Determination of the Dissociation Constants (pK_a) of Eight Amines of Importance in Carbon Capture: Computational Chemistry Calculations, and Artificial Neural Network Models

Abstract

This work focuses on determining the dissociation constants (pK_a) of eight amines, namely, 3-(Diethylamino) propylamine, 1,3-Diaminopentane, 3-Butoxypropylamine, 2-(Methylamino) ethanol, Bis(2-methoxyethyl) amine, α-Methylbenzylamine, 2-Aminoheptane, and 3-Amino-1-phenylbutane, within temperatures ranging from 293.15 K to 323.15 K. The thermodynamic properties of the protonated reactions were regressed from the pK_a work. In addition, the protonated order of both 3-(Diethylamino) propylamine and 1,3-Diaminopentane were determined using computational chemistry methods owing to their unsymmetrical structures. In addition to the experimental methods, the dissociation constants at the standard temperature (298.15 K) were also estimated using group functional models (paper–pencil) and computational methods. The computational methods include COSMO-RS and computational chemistry calculations. An artificial neural network (ANN) method was employed to model the data by collecting and combining the experimental properties to estimate the missing pK_a values. Although the ANN models can provide acceptable results, they depend on the availability of the data. Instead of using the experimental properties, they were generated using software such as Aspen Plus or CosmothermX. The simulated ANN model can also provide very good fits to the experimental constant values.

1. Introduction

Carbon dioxide (CO₂) is mainly generated by burning fossil fuels for human daily activities such as power generation, heating demands, and from refineries, steel, and cement production plants. CO₂ is considered one of the greenhouse gases that cause global warming [1]. There are many CO₂ capture technologies, such as using liquid solvents or solid sorbents to separate CO₂ from the other gases. For the flue gases with low CO₂ partial pressures, the aqueous amine solutions have been used because the solutions can quickly react with CO₂ while physical solvents are not very suitable to capture CO₂ at low pressures. For the different amine types, the reaction mechanisms between the amines and CO₂ are also very different [2]. As a result, the study of the protonation between amines and CO₂ is necessary to understand the reaction mechanism as well as model gas solubility in the solution [3].

Chowdhury et al. [4] and Tomizaki et al. [5] studied and reported the dissociation constants (pK_a) for cyclic amines, while Perrin [6] reported the dissociation constants for many alkanolamines. Both Versteeg et al. [7] and Sharma [8] studied the relationships between the dissociation constants and the reaction rate between CO₂ and aqueous amine solutions. The pK_a values of 2-(Butylamino)ethanol, m-Xylylenediamine, 3-Picolylamine, Isopentylamine, and 4-(Aminoethyl)-piperidine were recently measured and reported by Kumar et al. [9], while Nguyen et al. [10] reported the experimental values and explained the protonation mechanisms by computational chemistry calculation (DFT) for 1,4-Bis(3-aminipropyl) piperazine, 1,3-Bis(aminomethyl) cyclohexane, Tris(2-aminoethyl) amine, and 1-Amino-4-methyl piperazine. In addition, the constant values can be used to determine amines’ chemical and biological behaviors [9,10,11,12].

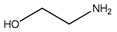
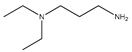
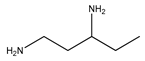
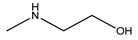
Some methods used to determine the dissociation constant values for amines include ultraviolet spectrophotometry, potentiometric titration, magnetic resonance, and conductimetric titration [13]. Among these methods, potentiometric titration is widely used because of its simplicity and convenience within the pH range of 2.00 to 11.00 [13,14,15]. In this study, the potentiometric titration method was used to determine and dissociation constant of Monoethanolamine (MEA), 3-(Diethylamino) propylamine, 1,3-Diaminopentane, 3-Butoxy-propylamine, 2-(Methylamino) ethanol, Bis(2-methoxyethyl) amine, α-Methylbenzylamine, 2-Aminoheptane, and 3-Amino-1-phenylbutane for the temperature range between 298.15 K to 313.15 K with an increment of 5 K. The average atmospheric pressure during the experiments was 95.8 (±0.8) kPa. The purpose of using monoethanolamine (MEA) is for validating the equipment. The compounds’ structures, suppliers, and purities are listed in Table 1.

Table 1. Chemical name, structures, suppliers, and mass purity (%) of the studied amines.

Full Name	IUPAC Name	Abbreviation Name	CAS Reg. No.	Molecular Structure	Molecular Mass (g⸳gmol−1)	Supplier	Mass Fraction Purity (%)
Monoethanolamine	2-Aminoethanol	MEA	141-43-5		61.08	Sigma-Aldrich (Oakville, ON, Canada)	≥99
3-(Diethylamino) propylamine	N′,N′-diethylpropane-1,3-diamine	DEAPA	104-78-9		130.23	Sigma-Aldrich	≥99
1,3-Diaminopentane	Pentane-1,3-diamine	EP	589-37-7		102.18	Sigma-Aldrich	98
3-Butoxypropylamine	3-Butoxypropan-1-amine	BPA	16499-88-0		131.22	Sigma-Aldrich	99
2-(Methylamino) ethanol	2-(Methylamino)ethanol	MAE	109-83-1		75.11	Sigma-Aldrich	≥98
Bis(2-methoxyethyl) amine	2-Methoxy-N-(2-methoxyethyl)ethanamine	BMOA	11-95-5		133.19	Sigma-Aldrich	98
α-Methylbenzylamine	1-Phenylethanamine	PEA	618-36-0		121.18	Sigma-Aldrich	99
2-Aminoheptane	[(2R)-heptan-2-yl]azanium	AH	123-82-0		115.22	Sigma-Aldrich	99
3-Amino-1-phenylbutane	4-Phenylbutan-2-amine	APB	22374-89-6		149.24	TCI (Portland, OR, USA)	98

Based on the structures in Table 1, the studied amines included two diamines (DEAPA and EP) and six monoamines (BPA, MAE, BMOA, PEA, AH, and APB). All six monoamines were primary or secondary amines that have high kinetic and CO₂ uptakes. The diamines were primary and tertiary amines. In addition, instead of directly measuring the kinetic rates between the aqueous amine solutions with CO₂, the dissociation constants (pK_a) can be used to rank the reaction rates for the studied amines. Furthermore, the dissociation constant can be used for further modeling CO₂ absorptions into the aqueous solutions. The studied amines are mainly monoamines and tertiary amines; therefore, they are expected to have lower heat of absorption than polyamines. As a result, these amines have a high potential for CO₂ capture.

2. Chemicals, Apparatus, and Experimental Procedures

The nine amines, namely, Monoethanolamine (MEA) (≥99% in mass purity), 3-(Diethylamino) propylamine (DEAPA) (≥99% in mass purity), 1,3-Diaminopentane (EP) (98% in mass purity), 3-Butoxypropylamine (BPA) (99% in mass purity), 2-(Methylamino) ethanol (MAE) (≥98% in mass purity), Bis(2-methoxyethyl) amine (BMOA) (98% in mass purity), α-Methylbenzylamine (PEA) (99% in mass purity), 2-Aminoheptane (AH) (99% in mass purity), and 3-Amino-1-phenylbutane (APB) (98% in mass purity) were purchased from Sigma Aldrich.

To measure the pH of the aqueous amine solutions, a 270 Denver Instrument pH meter (Denver Instruments, Arvada, CO, USA) was used in the titration method. Three pH buffer solutions were purchased from VWR (Mississauga, ON, Canada) and used to calibrate the pH meter. Buffer solutions of 4.00, 7.00, and 10.00 were used, and the uncertainties supplied by the manufacturer (VWR) were 0.02, 0.00, and 0.01 for the 10.00, 7.00, and 4.00 buffer solutions, respectively. Table S1 in the Supporting Information (SI) section summarizes the calibration data for the pH meter.

The equipment and experimental procedures were validated by determining the pK_a of monoethanolamine (MEA) and compared with the values in the literature [9,10,11,14,15]. Figure S1 in SI shows the comparisons of the dissociation constant values (pK_a) of MEA between this study and the data from the literature and is compared in Table S4. Hydrochloric acid solution 0.100 N (±0.002 N) was purchased from VWR International for the titration process. Nitrogen with 99.99% mass purity was purchased from Linde (Mississauga, ON, Canada) for flushing the space on the top of amine solutions to replace oxygen (O₂) and carbon dioxide (CO₂) present in the environment. The temperature of the solution inside the amine-storing beaker was controlled by an external water bath. The uncertainty of the temperature was 0.01 K. The aqueous amines were mixed to have a concentration of 0.0100 M within ±0.0002 M. The solutions were stirred at least for 20 min before starting the experiments.

In the beginning, 50 mL of the mixing solution was transferred into the storing beaker which had a stirring magnetic bar. During the experiment, the stirring speed of the bar was maintained at 30 rpm. The experiment started when the solution reached equilibrium and the temperature and pH became stable. The initial pH values of the solutions at equilibrium conditions were recorded. The storing beaker was always closed during the experiment to avoid oxidative degradation or vaporization. At each step of the titration process, 0.5 mL of the acid was added to the aqueous solution while stirring with the magnetic bar. After 20 to 30 s, the pH values were recorded as the mixtures reached equilibrium.

Measured pH and the details of the calculated pK_a values for MEA, before the thermodynamic corrections, are presented in Table S2. Table S3 shows the values of pK_a before and after the correction for MEA at 298.15 K.

3. Calculation of Dissociation Constant (pK_a)

To determine the dissociation constant values for the studied amines, the titration method was used to measure the pH of the solutions at each step after adding the acid to the solutions. The procedures employed are reported below to estimate the pK_a values for MEA as well as the other amines. The protonated mechanism of MEA and water is represented in Equation (1). In Equation (2), {MEAH⁺} is the protonated MEA molecule and {MEA} is the monoethanolamine molecule. Equation (2) was used to determine the pK_a values before the thermodynamic correction [10],

$${\mathrm{MEAH}}^{+}+{\mathrm{H}}_2\mathrm{O} \stackrel{K_a}{\leftrightarrow } \mathrm{MEA}+{\mathrm{H}}_3{\mathrm{O}}^{+}$$

(1)

$$\mathrm{p}{K_a}^{\mathrm{M}}=\mathrm{pH}+\log \frac{\left\{{\mathrm{M}\mathrm{E}\mathrm{A}\mathrm{H}}^{+}\right\}}{\left\{\mathrm{M}\mathrm{E}\mathrm{A}\right\}}$$

(2)

Equation (3) was used to calculate ionic strength (I), which is a function of the molecular concentration of ionization species (C_i) in the solution and the valency of species (z_i). The extended Debye–Hückel activity coefficient (γ) was calculated using Equation (4) with the adjustable parameter k_i. The value of the parameter was dependent on the ion sizes. The Supporting Information (SI) provides the details of the pK_a calculations as well as thermodynamic corrections with the parameters of A and B from the literature [16] and the values of k_i from Sumon et al. [17] Equation (5) was used to determine the true concentration of protonated MEA. For the first dissociation constant calculation, the value of I can be simply used as in Equation (3); however, the Albert et al. [13] method was used to determine I for the second pK_a, as reported in the literature [10]. Equation (6) was used to determine the dissociation constant after the thermodynamic correction (TC).

$$\mathrm{I}=0.5\sum {\mathrm{C}}_{\mathrm{i}}{\mathrm{z}}_{\mathrm{i}}^2$$

(3)

$${\mathsf{\gamma }}_{\mathrm{i}}={10}^{-\frac{\mathrm{A}{\mathrm{z}}_{\mathrm{i}}^2\sqrt{\mathrm{I}}}{1+\mathrm{B}{\mathrm{k}}_{\mathrm{i}}\sqrt{\mathrm{I}}}}$$

(4)

$$\left[\mathrm{M}\mathrm{E}\mathrm{A}{\mathrm{H}}^{+}\right]=\frac{\left\{\mathrm{M}\mathrm{E}\mathrm{A}{\mathrm{H}}^{+}\right\}}{{\mathsf{\gamma }}_{\mathrm{i}}}$$

(5)

pK_a = pK_a^M − TC

(6)

4. Results and Discussion

Based on the calculation steps mentioned above and in the Supporting Information section, the results of the first dissociation constants of MEA and the eight studied amines are listed in Table S4. The first pK_a values of MEA for various temperatures are also plotted in Figure S1 and reported in the SI section to compare them with the literature data. All the first dissociation constants of the studied amines and MEA are plotted in Figure 1.

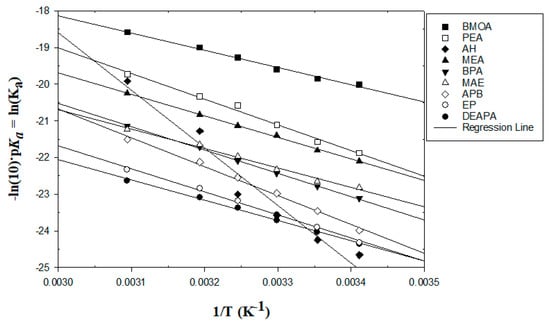
Figure 1. Linear relationship between the first dissociation constants and inverse temperatures of the amines studied.

First, the more negative values in Figure 1 have higher dissociation constant values. As the obtained data are reported in Table S4 and Figure 1, the six studied amines, namely, DEAPA, EP, APB, MAE, AH, and BPA, have higher dissociation constant values than MEA within the studied temperature range. Furthermore, two studied amines, BMOA and PEA, have lower constant values for the studied temperature range. In addition, AH has a high slope of the linear regression line which implies that the kinetic of the amine strongly depended on the temperature and the concentration. The six amines with higher pK_a values than MEA were expected to have higher reaction rates with CO₂ than MEA.

In addition, among the eight studied amines, two were diamines, DEAPA and EP. The values of the second dissociation constant are reported in Table S5 and Figure 2. As shown, the second pK_a of DEAPA was higher than that of EP. Based on the molecular structures of the two amines, DEAPA included one primary and one tertiary amino group, while EP had two primary amino groups. The tertiary amine tended to react slower with CO₂ than the primary amine; however, DEAPA had a higher second pK_a than EP, with two primary amino groups in the structure. Furthermore, tertiary amines have lower heat of absorption than primary amines. Therefore, DEAPA has great potential as an amine for CO₂ capture.

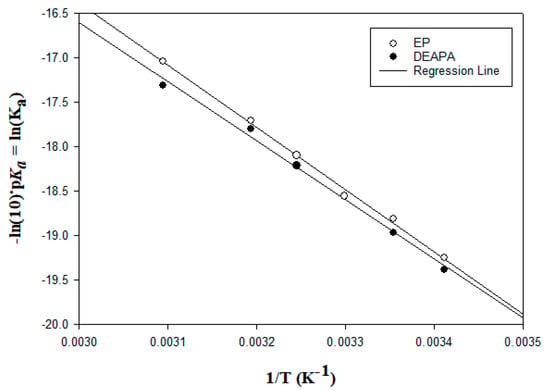
Figure 2. Linear relationship between the second dissociation constants with the inverse of temperature for diamines.

The coefficients of determination (R₂) of the linear regressions for Figure 1 and Figure 2 are reported in Table S6.

The standard state enthalpy change (ΔH⁰, kJ·mol⁻¹) and entropy change (ΔS⁰, kJ·mol⁻¹·K⁻¹) can be determined using the van’t Hoff equation [9,10,15]. These thermodynamic quantities (ΔH⁰ and ΔS⁰) can be regressed using data in Tables S4 and S5 and Figure 1 and Figure 2 by applying Equation (7). In the equation, the slope and intercept of the linear regressions are ($\frac{-\Delta {\mathrm{H}}^0}{\mathrm{R}}$) and ($\frac{\Delta {\mathrm{S}}^0}{\mathrm{R}}$), respectively. The universal gas constant (R, kJ·mol⁻¹·K⁻¹) value is 8.3145 × 10⁻³ kJ·mol⁻¹·K⁻¹. In addition, the standard state free energy of the reaction (ΔG⁰, kJ·mol⁻¹) was calculated using Equation (8). The calculated values of these thermodynamic quantities are reported in Table 2, Table 3, Table 4 and Table 5.

Table 2. The standard state enthalpy change (ΔH⁰/ kJ·mol⁻¹) and entropy change (ΔS⁰/ kJ·mol⁻¹·K⁻¹) of the first dissociation constants of the studied amines.

Amine	ΔH0 (kJ·mol−1)	ΔS0 (kJ·mol−1·K−1)
3-(Diethylamino) propylamine	46.05	−0.05
1,3-Diaminopentane	52.40	−0.02
3-Butoxypropylamine	52.83	−0.01
2-(methylamino) ethanol	44.27	−0.04
Bis(2-methoxyethyl) amine	39.21	−0.03
α-Methylbenzylamine	58.30	0.02
2-Aminoheptane	130.9	0.24
3-Amino-1-phenylbutane	65.68	0.03

Table 3. Standard state free energy of reaction (ΔG⁰, kJ·mol⁻¹) of the first dissociation constants of the studied amines.

Amine	Temperature T/K
	293.15	298.15	303.15	308.15	313.15	323.15
3-(Diethylamino) propylamine	59.38	59.59	59.78	59.88	60.13	60.81
1,3-Diaminopentane	59.27	59.25	59.37	59.41	59.47	60.01
3-Butoxypropylamine	56.35	56.51	56.53	56.58	56.53	56.79
2-(Methylamino) ethanol	55.62	56.17	56.30	56.28	56.35	57.04
Bis(2-methoxyethyl) amine	48.77	49.20	49.39	49.38	49.46	49.93
α-Methylbenzylamine	53.32	53.48	53.22	52.74	52.94	53.02
2-Aminoheptane	60.11	60.11	59.43	58.94	55.40	53.51
3-Amino-1-phenylbutane	58.48	58.16	57.92	57.76	57.61	57.78

Table 4. The standard state enthalpy change (ΔH⁰/ kJ·mol⁻¹) and entropy change (ΔS⁰/ kJ·mol⁻¹·K⁻¹) of the second dissociation constants of 3-(Diethylamino) propylamine and 1,3-Diaminopentane.

Amine	ΔH0 (kJ·mol−1)	ΔS0 (kJ·mol−1·K−1)
3-(Diethylamino) propylamine	55.33	0.03
1,3-Diaminopentane	58.18	0.04

Table 5. Standard state free energy of reaction (ΔG⁰, kJ·mol⁻¹) of the second dissociation constants of 3-(Diethylamino) propylamine and 1,3-Diaminopentane.

Amine	Temperature T/K
	293.15	298.15	303.15	308.15	313.15	323.15
3-(Diethylamino) propylamine	47.26	47.03	46.78	46.66	46.34	46.52
1,3-Diaminopentane	1.35	1.29	1.24	1.19	1.14	1.07

$$\ln {\mathrm{K}}_{\mathrm{a}}=-\ln ({10}^{\mathrm{p}Ka})=\frac{\Delta {\mathrm{S}}^0}{\mathrm{R}}+\frac{-\Delta {\mathrm{H}}^0}{\mathrm{R}\mathrm{T}}$$

(7)

ΔG⁰ = RT ln (10^pKa)

(8)

5. Estimation Protonated Order for the Diamines

There are two diamines in this study, namely, 3-(Diethylamino) propylamine and 1,3-Diaminopentane. As mentioned above, 3-(Diethylamino) propylamine’s structure has one primary and one tertiary amino group, while 1,3-Diaminopentane includes two unsymmetrical primary amino groups. It is important to know that the protonation order is required to model the solubility of CO₂ in amine solutions. To perform the study, commercial computational chemistry software (Gaussian (09 Revision B.01 SMP)) was used to optimize the molecular structures of the neutral amines with different models and basis sets. The molecular structures of the amines were built by using GaussView version 5.0.9. The optimization model was performed with implicit (without explicit water molecule) solvent and polarizable continuum model (PCM) as default. Then, the optimization structures would be reoptimized with protons at different amino groups. The energy (E) of the protonated amines was used to suggest the preferred amino group for the first and second pK_a. The structures with lower energies suggested the highest stable structures. For the computational chemistry methods, Hartree–Fock (HF), density functional theory (DFT/B3LYP), and the Moller–Plesset perturbation second order (MP2) were used. The basis sets chosen were 6-311G+(d,p), B3LYP/3-21G, and B3LYP/6-311G+(d,p), or HF, DFT, and DFT, respectively. For the MP2 calculation, the chosen basis set was 6-311G+(d,p). For the energy notation in Equation (9), E₁ represented the potential energy surface (PES) when the proton was attached to the primary amino group on the carbon chain, while E₂ represented the PES when the proton was attached to the primary amino group on the branch for (1,3-Diaminopentane) or the tertiary amino group for 3-(Diethylamino propylamine). The two geometrical structures for the two amines were optimized with water as a solvent and a polarizable continuum model (PCM).

ΔE (kJ·mol⁻¹) = E₁ − E₂

(9)

Based on the results reported in Table 6, the differences in PES (ΔE/ kJ·mol⁻¹) were positive for all calculation methods for 3-(Diethylamino) propylamine. This means that the E₁ was higher than E₂ or the protonated tertiary amino group was more stable than the protonated primary amino group in the structure. The results do not agree with what is reported in the literature [9,10,16], which suggested that the primary amino group should be protonated before the tertiary amino group. However, the functional groups in the structure can strongly affect the order of protonation for the amines. This conclusion will be studied further in the later parts of this study. As for 1,3-Diaminopentane, the differences were all negative; this implies that the protonated amino group on the chain structure was more stable than the protonated amino group on the branch.

Table 6. The difference in potential energy surface (PES) between protonated 3-(Diethylamino) propylamine and 1,3-Diaminopentane structures.

Model/Basis Set	ΔE (kJ·mol−1)
	3-(Diethylamino) propylamine	1,3-Diaminopentane
HF/6-311G+(d,p)	64.91	−7.13
DFT/B3LYP/3-21G	5.72	−17.71
DFT/B3LYP/6-311G+(d,p)	14.93	−6.13
MP2/6-311G+(d,p)	21.00	−8.65

6. Computational Estimation for the Dissociation Constants

In addition to the experimental measurements, the dissociation constants could be estimated by other methods such as the PDS [16] (Perrin, Dempsey, and Serjeant) method, the new PDS [17] method, the QSSG [18] method, the COSMO-RS method, the Van’t Hoff equation, the SHE [17] method, and the KHE [19] method. The first three methods were simply called functional group methods because the method suggested the base values for the primary, secondary, and tertiary groups. The functional groups around these amino groups would shift the base values. The shifted values depended on the type of functional groups and their positions. For the other methods, computational chemistry calculations were required to optimize the structure from which the Gibbs free energy would be determined before and after the protonation occurred. Based on the difference in the free energy, the values of dissociation constants can be determined.

6.1. Functional Group Estimations

The method can be used to estimate the first dissociation constant for the studied amines at 298.15 K based on the chemical structures. As mentioned above, the base values and the pK_a shift were predetermined by optimizing the structures and the experimental values of many chemicals; as a result, the estimated values’ accuracies improved when more experimental values were available for optimization. For further improvements, Sumon et al. [17] and Qian et al. [18] included more data to reoptimize the base and shift values. Sumon’s method is called the new PDS while Qian’s method is called the QSSG method in this study. The suggested base and shift values for the three methods are summarized in Table S7. By applying these methods to determine the dissociation constant values for the studied amines, the first pK_a at 298.15 K values are summarized in Table 7 below. 2-(Methylamino) ethanol was chosen to demonstrate the calculation method. Based on the structure in Table 1, this amine has a secondary amino group, (CH₃)– on the secondary amino, and –(OH) on the gamma (γ) position. For the PDS method, the first pK_a value of the amine would be 11.15 − 0.2 − 1.1 × 0.4 = 10.51. For the new PDS method, the first pK_a value would be 10.50, while the QSSR method suggests 10.2. By comparing the estimated values with the experimental values (9.84), the lowest error was 0.36 while the highest error was 0.67. Table 7 summarizes the estimated pK_a values for the three methods. As mentioned above, 3-(Diethylamino) propylamine and 1,3-Diaminopentane could be protonated at different locations; therefore, the superscript V1 was used to represent the primary amino protonating on the main chain while V2 stood for the tertiary amino or the branch primary amino protonating, as shown in Figure 3.

Table 7. The estimated pK_a values of the eight amines with three different methods at T = 298.15 K.

Solvent	pKa, PDS [19]	pKa, Sumon [20]	pKa, QSSR [21]	pKa [Exp.]
3-(Diethylamino) propylamineV1	10.63	10.44	10.24	10.44
3-(Diethylamino) propylamineV2	10.37	10.46	10.28
1,3-DiaminopentaneV1	10.64	10.46	10.28	10.38
1,3-DiaminopentaneV2	10.64	10.46	10.28
3-Butoxypropylamine	10.58	10.38	10.13	9.90
2-(Methylamino) ethanol	10.51	10.50	10.20	9.84
Bis(2-methoxyethyl) amine	10.19	9.98	9.24	8.62
α-Methylbenzylamine	10.77	10.60	10.60	9.37
2-Aminoheptane	10.77	10.60	10.60	10.53
3-Amino-1-phenylbutane	10.77	10.60	10.60	10.19

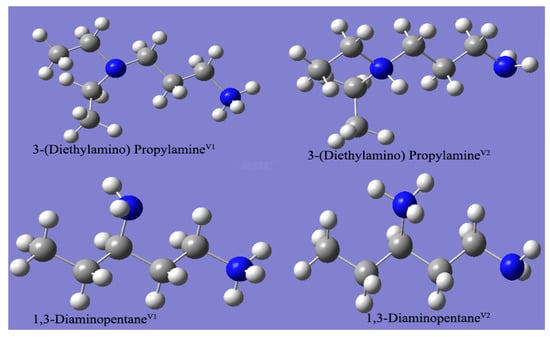
Figure 3. The protonating possibilities for 3-(Diethylamino) propylamine and 1,3-Diaminopentane. Blue: nitrogen, grey: carbon, and white: hydrogen.

6.2. Computational Chemistry Estimation

In addition to the functional group estimations such as the PDS or QSSR methods, the dissociation constants values of the amines at the standard conditions can be estimated by computational chemistry calculations. In particular, the SHE [17] method applied quantum computational chemistry calculations to determine amine pK_a values. In general, the dissociation mechanism of an amine was reported in Equation (10). By combing Equations (8) and (10), the dissociation constant at standard condition was determined by Equation (11) with R = 1.986 × 10⁻³ kcal·K⁻¹·mol⁻¹, and the unit of energy is kcal·mol⁻¹. Equation (12) was derived by expanding and simplifying Equation (11) as reported in the literature [17]:

$${\mathrm{B}\mathrm{H}}_{\left(\mathrm{a}\mathrm{q}\right)}^{+}\leftrightarrow {\mathrm{B}}_{\left(\mathrm{a}\mathrm{q}\right)}+{\mathrm{H}}_{\left(\mathrm{a}\mathrm{q}\right)}^{+}$$

(10)

$${\mathrm{p}K}_a=\frac{[{\mathrm{G}}_{\left(\mathrm{a}\mathrm{q}\right)}\left({\mathrm{H}}^{+}\right)+{\mathrm{G}}_{\left(\mathrm{a}\mathrm{q}\right)}\left(\mathrm{B}\right)-{\mathrm{G}}_{\left(\mathrm{a}\mathrm{q}\right)}\left({\mathrm{B}\mathrm{H}}^{+}\right)]}{1.3643}$$

(11)

$${\mathrm{p}K}_a=\frac{[{\mathrm{G}}_{\left(\mathrm{a}\mathrm{q}\right)}\left({\mathrm{H}}^{+}\right)+{∆}_{\mathrm{h}}{\mathrm{E}}_{\mathrm{e}\mathrm{l}}+{∆}_{\mathrm{h}}{∆\mathrm{G}}_{\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{e}\mathrm{l}}+{∆}_{\mathrm{h}}{\mathrm{E}}_{\mathrm{n}\mathrm{u}\mathrm{c}}]}{1.3643}$$

(12)

The values of ${\mathrm{G}}_{\left(\mathrm{a}\mathrm{q}\right)}\left({\mathrm{H}}^{+}\right)$ = −270.3 kcal·mol⁻¹, ${∆}_{\mathrm{h}}{\mathrm{E}}_{\mathrm{n}\mathrm{u}\mathrm{c}}$ = −9.4 kcal·mol⁻¹, and ${∆}_{\mathrm{h}}{∆\mathrm{G}}_{\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{e}\mathrm{l}}$ = 0 kcal·mol⁻¹ are reported in the literature [17]. Values of ${∆}_{\mathrm{h}}{\mathrm{E}}_{\mathrm{e}\mathrm{l}}$ were determined by optimization of the molecular structures. In addition, the SHE method used the implicit–explicit model, which added one additional water molecule to the amine. In addition, an empirical correction factor was included to minimize the errors between the estimated experimental values as in Equation (13). The values of C were −1.7 for cyclic amines and −0.7 for acyclic amines [17].

$${\mathrm{p}K}_a=\frac{[-270.3+{\mathrm{E}}_{\mathrm{e}\mathrm{l}}\left(\mathrm{B}·{\mathrm{H}}_2\mathrm{O}\right)-{\mathrm{E}}_{\mathrm{e}\mathrm{l}}\left({\mathrm{B}\mathrm{H}}^{+}·{\mathrm{H}}_2\mathrm{O}\right)-9.4]}{1.3643}+\mathrm{C}$$

(13)

However, as in Equation (11), the dissociation constant values could be calculated since ${\mathrm{G}}_{\left(\mathrm{a}\mathrm{q}\right)}\left(\mathrm{B}\right)$ and ${\mathrm{G}}_{\left(\mathrm{a}\mathrm{q}\right)}\left({\mathrm{B}\mathrm{H}}^{+}\right)$ could be found directly without further simplification as in the SHE method. This method is called the theoretical method in this study. All values of ${\mathrm{G}}_{\left(\mathrm{a}\mathrm{q}\right)}\left(\mathrm{B}\right)$, ${\mathrm{G}}_{\left(\mathrm{a}\mathrm{q}\right)}\left({\mathrm{B}\mathrm{H}}^{+}\right)$, ${\mathrm{E}}_{\mathrm{e}\mathrm{l}}\left(\mathrm{B}·{\mathrm{H}}_2\mathrm{O}\right)$, and ${\mathrm{E}}_{\mathrm{e}\mathrm{l}}\left({\mathrm{B}\mathrm{H}}^{+}·{\mathrm{H}}_2\mathrm{O}\right)$ were determined using Gaussian (09 Revision B.01 SMP). These molecular structures of the amines and amines–water were built using GaussView version 5.0.9. For the theoretical method, the structures were optimized using different methods (DFT/B3LYP and MP2) and the basis sets (6-31G(d) and 6-311G++(d,p)), while the SHE method used the DFT calculation method and 6-31G(d) basis set. All the amines’ geometrical structures were optimized with water as a solvent and the polarizable continuum model (PCM).

In addition to the quantum computational chemistry calculation methods mentioned, COSMO-RS can be used to determine the dissociation constant values with the same concept as in Equation (11) at the standard temperature (T = 298.15 K). In this study, CosmothermX (Version C30_1201) software was used to estimate the pK_a values for the studied amines with the TZVP calculation method. The results from these calculations were compared to the experimental values in Table 8. As mentioned above, the V1 superscript stands for the protonated main chain amino group while the V2 superscript stands for the branched or tertiary amino group.

Table 8. Comparison between the estimated pK_a values by different methods with experimental dissociation constants.

Amine	SHE Method		Theoretical Method			Cosmo-RS Method	Experimental Values
	pKa without Correction	pKa with Correction	DFT/B3LYP 6-31G(d)	DFT/B3LYP 6-311G++(d,p)	MP2 6-31G(d)
3-(Diethylamino) propylamineV1	8.81	8.11	6.95	3.69	6.60	10.36	10.44
3-(Diethylamino) propylamineV2	10.27	9.57	8.74	6.81	8.23	9.89
1,3-DiaminopentaneV1	9.47	8.77	5.01	3.21	5.38	10.65	10.38
1,3-DiaminopentaneV2	8.42	7.72	7.99	4.11	7.16	9.39
3-Butoxypropylamine	8.18	7.48	7.88	4.94	6.24	10.02	9.90
2-(Methylamino) ethanol	8.32	7.62	6.51	3.80	6.07	9.50	9.84
Bis(2-methoxyethyl) amine	6.65	5.95	4.45	1.70	3.76	7.07	8.62
α-Methylbenzylamine	7.69	6.49	5.20	2.13	4.74	9.29	9.37
2-Aminoheptane	8.78	8.08	7.21	4.30	6.31	10.43	10.53
3-Amino-1-phenylbutane	8.30	7.10	6.20	3.34	5.47	9.83	10.19

The value in bold was used as an example.

By comparing the group functional methods in Table 7, the original PDS method tended to predict higher values than Sumon’s method, which led to higher values than Qian’s method. In general, the estimated values by Qian’s method were closest to the experimental values than the other methods, on average. It should be mentioned that Qian’s method had more functional groups than the original PDS and Sumon’s method. In addition, Qian’s method included the effects of the group functional group on the ε (theta) position while the original PDS and Sumon’s methods included only the δ (delta) position. Therefore, the estimated values by Qian’s method were the closest to the experimental values.

In addition, when comparing the values between the group functional methods and chemistry computational methods in Table 7 and Table 8, the group functional methods were found to be more accurate than the computational methods. The functional group methods were also much faster and cheaper than the computational methods as they did not require high-performance computers and complex software while providing reasonable results. In addition, the estimates obtained using the Cosmo-RS calculation using CosmothermX (version C30_1201) were much better than both the SHE and the classical methods.

As mentioned earlier, 3-(Diethylamino) propylamine’s first pK_a can be associated with the tertiary amino position or V2 conformation in Figure 3. By comparing the estimated values by group functional methods and chemistry computational method (except the Cosmo-RS method), the pK_a values for the tertiary protonated scenario were closer to the experimental value than the first protonated scenario. On the contrary, the group functional methods estimated the same values for 1,3-Diaminopentane for both cases. The computational methods with different basis sets have different values for dissociation constants for the different amine geometries. In particular, the SHE method and Cosmo-RS calculation provided the closest values to the experimental values while the classical methods estimated the best values, although all the values did not perfectly match the experimental results. According to the structure presented in Table 1, the chain is considered the longest structure while the branch is attached to the chain. Logically, one primary amino belongs to the chain while the other is the branch. By the group contributions, the effect of the primary on the chain and branch is the same for each group. Although the ethyl group effect on the pK_a values was not studied, it will shift the original values. As observed in Table S7, the methyl group will reduce the original values; similarly, the ethyl group would have similar behavior with different values. By combining the logical analysis with the results reported in Table 6, the primary amino group attached to the chain would probably be protonated before the branched amino group.

7. Estimation of the Dissociation Constants at Various Temperatures by Computational Chemistry

The above methods were used to predict the pK_a values for the amines at the standard temperature (T = 298.15 K). However, it was necessary to estimate the constants at different temperatures. Therefore, to determine the pK_a values at various temperatures, a thermodynamic cycle would be employed. In this study, two different cycles would be used to calculate the constant values. Figure 4 represents a thermodynamic cycle which is called the “hydronium cycle”. Equation (14) was derived from Equation (11), as reported in the literature [20], where $∆{\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left({\mathrm{B}\mathrm{H}}^{+}\right)$, $∆{\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left({\mathrm{H}}_2\mathrm{O}\right)$, $∆{\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left(\mathrm{B}\right),$ and $∆{\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left({{\mathrm{H}}_3\mathrm{O}}^{+}\right)$ are the free solvation energies of BH⁺, H₂O, B, and H₃O⁺, respectively. The gas phase acidity of BH⁺ is represented by $∆{\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^{\mathrm{*}}$ and is defined by Equation (15) [20], while ${\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left(\mathrm{B}\right)$, ${\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left({{\mathrm{H}}_3\mathrm{O}}^{+}\right)$, ${\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left({\mathrm{H}}_2\mathrm{O}\right),$ and ${\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left({\mathrm{B}\mathrm{H}}^{+}\right)$ are the Gibbs free energies for B, H₃O⁺, H₂O, and BH⁺ in the gas phase. In addition, ${∆\mathrm{G}}^{0\mathrm{*}}$ is the free energy change which is associated with moving from the standard state that uses a concentration of 1 atm in the gas phase and 1 mol·L⁻¹ in the aqueous phase to a standard state that uses a concentration of 1·mol·L⁻¹ in both the gaseous and aqueous phases. Equation (16) defines the values of ${∆\mathrm{G}}^{0\mathrm{*}}$ for different temperatures [20].

$${\mathrm{p}K}_a=\frac{[{∆\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0+{∆\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left(\mathrm{B}\right)-{∆\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left({\mathrm{B}\mathrm{H}}^{+}\right)+{∆\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left({{\mathrm{H}}_3\mathrm{O}}^{+}\right)-{∆\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left({\mathrm{H}}_2\mathrm{O}\right)+{∆\mathrm{G}}^{0\mathrm{*}}]}{\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}\left(10\right)}$$

(14)

$${∆\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0={\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left(\mathrm{B}\right)+{\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left({{\mathrm{H}}_3\mathrm{O}}^{+}\right)-{\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left({\mathrm{B}\mathrm{H}}^{+}\right)-{\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left({\mathrm{H}}_2\mathrm{O}\right)$$

(15)

$${∆\mathrm{G}}^{0\mathrm{*}}=\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}\left(24.46\right)$$

(16)

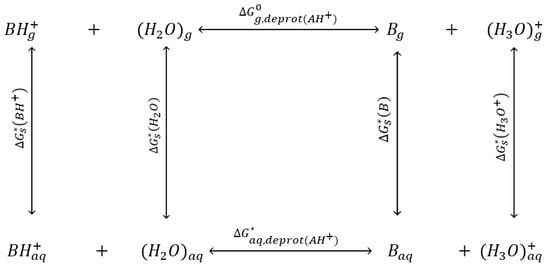
Figure 4. Hydronium thermodynamic cycle for calculating the dissociation constant.

The Gibbs free energy of the amines in the gaseous phase at various temperatures can be calculated by computational chemistry calculation. The solvation energies at various temperatures can be determined by Equation (17), as in the literature [20]. In the equation, CavE₂₉₈ and $∆{\mathrm{G}}_{\mathrm{s}}\left(298\right)$ are the cavitation energy and free energy of solvation at 298 K, respectively, which can be calculated by computational chemistry. The computational chemistry calculations can be used to determine the solvation-free energy of water (H₂O) and hydronium (H₃O⁺) at standard temperature (298.15 K). The values of −4.64, −5.05, and −5.12 kcal·mol⁻¹ of water for three calculations (DFT/B3LYP/6-31G(d), DFT/B3LYP/6-311++G(d,p), and MP2/6-31G(d), respectively) at 298.15 K are very different from the experimental value of −6.32 kcal·mol⁻¹ reported in the literature [21]. Similarly, the values of −77.63, −77.42, and −78.45 kcal·mol⁻¹ of hydronium (H₃O⁺) for three calculations (DFT/B3LYP/6-31G(d), DFT/B3LYP/6-311++G(d,p), and MP2/6-31G(d), respectively) at 298.15 K are much lower than the experimental values of −110.3 kcal·mol⁻¹ found in the literature [21]. Therefore, this study employed the experimental values of −6.32 kcal·mol⁻¹ and −110.3 kcal·mol⁻¹ at 298.15 K to improve the accuracy. Similar to the previous calculations, the computational chemistry calculations were performed by the methods and basis sets as DFT/B3LYP/6-31G(d), DFT/B3LYP/6-311++G(d,p), and MP2/6-31G(d), while the solvation model was the polarizable continuum model (PCM) with water as the solvent. The results of the calculations are summarized in Table 9.

$$∆{\mathrm{G}}_{\mathrm{s}}\left(\mathrm{T}\right)=∆{\mathrm{G}}_{\mathrm{s}}\left(298\right)+\left(\mathrm{T}-298\right)\frac{{\mathrm{C}\mathrm{a}\mathrm{v}\mathrm{E}}_{298}}{298}$$

(17)

Table 9. Dissociation constant values of the studied amines at various temperatures (K) for DFT1 (DFT/B3LYP/6-31G(d)), DFT2 (DFT/B3LYP/6-311G++(d,p)), and MP2 (MP2/6-31G(d)) calculations by hydronium thermodynamic cycle.

Amine	Temperature/K
	293.15			298.15			303.15			308.15			313.15			323.15
	DFT1	DFT2	MP2	DFT1	DFT2	MP2	DFT1	DFT2	MP2	DFT1	DFT2	MP2	DFT1	DFT2	MP2	DFT1	DFT2	MP2
3-(Diethylamino) propylamineV1	7.34	7.43	7.87	7.24	7.32	7.77	7.14	7.23	7.66	7.05	7.13	7.56	6.96	7.04	7.47	6.79	6.87	7.28
3-(Diethylamino) propylamineV2	9.16	10.61	9.53	9.03	10.45	9.40	8.91	10.31	9.27	8.79	10.16	9.15	8.68	10.02	9.03	8.46	9.76	8.80
1,3-DiaminopentaneV1	8.41	7.85	8.44	8.29	7.75	8.32	8.17	7.64	8.21	8.06	7.54	8.10	7.96	7.44	7.99	7.76	7.25	7.79
1,3-DiaminopentaneV2	5.34	6.94	6.62	5.30	6.94	6.63	5.26	6.77	6.46	5.23	6.69	6.38	5.19	6.61	6.30	5.12	6.45	6.16
3-Butoxypropylamine	8.32	8.71	7.50	8.18	8.57	7.40	8.04	8.44	7.31	7.91	8.31	7.21	7.79	8.18	7.12	7.55	7.94	6.95
2-(Methylamino) ethanol	6.90	7.54	7.33	6.81	7.43	7.24	6.72	7.33	7.14	6.63	7.24	7.05	6.55	7.15	6.96	6.40	6.97	6.79
Bis(2-methoxyethyl) amine	4.79	5.40	4.98	4.74	5.34	4.93	4.69	5.28	4.88	4.65	5.22	4.83	4.60	5.17	4.78	4.51	5.06	4.69
α-Methylbenzylamine	5.56	5.84	5.97	5.49	5.77	5.90	5.43	5.70	5.84	5.37	5.63	5.77	5.31	5.57	5.71	5.20	5.44	5.58
2-Aminoheptane	7.60	8.04	7.58	7.50	7.93	7.48	7.41	7.83	7.38	7.32	7.73	7.29	7.23	7.64	7.20	7.06	7.45	7.02
3-Amino-1-phenylbutane	6.58	7.07	6.72	6.49	6.98	6.63	6.41	6.88	6.55	6.33	6.80	6.47	6.26	6.71	6.39	6.11	6.55	6.24

By comparing the calculation values in Table 9 and the experimental values in Table S4, at the various temperatures, the calculation values obtained were very far from the experimental values. The differences could be the result of the errors between calculations and experimental values for each calculation or species in the cycle. For example, the significant differences for solvation-free energy of water and H₃O⁺ between computational chemistry calculations and experimental values were observed previously. Therefore, more species or components involved in the thermodynamic cycle will result in more errors. By comparison, 3-(Diethylamino) propylamine with the protonated tertiary amino had constant values which were closer to the experimental values. Similarly, 1,3-Diaminopentane with the protonated chain primary amino had constant values close to the experimental results. Therefore, the calculations confirm the reaction order or mechanism of the two diamines as discussed previously. Furthermore, to reduce the components in the cycle in Figure 4, the hydronium H₃O⁺ was replaced by the proton (H⁺) while the water molecule was completely removed, as in the protonated thermodynamic cycle in Figure 5.

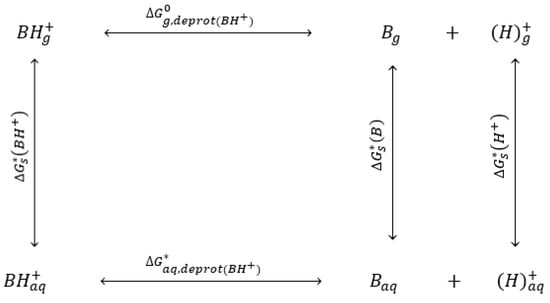
Figure 5. Protonated thermodynamic cycle for calculating the dissociation constants.

Because the proton does not include any electron, it could not be used in computational chemistry calculation optimization. The gas phase free energies of protons at various temperatures were obtained by fitting the data in the literature [22] from 0 K to 400 K. The values are reported in Table S8 in the SI section. In addition, Equations (18) and (19) were applied for the new thermodynamic cycle. In the equations, ${∆\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left(\mathrm{B}\right)$, ${∆\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left({\mathrm{B}\mathrm{H}}^{+}\right)$, and ${∆\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left({\mathrm{H}}^{+}\right)$ were the free solvation energies of B, BH⁺, and H⁺, while ${\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left(\mathrm{B}\right)$, ${\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left({\mathrm{H}}^{+}\right)$, and ${\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left({\mathrm{B}\mathrm{H}}^{+}\right)$ were Gibbs free energies of B, H⁺, and BH⁺ in the gas phase. The calculations were performed the same as previously, while the cavitation energy of the proton was calculated with DTF/B3LYP/6-311G(d,p). The calculation results are summarized in Table 10.

$${\mathrm{p}K}_a=\frac{[{∆\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0+{∆\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left(\mathrm{B}\right)-{∆\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left({\mathrm{B}\mathrm{H}}^{+}\right)+{∆\mathrm{G}}_{\mathrm{s}}^{\mathrm{*}}\left({\mathrm{H}}^{+}\right)+{∆\mathrm{G}}^{0\mathrm{*}}]}{\mathrm{R}\mathrm{T}\mathrm{l}\mathrm{n}\left(10\right)}$$

(18)

$${∆\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0={\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left(\mathrm{B}\right)+{\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left({\mathrm{H}}^{+}\right)-{\mathrm{G}}_{\mathrm{g}\mathrm{a}\mathrm{s}}^0\left({\mathrm{B}\mathrm{H}}^{+}\right)$$

(19)

Table 10. Dissociation constant values of the studied amines at various temperatures (K) for DFT1 (DFT/B3LYP/6-31G(d)), DFT2 (DFT/B3LYP/6-311G++(d,p)), and MP2 (MP2/6-31G(d)) calculations by protonated thermodynamic cycle.

Amine	Temperature/K
	293.15			298.15			303.15			308.15			313.15			323.15
	DFT1	DFT2	MP2	DFT1	DFT2	MP2	DFT1	DFT2	MP2	DFT1	DFT2	MP2	DFT1	DFT2	MP2	DFT1	DFT2	MP2
3-(Diethylamino) propylamineV1	10.45	7.13	10.09	10.19	6.93	9.85	9.95	6.74	9.61	9.71	6.56	9.38	9.48	6.38	9.16	9.04	6.03	8.73
3-(Diethylamino) propylamineV2	12.27	10.31	11.75	11.99	10.06	11.48	11.72	9.82	11.22	11.45	9.59	10.96	11.20	9.36	10.72	10.71	8.93	10.24
1,3-DiaminopentaneV1	11.51	7.56	10.66	11.24	7.35	10.40	10.98	7.16	10.15	10.73	6.96	9.91	10.48	6.78	9.68	10.01	6.42	9.24
1,3-DiaminopentaneV2	8.45	6.64	8.84	8.26	6.46	8.62	8.07	6.28	8.41	7.89	6.11	8.20	7.71	5.94	7.99	7.37	5.62	7.61
3-Butoxypropylamine	11.42	8.42	9.72	11.13	8.18	9.48	10.85	7.95	9.25	10.58	7.73	9.03	10.31	7.52	8.81	9.81	7.11	8.40
2-(Methylamino) ethanol	10.00	7.24	9.55	9.76	7.04	9.32	9.52	6.85	9.09	9.29	6.66	8.87	9.07	6.48	8.65	8.65	6.14	8.24
Bis(2-methoxyethyl) amine	7.90	5.11	7.20	7.70	4.95	7.01	7.50	4.80	6.82	7.31	4.65	6.64	7.12	4.51	6.47	6.77	4.23	6.14
α-Methylbenzylamine	8.67	5.54	8.19	8.45	5.38	7.98	8.24	5.21	7.78	8.03	5.06	7.58	7.83	4.90	7.39	7.46	4.61	7.03
2-Aminoheptane	10.71	7.75	9.80	10.46	7.54	9.56	10.22	7.35	9.33	9.98	7.16	9.10	9.75	6.97	8.89	9.32	6.62	8.47
3-Amino-1-phenylbutane	9.69	6.77	8.94	9.45	6.58	8.71	9.22	6.40	8.49	9.00	6.22	8.28	8.78	6.05	8.08	8.37	5.72	7.68

By comparing the calculation results in Table 9 and Table 10 and the experimental measurements in Table S4 for the first dissociation constants (pK_a), although the calculation results which were based on the protonated thermodynamic cycle were not very close to the experimental measurements, the protonated thermodynamic cycle calculations were much better than the hydronium thermodynamic cycle calculation results. The improvements could be the result of using the experimental data of the proton, rather than using all the calculation results of the proton. In addition, the basis set of 6-311G++(d,p) underestimated the calculation results while the basis set of 6-31G(d) overestimated the results. In addition, 3-(Diethylamino) propylamine with the protonated tertiary amino (V2) had constant values closer to the experimental values than the protonated primary amino version (V1), on average. For 1,3-Diaminopentane, the protonated chain primary amino 1,3-Diaminopentane (V1) had dissociation constant values closer to the experimental results than the protonated branch primary amino 1,3-Diaminopentane (V2) on average. The calculations confirm the reaction order or mechanism of the two diamines which have been discussed previously.

8. The Artificial Neural Network (ANN) Models for Estimating the Constant Values of the Studied Amines

8.1. ANN Model with Input Parameters

As observed in the results and previous discussions, the dissociation constants of the studied amines at various temperatures were quite far from the experimental measurements. Although the measurements provided the most accurate values, the purchase of the chemicals is expensive in addition to the cost of waste disposal. In addition, chemists and chemical engineers have a great interest in estimating the constant values of chemicals even before their synthesis. Therefore, many researchers have attempted estimating the constant values at various temperatures with higher accuracies.

For computational chemistry estimation, Khalili et al. [12] used the commercial software Gaussian to predict the dissociation constant values of 17 amines at 298.15 K with ±0.68 pK_a unit accuracy. Based on the Khalili–Henni–East (KHE) method [12], Sumon et al. [20] performed the calculations and improved the estimations to within ±0.28 pK_a unit accuracy at the standard temperature. Although computational chemistry calculations can be applied to estimate the pK_a for chemicals with known structures, the method could consume much CPU time and memory for large molecules. In addition to quantum chemistry calculations and quantitative structure–property relationship (QSPR) methods, artificial neural networks (ANNs) can be used to substitute experimental measurements. In summary, an ANN is a mathematical model which imitates the human brain to analyze information [23]. One of the advantages of an ANN is its flexibility to be applied in many fields using the nonlinear relationship in complicated systems without deep knowledge of the model; therefore, ANN applications have become very popular in solving engineering as well as scientific problems [24,25]. Habibi-Yangjeh et al. [25] predicted the dissociation constants of many different benzoic acids and phenol at standard temperature (298.15 K) by combining QSPR and ANN. The squared correlation coefficients (R²) of the ANN model for training, validation, and prediction were 0.9926, 0.9943, and 0.9939, respectively. Many scientists have combined two models (ANN and QSPR) to estimate the constant values of chemicals. One of the challenges was to convert chemical structures to numerical information to feed into the ANN model. Another challenge was that these works were performed at the standard temperature (298.15 K). In this study, the ANN model is used for predicting pK_a values for the amines at various temperatures.

First of all, data were collected to feed into the model (input data) and references (output) were obtained. The data can generally be divided into three segments, which included (1) properties that identified the chemicals (molecular weight, temperature, number of H, N, C, and O atoms), (2) properties associated with the dissociation constants (density, viscosity, refractive index, and sound velocity), and (3) referenced output (experimental measurement pK_a values). In this study, 1140 data points of 31 sets of amines associated with CO₂ capture were collected and are listed in Table S9 in the SI section.

In the ANN study, the data were divided into three groups for training, validation, and testing. For training purposes, of the entire dataset, 70% of the data was randomly chosen. Similarly, of the entire dataset, 15% was randomly chosen for validation while the remaining 15% of the dataset was selected for testing the ANN model. In addition, this study optimized the number of hidden layers, the number of neurons in each hidden layer, and the number of epochs with the optimal condition of minimizing the mean squared error (MSE) in the ANN model. Initially, only one hidden layer was applied while the number of neurons varied from 30 to 80. Figure S2 shows the performances which included the correlation® and mean squared error (MSE) of the ANN model.

Based on Figure S2, the ANN model performed well with one hidden layer when the number of neurons was equal to 40. In particular, the R_overall = 0.86156, MSE_train = 0.0288, MSE_validation = 0.0460, and MSE_test = 0.09044. To study the effect of additional hidden layers, an extra hidden layer was added with 40 neurons for the first layer, while the number of neurons for the extra hidden layer was varied from 10 to 50. Figure S3 shows the performances with R and MSE of the ANN model. As observed in Figure S3, the performances of the ANN model significantly improved by introducing the second hidden layer into the model. In particular, the model was optimized when the number of neurons was 39 with R_overall = 0.9075, MSE_train = 0.0069, MSE_validation = 0.0372, and MSE_test = 0.0597.

For further improvement, an additional third hidden layer was introduced into the ANN model. However, the performances of the ANN model did not improve; therefore, as a final scenario, this study used 40 and 39 neurons for the first and second hidden layers, respectively. The neurons, weights, and biases for the first, second, and output layers are reported in Table 11, Table 12 and Table 13, respectively. The overfitting in the ANN model happened when the model could predict the output with very high accuracy in the training process; however, the predictions would not fit well in the validating and testing processes. Therefore, balancing the accuracies between all processes is necessary to avoid overfitting issues. In addition, the studied ANN model chose the right balance between the variables and the hyperparameters which were the number of epochs, neurons, and batch sizes.

Table 11. Neurons, weights, and biases for the first hidden layer for the ANN model in this study.

Neuron	Temperature	Molecular Weight	Number of C	Number of H	Number of N	Number of O	Refractive Index	Sound Velocity	Density	Viscosity	Bias
1	−0.1606	0.0418	−0.2179	0.1791	−0.5387	0.5581	−0.0116	0.5601	0.3960	0.5408	0.1280
2	−0.0019	0.2824	−0.4485	0.6275	−0.4088	−0.0983	0.2342	0.2044	−0.2735	−0.9534	0.4230
3	0.3512	0.5736	−0.4307	−0.0813	−0.7615	−0.0966	0.6547	0.1445	−0.7132	−0.5333	0.3857
4	−0.7657	0.4059	0.2351	−0.1342	0.4731	0.5649	−0.5287	0.4273	−0.5889	0.4599	0.0970
5	−0.5625	0.6416	−0.0182	−0.5174	0.3660	0.6449	−0.1326	−0.6361	−0.2539	0.2892	−0.1645
6	0.0953	0.3919	−0.3118	0.3992	0.7698	−0.6674	−0.5810	−0.1775	−0.4318	−0.7450	0.1681
7	0.2029	0.7125	−0.5716	0.0432	−0.3829	0.6687	−0.4168	0.2658	0.2181	0.0705	−0.1781
8	−0.3264	−0.7266	0.3055	0.0234	−0.7161	0.0598	−0.5198	0.0999	0.6816	−0.4716	0.1862
9	−0.6917	0.3358	−0.2423	−0.3921	0.5583	0.2305	0.3588	−0.6494	0.4169	−0.7451	0.1513
10	−0.5985	−0.8256	−0.0713	0.6598	−0.2951	−0.1735	−0.0084	0.6206	0.4261	0.3258	−0.2165
11	0.7704	0.3803	0.4634	0.6663	−0.4879	0.6356	0.4890	0.1110	0.2620	−0.2092	0.0304
12	−0.3404	−0.5674	−0.7932	−0.5772	−0.4899	−0.2049	−0.5343	0.2947	−0.1619	−0.1266	0.0807
13	−0.0338	−0.6166	−0.3253	−0.7251	0.0677	0.6614	0.4311	−0.7018	−0.6937	−0.4153	0.1659
14	−0.2682	−0.5091	0.0480	0.3170	−0.7225	0.8834	−0.3158	0.0101	−0.4100	−0.1235	0.2524
15	0.2565	−0.1078	0.3414	−0.4316	−0.2166	0.0072	−0.7935	0.5236	−0.0566	−0.4636	−0.0757
16	0.3958	0.4307	−0.0701	0.2972	−0.6833	0.5825	0.6117	−0.5569	−0.6424	−0.5044	0.2795
17	0.0319	0.0469	−0.3511	0.0314	−0.9649	0.7494	0.4980	0.2465	−0.7343	0.5067	0.2693
18	−0.5768	−0.2701	0.6151	−0.5232	0.0859	−0.7951	−0.0321	0.0401	0.2094	−0.0761	0.3236
19	−0.1144	−0.7453	−0.0239	0.6069	0.8351	−0.2969	−0.0053	0.0238	−0.1657	0.5311	0.1203
20	−0.3066	0.4596	−0.4190	0.0733	−0.7205	−0.9337	−0.1272	−0.2780	−0.3781	0.2868	0.4707
21	−0.7033	−0.3322	−0.7593	0.0392	−0.3011	0.8993	0.5743	−0.6363	−0.5388	−0.5341	0.1583
22	−0.2757	0.5471	−0.7170	−0.3693	−0.8787	0.6861	−0.6731	−0.6895	0.0206	−0.1790	0.3536
23	0.0430	−0.5891	−0.5039	−0.0625	−0.5739	−0.1442	−0.3621	0.2378	−0.2223	−0.0527	0.3039
24	0.0180	0.8456	−0.2889	−0.6364	0.6036	−0.0969	−0.3055	0.2153	−0.3660	0.1361	0.1386
25	0.4003	0.1114	0.5461	−0.3675	0.6447	−0.0693	−0.7118	0.6243	−0.0737	0.0206	0.3567
26	0.2454	−0.4345	0.3552	0.4435	−0.8293	0.3049	−0.3266	−0.6133	−0.5094	−0.0145	−0.1643
27	−0.3604	0.1635	0.4420	0.7140	0.8929	0.0178	−0.2349	−0.6850	0.2051	0.4970	0.1628
28	0.3333	0.0583	0.3531	−0.1965	−0.3599	0.5106	−0.2346	−0.7218	0.7650	−0.3121	0.3366
29	−0.4641	−0.4724	−0.5901	0.2899	−0.0581	−0.5267	−0.3159	−0.8717	−0.0177	−0.0139	0.1253
30	0.1067	−0.4578	−0.2740	0.2515	−0.7895	−0.2120	0.1888	−0.3705	0.6872	−0.1911	0.3330
31	−0.3392	−0.1498	0.3646	0.6204	−0.1839	0.6582	−0.3199	0.1551	0.3568	0.1923	0.1583
32	0.4965	0.5742	−0.3691	0.1134	−0.0984	−0.8393	−0.8090	−0.2186	−0.6202	0.1156	0.2307
33	0.6700	0.2042	−0.0350	0.3204	0.3162	0.4469	−0.8651	0.5723	0.0352	0.3410	−0.2331
34	0.1773	−0.5900	0.4932	0.3290	−0.4802	−0.3170	0.5759	0.5560	−0.6513	−0.9507	0.3155
35	−0.2870	−0.0699	−0.0866	−0.2916	−0.1423	0.3922	0.7709	0.0266	−0.4360	0.1056	−0.1400
36	0.3352	−0.3374	−0.7176	−0.3203	0.6644	−0.0147	0.3215	0.2830	−0.7252	0.4149	0.3521
37	0.0020	−0.2064	−0.5518	−0.0655	0.2919	−0.6655	−0.6246	−0.6007	0.7581	0.5035	−0.1730
38	0.7213	−0.0464	0.2616	−0.7370	0.0446	−0.4197	−0.6358	−0.5214	−0.4455	0.3504	0.1515
39	0.0745	0.7063	0.3609	0.0959	−0.1461	−0.2016	−0.1824	0.7324	0.1838	−0.7503	0.2346
40	−0.7435	−0.4516	0.6738	−0.1484	−0.1391	0.3766	0.5637	0.3620	−0.5014	−0.2568	0.1497

Table 12. Neurons, weights, and biases for the second hidden layer of the ANN model in this study.

	First Hidden Layer
	Neuron	1			2		3		4		5		6		7		8		9		10		11		12		13		14		15		16		17		18		19		20
Second Hidden Layer	1	−0.1406			−0.5220		0.2620		0.0433		0.0436		0.2505		0.0772		0.3252		0.4780		−0.2089		0.1207		0.3259		−0.0076		−0.3707		0.2342		0.1582		−0.4062		0.2941		0.2141		−0.4805
	2	−0.0641			0.3851		−0.0597		0.2090		−0.2911		0.2493		0.0592		0.4414		0.1089		0.0300		0.0559		−0.1437		0.0879		0.1158		0.1559		0.3365		0.3371		−0.0560		0.2150		−0.0775
	3	0.1139			0.3216		−0.0013		0.2787		0.0364		0.1226		−0.4049		0.2608		0.1083		−0.2419		0.1292		−0.1896		−0.0055		−0.2848		0.2669		0.2151		0.0622		0.4145		−0.0195		−0.2681
	4	−0.3921			0.2468		−0.2404		0.0857		−0.1646		−0.1200		−0.2069		−0.2492		0.0629		−0.2256		−0.3930		0.0401		−0.0819		−0.3141		0.0236		0.1730		−0.2725		−0.3016		−0.0239		−0.3218
	5	−0.3081			0.2905		−0.2567		0.2731		−0.2699		−0.0662		0.0145		−0.4032		−0.3600		−0.2934		0.0785		0.2710		−0.0830		0.1712		−0.0867		0.3642		−0.0871		−0.4488		−0.1178		0.1331
	6	0.0524			0.5694		0.3378		−0.0142		−0.1306		0.3685		0.1986		0.0699		−0.3546		0.3959		0.2108		0.3006		0.3608		0.0919		0.2979		−0.1522		0.1566		0.3083		0.2956		0.1799
	7	0.1532			0.4936		0.1777		−0.0361		−0.3961		0.0101		0.0091		0.3864		0.2972		−0.2380		0.1046		−0.2154		−0.1241		0.3974		−0.0636		−0.0613		0.3664		0.0290		0.4316		−0.1164
	8	−0.2971			0.2172		−0.4004		−0.3254		0.2207		−0.0646		−0.0109		0.3193		0.3355		0.2138		0.1669		−0.0251		−0.1417		−0.0079		−0.1347		−0.1352		−0.1244		−0.1763		−0.2312		0.0903
	9	−0.2667			−0.5043		−0.4362		0.2141		0.1282		0.2850		0.4435		0.0080		0.3238		−0.4930		−0.3327		−0.1548		−0.1791		0.2022		−0.3028		−0.0363		−0.1057		−0.1486		0.1679		−0.0762
	10	−0.3028			−0.0350		−0.0890		−0.0354		0.3422		0.2009		−0.2660		0.0356		−0.1812		0.2848		−0.1420		0.3929		−0.2222		0.1075		−0.0936		−0.2289		0.3026		0.1279		0.0528		−0.0947
	11	0.2781			−0.1349		0.0426		0.0235		−0.2321		−0.1963		−0.1786		0.1776		−0.4179		−0.3884		0.0947		−0.4087		0.0784		−0.1527		0.1976		0.1873		0.3724		0.4615		0.3817		0.4288
	12	−0.3314			0.1522		−0.0697		−0.1476		−0.2753		0.2824		−0.4825		−0.3862		−0.2801		−0.2798		−0.4228		0.1474		−0.2675		−0.2088		0.0903		−0.1468		0.0241		−0.0179		0.0285		0.2227
	13	−0.0243			−0.3137		0.3234		0.3165		0.2108		−0.0599		−0.1065		−0.2375		0.0897		0.2386		0.2943		−0.3956		0.4071		−0.1538		0.1853		0.0392		0.1325		−0.2416		0.2460		−0.3155
	14	−0.4207			−0.4424		−0.4699		0.2896		−0.1649		0.1521		−0.1741		0.0379		−0.2452		−0.0617		−0.2094		−0.3117		0.3083		0.3793		0.3327		0.0777		−0.4512		−0.0947		0.2239		0.1765
	15	0.1307			0.1257		0.0679		−0.2171		−0.1956		0.0543		0.1855		0.1408		−0.0027		−0.2647		−0.4571		−0.0934		0.0649		0.3730		−0.0351		−0.2535		0.4531		0.1238		−0.0314		0.1276
	16	0.1312			0.1767		0.2067		−0.3377		−0.1273		0.4508		−0.0290		−0.2301		0.2660		−0.0051		0.2071		−0.2144		−0.0116		−0.0501		−0.3595		0.3049		0.0258		0.1592		−0.1188		0.4361
	17	0.0100			0.5449		0.3225		0.3089		0.1688		0.0145		0.2309		0.3835		0.2629		−0.2570		0.2010		−0.1687		0.3562		0.2249		−0.3358		0.2508		−0.2291		0.0774		−0.2082		0.3325
	18	−0.2277			−0.0677		−0.0486		−0.3494		−0.3043		0.2349		−0.1302		−0.0291		0.2950		−0.4888		0.2906		−0.0258		0.2462		0.2469		−0.4652		0.1856		0.0874		0.2405		−0.3172		−0.2777
	19	−0.1043			0.0572		−0.0568		0.2316		0.0118		0.4908		0.1115		0.2316		0.1884		0.1855		−0.1505		−0.3323		−0.3209		−0.1386		−0.1029		0.2485		−0.1091		0.1514		0.4495		0.0753
	20	−0.2704			−0.3722		0.2123		0.0795		−0.1884		0.1651		−0.4748		−0.3302		−0.1993		−0.0650		−0.2008		0.2241		−0.1425		0.0771		0.0132		−0.2348		−0.1603		−0.1179		0.0771		0.0409
	21	−0.4568			0.2047		0.0152		−0.3129		−0.4263		0.1829		−0.3396		0.0342		−0.3056		0.0135		0.2356		−0.3022		−0.1676		0.0394		0.3372		0.4071		0.1740		−0.3581		−0.0536		−0.0808
	22	−0.0709			−0.1581		−0.2812		0.3837		−0.1724		0.3719		0.3878		0.0189		−0.2325		−0.2006		0.4298		−0.3183		−0.3252		0.1380		−0.0273		−0.0010		0.1012		0.0870		0.3157		−0.1116
	23	0.0786			0.2550		−0.3996		0.1617		0.4286		−0.3293		0.2945		−0.6878		−0.0589		0.0038		0.3619		−0.5059		−0.3676		−0.1545		−0.0067		0.1836		−0.0754		−0.2292		0.0969		0.0506
	24	0.0422			0.0068		−0.1938		0.1053		−0.2720		0.0101		−0.0283		0.2374		−0.2937		−0.0122		0.1374		0.3433		−0.1765		0.2998		−0.0573		0.2604		0.1388		0.2053		−0.2033		0.5564
	25	0.2520			0.3857		−0.3463		−0.3316		−0.2794		−0.3172		−0.0038		−0.0044		−0.4220		−0.1891		−0.2214		−0.4116		0.0366		−0.0049		−0.0745		0.1595		0.0171		0.1823		−0.0339		0.3030
	26	0.0248			0.3386		0.0091		0.0098		−0.2635		0.4802		−0.0837		−0.0436		0.0693		0.3055		0.1646		0.3271		0.3730		0.0243		−0.4007		0.3458		−0.1571		0.2863		−0.1073		0.4638
	27	−0.1794			−0.3931		0.3003		−0.4865		−0.3378		0.2500		0.3262		−0.2257		−0.0038		−0.1156		−0.0936		−0.0671		−0.2760		−0.2080		0.4135		0.3486		−0.2006		0.2483		0.2931		−0.1503
	28	0.1610			0.2878		0.2982		−0.1795		0.2950		0.0791		−0.3599		−0.1901		−0.1720		0.3546		0.3006		0.0699		0.1269		0.1191		0.0898		0.4007		0.0054		−0.2089		0.2814		0.3455
	29	−0.2899			−0.0251		0.1417		0.1799		0.2286		−0.0092		−0.2084		−0.2463		−0.2812		0.1181		−0.3383		−0.0005		−0.3666		0.1527		0.2171		−0.0763		0.1146		−0.2853		0.3364		−0.1187
	30	0.0222			0.0368		0.3488		0.3453		−0.3677		0.1315		−0.2404		0.2383		−0.0613		−0.2496		−0.0408		0.1619		0.0431		−0.2558		0.0675		0.1443		0.4499		0.4638		0.2888		0.0531
	31	−0.0876			−0.3058		−0.3741		−0.1372		0.2921		0.0369		−0.2710		0.0701		−0.0215		−0.1588		0.3393		−0.4207		0.3685		0.1215		−0.3683		0.1407		−0.0506		−0.3704		0.2876		0.0111
	32	0.2372			0.1311		−0.1026		0.0616		−0.1637		0.1571		−0.1361		0.3294		−0.1954		0.0055		−0.0174		−0.2463		0.2527		−0.2722		−0.4205		0.1578		0.0866		−0.0876		0.4029		0.4013
	33	0.3074			0.5796		0.2672		0.1706		0.0452		0.2762		−0.1420		−0.2147		0.0023		0.1806		−0.1328		−0.0393		0.3985		0.1586		0.1846		0.2657		0.2756		0.4651		−0.2641		0.4316
	34	0.1582			0.4017		0.1298		0.2009		−0.2780		−0.2077		−0.1437		−0.2995		−0.3896		0.0455		0.0544		0.3745		−0.0589		0.2888		−0.2097		0.0206		0.1857		−0.2535		−0.5150		0.1893
	35	−0.2777			−0.1416		−0.0215		−0.0303		0.1246		−0.1345		0.0066		−0.2876		0.4103		−0.0667		0.1351		−0.2339		0.0424		−0.1074		−0.1454		0.0655		−0.5144		−0.1339		−0.3041		−0.1637
	36	0.0803			0.0987		0.4278		0.1621		0.0003		0.4169		0.1084		−0.4187		0.3001		0.2790		−0.2786		0.1928		−0.2995		−0.1375		−0.4427		−0.2169		0.1860		−0.0640		−0.0608		0.0502
	37	−0.0223			0.1187		0.1217		0.2629		0.2363		−0.2881		−0.1345		−0.0720		0.0416		−0.1344		0.1771		0.1962		−0.2916		0.2605		−0.2993		−0.1979		0.1469		−0.0677		0.2635		−0.0695
	38	0.3396			0.1540		−0.2236		−0.0463		−0.1797		0.2892		−0.3870		0.2219		0.2963		−0.0250		0.2840		0.3957		0.1636		−0.0511		−0.3449		−0.2259		0.1768		−0.0775		0.1079		0.0958
	39	0.0267			0.2729		−0.1904		−0.2475		−0.3583		0.0162		−0.3899		−0.1279		0.1726		−0.1347		−0.1325		0.0407		−0.1970		−0.0160		−0.4419		−0.3002		0.1439		0.2575		0.0403		−0.0307
Second Hidden Layer	First Hidden Layer
	Neuron		21	22		23		24		25		26		27		28		29		30		31		32		33		34		35		36		37		38		39		40		Bias
	1		0.0768	−0.2115		0.0147		−0.0994		−0.0585		−0.3543		−0.1715		0.2062		0.3290		0.2921		−0.5487		−0.3978		0.5125		−0.1825		−0.0264		−0.0328		0.3035		−0.1804		−0.2091		0.1079		−0.1644
	2		0.4092	0.5371		0.3804		0.0179		0.0640		0.3294		−0.3631		−0.2145		−0.1189		0.3614		−0.0715		0.3624		0.1609		0.4641		0.1006		0.4432		−0.2340		−0.3445		0.3538		−0.0251		0.4134
	3		−0.3651	−0.2190		−0.0987		0.4580		0.2708		0.2857		0.2903		0.3870		−0.2020		−0.1909		0.1149		−0.1917		0.2763		−0.2033		−0.4119		0.4892		−0.1086		0.1483		0.0987		0.0931		0.2474
	4		0.1350	−0.2927		0.2175		0.1051		−0.2861		−0.0382		−0.3253		0.3285		0.1030		−0.1720		0.3702		−0.2329		−0.1797		0.1661		0.0731		0.0200		−0.0478		0.0874		0.3169		0.1547		−0.0280
	5		−0.2425	0.0364		0.0037		−0.2898		−0.1407		0.1771		0.2238		−0.2577		−0.4197		0.1141		0.2041		−0.2762		0.0760		0.1236		0.0119		0.2809		−0.1828		−0.1005		−0.3647		0.3120		−0.0463
	6		0.4142	0.1872		0.2236		0.3866		−0.1688		−0.3020		0.2444		0.3114		−0.1808		0.2120		0.1345		−0.2245		−0.3553		−0.0980		−0.2091		0.3503		0.1050		0.3917		0.3177		0.0107		0.3189
	7		0.0223	0.4778		0.3185		0.1326		−0.2195		−0.2555		−0.4893		−0.2962		0.1763		0.5453		−0.0360		−0.2170		0.2171		0.1882		−0.4124		0.2948		−0.2496		0.0910		−0.0572		0.2494		0.3130
	8		0.3333	0.0980		0.3247		−0.2698		−0.3194		−0.0073		0.1240		−0.4326		−0.1819		−0.0623		−0.3973		0.0911		0.1929		−0.0298		0.3843		0.0455		−0.3282		−0.2059		−0.2972		−0.3177		−0.1035
	9		0.3598	0.3110		0.2687		−0.3894		−0.0076		0.2168		−0.2589		−0.0210		−0.0376		−0.5393		−0.2733		−0.1299		0.2692		0.0982		−0.0028		0.2771		−0.1642		0.3826		−0.4205		0.0409		−0.1543
	10		−0.0953	0.0665		0.3227		−0.3548		−0.2585		0.1379		−0.4123		−0.2009		−0.2568		−0.2654		0.0734		0.2714		0.3240		0.1576		−0.1206		0.1251		0.3158		−0.3566		−0.3726		0.2681		−0.2014
	11		0.0458	0.0744		−0.1277		−0.2280		0.0205		−0.1742		0.3784		−0.0088		−0.1059		0.0576		0.1523		0.3100		−0.2735		0.3601		−0.2291		0.1558		−0.4212		−0.0450		−0.1154		0.3918		0.3126
	12		0.2147	0.1505		0.2628		0.0269		−0.1339		0.3442		0.2972		−0.1315		0.3019		−0.0895		−0.1776		0.0536		−0.3029		−0.1803		0.0692		−0.0582		0.3272		−0.3341		−0.3433		−0.2139		−0.1349
	13		0.3632	−0.2730		−0.2979		−0.3590		−0.2084		−0.1768		0.3498		0.4246		0.1995		0.2020		0.0999		0.1912		−0.3977		0.2876		−0.1727		−0.4491		−0.2983		0.3381		−0.0804		0.2067		−0.1565
	14		0.1828	0.3223		−0.2847		−0.1042		−0.0538		−0.0545		−0.1139		−0.0173		0.1147		0.1866		−0.2594		−0.1400		0.0958		−0.2323		0.2645		−0.0352		0.0840		0.2827		−0.1351		−0.2243		−0.1283
	15		0.3233	0.3846		0.2227		0.2052		0.1877		0.0643		0.2911		0.2369		0.3335		0.3638		−0.0743		−0.0556		−0.4286		0.4726		−0.2963		0.4134		0.3043		0.0039		0.0831		−0.2960		0.3516
	16		0.1076	0.4335		−0.1987		0.3943		0.0108		0.1632		0.0260		−0.2115		−0.1259		0.4290		0.1836		0.0185		−0.0354		0.0629		−0.4009		0.3964		0.3355		−0.2840		−0.0638		−0.3073		0.3290
	17		0.0945	−0.0016		0.0906		0.1655		0.3999		−0.1266		0.1329		−0.2400		0.0474		−0.0254		−0.3284		0.3026		−0.4537		0.1651		0.2115		−0.0801		−0.2859		0.3218		−0.1546		0.4495		0.3774
	18		0.0656	0.0566		−0.4382		−0.0410		0.0271		0.1031		0.1107		0.4151		−0.1047		−0.1403		−0.2433		−0.3944		0.3803		−0.0117		0.2807		0.2279		0.3073		−0.2450		0.2814		0.2454		−0.1655
	19		−0.2544	−0.3225		0.2706		0.2289		0.1437		0.1439		0.2801		0.3142		0.0274		−0.2264		−0.3394		−0.1081		−0.4067		0.3922		−0.3898		0.2621		−0.2371		−0.1866		−0.0031		0.2040		0.3144
	20		0.3372	0.1532		0.3816		0.1402		0.0152		0.4948		−0.3293		−0.4918		0.4262		−0.5084		−0.5253		0.3098		0.3345		−0.1641		−0.3705		−0.1531		0.2976		−0.1324		−0.3610		0.0824		−0.0927
	21		−0.3999	−0.4606		−0.3476		0.0986		0.0051		0.0378		−0.0709		−0.0559		−0.2388		0.4424		0.1879		−0.4341		0.0372		−0.0603		0.1180		0.0371		−0.1459		0.0330		0.3200		0.2854		−0.1162
	22		−0.1028	−0.3448		−0.1991		−0.1618		0.2872		−0.3268		0.0497		−0.3798		−0.2699		−0.4961		0.2881		−0.3615		−0.0233		−0.2507		0.3174		−0.2758		0.2484		0.0631		0.3159		−0.2641		−0.0715
	23		−0.3099	−0.0873		0.0028		0.1242		−0.6426		−0.2623		−0.2061		0.0927		−0.0629		−0.4159		−0.0286		−0.4137		0.1579		−0.3793		−0.0194		−0.1521		0.3298		−0.3829		−0.0159		−0.1715		−0.0265
	24		−0.2692	0.3070		0.0665		−0.2796		−0.1868		0.4225		0.0645		0.3148		0.3030		0.3923		0.0418		−0.1556		−0.1325		−0.1062		−0.2433		0.1793		−0.3519		0.2869		0.2944		−0.2146		0.3654
	25		−0.1678	−0.3027		0.3130		−0.3195		0.2117		−0.3045		−0.3834		−0.2386		−0.4193		0.2101		0.0036		0.0073		0.3075		−0.0898		−0.0688		−0.0589		−0.0459		−0.1477		−0.1263		−0.0533		0.0114
	26		0.1722	0.2609		−0.0387		0.0130		0.1732		0.3656		−0.0309		0.1643		0.3881		0.3819		0.2843		−0.2041		−0.3372		−0.1243		−0.2628		0.1515		−0.0367		−0.3337		−0.2197		0.1892		0.3510
	27		−0.0566	−0.3334		0.3504		−0.3445		0.0224		0.2836		0.2706		−0.0897		−0.1879		−0.1814		−0.4275		0.0805		0.0043		0.1290		0.2662		−0.0484		0.2067		0.2821		0.0961		0.3103		−0.1659
	28		0.0355	0.2943		0.3186		0.0362		0.0576		−0.0247		−0.1003		0.0155		0.2863		0.1684		0.1270		0.2510		−0.3091		0.0321		0.0459		−0.0124		0.0469		−0.3546		0.3117		0.2399		0.3114
	29		−0.0427	0.0004		−0.3161		−0.2563		0.0967		−0.1734		0.2595		−0.1448		−0.1880		−0.0135		−0.1192		−0.0035		−0.3545		0.1559		0.0771		−0.5105		0.2219		−0.1221		−0.1376		−0.3183		−0.0795
	30		−0.2031	0.1744		−0.1012		0.0341		0.2824		−0.3173		0.2654		0.2101		−0.1753		0.3096		0.0469		0.1292		−0.4504		0.2142		0.0907		−0.2426		−0.2603		−0.1283		−0.2757		0.4494		0.3747
	31		−0.1771	−0.3055		−0.2837		−0.3544		0.1830		−0.0731		0.2997		0.4541		−0.0374		0.2708		0.1544		0.1015		0.1715		0.1272		0.1744		−0.2146		0.1630		0.2823		0.2248		−0.4986		−0.1474
	32		−0.2729	−0.4100		−0.0402		−0.2369		0.3211		−0.4620		−0.3468		−0.4386		0.2452		0.1687		−0.2917		−0.1681		0.2985		0.3626		0.1712		−0.0989		0.1732		−0.0771		−0.2158		0.0572		0.2211
	33		0.1280	−0.0678		0.4240		0.2189		0.3553		0.3110		0.3399		0.3294		−0.0337		0.0175		−0.0358		0.2161		0.2083		−0.1373		0.0923		0.1798		−0.0126		0.3294		0.3085		0.0494		0.2954
	34		−0.1181	0.4813		0.2657		−0.2980		−0.1540		0.0114		−0.5148		0.3089		0.0464		0.2665		0.1773		−0.2325		−0.0546		−0.2807		0.0767		−0.1897		−0.0663		−0.0438		0.3282		0.1695		0.2822
	35		0.4581	0.3894		0.1499		−0.2715		−0.2068		−0.1187		−0.1987		−0.2565		0.3042		−0.1692		0.0147		0.3637		0.1131		0.2892		0.2375		0.3863		0.3747		0.0534		0.0752		0.2193		−0.1500
	36		−0.3805	−0.2995		0.2911		0.1375		0.3437		−0.3888		0.2640		0.0043		−0.1504		0.4632		−0.3192		−0.1903		0.1491		0.4511		0.1718		−0.0885		0.2726		0.3631		0.1532		−0.2430		0.2411
	37		−0.1288	0.4878		0.3445		−0.0369		0.1648		−0.1732		0.1582		−0.2456		0.2495		0.0618		0.1647		0.3431		−0.2958		0.1673		0.0529		−0.1069		−0.2629		0.0394		0.2848		0.4427		0.3552
	38		0.1515	0.2402		−0.2384		0.3824		0.0711		−0.1920		0.3547		0.2359		−0.0921		0.1478		0.0240		0.0551		−0.2322		0.1581		0.0075		0.0301		−0.2963		0.2191		−0.0286		0.1005		0.3033
	39		−0.0981	−0.3711		0.0208		0.3721		0.2402		−0.1475		−0.4202		−0.2950		0.0904		−0.1111		0.0284		0.3176		−0.0301		0.4134		−0.0569		0.4671		−0.1343		−0.0426		0.3297		0.0781		0.2472

Table 13. Neurons, weights, and biases for the output layer for the ANN model in this study.

	Second Hidden Layer Neuron
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Weight	−0.2425	0.1079	0.1664	−0.3607	−0.4238	0.1753	0.3360	−0.2893	−0.3836	−0.2694	0.4022	−0.1757	−0.0361	−0.2227	0.3160	0.2980	0.1107	−0.2892	0.1082	−0.4448
	Second Hidden Layer Neuron
	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	Bias
Weight	−0.3494	−0.2602	−0.1228	0.1338	0.2542	0.1623	−0.1214	0.2947	−0.2579	0.1706	−0.1471	0.4089	0.4170	0.2894	−0.2602	0.1802	0.0809	0.4036	0.3339	0.2847

The ANN model architecture was described in Figure S4 for this study. The process of determining the best overall performance by running the model with many epochs varying from 140 to 200 is presented in Figure S5. Based on the results, the best performance for the overall MSE was at 166 epochs with a value of 0.026.

Figure S6 is a parity plot between the output and target for the entire dataset which included training, validation, and testing. The overall R was higher than 0.9; therefore, the ANN model provided a good estimation of the dissociation constants for a wide range of temperatures. Figure S7 shows the error histogram with only a few outliers. Based on the figure, the majority of the errors were close to the value of −0.06303, which almost overlaps with the zero line.

8.2. ANN Model with Optimized Input Parameters

Previously, the ANN model with the provided inputs resulted in high-accuracy prediction; however, the model required many of experimental data. In an effort to make the ANN model more robust and faster, a further study was performed on reducing the number of inputs to decrease the number of experimental input data as well as speed up the training processes. In the model, the temperatures were unchanged because they directly have impact on the pK_a values. This study focuses on the omission of some inputs to obtain an acceptable trade-off between the errors, complexities, and training speed.

From the previous full model, the study reduces the number of inputs such as density, refractive index, and the number of atoms (molecular weights) or combinations and examines the R_overall, MSE_train, MSE_validation, and MSE_test. The results are summarized in Table 14 below. The R_overall reached the highest values of 0.89225, while MSE_train, MSE_validation, and MSE_test were 0.00881, 0.02945, and 0.0798, respectively, when the sound velocity and refractive index were omitted. By comparison with the full model, the value of R_overall of the full model was a little higher than the R_overall of the reduced model, while the values of MSE_train, MSE_validation, and MSE_test of the full model were lower than the values of the reduced model. However, the differences were not large, and the reduced model did not require two sets of experimental datasets, which were the speed of sound and refractive index. Other combinations and the results are shown in Table 14.

Table 14. Comparisons of the reduced ANN models’ performance.

Removed Inputs	Roverall	MSEtrain	MSEvalidation	MSEtest
Density	0.8165	0.0139	0.1127	0.0882
Refractive Index	0.8295	0.0020	0.6125	0.1453
Sound Velocity	0.8425	0.0127	0.1369	0.0369
Viscosity	0.6939	0.0578	0.1931	0.1629
Molecular Weight (MW)	0.7976	0.0317	0.0973	0.1132
Sound Velocity & MW	0.8416	0.0053	0.0740	0.0903
Refractive Index & MW	0.8321	0.0084	0.0847	0.0905
Density & MW	0.7231	0.0058	0.1476	0.1427
Density & Sound Velocity	0.8871	0.0105	0.0661	0.0532
Density & Refractive Index	0.6270	0.0367	0.2419	0.1563
Density & Viscosity	0.8141	0.0038	0.1202	0.0782
Refractive Index & Sound Velocity	0.8922	0.0088	0.0295	0.0789
Refractive Index & Viscosity	0.6970	0.0028	0.1146	0.1953
Sound Velocity & Viscosity	0.7965	0.0080	0.1086	0.1048

Table 15, Table 16 and Table 17 summarize the weights and biases for the first, second hidden, and output layers of the reduced (refractive index and sound velocity) model.

Table 15. Neurons, weights, and biases for the first hidden layer for the reduced (refractive index and sound velocity) ANN model.

Neuron	Temperature	Molecular Weight	Number of C	Number of H	Number of N	Number of O	Density	Viscosity	Bias
1	−0.1124	0.6348	−0.1873	0.4645	0.1034	0.2243	0.0002	−0.1052	−0.1158
2	0.0615	−0.3450	−0.8294	−0.1796	−0.4868	−0.2349	0.0533	−0.3133	0.1328
3	0.5461	−0.0927	0.6757	0.2881	−0.6074	0.4297	−0.4679	−0.5559	0.1199
4	0.0927	0.5841	−0.1074	0.5233	−0.4246	−0.4336	−0.4754	0.5572	−0.1090
5	0.1490	−0.5444	0.6037	0.4292	0.4622	−0.4950	−0.2201	−1.0798	0.3012
6	0.5757	0.2660	−0.5993	0.0854	−0.4168	0.5109	−0.3404	0.8664	0.2324
7	0.5141	0.5379	0.4001	0.5429	−0.2441	0.4389	−0.5126	0.3049	0.1068
8	0.0563	0.2174	0.4328	0.5608	0.5297	−0.1892	−0.3629	0.4120	0.2365
9	0.4652	−0.3000	0.1158	0.7321	0.3856	−0.8809	0.3438	0.4824	−0.0531
10	0.7418	0.3283	−0.6438	0.7119	0.4064	−0.8005	−0.1244	−0.3977	0.1852
11	0.2276	0.8759	0.6164	0.8747	0.0400	0.3592	−0.8716	0.6410	−0.2100
12	0.1087	−0.7280	0.2788	0.0503	−1.2021	−0.0328	0.3785	−0.0224	0.3546
13	−0.5202	0.6770	−0.0261	−0.6915	0.8760	−0.9841	0.0394	0.6508	0.1744
14	0.0531	0.8788	0.9902	−0.0819	−0.3536	−0.1227	−0.2712	0.7150	0.1844
15	0.2421	0.8376	−0.6455	0.9184	0.6953	0.4072	−0.2738	0.8454	−0.1895
16	0.0890	0.4068	0.0635	0.5081	0.5596	−0.4588	−0.4789	−0.8583	0.2146
17	0.2639	−0.3405	−0.6563	−0.5088	0.1728	0.3697	−0.4624	−0.4943	0.1529
18	0.7855	−0.3594	0.5913	0.1127	0.3087	0.1566	0.6119	−0.3837	0.1080
19	0.1410	−0.0114	0.7488	−0.7060	−0.6965	0.3823	0.6775	−0.2402	0.2199
20	0.3099	−0.6274	−0.3260	−0.1632	−0.4577	−0.4790	−0.7153	0.0169	0.3601
21	0.4944	0.0026	0.5356	−0.0617	−0.0308	0.5477	−0.6159	−0.7886	0.3109
22	0.7639	−0.1264	0.2089	0.9107	−0.5838	−0.7296	0.6672	−0.2214	−0.2152
23	0.1166	0.1045	0.3700	−0.9411	0.8753	0.2054	0.3032	0.1617	−0.0329
24	0.0609	−0.1350	−0.1921	0.3794	−0.8310	0.6281	0.6988	−0.6927	0.2667
25	−0.6552	0.7355	−0.4250	0.3771	0.2129	−0.3710	−0.0342	−0.6665	0.3866
26	0.6890	−0.5657	0.6196	−0.2864	−0.3520	−0.2700	0.5165	0.5083	−0.1347
27	−0.6732	0.2030	0.5096	−0.1973	−0.9718	−0.6391	0.6424	−0.6936	0.2777
28	0.2173	0.5484	−0.3094	0.0621	0.1741	−0.6550	0.2073	0.4688	−0.0303
29	−0.6974	0.4656	0.1492	−0.3026	0.7717	0.9050	−0.7429	−0.6089	0.1536
30	0.1526	−0.4806	−0.6957	0.8162	−0.7643	0.4780	0.2927	0.7566	0.1915
31	0.0945	−0.5134	−0.2309	0.7205	0.9501	−0.5224	−0.5596	0.6869	0.0859
32	0.2465	−0.2837	−0.2653	0.6383	−0.7153	−0.4952	−0.4650	−0.5650	0.5163
33	0.0365	−0.7152	0.6098	0.8256	−0.3674	−0.8255	−0.1359	0.8580	−0.2322
34	0.5208	0.2592	−0.8057	0.1775	0.1458	0.3018	−0.5660	0.3805	−0.3196
35	−0.2938	−0.7255	0.7986	0.3319	−0.0357	0.0326	0.2618	0.4753	0.2338
36	0.0461	−0.5900	0.9098	−0.7344	−0.6309	0.5015	−0.2017	0.5709	0.3059
37	0.1191	0.5190	0.5997	−0.7229	−0.3856	0.8398	−0.3775	−0.2760	0.2416
38	0.9021	0.4589	−0.7767	0.2780	−0.1635	0.1610	−0.3135	0.6061	−0.2489
39	−0.2666	−0.0804	0.1347	0.1864	−0.7957	0.4831	−0.7491	−0.6082	0.6132
40	0.2850	0.7118	−0.7793	−0.2098	−0.5247	0.3116	−0.1219	0.4998	−0.1063

Table 16. Neurons, weights, and biases for the second hidden layer of the reduced (refractive index and sound velocity) ANN model.

	First Hidden Layer
	Neuron		1		2		3		4		5		6		7		8		9		10		11		12		13		14		15		16		17		18		19		20
Second Hidden Layer	1		−0.1130		0.2500		0.3210		−0.2440		−0.0862		0.2500		0.1120		0.1610		−0.0157		−0.0831		0.0158		−0.0696		−0.1380		−0.5570		−0.2110		−0.3910		0.0779		−0.0925		0.2760		0.2720
	2		0.1920		0.0169		−0.0515		−0.0243		0.2800		0.1490		0.0796		0.0199		−0.0004		−0.3660		0.0374		−0.2410		0.0160		−0.0773		0.1210		0.1660		−0.4440		−0.3050		0.2660		−0.0588
	3		0.3380		0.0986		−0.2280		0.1810		0.0651		0.2510		−0.1890		−0.2970		−0.0560		−0.3270		0.1470		−0.3060		−0.0109		0.0110		−0.0519		0.3530		0.0070		−0.1130		0.0289		0.0852
	4		0.0029		−0.2870		−0.1520		0.2410		−0.0852		−0.2720		−0.3080		0.2290		0.0400		−0.3450		−0.1940		−0.2340		−0.2220		0.2550		−0.2780		−0.1950		−0.2800		−0.3630		0.1030		0.2020
	5		−0.0007		0.1900		−0.3000		0.3990		0.0803		−0.0425		−0.0978		0.0110		−0.1940		−0.1910		0.2480		−0.1630		−0.4170		0.3800		−0.0309		0.1470		0.3210		−0.0858		−0.3130		0.0712
	6		0.0756		−0.3330		0.3130		−0.3870		0.3590		0.0350		0.3970		0.3560		−0.0578		0.1760		0.3720		0.3200		0.2500		0.1930		−0.2960		−0.2860		0.2310		0.0960		−0.1210		0.0331
	7		0.1040		−0.2420		0.4010		0.2160		0.0436		−0.0560		0.1370		0.2910		−0.1320		−0.0003		0.2710		−0.3060		−0.0497		0.1310		−0.1280		0.3250		−0.3770		0.2800		0.1590		0.2920
	8		−0.4420		−0.0948		0.2920		0.1810		0.4170		0.0836		−0.3010		0.2410		0.4190		−0.2300		0.3710		−0.3380		−0.1050		0.3020		−0.1650		0.1830		−0.0523		0.2230		0.1380		−0.4550
	9		−0.2180		0.0290		0.3720		0.0618		−0.2620		0.1110		0.4140		−0.2540		−0.2210		−0.0907		−0.0221		0.0773		−0.4180		−0.0377		0.0335		0.0189		−0.5090		0.2020		0.3530		−0.3040
	10		−0.2720		0.2590		−0.1100		−0.1360		0.2760		0.2640		−0.1120		−0.2390		−0.2080		0.1240		0.4520		0.3210		0.2330		−0.0212		0.0116		−0.1730		−0.3350		0.1470		−0.1530		0.3590
	11		−0.2510		0.3300		−0.2370		−0.0599		0.1830		−0.2230		−0.0796		−0.2410		−0.0792		0.1490		0.0378		0.3650		−0.2550		−0.4200		−0.0699		0.3110		−0.3300		−0.4470		−0.3490		0.1100
	12		0.0316		0.3330		−0.3090		−0.1350		0.0516		0.2210		0.0025		−0.2220		0.3730		−0.1260		−0.1940		−0.2900		−0.1520		0.3920		0.0601		−0.1390		0.2470		0.0685		−0.0674		0.1090
	13		−0.0388		−0.3170		−0.2070		−0.1660		0.2590		−0.2280		−0.2220		−0.1330		0.1220		0.3330		−0.1190		0.1020		0.0698		0.1670		0.1320		0.1160		−0.0554		−0.2800		0.1730		−0.0591
	14		0.0190		0.0555		0.1490		0.1250		0.0242		−0.3140		0.0072		0.1240		−0.0191		0.2440		0.0171		−0.1740		−0.3590		−0.4420		0.2790		−0.4100		−0.0249		−0.3060		0.0589		−0.2580
	15		−0.2480		−0.1440		0.1710		0.0332		0.2420		−0.3640		0.2500		0.3490		0.2740		−0.2760		−0.1150		−0.1000		0.1400		−0.3710		−0.2810		−0.0389		−0.0917		−0.4830		−0.0861		−0.3190
	16		0.2560		−0.3850		−0.1730		−0.2310		−0.2540		−0.2530		0.4930		0.0831		−0.1310		−0.3690		−0.1120		−0.3630		−0.3610		−0.1680		−0.0180		0.1160		0.2210		0.0690		−0.1470		−0.4690
	17		−0.0384		−0.3590		0.5390		−0.2420		−0.3240		−0.0394		0.2010		0.3080		−0.4700		0.2240		0.0091		0.0401		0.0514		0.1080		−0.2060		0.0955		−0.4210		0.3750		−0.0885		0.2980
	18		−0.2950		−0.3000		−0.1890		0.1410		−0.2440		0.0490		−0.2770		−0.2220		−0.2540		−0.1050		0.2530		−0.3600		0.0608		0.1560		−0.3110		0.1850		−0.1350		0.3540		0.0164		0.4220
	19		−0.2430		−0.3460		0.0064		−0.0890		0.1500		−0.1740		0.3440		−0.2930		0.3920		−0.1010		0.2510		0.0933		−0.1920		−0.2670		−0.2180		−0.0743		−0.0221		−0.2540		0.0888		−0.0590
	20		0.3380		−0.1120		0.0249		−0.2560		−0.2260		0.0755		−0.0957		0.0723		0.1660		−0.3140		−0.1740		−0.1030		0.2620		−0.0429		0.3520		−0.0546		−0.5240		−0.3140		−0.2880		0.2930
	21		0.3230		−0.2700		−0.1200		0.3670		−0.1290		0.2630		0.1230		0.0128		0.1540		0.1810		0.3660		−0.2640		0.0532		0.2870		0.2850		−0.3410		−0.0020		−0.1740		−0.1340		−0.0187
	22		0.0352		−0.0088		0.5040		−0.2230		−0.0909		−0.0749		0.3040		−0.1270		−0.1930		−0.2020		−0.1280		0.1080		0.3320		−0.0513		0.0652		−0.4480		−0.1390		0.2900		−0.3190		0.4650
	23		0.1490		−0.0417		−0.0190		0.0193		0.1130		0.4670		−0.3390		−0.0389		−0.6830		0.1560		−0.2640		0.3310		0.1060		−0.5160		−0.0698		−0.1700		0.0358		0.0629		−0.3860		0.3450
	24		−0.2800		0.3840		−0.2310		0.2820		−0.0917		−0.3810		0.1120		−0.4170		0.4020		0.2990		−0.1880		0.1770		0.1130		−0.1740		0.3190		0.4320		−0.1500		−0.1340		0.1130		−0.3120
	25		0.1340		−0.2330		0.3780		0.1480		0.3840		0.0049		0.4240		0.3490		−0.1530		0.0334		0.1990		0.0184		0.1930		0.4150		0.0104		−0.1710		−0.2410		−0.2550		0.2260		−0.0698
	26		0.1170		−0.0838		0.2580		−0.1580		−0.1960		0.2170		0.0862		0.1630		0.0054		−0.1030		−0.3430		0.1080		0.3290		0.0529		−0.2430		−0.0290		0.1090		−0.2080		0.0738		−0.0798
	27		−0.0954		−0.2500		−0.2370		0.0241		0.2720		−0.4600		−0.2940		−0.0971		0.0194		0.2640		0.3480		−0.3600		0.2010		0.1520		−0.0396		0.1520		0.2660		−0.2790		−0.0808		−0.1420
	28		−0.4080		−0.0986		0.1700		−0.0138		0.1070		−0.3740		−0.0988		0.1680		−0.3900		−0.2110		0.2860		−0.4180		0.2430		0.4610		0.3830		−0.2890		−0.1340		−0.1910		−0.1510		−0.3600
	29		0.2320		−0.1360		0.0196		−0.1240		−0.2440		−0.1990		0.3110		0.0540		0.2630		0.1390		0.0372		−0.0138		0.1140		−0.3000		−0.3360		0.3680		−0.0042		0.2600		−0.3650		0.2610
	30		−0.2010		−0.3090		0.0304		0.1500		−0.1350		−0.0872		0.0809		−0.0779		0.3430		−0.1970		0.2830		−0.0369		0.2690		−0.1400		−0.3710		0.3700		0.3680		0.0276		0.0356		0.0485
	31		−0.0109		0.2620		0.0684		−0.3730		0.3830		−0.3660		0.1570		0.0693		−0.3550		−0.1110		0.0335		0.0252		0.0903		−0.2630		−0.1930		0.3330		0.2560		−0.2560		−0.0864		0.0487
	32		0.1300		0.1450		0.2550		−0.1580		0.3840		0.2800		0.0257		0.3190		0.3320		−0.3570		0.0169		0.0013		−0.2150		0.2470		−0.3410		0.3160		−0.3590		−0.3670		−0.0673		−0.2200
	33		0.1370		−0.3300		0.5440		−0.3770		−0.1580		0.0080		0.2370		0.1800		−0.5010		−0.1450		−0.4210		0.0773		0.0540		−0.3490		−0.1650		−0.3110		−0.1160		0.2390		−0.0323		−0.1220
	34		0.3330		0.1900		0.1750		−0.1040		−0.3110		0.3150		−0.2790		−0.4850		−0.0676		0.1020		0.3610		−0.2340		0.1930		−0.2300		−0.2990		0.2350		0.0459		0.0252		0.3210		−0.1690
	35		−0.2650		−0.3780		0.2790		0.0695		−0.0657		−0.1310		0.0574		0.1130		0.2480		0.0132		0.0252		−0.4200		−0.0322		0.1710		0.2310		−0.2350		0.3410		−0.3970		−0.0309		−0.5530
	36		−0.4190		0.1270		0.2730		−0.2380		0.2420		0.1230		0.4570		0.0449		−0.1700		0.0361		0.4880		−0.2730		−0.2990		−0.1060		−0.1830		0.0858		−0.0591		0.1280		−0.2980		0.0320
	37		0.1960		−0.3640		−0.3330		0.3330		−0.0504		0.0437		−0.1210		−0.0168		−0.2780		0.4350		−0.2780		0.0938		−0.3890		−0.2170		0.2900		0.3750		0.3900		0.1480		0.0185		0.2540
	38		−0.1250		0.1690		0.3140		−0.3080		0.3440		−0.1110		−0.3820		−0.1420		−0.0428		0.1510		0.3200		−0.0004		−0.3230		−0.2000		0.3560		−0.2130		−0.2230		−0.1290		−0.1020		−0.2820
	39		0.2530		−0.3750		0.1610		−0.3010		0.4360		0.0415		0.1960		0.1800		0.1160		−0.0007		0.2630		−0.0127		−0.8470		0.3670		−0.2930		0.1230		0.0762		0.1090		−0.2980		0.2700
Second Hidden Layer	First Hidden Layer
	Neuron	21		22		23		24		25		26		27		28		29		30		31		32		33		34		35		36		37		38		39		40		Bias
	1	−0.2730		0.0241		0.0586		0.1230		−0.3640		0.4180		−0.0802		0.3160		−0.2580		0.2790		0.0292		0.0445		0.0115		0.2910		0.0121		0.4050		−0.1890		0.2620		0.2830		−0.2870		−0.1300
	2	−0.1890		−0.2880		−0.1730		−0.2920		−0.4680		0.0963		0.1120		−0.1130		−0.2070		−0.0012		−0.3620		0.1670		0.1280		0.3690		−0.0649		−0.1080		0.0911		−0.3640		0.1360		0.0472		−0.0060
	3	0.0824		−0.3320		0.0834		0.0689		0.2140		0.2460		−0.3180		−0.1520		0.0215		0.2540		−0.1190		−0.2150		0.1340		0.2970		−0.2680		0.0341		−0.1290		−0.1840		−0.3580		0.2840		−0.2810
	4	0.0893		0.2420		0.0307		0.3120		0.1910		0.3050		0.3240		0.3570		0.1880		0.3640		−0.2310		−0.2110		−0.2420		−0.0009		−0.2650		0.2470		−0.2180		−0.3790		0.2430		−0.2340		0.1110
	5	0.2660		−0.3340		0.1300		−0.3480		0.3930		−0.3470		−0.3070		0.4240		0.2150		0.3310		0.2440		0.2470		−0.0926		−0.2160		0.1730		0.0244		0.5080		−0.0909		0.2340		−0.0719		0.3590
	6	0.2710		0.0494		−0.3220		−0.3120		0.0197		−0.0076		−0.1170		−0.0111		−0.2800		0.1310		0.3040		0.3420		−0.0285		0.2520		0.2470		−0.3650		0.2370		−0.5280		0.2230		0.3720		−0.2220
	7	−0.0358		−0.0607		0.2880		0.1010		−0.1510		0.1890		−0.0261		−0.0277		0.3520		−0.2860		0.3980		0.2860		−0.0266		0.2570		−0.4420		−0.3840		−0.0780		−0.0569		0.2790		0.1100		0.3390
	8	0.1120		−0.0708		0.1320		0.2400		−0.2110		−0.0409		0.2030		0.2640		−0.2500		0.1240		0.2240		0.1500		−0.2300		−0.1210		−0.2290		0.1440		−0.2230		−0.0033		0.3100		0.3630		−0.1380
	9	−0.2270		0.2440		0.1670		0.0033		−0.1700		−0.3710		−0.1400		0.1080		−0.2710		0.2220		0.1310		0.1720		−0.3310		0.4130		0.1710		0.0056		0.2040		−0.0890		0.0505		0.1320		0.4180
	10	0.0282		−0.2740		−0.0571		−0.0259		−0.3390		0.2080		0.3370		0.4490		0.2060		0.2130		−0.0665		−0.1800		−0.2940		−0.2830		−0.0382		0.1600		0.3900		−0.4600		0.2140		0.3370		−0.0764
	11	−0.0297		0.2340		−0.1780		0.2200		0.2170		0.0996		−0.1510		0.1020		−0.2890		−0.1040		0.4440		−0.3110		−0.2700		0.1840		−0.1570		0.1150		−0.2330		−0.1200		−0.2480		0.1060		0.3660
	12	0.3220		−0.2130		0.4240		−0.3430		0.0036		0.2010		−0.3630		0.2500		0.0003		0.5270		0.0604		−0.1120		0.0187		0.0065		0.0328		−0.3520		0.5280		−0.0426		0.1910		0.2680		−0.0493
	13	0.3570		0.3450		0.3840		−0.1080		0.5010		0.3540		−0.2540		0.3480		0.4640		0.1770		0.2810		−0.0030		0.0358		0.2670		−0.0289		−0.2560		−0.1920		0.1600		0.3160		0.3140		−0.2050
	14	−0.0115		0.4120		−0.0639		−0.0970		0.1810		0.3550		−0.3820		−0.3680		0.0968		−0.2860		−0.1490		0.2160		−0.1550		0.2590		−0.5380		−0.1340		0.1890		−0.1370		−0.1760		−0.3930		0.4180
	15	0.0546		−0.2080		−0.2710		0.2860		−0.2560		−0.1530		−0.2860		−0.1730		−0.3360		0.1330		0.1880		−0.0471		0.2890		−0.1130		−0.1450		0.1470		−0.2460		0.1130		−0.2760		−0.2520		−0.0389
	16	−0.1790		−0.4350		−0.2260		0.0623		−0.1380		−0.2760		0.1010		0.3770		0.4480		0.3390		−0.2290		0.4560		−0.1200		0.4730		0.3230		0.2110		−0.1630		0.0827		0.1550		−0.1650		0.4360
	17	−0.0218		0.2120		−0.0201		0.2200		−0.0996		−0.0491		0.1340		−0.0855		0.0624		−0.0366		−0.2980		−0.0259		−0.0883		0.3030		0.0039		−0.2320		0.1990		0.1650		0.2060		0.1050		−0.0284
	18	−0.1460		−0.0002		0.2940		0.1470		−0.3310		0.0808		−0.0047		0.2240		0.3140		0.1410		−0.0268		−0.3220		0.2880		0.2940		0.0685		−0.0824		−0.2120		0.0935		0.2750		−0.0016		−0.0134
	19	−0.1430		0.3190		0.4000		−0.4270		−0.0802		−0.3670		−0.1450		0.3060		0.0910		−0.3340		0.2900		−0.1600		−0.2540		0.1960		0.3460		−0.0326		0.0948		0.0627		0.1100		−0.0681		−0.0467
	20	−0.0757		0.2630		0.4100		0.1670		−0.0939		0.3280		0.0689		−0.1040		0.2590		0.2390		−0.1910		−0.0578		0.0517		0.3660		0.2950		−0.5640		0.2400		−0.2340		0.2460		0.0994		−0.2430
	21	−0.3380		0.3370		0.2970		0.2730		0.3100		0.1590		−0.1330		−0.3640		0.2090		−0.2960		−0.3620		0.2770		−0.0921		0.2440		0.2370		−0.4540		0.4140		−0.0264		0.3810		0.1650		0.3660
	22	−0.0518		0.2050		−0.0306		0.3290		0.0575		−0.3510		0.0622		0.1970		−0.1130		−0.1160		−0.1040		−0.2270		0.3280		−0.2470		0.0266		0.1070		−0.4230		0.0395		−0.3440		−0.0499		−0.2410
	23	0.0831		0.1980		−0.0057		0.1180		0.4100		0.1190		0.2250		−0.0615		−0.4070		0.2060		−0.0358		−0.3850		−0.2600		0.1350		−0.3720		0.0546		0.0049		0.3020		−0.3770		−0.3620		0.3520
	24	0.1650		−0.3540		−0.0870		0.1900		0.1660		−0.3150		−0.3580		0.2960		0.1360		0.2370		0.1390		0.3780		0.2800		−0.0392		0.2460		−0.1910		−0.1820		−0.3840		0.1600		0.0449		−0.1320
	25	0.0142		−0.1400		0.0656		0.1770		0.1780		0.0130		−0.2910		−0.0520		0.2430		0.1050		−0.0088		0.1500		−0.2160		0.4340		0.0893		0.0348		0.0881		0.0479		0.1570		−0.0406		−0.0833
	26	0.1350		0.1630		0.0975		0.1040		−0.2940		0.2350		−0.0977		−0.0799		0.2770		−0.3640		0.1580		0.0133		−0.2110		0.0938		0.0750		−0.1290		−0.2430		0.0005		0.0342		0.1580		0.2940
	27	0.2840		0.1460		−0.2810		−0.0268		−0.1660		0.2460		−0.0308		0.2130		0.2660		0.0197		0.2720		0.4390		−0.1730		0.4530		0.0600		−0.1360		0.2340		−0.3820		−0.0679		0.4550		−0.0389
	28	−0.0367		0.3100		−0.0807		0.1320		−0.3480		0.3960		−0.0883		−0.2700		−0.2210		−0.0311		−0.0597		0.0086		0.1270		0.2940		0.2920		0.3870		0.4010		−0.1280		−0.2870		0.3280		0.4150
	29	0.1880		0.2810		−0.1410		−0.3250		−0.3330		0.3290		−0.2420		−0.3820		−0.1540		0.1030		−0.5220		0.0084		−0.0021		−0.0271		−0.3290		−0.0818		0.2060		0.1660		0.2080		−0.1210		0.3650
	30	−0.2180		−0.3470		0.4060		−0.0490		−0.1130		−0.0974		0.2960		−0.2990		−0.1380		0.0404		0.1530		0.3010		−0.2890		0.2020		0.0073		0.2320		0.5000		0.0542		0.0797		0.3700		0.3550
	31	0.3260		0.2310		0.0774		−0.0236		−0.2220		−0.2830		−0.3340		0.0838		0.1500		−0.2440		0.1750		0.1870		−0.3610		−0.1330		0.3800		−0.0907		−0.0522		0.2330		0.4460		−0.1470		−0.0919
	32	0.3100		0.1300		0.0115		0.0298		0.2330		−0.2130		−0.3090		−0.1380		0.2270		0.2880		−0.3850		0.2100		−0.3050		−0.2590		0.1610		0.2330		0.4720		0.0809		−0.2720		0.0171		0.4060
	33	0.2420		0.2010		0.2560		0.5010		0.5700		−0.4740		0.0251		−0.3590		−0.4110		−0.0292		−0.0418		−0.3860		0.1180		−0.1380		−0.2850		−0.1780		−0.4230		−0.2220		−0.2670		0.1840		−0.0154
	34	−0.1170		0.3720		−0.1490		0.3640		−0.0036		0.0038		−0.2390		0.1490		−0.2370		0.2480		−0.3150		−0.1940		−0.3910		−0.0069		−0.0771		−0.4080		−0.2070		−0.1090		0.2070		−0.1420		0.3260
	35	−0.3790		−0.0276		0.1140		−0.3410		0.1120		0.3910		−0.0957		−0.0765		0.3670		0.2200		0.1070		−0.2050		0.2610		−0.0786		0.1930		−0.3680		0.0401		−0.4460		0.3450		0.2160		0.4100
	36	−0.0678		0.2650		0.0287		−0.2950		−0.4210		0.4100		0.0842		0.2690		0.2560		0.2190		0.0226		−0.0609		−0.1530		0.0761		0.4220		−0.1060		−0.1370		−0.1380		0.3630		0.4110		−0.0845
	37	−0.0603		−0.1800		0.1390		−0.0983		0.1170		0.0986		0.1820		−0.1960		−0.0012		−0.1290		−0.2580		0.4070		−0.1000		0.3660		−0.1360		−0.6470		0.3620		−0.1590		−0.1610		0.0724		0.4610
	38	0.2140		−0.0106		−0.3590		0.3200		0.2470		0.0174		−0.0384		−0.1490		−0.3600		0.3110		−0.3310		−0.1590		0.3370		−0.1420		−0.0017		0.0373		−0.3480		0.3090		−0.0060		−0.3920		−0.1270
	39	0.4130		0.3740		0.0496		−0.0222		0.2280		−0.0449		−0.0397		0.5130		0.2090		0.2650		−0.5730		0.0793		0.1410		−0.1630		−0.2370		−0.4570		0.4560		0.0582		0.5070		0.2690		0.3590

Table 17. Neurons, weights, and biases for the output layer for the reduced (refractive index and sound velocity) ANN model.

	Second Hidden Layer Neuron
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Weight	−0.3520	−0.0192	−0.2240	0.2270	0.4230	−0.2280	0.4020	−0.3160	0.1970	−0.4330	0.1430	−0.1250	−0.3330	0.4030	−0.2460	0.1050	−0.1970	−0.0096	−0.3040	−0.3800
	Second Hidden Layer Neuron
	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	Bias
Weight	0.3080	−0.2810	0.3210	−0.0485	−0.3340	0.3540	−0.3420	0.1720	0.4340	0.3530	−0.4710	0.2820	−0.3130	0.2380	0.3790	−0.2280	0.1970	0.0030	0.2470	0.3220

Figure S8 shows the performance of the reduced ANN model with several epochs ranging from 140 to 200. The figure shows that the best output of the model was when the number of epochs reached 187.

Figure S9 shows the parity plot between the estimated and the experimental (target) values. The overall R was over 0.89, while Figure S10 represents the error histogram with very few outliers. Based on Figure S10, most of the errors were close to the value of 0.0136 while most of the errors were in the range of −0.0785 to 0.1057.

8.3. The Simulated ANN Model with Simulated Inputs

As observed in the previous sections, the ANN inputs included many other experimental measurements, such as densities, viscosities, and so on. It would consume more time to obtain all the measured data than directly measuring the pK_a. In addition, it is impossible to obtain all of the data to estimate the dissociation constants values at various temperatures if the chemicals are synthesized. Therefore, it would be more convenient to develop an ANN model that can estimate the dissociation constant values based on the simulated data. Therefore, the model is called the simulated ANN model in this study. In this section, the chemicals are used to obtain the ANN model, the same as in the previous ANN models. In addition to the temperatures (K), the molecular weight (MW), and the output values (pK_a) taken from the literature, the simulated data which include critical pressure (P_c/kPa), critical temperature (T_c/K), acentric factor (ω), the boiling temperature at 1 atm (T_b/K), flash point temperature (T_F/K), density (ρ/g⸳cm⁻¹), dynamic viscosity (η/cP), and vapor pressure (P_v/mbar), were used for the ANN model. In particular, critical pressures, critical temperatures, acentric factors, and boiling temperatures were obtained by the NIST estimation system from Aspen Plus V11.0, while flash point temperatures, densities, dynamic viscosities, and vapor pressures were calculated by CosmothermX (version C30_1201). In summary, the input of the ANN model includes 10 different types of data while the outputs are the same as the previous records. Because of the same number of inputs and outputs, the numbers of neurons for the two hidden layers are kept the same. The ANN structure for the model is the same as in Figure S4. After training, the obtained parameters were R_overal = 0.9988, MSE_overal = 0.0012, MSE_train = 0.0016, MSE_validation = 4.8433 × 10⁻⁵, and MSE_test = 1.1246 × 10⁻⁴. The weights and biases for the first, second hidden, and output layers are reported in Table 18, Table 19 and Table 20. The simulated ANN model performance with various epochs is shown in Figure S11. Figure S12 shows the parity plot between the estimated and the experimental values, while Figure S13 represents the error histogram of the simulated ANN model.

Table 18. Neurons, weights, and biases for the first hidden layer for the simulated ANN model.

Neuron	Temperature	Molecular Weight	Pc	Tc	ω	Tb	Flash Point	Density	Viscosity	Vapor Pressure	Bias
1	0.3791	−0.8085	−0.0754	−0.9132	0.3418	0.5538	−0.7291	−0.6512	−0.9860	0.4810	−2.0023
2	0.4746	0.8302	0.8654	−0.9043	−0.7836	−0.3686	0.2534	0.4265	−0.6060	−0.6293	−1.8939
3	−0.9678	1.0067	−0.7232	0.7869	0.8227	−0.3581	−0.4781	−0.0987	0.2129	−0.0762	1.7755
4	−0.7234	−0.5354	−0.8370	0.0832	−0.9282	−0.6581	0.8251	−0.2978	−0.0111	−0.7344	1.7409
5	0.9134	0.4450	0.7416	−0.5013	−0.8255	0.3571	−0.2302	0.1854	0.8122	0.8372	−1.6066
6	−0.2562	0.3493	−0.7441	1.1380	−0.5083	−0.0830	0.2571	−0.6824	−0.2094	1.2723	1.2660
7	0.1311	0.9507	−0.8731	0.2632	−0.7579	−0.5542	0.3877	0.0767	−0.3177	1.0348	−1.3825
8	−0.1516	0.9403	−0.8621	−0.8131	−0.1601	0.6607	−0.2984	0.9383	−0.4385	0.4668	1.3223
9	−0.8780	−0.3078	−0.7529	0.6730	−0.6046	0.4587	0.1584	−0.8601	−0.0597	0.9301	1.1700
10	0.5599	0.2238	0.5272	1.0303	−0.0462	0.3535	0.5984	1.0233	0.3259	0.8472	−1.0670
11	0.3167	0.4763	0.7830	0.0952	0.8615	−0.1111	0.3839	−0.8183	−0.7026	1.0308	−1.0445
12	−0.1015	−0.9264	0.4596	0.7620	0.6767	−0.1300	0.7635	0.2730	−0.9578	−0.5940	0.8757
13	0.2397	1.1468	−0.3341	0.5968	0.1786	−0.1154	1.2483	−0.7094	−0.5689	0.5591	−0.6607
14	0.4327	−0.9618	0.6721	−0.9927	0.3691	−0.0770	−0.9889	0.0254	−0.4886	−0.4149	−0.6969
15	0.1752	0.1638	0.5640	0.2419	−0.7975	1.0040	0.6430	0.4276	−0.8962	−0.4620	−0.6266
16	−0.0787	−0.5875	−0.0880	0.1842	0.3355	1.1467	1.0754	0.4767	0.1912	−0.9335	0.5461
17	0.8310	0.3786	−0.7886	0.1869	−0.7642	0.2922	1.0674	0.4767	0.0537	−0.9244	−0.3521
18	−0.1769	0.7507	0.1771	0.9779	0.1770	0.9286	−0.9233	0.8800	0.1105	0.0204	0.1429
19	0.6280	−0.1534	0.6922	0.0460	0.7548	−0.8116	−1.1484	0.7920	0.3856	0.3359	−0.2327
20	0.8099	−0.4914	0.2947	−1.1076	0.1261	−0.8730	−0.0074	−0.9000	0.4258	0.1104	−0.0017
21	0.6538	0.1012	0.4083	0.9067	−0.1955	−0.8266	−0.7945	0.8350	0.6301	0.7756	−0.1463
22	−0.0648	−0.4560	0.0470	−0.0373	0.9708	0.4811	−0.8173	−0.4484	0.7598	1.0971	−0.1087
23	−0.8342	0.7138	−0.2714	0.8072	0.3474	−0.6189	−0.1420	0.7397	−0.5940	−0.8895	−0.2606
24	−0.4484	−1.0355	−0.6716	−0.7935	−0.3745	−0.9331	−0.5373	−0.3708	−0.2612	−0.3261	−0.2835
25	0.1710	−0.9951	−0.8705	0.7688	0.4988	−0.2195	−0.2865	−0.8504	0.3641	0.5624	0.5392
26	0.3659	−0.2618	−0.2483	0.5968	0.5172	0.3471	−1.0394	0.3535	0.7768	−1.0728	0.6771
27	1.0669	0.4071	0.7614	0.2302	0.0432	−1.1352	0.3036	0.0534	−1.0864	−0.4443	0.7538
28	0.1242	−0.5401	0.7899	−0.4472	0.6723	1.1611	0.4083	−0.8136	−0.5353	0.7056	0.7908
29	−0.6794	0.0376	−0.4322	−0.5894	0.7935	−0.6744	−0.3704	0.4906	−0.7393	−0.7163	−1.0006
30	−0.4455	0.6158	0.7486	0.9645	0.6431	0.6781	−0.5696	0.2461	0.8275	0.4248	−0.9722
31	−0.1922	0.2504	0.7396	0.5626	0.8359	0.6437	−0.6817	0.9742	−0.0605	−0.2694	−1.1254
32	0.9841	−0.6248	1.3213	−0.1506	−0.5872	−0.2341	−0.7170	−0.2421	−0.1931	0.6931	1.1572
33	−0.3461	−0.6864	−0.6441	−0.1240	0.9806	0.8088	−0.4116	−0.0670	0.0843	1.1457	−1.3049
34	0.7468	0.5503	−0.8377	0.1024	1.0355	−0.6581	−0.6267	−0.6024	−0.0731	−0.0491	1.4496
35	0.8815	−0.3559	−1.0640	0.2585	0.4074	−0.0368	−0.0374	−0.4715	0.9178	0.7317	1.5280
36	−1.0656	−0.5278	0.3542	0.5742	−0.6614	−0.5160	0.7826	1.0751	−0.0855	−0.2976	−1.5972
37	−0.1119	−0.1186	−0.5653	−0.6578	−1.1791	−0.8569	0.3319	−0.7798	0.0706	0.9059	−1.6048
38	0.7690	0.0281	−0.2250	−0.2455	−0.7056	0.4202	−1.2924	0.8117	−0.1272	−0.5649	1.8023
39	1.1043	−0.0561	−0.1044	0.8983	0.5968	−0.2814	1.1681	−0.0199	−0.2836	0.2912	1.9324
40	0.7479	0.1511	−0.3996	0.8378	−0.3424	0.0579	0.9685	−0.7035	0.7730	0.2840	2.1333

Table 19. Neurons, weights, and biases for the second hidden layer of the simulated ANN model.

	First Hidden Layer
	Neuron		1		2		3		4		5		6		7		8		9		10		11		12		13		14		15		16		17		18		19		20
Second Hidden Layer	1		0.3675		−0.4129		−0.3632		−0.3588		−0.2176		−0.0267		0.3484		0.3196		−0.1697		−0.1709		−0.3583		0.3200		0.1792		−0.1927		−0.2804		0.1303		−0.2889		−0.1000		0.0965		−0.0488
	2		0.0723		0.0893		0.2059		0.2444		−0.4186		−0.4020		−0.3264		0.1877		0.2626		0.2094		−0.2386		0.2902		−0.1840		0.2470		−0.1751		−0.1253		0.2915		−0.0251		0.0453		0.2768
	3		0.2520		−0.0459		0.2321		−0.4832		0.3868		0.2867		−0.0423		0.0069		−0.0826		−0.1255		−0.1334		−0.1317		0.0078		0.1420		−0.1252		−0.3232		0.1581		0.0203		0.3040		−0.0614
	4		0.4175		−0.3582		0.0947		−0.2655		0.3440		0.1157		0.1400		0.2081		−0.2398		0.1097		−0.2520		−0.1662		0.4494		−0.1493		0.1973		0.2679		−0.0214		−0.0811		−0.2637		0.4300
	5		−0.0879		0.3366		−0.0763		−0.3183		−0.0477		0.0366		−0.0852		−0.3360		0.1690		0.0904		−0.0626		−0.0554		−0.3462		0.2023		0.0354		0.3661		−0.2668		−0.3407		−0.3864		0.2922
	6		0.0209		0.3113		−0.1321		−0.2340		−0.2750		0.3039		−0.3866		0.3813		0.0887		−0.1052		−0.2553		−0.2168		0.0243		−0.0599		−0.2273		0.3987		−0.2026		0.1238		−0.2777		0.0689
	7		−0.3080		0.2053		−0.3001		0.0640		−0.0090		0.3091		−0.2579		0.3353		−0.1685		0.3183		0.0014		0.1246		0.3819		0.1811		0.2232		−0.0066		0.3930		0.2130		0.1698		0.3030
	8		−0.0073		−0.2561		0.3986		−0.1968		−0.3530		−0.2169		−0.2618		−0.0461		0.0599		−0.2809		0.4086		−0.2643		−0.3737		−0.2666		−0.0633		0.1066		0.2228		−0.0179		−0.2473		0.2051
	9		0.1161		−0.0462		0.1493		0.1134		−0.2454		0.2519		0.1486		0.2451		0.3223		0.1135		−0.2602		−0.4068		0.2248		−0.1390		−0.0694		0.2290		0.3209		−0.2798		0.2943		−0.0195
	10		−0.1006		0.4132		−0.0918		−0.0236		0.3483		0.1348		−0.2190		0.0887		−0.1846		0.0750		0.3235		−0.2270		0.0389		0.1166		−0.2783		−0.0850		0.0414		−0.0632		−0.2019		0.5208
	11		0.2539		0.1689		0.3385		0.0161		0.1556		−0.0100		0.0744		0.2135		0.2024		0.0003		0.3023		0.3141		0.2711		0.2036		0.0149		0.2833		0.1908		−0.2238		0.3016		−0.2702
	12		−0.3592		−0.0462		0.1392		−0.3342		−0.2028		0.3489		0.1980		−0.2600		−0.1874		0.0458		−0.3512		−0.0885		0.0658		−0.3567		0.0946		−0.2922		0.2332		0.0328		−0.3001		−0.1538
	13		−0.2886		−0.3729		−0.1169		0.2808		0.2341		0.1289		0.0902		−0.2957		0.3308		−0.2536		−0.0484		0.2546		0.0342		0.2909		0.2895		0.4214		0.0593		0.3112		0.1030		−0.1277
	14		0.0138		0.2795		−0.3605		−0.0229		0.2648		0.1849		−0.2092		−0.1621		0.1922		0.0532		0.1551		−0.0228		0.2506		−0.2150		0.2870		0.2236		0.1281		0.3172		−0.1741		0.1862
	15		−0.0233		−0.1131		−0.0705		−0.3079		0.1192		−0.1939		0.1198		−0.2788		−0.4236		0.2974		0.2018		−0.2785		−0.1920		0.3985		−0.2390		−0.2483		0.1623		−0.0480		−0.1519		0.3837
	16		−0.1013		−0.1014		0.0239		0.1274		0.3778		0.3309		−0.3028		0.1922		−0.3277		−0.0402		−0.2290		−0.0610		−0.4548		0.0082		−0.0364		0.1288		0.1384		0.2139		−0.3628		−0.1981
	17		−0.0689		−0.0225		0.0828		0.0220		−0.1723		−0.0796		−0.3003		−0.4118		0.3329		−0.2405		0.2664		−0.4247		0.3493		0.1485		0.0030		0.1454		0.0842		−0.3032		0.4409		−0.3327
	18		0.4089		−0.1471		0.0197		−0.1433		0.3188		−0.2334		−0.1666		0.3047		0.2030		0.1801		0.3162		−0.2553		0.0271		0.1325		−0.0231		0.1256		−0.2650		−0.4236		−0.2432		−0.2862
	19		−0.2853		0.4080		−0.0046		−0.4050		0.2562		−0.1497		0.2916		0.3208		−0.1797		0.0102		−0.1906		−0.0893		−0.4142		−0.1010		0.0319		−0.3426		0.0227		−0.0607		−0.3114		−0.2433
	20		−0.3529		−0.3001		−0.3084		−0.0962		−0.2981		0.0110		−0.2989		−0.1328		−0.4082		−0.0031		0.1524		0.1811		0.1314		−0.4248		0.3186		−0.0809		−0.2305		0.2504		−0.2408		0.1477
	21		0.2171		−0.0027		−0.2431		−0.4023		−0.3551		−0.2860		0.2289		−0.2751		−0.0777		−0.1006		−0.1067		−0.0416		0.1949		0.1177		−0.2360		0.3695		−0.0246		0.1837		−0.0999		0.1438
	22		0.0998		0.2137		0.3127		0.2138		0.3085		−0.3175		0.1966		0.3467		−0.1056		0.0322		0.3431		−0.1981		0.3399		0.2871		−0.1244		0.2051		−0.4745		−0.1835		−0.2246		−0.2419
	23		0.1705		0.0087		0.0597		0.1643		−0.1616		0.4684		0.3213		−0.3196		0.2598		0.2103		−0.3800		0.1234		0.4029		0.0309		0.2855		−0.2844		0.0771		−0.3007		−0.2744		0.0795
	24		0.1822		0.0475		0.2643		0.3493		0.1944		0.3380		−0.4132		0.2575		−0.2732		0.0306		−0.2744		−0.0610		0.1496		0.0011		−0.2392		−0.2243		0.3115		−0.1077		0.3326		0.3206
	25		−0.0879		−0.3220		−0.0218		−0.4372		0.1675		0.4062		0.1276		−0.2029		0.3063		−0.1298		−0.1556		−0.3889		−0.0704		0.1230		−0.0527		−0.2653		−0.2306		0.1100		0.2157		0.1574
	26		0.0664		−0.2748		0.1905		−0.4100		−0.1411		0.4253		−0.1676		0.3268		0.1000		0.2088		−0.1635		0.0874		0.3895		0.2700		−0.1899		−0.2011		−0.3417		0.4476		0.3642		−0.2204
	27		−0.4107		−0.0125		0.0655		0.2521		−0.3257		0.2403		−0.0277		0.1031		−0.3835		0.0320		0.3745		−0.2255		−0.2633		0.1177		−0.2763		0.2297		0.3443		0.1277		−0.0795		−0.1062
	28		0.3569		0.0092		0.3149		0.2706		0.0290		0.1662		−0.1881		−0.3940		−0.3172		−0.4059		0.1257		−0.2374		0.1872		0.0076		−0.5490		0.3238		0.1654		−0.3454		0.1546		−0.3176
	29		−0.1188		−0.1834		−0.1737		−0.1057		−0.4265		−0.2526		0.3211		−0.3484		−0.0458		−0.2569		−0.3911		0.1499		−0.4155		0.1673		−0.2108		−0.0418		−0.0798		−0.1626		0.0003		0.4023
	30		−0.0506		−0.0415		−0.0595		0.2957		−0.1181		−0.4751		0.3638		−0.2912		0.2586		−0.3027		0.0055		−0.0266		0.1468		0.1001		−0.0611		−0.0706		−0.1491		−0.3745		0.0767		−0.4548
	31		0.0659		0.0940		0.1306		−0.4552		−0.4220		−0.0516		−0.2078		−0.2641		0.2216		0.1184		−0.0141		−0.5029		0.2138		0.1098		−0.1704		−0.0172		−0.2573		0.1849		0.0480		0.4035
	32		−0.1916		0.1135		−0.2770		0.2752		−0.2372		0.0198		−0.4276		−0.1118		0.0289		−0.4154		−0.4634		0.2876		−0.3036		0.3862		−0.0791		−0.2791		0.0479		−0.2018		0.1299		0.3007
	33		0.2503		0.3602		−0.4307		−0.3453		0.3625		0.4604		0.3820		0.1913		0.2390		0.0332		−0.2940		−0.0425		0.3309		0.0389		0.3755		0.0181		0.2091		−0.2622		−0.2552		−0.2866
	34		0.1769		0.2671		−0.0335		−0.1262		−0.0452		0.3025		−0.1254		−0.5197		0.2315		−0.0828		−0.0241		0.2819		−0.0379		−0.1626		0.3203		0.2423		−0.1577		0.2614		−0.3634		−0.1480
	35		0.1022		0.0818		−0.2743		0.0858		0.3471		0.0006		0.1746		−0.4219		−0.2315		0.2351		−0.2417		−0.1334		−0.2856		0.0773		−0.3517		−0.1749		−0.3622		−0.0222		−0.2148		−0.2513
	36		−0.0260		0.3176		0.2087		−0.3842		−0.1337		0.3318		0.2631		0.2989		−0.2377		−0.2938		0.0150		−0.3735		−0.2342		0.1842		0.2201		0.1427		−0.2026		−0.1728		−0.0199		−0.1311
	37		−0.1950		0.2480		0.2322		−0.2545		−0.1468		0.1649		−0.0072		0.1848		0.4621		−0.0661		−0.3462		−0.2857		−0.2961		0.0959		−0.0986		−0.4596		0.2270		−0.1956		0.2720		−0.0417
	38		0.2485		0.3513		0.3696		0.0124		−0.2639		−0.4020		−0.0510		0.3320		−0.1695		−0.2361		0.2063		0.1953		0.3381		−0.2229		0.0577		0.1992		0.4241		0.2030		−0.1337		0.2088
	39		−0.3112		−0.2523		−0.2838		−0.3482		0.1553		−0.0911		0.0574		−0.1409		0.4294		0.3296		−0.0641		−0.1471		−0.3774		−0.1647		−0.1976		0.2069		−0.1889		−0.0439		0.2317		−0.0299
Second Hidden Layer	First Hidden Layer
	Neuron	21		22		23		24		25		26		27		28		29		30		31		32		33		34		35		36		37		38		39		40		Bias
	1	0.2226		−0.2608		0.0453		0.1842		0.3802		0.3290		0.1709		−0.0622		0.0024		0.0261		−0.1708		−0.3243		0.3717		−0.2252		−0.1437		−0.1778		−0.1762		−0.0297		0.2895		0.0446		−1.5575
	2	0.2719		−0.2400		−0.1186		0.3518		0.2427		0.2026		0.3053		−0.4083		0.3909		−0.0256		−0.1569		−0.2815		−0.0096		−0.1602		0.2972		−0.2061		0.3052		−0.3843		0.0607		0.1708		−1.4321
	3	0.1953		0.0773		−0.4534		0.3047		0.0785		−0.4133		−0.2228		0.3620		0.1284		−0.2609		0.1174		0.4776		−0.2847		0.2270		0.2265		−0.4136		0.2257		0.4271		0.0681		0.0936		−1.3873
	4	−0.0985		0.3888		0.2197		0.1470		0.4458		−0.3077		−0.1670		0.0169		−0.0204		0.1570		−0.3843		0.2875		0.3486		0.1509		0.2176		−0.2237		−0.0117		0.1510		−0.0486		0.3012		−1.2745
	5	−0.3232		0.3340		−0.3841		0.1154		0.3722		−0.2058		−0.0271		−0.3964		−0.1351		−0.1587		−0.0116		−0.2605		−0.0021		0.1012		−0.0967		−0.2644		−0.2715		−0.1702		0.3740		0.2941		1.2221
	6	−0.0349		−0.1820		0.0064		0.4890		−0.3517		−0.0457		0.1152		0.3051		0.3575		−0.4647		0.0218		0.1592		0.1771		−0.2999		−0.0445		0.2098		−0.3868		−0.1852		−0.0070		0.2247		−1.1044
	7	−0.1340		−0.3960		0.3151		0.0273		0.1221		−0.3383		−0.1558		0.3246		−0.1259		−0.0895		−0.0662		0.2196		0.1996		0.2432		0.3399		0.4207		−0.1968		−0.1638		−0.1626		0.2776		1.0731
	8	−0.1941		−0.2767		−0.1628		−0.0663		−0.1757		−0.2890		0.3802		0.1999		0.2850		−0.1252		0.3092		0.0691		0.1730		0.2758		−0.3105		−0.1401		−0.2917		0.0089		−0.3895		0.2400		0.9720
	9	−0.3102		0.1905		0.0054		0.4023		0.1720		0.2708		0.2719		−0.1633		0.3319		0.3041		0.0221		0.0064		0.0560		0.3137		0.1141		0.4263		0.2396		−0.2858		0.0791		−0.4544		−0.8734
	10	0.1883		−0.3968		0.3798		−0.1657		−0.3879		0.2453		−0.2370		0.1195		0.2504		0.2241		0.2052		−0.0853		0.2344		0.3072		0.1086		0.0918		0.2928		−0.0868		0.4908		0.3090		0.8089
	11	−0.1266		−0.1461		−0.0775		−0.1708		−0.2759		−0.1844		0.2305		0.2191		−0.3120		0.2915		0.3444		0.2912		0.3031		−0.3567		−0.3334		0.2673		0.0425		0.2097		−0.3751		−0.3990		−0.7268
	12	−0.2875		−0.4759		−0.2336		−0.1944		−0.0694		−0.0782		−0.3519		0.2234		0.3426		−0.4138		0.2385		−0.2739		−0.2417		0.0311		−0.1176		0.3008		−0.1868		0.0218		0.2220		−0.0207		0.6471
	13	0.0945		−0.0462		0.1885		−0.3065		−0.1065		−0.1757		0.3354		−0.2363		0.0205		−0.2940		0.2696		0.0497		0.3650		−0.1506		0.2480		0.2689		−0.1105		0.0953		−0.2462		0.1376		0.5823
	14	−0.3362		0.3231		−0.1162		−0.1109		−0.3146		−0.3602		0.1314		−0.6308		0.1263		−0.0394		−0.0227		0.0407		−0.3351		−0.1949		−0.4061		0.1358		−0.2797		−0.1068		0.2548		0.1865		−0.4488
	15	−0.1203		0.1658		0.3925		−0.0093		0.0588		−0.3781		−0.2402		0.2309		0.1481		−0.2758		0.1338		−0.3087		−0.3797		0.2061		0.2861		−0.0862		−0.1171		0.2761		0.2922		0.3641		0.4241
	16	−0.1530		0.1709		−0.1940		−0.0764		−0.2111		0.1085		0.1984		0.2636		−0.4966		0.2216		0.2766		0.5385		0.3877		−0.3252		0.1792		0.1171		−0.2994		0.2245		−0.1811		−0.2816		0.3017
	17	−0.0077		−0.1449		0.1344		−0.0591		0.0105		0.0791		0.3838		−0.2934		−0.2890		−0.1440		−0.4468		−0.3551		−0.4352		−0.2409		0.0351		−0.2100		0.0776		0.0714		−0.1592		−0.0980		0.2468
	18	0.2247		−0.2536		−0.0402		0.5374		−0.2511		0.3167		0.4253		−0.1168		0.3176		−0.1549		−0.2237		0.0989		−0.2494		−0.2615		−0.2052		−0.1912		0.4256		−0.0761		0.0875		−0.2739		−0.1677
	19	−0.3651		0.1756		0.1493		−0.2964		0.2036		0.1695		−0.0040		−0.2456		−0.3901		0.1820		−0.1683		−0.3968		0.1064		−0.0707		−0.1593		−0.4150		0.1546		−0.2778		−0.4154		0.0397		0.0908
	20	0.2865		0.3705		0.3068		0.1852		−0.2399		−0.1673		−0.0507		0.2960		0.0209		0.3317		−0.3333		−0.2280		0.2478		−0.1563		−0.2799		−0.1685		−0.1899		0.1223		−0.2100		0.2353		−0.0041
	21	0.3414		−0.2998		0.2059		−0.2379		−0.1476		−0.2143		0.2478		−0.2011		−0.1115		0.4529		−0.3283		0.2279		0.4156		−0.3613		0.2046		0.2386		0.3757		0.0968		−0.3174		0.0175		0.0343
	22	−0.1978		−0.1063		0.0800		0.4500		0.1092		0.0955		0.3156		−0.3378		0.0930		−0.2154		−0.2246		−0.1173		0.2206		−0.1957		−0.0317		0.0603		0.3201		−0.0577		0.2594		0.2214		0.1757
	23	−0.2409		0.1009		0.2247		−0.1998		−0.0660		−0.4355		0.1241		−0.0855		−0.3083		−0.1067		−0.4979		−0.2220		−0.1595		0.2971		0.2765		0.1363		0.0806		0.3962		−0.1198		−0.1371		0.2539
	24	−0.4017		0.0301		0.3170		0.2072		−0.0273		−0.1784		0.1676		−0.3540		0.2144		0.3080		0.1259		0.1311		−0.0598		0.2239		−0.2608		−0.3756		−0.0302		0.3005		0.3345		0.1981		0.3645
	25	−0.0359		−0.1898		0.2651		0.0568		−0.1194		−0.2595		−0.3507		0.1059		−0.2591		−0.2291		0.3213		−0.2817		0.1568		0.3176		−0.0997		−0.3055		0.2819		−0.4165		0.1084		0.2803		−0.4166
	26	0.1062		−0.3647		−0.1803		0.0608		0.3979		−0.0412		−0.1382		0.3910		0.3869		0.0477		0.1759		−0.0841		−0.0487		−0.1390		−0.3939		−0.4250		−0.2347		−0.0489		0.0914		−0.1004		0.4910
	27	0.3074		−0.1479		−0.4109		0.1461		−0.3724		−0.4238		0.0204		0.0427		−0.0552		−0.1938		−0.0776		−0.3518		0.3355		0.2503		0.3114		0.1863		0.2145		0.0846		−0.3659		−0.1335		−0.5483
	28	−0.1918		−0.1527		−0.1167		−0.0149		−0.0741		−0.2527		0.3753		0.1018		−0.3310		0.0413		−0.1289		0.2394		0.0917		0.3111		0.2693		−0.2638		0.3091		−0.0517		−0.0540		−0.3865		0.6372
	29	−0.2643		−0.2059		0.0341		−0.1394		−0.3118		0.3653		−0.2946		−0.2437		−0.0694		−0.1189		−0.0010		0.4408		0.3802		0.1184		0.3108		−0.4254		−0.0029		0.2538		0.3449		0.0219		−0.6989
	30	0.4718		−0.2049		−0.0080		0.0787		−0.4437		0.3237		−0.1125		−0.4133		0.0253		0.0864		0.1934		−0.0010		−0.0245		0.1939		0.3577		0.3385		−0.0846		−0.2007		−0.2413		0.1990		−0.8035
	31	−0.0856		−0.1866		0.1180		−0.0087		−0.2604		−0.2210		0.3461		−0.4021		−0.0308		−0.3325		0.1662		0.0925		−0.4058		−0.1056		0.1260		0.0943		−0.2518		−0.3059		−0.2800		−0.2081		0.8609
	32	−0.3001		−0.1203		0.0977		0.1225		−0.1566		−0.1078		0.0368		0.1114		−0.1031		−0.0498		−0.1805		0.3014		0.2247		−0.2616		−0.3101		−0.4321		0.3029		0.0782		0.3135		0.3556		−0.9600
	33	0.2239		−0.3574		−0.3657		−0.1378		−0.1040		−0.1216		−0.2233		−0.4116		0.0662		−0.0371		−0.4825		0.4074		0.1529		0.2037		−0.0707		−0.0494		0.2155		0.2578		−0.2437		0.1757		1.0187
	34	0.0368		0.2221		−0.3119		−0.3275		0.1182		0.3658		−0.1383		−0.0264		−0.4255		0.4009		−0.2236		−0.3385		0.4065		−0.0556		−0.0839		−0.0818		−0.3409		0.2607		−0.1398		0.1946		1.0709
	35	−0.1744		−0.0638		0.2230		−0.1008		0.0888		−0.3382		−0.1680		0.2853		−0.2672		−0.2439		0.1251		0.2545		0.2314		0.1470		0.1274		−0.3669		0.2321		−0.2944		−0.2316		−0.3928		1.1753
	36	0.1350		0.2189		−0.1752		−0.0635		0.2924		0.3223		−0.2680		0.0014		0.2019		−0.0811		−0.2209		−0.2380		−0.2323		−0.3617		−0.0488		−0.3692		−0.3753		−0.3377		0.0469		−0.2969		−1.3156
	37	0.2099		0.1271		0.0223		−0.2607		0.3721		0.3413		0.1485		−0.2894		−0.0429		0.1758		−0.4344		−0.0366		−0.3691		0.3444		0.4241		0.2995		0.0680		−0.1413		0.1336		0.1817		−1.3629
	38	0.3851		−0.2410		−0.0101		−0.1786		0.3164		0.3778		0.1264		0.2387		0.2891		−0.2700		0.0743		0.1923		0.2754		−0.0541		0.2902		−0.1209		−0.2282		0.0630		−0.0635		−0.3089		1.4434
	39	−0.0616		0.3390		0.4548		0.1988		0.3229		0.2196		0.1233		0.4229		−0.2809		0.2354		−0.1973		−0.1215		0.2145		−0.1600		0.0229		0.2061		−0.1263		−0.1236		−0.2105		−0.4252		−1.5342

Table 20. Neurons, weights, and biases for the output layer for the simulated ANN model.

	Second Hidden Layer Neuron
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Weight	0.8320	−0.3520	−0.6236	0.8300	0.2183	0.4836	0.3338	1.0340	−0.4871	−0.9513	−0.5188	−0.2229	0.5155	−0.7244	0.1526	−0.6513	0.0370	−0.3207	−0.3903	−0.3953
	Second Hidden Layer Neuron
	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	Bias
Weight	−0.7215	−0.7665	−0.7620	0.2172	0.2657	0.8019	−0.3311	−0.7170	−0.3379	0.1952	−0.4010	0.4523	0.8320	−0.7341	−0.2346	0.4236	0.2719	−0.7039	0.0767	−0.7918

Based on the overall correlation coefficient and mean squared errors of the ANN model, as mentioned above, the model can provide a good estimation of the dissociation constants at various temperatures. When comparing the full, reduced, and simulated ANN models with the same ANN architecture, the overall correlation coefficients (R_overal), and mean squared errors (MSEs) for overall, training, validating, and testing of the three models were not very different. The simulated model has even lower mean squared errors with higher overall correlation coefficients than the other models. In addition, the simulated model is more convenient than the others because it uses the simulated data for the estimations.

9. Conclusions

The first and second pK_a of 3-(Diethylamino) propylamine, 1,3-Diaminopentane, 3-Butoxypropylamine, 2-(Methylamino) ethanol, Bis(2-methoxyethyl) amine, α-Methylbenzyl-amine, 2-Aminoheptane, and 3-Amino-1-phenylbutane were experimentally measured from the temperature range between 293.15 K to 313.15 K with 5 K increments and 323.15 K at atmospheric pressure. The dissociation constants of the amines decreased when the temperature increased. In addition, by employing the Van’t Hoff equation, the thermodynamic quantities of the reactions were determined for the eight amines studied. Among the amines, 3-(Diethylamino) propylamine and 1,3-Diaminopentane have unsymmetrical structures; it is, therefore, necessary to determine the protonation reaction orders for these amines. Computational chemistry calculations confirmed that the first pK_a values of 3-(Diethylamino) propylamine were associated with the tertiary amino while the first pK_a values of 1,3-Diaminopentane were associated with the primary amino group on the carbon chain.

In addition, the dissociation constant values of the studied amines at 298.15 K were calculated using functional group and computational chemistry methods. The paper–pencil methods provided faster calculations while keeping the predicted pK_a values at acceptable accuracy. As the paper–pencil methods could not determine the dissociation constants at any temperature but at 298 K, computational chemistry methods were used to perform the calculations using two different thermodynamic cycles. The two cycles resulted in different predictions. However, the calculated values were not very accurate; therefore, artificial neural network (ANN) models were tested to provide better accuracy. The models simply collected and combined experimental data of many amines to estimate the pK_a. Although the ANN models can produce very good estimations, the main drawback was to obtain the experimental data. If the required data were not available or the chemicals had not been synthesized, the dissociation constant values could not be determined. Instead of using the experimental properties, the software can be used to generate the data for the ANN model. The simulated ANN model was able to fit the experimental pK_a quite well.