Density, Excess Molar Volume and Vapor–Liquid Equilibrium Measurements at 101.3 kPa for Binary Mixtures Containing Ethyl Acetate and a Branched Alkane: Experimental Data and Modeling
Abstract
1. Introduction
2. Experimental Section
2.1. Material and Pure Component Properties
2.2. Density Measurement Apparatus and Method
2.3. VLE Measurement Equipment
2.4. Density at 298.15 K and VLE of the Hexane (1)–Ethyl Acetate (2) System
3. Experimental Results and Discussion
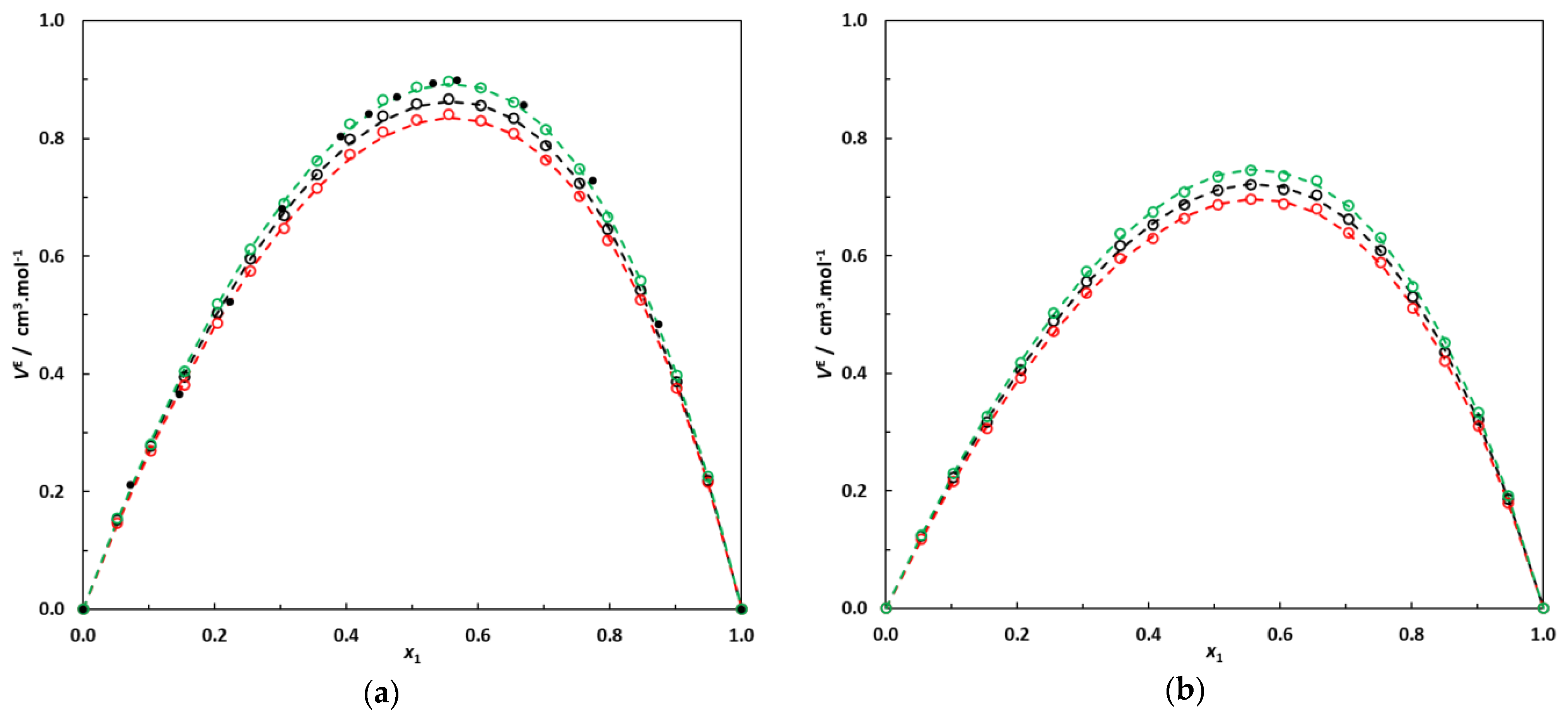
3.1. Density and Excess Molar Volumes
3.2. Pure Compounds’ Vapor Pressures
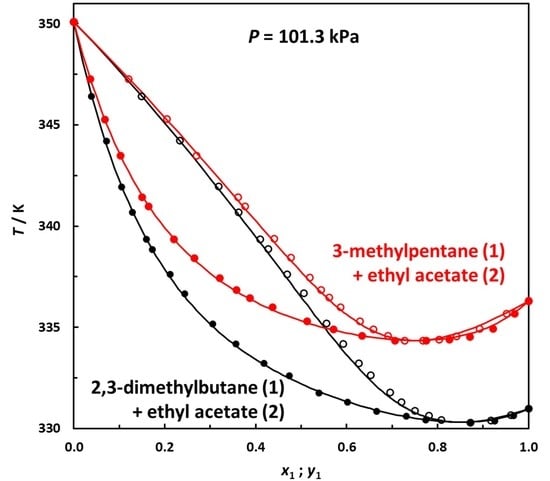
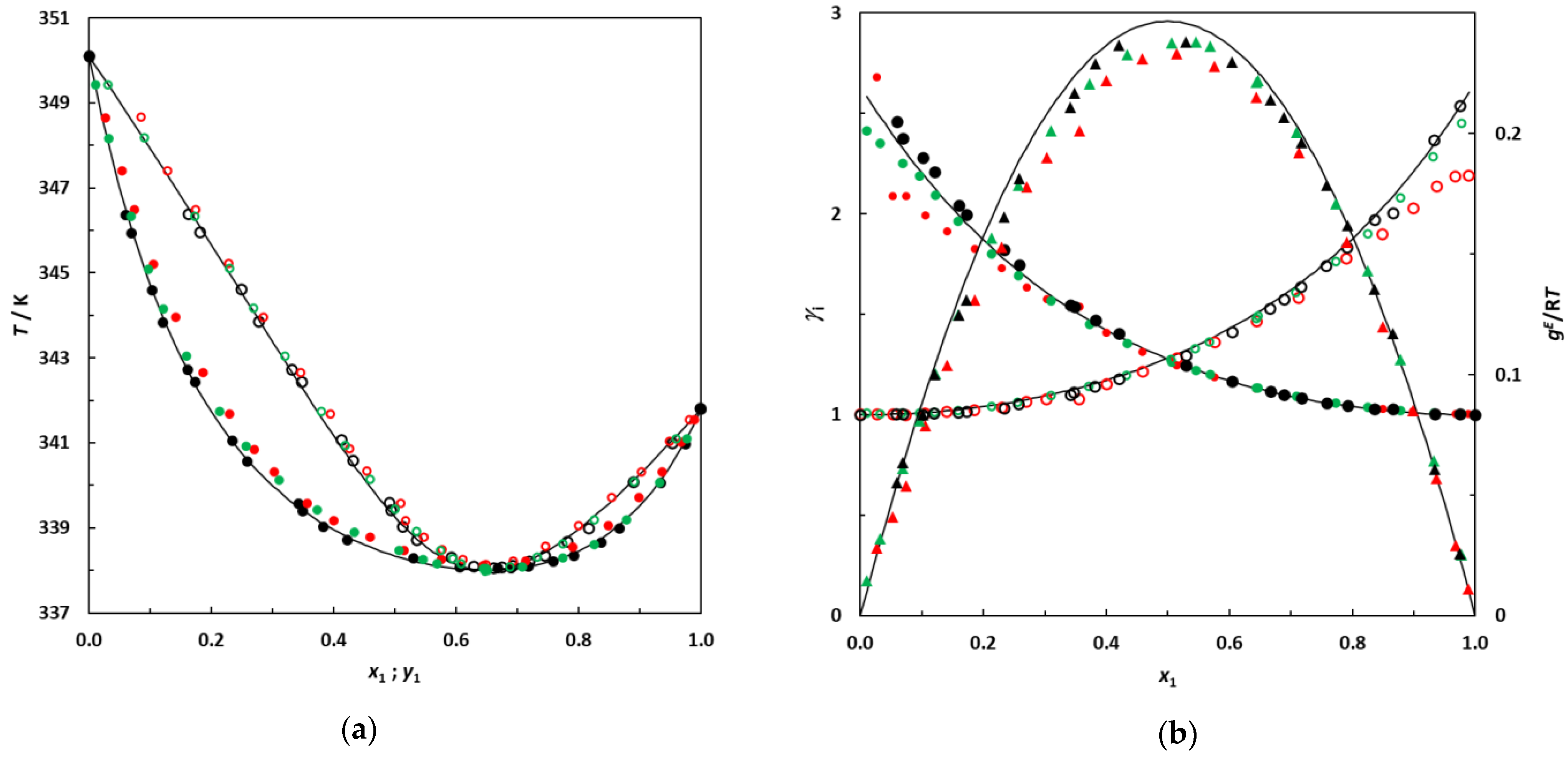
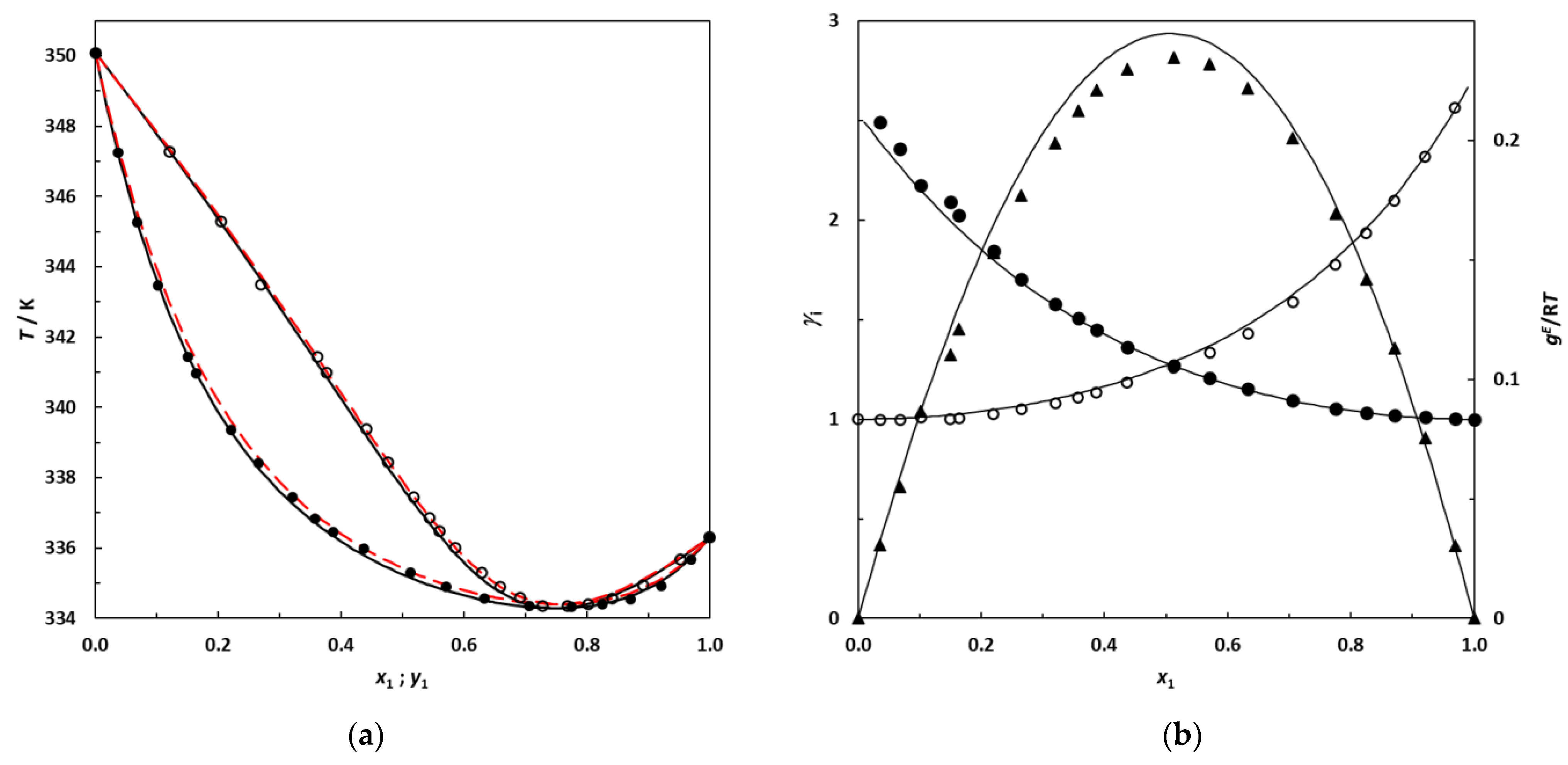
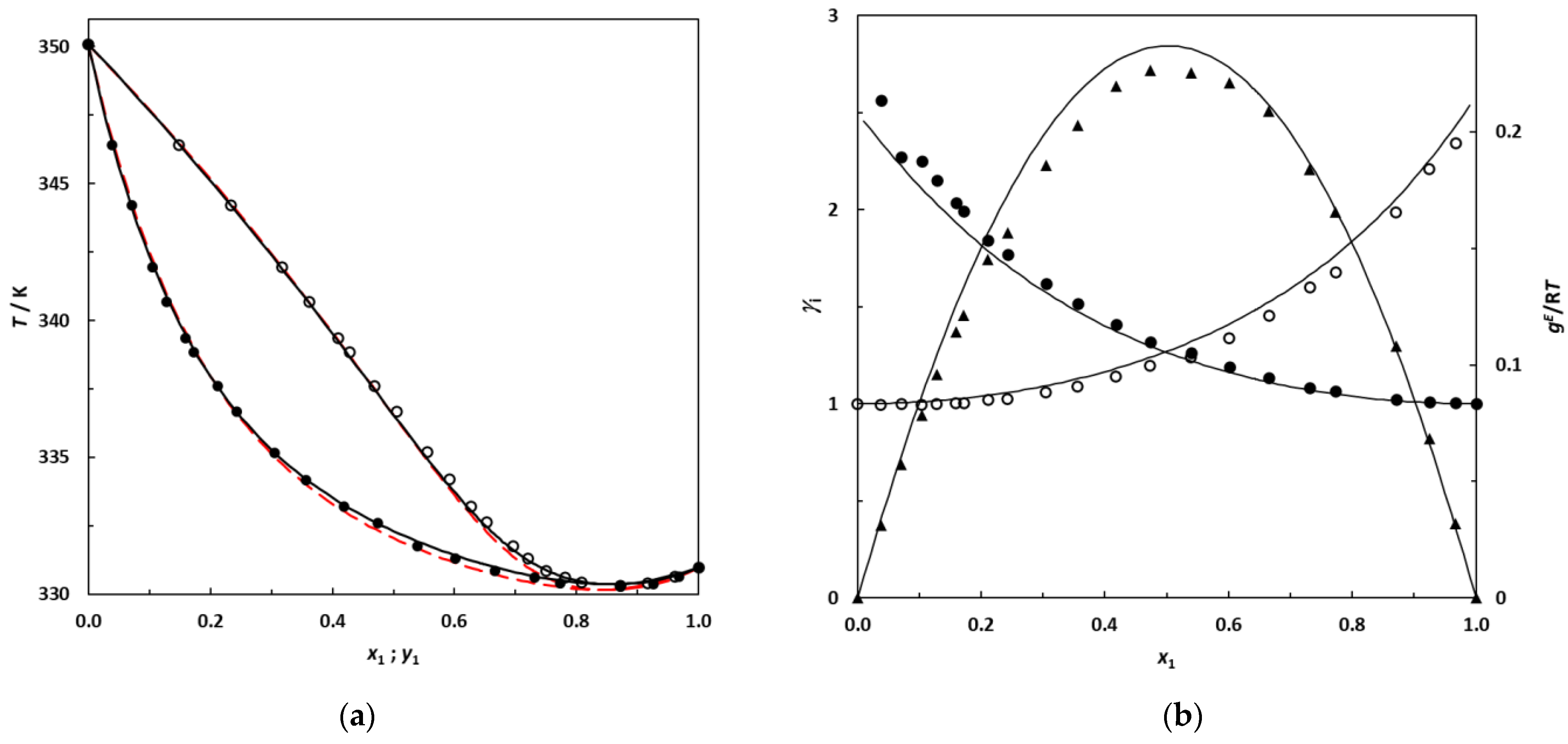
3.3. VLE Data and Consistency Checks
3.4. VLE Data Correlation
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grisales Diaz, V.H.; Willis, M.J. Ethyl acetate production from dilute bioethanol with low energy intensity. J. Clean. Prod. 2022, 376, 134137. [Google Scholar] [CrossRef]
- Çakmak, A.; Kapusuz, M.; Ozcan, H. Experimental research on ethyl acetate as novel oxygenated fuel in the spark-ignition (SI) engine. Energy Sources Part A Recovery Util. Environ. Eff. 2023, 45, 178–193. [Google Scholar] [CrossRef]
- Dabbagh, H.A.; Ghobadi, F.; Ehsani, M.R.; Moradmand, M. The influence of ester additives on the properties of gasoline. Fuel 2013, 104, 216–223. [Google Scholar] [CrossRef]
- Musyoka, S.K.; Khalil, A.S.G.; Ookawara, S.A.; Elwardany, A.E. Effect of C4 alcohol and ester as fuel additives on diesel engine operating characteristics. Fuel 2023, 304, 127656. [Google Scholar] [CrossRef]
- Gaspar, D.J.; Phillips, S.D.; Polikarpov, E.; Albrecht, K.O.; Jones, S.B.; George, A.; Landera, A.; Santosa, D.M.; Howe, D.T.; Baldwin, A.G.; et al. Measuring and predicting the vapor pressure of gasoline containing oxygenates. Fuel 2019, 243, 630–644. [Google Scholar] [CrossRef]
- Acosta, J.; Arce, A.; Martínez-Ageitos, J.; Rodil, E.; Soto, A. Vapor-Liquid Equilibrium of the Ternary System Ethyl Acetate + Hexane + Acetone at 101.32 kPa. J. Chem. Eng. Data 2002, 47, 849–854. [Google Scholar] [CrossRef]
- Park, S.J.; Han, K.J.; Choi, M.J.; Gmehling, J. Isothermal vapor-liquid equilibria and excess molar volumes for the ternary mixtures containing 2-methyl pyrazine. Fluid Phase Equilib. 2002, 193, 109–121. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, T.; Ma, Y.; Gao, J.; Xu, D.; Zhang, L.; Wang, Y. Vapour-liquid equilibrium measurements and correlation for separating azeotropic mixture (ethyl acetate + n-heptane) by extractive distillation. J. Chem. Thermodyn. 2020, 144, 106075. [Google Scholar] [CrossRef]
- Cripwell, J.T.; Schwarz, C.E.; Burger, A.J. Vapor-Liquid Equilibria Measurements for the Five Linear C6 Esters with n-Octane. J. Chem. Eng. Data 2016, 61, 2353–2362. [Google Scholar] [CrossRef]
- Fernández, L.; Pérez, E.; Ortega, J.; Canosa, J.; Wisniak, J. Measurements of the Excess Properties and Vapor-Liquid Equilibria at 101.32 kPa for mixtures of Ethyl Ethanoate + Alkanes (from C5 et C10). J. Chem. Eng. Data 2010, 55, 5519–5533. [Google Scholar] [CrossRef]
- Fernández, L.; Ortega, J.; Pérez, E.; Toledo, F.; Canosa, J. Multiproperty Correlation of Experimental Data of the Binaries Propyl Ethanoate + Alkanes (Pentane to Decane). New Experimental Information for Vapor-Liquid Equilibrium and Mixing Properties. J. Chem. Eng. Data 2013, 58, 686–706. [Google Scholar] [CrossRef]
- Ríos, R.; Ortega, J.; Fernández, L.; de Nuez, I.; Wisniak, J. Improvements in the Experimentation and the Representation of Thermodynamic Properties (iso-p VLE and yE) of Alkyl Propanoate + Alkane Binaries. J. Chem. Eng. Data 2014, 59, 125–142. [Google Scholar] [CrossRef]
- Ríos, R.; Ortega, J.; Fernández, L. Measurements and Correlations of the Vapor-Liquid Equilibria of Binary Mixtures and Excess Properties for Mixtures Containing an Alkyl (Methyl, Ethyl) Butanoate with an Alkane (Heptane, Nonane) at 101.3 kPa. J. Chem. Eng. Data 2012, 57, 3210–3224. [Google Scholar] [CrossRef]
- Pérez, E.; Ortega, J.; Fernández, L.; Wisniak, J.; Canosa, J. Contributions to the modeling and behavior of solutions containing ethanoates and hydrocarbons. New experimental data for binaries of butyl ester with alkanes (C5–C10). Fluid Phase Equilib. 2016, 412, 79–93. [Google Scholar] [CrossRef]
- Ortega, J.; Fernández, L.; Sosa, A.; Lorenzo, B.; Ríos, R.; Wisniak, J. New Advances in the Modeling and Verification of Experimental Information for Ester-Alkane Solutions: Application to a Batch-Distillation Case. Ind. Eng. Chem. Res. 2020, 59, 8346–8360. [Google Scholar] [CrossRef]
- Rios, R.; Ortega, J.; Sosa, A.; Fernández, L. Strategy for the Management of Thermodynamic Data with Application to Practical Cases of Systems Formed by Esters and Alkanes through Experimental Information, Checking-Modeling, and Simulation. Ind. Eng. Chem. Res. 2018, 57, 3410–3429. [Google Scholar] [CrossRef]
- Luis, P.; Wouters, C.; Sweygers, N.; Creemers, C.; Van der Bruggen, B. The potential of head-space chromatography for VLE measurements. J. Chem. Thermodyn. 2012, 49, 128–136. [Google Scholar] [CrossRef]
- Susial Badajoz, P.; García-Vera, D.; Marrero-Pérez, A.; Padrón-Guerra, N.; Mujica-González, T. Measurement of VLE Data by Using an Experimental Installation with Automatic Control: Modeling of Binary Systems of Methyl Acetate or Ethyl Acetate with n-Heptane or 2,2,4-Trimethylpentane at Both 0.1 and 1.5 MPa. J. Chem. Eng. Data 2019, 64, 5591–5608. [Google Scholar] [CrossRef]
- Pintos-Barral, M.; Bravo, R.; Roux-Desgranges, G.; Grolier, J.P.E.; Wilhelm, E. Excess molar heat capacities and excess molar volumes of (an n-alkylalkanoate + 2,2,4-trimethylpentane, or 2,2,4,4,6,8,8-heptamethylnonane) at T = 298.15 K. J. Chem. Thermodyn. 1999, 31, 1151–1164. [Google Scholar] [CrossRef]
- Awwad, A.M.; Jabra, K.A.; Al-Dujaili, A.H. Excess molar volumes of ethylacetate + hydrocarbons at 303.15 K: An interpretation in terms of the Prigogine-Flory-Patterson theory. Fluid Phase Equilib. 1989, 47, 95–102. [Google Scholar] [CrossRef]
- Ortega, J.; Toledo-Marante, F.J. Thermodynamic properties of (an ethyl ester + a branched alkane). XV. HEm and VEm values for (an ester + an alkane). J. Chem. Thermodyn. 2002, 34, 1439–1459. [Google Scholar] [CrossRef]
- Mohsen-Nia, M.; Modaress, H. Excess molar volume measurements of ternary mixtures [2-propanol+ethyl acetate+n-hexane] and their binary constituents at 298.15, 308.15 and 313.15 K. Phys. Chem. Liq. 2005, 43, 535–541. [Google Scholar] [CrossRef]
- Pereiro, A.B.; Rodríguez, A. Phase Equilibria of the Azeotropic Mixture Hexane + Ethyl Acetate with Ionic Liquids at 298.15 K. J. Chem. Eng. Data 2008, 53, 1360–1366. [Google Scholar] [CrossRef]
- Acosta, J.; Arce, A.; Rodil, E.; Soto, A. Densities, Speeds of Sound, Refractive Indices, and the Corresponding Changes of Mixing at 25 °C and Atmospheric Pressure for Systems Composed by Ethyl Acetate, Hexane, and Acetone. J. Chem. Eng. Data 2001, 46, 1176–1180. [Google Scholar] [CrossRef]
- Sastry, N.V.; Thakor, R.R.; Patel, M.C. Excess molar volumes, viscosity deviations, excess isentropic compressibilities and deviations in relative permittivities of (alkyl acetates (methyl, ethyl, butyl and isoamyl) + n-hexane, + benzene, + toluene, + (o-, m-, p-) xylenes, + (chloro-, bromo-, nitro-) benzene at temperatures from 298.15 to 313.15 K. J. Mol. Liq. 2009, 144, 13–22. [Google Scholar] [CrossRef]
- Loras, S.; Aucejo, A.; Muñoz, R. Phase equilibria in the systems 3-methylpentane + methylcyclohexane, diisopropyl ether + methylcyclohexane and 3-methylpentane + diisopropyl ether + methylcyclohexane at 101.3 kPa. Fluid Phase Equilib. 2002, 194–197, 957–968. [Google Scholar] [CrossRef]
- Kay, W.B. The Vapor Pressures and Saturated Liquid and Vapor Densities of the Isomeric Hexanes. J. Am. Chem. Soc. 1946, 68, 1336–1339. [Google Scholar] [CrossRef]
- Guerrero, H.; García-Mardones, M.; Pérez-Gregorio, V.; Gascón, I.; Lafuente, C. Experimental and VTPR-predicted volumetric properties of branched hexanes. Fluid Phase Equilib. 2013, 338, 141–147. [Google Scholar] [CrossRef]
- McConnell, C.G.; Van Winkle, M. Vapor-Liquid Equilibria in the Acetone−2,3-Dimethylbutane and Chloroform−2,3-Dimethylbutane systems. J. Chem. Eng. Data 1967, 12, 430–432. [Google Scholar] [CrossRef]
- García Baonza, V.; Cáceres Alonso, M.; Núñez Delgado, J. Study of the Equation of State of Liquid 2,3-Dimethylbutane at High Pressures. J. Phys. Chem. 1993, 97, 2002–2008. [Google Scholar] [CrossRef]
- Prokopová, O.; Blahut, A.; Čensky, M.; Součková, M.; Vinš, V. Comments on temperature calibration and uncertainty estimate of the vibrating tube densimeter operated at atmospheric pressure. J. Chem. Thermodyn. 2022, 173, 106855. [Google Scholar] [CrossRef]
- Zanghelini, G.; Athès, V.; Esteban-Decloux, M.; Giampaoli, P.; Vitu, S. Isobaric vapour-liquid equilibrium of α-terpineol highly diluted in hydroalcoholic mixtures at 101.3 kPa: Experimental measurements and thermodynamic modeling. J. Chem. Thermodyn. 2022, 171, 106806. [Google Scholar] [CrossRef]
- Zanghelini, G.; Esteban-Decloux, M.; Vitu, S.; Giampaoli, P.; Athès, V. β-Damascenone Highly Diluted in Hydroalcoholic Mixtures: Phase Equilibrium Measurements, Thermodynamic Modeling, and Simulation of a Batch Distillation. Ind. Eng. Chem. Res. 2022, 61, 18127–18137. [Google Scholar] [CrossRef]
- Muños-Rujas, N.; Rubio-Pérez, G.; Montero, E.A.; Aguilar, F. Isobaric Vapor-Liquid Equilibria at 50.0, 101.3, and 200.0 kPa. Density and Speed of Sound at 101.3 kPa and 298.15 K of Binary Mixtures HFE-7100 + 2-Propanol. J. Chem. Eng. Data 2020, 65, 4290–4298. [Google Scholar] [CrossRef]
- Ben Mahdoui, N.; Abidi, R.; Artigas, H.; Hichri, M.; Lafuente, C. Vapor-liquid equilibrium and excess properties of the binary mixtures formed by ethyl isobutyrate and n-alkanols. J. Chem. Thermodyn. 2019, 139, 105884. [Google Scholar] [CrossRef]
- Silva Vargas, K.; Katryniok, B.; Araque, M. Isobaric Vapor-Liquid Equilibrium Data for Six Binary Systems: Prop-2-en-1-ol (1)–Hexan-2-ol (2), Prop-2-en-1-ol (1)–Hexan-2-one (2), Hexan-2-one (1)–Hexan-2-ol (2), Prop-2-en-1-ol (1)–4-Methyl-pentan-2-ol (2), Prop-2-en-1-ol (1)–4-Methyl-pentan-2-one (2), and 4-Methyl-pentan-2-one (1)–4-Methyl-pentan-2-ol (2) at 101.32 kPa. J. Chem. Eng. Data 2021, 66, 1055–1067. [Google Scholar] [CrossRef]
- Ewing, M.B.; Sanchez Ochoa, J.C.S. Vapour pressures of n-hexane determined by comparative ebulliometry. J. Chem. Thermodyn. 2006, 38, 283–288. [Google Scholar] [CrossRef]
- Shaahmadi, F.; Thompson, C.; Burger, A.J.; Cripwell, J.T. Isobaric Vapor-Liquid Equilibria Measurements and Thermodynamic Modeling for the Systems Containing 2-Butanone, C3 Alcohols, and C4 esters: Part I—Binary Mixtures. J. Chem. Eng. Data 2022, 67, 676–688. [Google Scholar] [CrossRef]
- Willingham, C.B.; Taylor, W.J.; Pignocco, J.M.; Rossini, F.D. Vapor pressures and boiling points of some paraffin, alkylcyclopentane, alkylcyclohexane, and alkylbenzene hydrocarbons. J. Res. Natl. Bur. Stand. (U.S.) 1945, 35, 219–244. [Google Scholar] [CrossRef]
- Pavlíček, J.; Andresová, A.; Bogdanić, G.; Wichterle, I. Vapour-liquid equilibria in binary and ternary systems composed of 2,3-dimethylbutane, diisopropyl ether, and3-methyl-2-butanone at 313.15, 323.15 and 313.15 K. Fluid Phase Equilib. 2013, 344, 59–64. [Google Scholar] [CrossRef]
- Uusi-Kyyny, P.; Pokki, J.P.; Aittamaa, J.; Liukkonen, S. Vapor−Liquid Equilibrium for the Binary Systems of 3-Methylpentane + 2-Methyl-2-propanol at 331 K and + 2-Butanol at 331 K. J. Chem. Eng. Data 2001, 46, 754–758. [Google Scholar] [CrossRef]
- Rackett, H.G. Equation of state for saturated liquids. J. Chem. Eng. Data 1970, 15, 514–517. [Google Scholar] [CrossRef]
- Tsonopoulos, C. An Empirical Correlation of Second Virial Coefficients. AIChE J. 1974, 20, 263–272. [Google Scholar] [CrossRef]
- Van Ness, H.C.; Byer, S.M.; Gibbs, R.E. Vapor-Liquid Equilibrium: Part I. An Appraisal of Data Reduction Methods. AIChE J. 1973, 19, 238–244. [Google Scholar] [CrossRef]
- Fredenslund, A.; Gmehling, J.; Rasmussen, P. Vapor-Liquid Equilibria Using UNIFAC; Elsevier: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Wisniak, J. A new test for the thermodynamic consistency of vapour-liquid equilibrium. Ind. Eng. Chem. Res. 1993, 32, 1531–1533. [Google Scholar] [CrossRef]
- Wisniak, J.; Ortega, J.; Fernández, L. A Fresh Look at the Thermodynamic Consistency of Vapour-Liquid Equilibria Data. J. Chem. Thermodyn. 2017, 105, 385–395. [Google Scholar] [CrossRef]
- Liu, H.; Cui, X.; Zhang, Y.; Feng, T.; Zhang, K. Isobaric Vapor-Liquid Equilibrium for the Binary and Ternary System with Isobutyl Alcohol, Isobutyl Acetate and Dimethyl Sulfoxide at 101.3 kPa. J. Chem. Eng. Data 2017, 62, 1902–1909. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Weidlich, U.; Gmehling, J. A modified UNIFAC model 1. Prediction of VLE, hE and γ∞. Ind. Eng. Chem. Res. 1987, 26, 1372–1381. [Google Scholar] [CrossRef]
- Constantinescu, D.; Gmehling, J. Further Development of Modified UNIFAC (Dortmund): Revision and Extension 6. J. Chem. Eng. Data 2016, 61, 2738–2748. [Google Scholar] [CrossRef]



| Compound | CAS Number | Supplier | Mass Fraction Purity a | Mass Fraction Water Content b |
|---|---|---|---|---|
| Ethyl acetate (EA) | 141-78-6 | Sigma Aldrich | 0.999 | 0.0008 |
| Hexane | 110-54-3 | Merck | 0.993 | 0.0008 |
| 3-Methylpentane | 96-14-0 | Sigma Aldrich | 0.998 | 0.0005 |
| 2,3-Dimethylbutane | 79-29-8 | ThermoFisher Scientific | 0.998 | 0.0003 |
| Compound | Tb/K | ρ298.15K/g·cm−3 | ||
|---|---|---|---|---|
| This Work | Literature | This Work | Literature | |
| Ethyl acetate (EA) | 350.09 | 350.09 [6] 350.15 [10] | 0.89445 | 0.89431 [6] 0.89440 [10] |
| Hexane | 341.80 | 341.72 [6] 341.88 [10] | 0.65524 | 0.65507 [6] 0.65490 [10] |
| 3-Methylpentane | 336.30 | 336.30 [26] 336.10 [27] | 0.65972 | 0.65968 [21] 0.65973 [28] |
| 2,3-Dimethylbutane | 330.99 | 331.18 [27] 330.95 [29] | 0.65751 | 0.65700 [28] 0.65717 [30] |
| x1 b | ρ/g·cm−3 | VE/cm3·mol−1 | x1 | ρ/g·cm−3 | VE/cm3·mol−1 |
|---|---|---|---|---|---|
| 0.0000 | 0.89445 | 0.000 | 0.5546 | 0.73896 | 0.968 |
| 0.0512 | 0.87688 | 0.171 | 0.6052 | 0.72787 | 0.958 |
| 0.1032 | 0.85991 | 0.318 | 0.6555 | 0.71727 | 0.927 |
| 0.1557 | 0.84343 | 0.462 | 0.7023 | 0.70780 | 0.874 |
| 0.2043 | 0.82887 | 0.573 | 0.7529 | 0.69794 | 0.795 |
| 0.2542 | 0.81439 | 0.689 | 0.7923 | 0.69046 | 0.729 |
| 0.3056 | 0.80025 | 0.769 | 0.8506 | 0.67989 | 0.588 |
| 0.3547 | 0.78725 | 0.833 | 0.9014 | 0.67113 | 0.425 |
| 0.4052 | 0.77420 | 0.912 | 0.9496 | 0.66317 | 0.238 |
| 0.4558 | 0.76181 | 0.947 | 1.0000 | 0.65524 | 0.000 |
| 0.5054 | 0.75009 | 0.971 |
| x1 b | T = 293.15 K | T = 298.15 K | T = 303.15 K | |||
|---|---|---|---|---|---|---|
| ρ/g·cm−3 | VE/cm3·mol−1 | ρ/g·cm−3 | VE/cm3·mol−1 | ρ/g·cm−3 | VE/cm3·mol−1 | |
| 0.0000 | 0.90049 | 0.000 | 0.89445 | 0.000 | 0.88829 | 0.000 |
| 0.0519 | 0.88320 | 0.147 | 0.87723 | 0.152 | 0.87117 | 0.155 |
| 0.1026 | 0.86709 | 0.269 | 0.86120 | 0.277 | 0.85525 | 0.280 |
| 0.1539 | 0.85143 | 0.381 | 0.84561 | 0.394 | 0.83971 | 0.405 |
| 0.2042 | 0.83662 | 0.487 | 0.83087 | 0.504 | 0.82504 | 0.519 |
| 0.2546 | 0.82240 | 0.574 | 0.81672 | 0.595 | 0.81097 | 0.612 |
| 0.3047 | 0.80881 | 0.647 | 0.80321 | 0.670 | 0.79754 | 0.689 |
| 0.3554 | 0.79552 | 0.715 | 0.79000 | 0.739 | 0.78440 | 0.762 |
| 0.4053 | 0.78290 | 0.772 | 0.77745 | 0.799 | 0.77192 | 0.825 |
| 0.4551 | 0.77080 | 0.811 | 0.76542 | 0.839 | 0.75997 | 0.865 |
| 0.5061 | 0.75888 | 0.832 | 0.75359 | 0.859 | 0.74821 | 0.888 |
| 0.5553 | 0.74778 | 0.840 | 0.74257 | 0.866 | 0.73726 | 0.896 |
| 0.6039 | 0.73722 | 0.831 | 0.73208 | 0.857 | 0.72685 | 0.885 |
| 0.6542 | 0.72665 | 0.808 | 0.72158 | 0.834 | 0.71643 | 0.862 |
| 0.7030 | 0.71680 | 0.763 | 0.71180 | 0.788 | 0.70672 | 0.815 |
| 0.7537 | 0.70691 | 0.701 | 0.70199 | 0.723 | 0.69699 | 0.748 |
| 0.7969 | 0.69880 | 0.627 | 0.69395 | 0.646 | 0.68902 | 0.667 |
| 0.8462 | 0.68984 | 0.526 | 0.68506 | 0.542 | 0.68021 | 0.559 |
| 0.9010 | 0.68033 | 0.375 | 0.67563 | 0.387 | 0.67087 | 0.398 |
| 0.9491 | 0.67232 | 0.216 | 0.66771 | 0.219 | 0.66302 | 0.226 |
| 1.0000 | 0.66427 | 0.000 | 0.65972 | 0.000 | 0.65511 | 0.000 |
| x1 b | T = 293.15 K | T = 298.15 K | T = 303.15 K | |||
|---|---|---|---|---|---|---|
| ρ/g·cm−3 | VE/cm3·mol−1 | ρ/g·cm−3 | VE/cm3·mol−1 | ρ/g·cm−3 | VE/cm3·mol−1 | |
| 0.0000 | 0.90049 | 0.000 | 0.89445 | 0.000 | 0.88829 | 0.000 |
| 0.0538 | 0.88268 | 0.118 | 0.87671 | 0.123 | 0.87065 | 0.125 |
| 0.1030 | 0.86705 | 0.216 | 0.86116 | 0.223 | 0.85517 | 0.229 |
| 0.1542 | 0.85142 | 0.306 | 0.84560 | 0.318 | 0.83969 | 0.327 |
| 0.2049 | 0.83649 | 0.392 | 0.83074 | 0.406 | 0.82491 | 0.418 |
| 0.2547 | 0.82233 | 0.471 | 0.81665 | 0.489 | 0.81090 | 0.503 |
| 0.3054 | 0.80848 | 0.537 | 0.80288 | 0.556 | 0.79720 | 0.573 |
| 0.3563 | 0.79506 | 0.596 | 0.78953 | 0.617 | 0.78392 | 0.637 |
| 0.4059 | 0.78254 | 0.630 | 0.77708 | 0.653 | 0.77155 | 0.674 |
| 0.4540 | 0.77074 | 0.663 | 0.76536 | 0.686 | 0.75990 | 0.709 |
| 0.5052 | 0.75862 | 0.687 | 0.75331 | 0.711 | 0.74792 | 0.735 |
| 0.5553 | 0.74718 | 0.697 | 0.74195 | 0.721 | 0.73663 | 0.746 |
| 0.6054 | 0.73617 | 0.688 | 0.73101 | 0.712 | 0.72577 | 0.736 |
| 0.6546 | 0.72565 | 0.680 | 0.72056 | 0.703 | 0.71539 | 0.727 |
| 0.7037 | 0.71561 | 0.640 | 0.71059 | 0.662 | 0.70549 | 0.686 |
| 0.7521 | 0.70603 | 0.588 | 0.70108 | 0.609 | 0.69605 | 0.631 |
| 0.8018 | 0.69657 | 0.511 | 0.69169 | 0.530 | 0.68674 | 0.548 |
| 0.8506 | 0.68759 | 0.420 | 0.68278 | 0.436 | 0.67790 | 0.452 |
| 0.9007 | 0.67868 | 0.310 | 0.67395 | 0.321 | 0.66914 | 0.333 |
| 0.9466 | 0.67085 | 0.180 | 0.66619 | 0.186 | 0.66146 | 0.192 |
| 1.0000 | 0.66209 | 0.000 | 0.65751 | 0.000 | 0.65286 | 0.000 |
| Binary System | T/K | ||||
|---|---|---|---|---|---|
| Hexane–EA | 298.15 | 3.84392 | 0.67007 | 0.45232 | 0.20695 |
| 3-Methylpentane–EA | 293.15 | 3.29588 | 0.71386 | 0.46091 | 0.14146 |
| 3-Methylpentane–EA | 298.15 | 3.40859 | 0.74159 | 0.44523 | 0.09746 |
| 3-Methylpentane–EA | 303.15 | 3.52442 | 0.77610 | 0.41211 | 0.12022 |
| 2,3-Dimethylbutane–EA | 293.15 | 2.74556 | 0.67017 | 0.22393 | 0.03453 |
| 2,3-Dimethylbutane–EA | 298.15 | 2.84326 | 0.69501 | 0.23687 | 0.02754 |
| 2,3-Dimethylbutane–EA | 303.15 | 2.93939 | 0.73036 | 0.22997 | 0.03870 |
| P/kPa | T/K | |||
|---|---|---|---|---|
| Ethyl Acetate | Hexane | 3-Methylpentane | 2,3-Dimethylbutane | |
| 40.0 | 324.42 | |||
| 45.0 | 327.43 | |||
| 50.0 | 330.18 | 320.99 | 315.58 | 310.35 |
| 55.0 | 332.70 | 323.63 | 318.21 | 312.96 |
| 60.0 | 335.05 | 326.08 | 320.65 | 315.40 |
| 65.0 | 337.25 | 328.38 | 322.92 | 317.66 |
| 70.0 | 339.31 | 330.53 | 325.08 | 319.82 |
| 75.0 | 341.27 | 332.57 | 327.12 | 321.85 |
| 80.0 | 343.12 | 334.48 | 329.03 | 323.76 |
| 85.0 | 344.86 | 336.33 | 330.85 | 325.59 |
| 90.0 | 346.55 | 338.08 | 332.61 | 327.31 |
| 95.0 | 348.16 | 339.76 | 334.28 | 328.99 |
| 100.0 | 349.69 | 341.38 | 335.89 | 330.59 |
| 101.3 | 350.09 | 341.80 | 336.30 | 330.99 |
| T/K | |||||
|---|---|---|---|---|---|
| 350.09 | 0.000 | 0.000 | 1.000 | 0.000 | |
| 346.38 | 0.059 | 0.163 | 2.459 | 1.002 | 0.055 |
| 345.95 | 0.069 | 0.182 | 2.375 | 1.004 | 0.063 |
| 344.61 | 0.102 | 0.249 | 2.280 | 0.999 | 0.083 |
| 343.85 | 0.120 | 0.278 | 2.211 | 1.005 | 0.100 |
| 342.73 | 0.160 | 0.332 | 2.043 | 1.012 | 0.125 |
| 342.44 | 0.173 | 0.348 | 1.997 | 1.014 | 0.131 |
| 341.06 | 0.234 | 0.413 | 1.822 | 1.033 | 0.165 |
| 340.58 | 0.258 | 0.431 | 1.749 | 1.051 | 0.181 |
| 339.59 | 0.342 | 0.491 | 1.546 | 1.098 | 0.211 |
| 339.41 | 0.348 | 0.494 | 1.537 | 1.109 | 0.217 |
| 339.03 | 0.382 | 0.513 | 1.470 | 1.141 | 0.229 |
| 338.72 | 0.421 | 0.535 | 1.403 | 1.176 | 0.237 |
| 338.30 | 0.530 | 0.592 | 1.248 | 1.292 | 0.238 |
| 338.09 | 0.605 | 0.629 | 1.168 | 1.410 | 0.230 |
| 338.06 | 0.667 | 0.662 | 1.115 | 1.528 | 0.214 |
| 338.07 | 0.689 | 0.675 | 1.100 | 1.573 | 0.207 |
| 338.11 | 0.717 | 0.692 | 1.082 | 1.637 | 0.196 |
| 338.21 | 0.758 | 0.719 | 1.060 | 1.742 | 0.178 |
| 338.35 | 0.792 | 0.745 | 1.046 | 1.833 | 0.162 |
| 338.67 | 0.836 | 0.782 | 1.030 | 1.969 | 0.136 |
| 338.99 | 0.866 | 0.817 | 1.028 | 2.004 | 0.117 |
| 340.07 | 0.934 | 0.890 | 1.004 | 2.365 | 0.061 |
| 340.99 | 0.975 | 0.954 | 1.003 | 2.539 | 0.026 |
| 341.80 | 1.000 | 1.000 | 1.000 | 0.000 |
| T/K | |||||
|---|---|---|---|---|---|
| 350.09 | 0.000 | 0.000 | 1.000 | 0.000 | |
| 347.27 | 0.036 | 0.121 | 2.493 | 0.998 | 0.031 |
| 345.28 | 0.068 | 0.205 | 2.357 | 0.996 | 0.055 |
| 343.48 | 0.102 | 0.270 | 2.174 | 1.008 | 0.087 |
| 341.44 | 0.150 | 0.361 | 2.090 | 1.000 | 0.110 |
| 340.98 | 0.164 | 0.377 | 2.022 | 1.007 | 0.121 |
| 339.37 | 0.220 | 0.441 | 1.845 | 1.024 | 0.153 |
| 338.43 | 0.265 | 0.477 | 1.702 | 1.051 | 0.177 |
| 337.45 | 0.320 | 0.519 | 1.577 | 1.081 | 0.199 |
| 336.85 | 0.357 | 0.544 | 1.508 | 1.108 | 0.212 |
| 336.47 | 0.387 | 0.561 | 1.450 | 1.134 | 0.221 |
| 336.00 | 0.437 | 0.586 | 1.360 | 1.185 | 0.230 |
| 335.30 | 0.512 | 0.629 | 1.271 | 1.257 | 0.235 |
| 334.90 | 0.571 | 0.659 | 1.208 | 1.335 | 0.232 |
| 334.58 | 0.633 | 0.691 | 1.153 | 1.432 | 0.222 |
| 334.35 | 0.706 | 0.728 | 1.096 | 1.589 | 0.201 |
| 334.34 | 0.775 | 0.768 | 1.053 | 1.774 | 0.169 |
| 334.40 | 0.825 | 0.803 | 1.032 | 1.936 | 0.142 |
| 334.55 | 0.871 | 0.842 | 1.020 | 2.099 | 0.113 |
| 334.93 | 0.921 | 0.892 | 1.010 | 2.318 | 0.075 |
| 335.68 | 0.969 | 0.952 | 1.001 | 2.565 | 0.030 |
| 336.30 | 1.000 | 1.000 | 1.000 | 0.000 |
| T/K | |||||
|---|---|---|---|---|---|
| 350.09 | 0.000 | 0.000 | 1.000 | 0.000 | |
| 346.42 | 0.038 | 0.149 | 2.563 | 0.995 | 0.031 |
| 344.22 | 0.071 | 0.233 | 2.272 | 0.999 | 0.057 |
| 341.96 | 0.104 | 0.318 | 2.248 | 0.994 | 0.079 |
| 340.69 | 0.128 | 0.362 | 2.152 | 0.998 | 0.096 |
| 339.36 | 0.159 | 0.410 | 2.035 | 1.002 | 0.114 |
| 338.86 | 0.172 | 0.428 | 1.991 | 1.004 | 0.121 |
| 337.62 | 0.211 | 0.469 | 1.841 | 1.021 | 0.145 |
| 336.68 | 0.243 | 0.506 | 1.771 | 1.024 | 0.157 |
| 335.19 | 0.305 | 0.556 | 1.617 | 1.058 | 0.186 |
| 334.19 | 0.356 | 0.592 | 1.518 | 1.088 | 0.203 |
| 333.22 | 0.418 | 0.627 | 1.408 | 1.141 | 0.220 |
| 332.62 | 0.473 | 0.653 | 1.319 | 1.198 | 0.226 |
| 331.77 | 0.539 | 0.696 | 1.265 | 1.240 | 0.226 |
| 331.31 | 0.601 | 0.721 | 1.191 | 1.338 | 0.221 |
| 330.87 | 0.665 | 0.750 | 1.134 | 1.453 | 0.209 |
| 330.63 | 0.731 | 0.781 | 1.082 | 1.601 | 0.184 |
| 330.43 | 0.773 | 0.808 | 1.064 | 1.678 | 0.166 |
| 330.30 | 0.871 | 0.872 | 1.023 | 1.984 | 0.108 |
| 330.39 | 0.925 | 0.917 | 1.010 | 2.211 | 0.069 |
| 330.66 | 0.967 | 0.961 | 1.004 | 2.344 | 0.032 |
| 330.99 | 1.000 | 1.000 | 1.000 | 0.000 |
| Criterion | Fredenslund Test | Wisniak Test | |
|---|---|---|---|
| Δy ≤ 0.01 | Point Test 0.92 < Li/Wi < 1.08 | Area Test D ≤ 3 | |
| Hexane–EA | 0.006 | 0.962 < Li/Wi < 0.982 | 1.73 (L = 5.65; W = 5.85) |
| 3-Methylpentane–EA | 0.005 | 0.960 < Li/Wi < 0.985 | 1.74 (L = 5.99; W = 6.20) |
| 2,3-Dimethylbutane–EA | 0.012 | 0.957 < Li/Wi < 0.985 | 1.81 (L = 6.44; W = 6.68) |
| System | ||
|---|---|---|
| Hexane (1)–EA (2) | 0.655 | 338.05 |
| 3-Methylpentane (1)–EA (2) | 0.757 | 334.33 |
| 2,3-Dimethylbutane (1)–EA (2) | 0.877 | 330.30 |
| System | NRTL Parameters | NRTL | UNIFAC | |||
|---|---|---|---|---|---|---|
| Δg12/J·mol−1 | Δg21/J·mol−1 | Δy | ΔT/K | Δy | ΔT/K | |
| Hexane (1)–EA (2) | 1441.5 | 1575.9 | 0.0036 | 0.06 | 0.0070 | 0.38 |
| 3-Methylpentane (1)–EA (2) | 1665.9 | 1302.8 | 0.0027 | 0.08 | 0.0046 | 0.16 |
| 2,3-Dimethylbutane (1)–EA (2) | 1342.4 | 1496.0 | 0.0079 | 0.09 | 0.0080 | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caqueret, V.; Berkalou, K.; Havet, J.-L.; Debacq, M.; Vitu, S. Density, Excess Molar Volume and Vapor–Liquid Equilibrium Measurements at 101.3 kPa for Binary Mixtures Containing Ethyl Acetate and a Branched Alkane: Experimental Data and Modeling. Liquids 2023, 3, 187-202. https://doi.org/10.3390/liquids3020014
Caqueret V, Berkalou K, Havet J-L, Debacq M, Vitu S. Density, Excess Molar Volume and Vapor–Liquid Equilibrium Measurements at 101.3 kPa for Binary Mixtures Containing Ethyl Acetate and a Branched Alkane: Experimental Data and Modeling. Liquids. 2023; 3(2):187-202. https://doi.org/10.3390/liquids3020014
Chicago/Turabian StyleCaqueret, Vincent, Kaoutar Berkalou, Jean-Louis Havet, Marie Debacq, and Stéphane Vitu. 2023. "Density, Excess Molar Volume and Vapor–Liquid Equilibrium Measurements at 101.3 kPa for Binary Mixtures Containing Ethyl Acetate and a Branched Alkane: Experimental Data and Modeling" Liquids 3, no. 2: 187-202. https://doi.org/10.3390/liquids3020014
APA StyleCaqueret, V., Berkalou, K., Havet, J.-L., Debacq, M., & Vitu, S. (2023). Density, Excess Molar Volume and Vapor–Liquid Equilibrium Measurements at 101.3 kPa for Binary Mixtures Containing Ethyl Acetate and a Branched Alkane: Experimental Data and Modeling. Liquids, 3(2), 187-202. https://doi.org/10.3390/liquids3020014