Abstract
Interactions between DNA and graphene are paramount for a wide range of applications, such as biosensing and nanoelectronics; nonetheless, the molecular details of such interactions remain largely unexplored. We employ atomically detailed molecular dynamics simulations with an enhanced sampling technique to investigate the adsorption and mobility of double-stranded DNA along the basal plane of graphene, in an electrolytic aqueous medium. The study focuses on physiologically relevant conditions, using a buffer of [NaCl] = 134 mM. DNA physisorption is shown to be fast and irreversible, leading to deformation and partial melting of the double helix as a result of π–π stacking between the terminal nucleobases and graphene. Denaturation occurs primarily at the termini, with ensemble averaged H-bond ratios of 47.8–62%; these can, however, reach a minimum of 15%. Transition between free-energy minima occurs via a thermodynamical pathway driving the nucleic acid from a radius of gyration of 1.5 nm to 1.35 nm. Mobility along the basal plane of graphene is dominant, accounting for ~90% of all centre-of-mass translation and revealing that the DNA’s apparent diffusivity is similar to diffusion along the endohedral volume of carbon nanotubes, but one order of magnitude faster than in other 2D materials, such as BC3 and C3N.
1. Introduction
Ever since the pivotal work of Novoselov and Geim reported the experimental preparation of atomically thin graphene sheets [1,2], the latter have risen to the role of prototypical two-dimensional (2D) material due to their unique and peculiar electrical and physicochemical properties. Being the first crystalline 2D material, graphene is a mechanically very strong, transparent, and flexible conductor, and, as such, has found several applications in the field of electronics, namely sensing devices but also in the biological and medical fields for drug-delivery templates, diagnosis, and imaging agents [3,4,5,6,7]. As far as human health is concerned, the cytotoxicity and environmental impact of graphene-based materials needs to be thoroughly investigated [8]. Furthermore, graphene can be considered as the building block of other carbon forms, such as graphite, single-walled carbon nanotubes (SWCNTs), and buckminsterfullerenes, all of which exhibit the characteristic honeycomb lattice of sp2 hybridized carbon [9,10]. However, even employing state-of-the-art experimental techniques, it is currently quite challenging to simultaneously probe the structure and dynamics of bionanointerfaces down to the subnanosecond and subnanometer scales with atomic detail [11]. Classical experimental techniques in general yield only low-resolution information about shape, whereas others enlighten nothing about dynamics. A different approach is to study the phenomena occurring in real time, providing a self-consistent insight into thermodynamics and kinetics by using classical molecular dynamics (CMD) coupled with other enhanced sampling techniques.
It is well-known that nanoscopic solid surfaces can induce structural rearrangements and conformational alterations following nucleic acid adsorption [12], which are otherwise unobservable when DNA is in a bulk (isotropic) system. Bascom and Andriciocei demonstrated [13] that the B→A DNA transition can be modulated by the external surface of SWCNTs, but these seem to inhibit the complete relaxation of A-DNA to B-DNA as observed in the CMD simulations of Zhao and Johnson [14]. When the nucleic acid is encapsulated within these graphitic-like nanopores, the canonical B-DNA form is the thermodynamically stable conformation, as demonstrated by free-energy calculations previously performed by using a Dickerson dodecamer [15]. Clearly, when the solid surface is purely carbon based, as in the case of graphene or pristine SWCNTs, alterations in the nucleic acid structure or conformation are a direct consequence of the dominant role played by hydrophobic π interactions between the biomolecule’s nucleotides and the surface [14,15,16,17], which ultimately result in (physical) adsorption. Zhao observed that small (AGTC)2 and (AGTC)3 segments can become adsorbed onto carbon nanotubes and a graphite surface [16] is made by stacking five consecutive graphene layers, with the double-strand helix axis either parallel or perpendicular to the surface, according to a π–π stacking mechanism of the terminal nucleobase pairs on the surface. The studies by Kode and Ao, employing a combined experimental and simulation approach, verified that DNA@BN nanotube hybrids could exhibit enhanced dispersion yields in aqueous solutions when isopropyl alcohol was present in the system (60%), and attributed this finding to a polarity increase of the media [18]. Furthermore, the effect of solid substract curvature upon DNA adsorption has been the subject of previous studies. While employing single-stranded DNA (ssDNA) and SWCNTs [19] and BN nanotubes [20], it was observed that biomolecular adsorption onto the 1D solids was favoured by comparison to 2D graphite, and this can be attributed to the enhanced conformational flexibility of ssDNA arising from the existence of bare hydrophobic domains (nucleobases).
Hydrophobic interactions between graphene and other biologically relevant species, such as proteins, have recently been probed by using a model ovisporin peptide, whose secondary structure becomes randomized following contact with monoatomic pristine graphene [21]. The neurotransmitter dopamine can be detected in vivo by using carbon microelectrodes, and, as such, the atomic-level details of dopamine and dopamine-o-quinone diffusion dynamics along the basal plane of pristine graphene were investigated to access the impact of more complex microelectrode surface structures upon the kinetics of these analytes [22]. By using XNA and RNA strands of length equivalent to eight nucleobase pairs, Ghosh and Chakrabarti [23] observed that both nucleic acids undergo partial denaturation when exposed to a graphene surface while under physiological-like environments (310 K, 1 bar, [NaCl] = 150 mM). The influence of structural defects in a graphene lattice was recently investigated by Gao and Li [24], who concluded that defective graphene is more prone to initiate DNA unwinding than its pristine analogue. By drilling a hole onto atomically thin graphene membranes, Wilson and Aksimentiev [25] obtained nanopores of diameter 2.9–4.9 nm through which the electrophoretic transport of DNA was theoretically studied (voltage ~0.1–1 V) to address the issue of nucleic acid sequencing; surprisingly, it was observed that instead of promoting DNA capture/translocation through the nanopore, the effect of dielectrophoresis seems to block DNA passage due to an unexpected water compression in the nanopore.
The interactions of other 2D materials with double-stranded DNA have recently been investigated in a quest for surfaces with lower cytotoxicity and enhanced biocompatibility than pristine graphene. By using Pd (111) and Pd (100) surfaces, Gu et al. observed that DNA hexadecamers favour binding onto the (111) surface according to a flat conformation [26], where the biomolecule double-strand axis lies parallel to the solid surface, and this was interpreted in terms of binding energy. Similar nucleic acids, (ATCG)4, were exposed to C2N and C3N surfaces in a physiological-like environment: whereas the former seems to preserve the canonical DNA structure upon adsorption according to a perpendicular fashion onto the surface [27], the latter is able to induce a partial melting of the DNA double-strand after adsorption onto the C3N plane [28]. The behaviour observed for the C2N material was later replicated by changing the carbon-based solid into a pure phosphorene surface (black phosphorus) [29], and DNA adsorption was found to be thermodynamically more stable when the biomolecule contacts the solid according to a perpendicular configuration, where a terminal nucleobase pair directly contacts the solid; both CMD simulations and electrophoresis experiments concurred to verify that DNA is only minimally attracted towards phosphorene. On the other hand, and by using a shorter and slightly different DNA sequence, (AGCT)3, Deng et al. concluded that the double-strand physically adsorbs onto both BC3 and C3N nanosurfaces according to an upright/perpendicular orientation [30], resulting in a roughly 90° angle between the main axis of the biomolecule and the solid surface; physical adsorption is driven by strong π–π interactions between the terminal nucleobases and both BC3 and C3N. An identical adsorptive configuration was also observed when the dsDNA of the (ATCG)4 sequence was put into contact with MoSe2 nanosheets [31], revealing that the nucleic acid can favour vertical adsorption onto the surface via a mechanism mediated through terminal nucleobase pairs, regardless of the initial orientation toward MoSe2.
Here, we employ atomically detailed CMD calculations to probe the interactions between a B-DNA hexadecamer and a pristine (monoatomic) graphene surface immersed in aqueous solution under physiologically relevant conditions (310 K, 1 bar), while using NaCl to adjust the ionic strength of the medium at 134 mM (cf. Section 2.1). Simulations in the well-tempered metadynamics ensemble are also performed to generate free-energy landscapes in terms of two collective order parameters, namely the nucleic acid radius of gyration and the canonical Watson–Crick H-bond network (cf. Section 2.2). Results obtained are interpreted in terms of structural and equilibrium properties characteristic of canonical B-DNA double strands (Section 3). After summarizing the main findings, conclusions are established that serve as guidelines for future work (Section 4).
2. Models and Methodology
2.1. Molecular Models and System Setup
Atomically thin graphene sheets were prepared as 12 × 12 nm2 surfaces composed of hexagonally arranged carbon atoms and described by Steele’s Lennard–Jones (12, 6) potential (σ = 0.34 nm, ε = 28.0 K) [32], containing a total of 5694 sp2 carbon atoms, placed flat upon the (x, y) plane and kept fixed throughout each simulation. Lee and coworkers [33] computed the potential energy between graphene sheets and proposed σ = 0.341 nm and ε = 27.7 K to universally account for the van der Waals interactions in several graphitic systems, such as buckyballs, carbon nanotubes, and others. The advantages and drawbacks of using an empirical forcefield to describe aromatic carbons in graphene is clearly beyond the scope of the present work, and a recent review can be found elsewhere [4]. For the periodic boundary conditions not to influence the atomic surface density of the graphene sheet, the dimensions of the simulation box along the plane would have to be 11.93 × 12.05 nm2. By trimming the graphene sheet at , the atomic surface density, whose value is 0.573 Å−2 over most of the sheet, slightly increases to 0.665 Å−2 along the edges and to 0.704 Å−2 around the four vertices. The edge effects are illustrated in Figure 1, which shows a contour plot of Usf (x, y)/4εsf, where is the interaction potential between the graphene sheet and a Lennard–Jones probe (well depth εsf and size σsf = 0.34 nm located at a vertical distance of 0.34 nm from the sheet. This option allowed the effect of the atomic surface density to be evaluated in a single simulation, which substantially reduces the calculation time compared to a parametric analysis of several simulations with different surface densities.
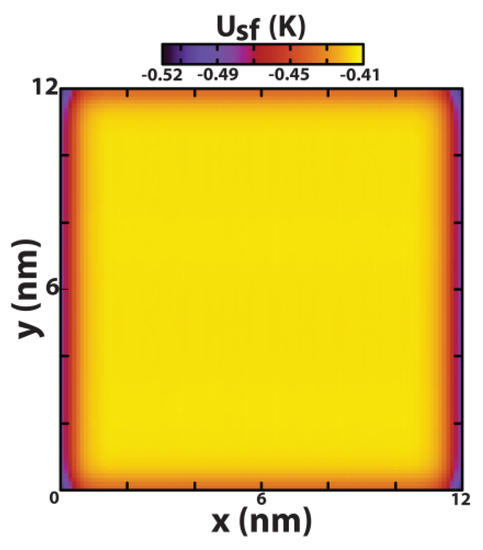
Figure 1.
Contour plot of Usf (x, y)/4εsf, where Usf (x, y) is the interaction potential between the graphene sheet and a Lennard–Jones probe (well depth εsf and size σsf = 0.34 nm) located at a vertical distance of 0.34 nm from the sheet.
The double-stranded DNA segment used in this work consists of an atomically detailed hexadecamer molecule (sequence: ATCGATCGATCGATCG, (ATCG)4, linear length: 5.1 nm, skeletal diameter: 2 nm, cf. Figure S1 in Supplementary Information), built by using the DNA-maker server [34] (http://structure.usc.edu/make-na/server.html, accessed on 1 October 2021) and according to a crystalline B-DNA conformation. Similar nucleic acids have been used before to study biomolecular adsorption onto other 2D materials, namely phosphorene surfaces [29], palladium [26], MoSe2 sheets [31], and C2N and C3N surfaces [27,28]. DNA with such sequences enables us to investigate two different types of terminal base pairs, namely A–T (containing two hydrogen bonds) and G–C (three hydrogen bonds), which have different interaction strengths with the graphitic surface. The nucleic acid is treated as a completely flexible entity, described by the AMBER99sb-ildn forcefield [35], including the refinements proposed to improve the description of backbone dihedrals [36].
In order to address the effect of initial configuration of the system, three different cases are considered: (i) nucleic acid in bulk aqueous electrolytic solution (DNA + H2O + NaCl), (ii) parallel, and (iii) perpendicularly oriented with respect to the graphene sheet (DNA + H2O + NaCl + graphene, Figure 2). In all cases, the DNA is initially placed at the (x, y) centre of the simulation cell and located at a minimum distance of 1.5 nm as measured between any atom in the double-strand and the solid surface (Figure S2 in Supplementary Information). The simulation boxes (DNA or DNA + graphene) are subsequently solvated by using a total of ~9 × 104 water molecules described by the TIP3P potential [37,38] (bulk density = 1 g/cm3) and the ionic strength of the medium adjusted with NaCl according to the Aqvist and Dang parameterization [39] to mimic physiological-like conditions (134 mM).
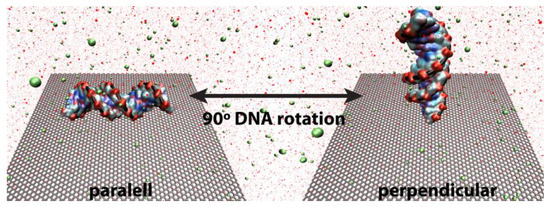
Figure 2.
Initial system setups, where parallel and perpendicular correspond to the DNA orientation toward a 12 × 12 nm2 graphene sheet aligned flat along the (x, y) plane. The sp2 carbon atoms are depicted as a honeycomb grey mesh representing the corresponding C–C bonds, and the DNA is coloured according to the chemical nature of the individual nucleobases (blue, N; red, O; and cyan, C) running through the phosphate skeleton (depicted as a black line). H2O molecules are represented by red dots and both Na+ and Cl− ions correspond to green spheres, [NaCl] = 134 mM. A bulk nucleic acid (without graphene) was also used as comparison benchmark, but its representation is omitted here for the sake of clarity.
2.2. Classical Molecular Dynamics (CMD) and Well-Tempered Metadynamics
CMD simulations were performed by using Gromacs 4.6.7 [40] and the Verlet’s algorithm to integrate Newton’s equations of motion with a 2 fs timestep. Molecular trajectories were visualized by using VMD 1.9.3 [41]. Physiological-like conditions were enforced upon the systems using a Nosé–Hoover thermostat [42,43] and a Parrinello–Rahman barostat [44] to maintain temperature and pressure at 310 K and 1 bar, respectively, while applying fully 3D periodic boundary conditions. It should be noted that previous work with DNA [16,24,26,27,28,29,30,31], using other 1D and 2D materials, was mostly focused on a temperature of 300 K, below the physiologically relevant value of 310 K. Both the Coulombic and van der Waals interactions were truncated by using a 1.5 nm potential cutoff, and long-range electrostatics were handled by using the particle-mesh Ewald summation method [45,46] with cubic interpolation while employing a maximum Fourier grid spacing of 0.12 nm. Dispersive interactions between unlike particles were calculated by using the classical Lorentz–Berthelot mixing rules [47,48]. After solvating the simulation box with the appropriate amount of H2O and NaCl, the system energy was minimized by using the steepest-descent method, followed by subsequent equilibration in the NVT ensemble during, at least, 1 ns. The system was then switched to the isothermal–isobaric ensemble, NpT, before beginning the production run of 0.5 μs.
Gibbs free-energy landscapes, at constant pressure and temperature, were obtained by using the well-tempered metadynamics framework of Barducci and Parrinello [49]. A detailed discussion on the method’s advantages and setbacks is beyond the scope of the present work and can be found elsewhere [50,51]. It suffices to say that the method biases Newton’s dynamics by adding a time-dependent Gaussian potential, V(Ω, t), to the classical Hamiltonian, preventing the system from becoming trapped in local energy minima and therefore resulting in an improved mapping of the thermodynamical phase space. The biasing potential V(Ω, t) is a function of the so-called collective variables (order parameters), , the latter being directly related to the microscopic coordinates of the real system, . In order to monitor the influence played by the solid surface on the DNA structure, we chose to employ two collective variables (n = 2) directly related to the double-strand structure: the radius of gyration () and the number of Watson–Crick H-bonds (). It is well-known that the radius of gyration, RGyr, gives a measure of a molecule’s compactness, and it is mathematically defined by Equation (1),
where N = 1014 is the total number of atoms in the double strand, mi is the mass of atom i, and ri is the positional vector of the atom relative to the molecular centre of mass. To quantify the number of Watson–Crick H-bonds (nHB), we employ the following switching function, Sij (r, t), as the second collective variable (),
where r0 = 0.35 nm, n = 8, m = 12, and rij (t) is the distance between atoms i and j at time t. For the hexadecamer employed in the present study, the maximum (theoretical) number of H bonds is obviously 40. The studies of Jayaraman and co-workers [52], with short (CGCG)2 segments in contact with hydrophilic and hydrophobic surfaces, demonstrated the adequacy of such an approach to quantify the Watson–Crick H-bond network and Deighan and Pfaendtner [53] employed a similar switching function to reconstruct the free energy of an explicitly solvated tryptophan-cage protein in H2O. Once the phase space has been thoroughly explored, three-dimensional free-energy (F (Ω)) surfaces are constructed by using a time-independent approach [51,54], and integrating , where ttot is the total simulation time, and τ is the time window over which the integration is performed. Cruz et al. [15,17,55] performed convergence tests while employing a Dickerson dodecamer and individual nucleobases confined within single-walled carbon nanotubes of variable diameters, using τ = 10 ns, and concluded that F (Ω) attained full convergence after an initial 40 ns of simulation time. All well-tempered metadynamics calculations were performed on the fly, patching the original Gromacs code with the Plumed 2.2.1 set of routines [56,57], and recording the temporal evolution of the relevant physical variables (geometrical distances, radius of gyration, Watson–Crick H-bonds, etc.).
3. Results
Initially located at a minimum distance of 1.5 nm away from the surface, the nucleic acid diffuses rapidly toward the graphene until reaching its surface (t ≤ 76 ns), and, henceforth, maintains a stable minimum distance of ca. 2.6 Å, indicating direct contact with the solid throughout the entire course of the simulations (Supporting Information Figure S3). Both the parallel and perpendicular initial configurations result in fast physisorption onto the graphene surface, via direct contact between the (AT) termini and the solid; however, the mechanism through which it occurs differs in its details. The parallel system has to undergo a 90° flipping of the molecular axis towards a perpendicular orientation, occurring in the range 6–12 ns, to enable and promote contact between the hydrophobic DNA termini (nucleotides) and the graphene sheet, mediated via the formation of π–π interactions between them (Figure 3, left). In the case of the perpendicular system (Figure 3, right), which possesses one of its termini already facing the graphene plane (AT pair), the nucleic acid rapidly approaches the solid in a quasiperpendicular fashion and becomes irreversibly physisorbed at ~76 ns.
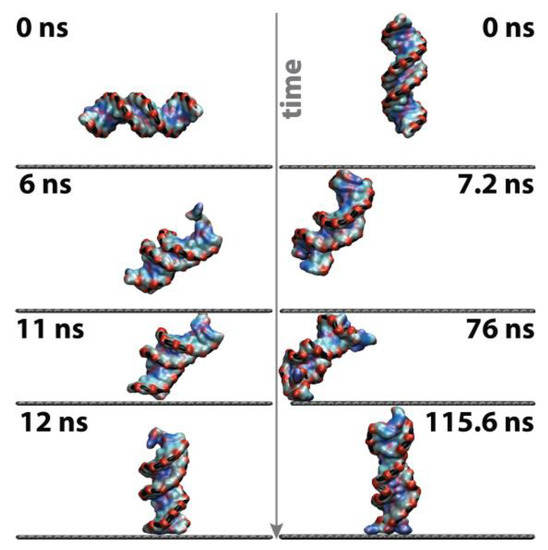
Figure 3.
Graphical depiction of the dynamics associated with the physisorption mechanism of the double-strand on graphene (left) parallel configuration, and (right) perpendicular orientation. A grey arrow indicates the increasing time scale. The nucleic acid is coloured according to the chemical nature of the nucleobases.
Although molecular adsorption onto the surface is irreversible during the observation time window (0.5 μs), forcing direct contact between the nucleic acid and graphene, it is, nonetheless, a dynamical process that confers mobility to DNA, allowing translation throughout the xy plane defined by the graphene surface; we will return to this issue and estimate an apparent self-diffusion coefficient for the physically adsorbed nucleic acid (cf. “3.6 Dynamics”).
3.1. Structural and Geometrical Features
An in-depth investigation was conducted by determining the temporal evolution of the main geometrical signatures characteristic of the systems DNA@bulk and DNA@graphene, and results thus obtained are graphically compiled in Figure 4. The root mean squared deviation (RMSD) corresponding to a time-averaged measure of intrastrand atomic displacements was computed by calculating the distance rij between atoms i and j at time t, and comparing with the same distance observed at time t = 0, according to , where N = 1014 is the total number of atoms in the DNA double helix. It should be noted that the benchmark system (DNA@bulk) exhibits a RMSD and RGyr fluctuating around 0.5 nm and 1.5–2 nm, respectively, similar to smaller Dickerson dodecamers under identical ionic strength with a mean RMSD of ca. 0.36 nm [15]. At a slightly higher salt concentration than the one employed here, [NaCl] = 0.154 mM, Ricci and Netz observed that RMSD ≈ 0.2–0.3 nm [58]. Previous studies with longer 12-mer structures of B-DNA mimicking experimental designs (length ~20 nm) have shown that the RMSD can reach 0.5–4 nm, depending on the particular ionic strength of the media [59].
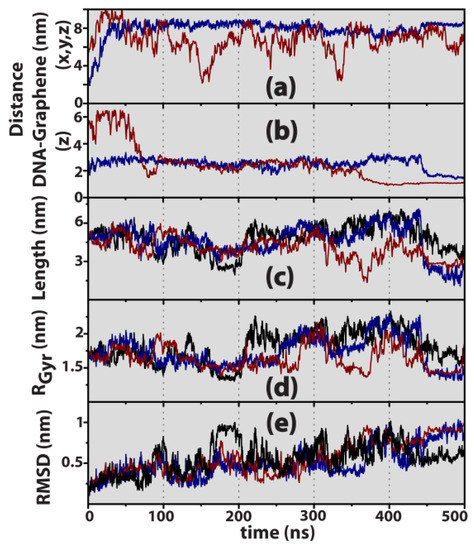
Figure 4.
Geometrical signatures of the nucleic acid structure. (a) Linear distance between the centre of mass of DNA and the centre of the graphene layer. (b) Distance between the centre of mass of DNA and graphene layer measured along the z direction normal to the graphene surface. (c) DNA length measured as the distance between opposite (AT) and (GC) termini, (5.1 nm @ t = 0 ns). (d) Radius of gyration, RGyr (1.69 nm @ t = 0 ns). (e) RMSD (0 @ t = 0 ns). Colours are attributed to bulk DNA (black), parallel (blue), and perpendicular (dark red) initial DNA orientations.
Data recorded in Figure 4 reveal that in the presence of graphene, and due to its hydrophobic nature leading to strong π–π interactions with the DNA nucleobases [14,15,16,60], the biomolecule interacts with the surface by undergoing structural deformations in the canonical B-form in order to accommodate physical adsorption occurring through one of its termini. In fact, the DNA length measured as the distance between opposite (AT) and (GC) terminal base pairs (Figure 4c) can decrease from the canonical bulk value of 5.1 nm to less than 3 nm upon contact with graphene, suggesting that for t > 0.35–0.4 μs the adsorbed nucleic acid tends to adopt a coiled conformation, resulting in a decrease of the end-to-end length. Gu and Zhao employed a DNA hexadecamer identical to ours to probe a C3N surface [28], and observed that, upon approach to the solid, the RMSD oscillates between a minimum of 0 nm and a maximum of 1.1 nm, in accordance with our own results of 0 ≤ RMSD ≤ 1 nm, as indicated in Figure 4e.
3.2. Molecular Thermodynamics
The energetics of adsorption are probed in terms of the corresponding Gibbs free-energy surfaces, obtained by using the well-tempered metadynamics framework [49]. It is represented as two-dimensional colour maps in Figure 5, built in terms of two order parameters: first, the radius of gyration (RGyr) and the number of canonical Watson–Crick H bonds (nHB), and secondly the temporal dependence that was averaged out according to the methodology previously described (cf. Section 2.2).
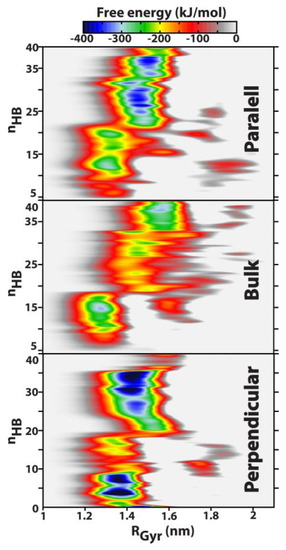
Figure 5.
Free-energy landscapes for the DNA systems studied in this work: parallel) the biomolecule is initially parallel-oriented toward the graphene sheet, bulk) corresponds to the nucleic acid in a [NaCl] = 134 mM solution without graphene (purely isotropic system), and perpendicular) when DNA is perpendicularly arranged (t = 0 ns) with respect to the solid surface. RGyr is the DNA radius of gyration, and nHB corresponds to the number of Watson–Crick hydrogen bonds in the double strand. Note that by definition, nHB = 40 corresponds to the maximum theoretical value.
The energetic surface obtained for bulk DNA corresponds to a purely isotropic system, where no restriction exists with regard to biomolecular translation within the 3D volume of the aqueous box. As a rule of thumb, it can be observed that the phase space explored in the well-tempered ensemble is broadly located within 1.1 nm RGyr 2 nm, and, apart from local free-energy minima, most significantly contained in a narrower region corresponding to RGyr 1.7 nm; a purely crystalline B-DNA dodecamer configuration exhibits RGyr ≈ 1.32 nm [15,55]. The phase space of RGyr in Figure 5 is a direct result of enhanced flexibility characteristic of the liquid state, which allows the nucleic acid to deform and relax its structure to accommodate solvation effects, and also is a consequence of molecular adsorption onto the solid surface and the ensuing structural deformation.
From the inspection of Figure 5, it now becomes clear that there is a thermodynamical pathway of consecutive free-energy minima, located in the region RGyr [1.25–1.59] nm, through which the biomolecule can travel by partially melting the Watson–Crick H bond network down to almost nHB = 5–6. This partial melting/denaturation has been theoretically and experimentally observed before—when double-stranded DNA segments were put in contact with other graphitic surfaces, such as single-walled carbon nanotubes [60,61]—being particularly evident at the double-strand termini. By using d(A)20–d(T)20 constructs, Shiraki and Naotoshi [60] attributed the partial denaturation to enhanced interactions between the nucleobases and the graphitic surfaces via π–π stacking.
While in the case of bulk DNA there are essentially two global free-energy minima, corresponding to a double-strand containing 15 and 38–39 H bonds, at RGyr = 1.28 nm and RGyr = 1.56 nm, respectively, the anisotropic systems with the graphene surface exhibit a much broader distribution of free-energy minima along the nHB order parameter, as a consequence of strong π–π interactions between the nucleic acid and the solid. From a maximum nHB = 40 hydrogen bonds characteristic of the ideal structure of a B-DNA hexadecamer, free-energy maps plotted in Figure 5 reveal that, in the presence of monoatomic graphene, a double-stranded DNA helix can undergo partial melting caused by a collapse of the Watson–Crick H bond network, resulting in nHB = 12–13 or even reaching such a small double-strand cohesion strength of ca. six H bonds. Furthermore, it is possible to identify two major sets of free-energy minima both above and below nHB ≈ 20, that is, at half of the maximum theoretical value of 40. In fact, when the double-strand integrity is maintained by 50% or more of the corresponding hydrogen bonds, the nucleic acid’s most (thermodynamically) favourable conformation corresponds to a radius of gyration of 1.45–1.5 nm, which decreases slightly to RGyr = 1.35 nm when double-strand integrity collapses following H bond breaking between the individual strands, and ultimately results in less than 50% existence of the canonical # H bonds.
3.3. Canonical Watson–Crick H-Bonds
Hydrogen bonds between complementary nucleotides are of a dynamical nature, and, similar to previous studies [61,62,63], herein we postulate that an H bond exists when the donor (D) and acceptor (A) are separated by no more than a distance of dD–A = 0.31 nm, and with a characteristic angle [63] between them of ∠ (D–H–A) ≤ 35°; the TIP3P potential employed [37,38] exhibits a radial distribution function for liquid water whose first O–O peak is located at ~0.3 nm [38]. These geometrical definitions have been used to perform a temporal analysis of simulation data, and the corresponding profiles thus obtained are graphically recorded in Figure 6, alongside average values determined for two ensembles corresponding to the initial and final windows of 0–0.3 μs and 0.3–0.5 μs, respectively.
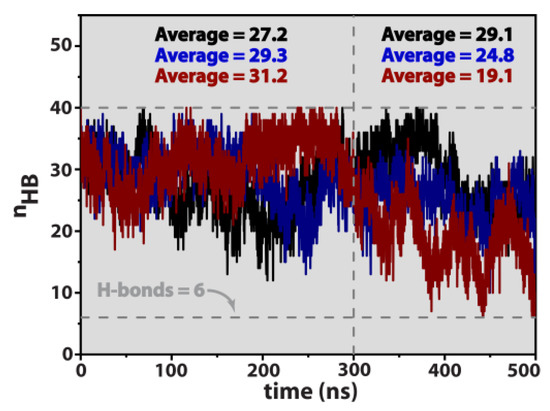
Figure 6.
Temporal profiles of the number of Watson–Crick hydrogen bonds, nHB, for the bulk nucleic acid (black), parallel (blue), and perpendicular system (dark red). Notice that the theoretical maximum number of H-bonds is 40. The inset values correspond to the ensemble averaged number of Watson–Crick H-bonds measured in the intervals 0–300 ns and 300–500 ns.
Data in Figure 6 reveals that the bulk system (black curve) roughly maintains the double-strand integrity throughout the entire observational time window, corresponding to, at least, 67.5–72.8% existence of the total number of canonical hydrogen bonds (H bond ratio) responsible for holding the two individual strands together. On the other hand, both the parallel and perpendicular configurations undergo partial denaturation of the double helix, an effect that is more pronounced for the latter arrangement. For time t ≥ 0.3 μs, the ensemble averages of hydrogen bonds correspond to 62% and 47.8%, for the parallel and perpendicular systems, respectively, which, in the latter situation can reach a lower threshold of 15%, corresponding to only six H bonds responsible for maintaining double-strand integrity.
In a recent study using bare palladium surfaces, a DNA hexadecamer similar to ours (sequence: (ATCG)4, cf. Section 2.1) was put in contact with {100} and [64] Pd facets, the systems immersed in electrolytic solutions of [KCl] = 150 mM, and studied by using a combination of molecular simulations and gel electrophoresis measurements [26]. It was then observed that physical adsorption of the nucleic acid was energetically favoured onto the Pd{111} facet and, furthermore, that physisorption resulted in significant conformational changes and H bond breakage in the double-stranded DNA adsorbed on Pd{111}, eventually reaching an H-bond ratio as low as 52.9%.
3.4. Intrastrand Hybridization
Partial denaturation/melting of the double strand is highly localized on the DNA termini, which comes as a consequence of direct contact between them and the hydrophobic graphene surface. In order to shed some light onto this effect, the internal double-helix structure, Θ, is probed by measuring the minimum distance of closest approach between each nucleotide, d(Πi, Πj)i,j = 1 − 32, at different observation times. The resulting contact maps in Figure 7 were obtained at 0.1 μs intervals. Note that the contact map at t = 0 μs corresponds to the pure (crystalline) form of the B-DNA hexadecamer. Evidently the distance between a nucleotide and itself is null, d(Πi, Πj) = 0 when i = j (e.g., the central diagonal coloured dark blue in Figure 7, is related to the intrastrand structure). Moreover, adjacent nucleotides belonging to the same single strand are always at a distance d(Πi, Πj)j = i + 1 < 0.4 nm. The stability of the interstrand structure is represented by the light blue diagonal, essentially determined by hydrogen bonding between complementary nucleotides located in different single strands. For example, the nucleotide pairs Π1–Π32 and Π16–Π17 defining the nucleic acid termini, exhibit the shortest contact distance between any group of atoms at 0 ns, and thus are coloured light blue.
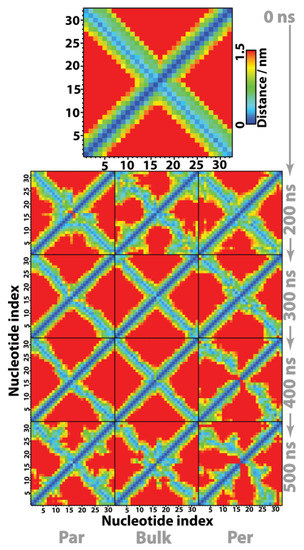
Figure 7.
Contact maps between individual DNA nucleotides. The distance between two nucleotides Πi and Πj is defined as the minimum distance between any pair of atoms (i, j: i ∈ Πi, j ∈ Πj); by definition d(Πi, Πj) = d(Πj, Πi) and d(Πi, Πj) = 0 when i = j. The terminal base pairs, defining the nucleic acid length, correspond to the first nucleotide H-bonded to the 32nd and nucleotide 16 H-bonded to the 17th one. Strand A runs from Π1→Π16 and the (complementary) B strand from Π17→Π32, where the pairs Π1–Π32 and Π16–Π17 correspond to the termini and define the nucleic acid length. Adjacent nucleotides that belong to the same strand are always at a distance d(Πi, Πj)j = i + 1 < 0.4 nm.
Overall, contact maps in Figure 7 indicate that after an initial period of 0–200 ns, corresponding to DNA equilibration to the liquid state and/or interaction with the graphene surface, the bulk system is the one where Θ remains closest to purely crystalline B-DNA, e.g., most of the double-helix internal structure is maintained throughout the study. This corroborates the previous observations regarding the canonical Watson–Crick H bond network, where it was shown that the average #H bonds = 29.1 (Figure 6), corresponding to an H bond ratio of 72.8%, strongly holds together the individual strands. Unlike the bulk molecule, the perpendicular system appears to be the one where DNA accommodates a larger degree of internal structure deformation, via a combined mechanism of coiling and melting of both termini. In fact, after 400 ns the double-strand regions defined by two (termini 1) and three (termini 2) nucleotides, running from 1–2/14–16 to the complementary 32–31/19–17, exhibit a minimum separation distance between them of 1–1.5 nm, clearly revealing denaturation of those termini. The parallel conformation lies in between the previous two situations, accommodating structural deformation without involving considerable/severe melting or denaturation of the double helix. Previous simulations have shown that even in the case of small DNA segments, adsorption on either graphene or the external surface of hydrophobic carbon nanotubes can result in melting of the terminal base pairs to accommodate structural deformation of the double strand upon adsorption [16].
3.5. Molecular Density Maps
Geometrical signatures characteristic of the nucleic acid show (cf. Figure 4b and Figure S3 in Supporting Information) that in the presence of graphene, DNA becomes constricted close to the solid surface due to strong hydrophobic interactions between the bare nucleobases at the termini and the sp2 carbon topology at the surface. To further probe this issue, we have determined two-dimensional density maps for the DNA centre of mass, using histogram reweighting with a bin width of 7 × 10−2 nm, and recorded the corresponding results in Figure 8 obtained for the whole simulation length (0.5 μs). Note that the graphene plate is located at the (z = 0) plane. The existence/absence of a graphene surface leads to two remarkably different situations regarding nucleic acid diffusion along the three-dimensional space. When no topological restrictions are present, as in the case of bulk DNA, the nucleic acid diffuses freely along the entire solvent environment as demonstrated by the quasi-isotropic distribution of molecular density in the (x, y) plane—the corresponding (x, z) and (y, z) density maps of bulk DNA have been omitted from Figure 8 for the sake of clarity and are recorded in the Supplementary Information (Figure S4).
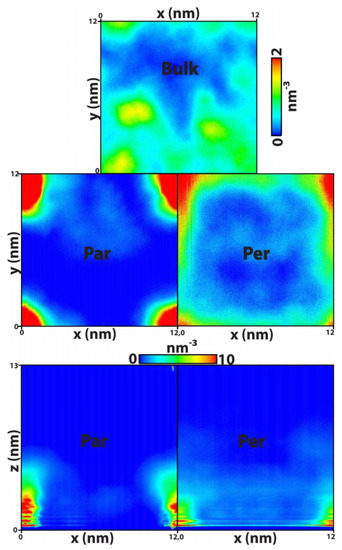
Figure 8.
Two-dimensional number density maps of DNA. Each surface was obtained by time-averaging out one dimension and calculating the corresponding histogram for the molecular centre of mass, using a bin width of 0.07 nm. The quasi-isotropic distribution of the nucleic acid observed in the bulk is essentially annihilated when the graphene sheet is introduced in the system, seating along the z = 0 plane; hydrophobic interactions between the DNA termini and the solid prevent the former from diffusing away from graphene. The (y, z) projections are similar to the (x, z) maps and thus omitted for the sake of clarity. Notice that the systems correspond to a total volume of (x, y, z) = 12 × 12 × 13 (nm3).
On the other hand, when the graphene sheet is present in the system the central area becomes less favourable for molecular translation, because of the edge effects, whilst essentially forcing DNA to explore a region of space located along the graphene edges and contained within a solvent slab defined by z < 5–6 nm, corresponding to the green–red regions (high density) evident in Figure 8. The reason for this is explained by Figure 1. For the chosen box dimensions in the (x, y) plane, the periodic boundary conditions artificially increase the atomic surface density of the graphene sheet along the edges with respect to the central zone and therefore influence the solid–fluid dispersive interaction potential per unit area in the same way. This effect is even more pronounced around the four vertices. The direct correlation between Figure 8 and Figure 1 shows that, on the one hand, the simulations were extended long enough to properly probe the entire plane of the graphene sheet and, on the other hand, small local changes in the atomic surface density due to surface defects of the pristine graphene can greatly influence the mobility of the DNA molecule.
3.6. Dynamics
Molecular mobility is usually addressed by using the Green–Kubo or Einstein formalisms to determine the corresponding self-diffusion coefficients [47,48], with both approaches being mathematically equivalent. Herein, we employ the Stokes–Einstein relation to access the apparent three-dimensional self-diffusion coefficient, , where is the mean squared displacement, r(t) is the positional vector of the DNA centre of mass at time t, the triangular brackets denote an ensemble average over all configurations, and n is the number of dimensions being considered. The three-dimensional mapping (n = 3) of MSD as a function of simulation time is graphically recorded in Figure 9a, along with its components considering molecular diffusion only in the xy plane (Figure 9b) and also along the z axis perpendicular to the graphene plane (Figure 9c). The grey lines correspond to the classical diffusional regimes [65], where MSD ∝ t2 (ballistic), MSD ∝ t (Fickian) and MSD ∝ t1/2 (single file).
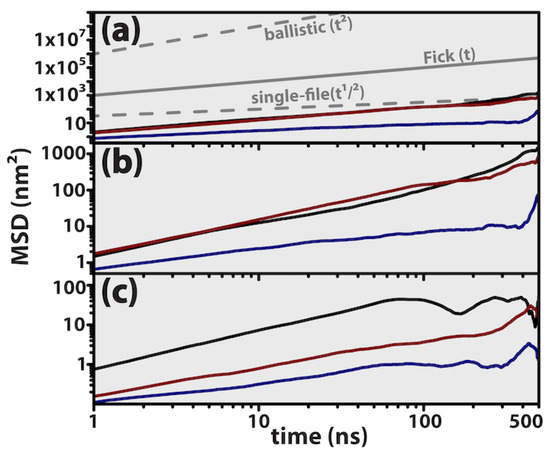
Figure 9.
Log-log plots of mean squared displacement (MSD) of the DNA centre of mass.Bulk nucleic acid (black). Parallel system (blue). Perpendicular system (dark red). The grey lines serve as guides to the eye and identify the classical diffusional regimes, namely ballistic, Fickian and single file, where the MSD is directly proportional to , and , respectively. (a) Diffusion along the three-dimensional space. (b) Translation in the xy plane parallel to graphene. (c) Diffusion along the z direction perpendicular to graphene.
Overall, molecular mobility is essentially Fickian for the DNA molecule diffuses according to a linear relation with time. Nevertheless, the parallel system initially starts diffusing according to an apparently single-file regime, migrating to Fickian-like diffusion after t > 300 ns, and this transition seems to be the consequence of enhanced molecular translation along the xy plane. Also evident from the inspection of Figure 9 is the predominance of mobility along the xy plane, as compared to translation along the z axis, when MSDz ≤ 0.1 MSDxy. Density maps in Figure 8 have already revealed that the nucleic acid mobility is hampered along the Z direction, being confined to translation along the graphene plane (xy) while being contained in a solvent slab of z < 5–6 nm.
Recent studies of ovispirin−1 adsorption upon pristine graphene concluded that the protein was not only prone to rapidly physisorb onto the solid substract, but also, at the same time, molecular diffusion became highly restricted to translation along the graphene surface [21], thus corroborating our own observations with DNA. Even smaller biomolecules like the neurotransmitter dopamine, in spite of being able to rapidly diffuse along the carbon surface, once physisorbed do not return to the bulk environment [22]. Other graphitic-like surfaces such as (1D) single-walled carbon nanotubes [14,16], exhibit a similar behaviour to 2D graphene, where the adsorbents can slide rather freely but always along the sp2 carbon mesh while maintaining direct contact with the surface. In contrast to what is observed with graphene, other two-dimensional materials induce different dynamics upon biomolecular diffusion. Gu and Zhou [27] employed a nucleic acid similar to ours to probe a C2N surface and observed that DNA migration along the transverse direction of the solid surface was highly restricted after binding, with the biomolecule maintaining an upright position—that is, perpendicularly aligned regarding the C2N plane. Recently, a slightly smaller DNA duplex was employed, (AGCT)3, to study the honeycomb lattices of both BC3 and C3N heterojunctions with graphene [30], having again been observed that double-stranded DNA binds perpendicularly to the two nanosheets, but nevertheless exhibits different dynamics on both, and this was interpreted in terms of the water distribution at the DNA/nanosheet interfacial region. Calculated diffusion coefficients varied in the region 3 × 10−11–12 × 10−11 m2/s, with average values of Davg = 8.65 × 10−11 m2/s (@C3N) and Davg = 3.64 × 10−11 m2/s−1 (@BC3).
Linear fittings of mean-squared displacement data in Figure 9a were performed in the region 0.2–0.5 μs, resulting in apparent diffusivities of Dapp = 6.99 × 10−10 m2/s (bulk), Dapp = 1.06 × 10−10 m2/s (parallel) and Dapp = 3.16 × 10−10 m2/s (perpendicular). The apparent diffusivity of the parallel system was estimated in the region 0.4–0.5 μs, to mitigate the effect of single-file diffusion occurring at very early times. As far as we are aware, there are no diffusion coefficients previously reported for a DNA hexadecamer adsorbed on graphene; nevertheless, earlier calculations employing a Dickerson dodecamer confined onto carbon nanotubes revealed that the nucleic acid would diffuse within the endohedral volume with self-diffusivities ranging from 5.4 × 10−10 m2/s up to 9.5 × 10−10 m2/s, and it was concluded that molecular diffusion was slower when the pristine nanotubes became electrically charged because of the electrostatic attraction between the nucleic acid and the nanotube walls [66]. Previous experimental measurements using very long DNA double strands, with thousands of base pairs, confined in glass slit-like pores revealed that the nucleic acid’s apparent self-diffusivity would be located in the region (2.7–9) × 10−12 m2/s, depending on the particular height of the glass substract and the length of the nucleic acid employed [67]. Recently, Jia and DuBay [22] used the small dopamine molecule to study biomolecular diffusion onto pristine graphene sheets, and determined that Davg = 1.92 × 10−9 m2/s for translation along the basal plane.
4. Conclusions
A double-stranded DNA hexadecamer has been employed herein to investigate the interactions between nucleic acids and pristine graphene sheets, under physiologically relevant conditions ([NaCl] = 134 mM, 310 K, 1 bar). Atomically detailed molecular dynamics calculations were performed, coupled with well-tempered metadynamics, to access the Gibbs thermodynamical free energies associated with DNA/graphene molecular interactions. Simulations showed that adsorption onto graphene occurs rather quickly (≤76 ns), and results in conformational changes and hydrogen bond breakage in the double helix, leading to partial melting of the double strand being highly localized on the DNA termini; this was attributed to strong π–π interactions between the terminal base pairs and the hydrophobic graphene surface.
Free-energy maps obtained, in terms of the double-strand radius of gyration and Watson–Crick H-bonds, revealed that in the presence of pristine graphene, the DNA double helix can undergo partial denaturation caused by a breakdown of the Watson–Crick H bond network, thus resulting in a minimum of 12–13 or even six H bonds responsible for maintaining the double-strand cohesiveness. The ensemble of free-energy minima is located within a region corresponding to an overall radius of gyration of RGyr = 1.35–1.5 nm. Transition between minima is dynamical in nature, which, studied in terms of Fickian apparent diffusivity, suggests that molecular translation (~10−10 m2/s) occurs essentially along the basal plane of graphene. Furthermore, it (i) is of the same order of magnitude as a Dickerson dodecamer moving within the endohedral volume of carbon nanotubes, but (ii) is faster than similar nucleic acids translation along the surface of other 2D solids such as BC3 and C3N (~10−11 m2/s).
The importance of the work being reported arises from the atomically informed knowledge of molecular interactions between nucleic acids and graphene, now becoming available to the scientific community, and is directly connected to the application of graphene in such broad fields as biosensing, nanofluidics, drug delivery, and all other fields where the bionanointerface is at the core. The recent experimental works by Krause and Tinnefeld clearly evidence the importance of understanding π–π stacking at a molecular level, in the context of DNA origami adsorption as studied by fluorescence methods [7,68]. In the context of nanoelectronics, however, a fundamental question remains unanswered: what would happen if the graphene electrical conductivity was to be increased, e.g., either by doping the carbon lattice with p-type dopants or by using other chemical functionalization techniques? If it is true that the DNA termini are hydrophobic, on the other hand, the outer skeleton is heavily charged (hydrophilic) as a consequence of the media-exposed phosphate ions (). This issue remains to be addressed in the future.
Supplementary Materials
The following supporting information can be downloaded from: https://www.mdpi.com/article/10.3390/liquids3020013/s1, Figure S1: B-DNA hexadecamer topology; Figure S2: Initial system setup; Figure S3: Minimum distance between DNA and graphene; and Figure S4: Two-dimensional density maps of bulk DNA.
Author Contributions
F.J.A.L.C. conceptualized the work, designed the numerical experiments, performed calculations and analysed data. F.J.A.L.C. and J.P.B.M. wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work received support from PT national funds (FCT/MCTES, Fundação para a Ciência e Tecnologia and Ministério da Ciência, Tecnologia e Ensino Superior) through projects UIDB/50006/2020 and UIDP/50006/2020. F.J.A.L.C. gratefully acknowledges FCT/MCTES for funding through program DL 57/2016-Norma Transitória (Ref. 654/2018-24), and also for funding the Advanced Computing Project 2021.09623. CPCA on Cirrus-A:INCD. The support of the Portuguese National Grid Initiative (https://www.incd.pt/, accessed on 1 October 2022) is greatly appreciated.
Data Availability Statement
The raw data required to reproduce these findings are available by request to the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef]
- Reina, G.; González-Domínguez, J.M.; Criado, A.; Vázquez, E.; Bianco, A.; Prato, M. Promises, facts and challenges for graphene in biomedical applications. Chem. Soc. Rev. 2017, 46, 4400–4416. [Google Scholar] [CrossRef] [PubMed]
- Pykal, M.; Jurecka, P.; Karlicky, F.; Otyepka, M. Modelling of graphene functionalization. Phys. Chem. Chem. Phys. 2016, 18, 6351–6372. [Google Scholar] [CrossRef]
- Sun, Z.; Fang, S.; Hu, Y.H. 3D Graphene Materials: From Understanding to Design and Synthesis Control. Chem. Rev. 2020, 120, 10336–10453. [Google Scholar] [CrossRef] [PubMed]
- Shankla, M.; Aksimentiev, A. Step-defect guided delivery of DNA to a graphene nanopore. Nat. Nanotechnol. 2019, 14, 858–865. [Google Scholar] [CrossRef]
- Kamińska, I.; Bohlen, J.; Yaadav, R.; Schüler, P.; Raab, M.; Schröder, T.; Zähringer, J.; Zielonka, K.; Krause, S.; Tinnefeld, P. Graphene Energy Transfer for Single-Molecule Biophysics, Biosensing, and Super-Resolution Microscopy. Adv. Mater. 2021, 33, 2101099. [Google Scholar] [CrossRef]
- Fadeel, B.; Bussy, C.; Merino, S.; Vázquez, E.; Flahaut, E.; Mouchet, F.; Evariste, L.; Gauthier, L.; Koivisto, A.J.; Vogel, U.; et al. Safety Assessment of Graphene-Based Materials: Focus on Human Health and the Environment. ACS Nano 2018, 12, 10582–10620. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mat. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Meyyappan, M. (Ed.) Carbon Nanotubes: Science and Applications; CRC Press: London, UK, 2005. [Google Scholar]
- Salmon, L.; Yang, S.; Al-Hashimi, H.M. Advances in the Determination of Nucleic Acid Conformational Ensembles. Ann. Rev. Phys. Chem. 2014, 65, 293–316. [Google Scholar] [CrossRef]
- Cervantes-Salguero, K.; Biaggne, A.; Youngsman, J.M.; Ward, B.M.; Kim, Y.C.; Li, L.; Hall, J.A.; Knowlton, W.B.; Graugnard, E.; Kuang, W. Strategies for Controlling the Spatial Orientation of Single Molecules Tethered on DNA Origami Templates Physisorbed on Glass Substrates: Intercalation and Stretching. Int. J. Mol. Sci. 2022, 23, 7690. [Google Scholar] [CrossRef] [PubMed]
- Bascom, G.; Andricioaei, I. Single-Walled Carbon Nanotubes Modulate the B- to A-DNA Transition. J. Phys. Chem. C 2014, 118, 29441–29447. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Johnson, J.K. Simulation of Adsorption of DNA on Carbon Nanotubes. J. Am. Chem. Soc. 2007, 129, 10438–10445. [Google Scholar] [CrossRef] [PubMed]
- Cruz, F.J.A.L.; De Pablo, J.J.; Mota, J.P.B. Endohedral confinement of a DNA dodecamer onto pristine carbon nanotubes and the stability of the canonical B form. J. Chem. Phys. 2014, 140, 225103. [Google Scholar] [CrossRef]
- Zhao, X. Self-Assembly of DNA Segments on Graphene and Carbon Nanotube Arrays in Aqueous Solution: A Molecular Simulation Study. J. Phys. Chem. C 2011, 115, 6181–6189. [Google Scholar] [CrossRef]
- Cruz, F.J.A.L.; De Pablo, J.J.; Mota, J.P.B. Free energy landscapes of the encapsulation mechanism of DNA nucleobases onto carbon nanotubes. RSC Adv. 2014, 4, 1310–1321. [Google Scholar] [CrossRef]
- Kode, V.R.; Hinkle, K.R.; Ao, G. Interaction of DNA-Complexed Boron Nitride Nanotubes and Cosolvents Impacts Dispersion and Length Characteristics. Langmuir 2021, 37, 10934–10944. [Google Scholar] [CrossRef]
- Iliafar, S.; Mittal, J.; Vezenov, D.; Jagota, A. Interaction of single-stranded DNA with curved carbon nanotube is much stronger than with flat graphite. J. Am. Chem. Soc. 2014, 136, 12947–12957. [Google Scholar] [CrossRef]
- Kode, V.R.; Thompson, M.E.; McDonald, C.; Weicherding, J.; Dobrila, T.D.; Fodor, P.S.; Ao, G. Purification and assembly of DNA-stabilized boron nitride nanotubes into aligned films. ACS Appl. Nano Mat. 2019, 2, 2099–2105. [Google Scholar] [CrossRef]
- Zheng, S.; Sajib, M.S.J.; Wei, Y.; Wei, T. Discontinuous Molecular Dynamics Simulations of Biomolecule Interfacial Behavior: Study of Ovispirin-1 Adsorption on a Graphene Surface. J. Chem. Theory Comput. 2021, 17, 1874–1882. [Google Scholar] [CrossRef]
- Jia, Q.; Yang, C.; Venton, B.J.; DuBay, K.H. Atomistic simulations of dopamine diffusion dynamics on a pristine graphene surface. Chem. Phys. Chem. 2022, 23, e202100783. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Chakrabarti, R. Unzipping of Double-Stranded Ribonucleic Acids by Graphene and Single-Walled Carbon Nanotube: Helix Geometry versus Surface Curvature. J. Phys. Chem. C 2016, 120, 22681–22693. [Google Scholar] [CrossRef]
- Gao, D.; Li, B.; Yang, Y.; Qu, Y.; Li, Y.-Q.; Zhao, M.; Liu, Y.; Liu, X.; Li, W. Defect-Induced Double-Stranded DNA Unwinding on Graphene. J. Phys. Chem. B 2021, 125, 2833–2840. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.; Aksimentiev, A. Water-Compression Gating of Nanopore Transport. Phys. Rev. Lett. 2018, 120, 268101. [Google Scholar] [CrossRef] [PubMed]
- Gu, Z.; Zhao, L.; Ge, C.; Liu, S.; Fang, G.; Chen, S.S.; Yang, Z.; Zhou, R. Facet-regulated adhesion of double-stranded DNA on palladium surfaces. Nanoscale 2019, 11, 1827–1836. [Google Scholar] [CrossRef] [PubMed]
- Gu, Z.; Zhao, L.; Liu, S.; Duan, G.; Perez-Aguilar, J.M.; Luo, J.; Li, W.; Zhou, R. Orientational Binding of DNA Guided by the C2N Template. ACS Nano 2017, 11, 3198–3206. [Google Scholar] [CrossRef]
- Zhao, L.; Gu, Z. Potential Unwinding of Double-Stranded DNA upon Binding to a Carbon Nitride Polyaniline (C3N) Nanosheet. J. Phys. Chem. B 2021, 125, 2258–2265. [Google Scholar] [CrossRef]
- Li, B.; Xie, X.; Duan, G.; Chen, S.H.; Meng, X.-Y.; Zhou, R. Binding patterns and dynamics of double-stranded DNA on the phosphorene surface. Nanoscale 2020, 12, 9430–9439. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, F.; Liu, Y.; Yang, Y.; Qu, Y.; Zhao, M.; Mu, Y.; Li, W. Orientational DNA binding and directed transport on nanomaterial heterojunctions. Nanoscale 2020, 12, 5217–5226. [Google Scholar] [CrossRef]
- Zhou, H.; Xie, Z.-X.; Liang, L.; Zhang, P.; Ma, X.; Kong, Z.; Shen, J.-W.; Hu, W. Theoretical investigation on the adsorption orientation of DNA on two-dimensional MoSe2. Chem. Phys. 2021, 551, 111329. [Google Scholar] [CrossRef]
- Steele, W.A. Molecular Interactions for Physical Adsorption. Chem. Rev. 1993, 93, 2355–2378. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Hodak, M.; Lee, R.S. Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential. Phys. Rev. B 2000, 62, 13104–13110. [Google Scholar] [CrossRef]
- Macke, T.J.; Case, D.A. Modeling Unusual Nucleic Acid Structures. In Molecular Modeling of Nucleic Acids; Leontis, N.B., SantaLucia, J., Eds.; American Chemical Society: Washington, DC, USA, 1998; pp. 379–393. [Google Scholar]
- Wang, J.; Cieplak, P.; Kollman, P.A. How Well Does a Restrained Electrostatic Potential (RESP) Model Perform in Calculating Conformational Energies of Organic and Biological Molecules? J. Comput. Chem. 2000, 21, 1049–1074. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Jorgensen, W.L. Transferable Intermolecular Potential Functions for Water, Alcohols, and Ethers. Application to Liquid Water. J. Am. Chem. Soc. 1981, 103, 335–340. [Google Scholar] [CrossRef]
- Noy, A.; Soteras, I.; Luque, F.J.; Orozco, M. The Impact of Monovalent Ion Force Field Model in Nucleic Acids Simulations. Phys. Chem. Chem. Phys. 2009, 11, 10596–10607. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; Van Der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comp. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Molec. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Nosé, S. A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical Dynamics: Equilibrium Phase-space Distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A Smooth Particle Mesh Ewald Potential. J. Chem. Phys. 1995, 103, 8577–8592. [Google Scholar] [CrossRef]
- Haile, J.M. Molecular Dynamics Simulation: Elementary Methods; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef] [PubMed]
- Sutto, L.; Marsili, S.; Gervasio, F.L. New Advances in Metadynamics. WIREs Comput. Mol. Sci. 2012, 2, 771–779. [Google Scholar] [CrossRef]
- Valsson, O.; Tiwary, P.; Parrinello, M. Enhancing Important Fluctuations: Rare Events and Metadynamics from a Conceptual Viewpoint. Ann. Rev. Phys. Chem. 2016, 67, 159–184. [Google Scholar] [CrossRef]
- Elder, R.M.; Pfaendtner, J.; Jayaraman, A. Effect of Hydrophobic and Hydrophilic Surfaces on the Stability of Double-Stranded DNA. Biomacromolecules 2015, 16, 1862–1869. [Google Scholar] [CrossRef]
- Deighan, M.; Bonomi, M.; Pfaendtner, J. Efficient Simulation of Explicitly Solvated Proteins in the Well-Tempered Ensemble. J. Chem. Theory Comput. 2012, 8, 2189–2219. [Google Scholar] [CrossRef]
- Laio, A.; Gervasio, F.L. Metadynamics: A Method to Simulate Rare Events and Reconstruct the Free Energy in Biophysics, Chemistry and Material Science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar] [CrossRef]
- Cruz, F.J.A.L.; Mota, J.P.B. Conformational Thermodynamics of DNA Strands in Hydrophilic Nanopores. J. Phys. Chem. C 2016, 120, 20357–20367. [Google Scholar] [CrossRef]
- Tribello, G.A.; Bonomi, M.; Branduardi, D.; Camilloni, C.; Bussi, G. PLUMED 2: New feathers for an old bird. Comp. Phys. Comm. 2014, 185, 604–613. [Google Scholar] [CrossRef]
- Consortium, T.P. Promoting transparency and reproducibility in enhanced molecular simulations. Nat. Methods 2019, 16, 670–673. [Google Scholar] [CrossRef] [PubMed]
- Ricci, C.G.; de Andrade, A.S.; Mottin, M.; Netz, P.A. Molecular Dynamics of DNA: Comparison of Force Fields and Terminal Nucleotide Definitions. J. Phys. Chem. B 2010, 114, 9882–9893. [Google Scholar] [CrossRef] [PubMed]
- Naskar, S.; Gosika, M.; Joshi, H.; Maiti, P.K. Tuning the Stability of DNA Nanotubes with Salt. J. Phys. Chem. C 2019, 123, 9461–9470. [Google Scholar] [CrossRef]
- Shiraki, T.; Tsuzuki, A.; Toshimitsu, F.; Nakashima, N. Thermodynamics for the Formation of Double-Stranded DNA–Single-Walled Carbon Nanotube Hybrids. Chem. Eur. J. 2016, 22, 4774–4779. [Google Scholar] [CrossRef]
- Alegret, N.; Santos, E.; Rodriguez-Fortea, A.; Rius, F.X.; Poblet, J.M. Disruption of small double stranded DNA molecules on carbon nanotubes: A molecular dynamics study. Chem. Phys. Lett. 2012, 525, 120–124. [Google Scholar] [CrossRef]
- Franklin, R.E.; Gosling, R.G. Molecular Configuration in Sodium Thymonucleate. Nature 1953, 171, 740–741. [Google Scholar] [CrossRef]
- Santosh, M.; Panigrahi, S.; Bhattacharyya, D.; Sood, A.K. Unzipping and Binding of Small Interfering RNA with Single Walled Carbon Nanotube: A platform for Small Interfering RNA Delivery. J. Chem. Phys. 2012, 136, 65106. [Google Scholar] [CrossRef]
- Agnihotri, S.; Zheng, Y.; Mota, J.P.B.; Ivanov, I.; Kim, P.C. Practical Modeling of Heterogeneous Bundles of Single-Walled Carbon Nanotubes for Adsorption Applications: Estimating the Fraction of Open-Ended Nanotubes in Samples. J. Phys. Chem. C 2007, 111, 13747–13755. [Google Scholar] [CrossRef]
- Karger, J. Transport Phenomena in Nanoporous Materials. Chem. Phys. Chem. 2015, 16, 24–51. [Google Scholar] [CrossRef] [PubMed]
- Cruz, F.J.A.L.; Mota, J.P.B. Dynamics of B-DNA in Electrically Charged Solid Nanopores. J. Phys. Chem. C 2017, 121, 16568–16575. [Google Scholar] [CrossRef]
- Balducci, A.; Mao, P.; Han, J.; Doyle, P.S. Double-Stranded DNA Diffusion in Slitlike Nanochannels. Macromolecules 2006, 39, 6273–6281. [Google Scholar] [CrossRef]
- Krause, S.; Ploetz, E.; Bohlen, J.; Schuler, P.; Yaadav, R.; Selbach, F.; Steiner, F.; Kaminśka, I.; Tinnefeld, P. Graphene-on-Glass Preparation and Cleaning Methods Characterized by Single-Molecule DNA Origami Fluorescent Probes and Raman Spectroscopy. ACS Nano 2021, 15, 6430–6438. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).