An Ab Initio Investigation of the Hydration of Tin(II)

Abstract

The structure of tin(II) is not well known in aqueous solution. The energies, structures, and vibrational frequencies of [Sn(H₂O)_n,]²⁺ n = 0–9, 18 have been calculated at the Hartree–Fock and second order Møller–Plesset levels of theory using the CEP, LANL2, and SDD effective core potentials in combination with their associated basis sets, or with the 6-31G* and 6-31+G* basis sets. The tin–oxygen distances and totally symmetric stretching frequency of the aquatin(II) ions were compared with each other, and with solution measurements where available.

1. Introduction

The structure of some metal ions in solution remain elusive [1,2]. Their toxicity to man and the environment is dependent on their oxidation state and speciation, which often depends on pH and the presence of counterions that solubilize the metal by complex formation. Computational chemistry can be useful in supporting and rationalizing proposed speciation models. However, for elements of high atomic number, a drawback is that there are typically few all-electron basis sets that can be used, and relativistic effects can play an important role. One workaround is to use effective core potentials, which replace the explicit description of core electrons by a core potential, which are then paired with basis sets describing the outermost electrons. Previously, some common effective core potentials for the aqua complexes of the heavy metals mercury(II) and thallium(III) (valence electron configuration 5d¹⁰) were benchmarked [3]. This work was extended to lead(II) with a valence electron configuration of 6s²5d¹⁰ [4]. We expand our work now to tin(II), which has a valence electron configuration of 5s²4d¹⁰. The presence of the ns² subshell, as with lead(II), will be shown to have a pronounced effect on the structures compared to those without it. Hemidirected structures (which tend to be favored at lower coordination numbers) have ligands that are not symmetrically distributed around the central ion, whereas holodirected structures have a symmetrical distribution.

In the gas-phase, it was reported that tin(II), lead(II), and mercury(II) easily underwent a proton transfer reaction and that the only species observed in the mass spectra were the deprotonated MOH⁺(H₂O)_n−1 ions, not the M(H₂O)_n²⁺ ions. These ions have anomalously high acidity in the gas phase as well as the solution phase. An ab initio study was carried out to rationalize this behavior, with a focus on the pathways to deprotonation [5]. In solution, it is believed that the relevant species are Sn²⁺ (aq) (pH < 2), SnOH⁺ (aq), Sn₂(OH)₂²⁺ (aq), Sn₃(OH)₄²⁺ (aq), Sn(OH)₂⁰ (aq) (pH = 5–8), and Sn(OH)₃⁻ (aq) (pH > 10) [2]. The polynuclear species form at higher concentrations, and the water content cannot be determined through potentiometric means.

The tin(II) ion in aqueous solution has been characterized by an X-ray study of a ~3 mol/L solution of the perchlorate salt [6]. The radial distribution curves showed peaks at 1.4 Å (Cl–O), 2.3 Å (O…O and Sn–O), 2.8 Å (Sn–O), 3.6 Å (Sn–Sn), and 4.2 Å. (Sn…O). Some hydrolyzed solutions were also examined, and the largest variation was in the 3.6 Å and 4.2 Å peaks, which suggested a greater degree of clustering as the hydrolysis increased. Essentially the same unhydrolyzed solution was studied by EXAFS [7], in which a Sn–O distance of 2.2–2.3 Å with four water molecules was found. They also reanalyzed the data of [6]. Regarding the hydrolysis products, potentiometric titrations suggested the existence of the species Sn₃(OH)₄²⁺(aq), in addition to Sn₂(OH)₂²⁺(aq) and SnOH⁺(aq) [8]. The crystal structure of the hydrolysis product Sn₃O(OH)₂SO₄, which is potentiometrically equivalent to Sn₃(OH)₄²⁺(aq), has been determined and shown to contain the discrete [Sn₃O(OH)₂]²⁺ ion [9,10].

A QM/MM-MD study has also been carried out on the tin(II) ion in aqueous solution [11]. It was found that the Sn–O distance peaked at 2.5 Å, with a shoulder at 2.65 Å. Gaussian fitting indicated peaks at 2.45 Å and 2.75 Å. A coordination number of eight was found. The power spectrum of the Sn–O stretching suggested peaks at 85 and 208 cm⁻¹.

2. Materials and Methods

Calculations were performed using Gaussian 98 [12]. This program version was the first to allow the analytical frequency calculation of molecules in which core electrons are described by effective core potentials (ECPs), and thus, many variants of these were tried. The MP2 calculations use the frozen core approximation. A stepping-stone approach was used for geometry optimization, in which the geometries at the levels HF/CEP-4G, HF/CEP-31G*, HF/CEP-121G*, HF/LANL2MB, HF/LANL2DZ, and HF/SDD were sequentially optimized. For minimum energy structures, the MP2/CEP-31G* and MP2/CEP-121G* calculations were also performed. Calculations were also carried out using the 6-31G* and 6-31+G* basis sets on the atoms of the water molecules (5d) with an effective core potential and basis set on the metal ion (denoted as ECP+6-31G* or 6-31+G*). For shorthand, we denoted the mixed basis sets as follows: CEP-121G* on Sn and 6-31G* on O, H, as basis set A; LANL2DZ on Sn and 6-31G* on O, H, as basis set B; and SDD on Sn and 6-31G* on O, H, as basis set C. The corresponding basis sets with diffuse functions were indicated by adding a “+” to the basis set name. Default optimization specifications were normally used. After each level, where possible, a frequency calculation was performed at the same level, and the resulting Hessian was used in the following optimization. Z-matrix coordinates constrained to the appropriate symmetry were used as required to speed up the optimizations. Since frequency calculations are done at each level, any problems with the Z-matrix coordinates would manifest themselves by giving imaginary frequencies corresponding to modes orthogonal to the spanned Z-matrix space. The Hessian was evaluated at the first geometry (opt = CalcFC) for the first level in a series in order to aid geometry convergence. We note that, for the heavy elements only, the three different CEP basis sets are equivalent (CEP-121G*) but differ for the oxygen and hydrogen atoms. We also note that the choice of core electrons defining the pseudopotential depends on the specific core potential (CEP and LANL2, [Kr]4d¹⁰; SDD, [Ar]3d¹⁰). In some cases, Gaussian 03 [13] and Gaussian 16 [14] were used to correct errors and omissions.

In many cases to follow, the symmetry of the minimum-energy complexes was the same as those previously found for bismuth [15]. To confirm these results, starting with high symmetry structures, systematic desymmetrization along the various irreducible representations was carried out [16,17]. We did not employ an implicit solvation model or additional electron correlation treatments for reasons described previously in [4]. The energies of all structures are found in Table S1.

3. Results

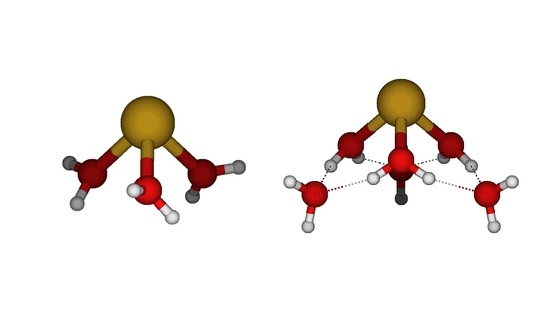
3.1. A Survey of Structures

Tin(II), as a lighter element in the same group as lead(II), might be expected to show similar properties. The point group symmetry for mono- through hexaaquatin(II) was usually found to be C_2v, C₂, C₃, C₂, C_s, and C₃. The diaquatin(II) species, like lead, ascends in symmetry to a planar C_2v structure at HF/LANL2MB. The tetraaquatin(II) species has C_2v symmetry at HF/LANL2DZ and C_s symmetry at HF/LANL2MB. The pentaaqua species has C₂ symmetry at HF/LANL2MB. At all levels for the pentaaqua species, if the pentacoordinate [5+0] species exists, it is competitive in energy with the [4+1], and the most stable form is dependent on the level of theory. For the hexaaquatin(II), the C₃ [3+3] form was always more stable than the C₃ [6+0] form, which occasionally had imaginary frequencies or reverted to the [3+3] form. We did not find stable hepta-, octa-, or enneaaquatin(II) structures. At the HF levels, the [6+12] form always contained at least an imaginary T mode.

The results of the systematic desymmetrization procedure [16] for aquatin(II) are as follows (see Figure 1 and Figure S1):

• The monoaquatin(II) remained as C_2v at all levels;
• The most stable diaquatin(II) remained as the bent C₂ at all levels except HF/LANL2MB (C_2v planar). The linear holodirected D_2d structure was approximately 50 kJ/mol higher in energy, but the unstable bent C_s structure was only slightly higher in energy (<1 kJ/mol for nonminimal basis sets). All attempts to generate a [1+1] structure instead resulted in proton transfer to give a SnOH⁺ + H₃O⁺ complex, which was 25–40 kJ/mol higher in energy;
• The most stable triaquatin(II) remained as the pyramidal C₃ at all levels. The two pyramidal C_3v structures were 12–25 kJ/mol higher in energy, whereas the planar holodirected D_3h and D₃ structures were 60–90 kJ/mol higher in energy. The stable [2+1] C_2v structure was 25–50 kJ/mol higher in energy;
• The most stable tetraaquatin(II) was usually the see-saw C₂, but it could be the C_2v #3 (HF/LANL2DZ, HF/B+) or C_s (HF/LANL2MB). The C_2v #3 was slightly higher in energy (<2 kJ/mol), with the other C_2v structures being higher (15–25 kJ/mol). The holodirected D_2d #1, #2, S₄, and D₂ structures were much higher in energy (50–80 kJ/mol). The C_s #2 [3+1] structure was always competitive in energy, and usually lower, than the tetracoordinate structure;
• The most stable pentaaquatin(II) was the square pyramidal C_s (if it exists), which is closely related to the C_2v #1 structure (<3 kJ/mol). The other three C_2v structures were ~25 kJ/mol higher in energy. The stable [4+1] and [3+2] structures were competitive in energy, and sometimes lower, depending on level of theory;
• The most stable hexaaquatin(II) was the distorted octahedral C₃ (if it exists). The octahedral T_h structure was ~30 kJ/mol higher in energy;
• Of the 16 different C_2v heptaaquatin(II) structures tried, none were stable, and either possessed imaginary modes or dissociated to a [6+1], [5+2], or [4+3] structure. Structures #1–#4, and #11, always dissociated. Structures #5–#8, and #16, usually remained as 7-coordinates. The remaining structures usually dissociated at most levels. Of the 7-coordinate C_2v structures, #8 and #16 were the lowest in energy. All of the 7-coordinate structures dissociated at HF/LANL2MB. Upon desymmetrization of the remaining 7-coordinate C_2v structures to C₂, nearly all dissociated to [6+1], [5+2], or [4+3] structures. The only exceptions, C₂ #10 and #15 at HF/CEP-31G*, possessed imaginary B modes, of which one corresponds to a water molecule moving to the second hydration shell;
• Of the octaaquatin(II) structures, two D_4h and two D_4d structures (point group order h = 16) were first examined. Multiple imaginary modes were present;

        ○

  For the D_4d #1 and #2 structures, desymmetrization along the A₂ imaginary mode gave the same S₈ structure; along the B₁ imaginary mode, they gave the same D₄ #2 structure; along the B₂ imaginary mode, they gave the C_4v #1 and #2 structures; and along the imaginary E₁ mode, they gave the same C_2v #1 structure (via C_s);

        ○

  For the D_4h #1 and #2 structures, desymmetrization along the A_1u imaginary mode gave the D₄ #2 structure found before; along the A_2g imaginary mode, they gave the same C_4h #1 structure; along the A_2u imaginary mode, they gave the C_4v #3 [4+4] and #4 structures; along the B_2g imaginary mode (D_4h #1), the D_2h #1 structure ascended in symmetry to D_4h #2; along the B_1g (D_4h #2) imaginary mode, they gave the D_2h #2 structure; along the B_1u imaginary mode, they gave the same D_2d #1 structure; along the B_2u mode, they gave the D_2d #2 and #4 structures, respectively; and along the E_g and E_u modes, they gave D_2h #3 and #4 (via C_2h and C_2v);

  

Examination of lower symmetry structures (h = 8) gave the following results:

○

For the S₈ #1 structure, all E₁ and B imaginary modes corresponded to the expulsion of water molecules to the second hydration shell. Desymmetrization along the B mode gave the [4+4] C₄;

○

For the D₄ #2 structure, the E mode corresponded to the expulsion of water molecules to the second hydration shell. Desymmetrization along the A₂ mode gave either a [4+4] C₄ structure or a C₄ #2 structure, whereas along the B₁ mode, it gave the D₂ #1 structure;

○

For the C_4h #1 structure, the imaginary E_u mode corresponded to the expulsion of two water molecules. Desymmetrization along the imaginary A_u mode for the most part gave either a [4+4] C₄ structure or ascended in symmetry to S₈; along the imaginary B_u mode at HF/CEP-4G and HF/LANL2MB, it gave a D_2d #5 and S₄ structure, respectively. This D_2d #5 structure was then rerun at all levels;

○

For the D_2d structures, desymmetrization along an A₂ imaginary mode would give an S₄ structure; along a B₁ imaginary mode, they gave a D₂ structure; along a B₂ imaginary mode, they gave a C_2v structure; along an E mode, they gave either a C₂ or C_s structure. Along the A₂ mode, an S₄ #2 or #4 structure typically resulted, or ascension in symmetry to the D_2d #5; along the B₁ mode, there was usually ascension to D₄ #2; along the B₂ mode, there was dissociation to a [6+2] or [4+4] structure; and along an E mode, dissociation would occur;

○

For the D_2h structures, desymmetrization along the imaginary A_u mode would give a D₂ structure, and along the imaginary B_ng modes, a C_2h structure was given. In all cases, these desymmetrized, and most ascended in symmetry to structures already found (D₂ #5, D₄ #2, C_4h #1). The B_nu modes corresponded to the expulsion of water molecules from the first hydration sphere;

  

Examination of lower symmetry structures (h = 4) gave the following results:

○

For the C_2v structures, desymmetrization along the A₂ mode would give a C₂ structure, and along the B₁ or B₂ mode, different C_s structures were given. For the C_2v structures, at least one of the imaginary B modes in each structure corresponded to dissociation to a [6+2] structure, whereas desymmetrization along the A₂ mode led to a [4+4] or [4+2+2] structure;

○

For the C₄ and S₄ structures, the imaginary E mode corresponded to dissociation to a [6+2] structure, whereas desymmetrization along the B mode to give a C₂ structure resulted in dissociation;

○

For the D₂ structures, at least one of the imaginary B₂ or B₃ modes corresponded to dissociation to a [6+2] structure, whereas desymmetrization along the B₁ mode to give a C₂ structure resulted in dissociation to a [6+2] or [4+4];

  

Based on these results, we must conclude that a stable 8-coordinate octaaquatin(II) ion cannot exist.

• Of the enneaaquatin(II) structures, four D_3h structures (point group order h = 12) were first examined. Multiple imaginary modes were present. Desymmetrization along the A₁” mode would yield D₃ structures; along A₂′, C_3h structures were given; and along A₂”, C_3v structures were given. A common D₃ #1 structure was found for most, and in some cases gave an additional [6+3] structure. Two possible C_3h structures were found, and in some cases gave an additional [6+3] structure. Four possible C_3v structures were found, and in some cases gave additional [6+3] structures. At least one of the degenerate modes corresponded to the expulsion of water molecule(s) from the inner coordination shell;

        ○

  For the D₃ structure, desymmetrization along the A₂ mode gave a C₃ #1 [6+3] structure. At least one of the E modes corresponded to the loss of water molecules from the first hydration shell.

        ○

  For the C_3h structures, desymmetrization along the A” mode gave either the C₃ #1 [6+3] structure above or a new C₃ #3 [6+3] structure (or occasionally [3+3+3]). At least one of the E modes corresponded to the loss of water molecules from the first hydration shell.

        ○

  For the C_3v structures, desymmetrization along the A₂ mode gave one of the C₃ [6+3] structures (or occasionally [3+3+3]) found above. At least one of the E modes corresponded to the loss of water molecules from the first hydration shell.

  

Based on these results, we must conclude that a stable 9-coordinate enneaaquatin(II) ion cannot exist.

To summarize these results, by using the systematic desymmetrization procedure, we have found stable structures for the mono- through hexaaquatin(II) complexes, and we have shown that hepta-, octa-, and enneaaqua structures do not exist on the potential energy surface. The hexaaquatin(II) C₃ structure is only stable at HF/CEP-31G*, HF/CEP-121G*, and MP2/CEP-31G*. The pentaaquatin(II) C_s structure is not stable at HF/CEP-4G, HF/LANL2DZ, and HF/SDD. In most cases, for systems with more than three water molecules, the most stable structure on the potential energy surface is tricoordinate, with the remaining water molecules in the second hydration sphere (the main exceptions being HF/CEP-31G* and HF/CEP-121G*). These results suggest that tin(II) would be tricoordinate trigonal pyramidal in an aqueous solution.

3.2. The Sn–O Distance

The average Sn–O distance as a function of coordination number is plotted in Figure 2 for all of the levels studied. The Sn–O distance always lengthened following an increase in the coordination number. We can see some gaps for n = 4–6 at some levels where no local minimum existed. The Sn–O distance using the minimal basis HF/LANL2MB was shorter than the other levels at the same hydration number by 0.1–0.3 Å, which tended to cluster together. The results using CEP-31G* were nearly coincidental with those of CEP-121G*. For all levels, there was a pronounced change in slope at n = 3. Within the cluster noted above, the Sn–O distance using the SDD basis set/pseudopotential on Sn (HF/SDD, HF/C, HF/C+) tended to be the longest (n = 1–5, 2.20–2.50 Å), whereas those using the LANL2DZ basis set/pseudopotential on Sn (HF/LANL2DZ, HF/B, HF/B+) were the shortest. This differed for lead, where the CEP basis set/pseudopotential tended to be the shortest [4]. The effect of the basis set/pseudopotential combination was more important than the presence or absence of correlation (HF vs. MP2). Metal–oxygen bond lengths to those oxygens making a smaller angle to the principal symmetry axis were longer, as was noted previously for aqualead(II) [4].

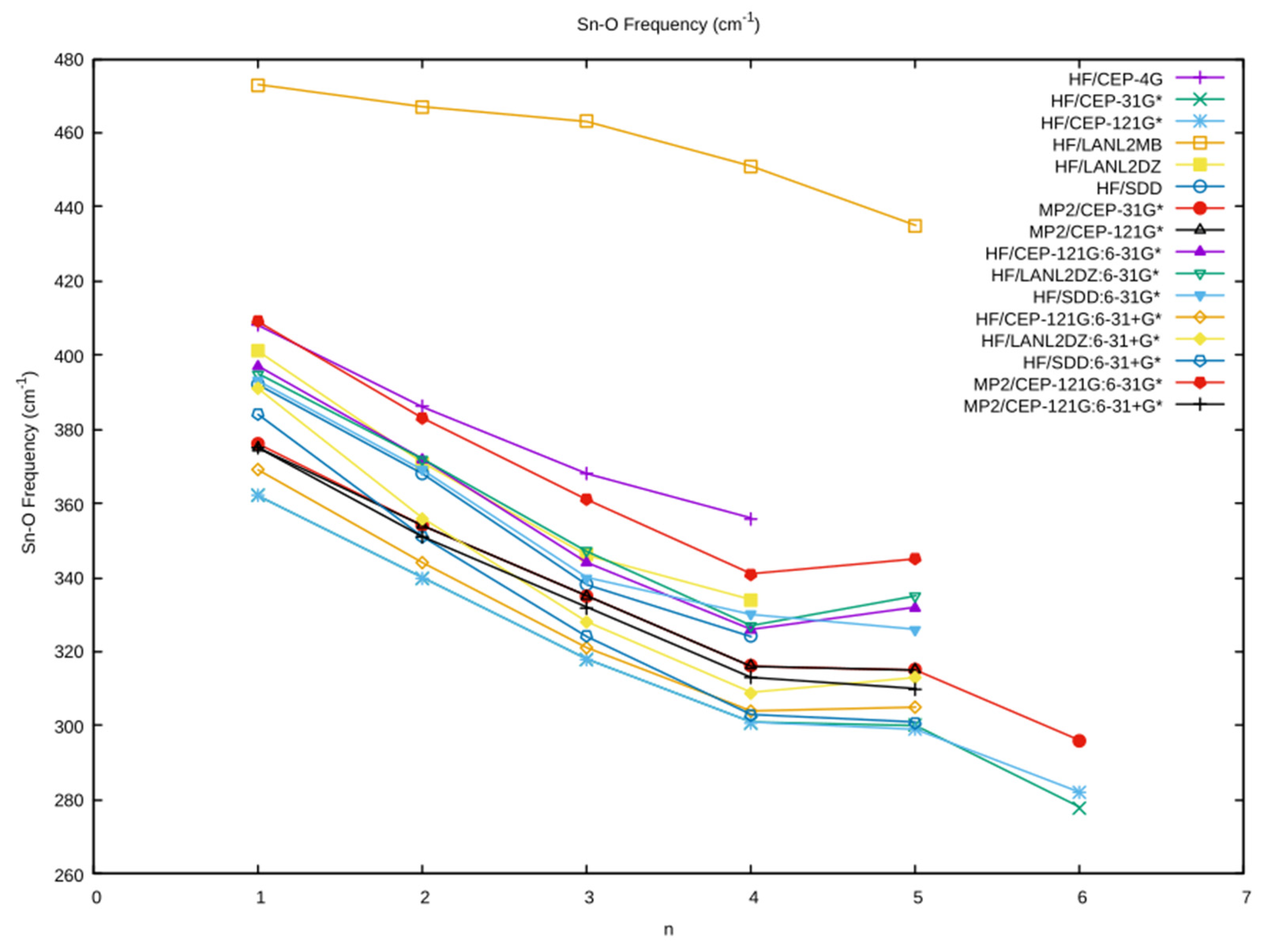
3.3. The Sn–O Vibrational Frequency

The vibrational frequency of the totally symmetric Sn–O stretch as a function of coordination number is plotted in Figure 3. As expected, the frequencies at the minimal basis HF/LANL2MB were much higher than the other levels which clustered together. For the most part, the vibrational frequency decreased as a function of hydration number. There was a levelling effect upon going from n = 4 to n = 5, because, for the square pyramidal n = 5, the character of the mode changed to be predominantly a Sn–O_apex stretch. The results using CEP-31G* were nearly coincidental with those of the CEP-121G*, and the MP2 values were ~15 cm⁻¹ higher than the HF values. The addition of diffuse functions (A+ vs. A) lowered the vibrational frequency by ~30 cm⁻¹, and correlation increased it by ~5–15 cm⁻¹. This was also true for the mixed basis set calculations. All other things being equal, the LANL2DZ frequencies were the highest, and the CEP frequencies were the lowest, with the SDD frequencies falling in the middle. The inverse relationship between average bond length and symmetric stretching frequency can be clearly seen.

4. Discussion

Because of the lack of experimental data on aquatin(II) complexes, certainty regarding the structure and vibrational frequencies of the aquatin(II) is lacking. We may compare a series of structures, such as [n+0] and [(n−m)+m]. For a hydration number of three, the tricoordinate [3+0] is always more stable than the [2+1] structure. For a hydration number of four, the tricoordinate [3+1] is usually more stable than [4+0], except for HF/CEP-31G* and HF/CEP-121G*, but they are competitive in energy. For a hydration number of five, the [4+1] and [3+2] structures are usually more stable than the [5+0], except for HF/CEP-31G* and HF/CEP-121G*, but all are still competitive in energy. For a hydration number of six, the [4+2] structure seems to be the most stable, with the [3+3] structure being competitive in energy. The picture emerging is that of a variable coordination number between three and six, with three (trigonal pyramidal) and four (see-saw) being the most likely.

We recently became aware [18] of a crystal structure determination of an aquatin(II) ion in the compound tin(II) perchlorate trihydrate [19]. The Sn–O distance was reported to be 2.201(7) Å. Examination of Figure 2, at n = 3, and

Table 1. Bond lengths (Å) of triaquatin(II). The theoretical levels A, B, and C are described in the text. HF = Hartree-Fock, MP2 = second-order Møller-Plesset, Expt. = experiment, XRD = X-ray diffraction, EXAFS = Extended X-ray absorption fine structure, LAXS = Large angle X-ray scattering.

Basis Set/Pseudopotential	HF	MP2
CEP-4G	2.2098	n/c
CEP-31G*	2.3001	2.2978
CEP-121G*	2.2963	2.2964
LANL2MB	2.0616	n/c
LANL2DZ	2.2202	n/c
SDD	2.2898	n/c
A	2.2624	2.2606
B	2.2397	n/c
C	2.3005	n/c
A+	2.2797	2.2887
B+	2.2610	n/c
C+	2.3241	n/c
Expt. XRD [19]	2.201(7)
Expt. XRD [20]	2.208(9)
Expt. EXAFS xtal. [20]	2.209(3)
Expt. EXAFS soln. [20]	2.219(3)
Expt. LAXS soln. [20]	2.206(2)

suggest that, if crystal packing forces are negligible, then the MP2/A+, HF/LANL2DZ, and HF/B+ levels give excellent agreement with the experiment. This result was confirmed by Persson and co-workers, who obtained 2.208(9) Å and obtained EXAFS results for the crystal and solution Sn–O distance of 2.209(3) and 2.219(3) Å, respectively, which quite importantly shows that the solution structure of tin(II) is the same as the solid. The LAXS measurement gives, at 2.206(2) Å, nearly the same value for the Sn–O distance [20].

The vibrational frequency for the n = 3 structure lay in the range 320–370 cm⁻¹. The effect of a second hydration sphere should be to increase this value somewhat. For most octahedral metal ions that we have previously examined, a rough rule of thumb is that, upon including a second hydration sphere, the vibrational frequency increases by 20q cm⁻¹, where q is the total charge on the octahedral ion. For tin(II), comparison of the vibrational frequencies of [Sn(H₂O)₃]²⁺ C₃, and [Sn(H₂O)₃]²⁺·(H₂O)₃ C_3v revealed a large ~85 cm⁻¹ increase in the vibrational frequency. This suggests that tin(II) should have an observable band in the isotropic Raman spectra corresponding to the totally symmetric stretching motion in the range of 400–450 cm⁻¹.

5. Conclusions

The common CEP, LANL2DZ and SDD pseudopotentials were paired with various basis sets to study the hydrated tin(II) ion. The calculations using minimal basis sets performed poorly. For the most part, the calculated structures were consistent with recent experimental results of a tricoordinate trigonal pyramidal hemidirected aqua complex. The careful use of symmetry can be used to both guide the search for new structures and also to rule out structures.