Machine Learning vs. Langmuir: A Multioutput XGBoost Regressor Better Captures Soil Phosphorus Adsorption Dynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. Laboratory Analysis
2.2. P Sorption Capacity
2.3. Machine Learning
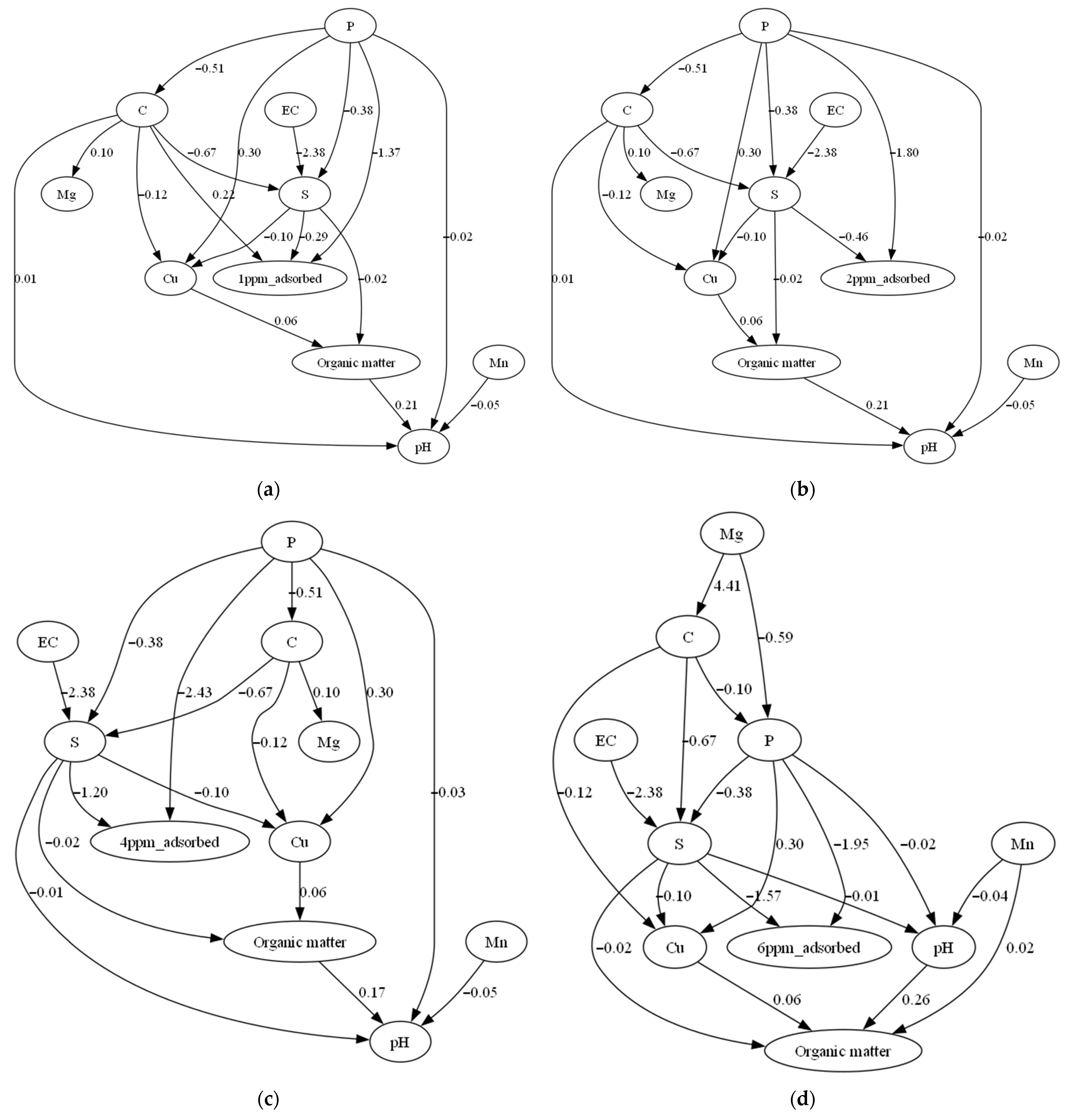
2.4. Causal Discovery
2.5. Comparison of the Langmuir Isotherms and the Multi-Output XGBoost Regressor on a Large Soil Dataset
3. Results
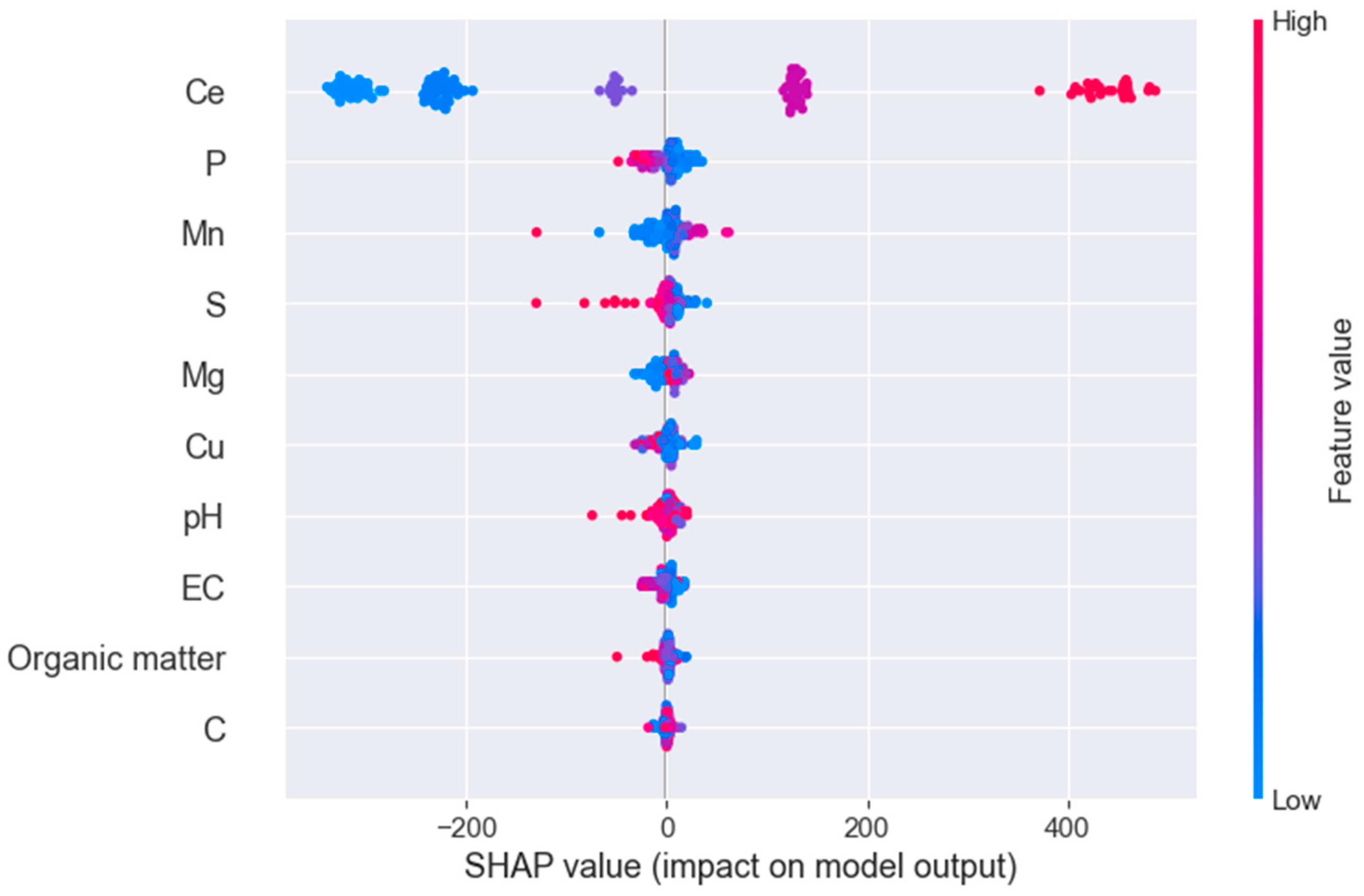
3.1. Feature Engineering
3.2. Causal Inference
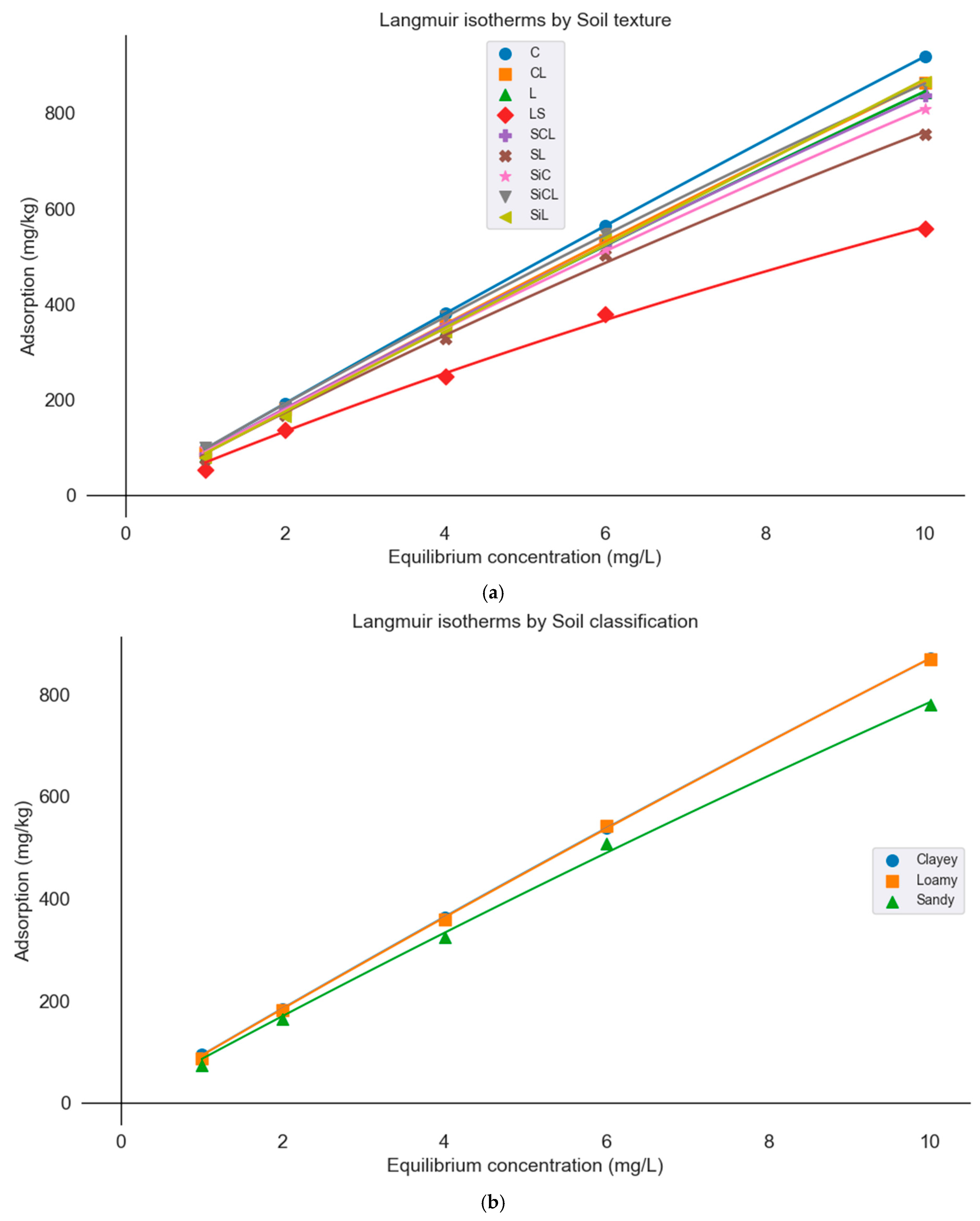
3.3. Langmuir Equations
3.4. Multiple Linear Regression Equations
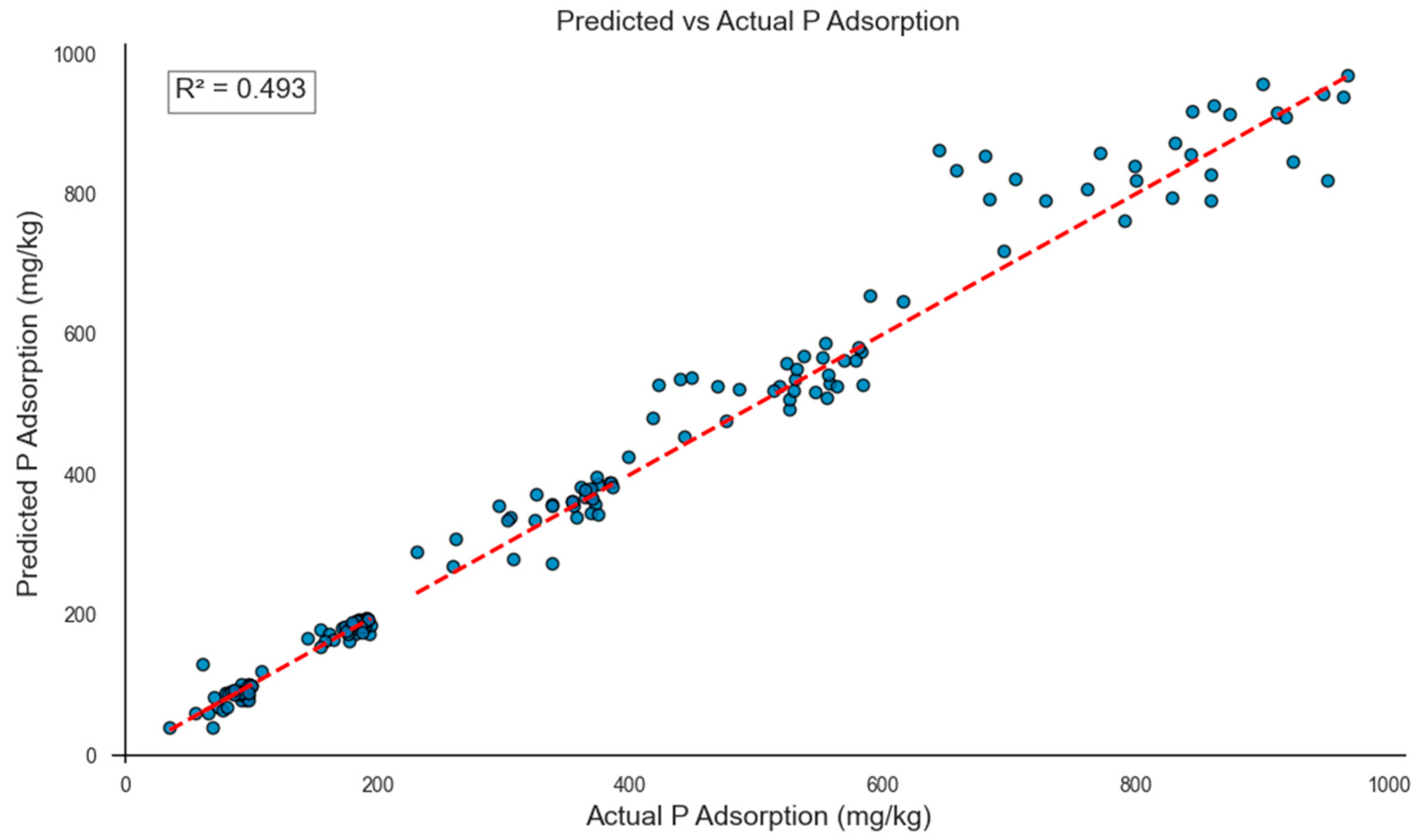
3.5. Multi-Output XGBoost Model Performance
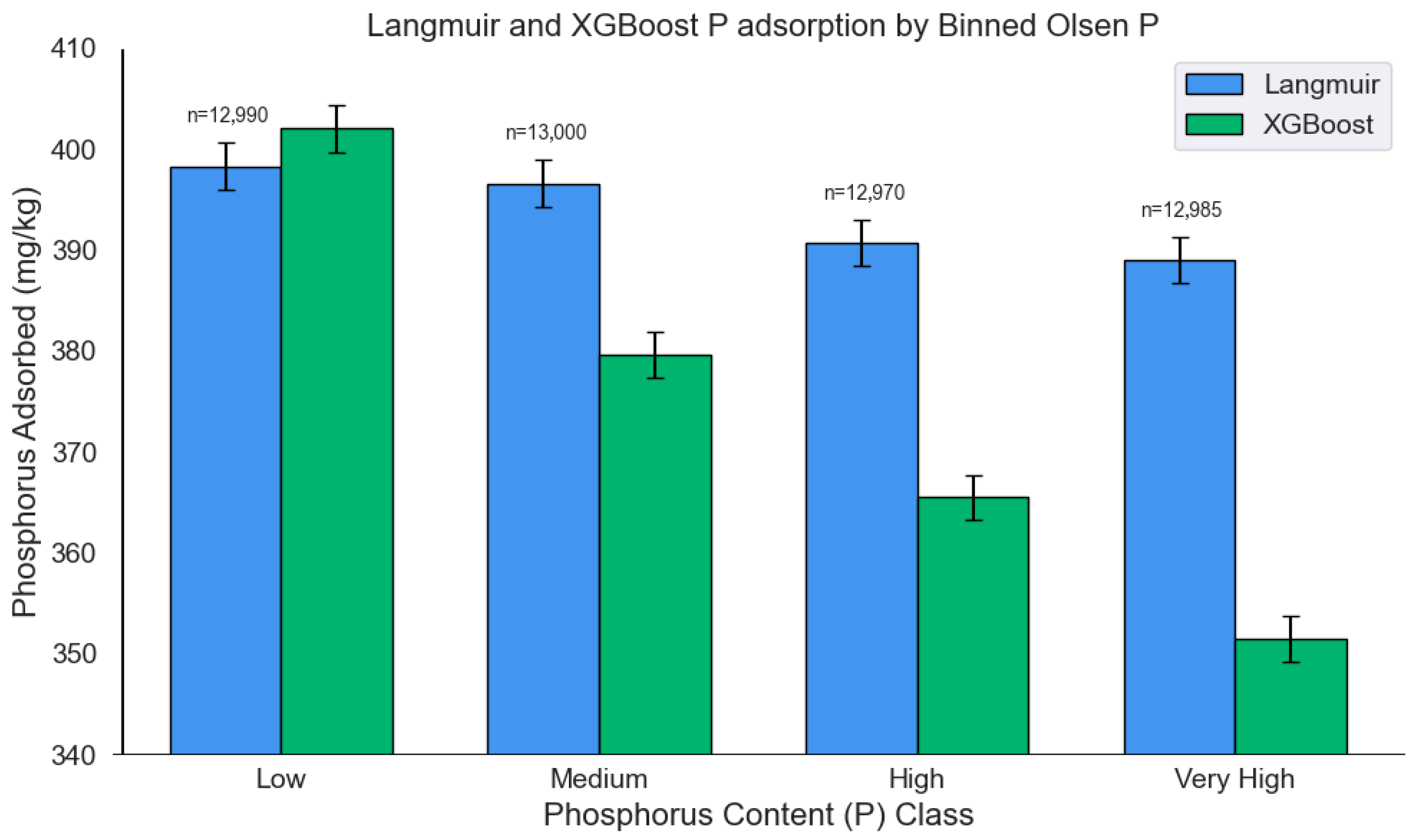
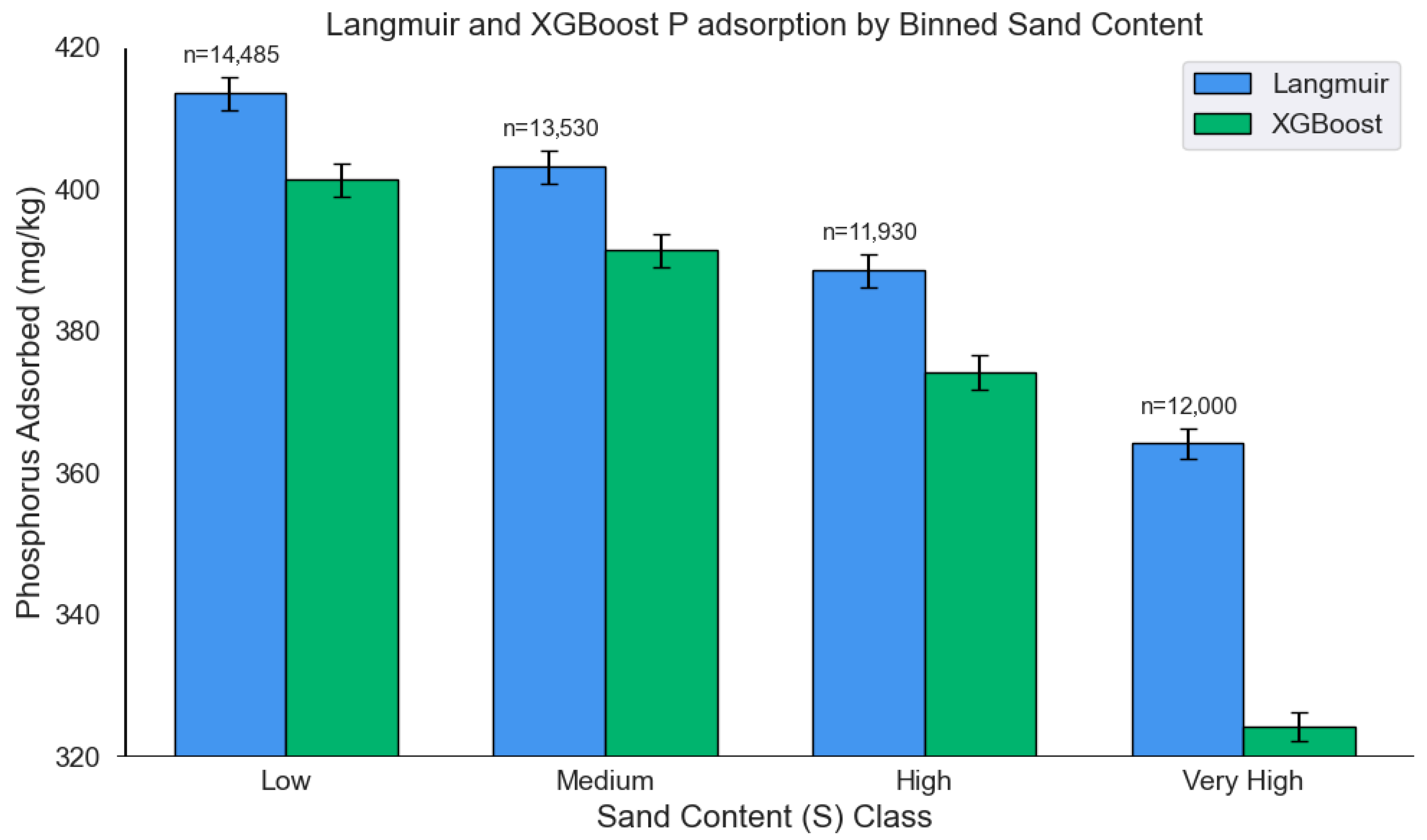
3.6. Performance of the Multi-Output XGBoost Model and Langmuir Isotherms on an Extended Soil Dataset
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| P | Phosphorus |
| RFE | Recursive Feature Elimination |
| MAE | Mean Absolute Error |
| DirectLiNGAM | Direct Linear Non-Gaussian Acyclic Model |
| DAG | Directed Acyclic Graph |
Appendix A
| Authors (Year) | Model Used | Key Findings |
| Olsen & Watanabe (1957) [12] | Langmuir, Freundlich | Introduced Langmuir model to estimate P adsorption maxima in soils. |
| Helyar et al. (1976) [13] | Langmuir | Studied phosphate adsorption behavior on Al oxides. |
| Nair et al. (1984) [31] | Standardized Langmuir protocol | Developed a standardized interlaboratory method for determining P sorption using Langmuir modeling. |
| Barrow (2008) [16] | Freundlich, Mechanistic models | Proposed improved description of sorption curves beyond isotherms. |
| Hussain et al. (2002) [47] | Langmuir, Freundlich | Compared isotherm performance under saline-sodic conditions. |
| Del Bubba et al. (2003) [20] | Langmuir | Estimated P adsorption maximum in sand filters using Langmuir. |
| Heredia & Fernández Cirelli (2007) [9] | Langmuir | Linked high P application to environmental risk based on sorption capacity. |
| Bolster & Sistani (2009) [14] | Langmuir | Investigated P sorption from animal manures; showed variability depending on manure type and application. |
| Dossa et al. (2008) [21] | Langmuir, Freundlich | Assessed impact of shrub residues on P sorption and desorption. |
| Lair et al. (2009) [48] | Langmuir | Investigated P sorption–desorption along soil weathering gradient. |
| Rossi et al. (2012) [49] | Langmuir (SWAT integration) | Tested Langmuir model performance within SWAT under high P conditions. |
| Dari et al. (2015) [19] | Langmuir, Freundlich | Proposed simplified method for estimating isotherm parameters. |
| Mihoub et al. (2016) [3] | Langmuir | Evaluated P sorption in calcareous soils and its role in sustainable P fertilizer management. |
| Yang et al. (2019) [44] | Freundlich | Showed influence of organic matter on P adsorption and desorption. |
| Wang et al. (2022) [30] | Modified Langmuir | Introduced a modified Langmuir equation to account for organic material influence on P adsorption in Mollisols. |
| Zawadzka et al. (2024) [18] | Langmuir | Applied Langmuir to model phosphate sorption in engineered media. |
References
- Kirkby, E.A.; Johnston, A.E. Soil and Fertilizer Phosphorus in Relation to Crop Nutrition. In The Ecophysiology of Plant-Phosphorus Interactions; White, P.J., Hammond, J.P., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 177–223. ISBN 978-1-4020-8435-5. [Google Scholar]
- Marschner, P. Marschner’s Mineral Nutrition of Higher Plants; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Mihoub, A.; Daddi Bouhoun, M.; Saker, M. Phosphorus Adsorption Isotherm: A Key Aspect for Effective Use and Environmentally Friendly Management of Phosphorus Fertilizers in Calcareous Soils. Commun. Soil Sci. Plant Anal. 2016, 47, 1920–1929. [Google Scholar] [CrossRef]
- Sgouras, I.D.; Tsadilas, C.D.; Barbayiannis, N.; Danalatos, N. Physicochemical and Mineralogical Properties of Red Mediterranean Soils from Greece. Commun. Soil Sci. Plant Anal. 2007, 38, 695–711. [Google Scholar] [CrossRef]
- Liu, D.; Xiao, Z.; Zhang, Z.; Qiao, Y.; Chen, Y.; Wu, H.; Hu, C. The Crop Phosphorus Uptake, Use Efficiency, and Budget under Long-Term Manure and Fertilizer Application in a Rice–Wheat Planting System. Agriculture 2024, 14, 1393. [Google Scholar] [CrossRef]
- Amarh, F.; Voegborlo, R.B.; Essuman, E.K.; Agorku, E.S.; Tettey, C.O.; Kortei, N.K. Effects of Soil Depth and Characteristics on Phosphorus Adsorption Isotherms of Different Land Utilization Types: Phosphorus Adsorption Isotherms of Soil. Soil Tillage Res. 2021, 213, 105139. [Google Scholar] [CrossRef]
- Oehl, F.; Oberson, A.; Tagmann, H.U.; Besson, J.M.; Dubois, D.; Mäder, P.; Roth, H.-R.; Frossard, E. Phosphorus Budget and Phosphorus Availability in Soils under Organic and Conventional Farming. Nutr. Cycl. Agroecosyst 2002, 62, 25–35. [Google Scholar] [CrossRef]
- Iatrou, M.; Papadopoulos, A.; Papadopoulos, F.; Dichala, O.; Psoma, P.; Bountla, A. Determination of Soil Available Phosphorus Using the Olsen and Mehlich 3 Methods for Greek Soils Having Variable Amounts of Calcium Carbonate. Commun. Soil Sci. Plant Anal. 2014, 45, 2207–2214. [Google Scholar] [CrossRef]
- Heredia, O.S.; Fernández Cirelli, A. Environmental Risks of Increasing Phosphorus Addition in Relation to Soil Sorption Capacity. Geoderma 2007, 137, 426–431. [Google Scholar] [CrossRef]
- Correll, D.L. The Role of Phosphorus in the Eutrophication of Receiving Waters: A Review. J. Environ. Qual. 1998, 27, 261–266. [Google Scholar] [CrossRef]
- Holman, I.P.; Howden, N.J.K.; Bellamy, P.; Willby, N.; Whelan, M.J.; Rivas-Casado, M. An Assessment of the Risk to Surface Water Ecosystems of Groundwater P in the UK and Ireland. Sci. Total Environ. 2010, 408, 1847–1857. [Google Scholar] [CrossRef] [PubMed]
- Olsen, S.R.; Watanabe, F.S. A Method to Determine a Phosphorus Adsorption Maximum of Soils as Measured by the Langmuir Isotherm. Soil Sci. Soc. Am. J. 1957, 21, 144–149. [Google Scholar] [CrossRef]
- Helyar, K.R.; Munns, D.N.; Burau, R.G. Adsorption of Phosphate by Gibbsite. J. Soil Sci. 1976, 27, 307–314. [Google Scholar] [CrossRef]
- Bolster, C.; Sistani, K. Sorption of Phosphorus from Swine, Dairy, and Poultry Manures. Commun. Soil Sci. Plant Anal. 2009, 40, 1106–1123. [Google Scholar] [CrossRef]
- Gjettermann, B. Modelling P Dynamics in Soil-Decomposition and Sorption: Technical Report; Concepts and User Manual; DHI Water & Environment: Hørsholm, Denmark, 2004. [Google Scholar]
- Barrow, N.J. The Description of Sorption Curves. Eur. J. Soil Sci. 2008, 59, 900–910. [Google Scholar] [CrossRef]
- Barrow, N.J. On the Reversibility of Phosphate Sorption by Soils. J. Soil Sci. 1983, 34, 751–758. [Google Scholar] [CrossRef]
- Zawadzka, B.; Siwiec, T.; Reczek, L.; Marzec, M.; Jóźwiakowski, K. Modeling of Phosphate Sorption Process on the Surface of Rockfos® Material Using Langmuir Isotherms. Appl. Sci. 2024, 14, 10996. [Google Scholar] [CrossRef]
- Dari, B.; Nair, V.D.; Colee, J.; Harris, W.G.; Mylavarapu, R. Estimation of Phosphorus Isotherm Parameters: A Simple and Cost-Effective Procedure. Front. Environ. Sci. 2015, 3, 70. [Google Scholar] [CrossRef]
- Del Bubba, M.; Arias, C.A.; Brix, H. Phosphorus Adsorption Maximum of Sands for Use as Media in Subsurface Flow Constructed Reed Beds as Measured by the Langmuir Isotherm. Water Res. 2003, 37, 3390–3400. [Google Scholar] [CrossRef] [PubMed]
- Dossa, E.; Baham, J.; Khouma, M.; Sene, M.; Kizito, F.; Dick, R. Phosphorus Sorption and Desorption in Semiarid Soils of Senegal Amended With Native Shrub Residues. Soil Sci. 2008, 173, 669–682. [Google Scholar] [CrossRef]
- Jones, J.B. Laboratory Guide for Conducting Soil Tests and Plant Analysis; Taylor & Francis: Abingdon, UK, 2001; ISBN 9780849302060. [Google Scholar]
- Magdoff, F.R.; Jokela, W.E.; Fox, R.H.; Griffin, G.F. A Soil Test for Nitrogen Availability in the Northeastern United States. Commun. Soil Sci. Plant Anal. 1990, 21, 1103–1115. [Google Scholar] [CrossRef]
- Walkley, A.; Black, I.A. An Examination of the Degtjareff Method for Determining Soil Organic Matter, and a Proposed Modification of the Chromic Acid Titration Method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Van Reeuwijk, L.P. Procedures for Soil Analysis; ISRIC: Wageningen, The Netherlands, 2002. [Google Scholar]
- Bouyoucos, G.J. Hydrometer Method Improved for Making Particle Size Analyses of Soils1. Agron. J. 1962, 54, 464–465. [Google Scholar] [CrossRef]
- Knudsen, D.; Peterson, G.A.; Pratt, P.F. Lithium, Sodium, and Potassium. In Methods of Soil Analysis; Agronomy Monographs; American Society of Agronomy, Inc.: Madison, WI, USA; Soil Science Society of America, Inc.: Madison, WI, USA, 1983; pp. 225–246. ISBN 9780891189770. [Google Scholar]
- Iatrou, M.; Papadopoulos, A.; Papadopoulos, F.; Dichala, O.; Psoma, P.; Bountla, A. Determination of Soil-Available Micronutrients Using the DTPA and Mehlich 3 Methods for Greek Soils Having Variable Amounts of Calcium Carbonate. Commun. Soil Sci. Plant Anal. 2015, 46, 1905–1912. [Google Scholar] [CrossRef]
- Jeffrey, A.J.; McCallum, L.E. Investigation of a Hot 0.01m CaCl2 Soil Boron Extraction Procedure Followed by ICP-AES Analysis. Commun. Soil Sci. Plant Anal. 1988, 19, 663–673. [Google Scholar] [CrossRef]
- Wang, Z.; Hou, L.; Liu, Z.; Cao, N.; Wang, X. Using a Modified Langmuir Equation to Estimate the Influence of Organic Materials on Phosphorus Adsorption in a Mollisol From Northeast, China. Front. Environ. Sci. 2022, 10, 886900. [Google Scholar] [CrossRef]
- Nair, P.S.; Logan, T.J.; Sharpley, A.N.; Sommers, L.; Tabatabai, M.; Yuan, T.L. Interlaboratory Comparison of a Standardized Phosphorus Adsorption Procedure. J. Environ. Qual. 1984, 13, 591–595. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification Using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Xu, D.; Shi, Y.; Tsang, I.W.; Ong, Y.-S.; Gong, C.; Shen, X. Survey on Multi-Output Learning. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2409–2429. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-Generation Hyperparameter Optimization Framework. arXiv 2019, arXiv:1907.10902. [Google Scholar]
- Shimizu, S.; Inazumi, T.; Kawahara, Y.; Washio, T.; Hoyer Patrikhoyer, P.O.; Bollen, K.; Sogawa, Y.; Hyvärinen, A.; Hoyer, P.O.; Bollen Shimizu, K. DirectLiNGAM: A Direct Method for Learning a Linear Non-Gaussian Structural Equation Model. J. Mach. Learn. Res. 2011, 12, 1225–1248. [Google Scholar]
- Niyogi, D.; Kishtawal, C.; Tripathi, S.; Govindaraju, R. Observational Evidence That Agricultural Intensification and Land Use Change May Be Reducing the Indian Summer Monsoon Rainfall. Water Resour. Res. 2010, 46, 1–17. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Smith, S.M.; Spirtes, P. Pairwise Likelihood Ratios for Estimation of Non-Gaussian Structural Equation Models. J. Mach. Learn. Res. 2013, 14, 111–152. [Google Scholar] [PubMed]
- Tukey, J.W. Comparing Individual Means in the Analysis of Variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef] [PubMed]
- Van Rossum, G.; Drake, F.L. Python Tutorial. History 2010, 42, 270–272. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Yang, X.; Chen, X.; Yang, X. Effect of Organic Matter on Phosphorus Adsorption and Desorption in a Black Soil from Northeast China. Soil. Tillage Res. 2019, 187, 85–91. [Google Scholar] [CrossRef]
- Iatrou, M.; Karydas, C.; Tseni, X.; Mourelatos, S. Representation Learning with a Variational Autoencoder for Predicting Nitrogen Requirement in Rice. Remote Sens. 2022, 14, 5978. [Google Scholar] [CrossRef]
- Iatrou, M.; Karydas, C.; Iatrou, G.; Pitsiorlas, I.; Aschonitis, V.; Raptis, I.; Mpetas, S.; Kravvas, K.; Mourelatos, S. Topdressing Nitrogen Demand Prediction in Rice Crop Using Machine Learning Systems. Agriculture 2021, 11, 312. [Google Scholar] [CrossRef]
- Hussain, A.; Ghafoor, A.; Anwar-ul-Haq, M.; Nawaz, M. Application of the Langmuir and Freundlich Equations for P Adsorption Phenomenon in Saline-Sodic Soils. Int. J. Agric. Biol. 2002, 5, 241–246. [Google Scholar] [CrossRef]
- Lair, G.J.; Zehetner, F.; Khan, Z.H.; Gerzabek, M.H. Phosphorus Sorption–Desorption in Alluvial Soils of a Young Weathering Sequence at the Danube River. Geoderma 2009, 149, 39–44. [Google Scholar] [CrossRef]
- Rossi, C.G.; Heil, D.M.; Bonumà, N.B.; Williams, J.R. Evaluation of the Langmuir Model in the Soil and Water Assessment Tool for a High Soil Phosphorus Condition. Environ. Model. Softw. 2012, 38, 40–49. [Google Scholar] [CrossRef]
- Iatrou, M.; Tziachris, P.; Bilias, F.; Kekelis, P.; Pavlakis, C.; Theofilidou, A.; Papadopoulos, I.; Strouthopoulos, G.; Giannopoulos, G.; Arampatzis, D.; et al. Data-Driven and Mechanistic Soil Modeling for Precision Fertilization Management in Cotton. Nitrogen. 2025, 6, 29. [Google Scholar] [CrossRef]
- Halliday, D.J.; Association, I.F.I. IFA World Fertilizer Use Manual; International Fertilizer Industry Association: Paris, France, 1992; ISBN 9782950629906. [Google Scholar]


| pH → | 4–6 | 6–7 | >7 | >7 | >7 | >7 | >7 |
|---|---|---|---|---|---|---|---|
| Clayey | 5 | 5 | 5 | 8 | 10 | 2 | 5 |
| Loamy | 9 | 10 | 10 | 9 | 9 | 9 | 6 |
| Sandy | 9 | 12 | 12 | 5 | 6 | 0 | 1 |
| CaCO3 → | 0% | 0–1% | 1–5% | 5–10% | 10–20% | 20–30% | >30% |
| Group | pH Range | CaCO3 Range | Description | Soil Texture |
|---|---|---|---|---|
| 1 | 4.30–6.20 | 0 | Acidic | Clayey, Loamy, Sandy |
| 2 | 6.25–7.96 | 0–0.9% | Neutral, low carbonate | Clayey, Loamy, Sandy |
| 3 | 6.83–8.18 | 1–10% | Alkaline, moderately calcareous | Clayey, Loamy, Sandy |
| 4 | 7.20–8.28 | 10.3–48.3% | Strongly alkaline, calcareous | Clayey, Loamy, Sandy |
| Soil Classification | Qm | K |
|---|---|---|
| Clayey | 11,822.86 | 0.0080 |
| Loamy | 12,899.80 | 0.0072 |
| Sandy | 8231.61 | 0.0106 1 |
| Soil Type | Qm | K |
|---|---|---|
| Clay (C) | 16,366.06 | 0.0059 |
| Clay loam (CL) | 14,959.94 | 0.0061 |
| Loamy (L) | 12,055.41 | 0.0075 |
| Silty loam (SiL) | 104,509.79 | 0.0008 |
| Loamy Sand (LS) | 2803.55 | 0.0251 |
| Sandy Clay Loam (SCL) | 8517.25 | 0.0109 |
| Sandy Loam (SL) | 4998.74 | 0.0180 |
| Silty Clay (SiC) | 6686.86 | 0.0138 |
| Silty Clay Loam (SiCL) | 6840.72 | 0.0144 1 |
| Equilibrium Concentrations (mg/L) | |||||
|---|---|---|---|---|---|
| Soil Type | 1 | 2 | 4 | 6 | 10 |
| Clay (C) | 98.2 ± 3.5 a | 93.6 ± 11.1 a | 93.3 ± 10.1 a | 92.4 ± 9.5 a | 91.2 ± 7.6 a |
| Clay loam (CL) | 92.3 ± 8.2 b | 91.8 ± 8.0 b | 90.7 ± 8.2 b | 90.6 ± 7.6 b | 87.5 ± 9.7 b |
| Loamy (L) | 81.8 ± 17.2 a | 88.5 ± 9.3 c | 86.6 ± 15.5 c | 88.5 ± 7.9 c | 83.6 ± 9.8 c |
| Loamy Sand (LS) | 52.6 ± 9.9 b | 68.3 ± 31.7 d | 62.2 ± 23.2 a | 63.4 ± 27.9 a | 55.8 ± 27.9 a |
| Sandy Clay Loam (SCL) | 86.7 ± 11.1 c | 90.1 ± 6.9 e | 89.4 ± 6.7 d | 87.7 ± 8.7 d | 83.8 ± 11.0 d |
| Sandy Loam (SL) | 75.7 ± 23.3 d | 83.2 ± 17.3 f | 81.7 ± 17.2 e | 83.4 ± 12.0 e | 75.1 ± 12.9 b |
| Silty Clay (SiC) | 98.5 ± 0.7 e | 87.3 ± 14.0 g | 86.4 ± 17.7 f | 85.9 ± 17.9 f | 81.0 ± 23.3 e |
| Silty Clay Loam (SiCL) | 99.8 ± 0.3 f | 91.8 ± 8.1 h | 93.8 ± 4.2 g | 91.5 ± 4.4 g | 86.2 ± 6.3 f |
| Silty loam (SiL) | 80.0 ± 24.9 g | 83.1 ± 21.1 i | 85.6 ± 12.5 h | 90.4 ± 7.7 h | 86.7 ± 7.4 g |
| Soil Class | Intercept | Sand | Clay | pH | EC | Organic Matter | P | Mg | Mn | Cu | Ce * | R2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sandy | 192.1 | −2.4 | −3.6 | −5.9 | 16.3 | −1.7 | −4.2 | 15.7 | 1.4 | 3.6 | 78.8 | 0.98 |
| Loamy | 48.0 | −1.2 | 1.9 | −4.3 | 4.0 | 0.9 | −1.9 | −3.5 | 0.9 | −0.3 | 86.9 | 0.94 |
| Clayey | 308.5 | −1.0 | 1.5 | −31.0 | −25.1 | −25.7 | 3.2 | 0.6 | −3.9 | −1.0 | 86.3 | 0.95 |
| Equilibrium Concentrations (mg/L) | |||||
|---|---|---|---|---|---|
| Soil Type | 1 | 2 | 4 | 6 | 10 |
| Clay (C) | 91.1 ± 12.9 a | 89.7 ± 8.5 a | 88.8 ± 8.2 a | 88.5 ± 7.6 a | 85.1 ± 7.4 a |
| Clay loam (CL) | 83.6 ± 14.6 a | 87.0 ± 8.9 a | 86.8 ± 7.9 a | 87.7 ± 6.5 b | 84.7 ± 6.3 b |
| Loamy (L) | 76.9 ± 14.4 a | 84.3 ± 8.8 a | 83.1 ± 8.6 a | 85.6 ± 6.9 a | 82.2 ± 7.0 a |
| Loamy Sand (LS) | 76.3 ± 10.9 b | 76.9 ± 9.5 a | 65.8 ± 7.4 a | 69.8 ± 7.6 a | 61.6 ± 7.3 a |
| Sandy (S) | 76.6 ± 11.1 c | 76.9 ± 10.2 b | 65.4 ± 5.1 b | 69.8 ± 7.6 b | 61.1 ± 6.6 b |
| Sandy Clay (SC) | 81.5 ± 10.1 d | 85.4 ± 6.4 b | 84.3 ± 6.3 b | 85.8 ± 3.3 c | 82.3 ± 3.3 c |
| Sandy Clay Loam (SCL) | 77.7 ± 12.7 e | 84.0 ± 8.0 c | 82.6 ± 8.2 c | 83.6 ± 6.5 a | 79.4 ± 6.8 a |
| Sandy Loam (SL) | 74.4 ± 12.8 a | 78.7 ± 9.8 c | 73.8 ± 10.4 a | 76.4 ± 9.8 a | 70.2 ± 10.7 a |
| Silty Clay (SiC) | 93.6 ± 10.0 b | 89.7 ± 7.0 c | 89.2 ± 7.7 c | 88.6 ± 7.3 d | 84.7 ± 7.2 d |
| Silty Clay Loam (SiCL) | 93.1 ± 9.5 c | 90.7 ± 5.7 d | 90.4 ± 5.8 a | 90.1 ± 5.4 a | 86.4 ± 5.5 b |
| Silty loam (SiL) | 84.6 ± 13.9 b | 87.9 ± 7.2 d | 87.2 ± 6.7 d | 89.0 ± 5.0 b | 85.4 ± 5.3 e |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iatrou, M.; Papadopoulos, A. Machine Learning vs. Langmuir: A Multioutput XGBoost Regressor Better Captures Soil Phosphorus Adsorption Dynamics. Crops 2025, 5, 55. https://doi.org/10.3390/crops5040055
Iatrou M, Papadopoulos A. Machine Learning vs. Langmuir: A Multioutput XGBoost Regressor Better Captures Soil Phosphorus Adsorption Dynamics. Crops. 2025; 5(4):55. https://doi.org/10.3390/crops5040055
Chicago/Turabian StyleIatrou, Miltiadis, and Aristotelis Papadopoulos. 2025. "Machine Learning vs. Langmuir: A Multioutput XGBoost Regressor Better Captures Soil Phosphorus Adsorption Dynamics" Crops 5, no. 4: 55. https://doi.org/10.3390/crops5040055
APA StyleIatrou, M., & Papadopoulos, A. (2025). Machine Learning vs. Langmuir: A Multioutput XGBoost Regressor Better Captures Soil Phosphorus Adsorption Dynamics. Crops, 5(4), 55. https://doi.org/10.3390/crops5040055







