Stochastic Cost Estimation in Transportation Infrastructure Projects Using Monte Carlo Simulation and Correlated Risk Variables

Abstract

Peru faces critical challenges in the development and maintenance of its national road infrastructure, comprising over 32,000 km, of which only 26% are classified as being in good condition. This infrastructural deficit significantly elevates logistics costs and undermines national competitiveness, particularly in key sectors such as agriculture and mining. In this context, improving the accuracy and reliability of cost estimation in road infrastructure projects is imperative to optimize resource allocation and mitigate the risk of cost overruns. This study proposes a stochastic cost estimation framework that integrates Monte Carlo simulation with correlation matrices, enabling the modeling of uncertainty and the complex interdependencies among critical cost drivers. The methodology was applied to the Oyon Ambo highway in Peru. Historical input cost databases were analyzed to define probabilistic distributions, and correlation coefficients were employed to represent the dependencies between variables such as material prices, labor productivity, and equipment efficiency. The stochastic model produced probabilistic cost forecasts with associated confidence intervals and quantified risk exposure. The findings demonstrate that the proposed integrated approach significantly enhances the precision and robustness of cost estimates, providing project managers and decision-makers with a rigorous, data-driven tool for risk-informed budgeting and strategic financial planning in complex infrastructure projects.

1. Introduction

Road infrastructure is a highly valued aspect of current policies aimed at achieving economic development and competitiveness, as it facilitates market integration, reduces logistics costs, and shortens transportation times [1,2,3]. Recent IDB estimates indicate that meeting SDG-consistent service levels by 2030 would require annual infrastructure investment of about 3.12% of regional GDP across water and sanitation, energy, transport, and telecommunications (with roughly 1.37% of GDP in transport), levels that remain above current investment trends [4]. As a consequence, road quality in the region ranks among the lowest globally, with a direct impact on competitiveness and production costs. In Latin America, logistics costs account for nearly 20% of total production costs, double the global average [5].

One of the critical factors exacerbating this situation is the frequent occurrence of cost overruns and delays in infrastructure projects. Globally, infrastructure investment projects show average cost overruns of 28%, but in Latin America this figure rises to 48% [6]. Moreover, it has been documented that around 75% of projects face budget increases and 65% experience schedule delays. Unlike other regions where these indicators tend to decrease, in Latin America they have continued to rise over time. This situation not only increases the fiscal burden but also generates uncertainty in execution and undermines the efficiency of public spending: the IDB estimates that between 20% and 53% of the budget allocated to public investment remains unexecuted due to administrative and technical delays [7].

In Peru, this problem takes on special significance. The country ranks 110th out of 141 in terms of road infrastructure quality according to the World Economic Forum [2], and faces paradigmatic cases such as the Nueva Carretera Central, whose budget doubled from S/11 billion to over S/24 billion after alignment adjustments during the study phase [8]. Adding to this is a troubling panorama of paralyzed works: by the end of 2023, the Comptroller General of the Republic reported 2298 projects halted with S/26.992 billion already invested, of which an additional S/13.772 billion would be required for completion [9]. Transport sector leads this group with 628 stalled works, many of them roads, mainly due to contractual breaches (23.5%) and lack of financing (22.4%) [10].

This combination of insufficient investment, poor construction quality, and frequent budget deviations seriously limits a country’s ability to effectively execute its infrastructure programs. The economic consequences are significant: it is estimated that if these gaps persist over the next decade, Latin America’s GDP would be 15 percentage points lower, with an accumulated loss close to USD 900 billion for the region.

In this context, the need to substantially improve cost estimation methodologies in road projects becomes evident, incorporating approaches that more realistically reflect the inherent uncertainty of this type of work. Traditional techniques, based on deterministic values, often underestimate the variability of inputs and the interdependencies among key factors such as material prices, labor productivity, and equipment efficiency. Hence, recent studies have proposed the use of stochastic tools such as Monte Carlo simulation to capture this complexity [11,12]. In a previous study [13], it was argued that Monte Carlo simulation is a suitable tool in contexts like Latin America, where the use of stochastic methods is still limited. Following this line of improvement, the present study proposes a stochastic cost estimation framework that integrates Monte Carlo simulation with correlation matrices, with the objective of explicitly modeling the relationships among interdependent variables using historical data or expert judgment.

Several international studies have demonstrated the usefulness of Monte Carlo simulation in estimating costs and schedules in construction projects, integrating correlation matrices to model interdependencies among variables. Research by Firouzi et al. [14], Moselhi and Roghabadi [15] and Sobieraj and Metelski [16] has shown that ignoring correlation among items can lead to underestimating project uncertainty, affecting the accuracy of contingency and schedule estimates. However, these approaches have been developed mainly in European, North American, or Asian contexts, where there is greater availability of data and specialized tools. In contrast, in Latin America—and particularly in Peru—the application of such methodologies is still incipient, requiring the development of practical, adaptable, and rapidly implementable tools that allow for a robust initial approach to quantitative risk analysis. Therefore, this research proposes a model tailored to Latin American conditions, with direct application to a case study in a Peruvian road project.

Unlike previous studies that apply Monte Carlo simulation under the assumption of independence among variables, this research explicitly incorporates correlations between critical cost factors such as prices, productivity, and operational efficiency [17,18,19,20]. This methodological differentiation is key in real-world contexts where these variables are strongly interrelated, yet the literature often treats them as independent. The proposed model, in addition to presenting a correlation structure adaptable through historical data and expert judgment, also enables its practical implementation in data-limited environments such as those prevalent in Latin America. With this, the study seeks to close a concrete gap in the quantitative risk analysis of infrastructure projects in the region.

2. Methodology

2.1. Methodological Framework of the Research

The methodology of this research is structured in three main phases, as shown in Figure 1. Phase 1 comprises the identification of the problem, the literature review, and the selection of the case study. In Phase 2, the stochastic model is developed through data collection, goodness-of-fit testing, the selection of probability distributions, and the construction of the correlation matrix. Finally, Phase 3 involves a simulation using the Monte Carlo method and the analysis of the resulting indicators. This comprehensive approach allows for a realistic representation of uncertainty and interdependencies among critical variables in road infrastructure projects.

2.2. Case Study Description

The model was applied to the improvement of a 49 km section of the Oyón–Ambo highway, located in the central-northern region of Peru, which connects Lima, Pasco, and Huánuco. This case was selected due to its technical and logistical complexity, as well as the availability of reliable historical data, making it representative for validating a stochastic cost estimation methodology under real conditions of uncertainty. This project has been the subject of previous research under a qualitative approach [21,22], and a quantitative approach using Monte Carlo Simulation [13]. However, unlike earlier studies that relied solely on Monte Carlo simulation, this research introduces correlation matrices to capture interdependencies among key variables, representing a significant methodological advancement in contexts such as LATAM.

2.3. Data Collection and Historical Database

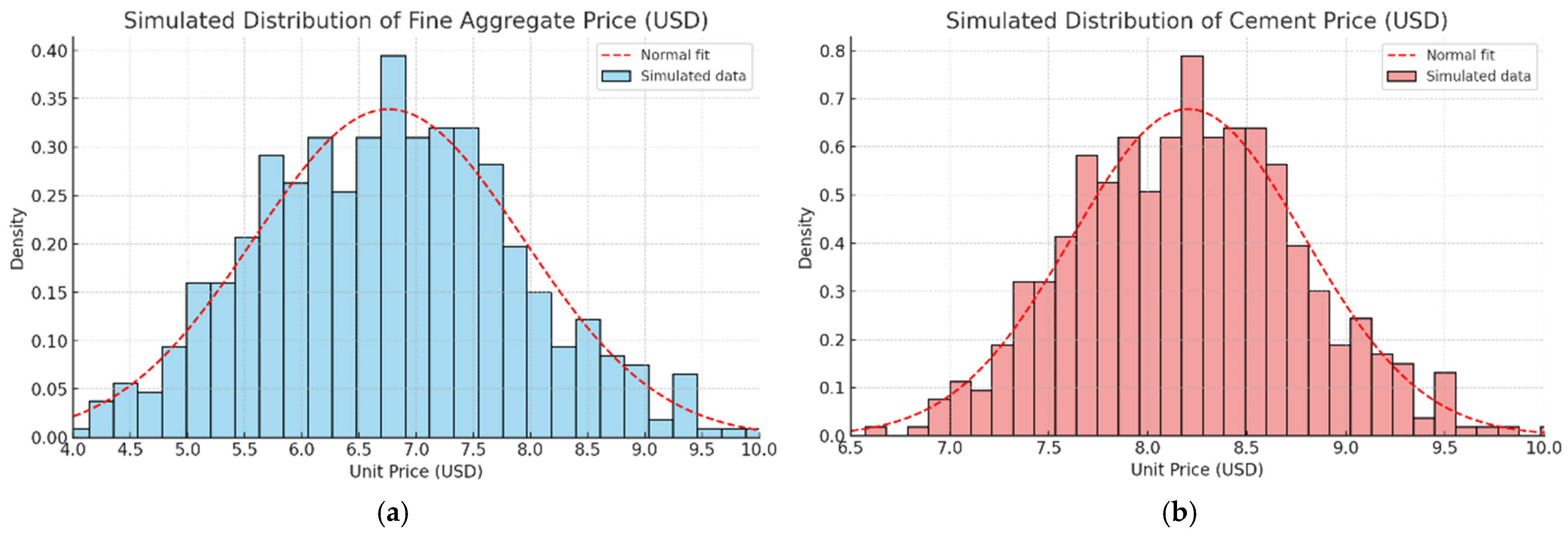
The model was based on the analysis of more than 500 unit records related to input prices, labor productivity, and equipment efficiency from road projects executed between 2019 and 2023 in the central-northern region of the country. The information sources included technical files from the Ministry of Transport and Communications (MTC), regional contractors’ databases, the Peruvian Unit Price Bank (BPU), and records from the National Public Investment System (SNIP). The data were cleaned to remove incomplete records and outliers. Subsequently, an exploratory analysis was conducted using statistical tools to identify the probability distribution of each variable. Goodness-of-fit tests such as Kolmogorov–Smirnov, as expressed in Equation (1), and Anderson–Darling were applied to validate the adequacy of the selected functions.

$$D=\underset{x}{\mathrm{s}\mathrm{u}\mathrm{p}}\left|F_n\left(x\right)-F\left(x\right)\right|$$

$$A^2=-n-{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left[\right(2i-1\left)\right(\ln F\left(X_i\right)+\ln (1-F\left(X_{n+1-i}\right))\left)\right]$$

(1)

The goodness-of-fit tests, shown in

Table 1. Goodness-of-fit tests for key variables of the stochastic model.

Variable	Test	Test Statistic (D/A2)	p-Value/Critical Level	Result
Portland Cement for Concrete	Kolmogorov–Smirnov	0.0508	0.9467	Normality not rejected
Portland Cement for Concrete	Anderson–Darling	0.2534	0.7590 (5%)	Normality not rejected
Fuel	Kolmogorov–Smirnov	0.0733	0.6293	Normality not rejected
Fuel	Anderson–Darling	0.6214	0.7590 (5%)	Normality not rejected
Fine aggregate	Kolmogorov–Smirnov	0.0543	0.9136	Normality not rejected
Fine aggregate	Anderson–Darling	0.4066	0.7590 (5%)	Normality not rejected
Coarse aggregate	Kolmogorov–Smirnov	0.0668	0.7405	Normality not rejected
Coarse aggregate	Anderson–Darling	0.3864	0.7590 (5%)	Normality not rejected

and Figure 2, confirmed that the key variables of the model, Portland cement for concrete, fuel, fine aggregate, and coarse aggregate—follow a normal distribution, with positive results in both Kolmogorov–Smirnov and Anderson–Darling tests.

For the Kolmogorov–Smirnov test, the test statistic is the largest vertical gap between the empirical and the theoretical cumulative distribution functions; for the Anderson–Darling test, it is a tail-weighted distance. Decisions are made by comparing the test statistic with its probability value or with a critical value.

Given the 2019–2023 time span, marked by COVID-19 and inflation shocks, we interpret unit-price observations as regime-conditional rather than strictly stationary. To preserve transferability, budgeting inputs should be deflated to constant currency (using official construction/producer price indices) and de-trended before distribution fitting; correlations (ρ) should be estimated on normalized series or residuals. In practical applications, we recommend calibrating the chosen percentile (as P90–P95) to contemporaneous indices at the time of funding decisions, treating the percentiles reported here as conditional on the 2019–2023 regime. This regime-aware reading mitigates spurious inferences from temporary shocks without changing the scope of this study.

The normal distribution is used to model phenomena with a central tendency and symmetrical variability, making it useful when values are evenly distributed around a mean. Its probability density function is given by (2), where μ represents the mean and σ the standard deviation. This distribution is applied in cost and schedule estimations when variations result from multiple independent factors, in accordance with the Central Limit Theorem.

$$f\left(x\right)={\displaystyle \frac{1}{\sigma \sqrt{2\pi }}}{e}^{-{\displaystyle \frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}}$$

(2)

The triangular distribution is used when information is limited and only the minimum (a), most likely (b), and maximum (c) values are known. This model, described in (3), is applied in cost and schedule estimation when subjective assessments are available but there is insufficient historical data to use more complex distributions.

$$f\left(x\right)=\left\{\begin{array}{c}{\displaystyle \frac{2\left(x-a\right)}{\left(b-a\right)\left(c-a\right)}};a\le x \le b\\ {\displaystyle \frac{2\left(c-x\right)}{\left(c-a\right)\left(c-b\right)}}; a\le x \le b\\ 0 ;in another cases\end{array}\right.$$

(3)

The Beta PERT distribution is a variant of the Beta distribution used to represent uncertainty in project activity estimates. It is defined in terms of the minimum (a), maximum (b), and mode (m) values, with its probability density function shown in (3).

$$f\left(x\right)={\displaystyle \frac{{\left(x-a\right)}^{\alpha -1}{\left(b-x\right)}^{\beta -1}}{B\left(\alpha ,\beta \right){\left(\beta -a\right)}^{\alpha +\beta -1}}}$$

(4)

where B(α, β) is the Beta function, and the expressions for α and β are represented as shown in (4).

$$\alpha =1+4{\displaystyle \frac{m-a}{b-a}}; \alpha =1+4{\displaystyle \frac{b-m}{b-a}}$$

(5)

2.4. Definition of Random Variables and Probability Distributions

Based on the historical data collected, the main random variables that significantly influence the cost estimation of the Oyón–Ambo project were identified and selected. These variables were grouped into three main categories: (i) input prices, (ii) labor productivity, and (iii) equipment efficiency. Each variable was analyzed individually to determine its statistical behavior and the probability distribution function that best represented its variability.

Specialized tools such as @Risk were applied to fit probability distribution functions to the collected data, using triangular distributions for inputs with low dispersion, PERT distributions for productivity rates and operating times, and normal distributions for symmetric variables with a large sample size. They were parameterized according to minimum, maximum, most likely values, or means and standard deviations. In total, 15 random variables, as shown in

Table 2. Variables and inputs with probabilistic behavior in the stochastic model.

Category	Random Variable	Type of Distribution
Input prices	1. Portland Cement price	Normal
	2. Fine aggregate price	Normal
	3. Coarse aggregate price	Normal
	4. Fuel price	Normal
	5. Steel price	Triangular
	6. Cost of plasticizer additive	Triangular
Labor productivity	7. Productivity in earthworks (m3/day)	PERT
	8. Productivity in granular base spreading	PERT
	9. Productivity in concrete placement	PERT
	10. Productivity in asphalt layer placement	PERT
Equipment efficiency	11. Hourly cost of front loader	Normal
	12. Hourly cost of compactor roller	Normal
	13. Roller efficiency (m3/h)	PERT
	14. Motor grader efficiency	PERT
	15. Hourly cost of concrete mixer truck	Triangular

, were modeled with their respective distributions, providing a solid statistical basis to simulate uncertainty scenarios and obtain more precise and realistic cost estimates.

Distribution types were selected based on previous studies [13] and data availability, goodness-of-fit, and variable nature, consistent with established cost-risk guidance. For unit input prices with sufficient observations and no rejection of normality (cement, fuel, fine and coarse aggregates; K–S and Anderson–Darling at α = 5%), we used Normal. Where data were sparse and bounded by procurement ranges (as steel price, plasticizer additive), we used Triangular, a recommended choice when only minimum/most-likely/maximum are credibly specified and tail behavior is uncertain. For labor productivity and equipment efficiency—bounded rates typically elicited from technical files as min–mode–max with potential skew—we used Beta-PERT, which emphasizes the most-likely value while respecting bounds.

These criteria are aligned with AACE guidance on selecting probability distributions [23,24,25] and with government handbooks that favor Triangular/PERT under limited data and elicitation settings [26,27]; our earlier study documents these same justifications and diagnostics in road-project applications.

2.5. Correlation Matrix and Interdependency Modeling

In stochastic cost modeling, assuming independence among random variables can lead to biased estimates of the project’s total risk. In real contexts, factors such as material prices, labor productivity, and equipment efficiency exhibit significant interdependencies. Ignoring these correlations limits the accuracy of uncertainty analysis and may underestimate the contingencies required to mitigate cost overruns.

To capture interdependencies, we computed a Pearson-based correlation matrix from the cleaned and temporally normalized historical data and retained only pairs with technical justification and |r| ≥ 0.30 (a pragmatic “moderate-effect” screening cut-off that balances signal and noise in data-constrained settings [28]). The selected correlations were then implemented in the simulation using @RISK’s correlation engine: Cholesky factorization was used to ensure a valid positive-definite matrix, and rank-correlated sampling (Iman–Conover) was applied to generate correlated draws while preserving each variable’s marginal distribution. The resulting correlation matrix is consistent with the variance–covariance structure shown in Equation (3) [26]

$$V=\left(\begin{array}{ccc}{v}_{11}& v_{12}& v_{13}\\ v_{21}& v_{22}& v_{23}\\ v_{31}& v_{32}& v_{33}\end{array}\right)=\left(\begin{array}{ccc}{\sigma }_1^2& {\rho }_{12}{\sigma }_1{\sigma }_2& {\rho }_{13}{\sigma }_1{\sigma }_3\\ {\rho }_{12}{\sigma }_1{\sigma }_2& {\sigma }_2^2& {\rho }_{23}{\sigma }_2{\sigma }_3\\ {\rho }_{13}{\sigma }_1{\sigma }_2& {\rho }_{23}{\sigma }_2{\sigma }_3& {\sigma }_3^2\end{array}\right)$$

Table 3. Correlated random variables in the stochastic model.

	Fuel	Heavy Machinery	Labor	Fine Aggregate	Coarse Aggregate	Roller	Compaction
Fuel	1.00	0.78
Heavy Machinery	0.78	1.00
Labor			1.00				0.65
Fine Aggregate				1.00	0.83
Coarse Aggregate				0.83	1.00
Roller						1.00	0.71
Compaction			0.65			0.71	1.00

summarizes the pairs of correlated random variables incorporated into the model, along with their respective correlation coefficients.

A Pearson-based correlation matrix, coupled with Iman–Conover rank mapping, is employed as a pragmatic first-order representation of co-movement under data constraints. This choice preserves marginal fits and propagates dependence for contingency sizing; however, it does not capture non-linear or asymmetric tail dependence, so extreme co-movements may be understated. The objective is to quantify the value of moving from independence to an empirically supported dependence structure rather than to fully characterize tail risk. Consistent with Firouzi et al. [14], richer copula models can reshape tail behaviour.

2.6. Monte Carlo Simulation Framework and Risk Metrics

Using @Risk [29], simulations with 10,000 iterations were executed to model cost uncertainty for the Oyón–Ambo section. This number of iterations was adopted based on prior Monte Carlo analyses conducted on the same project [13], which evaluated sample sizes of 5000, 10,000, and 50,000 iterations. The results demonstrated that convergence of key statistical outputs (mean, percentiles, and standard deviation) was achieved from approximately 10,000 iterations onward, indicating that higher sample sizes did not significantly improve accuracy. Therefore, this iteration count ensures reliable convergence while optimizing computational resources. The model incorporated triangular, PERT, and normal input distributions, enforced the empirically derived correlation matrix, and was applied to the project’s bill of quantities.

Each iteration produced a total-cost scenario, yielding a full probability distribution of project cost. We then computed decision-oriented outputs: expected total cost (mean), standard deviation, confidence percentiles (P10, P50, P90), 95% Value-at-Risk (VaR), and the probability of exceeding the base budget. Together, these metrics quantify central tendency, dispersion, tail risk, and budget-overrun likelihood, supporting contingency sizing, proactive financial management, and strengthened controls under uncertainty.

The simulation employed 10,000 iterations as a practical convergence threshold, consistent with prior runs on the same project [13]. Beyond this size, the principal outputs (mean and upper percentiles) exhibited no material variation, meeting the study’s precision requirements while maintaining computational efficiency.

2.7. Monte Carlo Workflow for Correlated Cost Estimation

Inputs comprise the fitted marginal distributions for each cost driver (Xi), a target correlation matrix (R), and the iteration count (N). Outputs include the empirical distribution of total cost, summary statistics (mean, P50, P90, P95), and exceedance probabilities relative to specified budget thresholds. The procedure fits appropriate marginal distributions to each driver and stores their parameters; generates N independent pseudo-random variates per driver and computes their ranks; imposes the target dependence via Iman–Conover rank mapping to approximate R while preserving empirical ranks; maps the correlated ranks to the physical space using the inverse CDFs of the marginals to obtain simulated cost deltas; aggregates the simulated drivers into total cost for each iteration to form the sample of totals; and finally computes the summary statistics and decision quantiles and evaluates budget exceedance probabilities. The process is listed below:

• Fit an appropriate marginal distribution to each driver Xi and store parameter estimates;
• Generate N independent pseudo-random variates and rank them per driver;
• Impose the target dependence using Iman–Conover rank mapping to match R while preserving the empirical ranks;
• Map the correlated ranks to physical space via the inverse CDFs of {Xi} obtaining simulated cost deltas per driver.
• Aggregate simulated drivers to total cost for each iteration; record the sample of totals.
• Compute summary statistics and decision quantiles (P50, P90, P95), and evaluate budget exceedance probabilities.

3. Results

3.1. Distribution of Results

The execution of the Monte Carlo simulation with 10,000 iterations produced a probabilistic distribution of the total estimated cost for the Oyón–Ambo road project, integrating the variability of the input variables and their respective interdependencies. From these results, the most likely budget execution scenarios were identified, as well as the levels of exposure to economic risk.

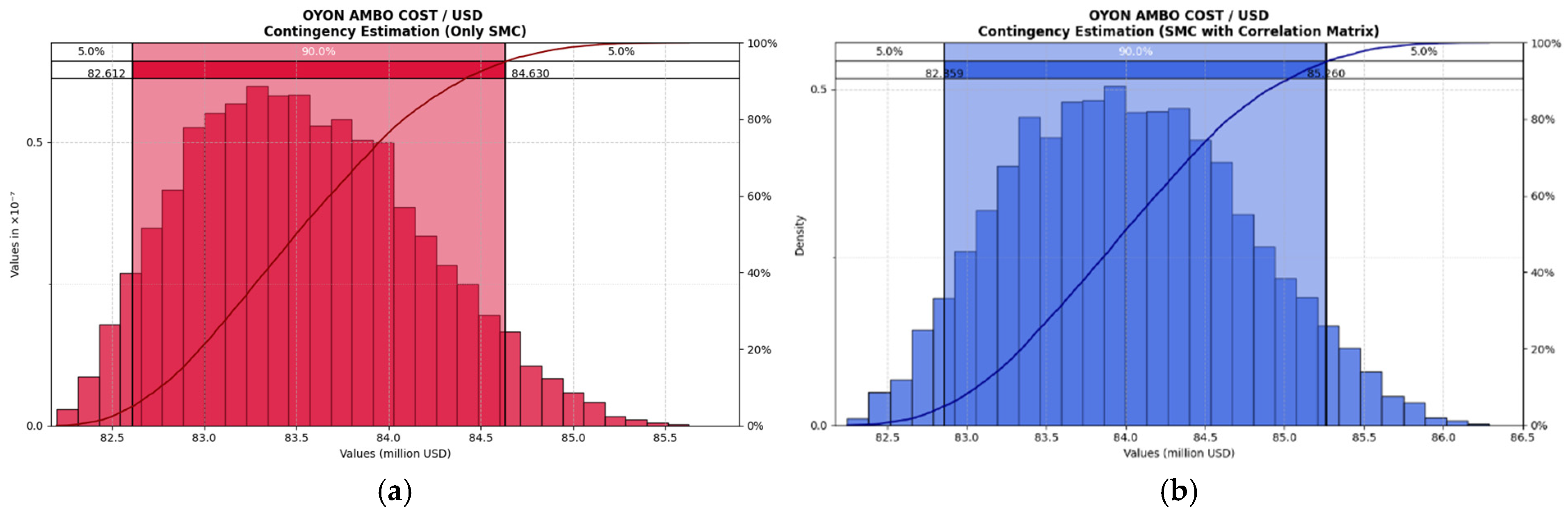
When comparing the results of both simulations shown in Figure 3, a significant difference is observed in the projected values for the 95th percentile of the project’s total cost. In the model without correlations, P95 was USD 84.63 million, while in the model incorporating correlation matrices this value increased to USD 86.26 million. This increase reflects a direct effect of the dependencies introduced among random variables, which amplify risk propagation within the system. The wider interval between the 5th and 95th percentiles suggests greater dispersion in the possible scenarios, translating into higher volatility in cost estimation. This behavior is consistent with statistical principles, which indicate that positive correlation among variables increases the joint variance of the system. Therefore, the results show that the use of correlation matrices not only alters the expected value but also affects the shape and spread of the simulated outcome distribution, which is particularly relevant for contingency estimation in contexts with multiple interrelated sources of uncertainty.

In the uncorrelated simulation (red curve), the distribution exhibits a slightly positive skew, with a longer right tail, indicating fewer high-cost scenarios. In contrast, the correlated model (blue curve) shows a more centered and compact distribution, with greater overall dispersion, reflecting a more uniform propagation of risk due to dependencies among variables.

This behavior is consistent with statistical theory: the incorporation of correlations among variables tends to increase joint variance and redistribute risk, making the curve more symmetric but broader. This results in more conservative and realistic estimates for budget planning.

3.2. Statistical Analysis

The main statistical indicators derived from both Monte Carlo simulations are presented below: one without considering correlations among random variables, and another integrating a correlation matrix. The objective is to contrast the effects of explicitly incorporating interdependencies on the shape and dispersion of the simulated total cost distribution. The results, as shown in

Table 4. Comparison of statistical indicators between simulations with and without correlation.

Indicator	Without Correlation (Red)	With Correlation (Blue)
Mean (USD million)	83.55	84.01
Percentile 10 (P10)	82.77	83.06
Percentile 50 (P50)	83.50	83.98
Percentile 90 (P90)	84.39	85.00
Standard deviation	0.61	0.73
Skewness	0.32	0.18
Kurtosis	−0.44	−0.52

, reveal relevant differences in the mean, key percentiles, and shape measures (skewness and kurtosis), showing greater dispersion and a slight reduction in kurtosis when correlations are considered.

3.3. Sensitivity Analysis

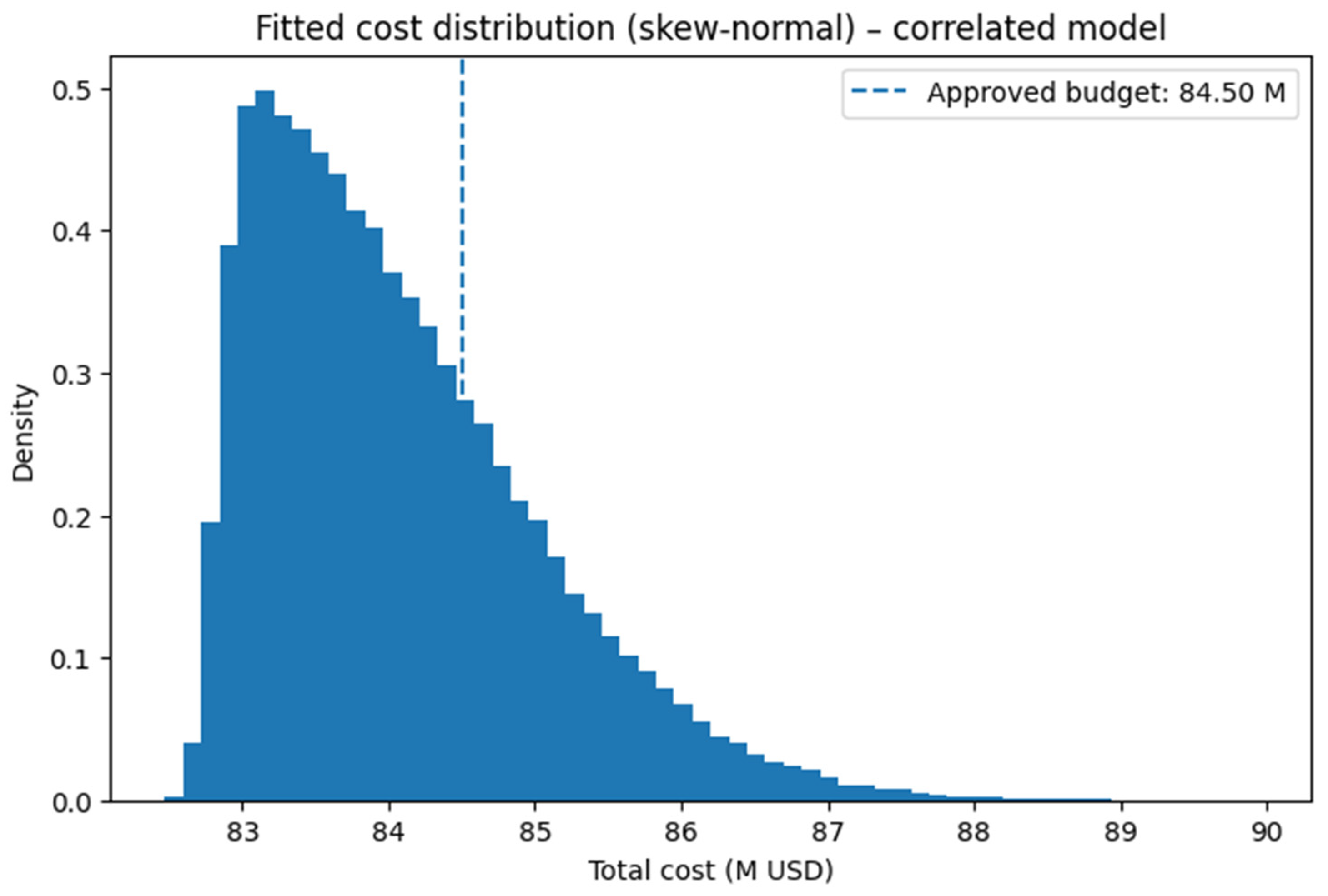
Based on the cost distribution of the correlated model reported in Section 3.1 (Mean = USD 84.01 M, P50 = USD 83.98 M, P90 = USD 85.00 M, and P95 = USD 86.26 M), exceedance probabilities were estimated for different budget thresholds:

• If the approved budget were USD 84.00 M, the probability of exceedance would be 45.4%.
• If the approved budget were USD 84.50 M, the probability of exceedance would be 28.7%.
• If the approved budget were set at P90 (USD 85.00 M), the residual risk would decrease to 16.8%.
• If the approved budget were set at P95 (USD 86.26 M), the residual risk would be ≈ 3.0%.

These figures were obtained by fitting a skew-normal distribution that reproduces the reported quantiles and evaluating the cumulative distribution function (CDF) at each threshold. Compared to the approved budget in the technical file, the probability of exceedance can be directly interpreted depending on where the budget lies relative to P50/P90/P95: if set around USD 84.5 M, the project faces moderate risk (~29%); if raised to P90, that risk falls to ~17%; and at P95, the residual risk reduces to ~3%.

Figure 4 shows the probability density of simulated project costs, highlighting the expected distribution around the mean and indicating the position of the approved budget. This visualization allows decision-makers to directly observe the likelihood of costs clustering around central estimates or deviating toward higher values.

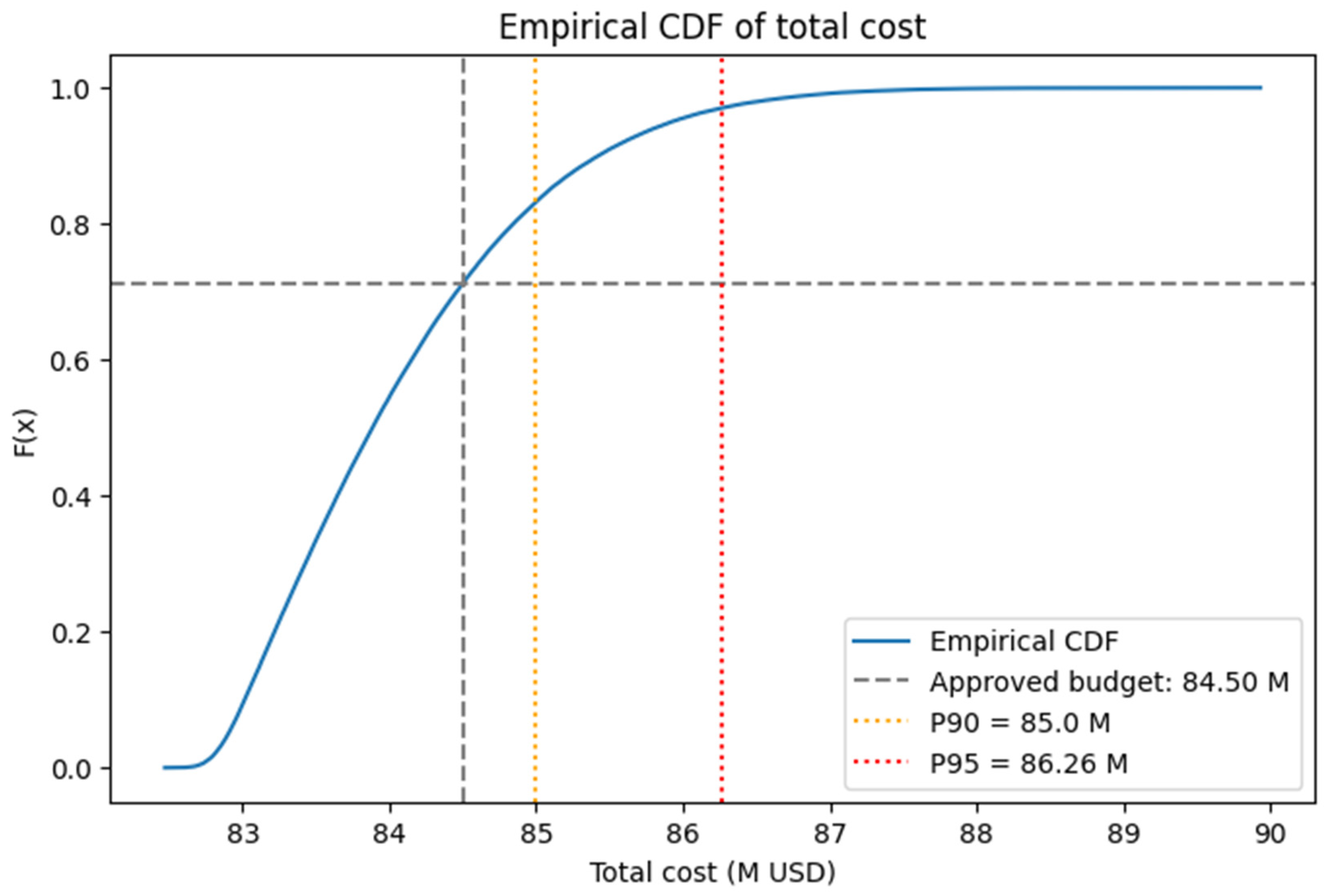
Figure 5 presents the CDF of simulated costs, which is particularly useful for interpreting exceedance probabilities. By comparing the position of the approved budget with the cumulative curve, one can directly quantify the risk of cost overruns. Together, these figures link the statistical analysis with practical financial decision-making, reinforcing the connection between percentiles (P50, P90, P95) and the residual budgetary risk identified in the sensitivity analysis.

4. Discussion

4.1. Comparison with Similar Methodology Studies

The results of this study’s stochastic cost estimation—particularly the inclusion of correlated risk factors—align with and extend findings from existing literature. The Monte Carlo simulations showed that incorporating correlation between cost drivers significantly widened the cost distribution and raised the high-end risk estimate. For instance, the 95th percentile (P95) cost forecast increased from about USD 84.63 million under an independence assumption to USD 86.26 million when correlations were modeled. This ~2% rise in the P95, coupled with a jump in the standard deviation (from 0.61 to 0.73), indicates greater volatility and a more conservative contingency requirement once interdependencies are acknowledged. Such behavior is consistent with statistical theory and has been observed by other authors—positively correlated inputs lead to higher joint variance and broader outcome ranges [30,31,32,33].

These findings corroborate prior studies emphasizing the critical role of accounting for correlations in project cost estimates [34,35,36,37]. Decades ago, Touran and Wiser [38] demonstrated that ignoring correlations among cost elements can severely underestimate total cost variance. More recently, Firouzi et al. [14] applied a copula-based Monte Carlo model and found that different dependency structures yield markedly different cost distribution shapes. They concluded that modeling such interdependencies (via copulas) improves the accuracy of total cost prediction. Likewise, Moselhi and Roghabadi underscored that correlation is “the most important issue” for accurate contingency estimation. In their fuzzy Monte Carlo approach, they even introduced subjective correlation techniques to handle situations with limited data on correlation coefficients [15]. Our results directly echo these studies: by explicitly integrating a correlation matrix, we obtain a more realistic risk profile, avoiding the underestimation of uncertainty that occurs when cost drivers are treated in isolation. This agreement with global research validates our methodological choice and highlights a key improvement over traditional Monte Carlo analyses that assume independent cost items.

Methodologically, our approach distinguishes itself by using actual historical data and expert judgment to construct the correlation matrix for cost variables. This is in contrast to earlier works that often assumed simplistic or no dependencies, or relied on preset correlation categories (“high/medium/low” subjective correlations as in Touran [39]. By capturing nuanced interdependencies, our model provides a refined risk quantification. Notably, Moselhi and Roghabadi’s fuzzy-simulation method achieved comparable accuracy to a full Monte Carlo by incorporating uncertainty in the correlation inputs—their “developed method” was shown to match the performance of a Monte Carlo with correlation even when run in an analytical (non-simulation) mode. This highlights that while the implementation may vary, the inclusion of correlation in cost risk models is indispensable for realism. In sum, the consensus across these studies is that acknowledging the interconnected nature of cost drivers leads to more robust and defensible estimates of contingency and risk exposure.

4.2. Global Context and Implications

Placing our findings in a global context, it becomes clear that advanced risk analysis techniques like ours are not just academic exercises but are crucial for addressing well-documented cost overrun trends. Worldwide, infrastructure projects commonly suffer cost overruns averaging around 28%, whereas in Latin America the average overrun soars to roughly 48%. Traditional deterministic estimating approaches—still prevalent in many projects—have been heavily criticized for contributing to these overruns due to their inability to represent uncertainty. They tend to produce point estimates that ignore variability and correlations, resulting in budgets that are too optimistic. Our Monte Carlo-based framework directly tackles this shortcoming by providing probability-based forecasts. For example, rather than a single-valued contingency, we can quantify the likelihood of exceeding the baseline budget. This probabilistic insight allows decision-makers to prepare more effectively for worst-case scenarios, a practice aligned with modern risk management but often missing in conventional estimates.

It is important to note that while quantitative risk analysis methods like Monte Carlo simulation are well-established in many developed regions, their adoption in developing contexts has lagged. The literature observes that most prior applications of Monte Carlo cost simulation with correlation have been in North America, Europe, or Asia, where abundant data and specialized tools facilitate such analyses. In contrast, in Latin America—and Peru in particular—the use of these stochastic methods is still incipient. This study contributes to bridging that gap by demonstrating a practical implementation tailored to a data-scarce environment. The current approach shows that even with limited historical information, a carefully constructed model can yield meaningful risk metrics [40,41,42]. The case of the Oyón–Ambo road project serves as an example of how integrating Monte Carlo simulation into local project planning can enhance estimate reliability, offering a template for similar efforts in the region.

The implications of our findings extend to improving contingency practices. By capturing a more realistic spread of possible costs, our model suggests contingencies that are neither overly conservative nor dangerously low, but rather calibrated to a chosen confidence level. In a recent related study of Peruvian road projects, Ariza and Zavala [13] reported that applying Monte Carlo–based quantitative risk analysis reduced uncertainty significantly, resulting in recommended cost contingencies between 1.34% and 11% of project budgets—far lower than the ~32% cost overruns historically observed on similar projects. This improvement underscores how embracing formal risk analysis can narrow the chronic gap between estimated and actual costs. In the current study, we similarly see that a rigorous stochastic estimation can elucidate a plausible contingency range (on the order of only a few percent of total cost for high-confidence budgeting), which can be compared against traditional ad hoc contingencies or past project outcomes. Such comparisons reveal that quantitative risk models can substantially improve the accuracy of budget forecasts, thereby enhancing financial control.

The results are in strong agreement with global research on cost estimation under uncertainty [12,43], while also shedding light on context-specific considerations. The enhanced accuracy and robustness of the cost forecasts obtained here—attributable to modeling correlations and uncertainty comprehensively—mark a valuable advancement for infrastructure project management in developing regions. This comparative perspective, juxtaposing our findings with those of other authors and methods, not only validates the effectiveness of our approach but also illustrates the differences in outcomes when modern stochastic methods are employed versus when traditional techniques fall short. By reflecting on these differences, it underscore the importance of methodological choice in cost estimation: incorporating interdependencies and probabilistic risk assessment leads to more reliable budgets, ultimately improving the likelihood of project success in both local and global settings.

4.3. Cost–Benefit and Value of Information (VOI)

Modeling dependencies among variables raised P95 from USD 84.63 M (independence) to USD 86.26 M (with correlations), i.e., +USD 1.63 M (~2%), and widened the cost distribution (standard deviation from 0.61 to 0.73). This thicker tail translates into material changes in exceedance risk at typical budgeting thresholds: with the correlated model, if the budget were USD 84.00 M the exceedance probability would be 45.4%; at USD 84.50 M, 28.7%; at P90 = USD 85.00 M, 16.8%; and at P95 = USD 86.26 M, about 3.0%. To assess whether incorporating correlations is worthwhile, we propose a conservative proxy for the expected underestimation cost, computed as the gap between the adopted threshold and P95 (with ρ) times the exceedance probability at that threshold. This metric approximates the minimum benefit (expected value) of aligning contingency to the true risk when dependencies are present.

Results, as shown in

Table 5. Exceedance Risk and Expected Overrun Proxy by Budget Threshold.

Budget Threshold	Exceedance Probability (%)	Gap vs. P95 with ρ (MUSD)	Expected Overrun Proxy (MUSD)
USD 84.00 M	45.4	2.26	1.03
USD 84.50 M	28.7	1.76	0.51
P90 = USD 85.00 M	16.8	1.26	0.21
P95 = USD 86.26 M	~3.0	0.00	0.00

, indicate that budgeting USD 84.50 M implies an expected overrun proxy ≈ USD 0.51 M, whereas budgeting P90 = USD 85.00 M reduces it to ≈ USD 0.21 M, and P95 = USD 86.26 M is effectively zero (≈0). Therefore, any analysis cost (data preparation, marginal fitting and ρ-matrix, simulation) below those expected values yields positive VOI. In large projects (>USD 80 M), the incremental effort to build/maintain a correlation matrix and run the model is small relative to the expected exposure avoided; moreover, the reduction in residual risk supports funding policies consistent with P90–P95 risk appetite.

The conservative expected-underestimation proxy is computed as Pr (Cost > Threshold) × max (P95 with ρ − Threshold, 0), where P95 with ρ is the 95th percentile under the correlated model. Intuitively, it treats P95 with ρ as a conservative stand-in for the size of the overrun whenever the budget is exceeded; multiplying by the exceedance probability yields a lower bound on the expected overrun that would arise if dependencies were ignored. This proxy does not integrate the full tail (as CVaR/expected shortfall) and therefore understates tail risk; it equals zero when Threshold ≥ P95 with ρ and is positive otherwise. It is suitable for quick cost–benefit/VOI screening with the evidence available here, while comprehensive funding decisions should also consider tail metrics and stress tests.

4.4. Limitations and Future Research

This study is constrained by data availability, distributional assumptions, and the chosen dependence structure. First, correlations among cost drivers were estimated from limited historical evidence and expert judgment; sampling error and potential non-stationarity (e.g., inflation regimes, FX shocks) may bias both the correlation matrix and the resulting tail risk. Second, the fitted marginal distributions and the skewness/asymmetry implied by our model are approximations; model misspecification can propagate to percentile-based contingencies. Third, linear correlation matrices capture co-movement but may under-represent tail dependence and asymmetric co-fluctuations. Future work should: (i) estimate dependencies empirically from multi-project panels and test vine-copulas against linear correlation; (ii) integrate dynamic price processes (e.g., SDEs for asphalt and steel) to link market volatility to budget risk; (iii) adopt hierarchical/Bayesian updating to recalibrate during execution; (iv) jointly model cost–schedule risk; and (v) back-test forecasts against realized outcomes, including extreme-value stress tests and bootstrap validation, to quantify calibration and improve transferability across contexts.

Furthermore, the fitting assumes stationarity after deflation, yet the 2019–2023 window likely embeds structural breaks (pandemic/inflation) and potential time-varying correlations. While our goal here is to quantify the VOI of modeling dependencies for contingency setting, a full time-series treatment (as break tests and segmentation, fitting distributions on residuals from ARIMA/ETS where needed, and rolling/regime-specific ρ) is outside this research. In practice, percentiles should be re-calibrated to contemporaneous construction/producer price indices at the time of funding decisions, and documented structural breaks should guide regime conditioning. When correlations appear time-varying, rolling-window or DCC-type diagnostics can be used; future extensions will incorporate these diagnostics and report CVaR alongside percentile metrics to strengthen out-of-sample applicability.

Linear correlation matrices capture average co-movement but under-represent tail dependence and asymmetric co-fluctuations; therefore, copula-based (as vine or t-copulas) dependencies are a priority for future work once broader panel data are available.

5. Conclusions

This paper advances stochastic cost estimation for transportation infrastructure by embedding correlated Monte Carlo simulation within a transparent risk framework. Relative to independence assumptions, modeling interdependencies among cost drivers produces a wider and more realistic cost distribution, materially lifting upper-tail percentiles (e.g., P90–P95) and, hence, contingency requirements. The approach yields interpretable outputs—exceedance probabilities for any budget threshold and sensitivity insights—that directly inform governance decisions on contingency sizing and risk appetite. In contexts where deterministic budgeting remains prevalent, these results demonstrate the practical value of probabilistic planning to reduce the likelihood and severity of cost overruns.

Beyond its empirical findings, the study offers a replicable template for agencies and practitioners operating under data constraints. By combining defensible marginal distributions with an explicit dependence structure, the method balances rigor and implementability, and can be progressively enriched with better data (panel histories), richer dependence models (copulas), and dynamic drivers (commodity price processes). The broader implication is clear: adopting correlated, percentile-based budgeting shifts practice from optimistic point estimates to risk-informed decisions, improving fiscal discipline and project credibility across the transportation sector.