A Machine Learning Approach to Traffic Congestion Hotspot Identification and Prediction

Abstract

Travel-time delays due to recurring congestion cause productivity loss, increase the likelihood of accidents, and lead to environmental pollution due to greenhouse gas emissions. The National Highway Traffic Safety Administration in the United States has listed several driver assistance technologies that are now common in most newer vehicles. While these technologies can help reduce the likelihood of traffic-related accidents, they do little to reduce recurring congestion in urban areas. Recurring congestion during rush hours is prevalent, for example, along Interstate 95 and Capital Beltway 495 in the Baltimore-Washington area. Such congestion also enhances the likelihood of crashes. Previous approaches to hotspot identification are primarily theoretical, which limits their practical applicability. In this paper, we develop a Machine Learning (ML) approach that integrates geospatial data with artificial neural networks to predict traffic congestion hotspots during rush hour. The approach uses live traffic sensor data. A case study from Maryland is presented. The result shows top hotspot segments across Maryland. Using a snapshot of hotspots at eight different time periods, the likelihood of hotspot locations is predicted using an artificial neural network. The framework is validated using live loop detector data (speed and volume) from Maryland freeways, particularly I-495 and I-95. The research can serve as a valuable tool for traffic congestion hotspot identification and travel-time prediction.

1. Introduction

Recurring traffic congestion is a major problem in urban areas, leading to travel-time delays, lost productivity, increased likelihood of accidents, and elevated levels of environmental pollution due to greenhouse gas emissions. The first key challenge in addressing recurring congestion is to identify pockets of hotspots so that travelers can be advised to adjust their travel schedules or take alternate routes when possible. Figure 1 shows a map of the top 15 congested highway segments in Maryland based on a 2017 rating. Figure 2 shows a 5.12 km (3.18 mile) stretch of Interstate 495 (I-495), also known as the Capital Beltway, which was rated as the most congested segment.

The recurring congestion along urban corridors is primarily caused by daily commuters. Many transportation agencies monitor traffic flow on major highways using sensors embedded beneath the road surface. These sensors are installed at key locations in each direction of a highway and collect real-time speed and volume data at regular intervals, such as every 15 min. For example,

Table 1. Speed data collected along key highway segments by underground sensors (Source: Maryland Department of Transportation).

Location	Average Speed	Last Reported
I-95 prior to I-295 North	60 MPH	11 July 2022, 1:40:15 p.m.
I-895 North past Harbor Tunnel Toll Booth, MM 8.7 South	Between 50–65 MPH	11 July 2022, 1:39:45 p.m.
I-895 North past Harbor Tunnel Toll Booth, MM 8.7 North	Between 50–65 MPH	11 July 2022, 1:39:45 p.m.
I-495 Outer Loop between Old Georgetown Rd and Fernwood Rd Outer Loop	50 MPH	11 July 2022, 1:40:15 p.m.
I-495 Outer Loop between Old Georgetown Rd and Fernwood Rd Inner Loop	57 MPH	11 July 2022, 1:40:15 p.m.
I-95 SB south of MD 175 South	60 MPH	11 July 2022, 1:40:14 p.m.
I-495 O/L prior to US-50 W off-ramp West	Over 65 MPH	11 July 2022, 1:40:15 p.m.

shows speed data for several key highway segments in Maryland.

As rush hour approaches, traffic density along many segments increases, leading to congestion. In this paper, we develop a geospatial framework leveraging ML to automatically detect and identify high-congestion segments along portions of I-495 and I-95 in Maryland. The scientific contribution of this study lies in the integration of a geospatial approach with a neural network using live traffic sensor data to identify hotspots, applying a 40-mph cutoff speed that can be adjusted as needed. The use of Artificial Neural Networks (ANNs) enables real-time processing of data to predict hotspot locations based on a snapshot of hotspots at eight different time periods. This framework provides a practical tool for identifying traffic congestion hotspots and estimating travel times.

Objectives

The overarching objective of this study is to develop and test a Machine Learning (ML)–based geospatial framework for identifying and predicting traffic congestion hotspots using real-time loop detector data. We articulate three specific objectives:

• To evaluate whether the integration of geospatial analysis with artificial neural networks improves hotspot prediction accuracy compared with baseline methods.
• To assess the potential for near real-time deployment by testing the framework on live loop detector data collected at 15-min intervals.
• To demonstrate applicability using a Maryland case study (I-495 and I-95) while outlining pathways for broader statewide implementation.

Based on these objectives, the study seeks to answer the following research questions: (1) Can the integration of geospatial data and ANNs improve congestion hotspot prediction accuracy? (2) Is the proposed framework computationally efficient for real-time traffic management deployment? (3) To what extent can the approach demonstrated on Maryland highways be generalized to other corridors at the state level and beyond?

While spatio-temporal deep learning models have been studied in the literature, this work makes a distinct contribution by embedding the analysis in a geospatial environment and applying it to real-time loop detector data from Maryland highways. The novelty of this study lies in demonstrating a practical, deployment-oriented framework that bridges theoretical advances with real-world implementation.

The contribution of this paper is not the proposal of a fundamentally new methodological algorithm but rather a proof-of-concept demonstration of how existing ML approaches can be operationalized in a geospatially explicit, real-time framework. The novelty lies in the practical integration of geospatial hotspot detection with ANN prediction using live loop detector data from Maryland highways, thereby bridging the gap between theoretical models and real-world deployment.

2. Literature Review

Predicting traffic hotspot corridors and travel times has been studied in previous works [1]. ML methods have also been applied to predict hotspots and travel times [2,3]. For instance, a Random Forest classifier was used to predict critical gaps at intersections under permissive left-turning phasing [4], while another study provided an analytical formulation for capacity reduction at signalized intersections due to dilemma zones [5].

Traditional approaches often rely on statistical models such as AutoRegressive Integrated Moving Average (ARIMA) and regression, whereas more recent studies explore advanced architectures including convolutional neural networks (CNNs), long short-term memory networks (LSTMs), and ensemble methods. These methods exploit spatio-temporal dependencies in traffic data and have reported high accuracy in both freeway and urban settings. For example, ref. [2] applied a deep spatio-temporal learning framework for traffic prediction and reported improved performance compared to baseline time-series models. Similarly, ref. [6] integrated multi-sensor data (including loop detectors, probe vehicles, and GPS trajectories) into an urban traffic state prediction framework, highlighting the importance of multi-source data for robust forecasting.

Several studies also provide quantitative benchmarks. Ref. [2] reported mean absolute percentage errors (MAPE) below 10% in congested conditions, while [6] achieved accuracy rates above 90% for short-term traffic state prediction. These benchmarks provide strong reference points against which proof-of-concept models, such as ours, can be evaluated.

While these approaches demonstrate the power of advanced deep learning, they often require substantial computational resources, long training datasets, and multi-source data integration, which may not be feasible for immediate deployment in all jurisdictions. In contrast, the present study emphasizes proof-of-concept feasibility by integrating geospatial hotspot identification with a lightweight ANN, trading methodological sophistication for computational efficiency and real-time applicability.

One drawback of existing methods for identifying and predicting congested road segments is that they generally do not utilize real-time sensor data. As a result, such approaches remain largely theoretical and cannot be readily applied in practice.

Although statistical approaches can provide meaningful traffic flow insights, they generally fail to capture complex non-linear relationships in the data. Such methods are typically used to find correlations in historical data to anticipate future traffic conditions. In contrast, Deep Neural Networks (DNNs) leverage large datasets to analyze network flow and identify patterns. DNNs are widely used in transportation due to their versatility, predictive accuracy, and ease of simulation in numerical models. Ref. [7] reviewed methods for predicting traffic congestion and identified two widely adopted techniques: (i) Convolutional Neural Networks (CNNs) based on image-processing methods; and (ii) time-series analysis using Long Short-Term Memory networks (LSTMs). While deep learning techniques generally outperform traditional statistical methods in accuracy, they are computationally intensive, resource-demanding, and not always mathematically interpretable.

Conventional traffic prediction models rely on aggregated flow data collected from various stations, and do not provide real-time congestion predictions for individual traffic nodes based on the state of neighboring nodes. Several studies, such as [8,9], propose scalable traffic flow prediction models using spatio-temporal data. Ref. [10] developed a decentralized deep learning model to predict the congestion state of urban traffic at a junction (network point) based on historical congestion data at neighboring junctions. The model can also predict the congestion state of newly introduced network points without historical data.

Rather than a binary congested/uncongested classification, the model assigns values between 0 and 1 to indicate congestion severity, defined as the ratio of average speed to the speed limit. In rare cases when the average speed exceeds the speed limit, the congestion value is capped at 1. A snapshot of each network point captures the congestion states of the junction and its neighboring junctions at fixed time intervals, represented as matrices for the entire network. Rows correspond to spatial sequences of network points, while columns represent temporal sequences.

The model employs two deep learning algorithms: Deep Traffic Flow-Convolutional Neural Network (DTF-CNN) and Long Short-Term Memory Traffic Flow (LSTM). In the DTF-CNN, two data groups are used as input: the traffic condition dataset from network point snapshots and traffic incident data (e.g., weather, accidents, events) [11], which can serve as engineered features related to traffic volume. Incident data is processed as a convolutional layer and iteratively trained to reduce its one-dimensional (1-D) array. The resulting 1-D values are then fed into a fully connected network to predict congestion values (0–1) for each network point at the next time interval based on historical spatio-temporal data. LSTM uses a recurrent neural network to predict congestion states for network points even when historical traffic data from other road segments is unavailable.

Many congestion prediction models are primarily based on a system-wide level, i.e., they utilize aggregated traffic flow data. For instance, refs. [11,12] and other similar studies used traffic parameters such as density, volume, and other aggregate traffic data to develop deep learning and ML traffic flow prediction models. However, understanding traffic disturbances at the individual vehicle level cannot rely on aggregated data.

Recent advances in wireless vehicle communications have enabled capturing traffic disturbances at the individual vehicle level. For example, ref. [3] proposed an ML approach based on online and offline models to predict traffic congestion for connected vehicles at an individual level. Vehicle trajectories provided by the Next Generation SIMulation (NGSIM) program were used for a segment of US-101 divided into ten equal sections. Traffic perturbations and trajectory information were captured via in-vehicle wireless communications, i.e., V2V (vehicle-to-vehicle) and V2I (vehicle-to-infrastructure), including real-time vehicular data such as speed, acceleration, location, and headway at a 0.1 s resolution.

In this framework, traffic states were treated as dependent variables, while mean speed and speed standard deviation (SSD) served as explanatory variables. The traffic state was classified into binary conditions—congested or uncongested—using K-means clustering after scaling density and flow values. The critical density was approximately 80 vehicles per mile per lane (vpmpl). Temporally (10- and 20-s intervals) and spatially lagged (each 200 ft section) models were developed using lagged values of the explanatory variables. Online and offline congestion prediction models were developed to reflect varying levels of connected vehicle market penetration (30%, 50%, and 100%).

Offline models were first calibrated and tested using historical traffic state datasets [3], while online models were trained with real-time information from the first 10 min of historical data to predict the next 5-min interval. The models were retrained every 5 min with updated data, using a maximum of 45 min of historical data to predict the following 5 min during rush hours. K-fold cross-validation was applied for model validation. For fully connected vehicles, all three ML-based techniques—logistic regression (LR), Random Forest (RF), and neural network (NN)—achieved similar precision (94–97%) in predicting congested states for both 10- and 20-s intervals. LR and RF outperformed NN in predicting uncongested states, with 10-s intervals yielding substantially better results than 20-s intervals.

Recent advancements in ML and artificial intelligence (AI) have significantly improved traffic congestion prediction, offering promising solutions for urban congestion challenges. Ref. [13] emphasized the importance of integrating big data from stationary sensors and probe vehicles to enhance short-term prediction accuracy. This shift towards real-time data utilization represents a significant advancement in traffic management capabilities. Similarly, ref. [14] proposed a weighted Markov model for mobility prediction that accounts for individual user behavior patterns by classifying users based on their trajectory characteristics. The model optimizes weighting coefficients for each class to improve prediction accuracy, demonstrating enhanced performance over traditional aggregated methods. This approach illustrates the benefit of combining machine learning classification with Markov-based modeling to capture stochastic variations in traffic patterns and supports potential real-time route optimization. Further highlighting the importance of spatio-temporal dynamics, ref. [15] proposed a Convolutional Long Short-Term Memory (CLSTM) model that efficiently integrates spatial and temporal information, outperforming traditional approaches and demonstrating the value of spatio-temporal integration for higher prediction accuracy.

In a quest to enhance predictive accuracy, ref. [16] introduced an ensemble ML strategy, combining predictions from XGBoost, LightGBM, and CatBoost models. This approach represents a significant advancement in applying ensemble learning within intelligent transportation systems, demonstrating its potential to substantially improve traffic flow prediction.

Addressing congestion propagation, ref. [17] developed a framework leveraging network embedding to infer congestion spread across road segments. Their method provides a novel perspective on congestion management, improving upon traditional approaches through predictive analytics. Ref. [18] focused on enhancing spatio-temporal deep learning algorithms by incorporating congestion patterns, offering improved prediction of traffic states in critically congested areas through graph theory and traffic flow fundamentals.

In the context of intersection traffic flow prediction, ref. [19] proposed an ML-based approach employing Recurrent Neural Networks (GRU) and Random Forests (RF), illustrating the adaptability of ML for real-time traffic control. Ref. [20] utilized real-time datasets collected via cameras and sensors for traffic flow prediction, showcasing the capabilities of deep learning in traffic management. Similarly, ref. [21] presented an LSTM-based model for short-term congestion prediction in LoRa networks, highlighting the integration of IoT and low-power network technologies in traffic monitoring. Additionally, ref. [22] introduced a deep stacked LSTM network for urban road traffic congestion prediction, integrating fuzzy logic and stochastic estimation algorithms to detect congestion levels effectively.

Despite these advancements, a significant research gap remains in the practical application of traffic congestion identification and prediction, primarily due to the limited availability of real-time sensor data. Existing statistical techniques, although useful for traffic flow insights, struggle with complex nonlinear traffic patterns.

To address this gap, the present study develops a ML framework that integrates geospatial analysis with neural networks to predict congestion hotspots during rush hours using live traffic sensor data. Unlike purely theoretical models, our method employs an ANN for real-time hotspot prediction, providing a practical improvement over existing approaches. By leveraging the ability of ANNs to learn from live data, the model identifies congestion hotspots and enhances travel-time prediction accuracy. Using live loop detector data from Maryland highways, our study demonstrates the feasibility of a practical tool for traffic congestion hotspot identification and travel-time prediction, contributing to the mitigation of travel-time delays, accident risks, and environmental pollution caused by recurring congestion.

While advanced architectures such as CNNs, LSTMs, and ensemble methods have been applied in previous research, this study deliberately focuses on a lightweight ANN to demonstrate proof-of-concept feasibility. This choice emphasizes real-time applicability and computational efficiency, while leaving exploration of more complex architectures for future work.

3. Commentary

While the literature review surveys prior work on traffic congestion prediction, it is equally important to critically examine the theoretical and methodological contributions of these studies. Prior research has made significant progress in modeling traffic congestion, particularly through statistical analysis, ML, and geospatial integration. Nevertheless, several limitations remain.

From a theoretical standpoint, many studies capture temporal dynamics but often underemphasize the spatial interdependencies inherent in traffic systems. Methodologically, although deep learning models have achieved high predictive accuracy, they frequently lack interpretability and require large datasets that are not always available in practical contexts. Regarding research objects, much prior work has focused on limited testbeds or corridor-specific studies, reducing the generalizability of their findings. Furthermore, existing studies often emphasize predictive performance without providing actionable insights for traffic management policies.

These limitations collectively highlight current gaps in the field. Specifically, the insufficient integration of spatial and temporal factors, reliance on data-rich environments, and limited practical deployment underscore the need for innovative approaches. The present study addresses these issues by proposing a geospatial–ANN framework that explicitly models spatial spillovers while remaining adaptable for real-time applications. By logically connecting the identification of prior shortcomings to the rationale for the proposed framework, this commentary underscores both the necessity and novelty of the study.

4. Methodology

There are several methods available to identify traffic congestion hotspots in the literature. For example, ref. [2] introduced an innovative ensemble-learning methodology for predicting potential traffic hotspots by analyzing daily traffic volume trends on highways. Utilizing Gradient Boost Regression Tree (GBRT) technology, this approach incorporates heterogeneous spatio-temporal data, including toll records, meteorological information, and calendrical data, to model traffic volume features and predict daily trends. Central to their method is the identification of potential traffic hotspots as locations with the Top-K traffic volumes, leveraging an ensemble-learning model fine-tuned with algorithmic parameters for accurate trend prediction. Specifically, the model is formulated as the following optimization problem:

$$\underset{F}{min}\sum _{j=0}^N{L}_f\left(y_j,F_{m-1}\left(x_j\right)+h_m(x_j;{\varphi }_m)\right)+\Omega \left(h_m\right)$$

(1)

$$F_m\left(X\right)=F_{m-1}\left(X\right)+h_m(x_j;{\varphi }_m)$$

(2)

where $L_f$ is the loss function that measures the difference between actual ($y_j$) and predicted traffic volumes $\left(F_{m-1}{x}_j+h_m(x_j;{\varphi }_m)\right)$; N is the number of observations in the training set; $F_{m-1}$ is the current model before adding the new tree; $h_m$ is the new decision tree to be added; ${\varphi }_m$ represents the parameters of the new tree; $\Omega$ is the regularization term penalizing the complexity of the new tree to avoid overfitting; and $X_j$ is the feature vector for the jth observation. Their system processes raw online toll data and external datasets to forecast traffic volumes and hotspot locations up to 30 days in advance, thereby enabling dynamic and proactive traffic management. This study’s integration of diverse data sources with advanced ML techniques provides a comprehensive framework for traffic trend analysis and hotspot detection, enhancing traffic flow management and reducing congestion.

Likewise, ref. [11] used a logistic regression method for traffic hotspot prediction to develop the relationship between accidents and several factors, such as road type, vehicle type, driver state, weather, and date. Given n factors that influence the occurrence of traffic accidents, represented as $x_1,x_2,\dots ,x_n$, the logistic regression model can be formulated as follows:

$$\mathrm{logit}\left(y\right)=ln\left({\displaystyle \frac{p}{1-p}}\right)=a_0+a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n$$

(3)

where y (taking values 0 or 1) indicates the presence of a traffic accident hotspot, p denotes the probability of a traffic accident occurring, $x_i$ (for $i=1,2,\dots ,n$) corresponds to the factors related to traffic accidents, $a_0$ represents the constant term, and $a_i$ (for $i=1,2,\dots ,n$) are the regression coefficients. This model can also be equivalently expressed in terms of the probability p as:

$$p={\displaystyle \frac{e^{a_0+a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n}}{1+e^{a_0+a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n}}}$$

(4)

Recently researchers have developed methods to identify hotspots for traffic crashes [11,23,24,25,26]. Ref. [26] discussed several methods for traffic crash hotspot prediction which we discuss here. Kernel Density Estimation (KDE) is used to estimate density of traffic crashes and is calculated using the formula:

$$f(x,y)=\sum _{i=1}^n{\displaystyle \frac{1}{2n{h}^2}}{W}_{i}K\left({\displaystyle \frac{d_i}{h}}\right)$$

(5)

where $f(x,y)$ are the density estimates at the crash location $(x,y)$; n is the number of fatal crash locations; h is bandwidth or kernel size; K is the kernel function; $d_i$ is the distance between the crash location $(x,y)$ and the crash location of the ith observation; and $W_i$ is the intensity of the crash based on severity and varies as per the assigned weights for different severity levels of crashes.

Next method discussed in the study is kriging which is an interpolation technique that models the spatial correlation of variables to predict values at unsampled locations as shown in Equation (6)

$$\widehat{Z}\left(x\right)=m\left(x\right)+\sum _{i=1}^n{\lambda }_i\left[Z\left(x_i\right)-m\left(x_i\right)\right]$$

(6)

where, $\widehat{Z}\left(x\right)$ is the estimated number of crashes based on n number of known crash frequencies at any given location. Also, $m\left(x\right)$ and $m\left(x_i\right)$ are the expected values of the random variables $Z\left(x\right)$ and $Z\left(x_i\right)$. For the estimation of a crash frequency at any location x, ${\lambda }_i$ is used as a kriging weight assigned to datum $Z\left(x_i\right)$.

Lastly, the researcher discussed about Network Kernel Density Estimation (NKDE) which is calculated using the formula:

$$K_y\left(x\right)=\left\{\begin{array}{cc}{\displaystyle \frac{k\left(d\right(x,y\left)\right)}{(n_1-1)(n_2-1)\dots (n_s-1)}}\hfill & \mathrm{for}d(y,x)\ge h,\hfill \\ 0\hfill & \mathrm{for}0\le d(y,x)\le h\hfill \end{array}\right.$$

(7)

where $K_y\left(x\right)$ is an equal split discontinuous kernel function, y is the kernel center, d is the shortest path distance between x and y, h is the bandwidth, and n is the degree of the node.

Similarly, ref. [27] combined signalized intersections and their adjacent road segments into meso-level units to identify the hotspots in the urban arterial using Empirical Bayesian (EB), Potential for Safety Improvement (PSI), and Full Bayesian (FB) methods. EB method refines expected crash frequencies by blending observed data with predictions from Negative Binomial (NB) models, addressing data over-dispersion. Formula for EB expected crash frequency is provided as:

$${\lambda }_i^{EB}={\lambda }_i^{NB}·\mathrm{weight}+y_i\times (1-\mathrm{weight})$$

(8)

$$\mathrm{weight}={\left(1+{\displaystyle \frac{{\lambda }_i^{NB}}{\phi }}\right)}^{-1}$$

(9)

where $\phi$ is the negative binomial inverse dispersion parameter, $y_i$ is the observed crash frequency, and ${\lambda }_i^{NB}$ is the negative binomial model predicted crash frequency. Another method discussed is PSI, which is the difference between EB expected crash frequency and the crash predicted from SPF, as in Equation (10). If PSI > 0, a site experiences more crashes than predicted and vice-versa.

$$PS{I}_i={\lambda }_i^{EB}-{\lambda }_i^{NB}$$

(10)

FB method addresses spatial correlations among traffic units on the same arterial using a Conditional AutoRegressive (CAR) model with a random effect term to capture variations and spatial correlations. Formulation for FB CAR model is provided as:

$$\begin{array}{cc}\hfill y_{ij}& \sim \mathrm{Negbin}({\theta }_i,r)\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill log(log\left({\lambda }_{ij}\right))& ={\beta }_0+{\beta X}_{ij}+{\phi }_{ij}\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill p\left({\phi }_{ij}\right|{\phi }_{-ij})& \propto exp\left[-{\displaystyle \frac{w_{j+}}{2{\sigma }_{\phi }^2}}{\left({\phi }_{ij}-\rho \sum _{i\ne j}{\displaystyle \frac{w_{ij}}{w_{j+}}}{\phi }_{ij}\right)}^2\right]\hfill \end{array}$$

(13)

where $y_{ij}$ is the crash frequency for meso-level unit i on arterial j; ${\theta }_i$ is the expected crash frequency; r is the over-dispersion coefficient; ${\lambda }_{ij}$ is the modeled crash rate; $X_{ij}$ is the vector of explanatory variables; ${\phi }_{ij}$ is the random effect term capturing spatial variation; $w_{ij}$ is a proximity matrix element indicating spatial relationship; and ${\sigma }_{\phi }^2$ is the variance of ${\phi }_{ij}$.

Ref. [28] developed a link-based model to identify congestion hotspots in urban road networks, presenting a novel approach that models vehicles moving through links (road segments) rather than nodes (intersections). This model introduces a balance equation for each link $ij$ as shown in Equation (14):

$$\Delta q_{ij}\left(t\right)=g_{ij}\left(t\right)+{\sigma }_{ij}\left(t\right)-d_{ij}\left(t\right)$$

(14)

where $g_{ij}\left(t\right)$ is the rate of vehicles entering the link directly from its origin node i, ${\sigma }_{ij}\left(t\right)$ is the rate of vehicles entering from adjacent links, and $d_{ij}\left(t\right)$ is the rate of vehicles exiting the link, constrained by the link’s capacity ${\tau }_{ij}$. Congestion is quantified when the sum of $g_{ij}\left(t\right)$ and ${\sigma }_{ij}\left(t\right)$ exceeds ${\tau }_{ij}$, leading to $\Delta q_{ij}\left(t\right)>0$. This framework allows for an analytical prediction of congestion levels both globally and locally within the network, providing a tool for urban planning and congestion mitigation strategies.

One major weakness of the aforementioned methods is that they are either too cumbersome or rely on results from small, jurisdiction-specific case studies. Moreover, they do not leverage real-time loop detector data, such as speed, flow, density, and spatial vehicle locations. In this context, the first author’s original work from 2000, which integrated a Geographic Information System (GIS) with a genetic algorithm, is noteworthy [29]. This seminal study established an integrated geospatial and numerical computation framework, combining the advantages of rapid numerical computation with spatial analysis.

In this paper, we identify hotspots using live loop detector data by developing an algorithm in a geospatial environment, following a methodology similar to that proposed by [29]. We then employ an ANN to predict the hotspot segments. An ANN is a system that learns to make robust predictions by: (1) using input data; (2) generating an initial prediction; (3) comparing the prediction to the desired output; and (4) adjusting its internal parameters to improve future predictions. ANNs are typically trained iteratively to enhance prediction accuracy, akin to a trial-and-error process. Readers are encouraged to consult standard references on ANN theory for further details.

For identifying hotspots, we use a threshold of 40 mph as the cutoff speed. This value is user-specified and can be reduced to 35 mph or 30 mph if desired. Any traffic below this user-defined speed is considered congested.

The 40 mph threshold was selected in accordance with Maryland DOT practice and common transportation engineering standards for defining freeway congestion. However, the cutoff parameter is flexible within the framework and can be adjusted to alternative values (e.g., 35 mph, 45 mph) or extended to flow- or capacity-based definitions. In the present study, no formal sensitivity analysis was conducted; future work will evaluate the robustness of results across different threshold settings.

We acknowledge that this binary threshold (hotspot vs. non-hotspot) is a simplification of real-world congestion dynamics, which are continuous and influenced by multiple factors (e.g., queue spillovers, shockwaves, incidents, weather). The binary definition provides a computationally tractable starting point and aligns with commonly used agency practices for defining congestion thresholds. In future extensions, the framework can be adapted to multi-class or continuous formulations that capture varying levels of congestion severity.

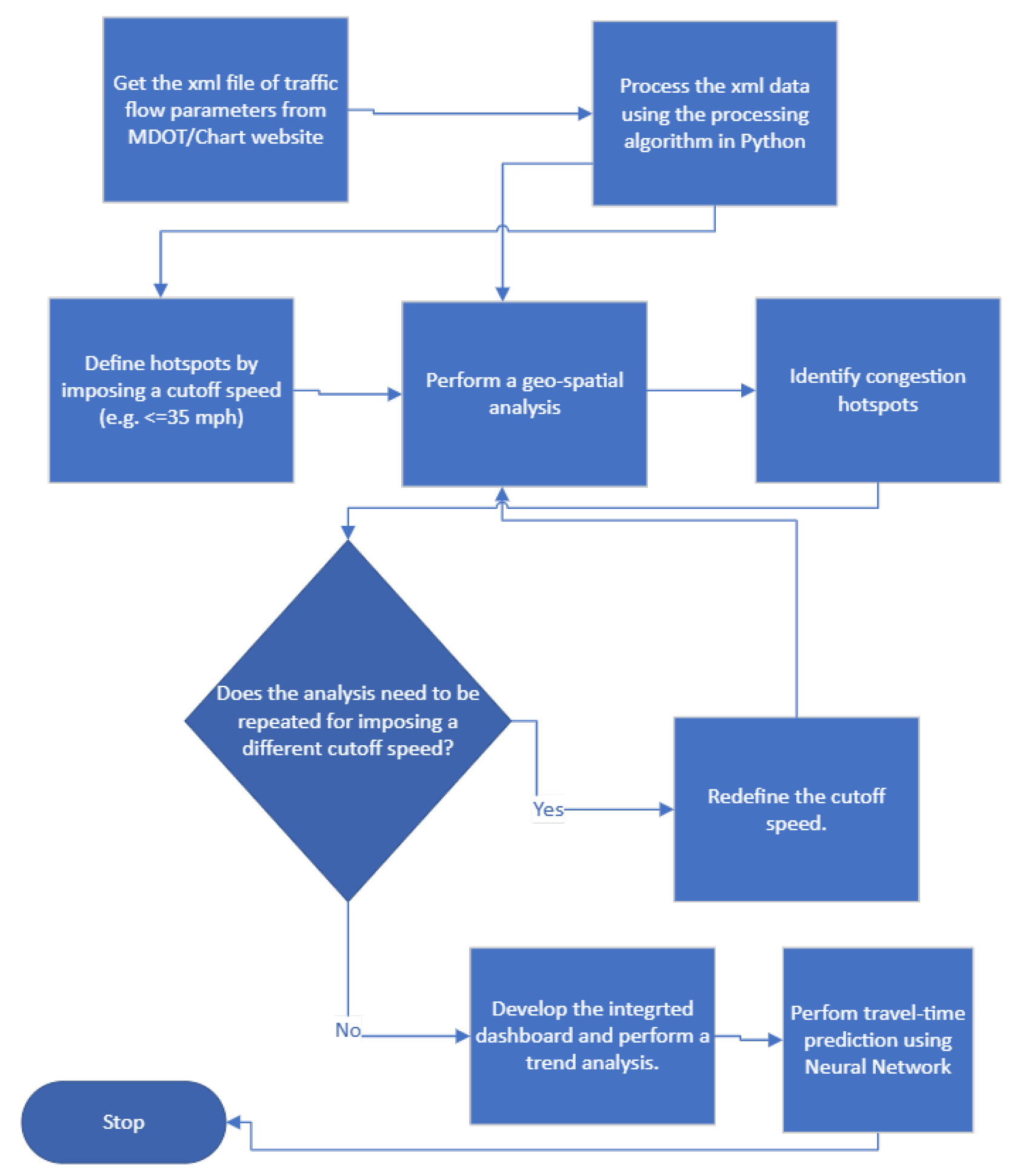
The methodological framework is illustrated in the flowchart in Figure 3. The analysis begins by parsing an XML file containing traffic flow parameters from loop detectors, and the geospatial analysis is performed using Python v3.8. We use a two-layer ANN to predict hotspot road segments in Maryland using real-time sensor data. A sigmoid activation function is applied in the second layer. The dataset outputs are binary, with 0 representing no hotspot and 1 representing the presence of a hotspot. The sigmoid function ensures that the output x is limited to a range between 0 and 1 and is expressed as:

$$S\left(x\right)={\displaystyle \frac{1}{1+e^{-x}}}$$

(15)

As the two possible outputs of the dataset are 0 and 1, and because the Bernoulli distribution naturally models such binary outcomes, the sigmoid function is an appropriate choice for the second layer. If the predicted value falls between 0.5 and 1, it is rounded up to 1; if it falls between 0 and 0.5, it is rounded down to 0.

5. Example

5.1. Identification of Hotspot Segments Along I-495/I-95

First, we analyze the I-495/I-95 corridor in Maryland to identify hotspot segments using the developed geospatial analysis. Figure 4a–l show the results taken at various time intervals during the morning and evening rush hours on 4 February 2022. The number of hotspot locations are shown in the bar chart in blue on the left and plotted on the spatial map as an orange marker on the right.

This study focuses on freeway corridors in Maryland, primarily I-495 and I-95, because these segments are among the most congested in the state and have reliable loop detector coverage. Although the analysis is currently limited to highways, the framework can be generalized to arterials and secondary roads when adequate data sources become available.

For this proof-of-concept study, we selected case days with high levels of data completeness to minimize issues of missing values or faulty sensor records. Although preprocessing steps included basic filtering and conversion of text-based speed data into numeric values, a formal protocol for handling missing data, sensor errors, and outliers was not implemented.

Future extensions of the framework will incorporate interpolation methods to estimate missing values, smoothing techniques to reduce noise and fluctuations in the sensor data, and anomaly detection algorithms to identify and correct erroneous or outlier measurements. These enhancements will systematically improve the robustness, accuracy, and reliability of the hotspot identification process, ensuring that the framework can handle incomplete or imperfect datasets more effectively in real-world applications.

5.2. Computational Efficiency Analysis

In this study, only 8 representative time points were used for evaluating computational efficiency. These time points were carefully selected to capture both peak and off-peak traffic conditions for which loop detector data were complete and validated. The purpose of using this smaller dataset was to provide a proof-of-concept demonstration of the model’s scalability and efficiency. The proposed framework is not limited to this dataset size; it is readily extendable to larger time series data, and its efficiency under real-time conditions will scale with additional input points.

The present analysis focuses on two representative weekdays (4 February and 10 November 2022). These dates were selected based on data completeness and their representation of typical morning and evening rush-hour patterns. The choice of limited case days was intended to demonstrate proof-of-concept while ensuring computational tractability. Using the selected time points and case days, we then analyzed the spatial and temporal evolution of congestion hotspots to illustrate how the framework captures traffic dynamics throughout the day.

It can be observed in Figure 4 that: (a) hotspots form and dissipate between 6–9 a.m. and 4–7 p.m. at varying rates; (b) congestion peaks and begins to dissipate around 9:30 a.m. and 5:30 p.m., respectively; and (c) a higher concentration of hotspots occurs along Beltway I-495 compared to I-95, confirming some of the top congested segments in the state as shown in Figure 1 and Figure 2.

5.3. Identification and Ranking of Hotspot Segments Statewide

In this example, we analyze speed data from key highway segments in Maryland at eight different time intervals on 10 November 2022, to identify the formation of hotspots at various locations along the highways studied. We use a threshold criterion of 40 mph to define hotspots. A sample subset of the actual dataset, comprising over 300 locations, is shown in

Table 2. Sample Dataset to Identify Hotspots.

Location	Color Code	Speed	Time	Speed1	Speed2	Speed3	Hotspot
I-270 @ MD 109 NORTH		50 MPH	11 October 2022, 12:40:05 p.m.	50	50	50	0
I-270 @ MD 109 SOUTH		Over 65 MPH	11 October 2022, 12:40:05 p.m.	65	65	65	0
I-270 @ MD 85 NORTH		Over 65 MPH	11 October 2022, 12:40:05 p.m.	65	65	65	0
I-270 @ MD 85 SOUTH		40 MPH	11 October 2022, 12:40:05 p.m.	40	40	40	1
I-270 bet Park Mills Rd and Scenic Overlook NORTH		Over 65 MPH	11 October 2022, 12:40:06 p.m.	65	65	65	0
I-270 bet Park Mills Rd and Scenic Overlook SOUTH		Over 65 MPH	11 October 2022, 12:40:06 p.m.	65	65	65	0
I-270 NB @ MSP Truck Weigh Station NORTH		Over 65 MPH	11 October 2022, 12:40:05 p.m.	65	65	65	0
I-270 NB @ New Design Road NORTH		Over 65 MPH	11 October 2022, 12:40:05 p.m.	65	65	65	0
I-270 NB @ New Design Road SOUTH		57 MPH	11 October 2022, 12:40:05 p.m.	57	57	57	0
I-270 NB approaching MD 85 NORTH		Over 65 MPH	11 October 2022, 12:40:05 p.m.	65	65	65	0

Hotspot column is set to 1 when congestion is detected. Color Code Legend: green: Normal Traffic, yellow: Congestion Detected.

. The columns labeled Speed1, Speed2, and Speed3 are intermediate dummy fields in which the text value of speed reported in the third column is converted into numeric digits through data cleansing and pruning. A hotspot is defined as follows:

$$H=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{X}_j>40\hfill \\ 1,\hfill & \mathrm{if}{X}_j\le 40\hfill \end{array}\right.$$

(16)

where H is a hotspot and $X_j$ is the speed value reported in the jth column.

This formula is equivalent to the following expression in the Excel spreadsheet: H = IF(NOT(X_j ≤ 40), 0, 1), where the IF function returns 0 if $X_j$ is greater than 40 (i.e., NOT($X_j\le 40$) is true) and 1 if $X_j$ is less than or equal to 40 (i.e., NOT($X_j\le 40$) is false).

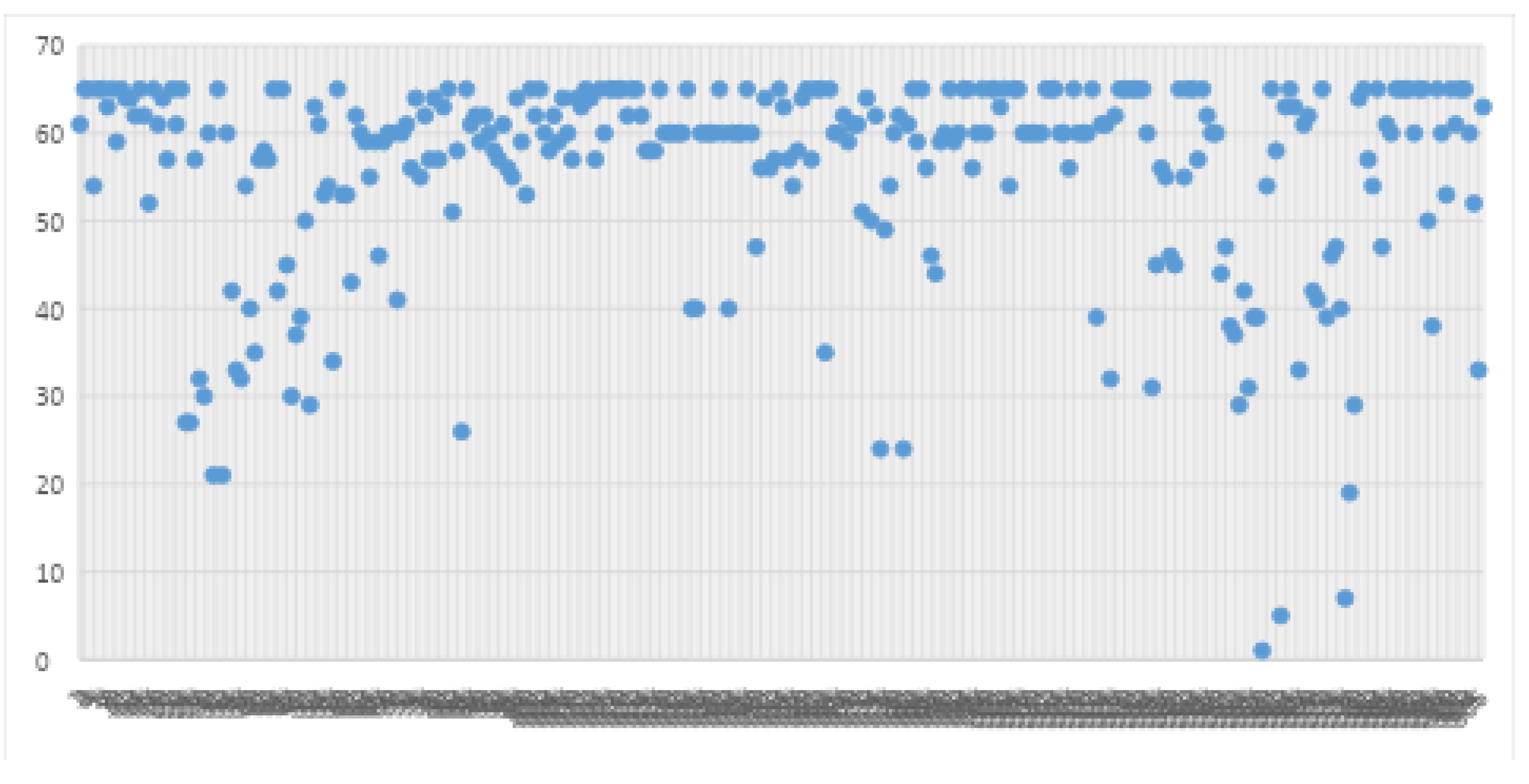
A sample speed distribution of sensor data from about 12:40 p.m. on 10 November 2022, is shown in Figure 5. The x-axis represents sensor locations, and the y-axis represents reported speed in mph. The red line indicates the threshold speed, below which locations are considered hotspots. In this example, the number of hotspots identified is 30.

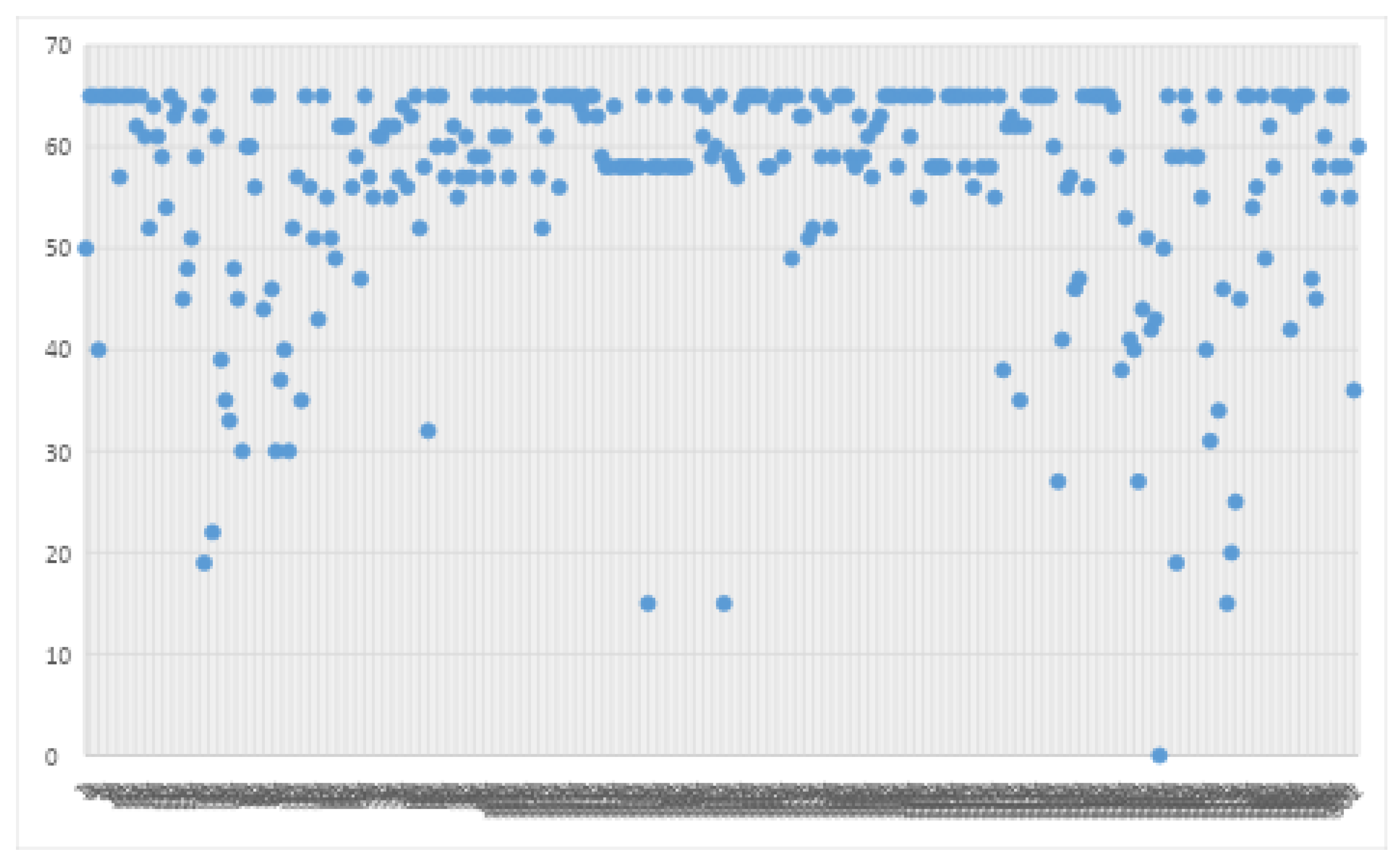
Another sample speed distribution of sensor data from about 2:07 p.m. on 10 November 2022, is shown in Figure 6. The total number of hotspots at this hour is 41, which is 11 more than that reported at 12:40 p.m., representing an increase of about 37%. Thus, it can be observed that the number of hotspots across the State begins to grow in the afternoon.

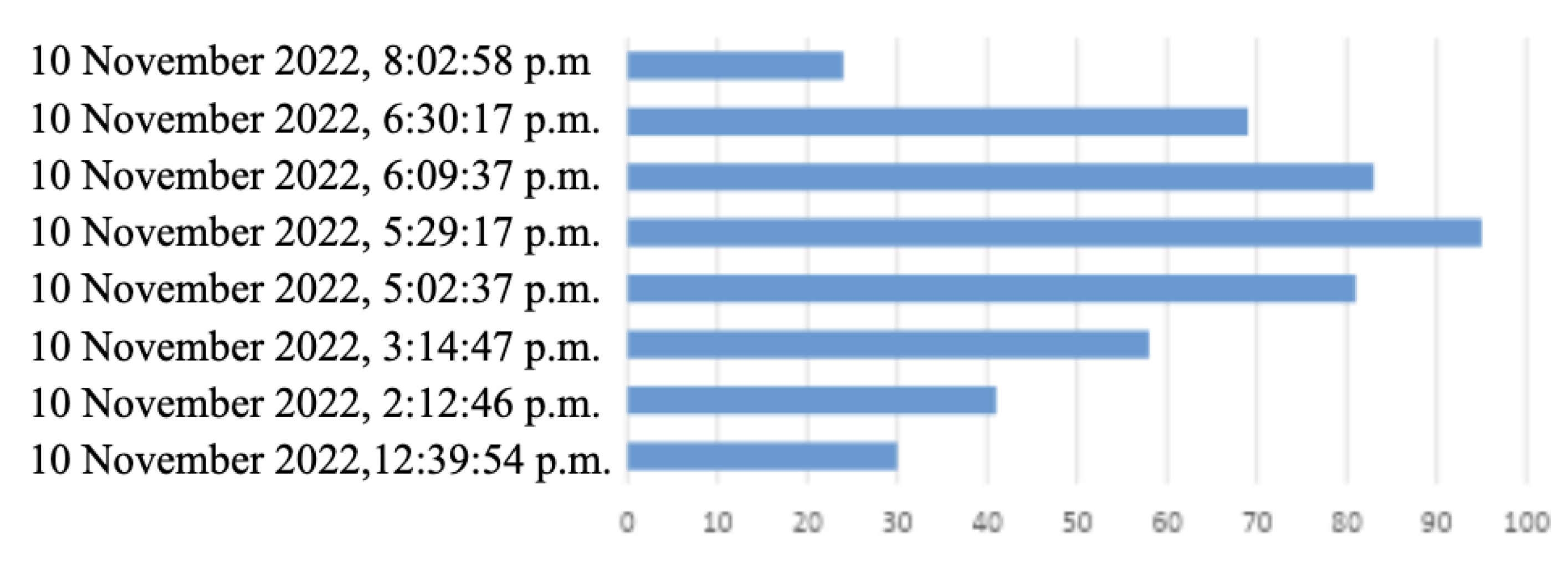
Figure 7 shows the number of hotspots identified across the eight time periods. The highest number of hotspots, 95, occurs at approximately 5:30 p.m.

Furthermore, we performed a ranking analysis to identify the top hotspots across the eight time periods using an Excel lookup function. The results are presented in

Table 3. Top Locations with Hotspots at the Eight Time Periods on 10 November 2022.

Location	12:39:54 p.m.	2:12:46 p.m.	3:14:47 p.m.	5:02:37 p.m.	5:29:17 p.m.	6:09:37 p.m.	6:30:17 p.m.	8:02:58 p.m.
I-495 I/L to MD-187 S INNER_LOOP	1	1	1	1	1	1	1	1
I-495 I/L to US-1 N NORTH	1	1	1	1	1	1	1	1
I-495 I/L to US-1 S NORTH	1	1	1	1	1	1	1	1
I-495 I/L to US-29 N NORTH	1	1	1	1	1	1	1	1
I-95/495 I/L to MD-214 W INNER_LOOP	1	1	1	1	1	1	1	1
I-95/I-495 I/L to MD-4 W INNER_LOOP	1	1	1	1	1	1	1	1
MD-185 S to I-495 I/L INNER_LOOP	1	1	1	1	1	1	1	1
MD-97 N to I-495 O/L NORTH	1	1	1	1	1	1	1	1
MD-97 N to I-495 O/L OUTER_LOOP	1	1	1	1	1	1	1	1

.

5.4. Hotspot Prediction Using ANN

We create a 2-layer ANN to predict the average likelihood of a hotspot statewide at a given time interval. We define the likelihood of a hotspot based on its deviation or skewness from the maximum number of hotspots, which is 95, observed at approximately 5:29 p.m. The input vector for the first layer represents time in hours and minutes (e.g., 1240 means 12:40 p.m., 1413 means 2:13 p.m.). The second input vector represents skewness, defined as follows:

$$S_i={\displaystyle \frac{h_i}{HH}}$$

(17)

where $S_i$ is the skewness at the ith time interval, $h_i$ is the number of hotspots at the ith time, and $HH$ is the highest number of hotspots reported (95 in our study). We round off the skewness to either 0 (if the skewness value is less than 0.5) or 1 (if the skewness value is equal to or greater than 0.5), which serves as the target for prediction. The resulting dataset is shown in

Table 4. The Dataset for Prediction.

Time Period	Number of Hotspots	Skewness	Target
1240	30	0.315789	0
1413	41	0.431579	0
1515	58	0.610526	1
1703	81	0.852632	1
1729	95	1	1
1810	83	0.873684	1
1830	69	0.726316	1
2003	24	0.252632	0

This dataset includes hotspot statistics and skewness values used to build the predictive model.

.

The ANN used in this study consists of two layers and two input features: time and skewness. This minimalist design was deliberately adopted to test the feasibility of integrating geospatial hotspot identification with neural network prediction while ensuring computational efficiency. The simplicity of the ANN also facilitates real-time implementation, although it does not fully exploit the modeling capacity of more advanced deep learning architectures.

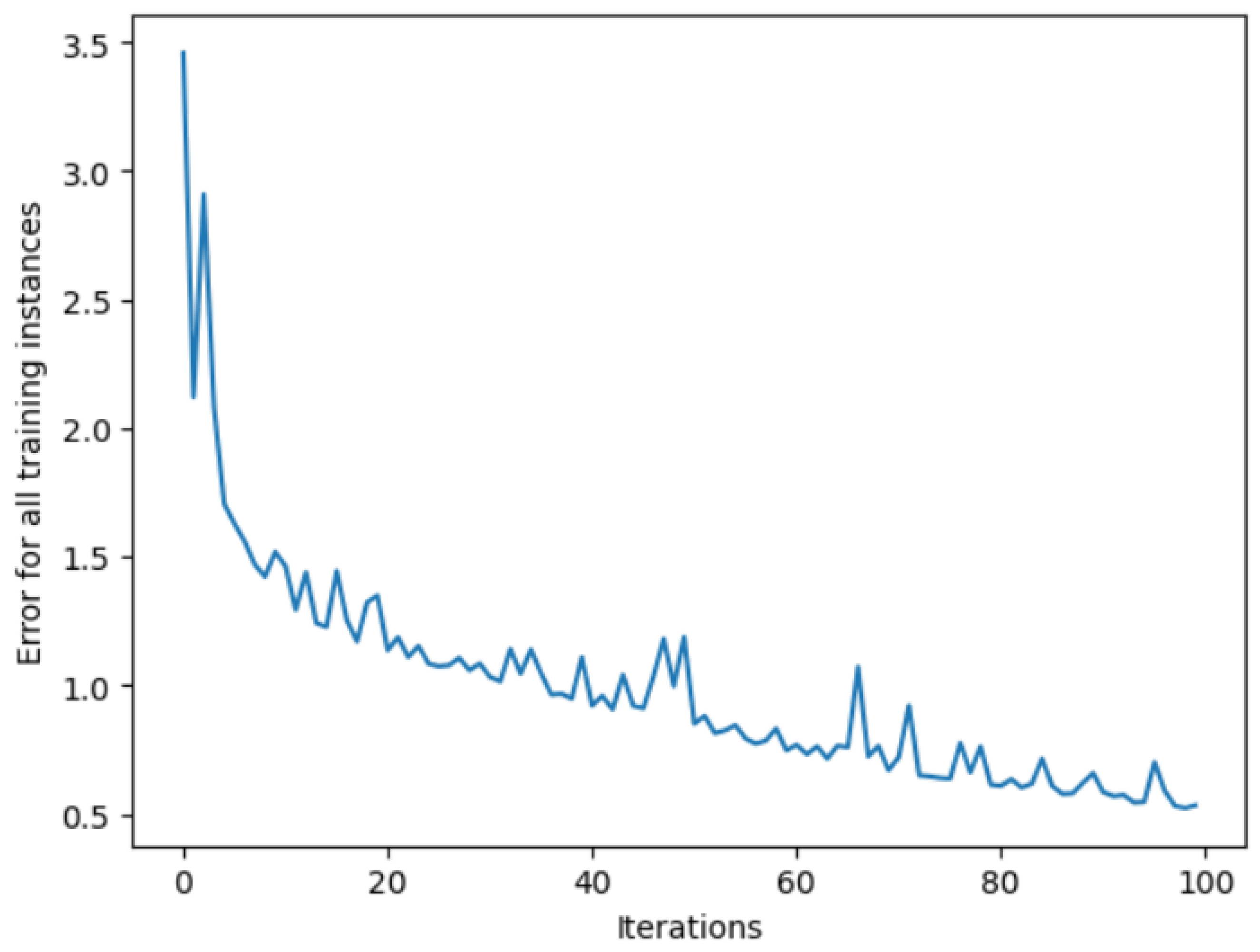
To illustrate the training process and demonstrate error minimization over successive iterations, we generate random input vectors and targets. Figure 8 shows the reduction in errors and their convergence across successive iterations. It can be observed that the error decreases from approximately 2.4% to 1.4% and then stabilizes. This indicates that the prediction results are acceptable, as a 1.4% error is relatively low. In this example, the learning rate is set to 0.1.

For our problem, the first input vector is constructed by normalizing the time interval with respect to 2400, representing 24:00 hours, and the second input vector is obtained by normalizing the number of hotspots by the total number of hotspots observed across the eight time periods studied. The resulting input vectors are shown in

Table 5. Construction of the Input Vectors.

Input_vector1	Input_vector2
1.935483871	0.062370062
1.6985138	0.085239085
1.584158416	0.120582121
1.409277745	0.168399168
1.388085599	0.197505198
1.325966851	0.172557173
1.31147541	0.143451143
1.198202696	0.04989605

The input vectors are computed features for training the prediction model.

.

Using the above input vectors and a learning rate of 0.5, the ANN achieves highly accurate predictions after training. The prediction error is reduced to approximately 0.6%, as shown in Figure 9.

The predicted values for the eight time periods are shown in Cell 88 of Figure 9, which, when rounded, perfectly correspond to the target values reported in the last column of Table 4.

The ANN was trained on a limited dataset consisting of eight time periods, selected to demonstrate proof-of-concept feasibility. While this allowed for tractable model development and testing, we acknowledge that the dataset size is insufficient to ensure statistical robustness or to fully guard against overfitting.

The predictive performance of the ANN was assessed using the misclassification error rate, defined as the percentage of instances where the predicted hotspot status differed from observed values. The model achieved a misclassification error of approximately 0.6% on the selected dataset. We note that additional validation measures, such as cross-validation, confusion matrices, Receiver Operating Characteristic (ROC) curves with Area Under Curve (AUC), and precision/recall statistics, were not implemented in this version due to the limited dataset size.

Although more complex deep learning architectures such as CNNs, LSTMs, and ensemble methods could provide enhanced predictive performance, they were not implemented here to maintain tractability and focus on proof-of-concept feasibility. The choice of a basic ANN reflects an emphasis on computational efficiency and deployment potential rather than methodological sophistication.

6. Results and Discussion

The results demonstrate that integrating geospatial analysis with artificial neural networks (ANNs) substantially enhances the prediction of congestion hotspots compared to baseline statistical methods. While descriptive statistics provide useful summaries of traffic flow patterns, the ANN–geospatial framework captures nonlinear spatial dependencies that traditional models fail to represent. For example, congestion clusters along I-495 were not only a function of volume counts but also strongly influenced by the spatial configuration of ramps and merges, which the ANN successfully learned.

From a theoretical perspective, these findings reinforce the argument that congestion is a spatially emergent phenomenon rather than a purely temporal one. This aligns with Liu et al. [2], who demonstrated that incorporating geospatial structures into traffic prediction models improves both accuracy and transferability across corridors [2]. Our results extend this theory by showing that spatial spillover effects—where congestion in one segment cascades into adjacent links—can be quantitatively captured using the proposed framework.

Practically, the framework offers several implications for transportation agencies. First, by highlighting congestion-prone zones before they reach critical thresholds, agencies can prioritize targeted interventions such as ramp metering, signal coordination, or dynamic message signs. Second, the results suggest that the framework can be adapted to other metropolitan areas with minimal recalibration, providing a scalable decision-support tool. Finally, the ability to visualize hotspot clusters in real time could support integration with connected-vehicle infrastructures, making proactive traffic management feasible.

Despite these contributions, limitations remain. The reliance on loop detector data may constrain applicability in regions with sparse sensor coverage. Future research should investigate fusing multiple data sources, such as probe vehicle and camera-based observations, to overcome these constraints. Nonetheless, the demonstrated gains in predictive accuracy suggest that the proposed approach provides both theoretical advancements and immediate practical value for urban traffic management.

We developed a geospatial framework to identify hotspots in real time using live sensor data along some of the most congested highways in Maryland, including Maryland sections of Capital Beltway 495 and I-95. The results show that sections of Capital Beltway I-495 are generally congested between 6–9 a.m. in the morning and 4–7 p.m. in the afternoon at varying rates. In the morning, the highest number of hotspots forms at about 9:12 a.m., and in the afternoon, the highest number of hotspots forms at about 5:30 p.m. More pockets of hotspots are formed along the Beltway than along I-95.

In this study, we restrict our analysis to loop detector data (speed, volume) due to its widespread availability and reliability for statewide monitoring. However, the framework is data-agnostic and can be extended to incorporate richer sources such as GPS trajectories, probe vehicle datasets, incident records, and weather information.

We developed a methodology to examine the formation of hotspots statewide in Maryland during the day. We found that the highest number of hotspots formed is 95 at about 5:30 p.m. We developed a ranking procedure to identify locations with hotspots at the eight-time intervals studied. The top locations where hotspots occurred at all eight time periods are: (1) I-495 inner loop to MD 187 south; (2) I-495 inner loop to US 1 north; (3) I-495 inner loop to US 1 south; (4) I-495 inner loop to US 29 north; (5) I-495 inner loop to MD 214 west; (6) I-495 inner loop to MD 4 west; (7) I-495 inner loop to MD 185 south; and (8) I-495 outer loop to MD 97 north. Thus, it is clear that I-495 inner loop at certain locations is more congested compared to the outer loop.

Using the information of time periods and corresponding number of hotspots, we developed two input vectors to construct a two-layer ANN to predict time periods during which a hotspot would form. The developed ANN, after training, had an error of about 0.6%. It correctly predicted the number of hotspots over the eight time periods studied.

The results presented in this section are primarily descriptive, focusing on the spatial and temporal distribution of congestion hotspots through maps, bar charts, and hotspot counts. These descriptive outputs are intended to illustrate proof-of-concept and feasibility rather than provide a full causal analysis. Future extensions of this work will include explanatory assessments of hotspot formation (e.g., bottleneck geometry, incident frequency, or spillback effects) and quantitative alignment of predicted hotspots with observed ground truth data.

The reported prediction error provides an indication of feasibility but does not include hypothesis testing or confidence intervals. Formal statistical reliability analysis was not conducted in this proof-of-concept study and will be addressed in future work.

The ANN predictions for the eight time periods showed close alignment with observed hotspot outcomes, achieving a low misclassification error (0.6%). Given the very small dataset size ($n=8$), this result should be interpreted as proof-of-concept rather than evidence of statistical generalizability.

The results should be interpreted as an applied proof-of-concept rather than a new methodological breakthrough. The study demonstrates the practicality of real-time hotspot prediction with operational data, providing a foundation for future work that will incorporate larger datasets, richer data sources, and advanced deep learning architectures.

The potential applications of this framework—such as integration into driver-facing apps or real-time dashboards for traffic management agencies—are speculative at this stage and not demonstrated in the present study. These should be viewed as future extensions, with the current contribution limited to proof-of-concept hotspot prediction using geospatial–ANN integration.

While recurring congestion locations are often familiar to both travelers and transportation agencies, the added value of this framework lies in its ability to process real-time sensor inputs and capture dynamic variations that cannot be anticipated solely from historical averages or traveler knowledge. This includes identifying earlier-than-usual congestion onset, abnormal queuing patterns, or unexpected disruptions. The framework is inherently data-agnostic and can be extended to incorporate archived historical patterns, predictive information about special events (e.g., stadium games, festivals, demonstrations), anticipated roadway capacity changes (e.g., work zones), and even weather forecasts. This integration would enable the model to provide forward-looking congestion alerts with sufficient timeliness to inform operational responses and traveler decision-making.

Compared to existing Intelligent Transportation Systems (ITS) and mobile applications that provide congestion forecasts, the contribution of this study lies in its scientific integration of geospatial hotspot identification with neural network prediction using state DOT loop detector data. The use of a lightweight ANN ensures computational efficiency, making the approach suitable for real-time application with minimal resources. Furthermore, because the framework is grounded in publicly available sensor infrastructure, it provides a transparent and replicable pathway for transportation agencies to operationalize congestion prediction without dependence on proprietary data sources.

7. Conclusions and Future Work

Predicting congestion hotspots is a prerequisite to active traffic management. The information generated by this framework could be used by transportation agencies to anticipate spillovers, allocate response resources, or adjust traffic control strategies, and by travelers to reconsider travel times, select alternate routes, or shift modes. These behavioral and operational responses can in turn disperse traffic loads, reducing the intensity of congestion at recurring hotspots. Thus, while this paper presents a proof-of-concept demonstration, it also provides a foundation for more comprehensive congestion mitigation strategies that integrate prediction, communication, and management.

In conclusion, while many ITS and commercial applications already provide congestion forecasts, the present study offers distinct advantages. First, it demonstrates a replicable proof-of-concept for operationalizing loop detector data in real time through a geospatial–ANN framework. Second, the method is lightweight and efficient, making it accessible to agencies with limited computational resources. Third, it provides a foundation that can be expanded with additional data sources (e.g., incidents, weather, planned events) to improve prediction robustness. These advantages highlight why the framework deserves attention as both a scientific contribution to traffic prediction methods and a practical tool for enhancing transportation systems management and operations.

Additional conclusions and future work are summarized below:

• Geospatial modeling is a powerful tool for detecting recurring congestion hotspots in real time using sensor data.
• Robust ML models can be developed for traffic forecasting and hotspot prediction in real time, aiding drivers in route guidance and effective rerouting strategies.
• Dynamic dashboards with geospatial maps can be deployed in conjunction with variable message signs to provide drivers with real-time traffic information.
• Mobile applications can be developed to provide advanced travel advisories, highlighting time windows with reduced congestion based on historical trends.
• The developed ANN prediction method can be extended to predict hotspots at other times of day.

It is important to note several limitations of the present study. The framework currently reduces congestion to a binary classification of hotspot versus non-hotspot using a 40-mph threshold. While this approach is consistent with practices adopted by transportation agencies and provides a tractable foundation for real-time hotspot detection, it simplifies the inherently continuous and multi-factorial nature of traffic congestion. In real-world settings, congestion dynamics are influenced by factors such as queue spillovers, shockwaves, weather conditions, and traffic incidents.

Another limitation is the geographic scope, which is restricted to Maryland freeway corridors, particularly I-495 and I-95. This excludes arterials and secondary roads where congestion is also significant. Future research will extend the framework to these roadway classes, leveraging probe vehicle, GPS, or municipal traffic management datasets to improve statewide and multimodal coverage.

A further limitation is the temporal scope of the analysis, restricted to two selected days and specific rush-hour periods. While sufficient for demonstrating feasibility, this approach does not capture broader variations such as seasonal trends, weekday–weekend differences, or incident-driven disruptions. Future research will extend the framework to multi-day, multi-season datasets to evaluate its robustness under diverse traffic conditions.

Future work will extend the framework beyond binary classification in several ways: (i) by developing multi-class models (e.g., mild, moderate, severe congestion) to capture gradations in traffic states; (ii) by employing regression-based models to predict continuous congestion metrics such as speed, density, or travel time; and (iii) by incorporating additional explanatory variables such as incident and weather data. These extensions will enhance the realism and applicability of the framework for traffic management and planning.

Another limitation is the use of a static 40-mph cutoff to define congestion. While this value aligns with Maryland DOT practice for identifying freeway congestion, it may not generalize across roadway types (e.g., arterials vs. expressways) or contexts (peak vs. off-peak conditions). To mitigate this concern, we emphasize that the framework is inherently flexible: the cutoff parameter is user-specified and can be adjusted to fit the characteristics of a given roadway network.

Additionally, the present analysis does not explicitly handle missing values, faulty sensor readings, or outliers. While these were minimized by selecting case days with high data completeness, future work will incorporate robust preprocessing protocols, including data imputation, noise filtering, and outlier detection, to enhance reliability.

The simplicity of the ANN architecture is another limitation. While sufficient for proof-of-concept and producing low prediction error, the model cannot capture the full complexity of spatio-temporal traffic dynamics. Future work will explore advanced architectures such as CNNs for spatial pattern recognition, LSTMs for temporal sequence learning, and GNNs for network-based traffic prediction. These methods are expected to improve generalizability and prediction robustness.

The small size of the training dataset (eight time periods) also raises the possibility of overfitting and limits statistical robustness. While the low prediction error demonstrates feasibility, future work will expand the dataset to include multiple days, seasonal variations, and incident-driven conditions. Larger training datasets will enable stronger validation protocols, cross-validation techniques, and improved generalizability.

The binary hotspot definition based solely on a 40-mph cutoff does not account for traffic flow variability, roadway capacity, or stochastic fluctuations. No sensitivity analysis of alternative thresholds was conducted in this study. Future extensions will include threshold sensitivity testing (e.g., 35, 40, 45 mph) and explore flow- and capacity-based definitions to provide a more comprehensive characterization of congestion.

A limitation of this study is the relatively weak validation protocol. While a misclassification error rate of 0.6% was achieved, the performance metric was narrow in scope, and no cross-validation, confusion matrix, or ROC/AUC analysis was conducted. These omissions limit the ability to assess robustness. Future research will implement more comprehensive validation procedures, including k-fold cross-validation and multiple performance measures (accuracy, precision, recall, F1-score, ROC/AUC), particularly with larger datasets.

The current results are descriptive. While maps and hotspot counts demonstrate feasibility, they do not fully explain the underlying causes of hotspot formation or provide statistical validation against observed ground truth. Future research will address this by incorporating causal analysis of congestion drivers and systematically comparing predicted versus observed hotspots using statistical performance metrics.

Another limitation is the absence of hypothesis testing, confidence intervals, and sensitivity analysis in the present work. While descriptive and predictive results demonstrate feasibility, they do not provide statistical measures of reliability. Future research will incorporate these procedures, including confidence intervals for prediction errors, hypothesis tests comparing predicted and observed congestion distributions, and sensitivity analyses of hotspot thresholds and ANN design choices.

Future extensions could incorporate dynamic thresholding methods, such as: (i) adopting Level of Service criteria that vary by roadway classification, (ii) using historical average operating speeds to set context-specific thresholds, or (iii) integrating adaptive cutoffs that adjust in real time based on observed traffic flow patterns. These modifications would improve the generalizability of the approach to a broader range of networks and operational conditions.