Deep Reinforcement Learning Approach for Traffic Light Control and Transit Priority
Abstract
1. Introduction
- Traffic signal priority for public transport. The model uses a CNN to process visual or spatial input to extract key features such as type of vehicle (public or private). Priority action might include allowing for green signals when public transport is detected. However, the reward signal is balanced in a way to prevent excessive congestion for non-priority vehicles. The CNN continuously extracts real-time features from traffic data. Based on these features, the DRL agent determines the most effective signal phase to prioritize public transport while maintaining overall traffic efficiency. The advantage of this approach is that the public transport efficiency improves without significantly disturbing general traffic.
- Experience with real-world network and traffic data. With advancements in technology, many major cities are now equipped with monitoring systems like surveillance cameras. However, most existing studies rely on experimental data to test their algorithms. Among the works that utilize real-world data, calibration and validation are, to the best of the authors’ knowledge, often not addressed or presented. In contrast, our study utilizes real-world data provided by the Agency of Mobility of Rome, collected over the course of one month. Furthermore, the network corresponding to these data represents a major corridor with 21 sequential traffic lights, unlike other studies that focus on idealized intersections.
- Complexity of intersection geometrical configuration and traffic light phases in a real-world scenario. The intersections in this study consist of multiple complex phases, including four-phase traffic lights with delayed turning movements, which present significant challenges for the DRL agent in decision making. This complexity is further heightened when considering multiple intersections, as the timing of left-turn movements for the eastbound approach and right-turn movements for the westbound approach must be coordinated with adjacent intersections to prevent spillback. A traffic management action that alleviates congestion at one intersection may inadvertently cause delays at upstream intersections. Therefore, turning movements are explicitly incorporated into the state representation to ensure that the agent can account for these interdependencies and optimize traffic flow across the network.
2. Literature Review
2.1. State Representation
2.2. Reward Function
2.3. Action Space Definition
2.4. Markov Decision Process
2.5. Bellman Equation
2.6. Deep Neural Networks
2.7. Transit Signal Priority Using DLR
3. Problem Definition
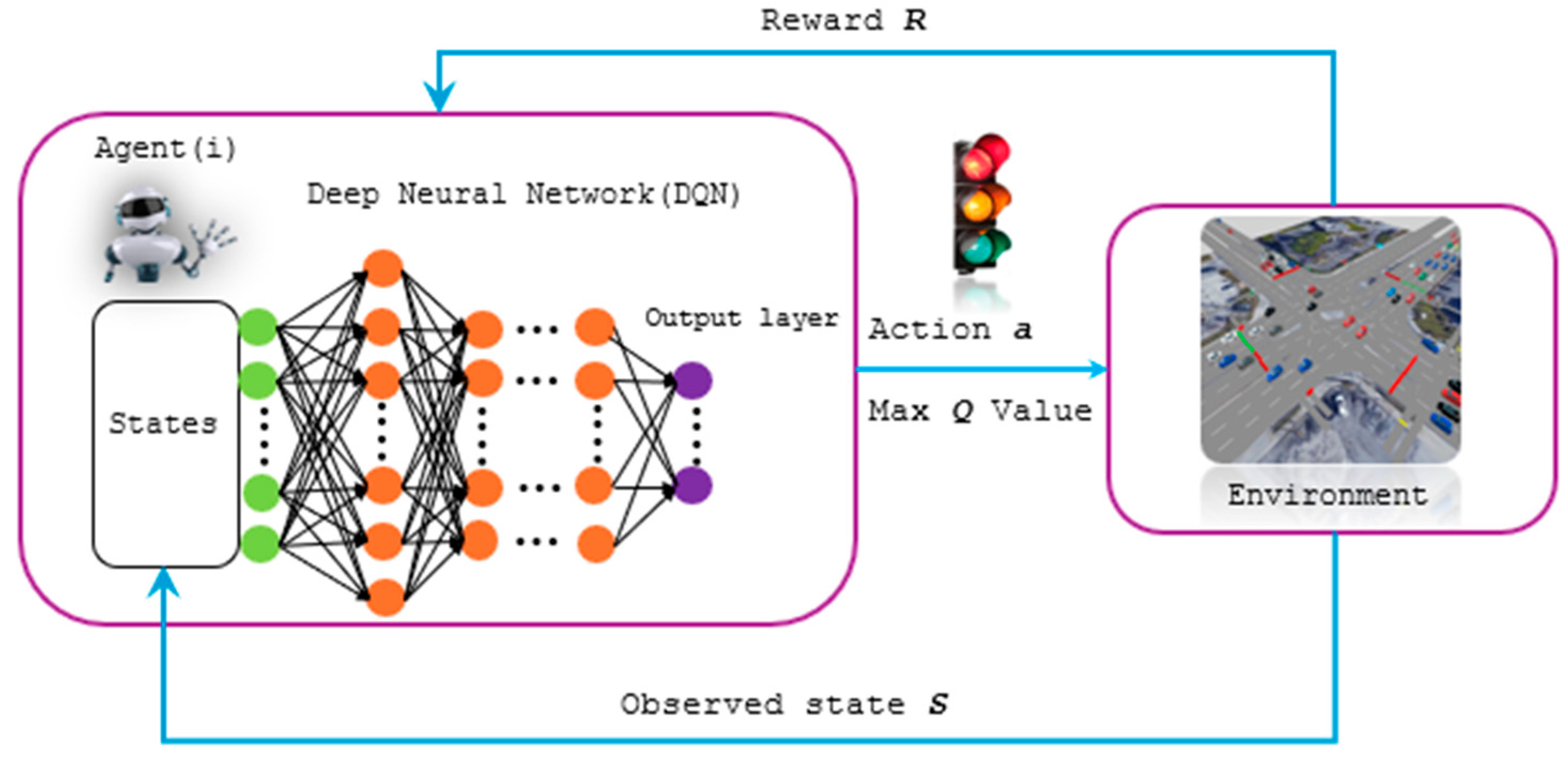
4. Framework
- Offline Stage: In the offline stage, a fixed timetable for the traffic lights is set. Data samples are collected by allowing traffic to flow through the system based on the fixed timetable. During this stage, the model logs the collected data samples.
- Training: The collected data samples are then used for training the model. The training process involves using the logged data samples to update the model’s parameters.
- Online Stage: After the model is trained, it proceeds to the online stage. In a regular time interval (Δt), the traffic light agent observes the current state (s) of its environment. The agent then performs an action (a) based on the observed state, which will determine whether it changes to another light phase or not. The action-selection strategy follows the ε-greedy strategy by combining exploration (doing random actions with probability ε) and exploitation (selecting the action with the maximum expected reward).
- Observing Rewards: After performing the action, the agent observes the environment and receives a reward (r) based on how much the action has improved the traffic conditions. The reward is a measure of the quality of the agent’s decision and indicates the impact of the action on traffic flow.
- Memory and Network Updates: The tuple (s, a, r) consisting of the observed state, performed action, and received reward is stored in a memory buffer. After a certain number of timestamps or a specific condition is met, the agent updates the network by using the logged data in the memory buffer.
4.1. Agent Design and Reward Calculations
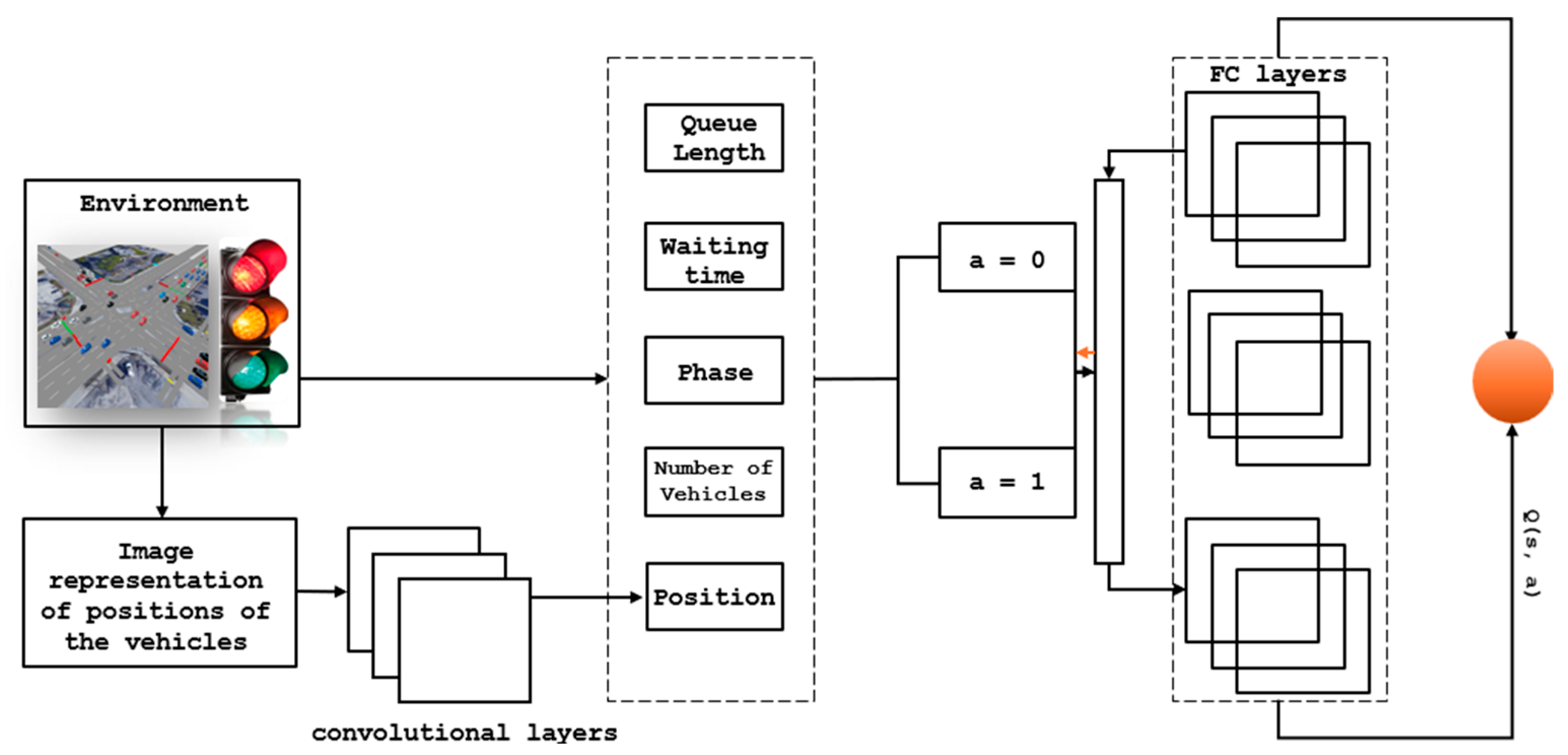
- S: It represents our state, which includes the queue length on the lane, the number of vehicles, and the average waiting time. The state also includes the position of the vehicle, as well as the current phase and the next phase.
- A: Action is defined as changing the light to the next phase (a = 1) or keeping the current phase (a = 0).
- R: Two different rewards were calculated for the scenario without TSP (hereafter scenario 1) and the scenario with TSP (hereafter scenario 2):
- The sum of the queue length: The queue length () for a specific lane is determined by counting the total number of vehicles in the queue plus the minimum gap between them.
- The sum of time loss for all vehicles due to driving below the ideal speed (the ideal speed includes the individual speed factor; slowdowns due to intersection).
- The number of traffic light switches involves counting the occurrences when the current phase of the traffic lights is either kept unchanged (C = 0) or changed to a different phase (C = 1).
- The sum of waiting time is the sum of the waiting time of all the vehicles across all lanes approaching the intersection ().
- The total number of vehicles that have passed the intersection during the time interval τ after the last action (n).
- The sum of the queue length: The queue length () for a specific lane.
- The sum of the time loss for private vehicles.
- The sum of the time loss for public transport ().
- The number of traffic light switches involves counting the occurrences when the current phase of the traffic lights is either kept unchanged (C = 0) or changed to a different phase (C = 1).
- The sum of waiting time is the sum of the waiting time of private vehicles across all lanes approaching the intersection ().
- The sum of the waiting time of public transport vehicles approaching the intersection .
- The total number of vehicles that have passed the intersection during the time interval τ after the last action (n).
4.2. Network Structure
4.3. Parameter Setting
5. Experimental Environment
5.1. Microsimulation
5.2. Simulation of Urban Mobility (SUMO)
- Road network file (net.xml): This file is responsible for creating the road network and configuring specific road characteristics (Figure 4).
- Traffic route file (rou.xml): In this file, traffic requirements are input, and traffic scenarios are generated accordingly.
- Queue output: Calculation of the actual queue in front of a junction based on lanes.
- Trip-info output (Trip information): Aggregated data on each vehicle’s trip (departure time, arrival time, duration, and route length)
- Emission output: All vehicle emission values for each simulation step
5.3. Simulation Characteristics
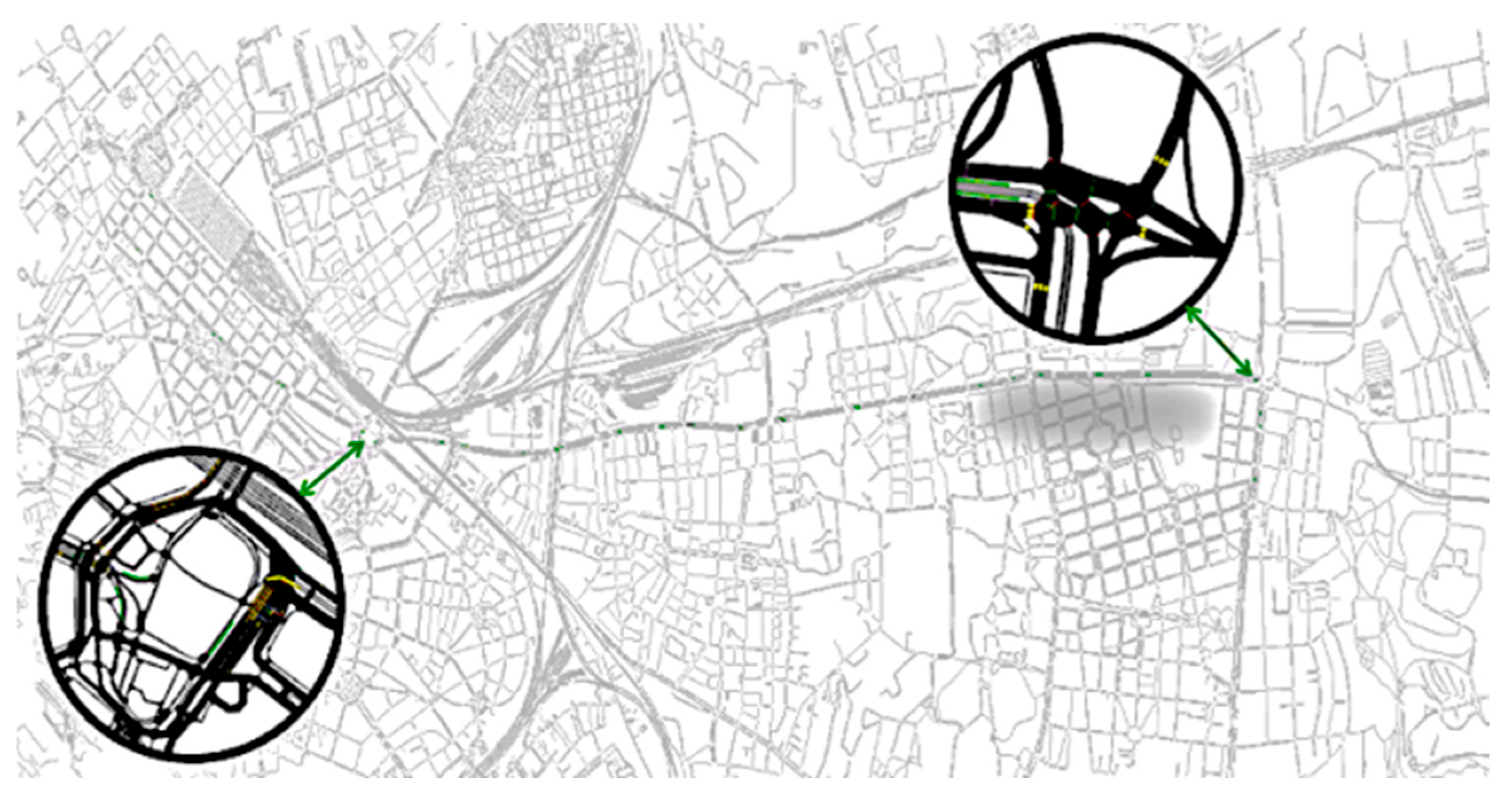
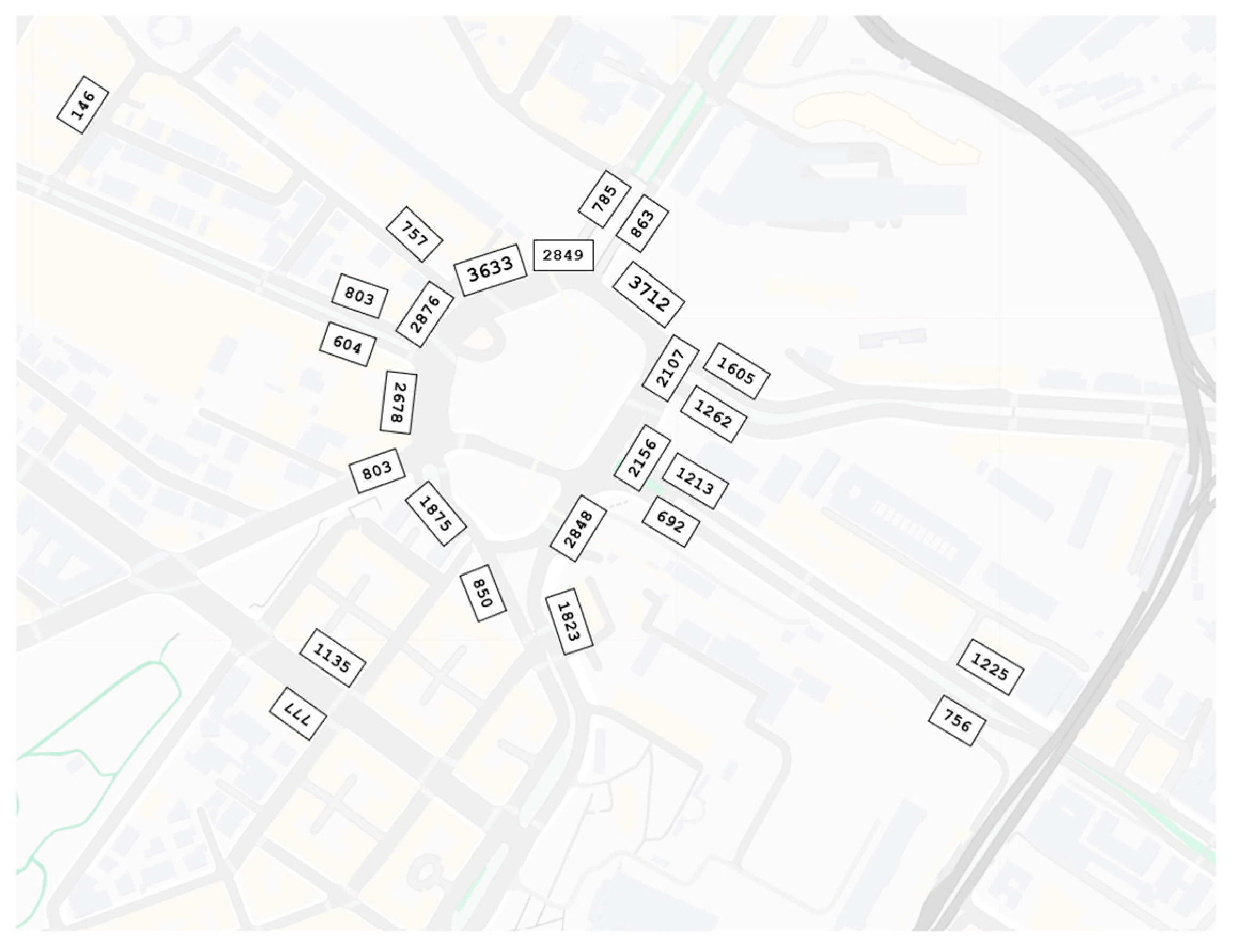
6. Study Area
7. Data Collection
8. Calibration
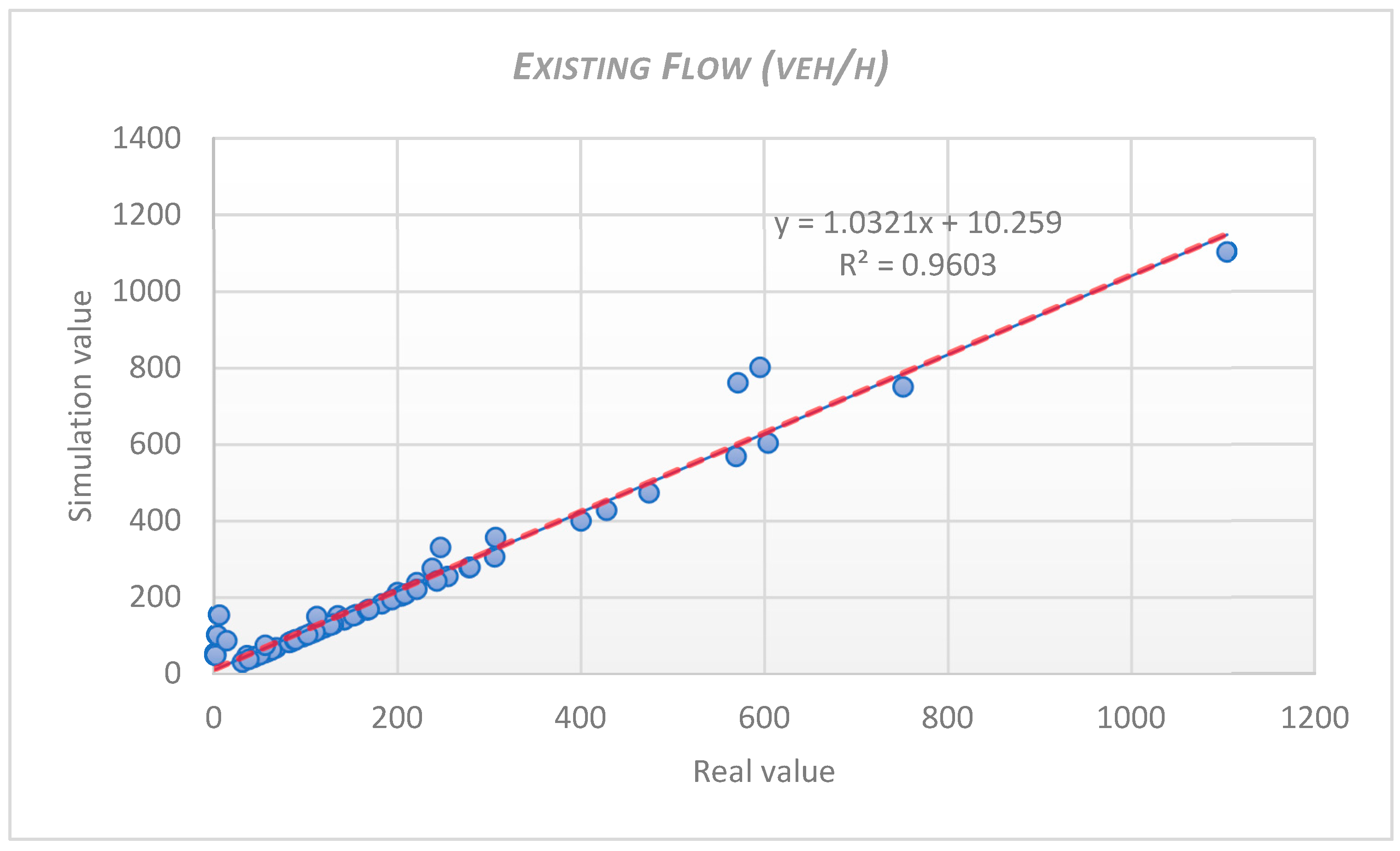
9. Validation
GEH Static
10. Results
10.1. Private Vehicles
10.2. Emissions
10.3. Public Transport (Trams)
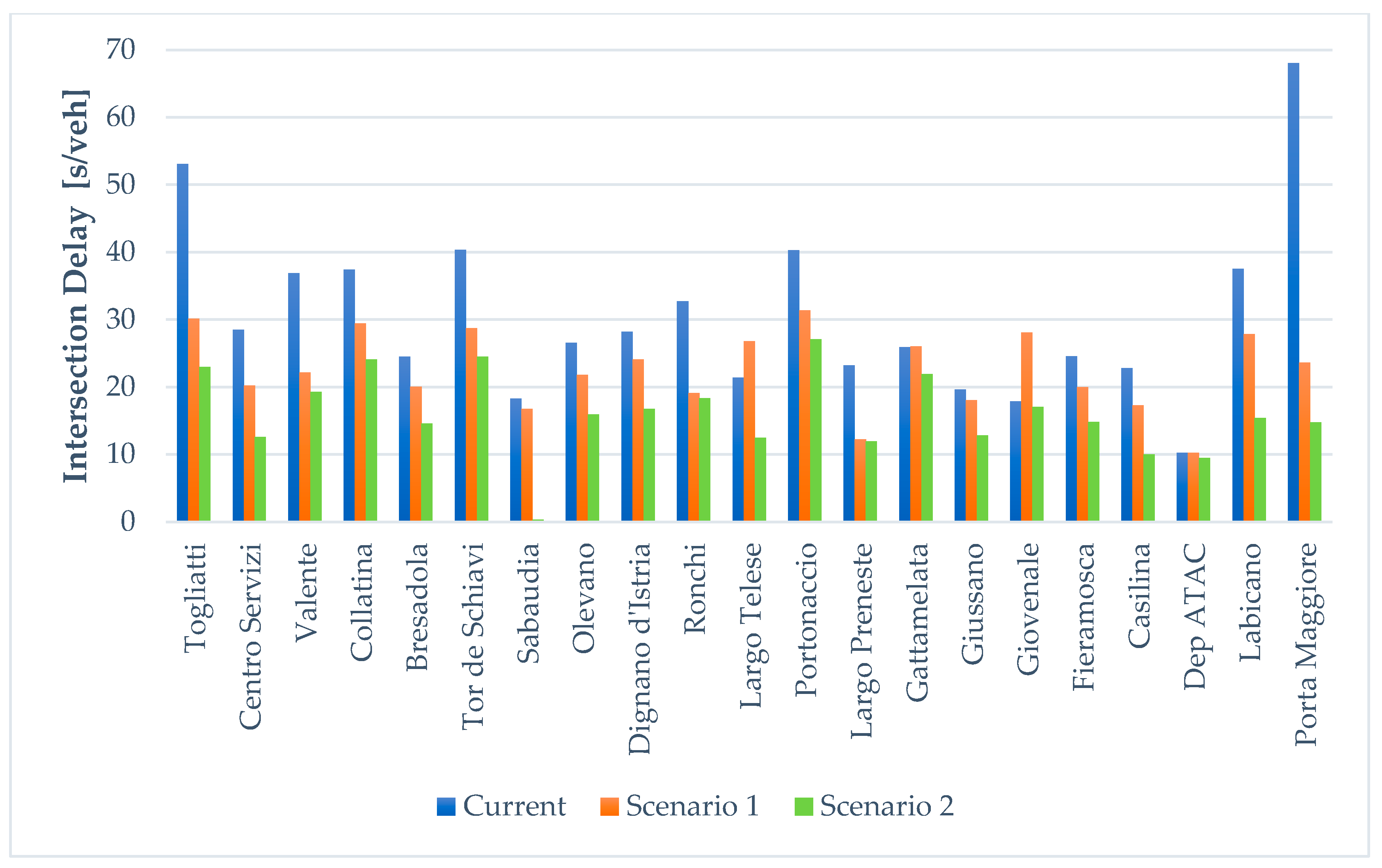
10.4. Intersection Delay
10.5. Private Vehicle vs. Public Transport
11. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mansouryar, S.; Shojaei, K.; Colombaroni, C.; Fusco, G. A Microsimulation Study of Bus Priority System with Pre-Signaling. Transp. Res. Procedia. 2024, 78, 507–514. [Google Scholar] [CrossRef]
- Wei, H.; Yao, H.; Zheng, G.; Li, Z. IntelliLight: A Reinforcement Learning Approach for Intelligent Traffic Light Control. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, London, UK, 19–23 August 2018. [Google Scholar]
- Wei, H.; Zheng, G.; Gayah, V.; Li, Z. Recent Advances in Reinforcement Learning for Traffic Signal Control: A Survey of Models and Evaluation. SIGKDD Explor. Newsl. 2021, 22, 12–18. [Google Scholar] [CrossRef]
- Dion, F.; Rakha, H.; Kang, Y.S. Comparison of Delay Estimates at Under-Saturated and over-Saturated Pre-Timed Signalized Intersections. Transp. Res. Part B Methodol. 2004, 38, 99–122. [Google Scholar] [CrossRef]
- Gershenson, C. Design and Control of Self-Organizing Systems; CopIt ArXives: Mexico City, Mexico, 2007; Volume 132. [Google Scholar]
- Varaiya, P. The Max-Pressure Controller for Arbitrary Networks of Signalized Intersections. In Advances in Dynamic Network Modeling in Complex Transportation Systems; Springer: New York, NY, USA, 2013. [Google Scholar]
- Kuyer, L.; Whiteson, S.; Bakker, B.; Vlassis, N. Multiagent Reinforcement Learning for Urban Traffic Control Using Coordination Graphs. In Machine Learning and Knowledge Discovery in Databases; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2008; Volume 5211. [Google Scholar]
- Mannion, P.; Duggan, J.; Howley, E. An Experimental Review of Reinforcement Learning Algorithms for Adaptive Traffic Signal Control. In Autonomic Road Transport Support Systems; Birkhäuser: Cham, Switzerland, 2016. [Google Scholar]
- Watkins, C.J.C.H.; Dayan, P. Q-Learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Balaji, P.G.; German, X.; Srinivasan, D. Urban Traffic Signal Control Using Reinforcement Learning Agents. IET Intell. Transp. Syst. 2010, 4, 177–188. [Google Scholar] [CrossRef]
- Arel, I.; Liu, C.; Urbanik, T.; Kohls, A.G. Reinforcement Learning-Based Multi-Agent System for Network Traffic Signal Control. IET Intell. Transp. Syst. 2010, 4, 128–135. [Google Scholar] [CrossRef]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Genders, W.; Razavi, S. Using a Deep Reinforcement Learning Agent for Traffic Signal Control; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Mazaheri, A.; Alecsandru, C. New Signal Priority Strategies to Improve Public Transit Operations in an Urban Corridor. Can. J. Civ. Eng. 2023, 50, 737–751. [Google Scholar] [CrossRef]
- Bie, Y.; Ji, Y.; Ma, D. Multi-Agent Deep Reinforcement Learning Collaborative Traffic Signal Control Method Considering Intersection Heterogeneity. Transp. Res. Part C Emerg. Technol. 2024, 164, 104663. [Google Scholar] [CrossRef]
- Li, M.; Pan, X.; Liu, C.; Li, Z. Federated Deep Reinforcement Learning-Based Urban Traffic Signal Optimal Control. Sci. Rep. 2025, 15, 11724. [Google Scholar] [CrossRef]
- Yu, J.; Laharotte, P.A.; Han, Y.; Leclercq, L. Decentralized Signal Control for Multi-Modal Traffic Network: A Deep Reinforcement Learning Approach. Transp. Res. Part C Emerg. Technol. 2023, 154, 104281. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal. Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Perera, A.T.D.; Kamalaruban, P. Applications of Reinforcement Learning in Energy Systems. Renew. Sustain. Energy Rev. 2021, 137, 110618. [Google Scholar] [CrossRef]
- Xiao, L.; Lu, X.; Xu, T.; Zhuang, W.; Dai, H. Reinforcement Learning-Based Physical-Layer Authentication for Controller Area Networks. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2535–2547. [Google Scholar] [CrossRef]
- Lu, X.; Xiao, L.; Xu, T.; Zhao, Y.; Tang, Y.; Zhuang, W. Reinforcement Learning Based PHY Authentication for VANETs. IEEE Trans. Veh. Technol. 2020, 69, 3068–3079. [Google Scholar] [CrossRef]
- Lin, Y.; Dai, X.; Li, L.; Wang, F.-Y. An Efficient Deep Reinforcement Learning Model for Urban Traffic Control. arXiv 2018, arXiv:1808.01876. [Google Scholar] [CrossRef]
- Bouktif, S.; Cheniki, A.; Ouni, A.; El-Sayed, H. Traffic Signal Control Based on Deep Reinforcement Learning with Simplified State and Reward Definitions. In Proceedings of the 2021 4th International Conference on Artificial Intelligence and Big Data, ICAIBD 2021, Chengdu, China, 28–31 May 2021. [Google Scholar]
- Bouktif, S.; Cheniki, A.; Ouni, A.; El-Sayed, H. Deep Reinforcement Learning for Traffic Signal Control with Consistent State and Reward Design Approach. Knowl. Based Syst. 2023, 267, 110440. [Google Scholar] [CrossRef]
- Gong, Y.; Abdel-Aty, M.; Cai, Q.; Rahman, M.S. Decentralized Network Level Adaptive Signal Control by Multi-Agent Deep Reinforcement Learning. Transp. Res. Interdiscip. Perspect. 2019, 1, 100020. [Google Scholar] [CrossRef]
- Liang, X.; Du, X.; Wang, G.; Han, Z. A Deep Reinforcement Learning Network for Traffic Light Cycle Control. IEEE Trans. Veh. Technol. 2019, 68, 1243–1253. [Google Scholar] [CrossRef]
- Zheng, G.; Zang, X.; Xu, N.; Wei, H.; Yu, Z.; Gayah, V.; Xu, K.; Li, Z. Diagnosing Reinforcement Learning for Traffic Signal Control. arXiv 2019, arXiv:1905.04716. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction. IEEE Trans. Neural. Netw. 2005, 9, 104281. [Google Scholar] [CrossRef]
- Gao, J.; Shen, Y.; Liu, J.; Ito, M.; Shiratori, N. Adaptive Traffic Signal Control: Deep Reinforcement Learning Algorithm with Experience Replay and Target Network. arXiv 2017, arXiv:1705.02755. [Google Scholar] [CrossRef]
- Wei, H.; Chen, C.; Zheng, G.; Wu, K.; Gayah, V.; Xu, K.; Li, Z. Presslight: Learning Max Pressure Control to Coordinate Traffic Signals in Arterial Network. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Vidali, A.; Crociani, L.; Vizzari, G.; Bandini, S. A Deep Reinforcement Learning Approach to Adaptive Traffic Lights Management. In Proceedings of the CEUR Workshop Proceedings, Grosseto, Italy, 16–19 June 2019; Volume 2404. [Google Scholar]
- Wu, T.; Zhou, P.; Liu, K.; Yuan, Y.; Wang, X.; Huang, H.; Wu, D.O. Multi-Agent Deep Reinforcement Learning for Urban Traffic Light Control in Vehicular Networks. IEEE Trans. Veh. Technol. 2020, 69, 8243–8256. [Google Scholar] [CrossRef]
- Noaeen, M.; Naik, A.; Goodman, L.; Crebo, J.; Abrar, T.; Abad, Z.S.H.; Bazzan, A.L.C.; Far, B. Reinforcement Learning in Urban Network Traffic Signal Control: A Systematic Literature Review. Expert. Syst. Appl. 2022, 199, 116830. [Google Scholar] [CrossRef]
- Chen, R.; Fang, F.; Sadeh, N. The Real Deal: A Review of Challenges and Opportunities in Moving Reinforcement Learning-Based Traffic Signal Control Systems Towards Reality. In Proceedings of the CEUR Workshop Proceedings, Ljubljana, Slovenia, 29 November 2022; Volume 3173. [Google Scholar]
- Shabestary, S.M.A.; Abdulhai, B. Deep Learning vs. Discrete Reinforcement Learning for Adaptive Traffic Signal Control. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Maui, HI, USA, 4–7 November 2018; Proceedings, ITSC; Volume 2018. [Google Scholar]
- Li, L.; Lv, Y.; Wang, F.Y. Traffic Signal Timing via Deep Reinforcement Learning. IEEE/CAA J. Autom. Sin. 2016, 3, 247–254. [Google Scholar] [CrossRef]
- Kiran, B.R.; Thomas, D.M.; Parakkal, R. An Overview of Deep Learning Based Methods for Unsupervised and Semi-Supervised Anomaly Detection in Videos. J. Imaging 2018, 4, 36. [Google Scholar] [CrossRef]
- Ling, K.; Shalaby, A. Automated Transit Headway Control via Adaptive Signal Priority. J. Adv. Transp. 2004, 38, 45–67. [Google Scholar] [CrossRef]
- Long, M.; Zou, X.; Zhou, Y.; Chung, E. Deep Reinforcement Learning for Transit Signal Priority in a Connected Environment. Transp. Res. Part C Emerg. Technol. 2022, 142, 103814. [Google Scholar] [CrossRef]
- Chu, T.; Wang, J.; Codeca, L.; Li, Z. Multi-Agent Deep Reinforcement Learning for Large-Scale Traffic Signal Control. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2901791. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholm, Sweden, 10–15 July 2018; Volume 5. [Google Scholar]
- Barcelo, J. Fundamentals of Traffic Simulation; Springer: New York, NY, USA, 2010; Volume 145. [Google Scholar]
- Krajzewicz, D.; Hertkorn, G. SUMO (Simulation of Urban MObility) An Open-Source Traffic Simulation. In Proceedings of the 4th Middle East Symposium on Simulation and Modelling, Berlin-Adlershof, Germany, 1–30 September 2002. [Google Scholar]
- Feldman, O. The GEH Measure and Quality of the Highway Assignment Models. In Proceedings of the Association for European Transport and Contributors, Glasgow, Scotland, 8–10 October 2012. [Google Scholar]






| Model Parameter | Value |
|---|---|
| Discount factor γ | 0.9 |
| Learning rate a | 0.001 |
| Exploration ϵ | 0.05 |
| Model update time interval | 4 s |
| Memory size | 20,000 |
| Parameter | Passenger Cars | Buses | Trams |
|---|---|---|---|
| Max Speed | 50 km/h | 50 km/h | 50 km/h |
| Speed Distribution | normc (1.00, 0.10, 0.20, 2.00) | normc (0.80, 0.08, 0.15, 1.50) | normc (0.80, 0.08, 0.15, 1.50) |
| Max Acceleration | 2.5 m/s2 | 2.5 m/s2 | 2.5 m/s2 |
| Max Deceleration | 4.5 m/s2 | 4.5 m/s2 | 4.5 m/s2 |
| Vehicle Length | 4 m | 12 m | 33 m |
| Maximum Capacity | 4 people | 70 passengers | 270 passengers |
| Minimum Gap | 1.0 m | 1.5 m | 2.5 m |
| Car-Following Model | Krauss | Krauss | Krauss |
| Speed Factor | Default | Default | Default |
| Emission Model | HBEFA3/PC_G_EU4 | HBEFA3 (City bus profile) | HBEFA3/PC_G_EU4 (Tram profile) |
| Traffic Flow Model | Poisson distribution | Frequency headway | Frequency headway |
| RMSE | RMSPE | MAPE | GEH |
|---|---|---|---|
| 44.77 | %27 | 10.04 | 89% < 4 |
| Current | Scenario 1 | Scenario 2 |
|---|---|---|
| 10,713,723 [m] | 4,943,131 [m] | 7,673,754 [m] |
| Emissions | Current | Scenario 1 | Scenario 2 |
|---|---|---|---|
| 196.90 [Kg] | 113.65 [Kg] | 142.52 [Kg] | |
| 9152.4 [T] | 6019.32 [T] | 7095.21 [T] | |
| 3918.75 [T] | 2482.90 [T] | 2979.57 [T] |
| Tram ID | Current | Scenario 1 | Scenario 2 |
|---|---|---|---|
| 5 | 548.67 | 443.42 | 318.08 |
| 14 | 680.62 | 507.69 | 420.38 |
| 19 | 377.18 | 233.09 | 156.64 |
| Intersection | Current [s] | Scenario 1 [s] | D1 [%] | Scenario 2 [s] | D2 [%] |
|---|---|---|---|---|---|
| Togliati | 53 | 25 | 53 | 30 | 43 |
| Centro servizi | 28 | 13 | 54 | 20 | 29 |
| Valente | 36 | 19 | 47 | 22 | 39 |
| Collatina | 37 | 23 | 38 | 29 | 22 |
| Bresadola | 24 | 13 | 46 | 20 | 17 |
| Tor de schiavi | 40 | 25 | 38 | 28 | 30 |
| Sabaudia | 18 | 8 | 56 | 16 | 11 |
| Olevano | 26 | 15 | 42 | 21 | 19 |
| Dignano d’istia | 28 | 16 | 43 | 24 | 14 |
| Ronchi | 32 | 19 | 41 | 19 | 41 |
| Largo telese | 21 | 14 | 33 | 26 | −24 |
| Portonaccio | 40 | 27 | 32 | 31 | 23 |
| Largo preneste | 23 | 12 | 48 | 12 | 48 |
| Gattamelata | 25 | 20 | 20 | 26 | −4 |
| Giussano | 19 | 12 | 37 | 18 | 5 |
| Giovenale | 17 | 17 | 0 | 28 | −65 |
| Fieramosca | 24 | 13 | 46 | 20 | 17 |
| Casilina | 22 | 9 | 59 | 17 | 23 |
| Dep Atac | 10 | 9 | 10 | 10 | 0 |
| Labicano | 37 | 15 | 59 | 27 | 27 |
| Porta maggiore | 68 | 16 | 76 | 23 | 66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mansouryar, S.; Colombaroni, C.; Isaenko, N.; Fusco, G. Deep Reinforcement Learning Approach for Traffic Light Control and Transit Priority. Future Transp. 2025, 5, 137. https://doi.org/10.3390/futuretransp5040137
Mansouryar S, Colombaroni C, Isaenko N, Fusco G. Deep Reinforcement Learning Approach for Traffic Light Control and Transit Priority. Future Transportation. 2025; 5(4):137. https://doi.org/10.3390/futuretransp5040137
Chicago/Turabian StyleMansouryar, Saeed, Chiara Colombaroni, Natalia Isaenko, and Gaetano Fusco. 2025. "Deep Reinforcement Learning Approach for Traffic Light Control and Transit Priority" Future Transportation 5, no. 4: 137. https://doi.org/10.3390/futuretransp5040137
APA StyleMansouryar, S., Colombaroni, C., Isaenko, N., & Fusco, G. (2025). Deep Reinforcement Learning Approach for Traffic Light Control and Transit Priority. Future Transportation, 5(4), 137. https://doi.org/10.3390/futuretransp5040137






