Abstract
While there are studies on bicycle crashes, no study has investigated the spatial analysis of fatal and injury bicycle crashes in the state of Ohio. This study fills this gap in the literature by mapping and investigating the bicycle crash-prone areas in the state. It analyzes fatal and injury bicycle crashes from 2014 to 2023 by utilizing four exploratory spatial data analysis techniques: nearest neighbor index, global Moran’s I index, hotspot and cold spot analysis, and local Moran’s I index at the state, county, census tract, and block group levels. Results vary slightly across techniques and spatial scales but consistently show that bicycle crash locations are clustered statewide, particularly in the state’s major metropolitan areas such as Columbus, Cincinnati, Toledo, Cleveland, and Akron. These urban centers have emerged as hotspots, indicating a higher vulnerability to bicycle crashes. While global Moran’s I analysis at the county level does not reveal significant spatial autocorrelation, a strong positive autocorrelation is observed at both the census tract (p = 0.01) and block group (p = 0.00) levels, indicating significant high clustering, signifying that finer geographical units yield more robust results. Identifying specific hotspots and vulnerable areas provides valuable insights for policymakers and urban planners to implement effective safety measures and improve conditions for non-motorized road users in Ohio. The study highlights the need for targeted mitigation strategies in high-risk areas, including comprehensive safety measures, infrastructure improvements, policy changes, and community-focused initiatives to reduce crash risk and create safer environments for cyclists throughout Ohio’s urban fabric.
1. Introduction
Bicycles have gained huge popularity as an active transport mode in Europe and elsewhere around the globe. Bike-sharing programs and dedicated bike lanes are common in these countries. Bicycling is beneficial for people—it improves health, reduces obesity, discourages motor vehicle usage, decreases vehicular traffic, reduces carbon footprints, and thereby cuts down on environmental pollution [1]. The transportation industry is a significant energy consumer and contributes to the production of primary pollutants and greenhouse gases (GHGs). In the United States in 2022, transportation was the major contributor to GHGs, accounting for 29% of all GHG emissions [2]. About 27% of US energy consumption in 2022 was from transportation [3], and 38% of all carbon dioxide emissions from burning fossil fuels [4] came from the transportation sector. In addition, transportation is also responsible for about 60% of carbon monoxide emissions [5]. Therefore, efforts to make bicycling an attractive and viable mode of transportation can facilitate a reduction in GHG and carbon monoxide emissions.
Studies have linked bicycle crashes to the built environment, bicycle infrastructure (bicycle lanes), motor vehicles, demographics, road network, traffic characteristics, and socioeconomic factors. Several studies conclude that infrastructure and the built environment are critical factors dominating the outcome of bicycle crashes [6]. One of the primary factors that leads to the seriousness of injury in a bicycle and motor vehicle collision is the high speed of the motor vehicle [7,8,9]. A speed of more than 80 km/h increases the possibility of fatality in a crash by 16 times than that of a speed of 32 km/h [8]. Although speeding-related crashes are not high, they result in high fatal injuries [10]. Other factors that are found to be critical are intoxication (either driver or bicyclist), inclement weather, lack of streetlights, crashes with trucks, head-on collisions, and involvement of older people [11,12].
Recent statistics on the safety of bicyclists tend to discourage people from choosing bicycles over motor vehicles, even for shorter routes [13,14,15]. Poor infrastructure, longer distances, mixed land use, and sometimes weather conditions add to the problem. Bicyclists are among the most vulnerable road user groups in terms of the probability of getting injured, as they ride on the same road as motor vehicles [16]. The literature shows that real and perceived safety do not necessarily coincide. While perceived safety without real safety creates a false sense of safety, absolute safety without perceived safety prevents people from using bicycles. Both types of safety are necessary to create a thriving cycling environment [7]. For example, in many communities in North America, the public perceives that using a bicycle is a perilous activity, causing a small proportion of people to use bicycle mode, while in many communities in Europe, there is no such public perception. In the European Union, the bike mode ratio is more than 30%, with some of the lowest total collisions in the world [17]. European countries such as the Netherlands, Sweden, and Norway have worked on reducing motor vehicle usage, and it is observed that they have been successful in increasing pedestrian and bicycle usage in recent times. Studies show that as the number of cyclists on the road increases, the probability of engaging in a collision also increases [17]. Although some studies find that the total number of general collisions increases with an increased number of road users, the collision per cyclist decreases [18]. This is known as the ‘safety in numbers’ hypothesis [19,20,21,22], which roughly means that after a certain level, bicyclists’ safety increases as the number of bicycle users increases.
There is a need to emphasize thorough research into the fatalities among bicycle users and determine factors that may affect the severity of crashes. Using a generalized linear logistic regression model to study fatal crashes, Bíl et al. [23] observed that the worst fatal crashes occur when the driver drives faster than the speed limit. Also, automobile users cause two times more fatal injuries to bicyclists as bicyclists do to themselves. Usually, cyclists are to be blamed when they deny the right-of-way to motor vehicles, leading to severe injuries for the cyclists themselves. Nighttime crashes, especially in areas without proper lighting, often result in fatalities. It is recommended to use reflective jackets, good lighting, taillights, and reflective elements to avoid nighttime crashes [23]. Additionally, having a dedicated bicycle lane is the best solution, complemented by lowering speed limits at critical junctions.
This study is based on analyzing bicycle crash data in Ohio from 2014 to 2023. It employs four exploratory spatial data analysis (ESDA) techniques to identify high-risk locations of crashes at the county, census tract, and block group levels. The techniques are the nearest neighbor index (NNI), global Moran’s I, hotspot and cold spot analysis, and local Moran’s I Index, also known as Local Indicators of Spatial Association (LISA). The primary objective is to find hotspots in Ohio with a high probability of bicycle crashes, requiring authorities’ immediate attention. The secondary objective is to find the best technique among the four spatial statistical methods that can be used for future studies. Measures that can be implemented to reduce crashes and encourage people to ride bicycles are also recommended in the study. While there are studies on bicycle crashes, no study has investigated the spatial analysis of fatal and injury bicycle crashes in the state of Ohio. This is the first exploratory study of its type that aims to fill this gap in the literature by mapping and investigating the bicycle crash-prone areas in the state so that planners, engineers, and policymakers can take necessary measures to combat bicycle crashes.
2. Literature Review
2.1. Existing Studies on Macrolevel and Microlevel Analysis of Non-Spatial Data
Researchers typically undertake crash analysis studies at two levels: macro and micro. Analysis at the micro level constitutes homogeneous road bodies like intersections and road segments that aid in identifying traffic attributes, lighting, design characteristics, and specific locations that lead to a high number of crashes and thus could suggest measures to alleviate the problem [24]. However, it is typically suggested that bicycle crashes should be analyzed at the macro level, which involves cumulating crashes over a geographical area that could be a census tract or county to explore the impact of land use, bicycle-related infrastructure, and socioeconomic factors [25]. This, however, makes the quantification of bicycle exposure difficult as bicycle crashes are fewer than motor vehicle crashes, are more severe, and involve built environment characteristics. When analyzing at the macro level, it is pertinent to consider the effects of spatial autocorrelation in crash statistics, as crashes are added up per geographic entity [26]. Nevertheless, researchers have developed crash prediction models at the macro and micro levels. One of the most common methods to develop crash models is with the help of the negative binomial (NB) distribution at the micro level because they are found to handle overdispersion commonly present in crash data [27] and limit the effects of exogenous variables over the entire population [28]. Many researchers have used the negative binomial distribution, and some of them have used it in its native form [17,29] while others modified it to create different models, such as the Random Parameter Negative Binomial (RPNB) model [16], Negative Binomial Log Link (NBLL) distribution [13], Zero Inflated Negative Binomial (ZINB) model [27], and Latent Segmentation Negative Binomial (LSNB) model [28]. The next most used method of analysis is the logit model [30], which has been used as a binary logistic regression [31], multinomial logit (MNL) [8,31], mixed logit (MXL) [7], generalized ordered logit (GOL), and generalized additive model (GAM) [11]. Alam [32] used case-based and logistic regression models to analyze fatal traffic crashes in Florida.
The mixed logit model typically produces better results than the simple multinomial logit model. Many models have been developed with the Bayesian framework [1,25,26,33], as it gives a broader and more robust approach to estimate models and is not based upon the asymptotic assumption usually found in the classical methods [26]. Unobserved heterogeneity is a significant problem that comes into play when data are aggregated at the macro level [16]. It arises when variables affecting the crash frequency are not measurable, or gathering such data can be almost impossible. Using the Bayesian spatial framework, the issue of unobserved heterogeneity is resolved [26]. In the long term, applying lower-cost road safety planning using macro-level Collision Prediction Models (CPMs) might be more practical than reactive safety improvement measures using micro-level CPMs [29]. Nonetheless, each method of analysis has its pros and cons, and no one method can be said to give accurate, universally applicable results.
2.2. Existing Studies on Spatial Data Analysis
Bayesian models are better than negative binomial (NB) models, as they consider the effects of spatial correlation when using variables such as environment, roadway, socioeconomic, and demographic characteristics associated with bicycle crashes [26]. Studies have found significant effects of spatial clustering and claimed that Bayesian models that took spatial autocorrelation into account performed better [24]. Some variables that show positive association with bicycle crashes are the total length of roadway with 15 mph and 35 mph speed limits, total number of dwelling units, total number of intersections per traffic analysis zone (TAZ), log of total employment in a TAZ, etc. [26]. Additionally, 30–40 mph speed is positively associated with bicyclist injury severity [8]. Perhaps roads with higher speeds and their infrastructure are inherently unattractive to bicyclists, resulting in lower to zero exposure and crashes. Apardian and Alam [34] claim that accessible roundabout crossings can be viewed as a viable travel demand management technique.
Ignoring the effects of spatial autocorrelation while analyzing data points does not produce convincing results [1,11,35]. The spatial distribution of crash points helps identify spatial variability in the occurrences of crashes and can link them to the type of built environment, road classes, and geographical areas [36]. Additionally, spatial analysis has linked crash incidence to aggregate measures of social and environmental characteristics in geographic areas to classify factors like the built environment variables, which explain the frequency of bicycle crashes [33]. Spatial analysis helps to understand the patterns and areas of high risk on an aggregated level. Research finds that models that consider spatial autocorrelation work better than those that ignore spatial autocorrelation effects [26,37,38].
Studies employ geospatial analytical techniques to map and investigate the spatial distribution of bicycle crash risk patterns in urban areas [39]. For instance, Chen [40] employs a Poisson lognormal random effects model using hierarchical Bayesian estimation and finds that TAZ-based bicycle crashes are spatially correlated. Chen [40] also finds that TAZs with more road signals, street parking signs, and automobile trips are linked to more bicycle crashes. These techniques include both ESDA and spatial regression techniques. By applying a geographically weighted negative binomial regression (GWNBR) model, Chun et al. [41] explored the spatial fabric of Seoul, finding that an increase in street slope and the total number of local buses lead to a decrease in bicycle-related crashes for certain TAZs, while an increase in the installation of bicycle lanes on the roadway is associated with an increase in bicycle crashes. By applying geographically weighted Poisson regression (GWPR) and GWNBR, the literature finds that traffic safety analysis zone (TSAZ)-based models result in superior performance compared to TAZ-based models, and that the relationships between built environment factors and traffic safety vary spatially, as reported by Obelheiro et al. [42]. By developing several network indicators using Graph theory, generalized linear regression, and full Bayesian techniques, Osama and Sayed [35] investigated the effects of these network indicators on cyclist safety and found that spatial effects were statistically significant in their models.
3. Datasets and Methodology
3.1. Datasets
The crash data were extracted from the Ohio Department of Transportation’s (ODOT) Transportation Information Mapping System (TIMS) website. TIMS provides a web mapping portal where information about Ohio’s transportation system can be explored, created, and shared. The system’s GIS Crash Analysis Tool (GCAT) uses Geographic Information Systems (GIS) to generate spatially referenced data. The GCAT aims to present a suitable highway safety crash analysis tool for ODOT and county engineers. The Ohio Department of Public Safety provides GCAT data that the ODOT modifies for analysis and engineering purposes. Ohio has 12 regional districts, 88 counties, 3164 census tracts, and 9468 block groups. This study’s analysis was performed at the state, county, census tract, and block group levels.
The crash data include columns for latitude and longitude, crash date, crash type, crash severity, day of the week, whether the crash occurred on a freeway, and whether the driver was distracted. While crashes are spatially located using latitude and longitude coordinates, if a location is missing or inaccurate, the ODOT manually assigns a location based on roadway inventories. The ODOT validates the data and addresses the issue of temporal stability before releasing the data on its website so that the results obtained from statistical analyses are reliable and can be generalized to a broader context. The data for bicycle crashes were consistent for the variables and the years we were interested in for the study. Although ODOT lists all crash severities, we focused on incapacitating, non-incapacitating, and fatal bicycle crashes across all road and weather conditions. The crash data included in our study spanned from 2014 to 2023, when 13,528 bicycle crashes occurred. GCAT has five categories of crash severity: property damage only (PDO), possible injury, incapacitating, non-incapacitating, and fatal. Out of 13,528, there were only 196 fatal crashes, which is insufficient to produce satisfactory results for spatial analysis. Therefore, we included incapacitating, non-incapacitating, and fatal crashes in our study, which totaled 8100. All the analyses were performed using ESRI’s ArcGIS Pro 3.3 version, with all crash points geocoded on the map. Shapefiles of counties, census tracts, and block groups were downloaded from the US Census Bureau website, which is available in the public domain. Figure 1 displays the frequencies, percentages, and linear percentages of fatal and injury bicycle crashes in Ohio in each year of the study. The figure shows that while the total numbers and thereby the percentages of bicycle crashes remained stable from 2014 to 2017, there was a declining trend from 2018 to 2020. While the crash numbers and their proportions were smaller in each year than those from 2014 to 2017, the general trend was upward from 2020 to 2023.
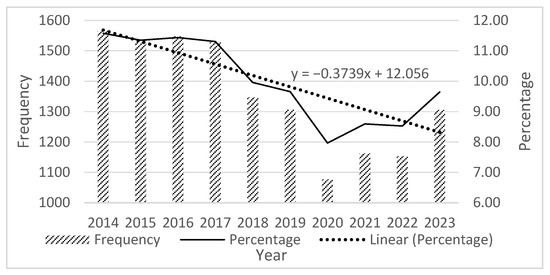
Figure 1.
Frequency, percentage, and linear percentage of fatal and injury bicycle crashes in Ohio, 2014–2023.
3.2. Methodology
Four ESDA techniques were used in our study: Nearest Neighborhood Index (NNI), Global Moran’s I Index, Hot Spot and Cold Spot Analysis (Getis-Ord Gi* Statistic), and Local Indicators of Spatial Association (LISA) or local Moran’s I Index. The reason for utilizing these ESDA techniques is that their strength lies in their ability to focus on and analyze specific features of geographical data and their data mining capability in the absence of an existing theoretical framework. ESDA tools are increasingly popular and considered standard techniques for analyzing and visualizing spatial data [43]. Also, we aimed to conduct the data analysis at first-order properties. As such, we did not apply K-function analysis or Ripley’s K statistic, which analyzes spatial data at a higher-order nearest neighbor level. Similarly, we did not intend to estimate any probability density function of a random factor. Therefore, we did not employ the non-parametric technique of Kernel Density Estimation (KDE), which uses kernels as weights.
3.2.1. Nearest Neighborhood Index (NNI)
NNI, also known as the Nearest Neighborhood Statistic or R statistic, is the ratio of the observed average distance and the expected average distance between the two nearest neighbors or points [43]. Equation (1) shows the calculation technique of the R statistic.
where is the observed and is the expected average distance between nearest neighbors. can be calculated from the observed pattern by calculating the distance between each point and all other points, where the nearest neighbors will have the shortest distances. On the other hand, can be calculated based on a theoretical random pattern. Equation (2) can be used to calculate :
where n is the number of points in the distribution and A is the study area. By calculating the value of the R statistic, we can say whether the observed pattern is dispersed, random, or clustered. If R > 1, the pattern is said to be more dispersed than random, and if R < 1, it means the pattern is more clustered than the random pattern. If R is close to 1, the pattern is random.
3.2.2. Global Moran’s I
Global Moran’s I (Equation (3)) is one of the measures of spatial autocorrelation for interval and ratio data and represents the similarity of points’ attributes and the proximity of those points. Global Moran’s I value typically lies between −1 and + 1. It is compared to its expected value E(I) (Equation (4)), where no spatial autocorrelation exists [43,44].
where n is the number of points in the distribution, wij is the spatial weights matrix, xi and xj are attribute values of neighboring units i and j, and W is the sum of all cell values in the weights matrix.
When I > E(I), the spatial pattern is said to be clustered, with nearby points showing similar characteristics. I~ = E(I) indicates a random pattern with points showing no pattern of similarity, and I < E(I) indicates a dispersed pattern with nearby points showing dissimilar characteristics or a negative spatial correlation.
3.2.3. Hotspot and Cold Spot Analysis
Global Moran’s I uses the measure of spatial autocorrelation to identify patterns (cluster, disperse, or random) of similar or dissimilar attributes at a certain geographical level. Unfortunately, it cannot inform us whether these patterns represent high values or low values. For example, when crashes are analyzed, a cluster pattern could represent a high number of casualties in a geographic unit surrounded by other geographic units with a high number of casualties or a geographic unit with a small number of casualties surrounded by other geographic units with a small number of casualties. This problem can be overcome by using the Getis-Ord Gi* statistic, shown by Equations (5)–(7) [45,46].
The expected G value for a threshold distance, d, can be defined by Equation (8).
where W is the sum of weights for all pairs of locations (), n represents the number of observations, wij is the measure of spatial weight between geographic units i and j, xj is the attribute value of geographic unit j, the mean of the xj values, and S is the standard deviation of the xj values.
The Getis-Ord Gi* statistic analyzes the attributes of each unit with respect to its neighboring unit and then produces a result. The result would show a spatial pattern that can be a cluster of high–high values, also called hotspots, or low–low values, also called cold spots [45,47]. The Getis-Ord Gi* statistic provides a more cross-sectional perspective of spatial patterns for two reasons. Firstly, it works at the local level of any geographical unit and is hence also called the local G-statistic. This produces better results as compared to an analysis at a larger aggregated level. Secondly, the presence of a single high value may not be statistically significant. However, a cluster of high values is significant and more alarming in the real world. This is also reasonable because the presence of a high crash value in a geographic unit must be a result of its neighboring factors that lead to a more substantial number of crashes.
3.2.4. Local Indicators of Spatial Analysis (LISA)
LISA or local Moran’s I analysis is also performed at the local level. Hence, the spatial autocorrelation value is derived for each areal unit, which gives better results than Global Moran’s I. The value of the local Moran statistic for an areal unit i is defined by Equations (9) and (10) [43,48].
where and are deviations from the mean is the standard deviation of the corresponding values of x, and is the row-standardized weight matrix.
A high LISA or local Moran’s I value indicates a cluster of high–high or low–low values of a variable among neighboring geographic units. In contrast, a low LISA or local Moran’s I value indicates a cluster of dissimilar values. LISA is one of the most effective spatial statistical methods as it works at a local scale, which helps to give better results [24].
4. Results
4.1. Nearest Neighborhood Index (NNI)
The NNI value for bicycle injuries and fatalities is 0.36, which is less than 1 and significant at a p-value of 0.00 (Table 1). This means that the crash points are clustered at a statewide level, which is also quite visible from looking at the distribution of crash points in Figure 2B. These injury and fatal crash points are highly clustered around the big cities in Ohio, namely, Cleveland, Columbus, Cincinnati, Toledo, Dayton, and Akron. The geographic boundaries of the study area at the county level, with labels provided for reference across Ohio, are depicted in Figure 2A. Meanwhile, the spatial distribution of crash points, which highlights localized clusters and broader regional patterns, is illustrated in Figure 2B.

Table 1.
Summary statistics of NNI of bicycle crashes in Ohio, 2014–2023.
4.2. Global Moran’s I
Global Moran’s I value for the bicycle crashes at the county level was found to be 0.10, with a p-value of 0.14 and a z-score of 1.46. This means the crash distribution pattern tends to be clustered and shows slight positive spatial autocorrelation, but this is not statistically significant. Looking at the z-score and the diagram in Figure 3A, one can deduce that the crash distribution represents a random pattern when considered at the county level.
Contrary to the findings at the county level, Global Moran’s I value for the bicycle crashes was found to be 0.17, with a p-value of 0.00 and a z-score of 33.57 at the census tract level. These results show a high positive spatial autocorrelation of the crash distribution points, which is statistically significant (Figure 3B). Hence, the bicycle crash points at the census tract level in Ohio show a high cluster pattern.
The value of Global Moran’s I at the block group level for bicycle crash injuries and fatalities was subsequently calculated. The results show a Moran’s I value of 0.14 with a p-value of 0.00 and a z-score of 49.47. Like census tract-level findings, these results also indicate high positive spatial autocorrelation, which is statistically significant (Figure 3C). This means that the bicycle crash point distribution at the block group level shows a high cluster pattern.
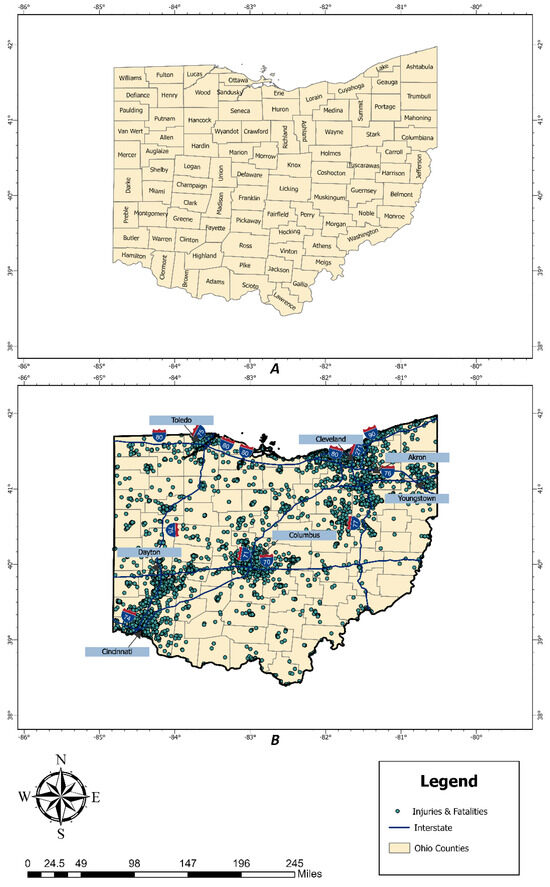
Figure 2.
County-level boundaries and spatial distribution of fatal and injury bicycle crash points in Ohio, 2014–2023: (A) Geographic boundaries of the study area at the county level, and (B) Distribution of fatal and injury bicycle crash points in different counties in Ohio.
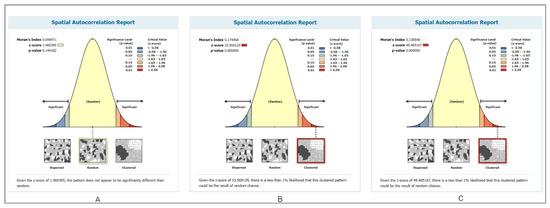
Figure 3.
Global Moran’s I diagrams of bicycle crashes in Ohio, 2014–2023: (A) county level, (B) census tract level, and (C) block group level.
4.3. Hotspot and Cold Spot Analysis (Getis-Ord GI* Statistic)
Global Moran’s I indicates whether there is any positive spatial autocorrelation between crash points at different spatial scales. Unfortunately, it cannot reveal whether the distribution pattern is a cluster of high or low numbers of bicycle crashes. Hotspot and cold spot analysis helps overcome this issue by comparing each geographical unit with its neighboring unit and then generating a result. Analysis was performed at three distinct spatial scales to find out the areas of high–high crash values, that is, areas with high number of bicycle injuries and fatalities surrounded by the areas with high number of such crashes, and areas of low–low crash values, that is, low number of bicycle injuries and fatalities surrounded by areas of low numbers of such crashes.
The hotspot analysis at the county level shows that six northeast Ohio counties are in the hotspot region with a 99% confidence level (Figure 4A). They are Cuyahoga, Summit, Lake, Geauga, Portage, and Medina. Four central Ohio counties, namely Delaware, Loraine, Fairfield, and Franklin, are also hotspots, but at a 95% confidence level, and Licking, Pickaway, Madison, and Butler counties at a 90% confidence level. The results, however, do not show any cold spot counties in Ohio. The results are expected as four big cities, namely Cincinnati, Columbus, Cleveland, and Akron, come under these counties.
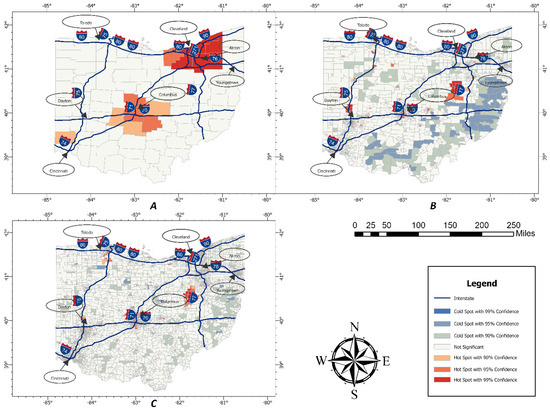
Figure 4.
Hotspot and cold spot analysis of bicycle crash points in Ohio, 2014–2023: (A) County level, (B) census tract level, and (C) block group level.
Next, hotspot analysis was performed at the census tract level to find out the census tracts with high and low values of bicycle crashes that resulted in injuries and fatalities. The results are better than those at the county level, as both hotspots and cold spots are observed at the census tract level. All the hotspots (99% confidence level) are in or around big cities like Toledo, Cleveland, Dayton, Columbus, Cincinnati, and Akron. Most cold spot census tracts (at 99% confidence level) are found near the eastern and southern parts of Ohio in counties like Jefferson, Trumbull, Columbiana, Monroe, Belmont, Pike, and Jackson (Figure 4B).
The last hotspot analysis was computed at the block group level, which is also the smallest unit of analysis in our study. The results are similar to those of the census tract analysis, as most of the hotspots (99% confidence level) are found in or around the big cities in Ohio (Figure 4C). Interestingly, cold spots are not as pronounced on the eastern part of Ohio as the results at the census tract level show.
4.4. Local Indicators of Spatial Association (LISA)
The last method this study applied is local Moran’s I, also known as LISA, for performing cluster analysis. Although hotspot and cold spot analysis gives areas of high and low values of bicycle crashes, it fails to give outliers, if any, in the data. LISA works on the proximity of one areal unit to the other, produces areas of high and low bicycle crashes, and indicates outliers, i.e., areas of high crashes surrounded by low crashes or areas of low crashes surrounded by high crashes. Anselin’s [48] local Moran’s I tool was first applied at the county level, and the results were considerably different from the hotspot analysis. As can be seen in Figure 5A, only two counties, namely Summit and Lake, have clusters of high–high bicycle crashes resulting in injuries and fatalities. This is possibly due to the metropolitan areas of Cleveland and Akron. On the other hand, Geauga, Portage, and Medina, three rural counties, are outliers in terms of having low–high bicycle crashes. The other counties with big cities were found to have non-significant bicycle crashes, and low–low clusters were found on the south and south-eastern part of Ohio.
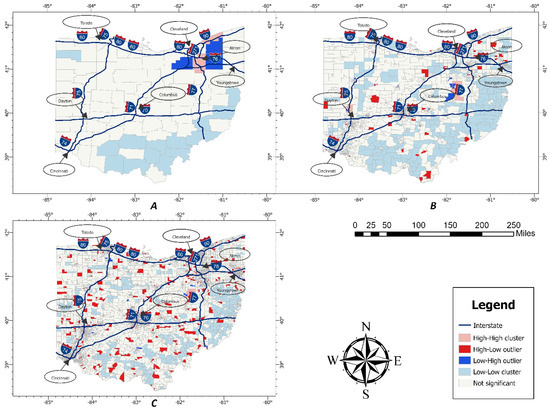
Figure 5.
LISA of bicycle crash points in Ohio, 2014–2023: (A) county level, (B) census tract level, and (C) block group level.
LISA was then applied at the census tract level (Figure 5B). Interestingly, here, high–high clusters are seen in or near Cincinnati, Toledo, Columbus, Dayton, and Cleveland metropolitan areas. Few patches of low–high outliers are seen around Cleveland, Akron, and Columbus. Again, low–low clusters of bicycle crashes are visible on the southern and eastern parts of Ohio.
The last analysis of bicycle crashes using LISA was performed at the block group level, and the results were remarkably similar to those of census tract level analysis, as shown in Figure 5C. High–high clusters of bicycle crashes are visible in or around big metropolitan areas like Toledo, Cleveland, Columbus, Akron, Dayton, and Cincinnati. High–low values of bicycle crashes can be observed scattered over the state, and low–low clusters of such crashes are noticeable in the eastern and southern parts of Ohio.
5. Discussion
The study applies spatial statistical analysis tools to spatially analyze the bicycle crashes that resulted in injuries and fatalities in Ohio from 2014 to 2023 at four spatial scales: state, county, census tract, and block group. An important finding of this study is that the results are slightly different for different methods and different spatial scales. As per the NNI value, the data points are clustered statewide, which seems a fair representation of crashes because points are clustered at specific locations, specifically in the big cities of Ohio. A study on all crashes in Indiana found that their data points were slightly clustered [49]. NNI results do not depend on the spatial scale and, as such, a constant value prevails for a given set of data points over the entire study area, like the state of Ohio, in this case.
Table 2 displays a summary of the findings of this study. The results from the Global Moran’s I value at the county level do not show significant spatial autocorrelation; hence, it is considered a random pattern. However, at the census tract and block group levels, Global Moran’s I values indicate a strong positive spatial autocorrelation with a z-score value as high as 49.50 for block groups and 33.60 for the census tract level. This is possible because the lower the geographical unit we consider, the better the results we expect. At the county level, points are clustered in a few counties with big metropolitan areas, while points are dispersed or random in the other counties. It is important to note that, unlike Getis-Ord Gi* and Local Moran’s I, Global Moran’s I does not work by considering each aerial unit with its neighboring unit. The computed Global Moran’s I value represents a global value for the entire study area—the state of Ohio in our study.

Table 2.
Summary statistics of the findings of the study.
The next method the study employed is hotspot and cold spot analysis, which gave marginally different results for the three spatial scales. The results at the county level show that only six counties are in the hotspot region with a 99% confidence level (Figure 4A), four counties are in the hotspot region at a 95% confidence level, and four counties are in the region of a 90% confidence level. The census tract and block group level analyses provide insightful results consistent with earlier studies [43,50]. At the census tract level, hotspots were found in and around the major cities in Ohio. Hotspots are present in the Toledo and Cleveland region. The census tract and block group results show that although Youngstown is a big city with Youngstown State University, no hotspots were found in or around this city. Contrarily, it turned out to be a cold spot region. Since Cincinnati is in a hilly region, people would be less likely to ride bicycles, reducing the chances of getting involved in crashes. However, hotspots are concentrated remarkably close to the Cincinnati region only. Holmes, Wayne, and Coshocton are three counties with hotspot regions despite having no big cities in these counties. The rest of the results are expected, as all other metropolitan areas are hotspots for bicycle crashes, confirmed by both census tract and block group results.
The last method, Local Moran’s I or LISA, was performed on the crash data points at three spatial scales. Analyzing spatially referenced traffic data at different scales helps to attain the best results, as different local-level information is analyzed, which helps to find the outliers [50]. As usual, the first analysis was performed at the county level, and the results differ from the hotspot and cold spot analysis methods. Local Moran’s I shows that only two counties, Summit and Lake, are associated with bicycle crashes of high–high numbers. This is possibly due to the presence of the metropolitan areas of Cleveland and Akron. On the other hand, Geauga, Portage, and Medina, which are rural counties, are outliers in terms of having low–high bicycle crashes. Other counties with big metropolitan areas show no significant local Moran’s I value.
A significant finding of this study is that most of the census tracts in metropolitan areas like Toledo, Cleveland, Columbus, Dayton, Cincinnati, and Akron have clusters of high bicycle crashes. High–low or low–high outliers are located around these regions. Comparable results are found at the block group level, except for around Holmes County, which also indicates a cluster of high–high values. The results of Local Moran’s I at the census tract and block group scales are compelling, as the big metropolitan areas are hotspots of high crash values. This is due to the high number of bicycle users in these regions and the presence of international universities. Unlike Nunn and Newby [49], who found border counties to have high-value clusters, this study shows counties with big cities to have clusters of high bicycle crashes. Their study included all crashes, unlike this study, which is solely based on bicycle crashes. Moreover, bicyclists are highly unlikely to travel interstate.
The results from the above analysis raise some critical questions about the safety of bicyclists in Ohio. Streets need to be safe to encourage more bicycling. Although we have yet to delve deeper into the reasoning, one significant takeaway from this study is that there is a need to study all the big cities separately to investigate the actual reasons behind these crashes and whether they are different for various locations. Cleveland, one of the most densely populated cities in Ohio, stands out as one of the hotspots for bicycle crashes in the state of Ohio. This could partially be explained by the ‘safety in numbers’ effect [19,20,21,22,51,52] because Cleveland ranks as Ohio’s best city for bicycling, potentially attracting more cyclists and thus increasing exposure to crashes. Columbus, the capital city with the highest population in the state of Ohio, is home to the most prominent university in Ohio, which explains the high number of bicycle crashes. Cincinnati and Toledo also have prominent universities and are the third and fourth most populous cities in Ohio, respectively. Therefore, it is likely that they will have a high number of bicycle users, especially during the late spring to the middle of the fall season. Nevertheless, further detailed investigation is required to find specific reasons for bicycle crashes in each city so that mitigation measures can be designed and applied appropriately.
6. Conclusions
The study’s findings reveal the need for more significant investment in bicycle-friendly infrastructure to enhance cyclist safety, particularly in urban areas with high crash densities. Addressing the challenges of urban sprawl and prioritizing active transportation modes, such as bicycling and walking, requires modifications to the built environment. This includes expanding bicycle lane networks, implementing bike-share programs, and promoting bicycling as a viable transportation mode.
From an engineering perspective, separating bicyclists from vehicular traffic through dedicated bike lanes, bicycle boxes at intersections, and improved visibility measures is crucial. Traffic-calming strategies, such as lower speed limits and enhanced road designs, can further reduce collisions. Public education efforts, mainly targeted educational campaigns, proper bicycling training, and stricter enforcement of traffic laws, can contribute to a safer environment for all road users [28].
Equitable resource distribution is essential to ensure that all communities receive adequate infrastructure improvements, regardless of their socioeconomic status. Historically underserved neighborhoods should not be neglected due to lower tax contributions; instead, investments should be made to create a safer and more inclusive urban landscape for bicyclists. By prioritizing these measures, policymakers can work toward making Ohio’s cities safer and more accessible for all bicycle users.
The census tract and block group level analysis provides more precise and meaningful results than broader spatial scales. Additionally, regions in and around big cities, like Toledo, Cleveland, Columbus, Dayton, Cincinnati, and Akron, were identified as hotspots for bicycle crashes. The high concentration of bicycle crashes in these major cities could result from potential contributing factors such as high automobile traffic volumes [18,53,54], a lack of dedicated bike lanes [18,55,56,57], and a lack of bicycle infrastructure [18,33,58].
The study highlights the need for targeted mitigation strategies in the relatively high-risk areas, which include comprehensive safety measures, infrastructure improvements, policy changes, and community-focused initiatives to reduce crash risk and create safer environments for cyclists throughout Ohio’s urban fabric. The findings join the growing body of research directed at the ever-increasing rate of bicycle crashes in the United States. Identifying specific hotspots provides valuable insights for policymakers and urban planners to implement effective safety measures and improve conditions for non-motorized road users in Ohio.
It is relevant to mention here that because this is the first exploratory study on the usage of ESDA techniques to investigate the spatial patterns of bicycle crashes in the state of Ohio, it did not dig into the crash locations and their underlying causes at the micro-fabric level of different cities. As such, the countermeasures are derived from both the study’s findings and from a general perspective. It is important to clarify that the study focuses on the geographic scale of block groups and larger; hence, a limitation of this study is that it does not focus on the micro-fabric level of geographic scale, such as individual street networks in specific cities. Although our study relies on reported bicycle crash incidents in Ohio, there is a possibility of underreporting, especially in cases involving minor crashes or pedestrian-related incidents. Furthermore, there may be inaccuracies or inconsistencies in the recorded latitude and longitude data that require manual corrections. Longer processing times may affect the currency of the crash data through the structured process established by ODOT for crash reporting [59].
Our next study, which is currently in progress, will utilize spatial regression models to investigate the contributing factors, including road infrastructure, traffic patterns, and socioeconomic factors, to inform the development of comprehensive bicycle safety strategies. It will also relate the spatial findings to specific infrastructure or policy measures within individual cities, namely, Columbus, Cleveland, Cincinnati, Toledo, Akron, and Dayton. Specifically, our future study will aim to address bicycle crash analysis at the micro-level scale [60,61], like the street network in the six cities above in the state of Ohio.
Author Contributions
Conceptualization, B.M.A. and M.R.; methodology, B.M.A. and M.R.; software, B.M.A.; validation, B.M.A., M.R. and Y.K.; formal analysis, B.M.A. and M.R.; investigation, M.R.; resources, B.M.A.; data curation, M.R.; writing—original draft preparation, M.R.; writing—review and editing, B.M.A. and Y.K.; visualization, B.M.A., M.R. and Y.K.; supervision, B.M.A.; project administration, B.M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is available from the following website: https://tims.dot.state.oh.us/tims, accessed on 17 July 2025.
Conflicts of Interest
Author Modabbir Rizwan was employed by Infrastructure Engineering Inc. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Guo, Y.; Osama, A.; Sayed, T. A cross-comparison of different techniques for modeling macro-level cyclist crashes. Accid. Anal. Prev. 2018, 113, 38–46. [Google Scholar] [CrossRef]
- EPA. Transportation Sector Emissions. Available online: https://www.epa.gov/ghgemissions/transportation-sector-emissions (accessed on 26 February 2025).
- EIA. Use of Energy Explained: Energy Use for Transportation. Available online: https://www.eia.gov/energyexplained/use-of-energy/transportation.php (accessed on 27 February 2025).
- EIA. U.S. Energy-Related Carbon Dioxide Emissions. 2023. Available online: https://www.eia.gov/environment/emissions/carbon/ (accessed on 27 February 2025).
- Statista. Carbon Monoxide Emissions from Transportation in the United States from 1990 to 2023, by Source. Available online: https://www.statista.com/statistics/999680/us-carbon-monoxide-emissions-from-storage-and-transport/#:~:text=Transportation%20CO%20emissions%20in%20the%20U.S.%201990%2D2023%2C%20by%20source&text=Carbon%20monoxide%20emissions%20from%20highway,the%20U.S.%20(excluding%20wildfires) (accessed on 27 February 2025).
- Vanparijs, J.; Panis, L.I.; Meeusen, R.; De Geus, B. Exposure measurement in bicycle safety analysis: A review of the literature. Accid. Anal. Prev. 2015, 84, 9–19. [Google Scholar] [CrossRef]
- Klassen, J.; El-Basyouny, K.; Islam, M.T. Analyzing the severity of bicycle-motor vehicle collision using spatial mixed logit models: A City of Edmonton case study. Saf. Sci. 2014, 62, 295–304. [Google Scholar] [CrossRef]
- Kim, J.-K.; Kim, S.; Ulfarsson, G.F.; Porrello, L.A. Bicyclist injury severities in bicycle–motor vehicle accidents. Accid. Anal. Prev. 2007, 39, 238–251. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Khattak, A.J.; Li, X.; Nie, Q.; Ling, Z. Bicyclist injury severity in traffic crashes: A spatial approach for geo-referenced crash data to uncover non-stationary correlates. J. Saf. Res. 2020, 73, 25–35. [Google Scholar] [CrossRef]
- Alam, B.M.; Spainhour, L.K. Contributing factors for young at fault drivers in fatal traffic crashes in Florida. J. Transp. Saf. Secur. 2009, 1, 152–168. [Google Scholar] [CrossRef]
- Chen, P.; Shen, Q. Built environment effects on cyclist injury severity in automobile-involved bicycle crashes. Accid. Anal. Prev. 2016, 86, 239–246. [Google Scholar] [CrossRef] [PubMed]
- Alam, B.M.; Spainhour, L.K. Contribution of behavioral aspects of older drivers to fatal traffic crashes in Florida. Transp. Res. Rec. 2008, 2078, 49–56. [Google Scholar] [CrossRef]
- Mukoko, K.K.; Pulugurtha, S.S. Examining the influence of network, land use, and demographic characteristics to estimate the number of bicycle-vehicle crashes on urban roads. IATSS Res. 2020, 44, 8–16. [Google Scholar] [CrossRef]
- Myhrmann, M.S.; Janstrup, K.H.; Møller, M.; Mabit, S.E. Factors influencing the injury severity of single-bicycle crashes. Accid. Anal. Prev. 2021, 149, 105875. [Google Scholar] [CrossRef]
- Dash, I.; Abkowitz, M.; Philip, C. Factors impacting bike crash severity in urban areas. J. Saf. Res. 2022, 83, 128–138. [Google Scholar] [CrossRef] [PubMed]
- Amoh-Gyimah, R.; Saberi, M.; Sarvi, M. Macroscopic modeling of pedestrian and bicycle crashes: A cross-comparison of estimation methods. Accid. Anal. Prev. 2016, 93, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Wei, F.; Lovegrove, G. An empirical tool to evaluate the safety of cyclists: Community based, macro-level collision prediction models using negative binomial regression. Accid. Anal. Prev. 2013, 61, 129–137. [Google Scholar] [CrossRef] [PubMed]
- Marshall, W.E.; Garrick, N.W. Evidence on why bike-friendly cities are safer for all road users. Environ. Pract. 2011, 13, 16–27. [Google Scholar] [CrossRef]
- Jacobsen, P.L. Safety in numbers: More walkers and bicyclists, safer walking and bicycling. Inj. Prev. 2015, 21, 271–275. [Google Scholar] [CrossRef]
- Elvik, R.; Bjørnskau, T. Safety-in-numbers: A systematic review and meta-analysis of evidence. Saf. Sci. 2017, 92, 274–282. [Google Scholar] [CrossRef]
- Fyhri, A.; Sundfør, H.B.; Bjørnskau, T.; Laureshyn, A. Safety in numbers for cyclists—Conclusions from a multidisciplinary study of seasonal change in interplay and conflicts. Accid. Anal. Prev. 2017, 105, 124–133. [Google Scholar] [CrossRef]
- Shoman, M.M.; Imine, H.; Acerra, E.M.; Lantieri, C. Evaluation of cycling safety and comfort in bad weather and surface conditions using an instrumented bicycle. IEEE Access 2023, 11, 15096–15108. [Google Scholar] [CrossRef]
- Bíl, M.; Bílová, M.; Müller, I. Critical factors in fatal collisions of adult cyclists with automobiles. Accid. Anal. Prev. 2010, 42, 1632–1636. [Google Scholar] [CrossRef]
- Apardian, R.E.; Alam, B.M. Pedestrian fatal crash location analysis in Ohio using exploratory spatial data analysis techniques. Transp. Res. Rec. 2020, 2674, 888–900. [Google Scholar] [CrossRef]
- Saha, D.; Alluri, P.; Gan, A.; Wu, W. Spatial analysis of macro-level bicycle crashes using the class of conditional autoregressive models. Accid. Anal. Prev. 2018, 118, 166–177. [Google Scholar] [CrossRef]
- Siddiqui, C.; Abdel-Aty, M.; Choi, K. Macroscopic spatial analysis of pedestrian and bicycle crashes. Accid. Anal. Prev. 2012, 45, 382–391. [Google Scholar] [CrossRef] [PubMed]
- Raihan, M.A.; Alluri, P.; Wu, W.; Gan, A. Estimation of bicycle crash modification factors (CMFs) on urban facilities using zero inflated negative binomial models. Accid. Anal. Prev. 2019, 123, 303–313. [Google Scholar] [CrossRef] [PubMed]
- Yasmin, S.; Eluru, N. Latent segmentation based count models: Analysis of bicycle safety in Montreal and Toronto. Accid. Anal. Prev. 2016, 95, 157–171. [Google Scholar] [CrossRef] [PubMed]
- Lovegrove, G.R.; Sayed, T. Using macrolevel collision prediction models in road safety planning applications. Transp. Res. Rec. 2006, 1950, 73–82. [Google Scholar] [CrossRef]
- Alam, B.M.; Spainhour, L. Logit and case-based analysis of drivers’ age as a contributing factor for fatal traffic crashes on highways and state roads in Florida. In Proceedings of the Transportation Research Board 93rd Annual Meeting, Washington, DC, USA, 12–16 January 2014; pp. 1–12. [Google Scholar]
- Yan, X.; Ma, M.; Huang, H.; Abdel-Aty, M.; Wu, C. Motor vehicle–bicycle crashes in Beijing: Irregular maneuvers, crash patterns, and injury severity. Accid. Anal. Prev. 2011, 43, 1751–1758. [Google Scholar] [CrossRef]
- Alam, B.M. Case-Based Analysis of Age and Sex Distribution of Drivers Causing Fatal Crashes: Evidence from Florida, USA. In ICTIS 2011: Multimodal Approach to Sustained Transportation System Development: Information, Technology, Implementation; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2011; pp. 1113–1121. Available online: https://ascelibrary.org/doi/10.1061/41177%28415%29141 (accessed on 17 July 2025).
- Kondo, M.C.; Morrison, C.; Guerra, E.; Kaufman, E.J.; Wiebe, D.J. Where do bike lanes work best? A Bayesian spatial model of bicycle lanes and bicycle crashes. Saf. Sci. 2018, 103, 225–233. [Google Scholar] [CrossRef]
- Apardian, R.; Alam, B.M. Methods of crossing at roundabouts for visually impaired pedestrians: Review of literature. Int. J. Transp. Sci. Technol. 2015, 4, 313–336. [Google Scholar] [CrossRef]
- Osama, A.; Sayed, T. Evaluating the impact of bike network indicators on cyclist safety using macro-level collision prediction models. Accid. Anal. Prev. 2016, 97, 28–37. [Google Scholar] [CrossRef]
- Loidl, M.; Traun, C.; Wallentin, G. Spatial patterns and temporal dynamics of urban bicycle crashes—A case study from Salzburg (Austria). J. Transp. Geogr. 2016, 52, 38–50. [Google Scholar] [CrossRef]
- Delmelle, E.C.; Thill, J.-C. Urban bicyclists: Spatial analysis of adult and youth traffic hazard intensity. Transp. Res. Rec. 2008, 2074, 31–39. [Google Scholar] [CrossRef]
- Chimba, D.; Emaasit, D.; Cherry, C.R.; Pannell, Z. Patterning Demographic and Socioeconomic Characteristics Affecting Pedestrian and Bicycle Crash Frequency. In Proceedings of the TRB 93rd Annual Meeting Compendium of Papers, Washington, DC, USA, 12–16 January 2014; Available online: https://trid.trb.org/view/1287401 (accessed on 17 July 2025).
- Loidl, M.; Wallentin, G.; Wendel, R.; Zagel, B. Mapping bicycle crash risk patterns on the local scale. Safety 2016, 2, 17. [Google Scholar] [CrossRef]
- Chen, P. Built environment factors in explaining the automobile-involved bicycle crash frequencies: A spatial statistic approach. Saf. Sci. 2015, 79, 336–343. [Google Scholar] [CrossRef]
- Chun, U.; Lim, J.; Lee, S.; Park, S. An analysis of bicycle accidents with respect to spatial heterogeneity. Sci. Rep. 2023, 13, 21812. [Google Scholar] [CrossRef]
- Obelheiro, M.R.; da Silva, A.R.; Nodari, C.T.; Cybis, H.B.B.; Lindau, L.A. A new zone system to analyze the spatial relationships between the built environment and traffic safety. J. Transp. Geogr. 2020, 84, 102699. [Google Scholar] [CrossRef]
- Lee, J.; Wong, D.W. Statistical Analysis of Geographic Information with ArcView GIS and ArcGIS; John Wiley & Sons, Incorporated: Hoboken, NJ, USA, 2005. [Google Scholar]
- Chen, Y. An analytical process of spatial autocorrelation functions based on Moran’s index. PLoS ONE 2021, 16, e0249589. [Google Scholar] [CrossRef] [PubMed]
- Ord, J.K.; Getis, A. Local spatial autocorrelation statistics: Distributional issues and an application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Zeren, F.; Akbulut, S.; Ozer, A.; Islek, H.; Bentli, R.; Mentese, E.Y. Spatial clustering and hot spot analysis of the COVID-19 pandemic in Malatya province. Medicine 2022, 11, 1030–1035. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Nunn, S.; Newby, W. Landscapes of risk: The geography of fatal traffic collisions in Indiana, 2003 to 2011. Prof. Geogr. 2015, 67, 269–281. [Google Scholar] [CrossRef]
- Cai, Q.; Lee, J.; Eluru, N.; Abdel-Aty, M. Macro-level pedestrian and bicycle crash analysis: Incorporating spatial spillover effects in dual state count models. Accid. Anal. Prev. 2016, 93, 14–22. [Google Scholar] [CrossRef]
- Wang, J.; Olivier, J.; Grzebieta, R.; Walter, S. Statistical errors in anti-helmet arguments. In Proceedings of the Australasian College of Road Safety Conference—“A Safe System: The Road Safety Discussion”, Adelaide, Australia, 6–8 November 2013. [Google Scholar]
- Aldred, R.; Goel, R.; Woodcock, J.; Goodman, A. Contextualising Safety in Numbers: A longitudinal investigation into change in cycling safety in Britain, 1991–2001 and 2001–2011. Inj. Prev. 2019, 25, 236–241. [Google Scholar] [CrossRef] [PubMed]
- Teschke, K.; Harris, M.A.; Reynolds, C.C.; Winters, M.; Babul, S.; Chipman, M.; Cusimano, M.D.; Brubacher, J.R.; Hunte, G.; Friedman, S.M. Route infrastructure and the risk of injuries to bicyclists: A case-crossover study. Am. J. Public Health 2012, 102, 2336–2343. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.J.; Scott, D.M.; Páez, A. A spatial modeling approach to estimating bike share traffic volume from GPS data. Sustain. Cities Soc. 2022, 76, 103401. [Google Scholar] [CrossRef]
- Morrison, C.N.; Thompson, J.; Kondo, M.C.; Beck, B. On-road bicycle lane types, roadway characteristics, and risks for bicycle crashes. Accid. Anal. Prev. 2019, 123, 123–131. [Google Scholar] [CrossRef]
- Vandenbulcke, G.; Thomas, I.; Panis, L.I. Predicting cycling accident risk in Brussels: A spatial case–control approach. Accid. Anal. Prev. 2014, 62, 341–357. [Google Scholar] [CrossRef]
- Pearson, L.; Reeder, S.; Gabbe, B.; Beck, B. Designing for the Interested but Concerned: A qualitative study of the needs of potential bike riders. J. Transp. Health 2024, 35, 101770. [Google Scholar] [CrossRef]
- Pearson, L.; Berkovic, D.; Reeder, S.; Gabbe, B.; Beck, B. Adults’ self-reported barriers and enablers to riding a bike for transport: A systematic review. Transp. Rev. 2023, 43, 356–384. [Google Scholar] [CrossRef]
- Apardian, B.; Alam, B.M. A study of the effectiveness of midblock pedestrian crossings: Analyzing a selection of high-visibility warning signs. Interdiscip. J. Signage Wayfinding 2017, 1, 26–59. [Google Scholar] [CrossRef][Green Version]
- Alam, B.M.; Spainhour, L. Behavioral aspects of younger at-fault drivers in fatal traffic crashes in Florida. In Proceedings of the Transportation Research Board 88th Annual Meeting, Transportation Research Board, Washington, DC, USA, 11–15 January 2009. [Google Scholar]
- Alam, B.M. Evaluation of Age as a Contributing Factor for Fatal Crashes in the State of Florida. Master’s Thesis, College of Engineering, Florida State University, Tallahassee, FL, USA, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).