High-Speed Railway Planning for Sustainable Development: The Role of Length Between Conventional Line and Straight Length

Abstract

The extension of high-speed rail (HSR) lines around the world is increasing. The largest network today is in China, followed by Spain, Japan, France, and Italy; currently, new lines are being built in Morocco and Saudi Arabia. The goal of the new lines built is to drastically reduce the time distances between the extreme railway terminals by intervening on the two main components of time: space and speed. The two components have been investigated in various fields of engineering for design conditions (ex ante/a priori). In the literature, there is no analysis of what happened in the realization of the projects (ex post/retrospective). The research problem that arises is to analyze the high-speed lines built in order to verify, given a pair of extreme terminals, how much the length is reduced by passing from a conventional line to a high-speed line, and to verify how this length is getting closer and closer to the distance as the crow flies. The reduction of spatial distance produces direct connections between two territories, making the railway system (HSR) more competitive compared to other transport alternatives (e.g., air travel). To address the problem posed, information and data are collected on European HSR lines, which constitute a sufficiently homogeneous set in terms of railway and structural standards. The planimetric characteristics of specially built lines such as HSR are examined. A test method is proposed, consisting of a model that is useful to compare the length along the HSR line, with direct lengths, and existing conventional lines. The results obtained from the elaborations offer a first answer to the problem posed, demonstrating that in the HSR lines realized the spatial distances approach the distance as the crow flies between the cities located at the extremes, and are always shorter than the lengths of conventional lines. The final indications that can be drawn concern the possibility of using the results obtained as a reference for decision-makers and planners involved in the transport planning process at national and international level. Future research directions should study the values of the indicators in other large HSR networks, such as those built in Asia, and more generally study all the elements of the lines specially built to allow better sustainable planning, reducing the negative elements found and increasing the positive ones.

1. Introduction

High-speed rail (HSR) is for all purposes a new mode that differs considerably from conventional rail as it has developed over the last two centuries. The HSR, with its main feature, which is the drastic reduction in travel times, competes with aircraft in a wider range of spatial distances than conventional rail lines. Because of its main features, today it is the most sustainable mode of transport for space distances up to 1000 km.

The Agenda 2030 of the United Nations assigns, in fact, to railway transport a relevant role for pursuing sustainable development at planetary level. The following Sustainable Development Goals (SDGs) underline the role of railway infrastructures and services [1] to ensure access to affordable, reliable, sustainable, and modern energy systems for all (SDG7); promote sustained, inclusive, and sustainable economic growth (SDG8); support economic development and human well-being, with a focus on affordable and equitable access for all (SDG9); reduce inequality within and among countries ensure equitable access for all (SDG10); and take urgent action to combat climate change and its impacts (SDG13).

The HSR lines allow the use of energy produced from renewable sources (SDG 7) and produce CO₂ emissions (SDG13) in a ratio of 1 to 5 or 1 to 10, based on the estimation methods used, compared to air transport [2,3,4,5,6].

The HSR built definitely improves the general economic conditions of the territories crossed (SDG8) by increasing the GDP by an annual differential value that can reach 1% [7]; this improvement allows the reduction of the economic gaps between the territories (SDG10) as happened in Spain with the construction of the high-speed lines [8].

The construction of high-speed lines offers highly competitive passenger services with air transport and conventional rail transport, allowing the pursuit of notable results in social equity [9,10,11,12].

It is important to note that, while many works in the literature emphasize the relevance of HSR for the sustainable development of people mobility at the national level, several works point out its limitations in some applications in terms of the increase in economic disparities; the environmental trade-offs during the construction phase; and the uneven accessibility under the use of conventional lines [13,14,15].

To pursue the goals of sustainable mobility at national level, different countries are working to develop railway networks, increasing the extension of HSR lines. Based on data from the Union Internationale des Chemins de Fer (updated October 2023), the total operative HSR lines in the world amount to 59,498 km. From a long-term perspective, the total extension will be 129,850 km. The largest network today is in China (40,493 km), followed by Spain (3917 km), which has overtaken Japan (3146 km) and France (2735 km) [16]. Towards this perspective, the European Union is implementing the Trans-European Transport Network (TEN-T) for pursuing the international goals [17,18]. All European countries follow integrated planning, designing and realizing processes considering the development of multiple aspects to individuate technical, geometrical, and functional characteristics of HSR lines. The general indications for the plans are those defined in the literature ranging in Europe from the TEN-T to the regional and local plans [19] to advanced systems for passenger mobility [20,21,22,23].

The TEN-T network has undergone successive evolutions; the current specification is defined by Regulation 1679 of June 2024 [24]. The network, as defined in 2024, has three time milestones: the completion of a core network by 2030, of an extended core network by 2040, and of a comprehensive network by 2050.

The intermediate target, to 2040, was introduced to allow the completion of the main cross-border sections that allow the networks of neighboring countries to be directly connected, mainly with reference to the sections of the railway networks. The importance of HSR is underlined by the same document which estimates that high-speed rail traffic is expected to double by 2030 and triple by 2050. This increase in demand is important because competitive high-speed passenger rail has a high potential for the decarbonization of transport.

One of the main objectives of the TEN-T network is sustainability, which must also be pursued with (…) the possibility of making greater use of more sustainable modes of transport, in particular by further developing an interoperable long-distance passenger rail network, including high-speed.

An analysis of the maps annexed to Regulation 1679 [25] shows (Figure 1) that the problems in the western part of the Union are that of connecting the HSR networks of the various countries with cross-border sections and that of completing the most extreme southern areas, while in the east, from the north of Greece to the Baltic republics, it is a question of building the main backbones, in this case, evidently already homogenized in a single network.

HSR increasingly improves its competitiveness with respect to other transport alternatives (e.g., travel by air) as the travel times that the new lines allow [26,27] are reduced. The competition between the HSR and the aircraft has been studied in relation to different aspects [28,29,30,31]. HSR is decisive for sustainable development based on the different impacts that the two modalities have on a social, economic, and environmental level. The literature has addressed these issues in depth starting from the environmental problems related to greenhouse gases [13,32,33] and on life [34], by social problems [35], by economic problems related to the growth of a territory [36,37,38], and the economic sustainability of the infrastructure [39].

The primary objective of the HSR lines is to minimize temporal distances between the extreme railway’s terminal. The two crucial factors of an HSR line, to reduce time compared to existing conventional lines, are the following:

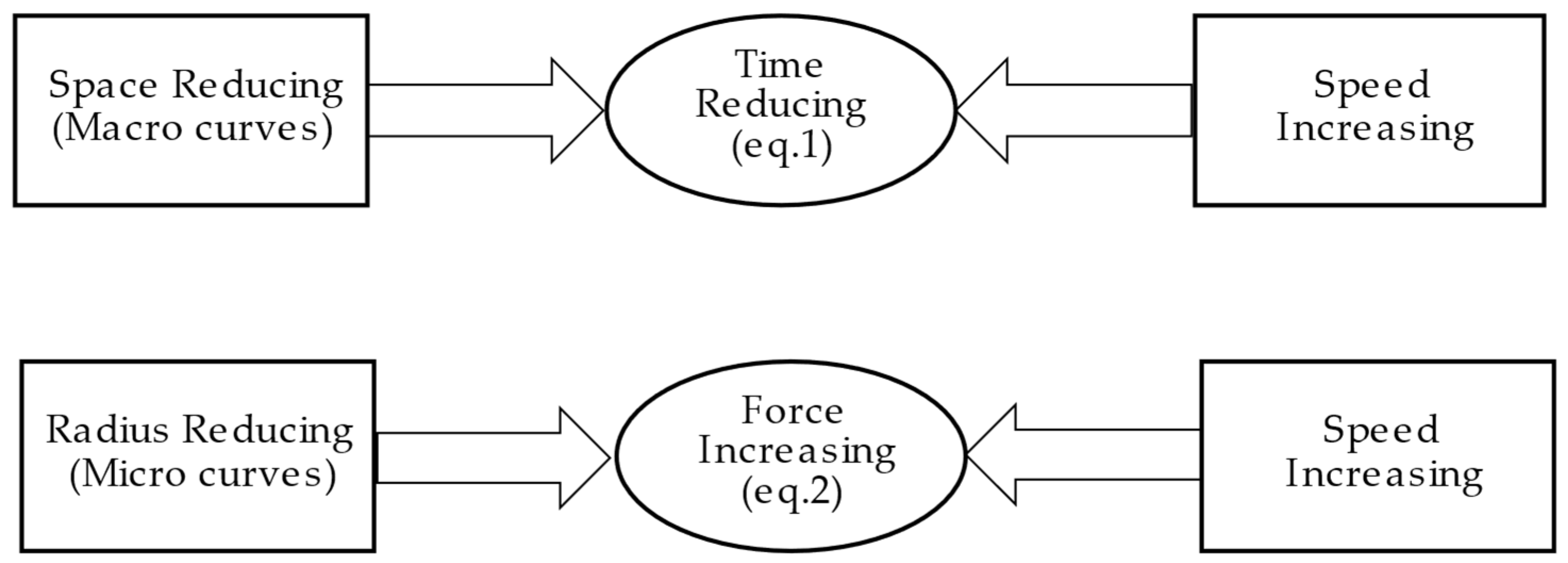
• The reduction in the spatial distance between the two ends of the line;
• The increase in travel speeds.

The problems connected with the two factors are deepened and developed in two different fields of engineering, although strongly integrated, as follows:

• On the one hand, the reduction in spatial distance is a problem more connected to civil engineering;
• On the other hand, the increase in speed, and therefore in the mechanical characteristics of railway trains, is a problem more connected with industrial engineering.

When considering the role of time as a dependent variable, these two factors emerge as foundational elements in the two fundamental equations of physics. They show the importance of each, assessed individually, and the importance of their interaction, particularly in the planimetric curves.

Spatial distance, or length, in the field of engineering, has a central role in the planning of a new line. As far as speed is concerned, there is a lot of work, and important experiments are underway, relating to the possibility of making trains with much higher speeds than the current ones: from Maglev magnetic leavening trains [40], to Hyperloop class vacuum trains [41,42], to the more advanced versions of the Shinkansen [43].

The vehicle–line interaction has been very in-depth with many works; it is possible to recall reference publications on the dynamics of the interaction with the different vertical and lateral effects [44,45]. The two factors have had different levels of development, while the problems of increasing speed have been studied by proposing new trains and new technologies, as mentioned above, the problems of length have been little addressed, compared to the lines designed and built [46].

The line extension influences the construction costs in the realization phase, but also the management costs in the next operative phases of a new high-speed rail line [47]. Spatial length represents a structural factors of a HSR network, because it linearly influences the temporal distances between extreme city nodes [48]. The temporal distance is therefore important in the study of the centrality of the nodes of a network [49,50,51,52]. A correct planning of an HSR line should aim to reduce temporal distances and then to increase sustainable mobility in terms of social, economic, and environmental goals. These principles are the inspiration for many railway projects, together with other ecological or geological principles, however declined [53].

The available scientific works investigate the railway horizontal and vertical alignment design, aimed at individuating a near-optimal solution connecting given railway start and end points [53] using direct (genetic algorithms) [54,55,56,57,58] and indirect (discrete algorithms) [59,60,61,62] methods. The problem is especially studied in topographically complex mountainous territories to identify the best truck alternative that meets different constraints [53]. In most cases, the problem regards the design of a single link at the local level for increasing quality or management processes [62]. These studies provided indications for design parameters related to passengers’ comfort, lateral stability, and maintenance cost [63].

The main scientific and technical works produced in the last 20 years have been reviewed and verified. In all the articles present in the literature, the methodologies for setting up the best project for a new infrastructure are continuously improved. It emerges that there are no articles in the accessible technical–scientific literature that verify three significant synthetic elements: actual lengths of the built HSR lines; lengths of existing conventional lines for the same connections between end nodes; and lengths of the theoretical lines (straight lines as the crow flies) between the extremes which constitute the lower limit and therefore determine the shortest theoretical time.

A review of the extant literature reveals the existence of numerous high-quality works that present methods for obtaining the best planning, thereby providing ex ante theoretical indications. There are no studies available in the literature regarding the relationship between the three lengths defined above, i.e., there is no analysis on what has been achieved with the new HSR lines compared to the conventional and straight ones. That is, there is no ex-post theoretical analysis of what is actually possible to achieve, between theoretical limits and real applications. The possibility of having a scientific analysis that identifies the real limits for the lengths of the HSR lines has important practical results because it allows technicians, designers, and planners to compare themselves with the real realizations and not with the theoretical distances, verifying the exchange between each percentile of more or less elongation, compared to the real ones, and the related savings or costs.

The purpose of this paper is to review the existing HSR lines to verify how the planimetric characteristics, and in particular the line spatial extension with the reduction in small and large-scale tortuosity, produce direct connections between territories.

The method used is to estimate a set of models for quantifying the reduction in distance between existing conventional and HSR railway lines, when compared to the straight line between two connected cities, also called the distance as the crow flies. The proposed models aim to reproduce the lengths of the existing HSR lines with respect to the distances of the conventional lines and the straight lengths as the crow flies. The following work is intended to provide a comprehensive overview of the subject matter. To accomplish the objectives of this paper and to implement the proposed method, information and data about the HSR lines are to be collected. A set of European railway lines realized in France, Italy, and Spain constitutes the specific observation field of this study. Elaborations of the available data allow the interpretation of the distance reduction respect to the distance as the crow flies, obtained before with the realization of the conventional railway lines and after with the HSR lines.

The main results of this paper are connected to the following: the review of existing planimetric characteristics of the HSR lines in Europe; the proposed method and their experimentation at the European level; and the real average quantity of HSR length respect to the straight line.

The results obtained from elaborations show the objective of planners to improve the performance of connections among territories, reducing the lengths. Decision makers involved in the integrated planning process at regional, national, and international level could use the proposed method for measuring sustainability indicators related to the temporal distances in an aggregate way. At the same time, the obtained results constitute a basis for measuring other components of sustainable development.

Following the main issues raised in this introduction, this paper has three sections. Section 2 describes the proposed model for reproducing the existing line lengths, leaving from basic equations of physics. Section 3 reports the main results obtained from the application of the model. Section 4 closes the paper with the discussion and main conclusive remarks.

2. The Proposed Model

The proposed model aims to verify what the relationships are between the lengths of the HSR lines, those of the conventional lines that insist on the same sections, and the corresponding lengths as the straight lines.

The hypotheses that are the basis of the present work are the basic equations of classical physics and the knowledge (and availability) for each HSR line that connects two terminals placed at the ends, of the lengths of the HSR line, of the distance as the crow flies (straight length), of the conventional line. The thesis to be demonstrated is that the average value of the HSR length is always less than the conventional length and greater than the distance as the crow flies and that the calibrated parameters to compare the different lengths are statistically valid and therefore usable for the strategic planning of new lines.

That is, it needs to investigate that HSR lines are shorter than conventional lines and tend to get very close to the distance as the straight lines between the HSR terminals placed at the ends. To verify the thesis the formulations of classical physics for the relationships between time, space, and speed and those for centrifugal forces (Section 2.1) are first recalled, then the formulation of linear regression models (Section 2.2) is recalled, specifying the variables with respect to which the statistical relationships are investigated on the basis of the characteristics freely readable by the special lines built for HSR (Section 2.3).

2.1. The Basic Equations

The two main factors that determine the value of the time distance are the spatial distance and the speed at which the line can be travelled. Here, the physical principles that allow the formalization of the relationships between variables are recalled.

The first factor is highlighted experimentally given that the reduction in the distance between the two extremes, with all other conditions being equal, in the hypothesis of speeds equal to conventional ones, leads to an equal reduction in travel times.

The basic equation of uniform rectilinear motion that represents this experimental result is as follows:

t = s/v

(1)

with

t as the time distance between the two extreme terminals;

s as the spatial distance evaluated along the path of the line;

v as the speed of travel of the line along the path.

From Equation (1), it immediately emerges that if the spatial distance passes from s₁ (conventional) to s₂ (HSR), assuming that s₂ is half of s₁, it follows that t₂ will be half of t₁ at the same speed. Then, for any percentage of reduction in spatial distance, there is the same percentage of reduction in temporal distance.

The second factor emerges again from Equation (1); in fact, it turns out that if the speed passes from v₁ (conventional) to v₂ (HSR), assuming that v₂ is twice as fast as v₁ (v₂ = 2 v₁), it follows that t₂ will be half of t₁ at the same distance (t₂ = 1/2 t₁). In the same way, for any percentage increase in speed, there is the same percentage of reduction in time distance.

Equation (1), in its simplicity, brings out the linearity of the reduction in time with the reduction in space and with the increase in speed. The planning problem is therefore to operate independently on the two variables s and v, giving to the maximum the reduction in the spatial distance and to the maximum the increase in speed.

In real situations, the two factors operate independently in straights, while they are not independent, in curves; in fact, it is possible to see how the speed that trains can reach and maintain depends on the planimetric and altimetric layout. Assuming that a flat track is built and assuming that trains are built that have very high powers that allow them to reach the desired speeds, the limitations arise from the passage along the curves due to the activation of centrifugal forces.

The reference equation for centrifugal forces is as follows:

F = m (v²/R)

(2)

with

F as the centrifugal force;

m as the mass of the train;

v as the speed on the curve;

R as the radius of the curve.

From Equation (2), it emerges that the speed cannot increase with the power available to the train, because the centrifugal force in the curve can generate the derailment of the train. Equation (2) can be reported in terms of acceleration towards the exit from the track, simplifying the mass m on the two sides of the equation. So, to reduce this acceleration, it is therefore necessary to make curves with a large radius (denominator), or reduce the speed (numerator).

The reduction in speed along curves, compared to that on the straight, requires that the train must begin to reduce speed long before entering the curve, and after the curve must accelerate to return to cruising speeds, from which two more time increments derive.

In a synthetic way, we can therefore define macro-curves as those connected to the large folds that the route makes to reach intermediate points that are not on the direct line between the extremes, i.e., large curvatures of the route usually defined at the planning scale. In the same way, the usual curves properly so-called, introduced in the planning to adapt the layout to the orography, can be defined as micro-curves. As macro-curves and micro-curves increase, the travel time increases. Figure 2 shows the scheme of the theoretical relations given by the principles of dynamics, where evidently the reduction in time is a positive element while the increase in centrifugal acceleration is a negative element.

In the next section, the formulation of the multiple linear regression model is recalled, which allows for investigating the relationships between the characteristics of the lines on the basis of the HSR achievements in various countries.

2.2. Model Specification

A multiple regression linear model is used to analyze the relationship between the different distances.

The general functional form of the model is the following:

y = f (x; β) + ε

(3)

where

x is the vector of independent variables (or attributes);

y is the dependent variable;

β is a vector of unknown parameters;

f () is a function;

ε is the error.

Given the model expressed by Equation (3), it is assumed that f () is linear,

y = β₀ + Σ_j=1,k β_j x_j + ε

(4)

where β₀ and β_j are parameters of vector β.

The vector of parameters, β, can be estimated by means of the ordinary least squares (LS) method. LS operates by choosing, among the infinite possible plans defined by Equation (4), the one that minimizes the sum of the squares of the deviations between the values observed and the values estimated by model (4).

The chosen vector β_LS, is the one for which results the following:

β_LS = argmin Σ_i=1,n ε²_i = argmin Σ_{i=1, n} (y_i − (β₀ + Σ_{j = 1,k} β_j x_j,i))²

(5)

with

β_LS, vector of parameters that minimizes Equation (5);

ε, observed deviations for each HSR line i;

y_i, average HSR length observed for the HSR line i;

x_j,i, attribute j observed for HSR line i.

It is useful to calculate a multiple correlation index, denoted by R², which measures the intensity of the linear link between the dependent variable y and the vector of explanatory variables, x. The R² index is equal to the following:

R² = 1 − RSS/TSS

where

RSS = Σ_i=1,n (y_i − (β₀ + Σ_j=1,k β_j x_j,i))² is the residual deviance;

TSS = Σ_i=1,n (y_i − y)² is the total deviance;

y is the average value of the dependent variable.

2.3. Variables Used

The investigation concerns the HSR realized in Europe, referring to the networks of France, Italy, and Spain.

Figure 3 shows the map of the selected European lines of the TEN-T network, and of which the database is available [64,65,66].

The database has been built starting from available information about the HSR lines investigated. Attributes that are valid for the model to be estimated and that can be found in the technical literature in a simple way have been sought, in order to allow the replicability of the model estimation in other national contexts.

In Italy, the investigated HSR lines are six [64]. These lines connect the main metropolitan Italian cities from north (Torino–Milano–Rome) to south (Rome–Naples–Salerno).

In France, the investigated HSR lines are six [65]. These lines connect the main metropolitan French cities from east to west (e.g., Strasbourg–Paris) and from north to south (e.g., Paris–Lyon–Marseille).

In Spain, the investigated HSR lines are four [66]. These lines connect the main metropolitan Spanish cities from east to west (Barcelona–Madrid) and from north to south (Valladolid–Madrid–Malaga).

It is necessary to point out that the system of lines considered is homogeneous internally, both in terms of the characteristics of the supply system and those of demand. As far as the demand is concerned, it is easy to highlight that the three countries belong to the European Union and therefore have a shared legislative and economic apparatus, the lifestyles are similar belonging to the same Latin culture. As regards the HSR infrastructure supply, it should be noted that the three countries have the same standard gauge and are converging towards the same ERTMS control system. It can be remembered that the conventional lines in Spain have a different gauge, while it was decided to implement the HSR with the standard gauge. Shared gauge and control enable full interoperability for HSR passenger services. Tests are underway to carry out HSR Milan–Paris services, between Italy and France, and the economic verification of the company that manages HS services in Italy is also underway, for the activation of HSR services in Spain.

Based on what was seen in Section 2.1 above, the minimum travel time depends on s and v. The dependence on v is, in short, a dependence on the type of train with the related engines available and on the type of power supply. While, as highlighted in Equation (1), the dependence on s depends only on the path built and therefore, specifically, on the length of the path. In fact, as seen, by fixing v, there is a linear relationship between time and space. All the various types of length (space) considered are then defined, to verify if there is a reduction in length from conventional to HSR lines, and if there is, how much it is worth. This analysis is carried out both on the overall system of lines and on that of each of the three countries considered.

The lines considered represent more than 61% of the total high-speed lines built in Europe, and approximately 13% of the lines built worldwide.

It should be considered that the three reference countries are important because the lines, in these countries, are all planned, designed, and built specially for high speed and are not upgrades of existing lines. The lines considered in the document used as reference UIC [16], following the formal definition provided by the European directive [24], are high-speed lines, as follows:

• Lines specially built for high speed (equal to or greater than 250 km/h);
• Lines specially upgraded for high speed (around 200 km/h);
• Lines specially upgraded for high speed which have special features as a result of topographical, relief, or town-planning constraints (speeds may be lower).

Based on these considerations, the values of 61% and 13% are significantly lower than those relating only to the lines built for high speed. The sample is therefore largely representative of the European situation with about 84% specially built for HSR, and significant on an international scale. It will be useful, as reported in the conclusions, to extend the proposed method to the large Asian HSR systems of China and Japan.

The model is focused on the difference between the existing HSR line distances and the distances as a straight line or as the crow flies.

A smaller difference between HSR length and length as the crow flies represents a more direct connection between the two cities. This produces better performances in terms of travel times.

The lengths considered are the following:

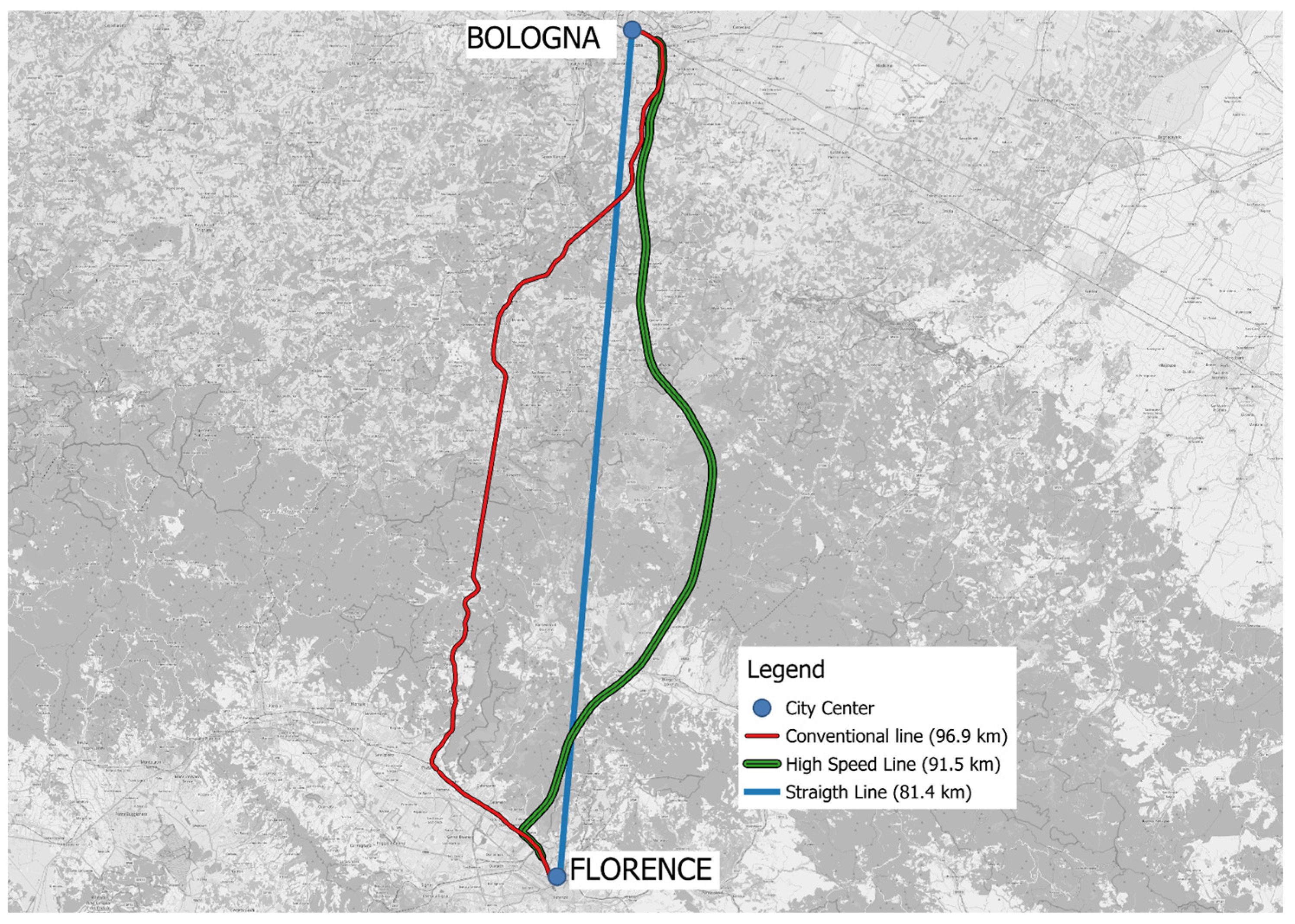
• HSR length or length of the HSR railway line which connects two cities;
• Conventional length, or length of the conventional railway line which traditionally connects two cities;
• Straight line or length as crow flies or minimum distance between two cities, calculated on the straight line joining the representative centers of the single urban areas.

Starting from the available data, a set of variables has been selected, and named generic, specific, and dummy.

The generic variables represent the length measured in kilometers, as follows:

• l_HS indicates the HSR line;
• l_CN indicates the conventional line;
• l_SL indicates the straight line or crow flies line.

The specific variables represent the lengths measured in kilometers of each line in the selected countries, Italy, France, and Spain, of each of the following:

• HSR line present in Italy, indicated as l_HS,IT, in France, indicated as l_HS,FR, and in Spain, indicated as l_HS,ES;
• Conventional line present in Italy, indicated as l_CV,IT, in France, indicated as l_CV,FR, and in Spain, indicated as l_CV,ES;
• Straight line connection present in Italy, indicated as l_SL,IT, in France, indicated as l_SL,FR, and in Spain, indicated as l_SL,ES.

The dummy variables are related to the specific country where each HSR line is located, as follows:

• In Italy (IT), the variable that assumes value 1 if the line connects two Italian cities, and 0 otherwise;
• In France (FR), the variable that assumes value 1 if the line connects two French cities, and 0 otherwise;
• In Spain (ES), the variable that assumes value 1 if the line connects two Spanish cities, and 0 otherwise.

3. Calibration Results

The calibration of the models is developed in order to first verify the relationship between the length of HSR railway tracks and the length of conventional tracks and straight distances; the relationships are also calculated for individual countries. In a second phase, the conventional length is set as a dependent variable to analyze how it depends on the average straight length.

The overall hypothesis is that the conventional line has the longest length and that the length of the HSR line is always between the conventional and the straight line.

To highlight the three lengths considered in relation to an experimental case, a section of the Italian HSR network is represented in Figure 4. The section is the Bologna–Florence which is a link built in one of the most orographically tormented Italian areas. In fact, the link crosses the important mountains of the Apennines. Figure 4 shows the three lengths relating to direct connection, HSR, and conventional line.

3.1. HSR Length Dependent Variable

Adopting the linear functional form described by Equation (4), the first group of models aims at reproducing the HSR line length, with the following assumptions:

• The variable l_HS is the dependent variable (y);
• The generic, specific, and dummy variables, representing the conventional lines, are the independent variables (x).

For each specified model,

Table 1. Models for reproducing the HSR line length (l_HS).

Model	R2	β
		βCN	βCN,IT	βCN,FR	βCN,ES	βSL	βSL,IT	βSL,FR	βSL,ES	βFR	βES	βFR+ES
1.1	0.986	0.88
1.2	0.985					1.15
1.3	0.989	0.47				0.53 *
1.4	0.987	0.85								21.07 *
1.5	0.987	0.90									−28.4 *
1.6	0.986	0.89										−5.53 *
1.7	0.986					1.08						27.03 *
1.8	0.989	0.43 *				0.57 *						8.45 *
1.9	0.987		0.94	0.89	0.85
1.10	0.987						1.12	1.12	1.22
1.11	0.989		0.94	0.65	0.85					113.52 *
1.12	0.988		0.94	0.89	0.92						−38.09 *
1.13	0.987		0.94	0.87	0.84							7.10 *
1.14	0.979						1.12	1.12	1.27		−18.37 *
1.15	0.992						1.12	0.74	1.22	141.39
1.16	0.988						1.12	1.00	1.11			42.98 *

* statistical parameter t-student (t) values are in the interval: −1.92 < t< 1.92; IT: Italy; FR: France; ES: Spain; FR + ES: France and Spain; l_HS: HSR length; l_CN: conventional length; l_SL: straight line length; l_HS,IT: HSR length in Italy; l_CN,IT: conventional length in Italy; l_SL,IT: straight line length in Italy; l_HS,FR: HSR length in France; l_CN,FR: conventional length in France; l_SL,FR: straight line length in France; l_HS,ES: HSR length in Spain; l_CN,ES: conventional length in Spain; and l_SL,ES: straight line length in Spain.

reports the values of the calibrated parameters β_LS and the values of the statistical indicators. The parameters with a low statistical significance are indicated with “*”.

As an example, the specification of Model 1.2 is as follows:

$${\mathrm{l}}_{\mathrm{HS}}={\beta }_{\mathrm{SL}}{\mathrm{l}}_{\mathrm{SL}}$$

which, with the calibrated parameter, becomes the following:

l_HS = 1.15 l_SL

By setting the l_HS equal to 100, it is possible to highlight the percentage increase or decrease in each of the specific lengths identified. So, for example, the straight-line length l_SL according to model 1.2, will be equal to the following:

l_SL = 100/1.15 = 87

In the first part of Table 1, the models that give l_HS from l_SL or l_CN are reported to introduce other country variables. In the second part, the attention is on the average length of each country.

3.2. Conventional Length Dependent Variable

Adopting the linear functional form described with Equation (4), the second group of models aims at reproducing the conventional line length with the following assumptions:

• The dependent variables (y) are specific for each country as follows:

  ○

  The variable l_CV,IT for Italy;

  ○

  The variable l_CV,FR for France;

  ○

  The variable l_CV,ES for Spain;

• The independent variables (x) are the following:

  ○

  The variable l_SL,IT for Italy;

  ○

  The variable l_SL,FR for France;

  ○

  The variable l_SL,ES for Spain.

For each specified model,

Table 2. Models for reproducing the conventional line length (l_CV).

Model	R2	β
		βSL	βSL,IT	βSL,FR	βSL,ES	βFR	βES	βFR+ES
2.1	0.988		1.19
2.2	0.992			1.26
2.3	0.990				1.43
2.4	0.988	1.307
2.5	0.993	1.331				−16.002 *
2.6	0.995	1.258					56.236
2.7	0.993	1.190						49.230
2.8	0.994	1.307
2.9	0.988		1.186	1.258	1.431
2.10	0.992		1.186	1.001	1.431	94.268
2.11	0.990		1.186	1.258	1.369		23.283 *
2.12	0.988		1.186	1.121	1.297			50.543 *

* statistical parameter t-student (t) values are in the interval: −1.92 < t < 1.92; IT: Italy; FR: France; ES: Spain; FR + ES: France and Spain; l_SL: length of the straight line; l_SL,IT: length of the straight line in Italy; l_SL,FR: length of the straight line in France; and l_SL,ES: length of the straight line in Spain.

reports the values of the calibrated parameters β_LS and the statistical indicators. The parameters with a low statistical significance are indicated with “*”. Table 2 reports the increase in conventional length respect to the other considered.

As an example, the specification of Model 2.8 is as follows:

$${\mathrm{l}}_{\mathrm{CV}}={\beta }_{\mathrm{SL}}{\mathrm{l}}_{\mathrm{SL}}$$

which, with the calibrated parameter, becomes the following:

l_CV = 1.307 l_SL

4. Discussion

The HSR lines are fundamental to reducing temporal distances among urbanized territories. From a long-term perspective, these reductions contribute to achieving the SDG at the global level. In line with this perspective, since 2000, the European Union has been investing in the construction of a homogeneous railway network as a relevant component of the TEN-T [24]. A great part of these investments regards the realization of high-speed rail infrastructures. The final aim is to realize a set of direct connections between the European cities. This paper has reviewed the operative HSR lines in France, Italy, and Spain.

From the calibrated models, some remarks emerge that could be better evidenced if represented in Figure 5.

The figure represents a different aspect that emerges from the models. The length of the existing conventional lines is set as a reference, i.e., equal to 100, as proposed in Section 3.1. The following considerations can be made:

• The average HSR line length (l_HS) of the three countries increases by 13% when compared with the distance between analyzed railway terminals as the average straight line (l_SL) (mod 1.2), but decreases of 13.6% compared with the average conventional lines (mod 1.1);
• The average straight-line length in Italy and in France is reduced by 10.7% and in Spain by 18%;
• The average conventional line length (l_CN) in Italy has a percentage increase in distance of 6%; the same percentage increase of 12.4% in France; and of 17.6% in Spain (mod 1.9), with respect to average HSR length.

The obtained results confirm that the realized HSR lines reduce the length with respect to the conventional lines, tending to the length of the line as the crow flies between two extreme cities.

From what was obtained from the analysis of the HSR lines actually built, it emerged that they are always shorter than conventional ones. It is useful to note that this reduction in the distance between the extremes together with the increase in speed makes it possible to reduce travel times, allowing us to compete with the aircraft on average distances on a national scale of 500–1000 km as the crow flies, confirming the consolidated literature results [67].

In their work, Givoni and Dobruszkes [67] consider more than 50 active lines as of 2013; each of them has been classified in relation to the travel time between the terminals that define the extremes and the percentage of demand it has acquired in the (bimodal) comparison with air transport. The HSR travel time for which the demand is split almost equally between the two modes is approximately 3 and a half hours. Below, demand grows strongly towards HSR, and above it reduces. An example of a service that is located in this central area and that in a few years has conquered an important percentage of demand is the line that connects the two most important Italian cities: Rome and Milan.

The straight distance is approximately 500 km. The current average time for high-speed rail services is 3 h. The average time by air transport is approximately 3 and a half hours including flight time, access, and exit time from the city center to the airports, and control time. The values of the modal times are similar to those obtainable for distances of the same order of magnitude. The comparison between these times explains the great result in terms of diverted demand that moved from the plane to the train, and explains even more the growth of previously non-existent induced demand, and the one relative to economic growth [9,49,67,68,69,70,71,72] demand (diverted, induced, by economic growth) which is constantly confirmed in the HSR, as can be easily verified by the daily offer on the Rome–Milan route of over 50,000 seats.

The real results therefore demonstrate that a valid plan of the HSR for direct connections between territories, with the reduction in distances and the increase in speeds, is a necessary (but not sufficient) element for success in national competition with other modes and services.

The tables and figures show a greater reduction in Spain when switching from conventional to HSR, this is due to the lengths of conventional which are much longer than direct lengths. Despite the sharp reduction, Spain has higher percentage lengths of HSR lines (22%) than those of France and Italy (12%).

These further results in the comparison between lines specially built for high speed and conventional lines demonstrate what was assumed in the introduction: pursuing sustainability objectives defined by Agenda 2030. In fact, the HS lines, by reducing the spatial and therefore temporal distances between territories compared to conventional ones, profoundly modify demand, contributing decisively, on average national distances, to pursuing the indicated SDGs.

5. Future Research and Conclusions

The work carried out has some limitations related to several factors; these limits allow us to glimpse important future developments for research. The first factor depends on the limited set of countries analyzed. In fact, as we have seen, the whole is strongly representative of European countries but constitutes just over 10% of the lengths of lines built worldwide. The second factor is the lack of consideration of the altimetric characteristics that influence the design of railway tracks in terms of tunnels and viaducts. The third factor is related to the urban densities of the territories crossed and therefore to the amount of population affected by the line.

The three factors set out above provide important indications for future developments. It is certainly interesting to analyze, through the proposed approach, the lines built in Asia (mainly China and Japan), comparing them with the results presented in this article which are related to Europe. In the same way, it may be interesting to verify what is happening in Africa with the first HSR lines built in Morocco. The second line concerns the internalization of the orographic conditions of the territory concerned. These developments can be useful, considering the binding obligation at the design stage not to have gradients higher than very low targets (3.5% in France), further reduced if the transit of freight trains is envisaged (1.25% in Italy). The third factor determines the possibility of future research that considers the presence of metropolitan areas close to the line and therefore the definition of the route with attestations of the line outside the cities or inside through stations and underground urban routes.

Further future research may concern the relationship between costs and lengths. At present, the literature proposes average costs for the construction of HSR infrastructures depending on the country. The only thing that emerges from these data is that by reducing lengths, costs are reduced. The second line of development proposed above could be developed to see the relationship between making a slightly longer and flatter track and making a shorter track with more slopes.

The future research identified can in turn be developed with various levels of aggregation: from considering the overall aggregate values on a global scale, to considering, at the other extreme, the disaggregated values for each country.

It is possible to draw some conclusions from the work carried out.

A first conclusion concerns the possibility of identifying, already at the time scale of strategic planning, sufficiently valid values for the lengths of the lines to be planned, without the need to develop the design process, at the various stages, according to the standards of each country. The estimated parameters make it possible to define, both in the case that a conventional railway line already exists and in the case that it does not, the length of the HSR line to be planned and therefore to determine its maximum costs in relation to the average costs of the country. The estimated parameters therefore make it possible to orient planning towards sustainable development, making it easy to verify whether the objective of reducing the temporal distance between extremes is pursued by the plan and to what extent it is pursued.

It is therefore important to note, even if at a very aggregate level, that the increases in the lengths of HSR lines are always halfway between conventional and direct lines. It is interesting to note that this happens both for territories with high orographic movements, such as Spain, and for those with medium movements, such as Italy, and for flat ones, such as France.

These considerations, compared with the future developments seen above and with the scientific and technical literature on HSR lines, identify a strong gap in the knowledge of what happened in the construction of the specially built lines and then in their operative phases. This implies the possibility of a large field of research, little to not yet explored, where the lines created are analyzed by comparing both the levels of efficiency and the levels of effectiveness. Further information and data placed in the scientific field make it possible to improve the lines that still need to be planned, increasingly confining the negative components.

The proposed work can be of great importance for designers because the results obtained can be reference elements for new lines in the design phase. The results can also be useful for public decision-makers because they allow them to have an aggregate estimate of the lengths and therefore the costs of building a line, when only the extremes are defined. The results are also interesting for researchers in the field because they allow them to develop analyses on the types of projects, allowing them to deepen their knowledge of the components.