Abstract
The autonomous vehicle is an innovative field for the application of machine learning algorithms. Controlling an agent designed to drive safely in traffic is very complex as human behavior is difficult to predict. An individual’s actions depend on a large number of factors that cannot be acquired directly by visualization. The size of the vehicle, its vulnerability, its perception of the environment and weather conditions, among others, are all parameters that profoundly modify the actions that the optimized model should take. The agent must therefore have a great capacity for adaptation and anticipation in order to drive while ensuring the safety of users, especially pedestrians, who remain the most vulnerable users on the road. Deep reinforcement learning (DRL), a sub-field that is supported by the community for its real-time learning capability and the long-term temporal aspect of its objectives looks promising for AV control. In a previous article, we were able to show the strong capabilities of a DRL model with a continuous action space to manage the speed of a vehicle when approaching a pedestrian crossing. One of the points that remains to be addressed is the notion of discrete decision-making intrinsically linked to speed control. In this paper, we will present the problems of AV control during a pedestrian crossing, starting with a modelization and a DRL model with hybrid action space adapted to the scalability of a vehicle-to-pedestrian (V2P) encounter. We will also present the difficulties raised by the scalability and the curriculum-based method.
1. Introduction
The rapid spread of Advanced Driver Assistance Systems (ADAS) in the car market and the ever-increasing computerization of our means of transport are leading us towards the automation of vehicles. This field, known as autonomous vehicle (AV), has made recent advances with the help of machine learning—more specifically, deep reinforcement learning (DRL), which is a subdomain of reinforcement learning and deep learning. The control and decision-making of a road agent are extremely complex to achieve due to the complexity of the road network. Autonomy requires good perception of the environment (detection of agents and road conditions), understanding of driving hazards (trajectory prediction) and safe cooperation with other road users. In fact, an autonomous model must be capable of addressing several objectives, such as user safety, passenger comfort and time efficiency. Research shows that it is possible to access environmental information using fixed or vehicle-mounted sensors [1,2]. These tools provide a robust visualization of the environment in digital format.
Based on this perception of the environment, our focus is on the interaction of an AV with a highly vulnerable road user, the pedestrian, during a pedestrian crossing. The pedestrian is a complex agent with which to cooperate. It is difficult to predict its trajectory due to the great uncertainty in its actions [3]: the pedestrian agent may change its mind and therefore its objective, or it may fall or have a perception that puts it in danger. Thus, it is very important to comply with the legislation of the country in question, as pedestrians have priority over vehicles in many Western countries. In the event of a pedestrian–vehicle encounter, the AV must decide on the order of passage of the agents at the meeting point (such as crossing paths at a pedestrian crossing) and act accordingly.
The decision-making can then be handled separately from real-time vehicle control. This separation is important because it contributes to the addition of communication with the pedestrian thanks to the first part. AVs and pedestrians can be represented as conflicting agents (their actions are influenced by those of other agents) [4] whose trajectory we want to optimize. The most interesting way to design this conflict is to define those agents as cooperative agents. They share two common goals: respecting the rules of the road and ensuring safety for all.
The vehicle has several communication methods with the pedestrian. First, the AV can communicate indirectly via its speed curve. The vehicle speed profile is widely known as a determinant of pedestrian decision [5,6]; to the best of our knowledge, the first work that exploited this property is presented in [7]. As indicated by [8], we can assume that each pedestrian has a decision threshold that strongly depends on the speed of the vehicle. In the same way, article [9] stated that deceleration is a determining factor for the pedestrian trajectory. Second, the AV can communicate directly via its light signals according to the model decision. The communication techniques are highly studied in the literature [10,11,12]. The visual signal is important because it is a very powerful communication tool, providing direct communication and reducing uncertainty and ambiguity.
The article proposes deep reinforcement learning (DRL) as a promising approach for AV control, particularly for managing the vehicle speed during pedestrian crossings. It presents a DRL approach with a hybrid action space aiming at addressing the challenges encountered in vehicle-to-pedestrian encounters. Furthermore, the paper suggests a curriculum-based scalability approach for autonomous vehicle (AV) control at crosswalks and discusses the challenges encountered in implementing this approach.
This paper is organized as follows. Section 2 lists related work on the application of the DRL model to the simulation of vehicle-to-pedestrian (V2P) interactions, including articles that influenced the writing of this article, and presents a brief overview of the usable techniques and DRL models with specific action space managing V2P interactions. Section 3 describes the studied use-case and our scalability approach. Section 4 details the proposed innovative approach based on hybrid DRL. Section 5 describes the simulation environment and presents the results of the proposed approach. Finally, we conclude in Section 6.
2. Related Works
2.1. V2P Interaction
Numerous tools exist for managing vehicle actions; yet, the literature concerning V2P interaction predominantly concentrates on vehicle control for collision avoidance measures and estimating pedestrian trajectories. The simplest method is to apply an emergency brake when the system detects a collision or when a pedestrian intends to cross the road. Other more complex and deterministic methods, such as quadratic programming, enable continuous control of the vehicle. For example, an intelligent driver model (IDM) can be used to adjust the vehicle speed by taking into account the car position and the estimated time at which the pedestrian leaves the road. The drawback of these techniques is their lack of adaptability to changes in pedestrian behavior. The DRL methods are more responsive and efficient, using continuous action space-based policies such as Deep Deterministic Policy Gradient (DDPG) and Proximal Policy Optimization (PPO) [13,14,15,16].
Firstly, it is important to point out that we are going to limit our study to vehicle control and decision-making, excluding the preceding perception part. The first logical approach for an AV that adapts to the actions of pedestrians is to focus on them. If we know the pedestrian future states, we can react more quickly, which makes it much easier to optimize the vehicle actions. We can detect the pedestrian and follow his trajectory over time using a camera, then estimate his next actions, as in [17]. This uses a model for predicting pedestrian trajectory, creating hazardous areas and warning the vehicle if there is an overlap with its own trajectory. We can also build a realistic pedestrian model to improve the learning of the vehicle control model. Theoretical models can be used for this purpose [18]. One of the most important points for the vehicle in the pedestrian actions is when the pedestrian decides whether to cross or not. Ref. [8] uses a theoretical model with the notion of a crossing trigger linked to a threshold (itself dependent on the state of the environment). Ref. [19] draws a pedestrian trajectory during a crossing (speed curve). Decision prediction models can also be used [20] to estimate this point.
The second approach confronts the vehicle with a worst-case scenario: avoidance is required to prevent an accident. On the one hand, the article [21] uses a DRL model learning directly from real data. As the aim of the model is to model the pedestrian as realistically as possible, it sets up a reward that compares the resulting trajectory with a real one. This work highlights the adaptive capacity of the pedestrian to avoid a vehicle. On the other hand, article [22] developed pedestrian models to test the robustness of AV models facing dangerous behavior. We can also use an avoidance model in which the model is given control of the speed and steering wheel with the aim of avoiding an accident [23].
The choice of DRL tools is highly dependent on the chosen action space. There are DRL models with discrete action space. There are numerous DRL tools of this kind that can be used, including Deep Q Learning (DQN) and its derivatives. In the context of avoidance, such an algorithm can be used to induce a lane change [24]. It can also be used to decide whether to activate an emergency stop [25] or not. For example, in [26], there are DRL models with continuous action space, where the model decides on vehicle deceleration (braking intensity).
2.2. Hybrid Action Space
In the presented use-case, we need a so-called hybrid action space (action space with continuous and discrete actions) with multiple objectives (ensuring passenger safety and time efficiency). We will list the different solutions from the state of the art:
To deal with a multi-objective model, Multi-Task Learning consists of managing several tasks at the same time. The main example for this idea is the Hindsight Experience Replay (HER) method [27]. HER separates the different objectives of the reward to promote targeted actions, despite the episode’s failure in its realization. It converges more quickly toward the complex actions we want to achieve. To do this, it first separates the reward into several distinct objectives (multi-task). Then, it stores the rewards of the different tasks in a replay buffer (separately). However, HER is not very efficient against shaped rewards (discrete rewards). Designing a non-sparse/shaped reward related to the model decision-making in our environment is very difficult. Moreover, to define the importance of each part of the reward, the only solution is to modify the frequency of their appearance in the replay buffer. DIStill and TRAnsfer Learning (Distral) [28] is an algorithm that separates different tasks into child models. Compared to federated learning, each model does not need a different data set but seeks to achieve its objective while being constrained by the general model. Importance Weighted Actor–Learner Architecture (IMPALA) [29] proposes a modification of the weight of each part of the reward for each distributed model.
To deal with the hybrid action space, Parameterized Action Space, a DRL subdomain, consists in hierarchically classifying discrete and continuous actions in the same model—a discrete action is linked to a set of continuous actions. The two following models start from DRL models on discrete or continuous actions only to build a parametric model on top. The action space hierarchy expresses the dependency between discrete and continuous actions. This approach significantly increases the number of outputs of the model. The parameterized DDPG [30] transforms the actor of the DDPG to ask him in the output: both discrete choice and the continuous values relative to the various discrete choices. All these data are then returned to the critic, which, just like the DDPG, returns as output an estimate of the reward with respect to the actions and the given state. It uses an epsilon-greedy degressive exploration on discrete actions and continuous actions with uniform laws. The P-DDPG model thus proposes a decision model able to perform a discrete choice and to optimize the continuous variables related to this choice.
The parameterized DQN [31] uses the same structure as the DQN to determine the discrete action to be carried out with the help of an estimate of the reward that one seeks to optimize (Q(a,s)). However, it adds an actor that calculates the continuous variables in the same way as a classical DDPG. In this case, the only difference is that it relies on the critic (model estimating Q) to achieve a good classification. It eventually compares the rewards obtained according to the discrete choice. The article also describes the techniques for limiting the values of the gradients. The squashing technique is the one that gives the best results in the tests we have been able to perform. This supports the theory of the article proposing the PATRPO model [32], which states that squashing is more interesting in learning than invert-gradient. This article also introduces multiple models, such as parameterized TRPO and SVG. Unfortunately, it does not explain how the TRPO-based algorithm is built [33]. Referring to the construction of the PASVG, it uses a two-step actor, one for the discrete part and another for the continuous part, with the discrete choice as an argument.
As we want to build a scalable model, Hybrid-Proximal Policy Optimization (HPPO) [34] inspired us because it separates discrete and continuous action choices using PPO models. It uses a critic that groups the result obtained by all the models at the same time. The notion of a generic critical model is an interesting one, as it allows us to judge the actions of several models (agents) at the same time. In the same way, a vehicle, whatever its actions, will want to build a model capable of ensuring the safety of other users, and the different choices of actions can be highly dependent (two groups of actions can be effective, while a mixture of the two can under-perform). Therefore, we can set scenario-related objectives over and above those directly linked to model actions. This observation leads us to distinguish between decision-making as a choice of trajectory and ongoing actions as respect for the choices already made by the decision model.
The addition of new agents considerably increases the complexity of the model, as it requires cooperation between agents. The article [35] seeks to train a realistic pedestrian model able to adapt to vehicles by seeking to avoid a collision, with or without a learning AV. In this use case, our focus is solely on the AV; thus, we keep a static pedestrian model.
3. Modeling of the Problem
To train a DRL model, we need to build a simulation environment for a V2P interaction. We consider a common scenario: a straight road with a pedestrian crossing. The vehicle agent must drive on the road, while the pedestrian agent wants to cross the road. The objectives of the vehicular agent are to ensure its own safety and that of other users, to limit the time lost due to necessary interactions in the environment and to offer a certain level of passenger comfort. The use of a DRL model also leads us to model the environment as a Markov Decision Process (MDP). Thus, we must define (S, A, P and R), with S representing the state space, A the action space, P the probabilities of transitions between states and R the reward function. The state space gathers movement information of the agents (both vehicle and pedestrian) as well as general road information. Information about the road is static information: it does not vary throughout the scenario. The action space can vary depending on the degree of control over the vehicle. In this article, we control the vehicle speed using the accelerator pedal; we consider this tool sufficient to represent the action of a human driver facing a pedestrian. The steering wheel is not taken into account, as we assume that it should only be used to avoid an emergency situation. The transition probabilities here are inherent to the applied laws of physics. When employing multiple DRL models in the same environment, objectives can be chosen by adjusting the reward function R. We model the pedestrian from the previous articles, improved to include new vehicles and new lanes. Gap acceptance analysis is performed for each lane crossed in the diagram in Figure 1 but the decision to cross is based on the vehicles on the lanes in the pedestrian’s remaining path.
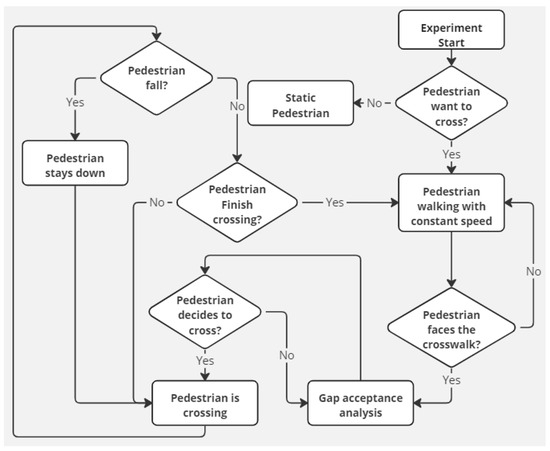
Figure 1.
Pedestrian model diagram.
3.1. Simple Environment Model: Single-Lane Crossing with V2P Interaction
In [36], a classic interaction between two agents is defined: a pedestrian and an autonomous vehicle. They operate on a one-lane (and one-way) road. We place the agents in positions that may cause conflict with each other: both agents must pass through the same road section, their trajectories are incompatible if the agents want to avoid a collision. The AV and the pedestrian must cooperate to safely and efficiently pass the crosswalk. The pedestrian model aims at crossing the road without causing a collision with the vehicle. Before and after the crosswalk, the agent walks at a constant speed. When he reaches the pedestrian crossing, it needs to decide whether to cross or not. As mentioned above [8], the gap between his crossing time and the vehicle’s arrival time is used to decide whether the pedestrian should cross. If his safety confidence is high enough, he chooses to cross. This feeling is represented by the critical gap: an estimate of his crossing time plus a parameter related to his ability to judge and behave cautiously (a constant related to the pedestrian). The pedestrian modeling part was carried out using data from the same article.
In the same paper [36], the vehicle has a hybrid action space, since it must choose whether to pass before or after the pedestrian (discrete action) and must control its speed to avoid any accident while making the choice it made earlier. This important distinction is the main reason why we have completely separated the discrete part from the continuous part in the action space. Before splitting the decision model into two parts, the hierarchization of objectives had led to a bias in learning, which could result in only the safety-related part being trained. A first model plans the trajectory of the vehicle with the aim of preventing an accident and being able to carry out the chosen plan (). The second model controls the vehicle speed with the objective of respecting the plan (), either preventing an accident and/or maintaining a constant speed. For decision-making, the DRL model should perform better than unsupervised classification algorithms, and labeling of the training data is not needed as for classical supervised classification. The two models obtain the same state space, but we define the following two different reward functions:
- Decision-making:
- Speed control:
where D is the difference between minimum braking distance and V2P distance; indicates the car speed limit; indicates the actual car speed; if the worst-case scenario results in an accident (i.e., a collision between the vehicle and the pedestrian, triggered when both agents are in the intersection simultaneously); and if the AV and the pedestrian fail to enter the crosswalk in the appropriate sequence as per the signaled intention (i.e., the vehicle yields if it displays a green signal, whereas it proceeds first if it displays a red signal).
3.2. Generalized Environment Model: Multiple Lane Crossing with Several Pedestrians and Vehicles
When we add a pedestrian, we mechanically increase the size of the state space. It seems rather inefficient to train a decision model for each new agent added to the environment model, as this would require a very large number of models, which we want to avoid. To solve this problem, we could use a discretized 2D map of the environment, which would then have to be vectorized using, for example, an autoencoder to preserve the information contained in the map and keep a fixed size at the model input. This method is a widely recognized approach in existing literature but we decided not to use it for two reasons. Firstly, the construction of a 2D map requires a certain amount of discretization of the environment, which limits the precision of the state space. Secondly, the vectorized state from a 2D map will be strictly subject to the shape of the road and its surroundings, making the generalization very difficult. We opt for a better solution, where discrete (order of passage) and continuous (acceleration) parts are treated differently as follows:
In the continuous part, we apply the model for each pedestrian separately. The only thing we need is a tool able to output a vehicle acceleration based on the vehicle’s various actions (relative to each pedestrian). We suggest using the minimum function to select the lowest acceleration in the continuous part: we give priority to the V2P interaction requiring the lowest vehicle acceleration; therefore, we ensure the safety of pedestrians. The model always takes the worse possible case. In this MDP, a pedestrian can appear during the scenario if we add a parameter stating that the pedestrian exists or not. Its appearance can induce changes in the vehicle actions; so, we need to make a new decision in the current scenario.
In the discrete part, the separation of the decision model over the pedestrians (having one discrete action per pedestrian) adds more complexity. As the decision model produces a discrete action for each pedestrian, we need a way to select the appropriate action to apply. We examined two potential solutions but ultimately decided to reject them due to their drawbacks. In the first solution, we prioritize a specific action as a green signal over a red signal. We opted against this approach due to its impact on convergence and even on results due to unbalanced label occurrence. In the second solution, we select the majority decision (take the most occurring action). This approach could lead to a necessary course of action for a pedestrian being ignored and, therefore, cause an accident. We opted for the safety-first solution, keeping the list of discrete actions and applying them in relation to the distance from pedestrians (light signal) and the possibility of an accident (pedestrian on the road). We apply the discrete action of the closest pedestrian for the light signal to avoid ambiguity (for example: display cross but stop only for another pedestrian) and apply the decision related to the pedestrian alone to calculate the acceleration. This modification of the decision model action acts as a supervisory tool. New pedestrians may appear in the scenario, and the vehicle must adapt to them. The scalability proposed above enables dynamic management of the display and decision-making; thus, our decision model can easily take this new pedestrian into account.
We define our multi-agent model environment as one where several agents controlled by our model must interact with each other. In such a multi-agent environment, the actions of one agent (AV) are correlated with those of other agents (AV or pedestrians). In our use-case, AV actions must be consistent to avoid accidents. AV agents can be considered cooperative with a common goal or competitive with a personal goal that may conflict with the goals of other agents. We suggest the cooperative point of view as we want to build a common crossing plan. To support this kind of action, we can add the status of one or more other vehicles to the decision model input. If all the vehicles wish to be kept in the model input, the curriculum-based approach can be applied: the discrete part giving all the discrete actions of the AV agents (with no model separation per pedestrian or AV like the continuous part approach).
If all the vehicles are in the same lane, cooperation is easy, because when a stop occurs, the preceding vehicles go first and the following ones wait behind the vehicle stopping. If a lane is added, the vehicles must also take into account the vehicles arriving in the other lanes in order to make a coherent decision. This decision-making process is complex and depends on many parameters, so it is very challenging to define and list all the optimal decisions related to the environment. The use of a simulation to test all possible scenarios (crossing order) and find the best solutions proves its worth. Scalability is a major point to take into account if we want the decision model to work properly. The addition of pedestrians, vehicles and lanes increases the environment complexity. According to our preliminary observations, a curriculum-based approach stands out as the most viable method to ensure convergence and model adaptability to an environment that is highly scalable in terms of size and number of agents.
4. Addressing the Problem with H-DRL
4.1. Our Scalable MDP
As mentioned in Section 3.1, we decided to separate the continuous models from the discrete model. They each output a part of the global action space of the MDP. The continuous part controls the acceleration of the vehicle while the discrete part chooses whether or not it should yield to the pedestrian.
The state space gathers movement information on all agents—position and speed—and parameters that help convergence—deviation from the speed limit, safety factor and presence of pedestrians in certain zones. Table 1 also includes previous actions taken by the vehicle. Actions range from braking to acceleration for the continuous part and from red to green signal for the discrete part. When the scenario begins, the vehicles drive at the speed limit, are randomly placed in the lines and their positions are optimized to provoke interaction with the pedestrians. The speed limit is set to 10 m/s. For the pedestrian part, we choose a speed range based on a literature review of pedestrian speed [19]. Their starting positions vary in proximity to the pedestrian crossing. We choose the car point of view; so, we assume that the pedestrian agent appears in the environment once detected by a vehicle.

Table 1.
State space with multiple pedestrians, cars and lines.
Scalability leads us to modify the model input. For the continuous model, we obtain an acceleration for each vehicle relative to a pedestrian. Therefore, the input is composed of the data of a pedestrian i, a car j and the road. For the discrete model, we take all the vehicle and road data, plus the data for pedestrian i. The supervision tool, described in Section 3.2, will output a concatenation of the two modified actions to be provided to the environment. The action space of the environment is a list of vehicle actions, i.e., a merger of the discrete action of each vehicle (signaling) and the selected continuous action of each vehicle (acceleration).
Having defined the state space and action space, we still need to redefine the rewards of Section 3.1. The rewards of the continuous part can be applied to each vehicle independently, so no modification is required. For the discrete part, we can sum the trajectory and safety errors of each vehicle to obtain a global reward or keep the errors of each vehicle without taking into account the intrinsic dependence of the vehicle trajectories. In all cases, the reward error for each vehicle includes those detected for each pedestrian. We need to modify the discrete reward to take into account the addition of new lanes. A risk of accident must be considered if the pedestrian is sufficiently close to the car lane. In the same way, signalization must react to any important change in pedestrian positions, i.e., at each lane change.
4.2. H-DRL Model
The use of the PPO structures our algorithm in two parts: a loop between the generation of batches on the environment with the current models, and a learning process on the same models based on the obtained batches. Batch generation is shown in Figure 2. At the start of the scenario, the discrete model is applied to each vehicle. We have a trajectory plan for each vehicle, which enables us to select the right continuous model to be applied throughout the scenario. The results obtained throughout the scenario (state, action, reward and log probability) are stored in a batch according to the decision taken by the discrete actor (our decision model). The discrete actor adds a line to its batch for each scenario (or new pedestrian); so, it needs enough scenarios per batch (maximum 80 steps per scenario). It sums up the errors obtained during the experiment. Each type of error incurs a penalty only once, rather than on a per-step basis. In this way, the vehicle will be penalized in the same way, regardless of how long the pedestrian has been endangered. It is important to remember that the input state of each model is modified to match the point of view of the vehicle in question. This modification process is described in detail in Section 3.2. For the learning part, we train the decision model on the different batches retrieved in the previous section. We can imagine a slower learning process for the discrete model due to having a much smaller batch size. The dependency between the continuous models and the discrete one is unique. On one hand, the discrete model chooses the data for the continuous part. On the other hand, the continuous part results will impact the discrete reward.
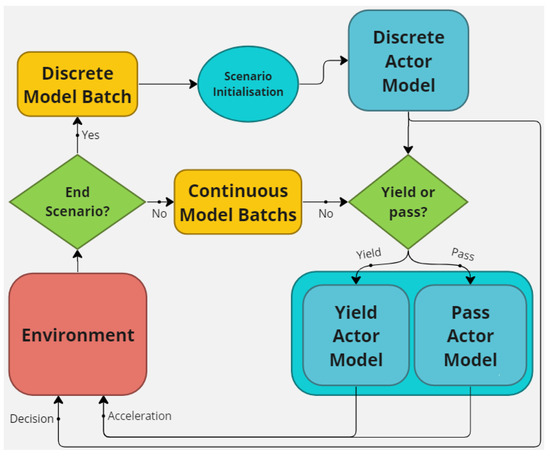
Figure 2.
Environment iterations diagram.
5. Simulation and Results
Before any analysis, we need to ensure that the different parts of the decision model converge. The higher the number of agents, the higher the complexity, and therefore, the longer the convergence time.
5.1. Methodology for Evaluating the Performance
The most important point in performance evaluation is the absence of accidents. The safety of pedestrians is the most decisive factor in AV decision-making. To guarantee safety, a fail-safe mode can be activated if the basic model proves insufficient in critical situations. The second objective we need to evaluate is the efficiency of the interaction. The simplest way to do this is to compare the average agent exit time and the average agent speed (and standard deviation to check for disparities in results) with a nominal vehicle. This nominal vehicle follows classic human behavior by stopping in front of the crosswalk if possible. Other elements can be taken into account, such as agent comfort during interaction. We can observe the average minimum speed reached, to judge the model’s ability to limit stops. We can also observe the stopping time of each agent, which we want to be as short as possible. It is important to separate the evaluation of the discrete and continuous parts of the decision model. By using the same nominal vehicle, it can be forced to adopt the same trajectory choices in order to compare it with the continuous part and, therefore, judge its performance. Conversely, the evaluation of the discrete part is based solely on the reward. Another method that could be used to validate the reliability of the model is stress testing. The pedestrian model is replaced by a dangerous one that tests critical situations (the most dangerous for the pedestrian) or makes a list of possible interaction cases as unit tests.
5.2. Results for a Single Vehicle/Pedestrian Interaction
To visualize the model actions over a standard episode, we have provided an example of each scenario. In the scenario where the car is the first to enter the crosswalk, the speed and acceleration of the AV must be very constant and stable, which is the case in Figure 3. In this example, the pedestrian has to wait almost two seconds for the car to pass before entering the crosswalk. The discrete model may choose to go first because the AV cannot stop before the crosswalk or the pedestrian is too far from the crosswalk. In this case, the vehicle displays a red signal to indicate to the pedestrian not to cross.
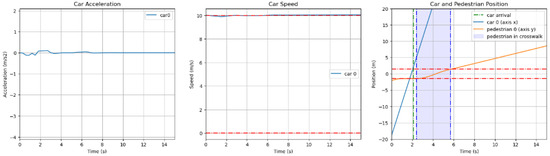
Figure 3.
The three diagrams illustrate the vehicle acceleration, vehicle speed and position of the two agents over time in a scenario where the car arrives first.
In the scenario where the car yields to the pedestrian (see Figure 4), the car speed profile consists of three stages. Firstly, the car reduces speed to give the pedestrian sufficient distance to cross. Secondly, the control model adjusts the speed to enable the car to leave as quickly as possible while maintaining a safe distance. When the pedestrian leaves the crossing zone completely, the car accelerates rapidly to reach the maximum speed. The car must adapt its speed according to unexpected events, such as a pedestrian falling on the road. In the example, the pedestrian has fallen, stopping his crossing for two seconds. The vehicle adapted by reducing speed and delaying its phase 2.
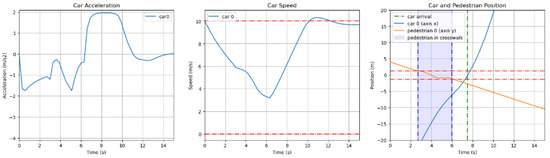
Figure 4.
The three diagrams respectively illustrate the vehicle acceleration, vehicle speed and position of the two agents over time in a scenario where the pedestrian crosses first.
5.3. Limitations and Perspectives
Preliminary tests indicated that substantial effort is needed when incorporating new agents into the system. The identified difficulties are as follows:
- The addition of new vehicles influences the actions required by the AVs, potentially leading to changes in the distribution of scenarios. For instance, if one vehicle prevents a pedestrian from crossing, another vehicle may be inclined to reject the pedestrian priority if the pedestrian’s waiting time is not affected by this decision. In addition, achieving convergence in the discrete part of the decision model requires a balanced distribution in the decision-making process, particularly in determining whether the AV should yield or not. Consequently, there is a need for further design work on scenario construction to ensure robustness and adaptability.
- The interdependency of actions among agents significantly influences the interaction between individual vehicles and pedestrians. For instance, if one vehicle prevents a pedestrian from crossing, another vehicle that is yielding must adjust its speed according to the pedestrian reaction to the first vehicle. Consequently, adjustments must be made to refine result estimations. We suggest prioritizing the overall success of the scenario or conducting direct comparisons with other methods.
- The actions of vehicles can occasionally be misunderstood by pedestrians, potentially leading to safety hazards. Similarly, a vehicle signal may be perceived by multiple pedestrians simultaneously, resulting in unintended communication effects. For instance, a pedestrian may only perceive one vehicle yielding while another vehicle does not. Designing appropriate reward functions and signaling models is essential to incentivize cooperation among vehicles and improve communication effectiveness.
6. Conclusions
In the present paper, we propose a solution for the AV to control its speed in the face of a variable number of other road users and in different road conditions. We have extended the MDP of a simple V2P interaction to allow the addition of new agents, whether vehicular or pedestrian, and even the addition of new lanes. AV agents use a light signal as a communication tool and control their acceleration in real time. The structure of this action space requires it to be used on a hybrid DRL model, supporting the agent scalability of the environment model. We achieve this goal by modifying model inputs and adding vehicle action supervision. Initial results are conclusive, with the decision model converging and adopting good behavior, thus opening the way for further study of model cooperation abilities via learning data. The success of our first tests encourages us to develop a model capable of handling a large number of situations with a variable number of agents (pedestrians or vehicles). Our next objective will then be to build a physical demonstrator to validate the applicability of our model to real-life conditions. To achieve this goal, we need to increase the model robustness by adding data uncertainty with error ranges in sensor data. This sim-to-real transfer work is necessary to limit the loss of performance of the simulation-based model. In addition, the possibility of building a multi-agent model integrating V2V communication seems promising in the field of multi-agent cooperation between vehicles. However, to do so, further work is required on modeling the issue using the frame of multi-agent deep reinforcement learning.
Author Contributions
Conceptualization, A.B., A.L., N.G. and A.A.-T.; methodology, A.B., A.L., N.G. and A.A.-T.; software, A.B.; validation, A.B., A.L., N.G. and A.A.-T.; formal analysis, A.B. and A.L.; investigation, A.B.; resources, N.G. and A.A.-T.; data curation, A.B. and A.L.; writing—original draft preparation, A.B. and A.L.; writing—review and editing, N.G. and A.A.-T.; visualization, A.B.; supervision, A.L., N.G. and A.A.-T.; project administration, N.G. and A.A.-T.; funding acquisition, A.A.-T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out as part of the VASIS project, a public research initiative funded by the Bourgogne Franche-Comté region.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
https://github.com/BrunoudA/Hybrid-DRL (accessed on 1 January 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, S.; Yu, B.; Tang, J.; Zhu, Q. Towards Fully Intelligent Transportation through Infrastructure-Vehicle Cooperative Autonomous Driving: Challenges and Opportunities. arXiv 2021, arXiv:2103.02176. [Google Scholar]
- Lu, L.; Dai, F. Digitalization of Traffic Scenes in Support of Intelligent Transportation Applications. J. Comput. Civ. Eng. 2023, 37, 04023019. [Google Scholar] [CrossRef]
- Koren, M.; Alsaif, S.; Lee, R.; Kochenderfer, M.J. Adaptive Stress Testing for Autonomous Vehicles. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 1–7. [Google Scholar]
- Zhang, M.; Abbas-Turki, A.; Lombard, A.; Koukam, A.; Jo, K. Autonomous vehicle with communicative driving for pedestrian crossing: Trajectory optimization. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; IEEE: New York, NY, USA, 2020; pp. 1–6. [Google Scholar]
- Zimmermann, R.; Wettach, R. First Step into Visceral Interaction with Autonomous Vehicles. In Proceedings of the AutomotiveUI ’17: 9th International Conference on Automotive User Interfaces and Interactive Vehicular Applications, New York, NY, USA, 24–27 September 2017; pp. 58–64. [Google Scholar]
- Jayaraman, S.K.; Creech, C.; Robert, L.P., Jr.; Tilbury, D.M.; Yang, X.J.; Pradhan, A.K.; Tsui, K.M. Trust in AV: An Uncertainty Reduction Model of AV-Pedestrian Interactions. In Proceedings of the HRI ’18: Companion of the 2018 ACM/IEEE International Conference on Human-Robot Interaction, New York, NY, USA, 5–8 March 2018; pp. 133–134. [Google Scholar]
- Gupta, S.; Vasardani, M.; Winter, S. Negotiation Between Vehicles and Pedestrians for the Right of Way at Intersections. IEEE Trans. Intell. Transp. Syst. 2019, 20, 888–899. [Google Scholar] [CrossRef]
- Manski, C.; Manuszak, M.; Das, S. Walk or wait? An empirical analysis of street crossing decisions. J. Appl. Econom. 2005, 20, 529–548. [Google Scholar]
- Ackermann, C.; Beggiato, M.; Bluhm, L.F.; Löw, A.; Krems, J.F. Deceleration parameters and their applicability as informal communication signal between pedestrians and automated vehicles. Transp. Res. Part F Traffic Psychol. Behav. 2019, 62, 757–768. [Google Scholar] [CrossRef]
- Rasouli, A.; Tsotsos, J.K. Autonomous vehicles that interact with pedestrians: A survey of theory and practice. IEEE Trans. Intell. Transp. Syst. 2019, 21, 900–918. [Google Scholar] [CrossRef]
- Dey, D.; Matviienko, A.; Berger, M.; Pfleging, B.; Kuhl, B.M.; Terken, J.M.B. Communicating the intention of an automated vehicle to pedestrians: The contributions of eHMI and vehicle behavior. IT Inf. Technol. 2020, 63, 123–141. [Google Scholar] [CrossRef]
- Dey, D.; Habibovic, A.; Pfleging, B.; Martens, M.; Terken, J. Color and Animation Preferences for a Light Band eHMI in Interactions Between Automated Vehicles and Pedestrians. In Proceedings of the CHI ’20: Proceedings of the 2020 CHI Conference on Human Factors in Computing Systems, Honolulu, HI, USA, 25–30 April 2020. [Google Scholar]
- Lillicrap, T.; Hunt, J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Zhang, M.; Abbas-Turki, A.; Mualla, Y.; Koukam, A.; Tu, X. Coordination Between Connected Automated Vehicles and Pedestrians to Improve Traffic Safety and Efficiency at Industrial Sites. IEEE Access 2022, 10, 68029–68041. [Google Scholar] [CrossRef]
- Brunoud, A.; Lombard, A.; Zhang, M.; Abbas-Turki, A.; Gaud, N.; Koukam, A. Comparison of Deep Reinforcement Learning Methods for Safe and Efficient Autonomous Vehicles at Pedestrian Crossings. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 2556–2562. [Google Scholar]
- Møgelmose, A.; Trivedi, M.M.; Moeslund, T.B. Trajectory analysis and prediction for improved pedestrian safety: Integrated framework and evaluations. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Republic of Korea, 28 June–1 July 2015; pp. 330–335. [Google Scholar]
- Wei, S.; Zou, Y.; Zhang, T.; Zhang, X.; Wang, W. Design and Experimental Validation of a Cooperative Adaptive Cruise Control System Based on Supervised Reinforcement Learning. Appl. Sci. 2018, 8, 1014. [Google Scholar] [CrossRef]
- Bosina, E.; Weidmann, U. Estimating pedestrian speed using aggregated literature data. Phys. A Stat. Mech. Appl. 2017, 468, 1–29. [Google Scholar] [CrossRef]
- Yau, T.; Malekmohammadi, S.; Rasouli, A.; Lakner, P.; Rohani, M.; Luo, J. Graph-SIM: A Graph-based Spatiotemporal Interaction Modelling for Pedestrian Action Prediction. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8580–8586. [Google Scholar]
- Nasernejad, P.; Sayed, T.; Alsaleh, R. Modeling pedestrian behavior in pedestrian-vehicle near misses: A continuous Gaussian Process Inverse Reinforcement Learning (GP-IRL) approach. Accid. Anal. Prev. 2021, 161, 106355. [Google Scholar] [CrossRef]
- Corso, A.; Du, P.; Driggs-Campbell, K.; Kochenderfer, M.J. Adaptive Stress Testing with Reward Augmentation for Autonomous Vehicle Validation. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 163–168. [Google Scholar]
- Li, J.; Yao, L.; Xu, X.; Cheng, B.; Ren, J. Deep reinforcement learning for pedestrian collision avoidance and human-machine cooperative driving. Inf. Sci. 2020, 532, 110–124. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, X.; Sun, J. Automated vehicle’s behavior decision making using deep reinforcement learning and high-fidelity simulation environment. Transp. Res. Part C Emerg. Technol. 2019, 107, 155–170. [Google Scholar] [CrossRef]
- Chae, H.; Kang, C.M.; Kim, B.; Kim, J.; Chung, C.C.; Choi, J.W. Autonomous Braking System via Deep Reinforcement Learning. arXiv 2017, arXiv:1702.02302. [Google Scholar]
- Fu, Y.; Li, C.; Yu, F.R.; Luan, T.H.; Zhang, Y. A Decision-Making Strategy for Vehicle Autonomous Braking in Emergency via Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2020, 69, 5876–5888. [Google Scholar] [CrossRef]
- Andrychowicz, M.; Wolski, F.; Ray, A.; Schneider, J.; Fong, R.; Welinder, P.; McGrew, B.; Tobin, J.; Abbeel, O.P.; Zaremba, W. Hindsight Experience Replay. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; Volume 30. [Google Scholar]
- Teh, Y.W.; Bapst, V.; Czarnecki, W.M.; Quan, J.; Kirkpatrick, J.; Hadsell, R.; Heess, N.; Pascanu, R. Distral: Robust Multitask Reinforcement Learning. arXiv 2017, arXiv:1707.04175. [Google Scholar]
- Espeholt, L.; Soyer, H.; Munos, R.; Simonyan, K.; Mnih, V.; Ward, T.; Doron, Y.; Firoiu, V.; Harley, T.; Dunning, I.; et al. IMPALA: Scalable Distributed Deep-RL with Importance Weighted Actor-Learner Architectures. arXiv 2018, arXiv:1802.01561. [Google Scholar]
- Hausknecht, M.; Stone, P. Deep Reinforcement Learning in Parameterized Action Space. arXiv 2016, arXiv:1511.04143. [Google Scholar]
- Xiong, J.; Wang, Q.; Yang, Z.; Sun, P.; Han, L.; Zheng, Y.; Fu, H.; Zhang, T.; Liu, J.; Liu, H. Parametrized Deep Q-Networks Learning: Reinforcement Learning with Discrete-Continuous Hybrid Action Space. arXiv 2018, arXiv:1810.06394. [Google Scholar]
- Jang, S.; Son, Y. Empirical Evaluation of Activation Functions and Kernel Initializers on Deep Reinforcement Learning. In Proceedings of the 2019 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Republic of Korea, 16–18 October 2019; pp. 1140–1142. [Google Scholar]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.I.; Abbeel, P. Trust Region Policy Optimization. arXiv 2015, arXiv:1502.05477. [Google Scholar]
- Fan, Z.; Su, R.; Zhang, W.; Yu, Y. Hybrid Actor-Critic Reinforcement Learning in Parameterized Action Space. arXiv 2019, arXiv:1903.01344. [Google Scholar]
- Trumpp, R.; Bayerlein, H.; Gesbert, D. Modeling Interactions of Autonomous Vehicles and Pedestrians with Deep Multi-Agent Reinforcement Learning for Collision Avoidance. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 4–9 June 2022; pp. 331–336. [Google Scholar]
- Brunoud, A.; Lombard, A.; Abbas-Turki, A.; Gaud, N.; Kang-Hyun, J. Hybrid Deep Reinforcement Learning Model for Safe and Efficient Autonomous Vehicles at Pedestrian Crossings. In Proceedings of the 2023 International Workshop on Intelligent Systems (IWIS), Ulsan, Republic of Korea, 9–11 August 2023; pp. 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).