Evaluation of Lithium-Ion Battery Performance under Variable Climatic Conditions: Influence on the Driving Range of Electric Vehicles
Abstract
1. Introduction
2. Theoretical Foundations
3. Modeling and Simulation
3.1. Experimental Prototype
3.2. Tests at Constant Intensity
4. Experimental Tests
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A critical review of thermal issues in lithium-ion batteries. J. Electrochem. Soc. 2011, 158, R1. [Google Scholar] [CrossRef]
- Lu, R.; Yang, A.; Xue, Y.; Xu, L.; Zhu, C. Analysis of the key factors affecting the energy efficiency of batteries in electric vehicle. World Electr. Veh. J. 2010, 4, 9–13. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Belt, J.R.; Ho, C.D.; Miller, T.J.; Habib, M.A.; Duong, T.Q. The effect of temperature on capacity and power in cycled lithium ion batteries. J. Power Sources 2005, 142, 354–360. [Google Scholar] [CrossRef]
- Lu, Z.; Yu, X.L.; Wei, L.C.; Cao, F.; Zhang, L.Y.; Meng, X.Z.; Jin, L.W. A comprehensive experimental study on temperature-dependent performance of lithium-ion battery. Appl. Therm. Eng. 2019, 158, 113800. [Google Scholar] [CrossRef]
- Liao, L.; Zuo, P.; Ma, Y.; Chen, X.; An, Y.; Gao, Y.; Yin, G. Effects of temperature on charge/discharge behaviors of LiFePO4 cathode for Li-ion batteries. Electrochim. Acta 2012, 60, 269–273. [Google Scholar] [CrossRef]
- New European Driving Cycle (NEDC). Available online: https://es.wikipedia.org/wiki/New_European_Driving_Cycle (accessed on 22 January 2023).
- Emission Test Cycles ECE, 1.5.; +EUDC/NEDC Revision: 2013-07, DieselNet. Available online: https://dieselnet.com/standards/cycles/ece_eudc.php (accessed on 19 January 2023).
- World Harmonized Light-Duty Vehicle Test Procedure (WLTP). Available online: https://es.wikipedia.org/wiki/WLTP (accessed on 20 January 2023).
- Emissions Standards Reference Guide. EPA Federal Test Procedure, FTP-75, EPA Federal Test: FTP 72/75 (1978)/SFTP US06/SC03 (2008). United States Environmental Protection Agency. Available online: https://www.epa.gov/emission-standards-reference-guide/epa-federal-test-procedure-ftp (accessed on 5 January 2023).
- Japanese JC-08 Cycle, Emissions Test Cycles, DieselNet. Available online: https://dieselnet.com/standards/cycles/jp_jc08.php (accessed on 21 January 2023).
- Steinstraeter, M.; Heinrich, T.; Lienkamp, M. Effect of low temperature on electric vehicle range. World Electr. Veh. J. 2021, 12, 115. [Google Scholar] [CrossRef]
- Iora, P.; Tribioli, L. Effect of ambient temperature on electric vehicles’ energy consumption and range: Model definition and sensitivity analysis based on nissan leaf data. World Electr. Veh. J. 2019, 10, 2. [Google Scholar] [CrossRef]
- Lindgren, J.; Lund, P.D. Effect of extreme temperatures on battery charging and performance of electric vehicles. J. Power Sources 2016, 328, 37–45. [Google Scholar] [CrossRef]
- Taggart, J. Ambient temperature impacts on real-world electric vehicle efficiency & range. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 22–24 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 186–190. [Google Scholar]
- Pan, C.; Dai, W.; Chen, L.; Chen, L.; Wang, L. Driving range estimation for electric vehicles based on driving condition identification and forecast. AIP Adv. 2017, 7, 105206. [Google Scholar] [CrossRef]
- Hao, X.; Wang, H.; Lin, Z.; Ouyang, M. Seasonal effects on electric vehicle energy consumption and driving range: A case study on personal, taxi, and ridesharing vehicles. J. Clean. Prod. 2020, 249, 119403. [Google Scholar] [CrossRef]
- Yuksel, T.; Michalek, J.J. Effects of regional temperature on electric vehicle efficiency, range, and emissions in the United States. Environ. Sci. Technol. 2015, 49, 3974–3980. [Google Scholar] [CrossRef]
- Ahmed, N.K.; Kapadia, J. Seasonality Effect on Electric Vehicle Miles Traveled in Electrified Vehicles. SAE Int. J. Altern. Powertrains 2017, 6, 47–53. [Google Scholar] [CrossRef]
- Dominguez-Jimenez, J.A.; Campillo, J.E.; Montoya, O.D.; Delahoz, E.; Hernández, J.C. Seasonality effect analysis and recognition of charging behaviors of electric vehicles: A data science approach. Sustainability 2020, 12, 7769. [Google Scholar] [CrossRef]
- Thiel, C.; Amillo, A.G.; Tansini, A.; Tsakalidis, A.; Fontaras, G.; Dunlop, E.; Taylor, N.; Jäger-Waldau, A.; Araki, K.; Nishioka, K.; et al. Impact of climatic conditions on prospects for integrated photovoltaics in electric vehicles. Renew. Sustain. Energy Rev. 2022, 158, 112109. [Google Scholar] [CrossRef]
- Smith, K.; Earleywine, M.; Wood, E.; Neubauer, J.; Pesaran, A. Comparison of Plug-In Hybrid Electric Vehicle Battery Life Across Geographies and Drive-Cycles; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2012; Volume 1, No. NREL/CP-5400-53817.
- Pascoe, P.E.; Anbuky, A.H. A VRLA battery simulation model. Energy Convers. Manag. 2004, 45, 1015–1041. [Google Scholar] [CrossRef]
- Pattipati, B.; Pattipati, K.; Christopherson, J.P.; Namburu, S.M.; Prokhorov, D.V.; Qiao, L. Automotive Battery Management Systems; IEEE: Piscataway, NJ, USA, 2008; pp. 581–586. [Google Scholar]
- Capacity and Battery Ratings Review.Battery Application & Technology. Engineers Edge. Available online: https://www.engineersedge.com/battery/capacity_battery_ratings.htm (accessed on 22 January 2023).
- Chen, K.; Li, X. Accurate determination of battery discharge characteristics—A comparison between two battery temperature control methods. J. Power Sources 2014, 247, 961–966. [Google Scholar] [CrossRef]
- Park, C.; Lahiri, K.; Raghunathan, A. Battery discharge characteristics of wireless sensor nodes: An experimental analysis. In Proceedings of the 2005 Second Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks, IEEE SECON 2005, Santa Clara, CA, USA, 26–29 September 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 430–440. [Google Scholar]
- BTU-501: Basics about Discharging. Battery University. 2017. Available online: https://batteryuniversity.com/article/bu-501-basics-about-discharging (accessed on 22 January 2023).
- Hausmann, A.; Depcik, C. Expanding the Peukert equation for the battery capacity modeling through inclusion of a temperature dependency. J. Power Sources 2013, 235, 148–158. [Google Scholar] [CrossRef]
- Armenta-Déu, C.; Carriquiry, J.P.; Guzmán, S. Capacity correction factor for Li-ion Batteries: Influence of the Discharge Rate. J. Energy Storage 2019, 25, 100839. [Google Scholar] [CrossRef]
- Chang, K.T. Geographic information system. In International Encyclopedia of Geography: People, the Earth, Environment and Technology: People, the Earth, Environment and Technology; Wiley-Blackwell: Hoboken, NJ, USA, 2016; pp. 1–9. [Google Scholar]
- Longley, P.A.; Goodchild, M.F.; Maguire, D.J.; Rhind, D.W. Geographic Information Systems and Science; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Jones, C.B. Geographical Information Systems and Computer Cartography; Routledge: Abingdon-on-Thames, UK, 2014. [Google Scholar]
- Thill, J.C. Geographic information systems for transportation in perspective. Transp. Res. Part C Emerg. Technol. 2000, 8, 3–12. [Google Scholar] [CrossRef]
- Taylor, P.J.; Johnston, R.J. Geographic information systems and geography. In Ground Truth: The Social Implications of Geographic Information Systems; Guilford Press: New York, NY, USA, 1995; pp. 51–68. [Google Scholar]
- Raju, P.L.N. Fundamentals of geographical information system. In Satellite Remote Sensing and GIS Applications in Agricultural Meteorology; World Meteorological Organisation: Geneva, Switzerland, 2006; p. 103. [Google Scholar]
- Gibson, R.; Erle, S. Google Maps Hacks; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2006. [Google Scholar]
- Mehta, H.; Kanani, P.; Lande, P. Google maps. Int. J. Comput. Appl. 2019, 178, 41–46. [Google Scholar] [CrossRef]
- Santos, L.; Coutinho-Rodrigues, J.; Antunes, C.H. A web spatial decision support system for vehicle routing using Google Maps. Decis. Support Syst. 2011, 51, 1–9. [Google Scholar] [CrossRef]
- Wang, F.; Xu, Y. Estimating O–D travel time matrix by Google Maps API: Implementation, advantages, and implications. Ann. GIS 2011, 17, 199–209. [Google Scholar] [CrossRef]
- Rahman, M.M.; Mou, J.R.; Tara, K.; Sarkar, M.I. Real time Google map and Arduino based vehicle tracking system. In Proceedings of the 2016 2nd International Conference on Electrical, Computer & Telecommunication Engineering (ICECTE), Rajshahi, Bangladesh, 8–10 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–4. [Google Scholar]
- Emirler, M.T.; Wang, H.; Aksun Güvenç, B.; Güvenç, L. Automated robust path following control based on calculation of lateral deviation and yaw angle error. In Proceedings of the Dynamic Systems and Control Conference, Columbus, OH, USA, 28–30 October 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 57267, p. V003T50A009. [Google Scholar]
- Maharaj, B.S.; King, G. Representative Driving Cycles for Trinidad and Tobago with Slope Profiles for Electric Vehicles. Transp. Res. Rec. 2022, 03611981221138526. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Kobayashi, Y.; Shirai, K. Remaining driving range estimation of electric vehicle. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–7. [Google Scholar]
- Petal Maps. GPS and Navigation. Available online: https://www.petalmaps.com (accessed on 23 January 2023).
- Sygic GPS Navigation & Maps. Available online: https://maps.sygic.com (accessed on 23 January 2023).
- Geo Tracker. GPS Tracker. Available online: https://play.google.com/store/apps/details?id=com.ilyabogdanovich.geotracker&pli=1 (accessed on 15 November 2022).
- Armenta-Déu, C.; Cattin, E. Real Driving Range in Electric Vehicles: Influence on Fuel Consumption and Carbon Emissions. World Electr. Veh. J. 2021, 12, 166. [Google Scholar] [CrossRef]
- Swift, A. Calculation of vehicle aerodynamic drag coefficients from velocity fitting of coastdown data. J. Wind Eng. Ind. Aerodyn. 1991, 37, 167–185. [Google Scholar] [CrossRef]
- Sudin, M.N.; Abdullah, M.A.; Shamsuddin, S.A.; Ramli, F.R.; Tahir, M.M. Review of research on vehicles aerodynamic drag reduction methods. Int. J. Mech. Mechatron. Eng. 2014, 14, 37–47. [Google Scholar]
- Hucho, W.; Sovran, G. Aerodynamics of road vehicles. Annu. Rev. Fluid Mech. 1993, 25, 485–537. [Google Scholar] [CrossRef]
- Wąsik, M.; Skarka, W. Influence of the windscreens inclination angle on the aerodynamic drag coefficient of the cars designed for the race shell eco-marathon based on Numerical simulations. Zesz. Nauk. Inst. Pojazdów Politech. Warsz. 2015, 3/103, 135–141. [Google Scholar]
- Armenta-Déu, C.; Giorgi, B. Influence of climatic changes onto the performance of electric vehicles. J. Automob. Eng. Appl. 2022, 9, 43–58. [Google Scholar]
- Armenta-Déu, C.; Boucheix, B. Seasonal Temperature Impact on the Driving Range of Electric Vehicles: Effects on Carbon Emission Saving. J. Altern. Energy Sources Technol. 2022, 12, 10–34. [Google Scholar]
- Armenta-Déu, C.; Giorgi, B. Analysis of influence of variable meteorological conditions on driving range of EV. Future Transp. 2023; review in process. [Google Scholar]
- Boucheix, B. Control of Electric Vehicle Driving Range in Environmental Variable Conditions; Internship Report; Polytech Clermont Ferrand: Aubière, France, 2022. [Google Scholar]
- Google Earth. Available online: https://www.google.com/earth/version/ (accessed on 23 May 2022).
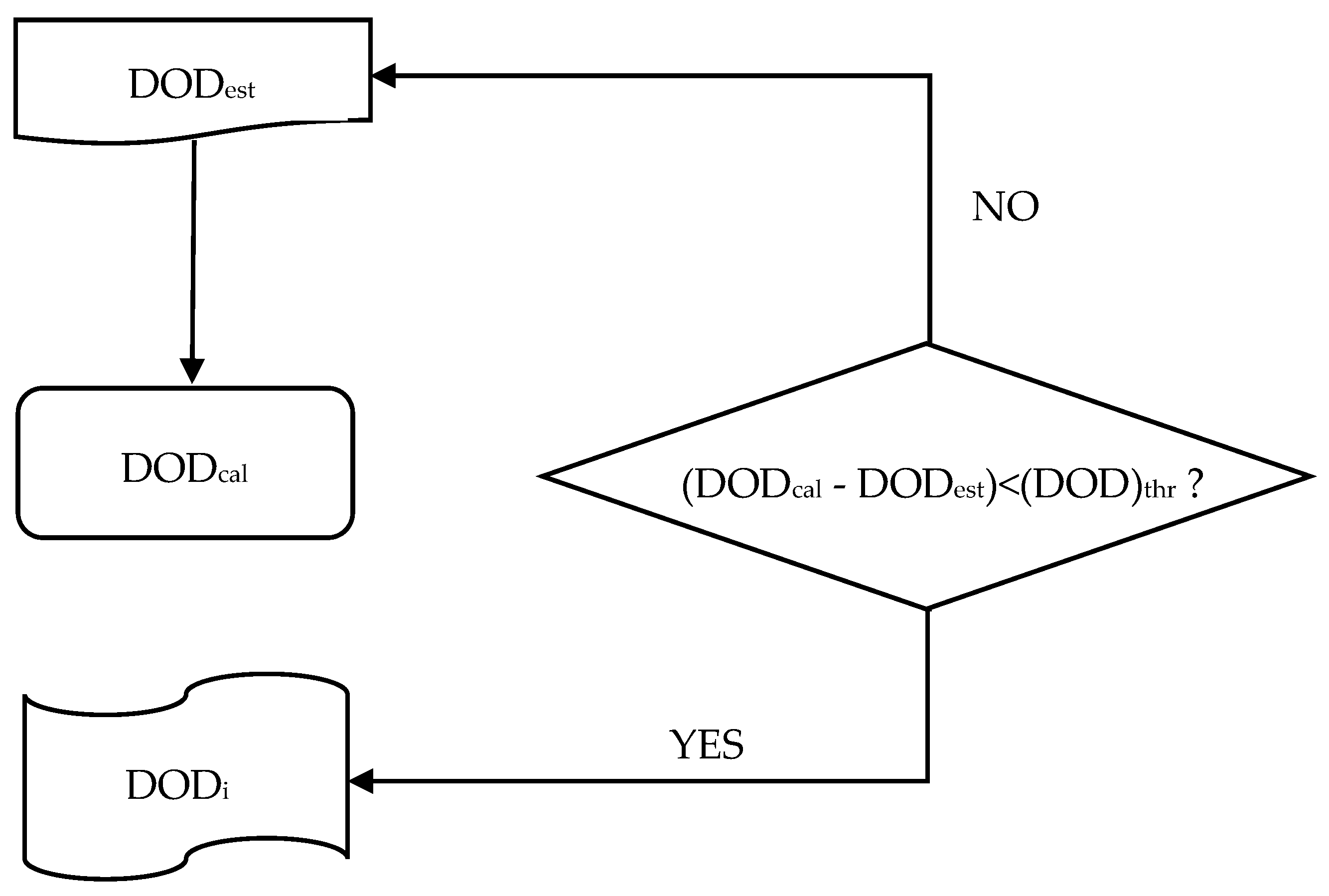











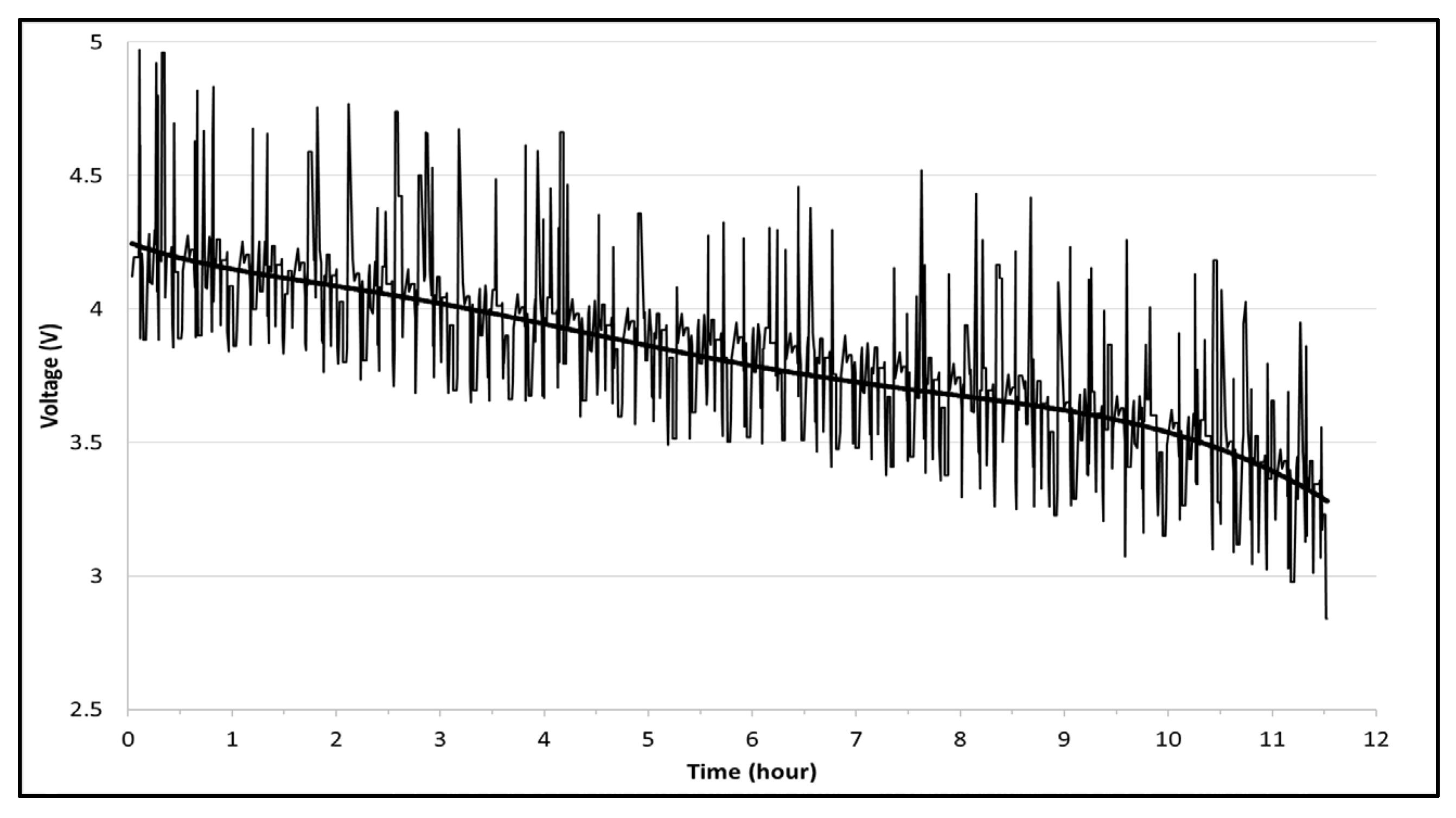
| Constant Ambient Temperature | 538 km |
|---|---|
| Variable ambient temperature | 494.5 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Armenta-Déu, C.; Boucheix, B. Evaluation of Lithium-Ion Battery Performance under Variable Climatic Conditions: Influence on the Driving Range of Electric Vehicles. Future Transp. 2023, 3, 535-551. https://doi.org/10.3390/futuretransp3020031
Armenta-Déu C, Boucheix B. Evaluation of Lithium-Ion Battery Performance under Variable Climatic Conditions: Influence on the Driving Range of Electric Vehicles. Future Transportation. 2023; 3(2):535-551. https://doi.org/10.3390/futuretransp3020031
Chicago/Turabian StyleArmenta-Déu, Carlos, and Benjamin Boucheix. 2023. "Evaluation of Lithium-Ion Battery Performance under Variable Climatic Conditions: Influence on the Driving Range of Electric Vehicles" Future Transportation 3, no. 2: 535-551. https://doi.org/10.3390/futuretransp3020031
APA StyleArmenta-Déu, C., & Boucheix, B. (2023). Evaluation of Lithium-Ion Battery Performance under Variable Climatic Conditions: Influence on the Driving Range of Electric Vehicles. Future Transportation, 3(2), 535-551. https://doi.org/10.3390/futuretransp3020031







