Development of a Signal-Free Intersection Control System for CAVs and Corridor Level Impact Assessment

Abstract

Assuming a full market penetration rate of connected and autonomous vehicles (CAVs) would provide an opportunity to remove costly and inefficient traffic lights from intersections, this paper presents a signal-free intersection control system relying on CAVs’ communicability. This method deploys a deep reinforcement learning algorithm and pixel reservation logic to avoid potential collisions and minimize the overall delay at the intersection. To facilitate a traffic-oriented assessment of the model, the proposed model’s application is coupled with VISSIM traffic microsimulation software, and its performance is compared with other intersection control systems, including fixed traffic lights, actuated traffic lights, and the Longest Queue First (LQF) control system. The simulation result revealed that the proposed model reduces delay by 50%, 29%, and 23% in moderate, high, and extreme volume regimes, respectively, compared to another signal-free control system. Noticeable improvements are also gained in travel time, fuel consumption, emission, and Surrogate Safety Measures.

1. Introduction

Due to rapid population growth and the increased number of vehicles, traffic congestion, collisions, and pollution have become leading causes of decreased living standards. In the USA in 2017, traffic congestion caused 8.8 billion hours of delay and 3.3 billion gallons of fuel waste, resulting in a total cost of 179 billion USD. Several studies have proved that human errors are pivotal in traffic congestion and accidents, and driver error contributes to up to 75% of roadway crashes worldwide. Intersections are crucial in traffic delays and collisions among urban traffic facilities. In the United States, 44% of reported traffic accidents occur at urban intersections, leading to 8500 fatalities and around 1 million injuries annually [1].

In conventional intersection control systems, an intersection controller such as a traffic light dictates the rules to the vehicles. However, recent advances in vehicles’ communication systems demand that there is communication between vehicles or between vehicles and the controller system to take full advantage of the CAVs’ communication capabilities. Based on this idea, CAV-based intersection control logic has been a point of interest for the last couple of decades. Several approaches such as trajectory planning, real-time optimization, and rule-based intersection control logics have been developed to establish purposive communication between facilities at the intersections. However, the most critical task in developing an intelligent intersection control system is to make the algorithm adjustable with stochastic or unprecedented circumstances. Existing CAV-based control systems are mostly based on fixed rules or conventional multi-objective optimization methods and are unlikely to produce a satisfactory outcome in unprecedented or rare circumstances, which is the main challenge for intersection control systems.

Considering CAVs as a revolution in the transportation industry, most public and private transportation-oriented agencies are involved with this phenomenon. In 2016 the U.S. Department of Transportation (USDOT) awarded a cooperative agreement collectively worth more than 45 million USD to three pilot Connected Vehicle (CV) sites in New York City, Wyoming, and Tampa [2]. Well-known car manufacturers, including Toyota, Honda, and Hyundai, are involved with the pilot program in Tampa [2]. In 2018, Waymo (Google) announced that its AVs have successfully driven 8 million miles on U.S. public roads [3]. Several companies such as TESLA and Cadillac have commercially produced level 3 to 4 CAVs [3]. General Motors is investing more than 20 billion USD until 2025 on its electric and CAV production [3]. In 2018, AUDI announced that the company would invest 16 billion USD on electric vehicles and AVs over the next five years. Ford has built an AV testing facility in Miami and noticeably increased its partnerships and investments in technology companies; building fully automated vehicles by the end of 2021 is the primary goal of the Ford company [3].

According to the astounding performance of deep reinforcement learning (DRL) in decision making in stochastic environments within the last few years in different areas from image processing to drought prevention, this relatively new method is deployed in this paper as an optimization logic to manage vehicles at the intersection [4]. In this method, each approaching vehicle to the intersection is considered a separate agent capable of coordinating with other agents if required. The intersection is divided into virtual grid areas, and each agent tries to reserve its desired areas ahead of time. A DRL optimization logic controls vehicles to avoid collisions and minimize overall delays at the intersection. The proposed model’s performance is compared with conventional and signal-free intersection control systems in a corridor of four intersections in VISSIM software. The proof of concept test proves that the proposed method outperforms conventional and signal-free intersection control systems in mobility, environmental, and safety measures.

The developed CAV management system can improve its performance or adjust to new circumstances during its life cycle, which is the main challenge in existing control systems. It also assumes individual vehicles are independent agents, each having its own optimization logic, and coordinating with other agents only if required, which is most likely how fully automated vehicles will act in the future. Deployment of the pixel reservation logic and the optimization algorithm have guaranteed collision-free maneuvers [5], making the optimization model more efficient by allowing it to target the traffic measures only.

Performance of the proposed model is compared with conventional and CAV-based intersection control systems, including fixed traffic lights, actuated traffic lights, and another CAV-based control system, in a corridor of four intersections. Based on the simulation results, the DQN noticeably outperforms all other control systems in all measures.

2. CAV-Based Intersection Control Systems

Based on the existing literature, CAV-based intersection control systems are clustered into four main groups, including (1) rule-based, (2) online optimization-based, (3) trajectory planning-based, and (4) ML-based algorithms.

2.1. Rule-Based Intersection Control Systems for CAVs

Most rule-based intersection logics are based on the intersection space reservation approach. The space reservation approach was initially developed in 2004 by Dresner et al. [5]. This method divides the intersection area into an n × n grid of reservation tiles. Each approaching vehicle to the intersection attempts to reserve a time–space block at the intersection area by transmitting a reservation request to the intersection manager, including its information such as speed and location. According to the intersection control policy, the intersection manager decides whether to approve and provide more passing restrictions to the vehicle or reject the reservation request. Dresner et al. deployed a “First Come First Serve” (FCFS) control policy, assigning the passing priority to the vehicle with the earliest arrival time. All other vehicles must yield to the vehicle with priority. In a following study, Dresner et al. [6] added several complementary regulations to the FCFS policy to make it work more reliably, safely, and efficiently. Simulation results revealed that the FCFS policy noticeably reduces intersection delay compared to traffic light and stop sign control systems.

Zhang et al. [7] proposed a state–action control logic based on Prior First in First Out (PriorFIFO) logic. They assumed spatial–temporal and kinetic parameters for vehicle movement based on a centralized scheduling mechanism. This study aimed to reduce the control delay for vehicles with higher priority. The simulation results with a combination of high-, average-, and low-priority vehicles showed that the algorithm works well for vehicles with higher priority, meanwhile, causing some extra delays for regular vehicles with lower priority.

Carlino et al. [8] developed an auction-based intersection control logic based on the Clarke Groves tax mechanism and pixel reservation. In this approach, if commonly reserved tiles exist between vehicles, an auction is held between the involved vehicles. All vehicles in each direction contribute to their leading vehicle to win the auction, and the control logic decides which leading vehicles receive a pass order first. The bid’s winner and its contributors (followers) have to pay the runner-up’s bid amount with a proportional payment (based on their contribution value in the bid). A “system wallet” component was added to auction-based intersection control to ensure low-budget vehicles or emergency vehicles would not be over-delayed. A comparison of simulation results showed that the auction-based control logic outperforms the FIFO logic.

2.2. Online Optimization Intersection Control Logic for CAVs

Yan et al. [9] proposed a dynamic programming-based optimization system to find the optimal vehicle passing sequence and minimize intersection evacuation time. In this algorithm, the optimizer agent clusters vehicles into several groups so that each group of vehicles can pass the intersection simultaneously without a potential collision. Since vehicles were clustered into several groups, the conventional problem of finding an optimal passing order of vehicles was transformed into partitioning the vehicles into different groups and finding optimal group sequences to minimize the vehicle evacuation time. In this method, approaching vehicles at the intersection provide their data to the controller agent, and the controller agent has to run the dynamic programming optimization whenever a new vehicle is detected. However, if a group of vehicles is authorized to pass the intersection, the calculation process is delayed till the whole group passes the intersection.

Wu et al. [10] deployed a timed Petri Net model to control a simple intersection with two conflicting movements. The intersection control was considered a distributed system, with parameters such as vehicles’ crossing time and time–space between successive vehicles. Two control logics, including (1) central controller and (2) car-to-car communication, were developed and tested. In central controller logic, approaching vehicles to the intersection provide their information to the controller center, and the controller center has to provide an optimized passing order for the vehicles, while in car-to-car control logic, each leading vehicle collects its followers’ data, and if the distance between them is shorter than a threshold, they are considered a group. In the latter system, only leading vehicles of groups communicate with each other, and the passing order priority for each group is defined by its leader’s proximity to the intersection. The optimization task was decomposed into chained subproblems by a backtracking process, and the final optimal solution was found by solving single problems and applying forward dynamic programming to find the shortest path from the original problem to the last problem in the graph. The simulation results revealed that both control logics have the same performance in delay reduction, resulting in almost the same queue length.

Fayazi et al. [11] deployed a Mixed-Integer Linear Programming (MILP) approach to optimize CAVs’ arrival time at the intersection. In this approach, the intersection controller receives the arrival and departure times from approaching vehicles and optimizes the vehicles’ arrival times. The optimization goal is to minimize the difference between the current time and the last vehicle’s expected arrival time at the intersection. To ensure all vehicles are not forced to travel near the speed limit, a cost value was defined as a function of the difference between the assigned and desired crossing time for each vehicle. Several constraints, such as speed limit, maximum acceleration, minimum headway, and minimum cushion for conflicting movements, were applied to the model. The two-movement intersection simulation results showed that the MILP-based controller reduces average travel time by 70.5% and average stop delay by 52.4%. It was also proved that the control logic encourages platooning under a specific gap setting.

Lee et al. [12] proposed a Cumulative Travel-time Responsive (CTR) intersection control algorithm under CAVs’ imperfect market penetration rate. They considered the elapsed time spent by vehicles from when they entered the network to the current position as a real-time measure of travel time. The Kalman filtering approach was deployed to cover the imperfect market penetration rate of CAVs for travel time estimation. Simulations were run in VISSIM for an isolated intersection with 40 volume scenarios covering the volume capacity ratio ranging from 0.3 to 1.1 and different CAV market penetration rates. Simulation results showed that the CTR algorithm improved mobility measures such as travel time, average speed, and throughput by 34%, 36%, and 4%, respectively, compared to the actuated control system. The CO₂ emission and fuel consumption were also reduced by 13% and 10%. It was also revealed that the CTR would produce more significant benefits as the market penetration rate passes the threshold of 30%. In general, more benefits were observed as the total intersection volume increased.

2.3. Trajectory Planning Intersection Control Logics for CAVs

Lee et al. [13] proposed a trajectory planning-based intersection control logic named Cooperative Vehicle Intersection Control (CVIC). The control algorithm provided a location–time diagram (trajectory) of individual vehicles and minimized the length of overlapped trajectories (conflicting vehicles). The optimization task was modeled as a Nonlinear Constrained Programming (NCP) problem. To ensure an optimal solution was achieved, three analytical optimization approaches, including the Active Set Method (ASM), Interior Point Method (IPM), and Genetic Algorithm (GA), were deployed. All three algorithms were implemented in parallel, and the first acceptable solution was implemented. Minimum/maximum acceleration, speed, and safe headway were considered the optimization problem’s constraints. A simulation testbed was developed in VISSIM to compare the proposed algorithm’s efficiency with actuated traffic signals under different volume conditions. The simulation results revealed that the proposed algorithm improved stopped delay, travel time, and total throughput by 99%, 33%, and 8%, respectively. A 44% reduction in CO₂ emission and fuel consumption was also achieved. It was also revealed that the CVIC is more advantageous when the intersection operates under oversaturated conditions.

Based on the assumption that vehicle trajectories can be defined as cubic interpolated splines, having the flexibility to reflect delays from the given signal timing, Gutesta et al. [14] developed a trajectory-driven intersection control for the CAVs. Vehicle trajectories were developed for several vehicles passing multiple intersections. The optimization goal was to minimize the sum of all trajectory curves (which reflect control delays) conditioned to meeting safety constraints. Traffic constraints such as speed limits were reflected in the model by adjusting the trajectory slopes. A Genetic Algorithm (GA) was deployed to evaluate all possible combinations of optimized single-vehicle trajectories. In addition, an artificial neural network (ANN), trained with available traffic stream factors, was deployed to achieve a short-term prediction of vehicle delays to be integrated with the optimization model. The simulation results revealed that the proposed control algorithm improves traffic measures under stable and unstable traffic conditions, even with CAVs’ low market penetration rate.

Krajewski et al. [15] proposed a decoupled cooperative trajectory optimization logic to optimize and coordinate CAVs’ trajectories at signalized intersections. The optimization goal was to minimize delay by coordinating conflicting movements such as straight going and left turns. The state-space of each vehicle had three dimensions: position, speed, and time. The optimization task was transformed into a graph (nodes representing the states and edges representing possible transitions between pairs of states) with a combined cost function of delay and comfort. The “decoupled” term refers to splitting the optimization problem into two stacked layers, (1) the Trajectory Layer (TL) and (2) the Negotiation Layer (NL). The TL’s task was to calculate trajectories for individual vehicles, and the NL’s task was to coordinate all trajectories to prevent potential collisions. The latter task was achieved by setting constraints for each vehicle’s TL algorithm, and the cost function was a weighted sum of the individual cost functions. The weight could also prioritize specific vehicle types. Simulation results revealed that the proposed algorithm reduces the cost value by 28% compared to the intelligent driver model replicating human-driven vehicles.

2.4. Machine-Learning-Based Intersection Control Logics for CAVs

Recent access to abundant and cheap computation and storage resources has made ML approaches popular in solving stochastic problems in different fields. Over the last few years, some researchers have deployed ML techniques to optimize single/multi-intersection traffic signal controls or develop signal-free control logic for CAVs. A selection of ML-based interaction control systems is reviewed in this section.

Lamouik et al. [16] developed a multiagent control system based on deep reinforcement learning to coordinate CAVs at the intersection. Each vehicle transfers five features to the controller agent in this method, including position, speed, dimension, destination, and priority. The controller agent has three possible responses for each vehicle, including acceleration, deceleration, and keep-same-speed. The reward value is a function of speed, priority, and collision. The controller agent was expected to avoid collisions and prioritize vehicles with a higher priority or higher speed in the training process. The controller agent was trained after several training epochs. However, the simulations were not run in a traffic network setting, and no traffic measures were assessed in this study.

Tong Wu et al. [17] developed a multiagent deep reinforcement learning algorithm to optimize several traffic lights in a corridor. Each traffic light was considered an agent, with actions being green lights for different phases. The reward value was set as a function of real-time delay for each vehicle, weighted by its priority. The innovation in this study was information exchange between controller agents so that each agent could estimate the policy of the other agents. According to other agents’ estimated policies, each agent could adjust the local policy to achieve the optimal global policy. Two networks with different intersections numbers were developed in SUMO for assessment purposes. Simulation results revealed that the proposed model outperforms independent deep Q-learning (no exchange of information between agents) and deep deterministic policy gradient (single-agent controlling all intersections). It was also shown that the model outperforms self-organizing and fixed-time traffic lights.

Touhbi et al. [18] developed a reinforcement-learning (RL)-based adaptive traffic control system. The main goal was to find the impact of using different reward functions, including queue length, cumulative delay, and throughput, on intersection performance. Unlike previous studies, which considered queue or delay as states, in this study, the state value was defined as a maximum residual queue (queue length divided by lane length) to reflect the traffic load on each phase. The learning process for a four-way single-lane intersection took 100 epochs of 1 hr simulation runs, and the simulation results revealed that the proposed algorithm remarkably outperforms the pretimed traffic signals. The analysis of different reward function deployments showed that each function’s efficiency highly depends on the traffic volume.

Yuanyuan Wu et al. [19] developed a decentralized coordination algorithm for CAVs’ management at the intersection. Each vehicle was considered an agent, and each agent’s state included its lane, speed, and moving intention. The intersection area was divided into an n × n grid, and each vehicle was supposed to reserve its desired pixel ahead of time. Vehicles could enter either a coordinated or an independent state, based on having a reserved pixel in common or not. Conventional multiagent Q-learning was deployed in this study, meaning that new states and their Q-values were added to a matrix as they came up, and the controller agent had to refer to a specific cell in the matrix to make a decision. Aligned with the multiagent optimization goal, each agent’s effort to maximize its Q-value resulted in a maximized global reward for all agents. Simulation results revealed that the proposed model outperforms the FCFS method, fixed-time traffic lights, and the LQF control system in delay reduction.

3. Methodology

3.1. Deep Reinforcement Learning and Deep Q-Networks

DRL process can be expressed as an agent taking actions; the environment responding to the agent by presenting new state and reward based on the last act’s quality. The agent seeks to maximize the reward over a series of interactions with the environment in discrete time steps (t) [20]. DQN formulation for estimating return values, called Q-function, is presented in Equation (1).

$$Q\left(s,a\right)=r+\mathsf{\Upsilon }maxQ\left(s^{\prime },a^{\prime }\right)$$

(1)

where:

• $Q\left(s,a\right)$ or Q-value defines the value of the current state–action pair.
• $Q\left(s^{\prime },a^{\prime }\right)$ defines the value of the next state–action pair.
• $\mathsf{\Upsilon }$ or “discount rate” ranges from zero to one and defines the present value of future rewards. If $\mathsf{\Upsilon }=0$, the agent is myopic, only concerned with maximizing the immediate reward. As $\mathsf{\Upsilon }$ approaches one, the agent cares more about future rewards and becomes more farsighted.
• $r$ is the immediate reward for the current actions.

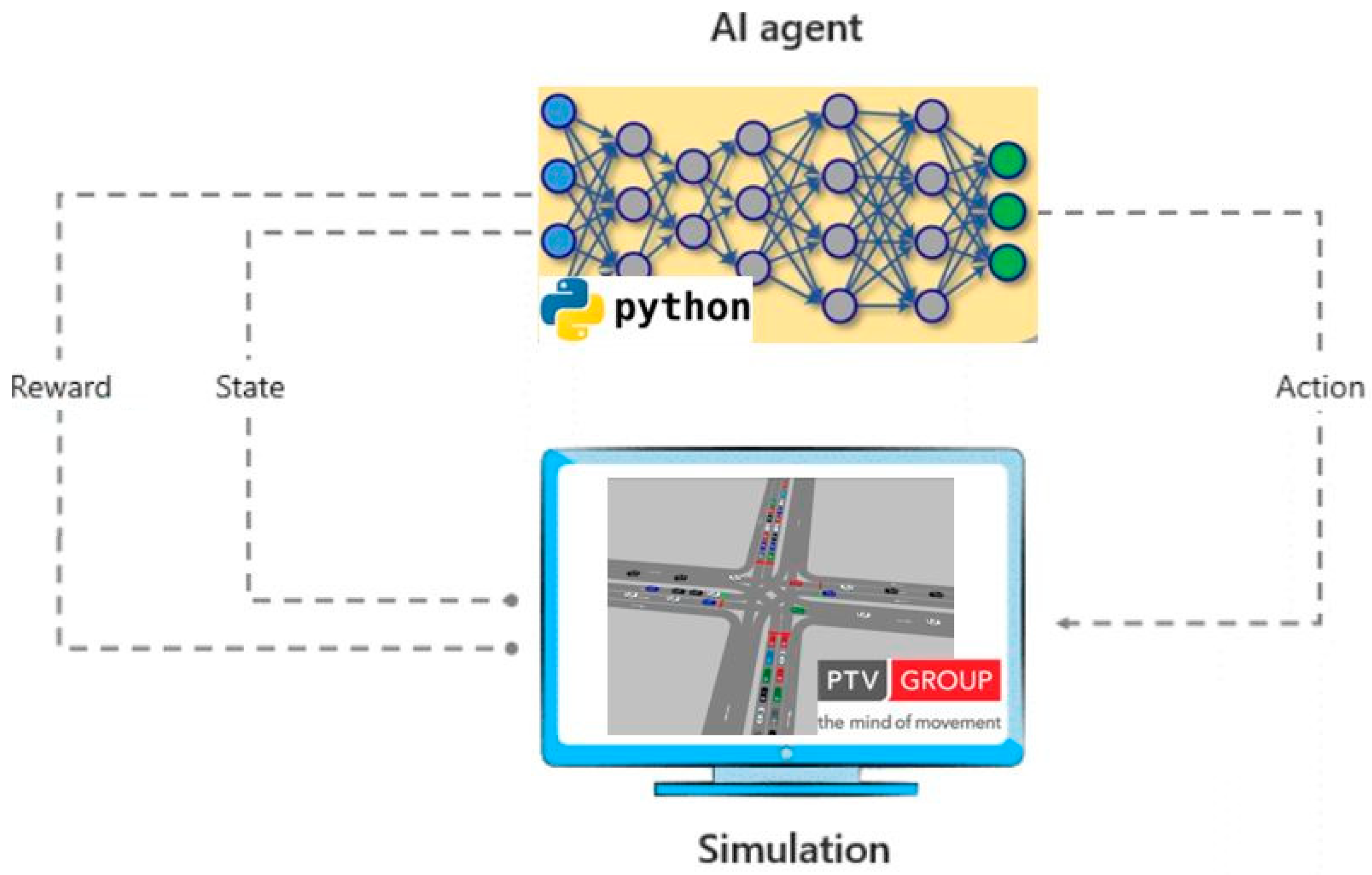
AI training and trial and error processes are usually performed in simulation testbeds, enabling a trained agent to tackle a broad scope of real-world scenarios. In the DQN approach, states are the input layer of the neural network, and the neural network’s output layer is an estimation of Q-values for all possible actions in the current state. The training occurs by updating the neural network weights based on a batch of recent historical data (states, actions, Q-values). In this study, the simulation testbed is developed in VISSIM software, and the DQN is developed as a Python application; a high-level training process of a DQN agent appears in Figure 1.

3.2. Training Environment, States, and Reward Function

The environment is a 4-way intersection including three lanes at each approach with dedicated left and right turn lanes. Traffic volume production, roadway configurations, and vehicles are set up in VISSIM software. The deep queue network (DQN) control system application is developed in Python and coupled with VISSIM through the COM interface. The intersection area is divided into 2.5 × 2.5 m² grid tiles, known as pixels or cells. The pixel reservation approach was initially proposed by Dresner et al. [5], and several researchers have used this method to manage CAVs at the intersection. This paper is inspired by a more recent pixel-reservation-based study by Wu et al. [19].

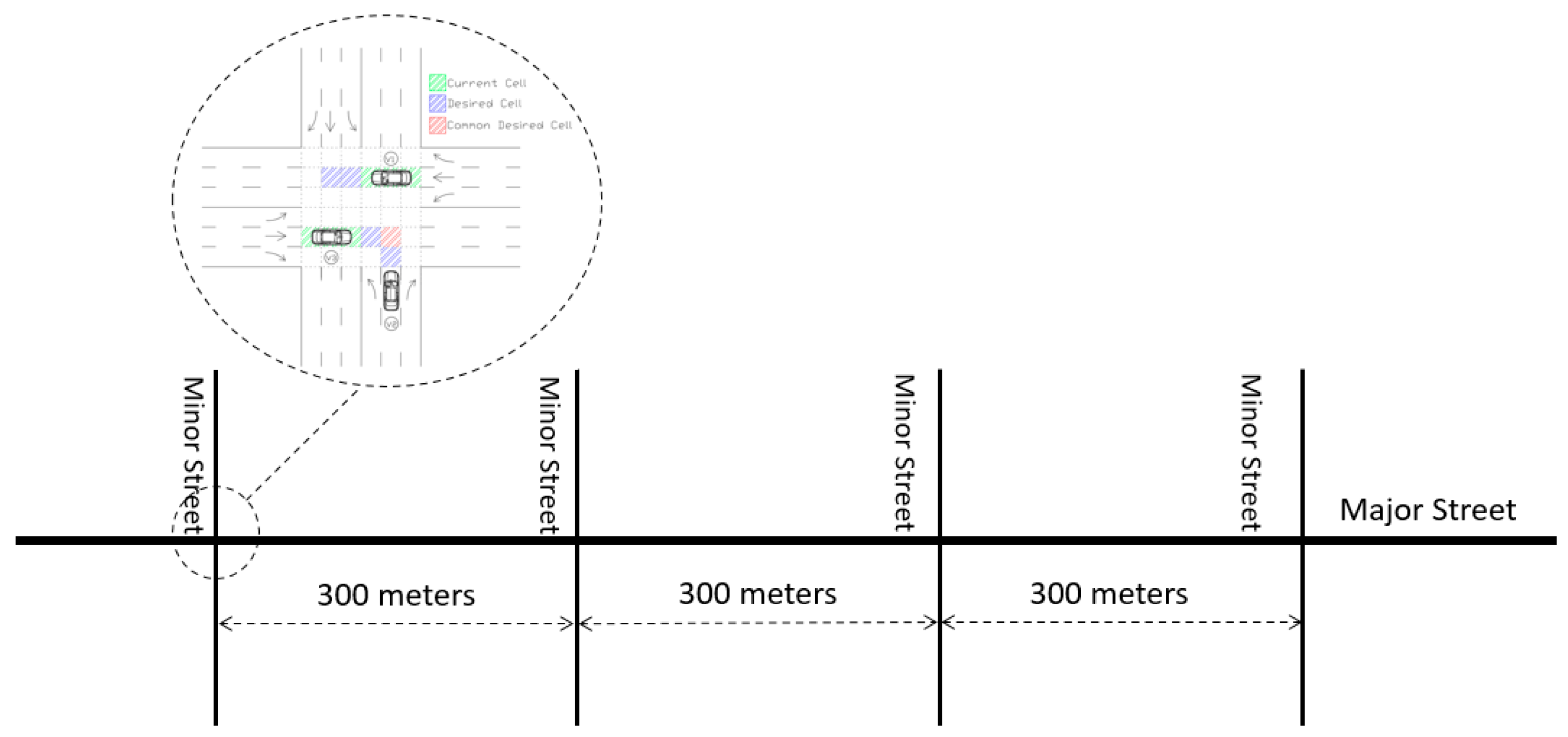
The maximum speed is 40.2 km/h, and the simulation resolution is set to 1 s/step, meaning that each vehicle would be surveying a maximum length of 11.17 m at each step ($V\Delta t=11.7\times 1$ = 11.17). Therefore, the grid zones are extended to 11.17 m (5 cells) upstream of the intersection for each approaching section. The proposed algorithm takes control of the vehicles as soon as they enter the gridded area. Assuming a vehicle length of 4.90 m (Ford Fusion 2019), each vehicle would occupy either two or three cells at each time step. The environment’s physical settings and definition of current cells, desired cells, and commonly desired cells appear in Figure 2. The maximum value between survey and stop distances defines the number of desired cells for each vehicle. The survey distance includes the number of desired cells if the vehicle accelerates or keeps moving at the maximum speed. The stop distance covers the required cells for the vehicle to stop. Since, while reserving cells, it is unknown whether the vehicle would be commanded to accelerate or decelerate for the next step, it is required to reserve enough cells to cover both scenarios.

Based on classical physics theory, the survey distance equals ($V\Delta t+\frac{1}{2}a\Delta t^2$) if the vehicle is moving slower than the maximum speed and can still accelerate, or it equals ($V\Delta t$) if the vehicle is already moving with the maximum speed, and the stop distance equals ($\frac{V^2}{2a}$). The acceleration and deceleration rates are set to 3.5 and 7 $\mathrm{m}/{\mathrm{s}}^2$. The stop and survey distance formulas are shown in Equation (2).

$$DS=\left\{\begin{array}{ll}max\left(\left[\frac{V^2}{2a}\right], \left[V\Delta t+\frac{1}{2}a\Delta t^2\right]\right)& V<V_m\\ max\left(\left[\frac{V^2}{2a}\right], \left[V\Delta t\right]\right)& V=V_m\end{array}\right.$$

(2)

where:

• $\Delta t$: each step’s time length.
• V: current speed.
• $a$: acceleration or deceleration capability.
• DS: number of desired cells.

If the algorithm detects a shared desired cell between vehicles, they will enter a coordinated state; otherwise, they will be in an independent state. For example, vehicles 2 and 3 in Figure 2 are in a coordinated state since they have reserved common cells. Each leading vehicle’s state includes its current speed, current cell, and the queue length behind it. Possible actions for each vehicle to avoid collision are acceleration, deceleration, or maintaining the current speed. Equations (3) and (4), present the state and possible actions. Maximum acceleration and deceleration rate for CAVs is assumed to be same as Ford Fusion 2019 hybrid specifications.

$$Stat{e}_i=\left(Spee{d}_i, Current Cel{l}_i, Queu{e}_i\right)$$

(3)

$$Actio{n}_i=\left(-acc,+acc, maintain curent speed\right)$$

(4)

Each leading vehicle’s reward at each time step is the summation of the delay of all vehicles in its direction. Assuming that the distance traveled by the vehicle $V_i$ at the time step t is $L_i$, then the optimal time required to pass the distance equals $(\frac{L_i}{V_m}$). Each approach’s delay value equals the reward function and is calculated based on Equation (5).

$$r\left(t\right)=-{\displaystyle \sum }_{i=1}^n\left(\Delta t-\frac{L_i}{V_m}\right)]$$

(5)

RL’s goal is to optimize the total return (reward) at the end of each episode and not the immediate reward. Therefore, being independent in this environment does not necessarily result in acceleration or maintaining the maximum speed.

3.3. Distributing Rewards between Agents

Since being in an independent state does not require interactions with other agents, the agent receives an individual reward (Equation (6)). Meanwhile, a coordinated state requires interaction with other agents, and the agent earns a joint reward (Equation (7)). The ultimate optimization goal is to maximize the total distributed reward at each step, known as the global reward (Equation (8)). This method is known as multiagent deep queue network (MDQN).

$$R\left(s_i,a_i\right)=r_i$$

(6)

$$r\left(s_j,a_j\right)={\displaystyle \sum }_{b=1}^h{r}_{jb}$$

(7)

$$R\left(S,A\right)={\displaystyle \sum }_{b=1}^N{r}_{\left(i or j\right) b}$$

(8)

where:

• Subscripts $i$ refer to an agent being in an independent state;
• Subscripts $j$ refer to an agent being in a joint state;
• (s,a) refers to taking a specific action (a), in specific state (s);
• $h$ is the number of agents involved in a joint state;
• N is the total number of agents in an environment;
• R is the global reward.

3.4. Transition from Independent to Coordinate State or from Coordinated to Independent State

Any transition from an independent state to a coordinated state or vice versa requires specific settings for updating Q-value in MADQN. Three possible transition types are explained below:

Type 1: when an agent moves from a coordinated state to another coordinated state or from an independent state to another independent state, the coordinated or independent Q-value is updated by:

$$Q{\left(s,a\right)}_{i or j}=r{\left(s,a\right)}_{i or j}+\mathsf{\Upsilon }maxQ{\left(s^{\prime },a^{\prime }\right)}_{i or j}$$

(9)

Type 2: when an agent moves from a coordinated state to an independent state, the joint Q-value is updated by:

$$Q{\left(s,a\right)}_j={\displaystyle \sum }_j^h[r{\left(s,a\right)}_j+\mathsf{\Upsilon }maxQ{\left(s^{\prime },a^{\prime }\right)}_i]$$

(10)

Type 3: when an agent moves from an independent state to a coordinated state, the independent Q-value is updated by:

$$Q{\left(s,a\right)}_i=\left[r{\left(s,a\right)}_i+\mathsf{\Upsilon }\frac{1}{h}maxQ{\left(s^{\prime },a^{\prime }\right)}_i\right]$$

(11)

Based on the existing literature [5,6], the pixel reservation system guarantees a collision-free vehicle maneuver system by itself. Therefore, unlike most other RL-based AV management systems, collision avoidance is not considered in the reward function as an optimization goal.

3.5. Training Settings and Learning Performance

For training purposes, traffic volume is set to 2500 and 1500 Veh/h on major and minor streets. Vehicles are stochastically generated with a constant random seed by VISSIM software for 900 s. Initial Epsilon (ε) value is set to 1, which may cause long queues. Therefore, intersection legs are extended 2 km in each direction to reflect the potential queue length. The total epoch length is set to 1500 s to ensure that all generated vehicles have evacuated the intersection at the end of each epoch. The hardware used for simulation is Dell tower Cor i9 with external GPU.

The simulation resolution is set to 1 step/s, and the random seed is kept constant during all training iterations. As mentioned previously in the Methodology Section, to improve the DQN performance, a lagged copy of the neural network estimates the target Q-values. The target neural network parameters are updated every five epochs (target network update frequency). The replay memory size, which defines how many of the latest experiences will be stored in the memory for training purposes, is set to 10,000. The minibatch size, which defines the size of random data set from replay memory to be forwarded to the neural network, is set to 32. The training process hyperparameter settings appear in

Table 1. Training process hyperparameters’ settings.

Hyperparameter	Value
Number of steps per epoch	1500
Step size (Δt), equal to simulation resolution	1 s
Replay memory size	10,000
Minibatch size	32
Target network update frequency	5 epochs
Initial ε	1
ε-decay factor	0.999
Discount (γ)	0.9

.

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

Figure 3 shows that the global reward converges to a maximum value after 3500 training epochs, which means an overall delay reduction for the intersection.

4. Proof of Concept Test

The trained model is applied to a corridor of four intersections to assess its impact on traffic flow in an extensive network. The testbed layout is shown in Figure 4.

The DQN control system’s performance is compared with other conventional and CAV-based intersection control systems, including (1) fixed traffic signal, (2) actuated traffic signal, and (3) Longest Queue First (LQF) control logic, which was developed by Wunderlich et al. [21]. In this algorithm, the phases have no specific order and are triggered based on queue length in different approaches. In our study, the LQF logic is modeled based on pixel reservation for connected and autonomous vehicles, so the only difference between LQF and DQN would be the optimization approach. The speed limit is 40.2 km/h, and three different volume regimes (with different random seeds for vehicle production), described below, are considered for evaluation purposes:

• Moderate volume: approximately 1150 and 850 Veh/h on the major and minor streets, respectively. This volume combination leads to Level Of Service (LOS) B for the major street and LOS C for the minor street.
• High volume: approximately 1600 and 1100 Veh/h on the major and minor streets, respectively. This volume combination leads to LOS D for both major and minor streets.
• Extreme volume: approximately 2000 and 1300 Veh/h on the major and minor streets, respectively. This volume combination leads to LOS F or congestion for major and minor streets.

The LOS is calculated based on the Highway Capacity Manual (HCM) 6th edition in Vistro, assuming the intersection operates under an optimized traffic light. Vistro is a traffic analysis and signal optimization software. Simulation time and resolution are set to 60 min and two steps/sec, respectively; accordingly, 20 simulation runs with different random seeds are run in VISSIM software for each scenario.

4.1. The Target Traffic Measure Comparison

Since the control system’s optimization goal is to minimize the delay, the delay is specified as the target traffic measure. A comparison of the average delay between different control systems appears in Figure 5. According to the figure, the DQN effectively reduces delay in all volume regimes, specifically in moderate volumes, with a 50% delay reduction compared to the second-best control system. Delay reductions of 29% and 23% are achieved compared to the second-best control systems in high and extreme volume regimes, respectively.

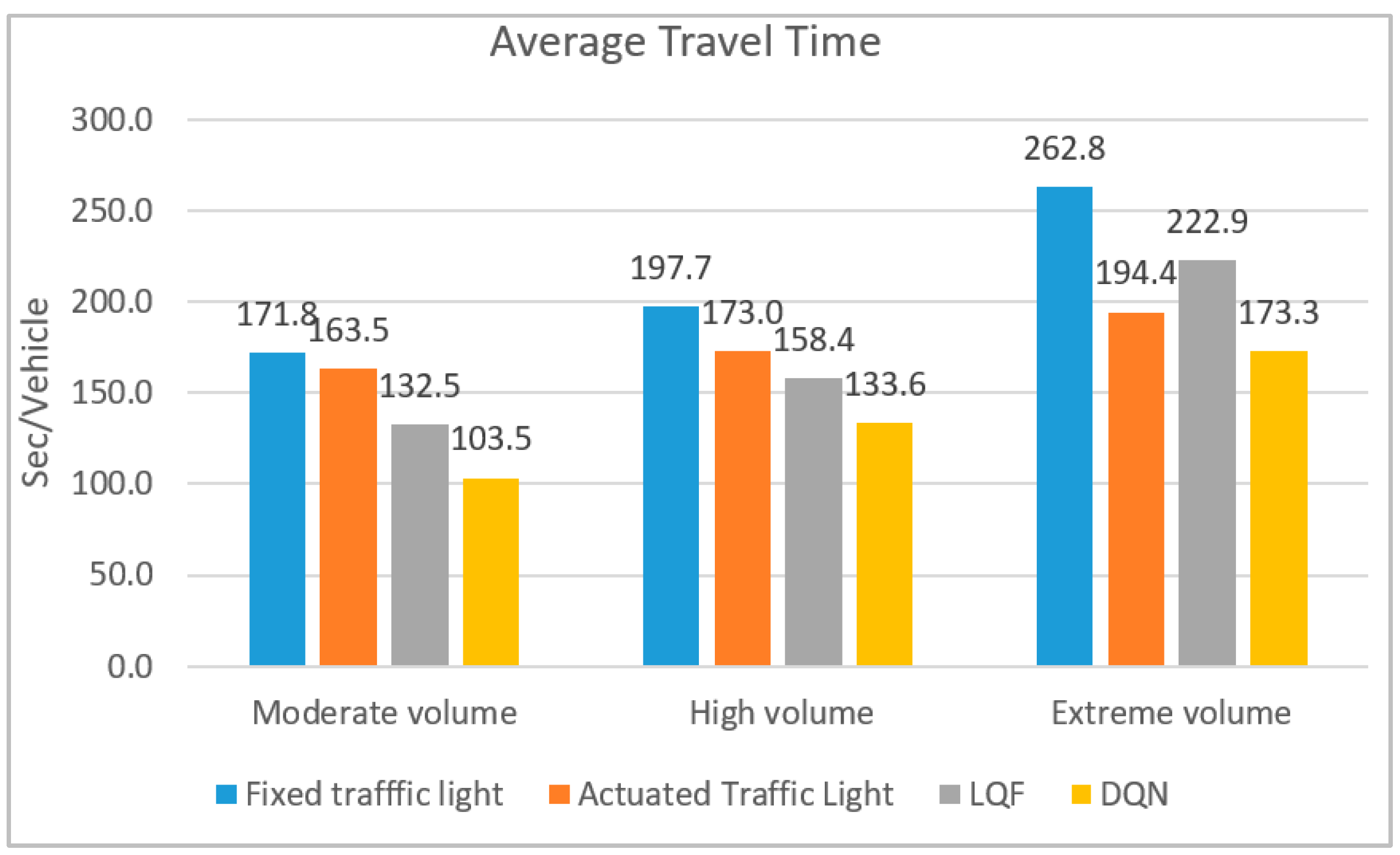
Followed by delay reductions, travel time improvement is also expected. The average travel time values shown in Figure 6, reveal that 22% and 16% travel time reductions are gained compared to the LQF control system in moderate and high volume circumstances, respectively. In the extreme volume regime, the proposed control system outperforms the actuated control system with an 11% travel time reduction.

4.2. Other Measures Comparison

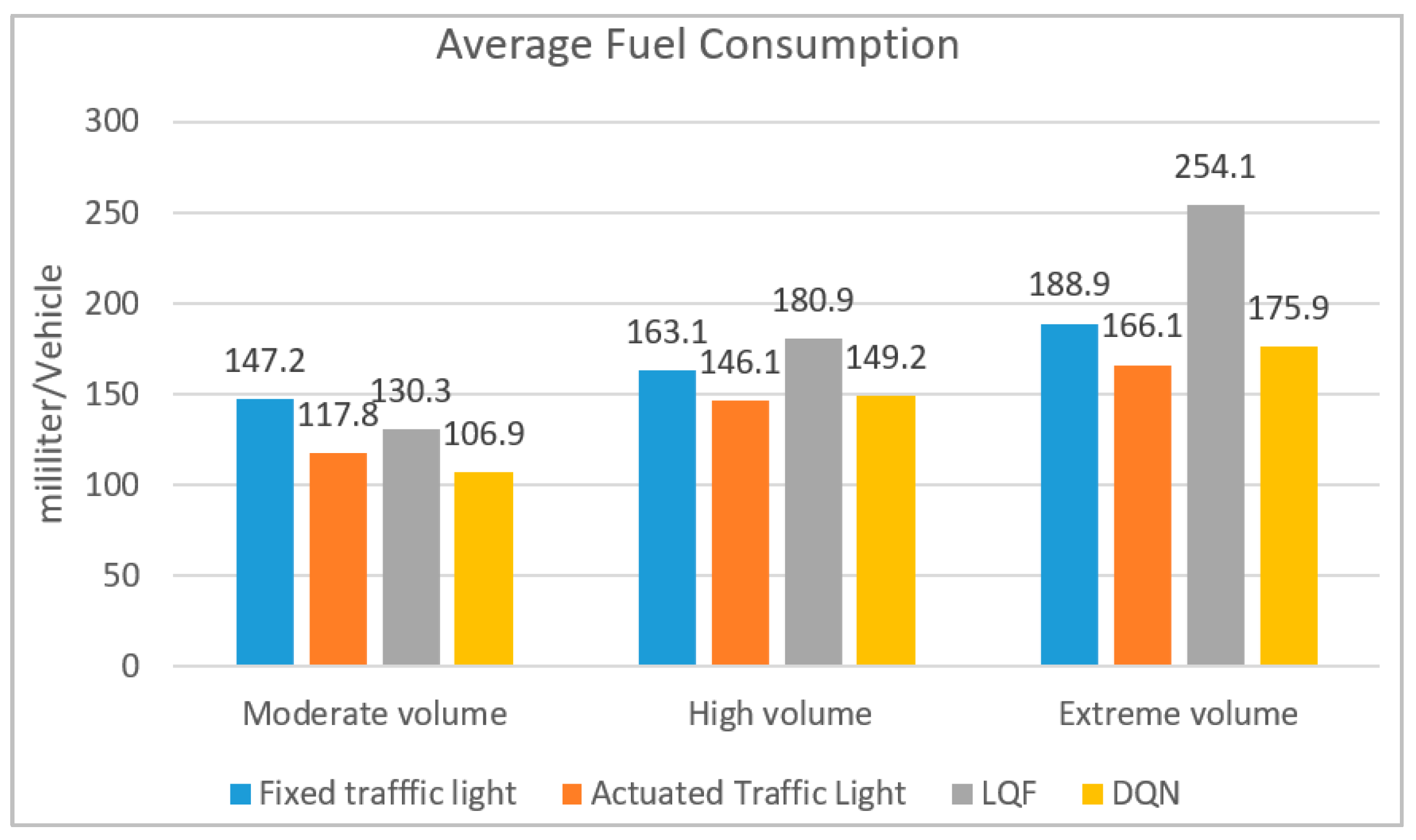
Along with target traffic measures, the environmental and safety impacts of the model are also evaluated. Fuel consumption and CO₂ emission are calculated based on the VT-Micro model. This model can estimate the emissions and fuel consumption for individual vehicles based on instantaneous acceleration and speed [22]. The average fuel consumption results appear in Figure 7; the DQN gains a 9% fuel consumption reduction in the moderate volume regime compared to the actuated control system. The actuated traffic light outperforms DQN with 2% and 6% fuel consumption reductions in high and extreme volume regimes, respectively. However, the proposed control system noticeably outperforms the other pixel-reservation-based model (LQF) in all volume regimes.

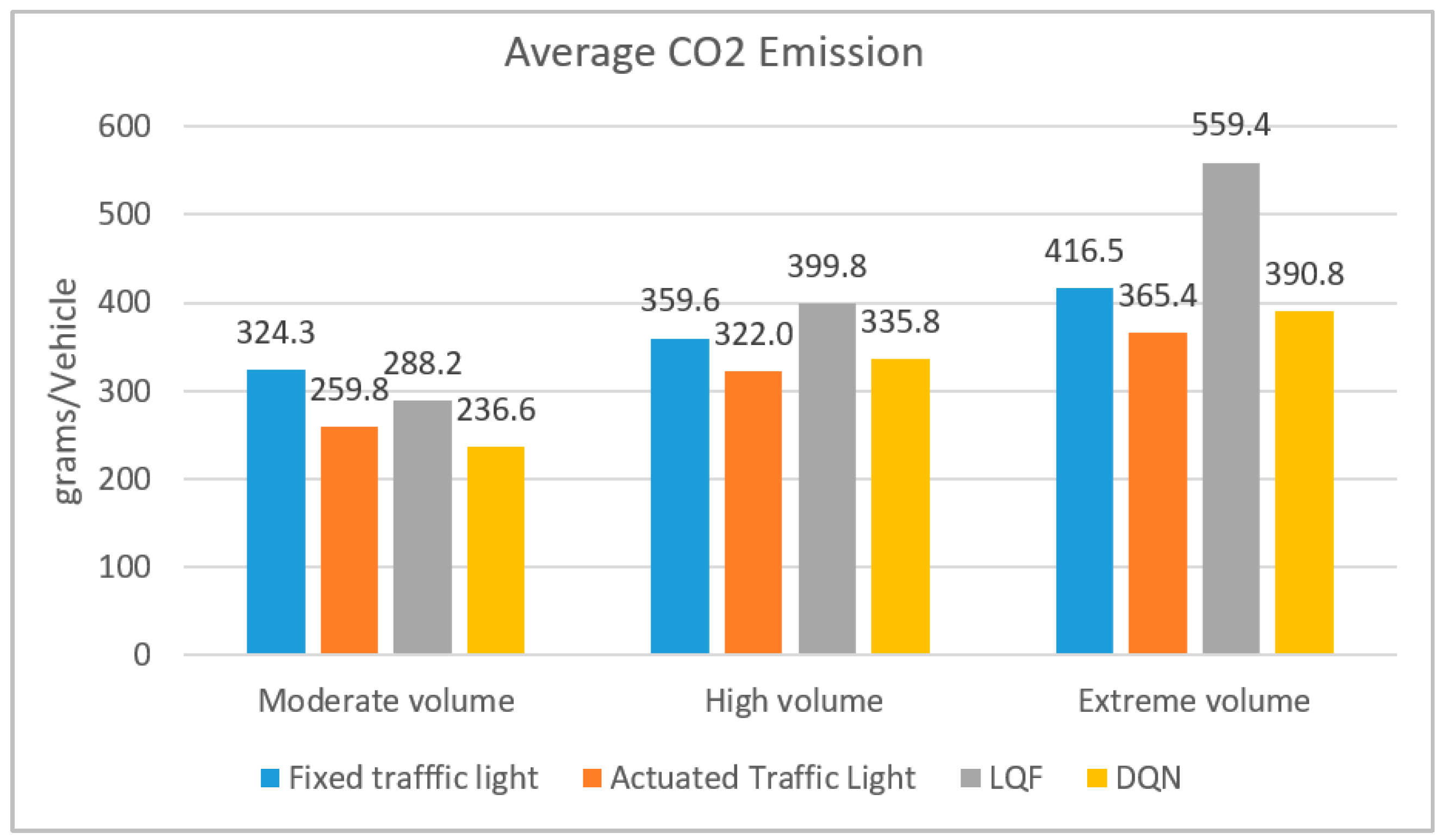
As shown in Figure 8, average CO₂ emission follows the same pattern as average fuel consumption. The DQN outperforms actuated traffic lights with a 9% CO₂ emission improvement. However, the actuated traffic light performs better than DQN with 4% and 7% less CO₂ emission in high and extreme volume regimes, respectively.

Despite acceleration and deceleration rates for DQN being limited to fixed values only, fuel consumption and emission improve slightly in moderate and high volume regimes, and a slight increment occurs in the extreme volume condition. Fuel consumption and CO₂ emission are estimated based on VISSIM software built-in models.

Among various Surrogate Safety Measures, the post-encroachment time (PET) is a well-fitting measure used to identify safety threats for crossing vehicles at an intersection. It represents the time between the departure of the encroaching vehicle from the conflict point and the vehicle’s arrival with the right-of-way at the conflict point [23]. Safety analysis is performed in the SSAM software, automatically identifying, classifying, and evaluating traffic conflicts in the vehicle trajectory data output from microscopic traffic simulation models. The comparison of PET for different traffic control systems appears in Figure 9 According to the figure, pixel-reservation-based logics, including DQN and LQF, have an almost equal PET. Both perform better than the actuated traffic light, specifically in extreme volume regimes with a 22% improvement in PET. Pixel-reservation-based control systems consist of more stop-and-go, which increases the chance of an accident in regular intersections. Therefore, even a minor improvement in PET compared to conventional control systems is noticeable.

4.3. Statistical Analysis of the Simulation Results

According to the t-test results performed on the simulation results between the DQN and other control systems, gains from DQN compared to the fixed traffic light are statistically significant for all measures in all volume regimes. The proposed model’s minor losses or gains in fuel consumption and emission are not statistically significant (with a confidence interval of 95%) compared to the actuated traffic lights. DQN gains compared to LQF are statistically significant in all measures except for safety, which is predictable since both models are based on pixel reservation logic to avoid collisions. The t-test results appear in

Table 2. p-values for t-test results.

	Fixed Traffic Light
	Moderate Volume
	Delay	Travel Time	Fuel Consumption	CO2 Emission	PET
DQN	<0.05	<0.05	<0.05	<0.05	<0.05
	High Volume
	Delay	Travel Time	Fuel Consumption	CO2 Emission	PET
	<0.05	<0.05	<0.05	<0.05	<0.05
	Extreme volume
	Delay	Travel Time	Fuel Consumption	CO2 Emission	PET
	<0.05	<0.05	<0.05	<0.05	<0.05
	Actuated Traffic Light
	Moderate volume
	Delay	Travel Time	Fuel Consumption	CO2 Emission	PET
DQN	<0.05	<0.05	>0.05	>0.05	<0.05
	High Volume
	Delay	Travel Time	Fuel Consumption	CO2 Emission	PET
	<0.05	<0.05	>0.05	>0.05	<0.05
	Extreme volume
	Delay	Travel Time	Fuel Consumption	CO2 Emission	PET
	<0.05	<0.05	>0.05	>0.05	<0.05
	LQF
	Moderate volume
	Delay	Travel Time	Fuel Consumption	CO2 Emission	PET
DQN	<0.05	<0.05	<0.05	<0.05	>0.05
	High Volume
	Delay	Travel Time	Fuel Consumption	CO2 Emission	PET
	<0.05	<0.05	<0.05	<0.05	>0.05
	Extreme volume
	Delay	Travel Time	Fuel Consumption	CO2 Emission	PET
	<0.05	<0.05	<0.05	<0.05	>0.05

.

5. Conclusions and Future Directions

Most existing CAV-based intersection control systems are based on costly physical traffic lights, which will no longer be a necessity in a full MPR of AVs. Moreover, they are based on traditional multi-objective optimization methods, and are not reliable when facing unprecedented circumstances after deployments such as gradual traffic pattern changes or incidents. To cover the existing shortcomings, this paper presented a signal-free intersection control system for CAVs based on a pixel reservation, and DQN logic. The DQN model is capable of decision making in unprecedented situations and adapting to new traffic patterns over time. The pixel reservation logic guarantees collision-free maneuvers that allow the DQN to target delay reduction as the only optimization goal. The traffic volume and vehicle arrival’s random seed are constant during 3500 epochs of model training iterations. However, the trained model can deal with any volume combination or stochastic vehicle arrivals due to the chain impact of the agent’s random actions in a DQN training course, known as exploration. The DQN is developed as a Python application, controlling individual vehicles in VISSIM software.

Performance of the proposed model is compared with conventional and CAV-based intersection control systems, including fixed traffic lights, actuated traffic lights, and LQF, in a corridor of four intersections. Based on the simulation results, the DQN noticeably outperforms the LQF control system with up to 50% and 20% delay and travel time reduction. Both CAV-based control systems have shown the same performance in safety measures. However, the DQN outperforms the LQF in fuel consumption and CO₂ emission by up to 30%. Although the proposed model is based on fixed acceleration and deceleration rates, it does not cause any significant losses in fuel consumption and CO₂ emission compared to the conventional intersection control systems, which is a promising result.

This study’s future directions can be (1) developing a passenger throughput optimization-based or emergency vehicle priority-based control system by adjusting the reward function, (2) assuming several accelerations and declaration rates for each vehicle to improve environmental measures, and (3) using other DRL methods such as Double DQN and Prioritized Experience Replay to improve the model’s performance.