The Space-Based Car-Following Model: Development and Application for Managed Motorway System Safety Evaluation

Abstract

Traffic safety studies need more than what the current micro-simulation models can provide, as they presume that all drivers exhibit safe behaviors. Therefore, existing micro-simulation models are inadequate to evaluate the safety impacts of managed motorway systems such as Variable Speed Limits. All microscopic traffic simulation packages include a core car-following model. This paper highlights the limitations of the existing car-following models to emulate driver behaviour for safety study purposes. It also compares the capabilities of the mainstream car-following models, modelling driver behaviour with precise parameters such as headways and time-to-collisions. The comparison evaluates the robustness of each car-following model for safety metric reproductions. A new car-following model, based on the personal space concept and fish school model is proposed to simulate more accurate traffic metrics. This new model is capable of reflecting changes in the headway distribution after imposing the speed limit from variable speed limit (VSL) systems. This model can also emulate different traffic states and can be easily calibrated. These research findings facilitate assessing and predicting intelligent transportation systems effects on motorways, using microscopic simulation.

1. Introduction

The car-following (CF) phenomenon within traffic flow has been studied extensively for the past 60 years. Different models target specific measures as the objective parameters in order to reproduce this phenomenon. Most CF models are focused on reproducing the average traffic metrics such as average traffic flow, speed or density [1], where reproduction of the fundamental traffic diagrams were the main purpose. Other CF models concentrated on individual vehicle trajectory reproduction to minimize the model errors in individual vehicles’ metrics such as space, speed and acceleration profile [2,3].

Comparing mainstream CF models has been the main focus for researchers [4,5]. Kikuchi et al. [6] assessed the impacts of Adaptive Cruise Control System (ACCS) on traffic flow and safety. They investigated General Motors (GM) CF models and a fuzzy rule-based CF model by the University of Delaware (called the UD model). Kikuchi et al. identified the UD model to be more suitable for their sensitivity tests. They used Minimum Spacing (MS) and the total time of having too short spacing for a car that not even an emergency brake would not save from a collision as their main metrics. However, these tests were only performed on a simulation test bed. They artificially introduced a perturbation in the simulation at the beginning of a traffic platoon and assessed stability of the traffic flow. Brackstone et al. [7] also investigated the effect of an ACC (Adaptive Cruise Control) through an assessment of the percentage likelihood of a car being involved in a collision. Ranjitkar and Nakatsuji [8] compared CF models against the prediction error in spacing, speed and acceleration in individual levels, while Panwai and Dia [9] compared CF models within different commercial simulation models against a spacing prediction error. Despite such studies, there is a lack of studies that have compared the CF models against more precise safety-related parameters such as individual short headways and time-to-collision (TTC) events. Other evaluations targeted mostly average metrics such as average speed or volume in the aggregate level, and space and speed errors at an individual level. Therefore, a comparison of CF models, based on a very precise metric related directly to safety, against observed data, is an existing gap in traffic modelling.

Microscopic simulation models provide a powerful tool to dynamically model transport systems, which allow traffic engineers to evaluate different strategies for transport networks to assess travel time, emission, and fuel consumption. CF models are one of the main components of any microscopic simulation model. Without an accurate safety-tuned CF model, micro-simulation for safety studies cannot be precise. CF is the interaction of nearby vehicles in the same lane, and so has a major role in traffic safety measure reproduction. The potential of micro-simulation to evaluate safety-related factors has been acknowledged [5,10], albeit with limited advancement to analyse traffic safety. Archer [11] used micro-simulation within signalized and unsignalized urban intersections, calculating certain safety indicators based on the concept of “conflicts”. Overall, research on the accuracy and applicability of the CF models for safety simulation studies is limited, and recent attempts to modify existing CF models [5,12] are still far from accomplishing the required model for safety studies. An extensive literature review of CF models [13,14] acknowledges a lack of safety measure accuracy.

Firstly, this research develops and validates a new CF model that is based on the concept of driver-vehicle personal space and fish schools. This enables traffic analysts to be more confident in the use of microscopic simulation models to evaluate the impact of different traffic scenarios in terms of their safety improvement impact. This step forward enables simulation models to predict near-miss crash risks.

Secondly, this study compares the performance of the proposed model against the mainstream CF models in terms of the produced safety indicators such as total time collision (TTC) and headways. Real freeway trajectory data was sourced from the Next Generation Simulation (NGSIM).

Thirdly, the proposed new CF model is applied to variable speed limit (VSL) in a managed motorway system. While there are a large number of managed motorway systems such as VSL or ramp metering implemented in many countries, there is little support showing the safety effects of these systems [15]. Furthermore, existing microscopic models do not offer the confidence to evaluate the safety effects of ITS applications such as VSL [16]. There are limited studies that show the impact of variable speed limits (VSLs) on safety e.g., [17,18,19,20] in a simulated environment, and few questioned if CF models, embedded in their simulation model platform, are reliable in mimicking the VSL impact on drivers’ headway and TTC as it does in real life. This research proposes a CF model that is particularly more robust in simulating the safety impact of managed motorway systems.

This paper starts by presenting the salient features of selected mainstream CF models for comparison in Section 2. Thereafter, Section 3 presents the new Space Based Model (SBM). Section 4 then elaborates on the calibration and comparison methodology. Section 5 presents the testing and validation of the SBM. This is followed by Section 6, which compares the CF models against the observed data to determine their strength and level of accuracy in the reproduction of safety metrics. In Section 7 the application of SBM in evaluating the safety impact of a variable speed limit (VSL) system is examined. Lastly, the significance and implications of the SBM are given in the Section 8.

2. Existing CF Models

An extensive literature review was conducted, and five mainstream CF models were identified for the purpose of evaluating their robustness in reproducing safety indicators. They are Gazis-Herman-Rothery, the intelligent driver model, the psychophysical model, the Gipps CF model, and cellular automaton. A detailed examination of the formulation for each model was sourced from the original authors and papers, and are summarized below.

(A)

The Gazis-Herman-Rothery (GHR) Model

GHR is regarded as the most well-known CF model, and was developed by Chandler et al. [1] who investigated the acceleration of the follower as a function of the follower’s speed, relative speed, spacing and driver reaction time delay. Their mathematical model is developed from an experiment using an instrumented car at General Motors. They discovered that spacing is not significantly correlated to acceleration, while speed differences are highly correlated to the acceleration that drivers choose. The general formula of GHR type models is shown in Equation (1).

$${\mathrm{a}}_{\mathrm{n}}\left(\mathrm{t}\right)={\mathrm{c} \mathsf{\nu }}_{\mathrm{n}}^{\mathrm{m}}\left(\mathrm{t}\right)\frac{∆\mathsf{\nu }\left(\mathrm{t}-\mathrm{T}\right)}{∆{\mathrm{x}}^{\mathrm{l}}\left(\mathrm{t}-\mathrm{T}\right)}$$

(1)

where:

${\mathrm{a}}_{\mathrm{n}}$: acceleration;

${\mathsf{\nu }}_{\mathrm{n}}$: follower vehicle speed;

$∆\mathrm{x}$: relative spacing;

$∆\mathsf{\nu }$: relative speeds;

T: reaction time;

m, l and c: the constants to be determined.

$\mathrm{m}$ indicates how vehicle speed affects acceleration implemented at time $\mathrm{t}$ by a driver. $\mathrm{l}$ represents how relative spacing $∆\mathrm{x}$ contributes to the car-following phenomenon. $\mathrm{c}$ is the sensitivity or scaling constant which relates to $\mathrm{T}$. Chandler et al. [1] recommended that when $\mathrm{l}=\mathrm{m}=0$, the suitable range for $\mathrm{c}=0.17 \mathrm{to} 0.74$, and $\mathrm{T}=1.0 \mathrm{to} 2.2$. However, a variety of $\mathrm{l}$ and $\mathrm{m}$ were suggested by different studies to calibrate and validate the GHR model. Brackstone and McDonald [4], in a comprehensive literature review of GHR-type CF models, identified the parameter combinations that are less contradictory and compared these with the rest of the studies. The parameter values for acceleration and deceleration phases for GHR-type models are summarized in

Table 1. Estimation of GHR model parameters (adapted from Brackstone & McDonald [4]).

Source	m	l
Chandler et al. (1958)	0	0
Herman and Potts (1959)	0	1
Hoefs (1972) dcn no brk/dcn brk/acn	1.5/0.2/0.6	0.9/0.9/3.2
Treiterer and Myers (1974) dcn/acn	0.7/0.2	2.5/1.6
Ozaki (1993) dcn/acn	0.9/−0.2	1/0.2

Note: dcn: deceleration; acn: acceleration; brk: deceleration with brakes; no brk: deceleration without brakes.

. These values are used during the simulation of the NGSIM data.

(B)

The Intelligent Driver Model

Treiber, Hennecke, & Helbing [21] proposed a deterministic continuous CF model, named the Intelligent Driver Model (IDM), which belongs to Optimal Velocity Models (OVM). Bando et al. [22] and Treiber et al. [23] demonstrated that IDM is an accident-free model because of the dependency on the relative speed, while in the OVM models, accidents happen easily. IDM shows self-organized attributes, hysteresis results and accommodates complex states. Some of the benefits of the model are; it is easily quantifiable and has realistic parameter values; the mean fundamental diagrams can be easily calibrated; and the numerical simulation of the model is fast. Furthermore, in contrast to other CF models, a corresponding macroscopic model is available. IDM also eliminates the limitations of the Gipps CF model, which does not show instability or hysteresis effects for vanishing fluctuations. The IDM assumes that acceleration is a continuous function of the speed ${\mathrm{v}}_{\mathsf{\alpha }}$, the gap ${\mathrm{s}}_{\mathsf{\alpha }}$, and the speed difference (approach rate) $∆{\mathrm{v}}_{\mathsf{\alpha }}$ from the vehicle ahead. The IDM is presented in Equation (2).

$$\dot{{\mathrm{v}}_{\mathsf{\alpha }}}={\mathrm{a}}^{\left(\mathsf{\alpha }\right)}[1-{\left(\frac{{\mathrm{v}}_{\mathsf{\alpha }}}{{\mathrm{v}}_0^{\left(\mathsf{\alpha }\right)}}\right)}^{\mathsf{\delta }}-{\left(\frac{{\mathrm{s}}^{\ast }\left({\mathrm{v}}_{\mathsf{\alpha }},∆{\mathrm{v}}_{\mathsf{\alpha }}\right)}{{\mathrm{s}}_{\mathsf{\alpha }}}\right)}^2]$$

(2)

where:

${\mathrm{v}}_{\mathsf{\alpha }}:$ speed;

${\mathrm{s}}_{\mathsf{\alpha }}$: spacing;

${\mathrm{s}}^{\ast }$: desired minimum gap;

$∆{\mathrm{v}}_{\mathsf{\alpha }}:$ speed difference from the leader;

$\mathsf{\alpha }:$ each vehicle own characteristics;

$\mathrm{a}:$ maximum acceleration;

${\mathrm{v}}_0:$ desired speed.

Treiber et al. [23] state that ${\mathrm{a}}^{\left(\mathsf{\alpha }\right)}\left[1-{\left(\frac{{\mathrm{v}}_{\mathsf{\alpha }}}{{\mathrm{v}}_0^{\left(\mathsf{\alpha }\right)}}\right)}^{\mathsf{\delta }}\right]$ stands for the acceleration in a free flow situation $({\mathrm{s}}_{\mathsf{\alpha }}\to \infty )$. $\mathsf{\delta }$ is usually between 1 and 5. The $\mathsf{\delta }$ range causes the real acceleration behaviour place between a constant acceleration of $\mathrm{a}$ if $\left(\mathsf{\delta }\to \infty \right)$ and an exponential function $\left(\mathsf{\delta }=1\right)$. The tendency to deceleration in the IDM is shown in Equations (3) and (4).

$$-{\mathrm{b}}_{\mathrm{int}}\left({\mathrm{s}}_{\mathsf{\alpha }},{\mathrm{v}}_{\mathsf{\alpha }},∆{\mathrm{v}}_{\mathsf{\alpha }}\right)≔-{\mathrm{a}}^{\left(\mathsf{\alpha }\right)}{\left(\frac{{\mathrm{s}}^{\ast }}{{\mathrm{s}}_{\mathsf{\alpha }}}\right)}^2$$

(3)

$${\mathrm{s}}^{\ast }\left(\mathrm{v},∆\mathrm{v}\right)={\mathrm{s}}_0^{\left(\mathsf{\alpha }\right)}+{\mathrm{s}}_1^{\left(\mathsf{\alpha }\right)}\sqrt{\frac{\mathrm{v}}{{\mathrm{v}}_0^{\left(\mathsf{\alpha }\right)}}}+{\mathrm{T}}^{\mathsf{\alpha }}\mathrm{v}+\frac{\mathrm{v}∆\mathrm{v}}{2\sqrt{{\mathrm{a}}^{\left(\mathsf{\alpha }\right)}{\mathrm{b}}^{\left(\mathsf{\alpha }\right)}}}$$

(4)

where:

${\mathrm{s}}_0:$ minimum jam distance;

T: safe headway.

The braking term depends on the proportion of the “desired minimum gap” ${\mathrm{s}}^{\ast }$ and the real spacing ${\mathrm{s}}_{\mathsf{\alpha }}$. The “desired minimum gap” ${\mathrm{s}}^{\ast }$ changes according to the velocity and approach rate. In Equation (4), the driver maintains the ${\mathrm{s}}_0$ minimum jam distance and additional safety distance ${\mathrm{T}}^{\mathsf{\alpha }}\mathrm{v}$, where T is the safe headway within a congested moving traffic situation. The last term of Equation (3) is an “intelligent” breaking strategy where drivers limit themselves to a desired braking deceleration in normal circumstances (a vehicle approaching a standing vehicle from a long distance).

(C)

The Psychophysical Model (Wiedemann)

Psychophysical models presume that a driver does not respond until passing an action point. These models determine how drivers react to the perceived situation of distance and speed differences by adapting their driving behaviour [24]. As proposed by Wiedemann and Reiter [24], the perception of change for the follower driver in psychophysical models is the observed size of the vehicle ahead. The formulation is not detailed here (refer to details in Wiedemann & Reiter [24]). Todosiev [25] has conducted a comprehensive investigation on these perception thresholds.

The psychophysical model originated from Michaels and Cozan [26] who discussed CF behaviour in terms of a psychophysical aspect of follower vehicles and assumed that drivers can predict relative speed differences of a vehicle in front via changes in visual angle. This idea led the Karlsruhe Institute of Technology in Germany [27] to develop other simulation applications. The Wiedemann car-following model was proposed in 1974. Subsequently, some researchers, namely Kumamoto et al. [28], Burnham and Bekey [29], and Lee and Jones [30] have used similar models based on Wiedemann. In this research, we will use the formulations from Wiedemann & Reiter [24] in Section 6.1 to compare the TTC and headway performance across the five models.

(D)

The Gipps Model

Safety distance or collision avoidance models set up a safety distance in the Gipps model. The Gipps model [31] is successful in switching between free flow and following situations. The proposed speed is given in Equation (5). This model assumes the follower can estimate all parameters with the exception of ${\mathrm{b}}_{\mathrm{n}-1}$. The extra safety margin added to calculate a safe distance is named θ. Gipps assumed θ = T/2.

$$\begin{array}{ll}{\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}+\mathsf{\tau }\right)=& \min \{{\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)+2.5{\mathrm{a}}_{\mathrm{n}}\mathsf{\tau }\left(1-{\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)/{\mathrm{V}}_{\mathrm{n}}\right)\sqrt{\frac{0.025+{\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)}{{\mathrm{V}}_{\mathrm{n}}}}, \\ & {\mathrm{b}}_{\mathrm{n}}\mathsf{\tau }+\sqrt{{\mathrm{b}}_{\mathrm{n}}{}^2{\mathsf{\tau }}^2-{\mathrm{b}}_{\mathrm{n}}\left[2\right[{ \mathrm{x}}_{\mathrm{n}-1}\left(\mathrm{t}\right)-{\mathrm{s}}_{\mathrm{n}-1}-{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)\left]-{\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)\mathsf{\tau }-{\mathrm{v}}_{\mathrm{n}-1}{\left(\mathrm{t}\right)}^2/ \hat{\mathrm{b}}\right]}\}\end{array}$$

(5)

where:

${\mathrm{a}}_{\mathrm{n}}$: Maximum acceleration;

b_n: Maximum deceleration;

${\mathrm{s}}_{\mathrm{n}}$: vehicle size;

${\mathrm{V}}_{\mathrm{n}}$: Desired speed;

${\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)$: vehicle location $\mathrm{t}$;

${\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)$: the speed of vehicle n at time;

$\mathrm{t}$$\mathsf{\tau }$: the apparent reaction time;

$\hat{\mathrm{b}}:$ driver of vehicle n estimation about ${\mathrm{b}}_{\mathrm{n}-1}$.

(E)

The Cellular Automaton Model

Nagel & Schreckenberg [32] introduced a stochastic discrete cellular automaton model to simulate freeway traffic, the focus being traffic jams and a smooth transition between free flows and start-stop situations and modelling shockwaves. The discrete computational model defines an L-sited array which may be either occupied by one vehicle or empty. Each vehicle has an integer velocity between 0 to ${\mathsf{\nu }}_{\max }$. Any simulation update in the Nagel-Schreckenberg model includes the four following steps:

Acceleration: if velocity $\mathsf{\nu }$ < ${\mathsf{\nu }}_{\max }$ and $∆\mathrm{x}$ > $\mathsf{\nu }$ + I, then speed is progress by one $\mathsf{\nu }$  $\to$  $\mathsf{\nu }$ +1.

Slowing (due to other cars): if a vehicle at site $\mathrm{i}$ sees the next vehicle at site $\mathrm{i}+\mathrm{j}$ (with j < $\mathsf{\nu }$), it decreases velocity to $\mathrm{j}-1$.

Randomization: with likelihood p, the follower car’s speed, if greater than zero, declines by one $\mathsf{\nu }$ → $\mathsf{\nu }$ − 1.

Car motion: each vehicle advances v sites.

Krauss, Wagner, & Gawron [33] introduced the continuous model of the Nagel- Schreckenberg model which had velocity and space as continuous variables. The rules to update the state are as shown in Equation (6).

$$\begin{array}{c}{\mathrm{v}}_{\mathrm{des}}=\min \left[\mathrm{v}\left(\mathrm{t}\right)+{\mathrm{a}}_{\max },{\mathrm{v}}_{\max },{\mathrm{s}}_{\mathrm{gap}}\left(\mathrm{t}\right)\right],\\ \mathrm{v}\left(\mathrm{t}+1\right)=\max \left[0,{\mathrm{v}}_{\mathrm{des}}-{\mathsf{\sigma } \ast \mathrm{n}}_{\mathrm{ran},0,1}\right],\\ \mathrm{x}\left(\mathrm{t}+1\right)=\mathrm{x}\left(\mathrm{t}\right)+ \mathrm{v}\left(\mathrm{t}+1\right)\end{array}$$

(6)

where:

${\mathrm{s}}_{\mathrm{gap}}\left(\mathrm{t}\right):$ spacing;

${\mathrm{a}}_{\max }:$ maximum acceleration;

${\mathrm{n}}_{\mathrm{ran},0,1}:$ random number between 0 and 1;

$\mathsf{\sigma }$: maximum deceleration due to noise.

3. Space-Based Model (SBM) Development

The SBM is designed to make microscopic simulation able to evaluate safety impacts after application of an intelligent transportation system such as VSL. The model allows the modeller to track the effects of any calibration parameter on the CF behaviour. The model parameters correspond to the actual driver behaviour element.Although the model targets individual driver metrics such as headway, it can also reproduce the macroscopic traffic flow metrics such as average volume and average speed. Therefore, the fundamental traffic diagrams can also be reproduced. Finally, the model takes a shorter time to complete simulation.

The SBM uses the concept of human personal space as the region surrounding a person which they regard as psychologically theirs [34]. Humans feel comfort or discomfort according to the space in which they are situated. This space could be at rest or in motion. The assumption in this model is that a driver has a similar space when driving and that a driver has a spatial understanding of the vehicle’s external representation, and, consequently, it introduces driver-vehicle personal space.

In addition to the driver-vehicle personal space, SBM is based on the notion of group movement to model a platoon of vehicles. For this, fish or birds’ movement in a school or group has inspired the modelling of a platoon of driver-vehicles. The idea for the SBM presented in this research is from the simulation of schools of fish [35,36] and also, as previously described, the concept of driver-vehicle personal space. The proposed CF model assumes three behaviour patterns, based on the space between drivers, (1) attraction, (2) parallel adaptation, and (3) repulsion.

In the SBM, the space between leader and follower is divided into three zones. If vehicles are too close, the leader vehicle is in the repulsion zone and will decelerate. When vehicles are further apart, the driver is in the parallel adaptation zone, where the driver mimics his leader’s speed. Finally, after the parallel adaptation zone, the driver will try to catch up with the leader and therefore accelerate.

In other words, under a certain short distance the driver feels unsafe and tries to avoid a collision. This threshold is called repulsion distance (${\mathrm{D}}_{\mathrm{rep}}$). In further distances, the driver tries to achieve a similar speed to the leader car to keep moving in harmony with the rest of the platoon. The maximum distance a driver attempts to drive with a similar velocity as the leader is called parallel adaptation distance (${\mathrm{D}}_{\mathrm{par}}$). Beyond the parallel adaptation distance, the driver feels far from the leader and tries to catch-up again with the leader or driver with desired speed. The zoning in the SBM is shown in Figure 1.

The formulation of the SBM is as follows. Firstly, the definitions of the zoning thresholds (Repulsion and Parallel adaptation) are shown in Equation (7).

$$\begin{array}{c}{\mathrm{D}}_{\mathrm{rep}}=\left(\frac{{\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)}{2.5+0.1{ \ast \mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)}\right){ \ast \mathrm{s}}_{\mathrm{n}}+{ \mathrm{D}}_{\mathrm{jam}}+{\mathsf{\sigma }}_{\mathrm{n}}\\ {\mathrm{D}}_{\mathrm{par}}={ \mathsf{\gamma } \ast \mathrm{D}}_{\mathrm{rep}} \end{array}$$

(7)

where:

${\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)$: speed of vehicle n at time t;

${\mathrm{D}}_{\mathrm{rep}}$: Repulsion threshold;

${\mathrm{D}}_{\mathrm{par}}$: Parallel adaptation threshold;

$\mathsf{\gamma }:$ The calibration parameters;

${\mathrm{s}}_{\mathrm{n}}$: Length of vehicle n (follower vehicle);

${\mathsf{\sigma }}_{\mathrm{n}}$: A normal random number for vehicle $\mathrm{n}$;

${ \mathrm{D}}_{\mathrm{jam}}$: Spacing in stop condition.

Equation (7) plays an important role in the behaviour of the SBM. Repulsion distance is defined as multiples of vehicle length and speed. However, as we know that when vehicles travel at higher speeds, they drive closer with a shorter headway. Therefore, $0.1{ \ast \mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)$ included in $\left(\frac{{\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)}{2.5+0.1{ \ast \mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)}\right){ \ast \mathrm{s}}_{\mathrm{n}}$, to apply such effect. When speed increases, the repulsion distance increases at a slower rate and so we can expect shorter headways at higher speeds. ${\mathrm{D}}_{\mathrm{jam}}$ is defined as a distance that stopped vehicles consider to be theirs. Finally, ${\mathsf{\sigma }}_{\mathrm{n}}$ represents the distribution within the population. After defining the repulsion zone, the parallel adaptation distance ${\mathrm{D}}_{\mathrm{par}}$ is simply defined as a multiple of repulsion distance. In our experiments, we determined that a value of 2 is an appropriate value for $\mathsf{\gamma }$ based on our observation from the NGSIM data.

According to the defined zones, the driver determines speed in the next simulation time step according to the following Equations (8)–(10).

$$\begin{array}{c}\mathrm{Repulsion} (∆{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)<{\mathrm{D}}_{\mathrm{rep}}{ \mathrm{and} \mathrm{v}}_{\mathrm{n}-1}\left(\mathrm{t}\right)\ne 0):\\ {\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}+∆\mathrm{t}\right)={\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)+{\mathrm{D}}_{\mathrm{diff}}/\left(\mathsf{\phi }\times \left(∆\mathrm{t}\right)\right)+{\mathsf{\sigma }}_{\mathrm{n}}\left(0,0.05\right)\end{array}$$

(8)

$$\begin{array}{c}\mathrm{St}. {\mathrm{D}}_{\mathrm{diff}}=∆{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)-{\mathrm{D}}_{\mathrm{rep}}\\ \mathsf{\phi }=\{\begin{array}{c}\mathrm{if} ∆{\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)>\left(\frac{∆{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)}{2\times {\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)}\right) 1 \\ \mathrm{else} 2.4\end{array}\\ \mathrm{Parallel} \mathrm{adaptation} ({\mathrm{D}}_{\mathrm{rep}}<∆{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)<{\mathrm{D}}_{\mathrm{par}}):\\ {\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}+∆\mathrm{t}\right)={\mathrm{v}}_{\mathrm{n}-1}\left(\mathrm{t}\right){ \ast \mathsf{\sigma }}_{\mathrm{n}}\left(0.1,{ \mathrm{v}}_{\mathrm{n}-1}\left(\mathrm{t}\right)/{\mathrm{V}}_{\mathrm{n}}\right)\end{array}$$

(9)

$$\begin{array}{c}\mathrm{Attraction} (∆{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)>{\mathrm{D}}_{\mathrm{par}}):\\ {\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}+∆\mathrm{t}\right)=\min ({\mathrm{V}}_{\mathrm{n}},{\mathrm{v}}_{\mathrm{n}}^{\mathrm{f}}\left(\mathrm{t}\right),({\mathrm{v}}_{\mathrm{n}-1}\left(\mathrm{t}\right) \ast ∆{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)/{\mathrm{s}}_{\mathrm{n}}))\\ \mathrm{St}. {\mathrm{v}}_{\mathrm{n}}^{\mathrm{f}}\left(\mathrm{t}\right)={\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)+{\mathrm{a}}_{\mathrm{n}} \ast ∆\mathrm{t}\end{array}$$

(10)

where:

${\mathrm{D}}_{\mathrm{diff}}:$ differentiation of vehicle’s spacing $∆{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)$ with repulsion distance;

$\mathsf{\phi }$: parameter to change the reaction of driver between pure and tolerated repulsion;

$∆\mathrm{t}$: apparent reaction time, a constant for all vehicles and equal to simulation step;

$∆{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right):$ spacing between follower and leader vehicle;

$∆{\mathrm{v}}_{\mathrm{n}}\left(\mathrm{t}\right)$: speed difference between follower and leader vehicle;

${\mathrm{a}}_{\mathrm{n}}$: maximum acceleration the driver of vehicle n wishes to undertake;

${\mathrm{V}}_{\mathrm{n}}$: speed at which the driver of vehicle n wishes to travel;

${\mathrm{v}}_{\mathrm{n}}^{\mathrm{f}}\left(\mathrm{t}\right):$ feasible speed for vehicle n according to an and current speed.

Equation (8) is also important in defining the SBM performance. In this equation, ${\mathrm{D}}_{\mathrm{diff}}$ determines how close the vehicle is to its leader than the repulsion distance. Therefore, for example if ${\mathrm{D}}_{\mathrm{rep}}$ is 30 m and current spacing is 25 m, then ${\mathrm{D}}_{\mathrm{diff}}$ will be −5. Therefore ${\mathrm{D}}_{\mathrm{diff}}$ is a negative value which causes a speed reduction of the follower vehicle. ${\mathrm{D}}_{\mathrm{diff}}$ is placed in the follower vehicle speed formulation and it is divided by $\mathsf{\phi }\times \left(∆\mathrm{t}\right)$ where, $\mathsf{\phi }$ determines how sharply the vehicle should decelerate. In this expression, the model will smartly consider the speed differences with the leader. If the driver did not perceive a considerable speed difference with the leader, $\mathsf{\phi }$ is a high value of 2.4, otherwise it is 1. This $\mathsf{\phi }$ allows the model to appropriately experience short TTC and headways. Having ${\mathrm{D}}_{\mathrm{diff}}$ divided by $∆\mathrm{t}$, causes the speed formulation, independent from the simulation step. The proposed speed for the next simulation step will be appropriate according to the simulation step of any experiment. In Equation (8), there is also a population distribution term of ${\mathsf{\sigma }}_{\mathrm{n}}\left(0, 0.05\right)$.

Equation (9) defines the speed when the vehicle is in the parallel adaptation zone. In this equation speed will be simply the leader’s speed with a random variation value. However, the random number is chosen from a distribution depending on the portion of vehicle speed to the desired speed in order to make the random number value appropriate to the absolute speed magnitude.

Equation (10) determines the speed in the attraction zone. The driver wants to catch up with the desired speed. The speed is the minimum of desired speed ${\mathrm{V}}_{\mathrm{n}}$, feasible speed ${\mathrm{v}}_{\mathrm{n}}^{\mathrm{f}}\left(\mathrm{t}\right)$ according to the desired acceleration and also a portion of its leader speed. The last term in this equation, $({\mathrm{v}}_{\mathrm{n}-1}\left(\mathrm{t}\right) \ast ∆{\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)/{\mathrm{s}}_{\mathrm{n}}))$ is to keep the model stable according to the leader speed, and spacing when the leader speed is too low. When the remaining spacing is not sufficient to let the follower car drive with its own desired speed, this third term is the deterministic term. The advantages of employing the SBM are that it is self-organized and any perturbation in the leader trajectory will be managed. It specifically performs better for more precise detailed traffic metrics such as headways and time-to-collision and other safety-related indicators such as speed deviation. The SBM is easy to calibrate for safety metrics because of its simple structure. Since the SBM divides the driving phases into three, it is relatively easy to conduct a more focused calibration. For example, if the focus is short distance measures, then the focus should be on the repulsion zone.

4. Model Calibration and Comparison Methodology

4.1. Data Selection and Preparation

For the purpose of model calibration, testing and validation of NGSIM data has been used. The NGSIM program collected comprehensive vehicle trajectory information on a series of motorways including US 101, the Hollywood Motorway, southbound in Los Angeles, CA, USA, on 15 June 2005. The area covered roughly 640 m and included five mainline lanes and around 3000 vehicles over 15 min of data, from 7:50 to 8:05 a.m. The major focus of this analysis is CF and therefore among all the available trajectories, those trajectories where either themselves or their leader experienced lane changes have been excluded using computer codes developed in MATLAB.

4.2. Safety Indicators Selection

A comprehensive review of the different types of safety indicators (surrogate safety measures) have been explored, and further details can be found in [37]. The most common type of motorway crashes are rear-end crashes. As rear-end crashes are of interest in this research, and in order to assess safety in microscopic simulation models, TTC and short following headways are preferred, which directly show the rear-end safety risks.

The safety indicators in this study are headway = $\frac{∆\mathrm{x}}{\mathrm{v}}$ and TTC = $\frac{∆\mathrm{x}}{∆\mathrm{v}}$. It is important to understand the relationship between the two indicators. Headway is the change in distance over speed $\frac{∆\mathrm{x}}{\mathrm{v}}$ and TTC is the change in distance over change in speed $\frac{∆\mathrm{x}}{∆\mathrm{v}}$. Generally, short headways occur more frequently than short TTCs. Short headway does not necessarily end in a crash, because it must happen simultaneously with instability in the traffic where drivers cannot react in time. On the other hand, TTC only applies when the follower vehicle speed is higher than the leader. TTC includes both a short headway and an instability. That means a short headway eventually needs to end in a short TTC to cause any serious risk. Therefore, short headways can show a potential risk of a crash in case of any instability, while TTC shows a current risk of crash that is occurring. Therefore, a CF model that can present both indicators with a higher level of accuracy is a more robust model for safety analysis.

4.3. Models Calibration and Evaluation

To compare the performances of the models, each model needs to be calibrated and its specific parameters to be optimised. For the optimization of each of the models, the sum of UTheil’s Inequality Coefficient is used as the objective function to be minimized. This coefficient is a statistical measure that compares the estimated values to the observed. Hourdakis et al. [38] stated that UTheil’s Inequality is more sensitive and accurate than goodness-of-fit measures. Similarly, Xin et al. [39] used Theil’s Inequality Coefficient for the calibration of their CF model. Some research also simultaneously calibrates speed and space [40]. In this study, the speed and spacing are simultaneously calibrated to gain optimum reproduced headways (see Equation (11)).

$${\mathsf{\epsilon }}_{\mathrm{model}}=\frac{\sqrt{\frac{1}{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{v}}_{\mathrm{obsv}}^{\mathrm{i}}-{\mathrm{v}}_{\mathrm{sim}}^{\mathrm{i}}\right)}^2}}{\sqrt{\frac{1}{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{v}}_{\mathrm{obsv}}^{\mathrm{i}}{}^2}+\sqrt{\frac{1}{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{v}}_{\mathrm{sim}}^{\mathrm{i}}{}^2}}+\frac{\sqrt{\frac{1}{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{x}}_{\mathrm{obsv}}^{\mathrm{i}}-{\mathrm{x}}_{\mathrm{sim}}^{\mathrm{i}}\right)}^2}}{\sqrt{\frac{1}{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{obsv}}^{\mathrm{i}}{}^2}+\sqrt{\frac{1}{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{sim}}^{\mathrm{i}}{}^2}}$$

(11)

where:

${\mathrm{v}}_{\mathrm{obsv}}:$ Observed speed;

${\mathrm{v}}_{\mathrm{sim}}:$ Simulated speed;

${\mathrm{x}}_{\mathrm{obsv}}:$ Observed spacing;

${\mathrm{x}}_{\mathrm{sim}}:$ Simulated spacing;

$\mathrm{n}$: Number of observations.

Next, a Genetic Algorithm (GA) is implemented to minimize the objective function for each trajectory and to calibrate CF model parameters. This is done by developing MATLAB codes to optimise each of the CF models by running them against all the NGSIM trajectories of the leader and the follower cars. To do this, the follower and leader locations are reset to the actual position and then by taking the leader’s trajectory and applying different CF models, simulation is carried out to simulate the follower car.

5. SBM Testing Results

5.1. Simulation Results of SBM Based on One Pair of Cars

Figure 2a,b illustrates a trajectory of a pair of following vehicles, simulated using the SBM CF and Gipps CF models. The trajectories are from the NGSIM data, which shows that, while the SBM is stable and no collision occurs, it is able to create short headways and TTCs close to the actual trajectory. The noticeable characteristic in the speed profile in Figure 2a is that the Gipps-modelled follower is closely following the leader car profile and any small movement of the leader vehicle will be exactly emulated which may not necessarily occur in real life. The SBM speed profile varies more freely and closer to the behaviour of the observed following vehicle. In Figure 2b, the SBM is also more successful in mimicking the shorter headways than the Gipps model. In Figure 2b, the numbers of TTC events are also illustrated. The frequency of TTC events below 3 s in the SBM is equal to the observed data while the calibrated Gipps model does not have any TTC below 3 s.

5.2. Simulation Results of SBM Traffic Flow Measures

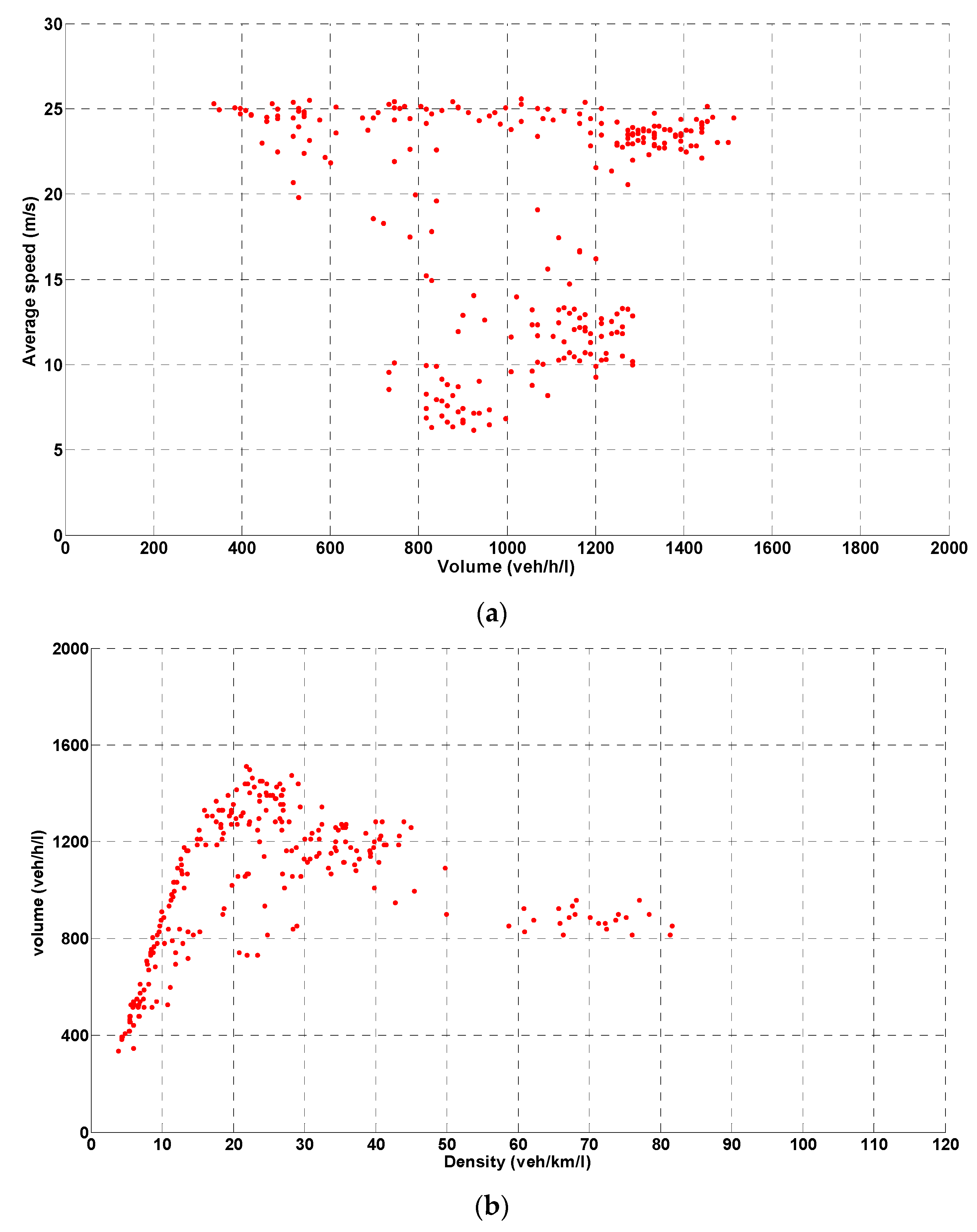
After testing the SBM for a single following vehicle, it is necessary to test the ability of the SBM to create the traffic flow. A random vehicle generator and the SBM CF were coded in MATLAB, and a single straight traffic lane was simulated. Figure 3a,b illustrates the speed-flow and flow-density diagrams respectively from the simulation using the SBM. The range of volume gradually increased from 500 to 2300 veh/h. Simulated detectors were created along the road in a certain cross section of the lane to measure average speed, volume and density of every 5 min of traffic flow data.

6. Performance Comparison of SBM with Other Selected CF Models

Table 2. Calibrated Parameter Values for Various Models.

GHR		IDM		Wiedemann		Gipps		CA		SBM
Parameter	value	Parameter	value	Parameter	value	Parameter	value	Parameter	value	Parameter	value
Constant C	1.1	Tsafe	1.12	AXadd	1.3	an	3.06	amax	3	${\mathrm{V}}_{\mathrm{n}}$	24.94
l Dec	1.2	$\mathsf{\alpha }$	3.00	AXmult	2.19	T	0.7	vmax	20	${\mathrm{a}}_{\mathrm{n}}$	2.75
m Dec	0.7	amax	1.48	BXadd	2.39	bn	−5.01	σ	3	$\mathsf{\gamma }$	2
l Acc	0.1	bDes	1.5	BXmult	1.32	B	−6.44
m Acc	0	S1	0.67	CX	42.77	θ	0.48
		S0	2.13	EXadd	1.16
		Vdes	25.03	EXmult	0.59
				OPDVadd	1.034
				OPDVmult	1.25

shows the calibrated parameters for each CF model using the NGSIM data. After the calibration process, simulation of the NGSIM trajectories was run with MATLAB for each model using the parameters in Table 2. Most models contained stochastic parameters randomly drawn from a distribution.

Each model was run with 30 iterations and their average results used for model comparison. The stochastic terms for each model are set as recommended by their developers. All random numbers were drawn from a normal distribution with mean values from the calibration phase. In IDM, these stochastic terms included: desired speed, maximum desired acceleration, desired deceleration rate, and safe headway; in Wiedemann: desired speed, NRND, RND1, RND2, and RND3, which indicate the randomness of driver differences in the psychophysical model [24]. In the Gipps model: desired speed, maximum desired acceleration, and desired deceleration rate. In CA model: desired speed, maximum desired acceleration and ${\mathrm{n}}_{\mathrm{ran},0,1}$ in the model structure. The GHR model is proposed mostly as a deterministic model and model designers did not introduce any stochastic parameters in the model structure. This is the only model that does not need to run multiple times and only its optimum result is compared with the rest of the models.

Two important measures were calculated to compare models’ performances: firstly, the frequency of the critical safety events in the total simulation experiment. Although the magnitude of safety indicators can show the severity of an event, the frequency of risky events is as important. Minderhoud and Bovy [41] reported from the literature several values for critical time-to-collision, namely 5, 4, 3.5, or 3 s. On the other hand, a short headway or tailgating phenomenon where a driver follows its leader with a shorter headway time than his or her own reaction time is an appropriate measure for evaluating safety on motorways. Driver reaction time is reported to vary between drivers from less than one second to about two seconds [42]. In this research, we have headways less than 1 s as the short headways and risky events. Therefore, according to the literature, TTC values of less than 3 s and headways less than 1 s are chosen as the critical events.

Secondly, the error in estimation of space, speed, acceleration, and headway in every simulation step was investigated. For example, the headway RMSE is the average of the error between the real follower car and simulated vehicle in every deci-second of simulation of all the simulated trajectory pairs. The RMSE is the square root of the variance of the residuals in Equation (12).

$$\mathrm{RMSE}=\sqrt{\frac{1}{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\left(\frac{{\mathrm{x}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{i}}}{{\mathrm{y}}_{\mathrm{i}}}\right)}^2}$$

(12)

where:

${\mathrm{x}}_{\mathrm{i}}$: Simulated value;

${\mathrm{y}}_{\mathrm{i}}$: Real value at time $\mathrm{i}$;

$\mathrm{n}$: Number of observations.

6.1. TTC and Headway Results

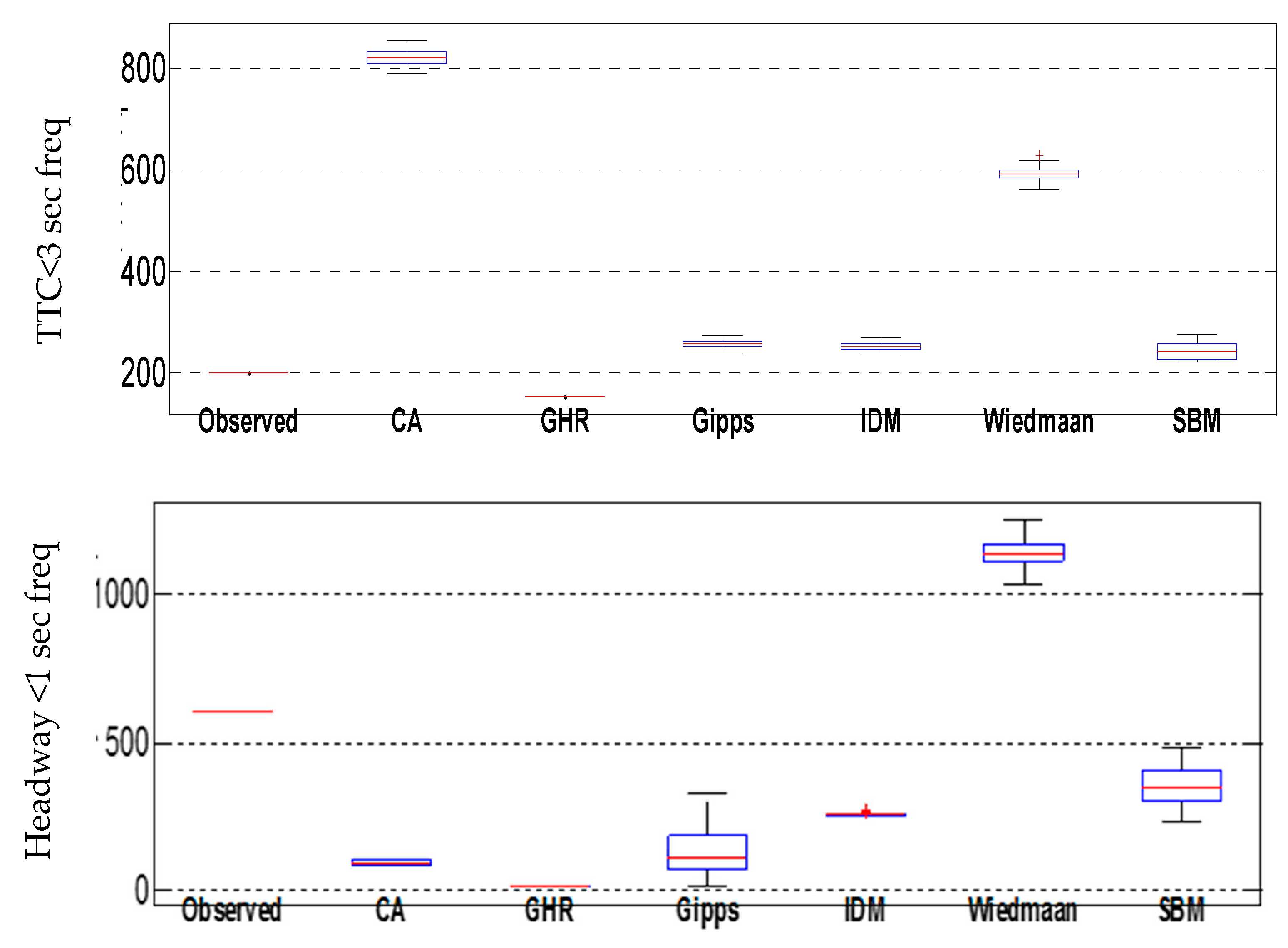
The results given in

Table 3. t-Test results for each CF model’s critical number of TTCs against observed, significance level 95%.

	TTC Freq < 3 s			Headway Freq < 1 s
CF model	−0.05%	Mean	+0.05%	−0.05%	Mean	0.05%
‘CA’	−628.11	−619.43	−610.75	477.91	511.46	545.01
‘GHR’	39.31	48	56.68	555.44	589	622.55
‘Gipps’	−63.54	−54.86	−46.18	450.08	483.63	517.18
‘IDM’	−59.74	−51.06	−42.38	314.94	348.5	382.05
‘Wiedemann’	−398.78	−390.1	−381.41	−567.95	−534.4	−500.84
‘SBM’	−49.88	−41.2	−32.51	211.44	245	278.55

represent the mean of observed data minus the mean of each CF model, both critical TTC and headways. From Table 3, the t-test results show that for both critical TTC and headways, the SBM model has the minimum difference with the observed data, and is significantly better in comparison with the other models. To illustrate, the mean of TTCs < 3 s in the observed data minus the mean of the critical TTCs in the SBM is estimated to be −41.2, and a 95% confidence interval for the difference of the means is [−49.88, −32.51], in comparison with the CA model, which is estimated to be −619.43, and [−628.11, −610.75].

Figure 4 presents the frequency of TTC and short headways against observed data. The closest frequency to the observed is the best predicting model. As seen from Figure 4, SBM has the closest reproduction of safety indicators of frequency of short TTC events (<3 s) and short headway (<1 s) events. The main purpose of this research is the simulation of the risky events frequency while other general metric predictions stay in an acceptable range. After SBM, the Gipps model is the next closest with 70% of the observed short TTCs. For short headways, IDM, with 40% of observed short headways, is the second-best model. The results also imply that GHR, Gipps and IDM models are too safety cautious because of the safety assumptions in their model that prevent them from acquiring realistic safety indicator frequencies. On the other hand, in terms of short TTC frequency, CA and Wiedemann models are 600 and 300 more than the actual observed data of 200 respectively.

The above analysis compares the capabilities of the mainstream car-following models emulating driver behaviour within precise parameters such as headways and time-to-collisions. The above shows that SBM can offer more confidence in using microscopic simulation models to evaluate the impact of different traffic scenarios in terms of their safety improvement impact, particularly frequency of short TTCs and short headways.

6.2. Model Validation

For the validation of SBM, a separate dataset of the NGSIM data from another location on a segment of Interstate 80 located in Emeryville, CA, USA on 13 April 2005, was utilized. To choose the trajectories according to our requirements, out of 45 min of data, we chose 4:00 to 4:15 p.m., which included different speed regimes. Only vehicle trajectory pairs which did not experience lane changes were selected. The simulation for the 724 trajectory pairs was conducted and the frequency of the short TTC and error in the headway reproduction was measured. The simulations were carried out in thirty iterations for all the datasets and then the overall average outcome was used for comparison. At thirty iterations, the results were optimized.

The simulation results in Figure 5 illustrate that even for this new set of data of the motorway, the SBM is the most robust CF model amongst the CF models in TTC and short headway frequency reproduction. The headway prediction in Figure 5 is almost as accurate as the CA and the Gipps model, and with 95% level of confidence, no model significantly reproduces more accurate headways than SBM.

7. SBM Application for Safety Evaluation of VSL

It is currently not straightforward for traffic authorities to determine whether the application of a VSL system or a ramp metering (RM) system improves safety and if this improvement is significant. Therefore, there is a clear demand to have a micro simulation model which reflects the estimated changes in traffic measures after employing a managed motorway system such as VSL or RM.

Unfortunately, no detailed traffic data were available before and after the application of a VSL at the time of this study, so it is unclear how traffic measures will change. For instance, changes in headway distribution are unknown after the application of VSL systems in motorways. This lack of data inhibits modelers to know how they should model the effect of a VSL on a motorway. Although decreasing speed can be a measure of less severe crashes, other important safety measures such as short headways and TTCs among vehicles are equally as important.

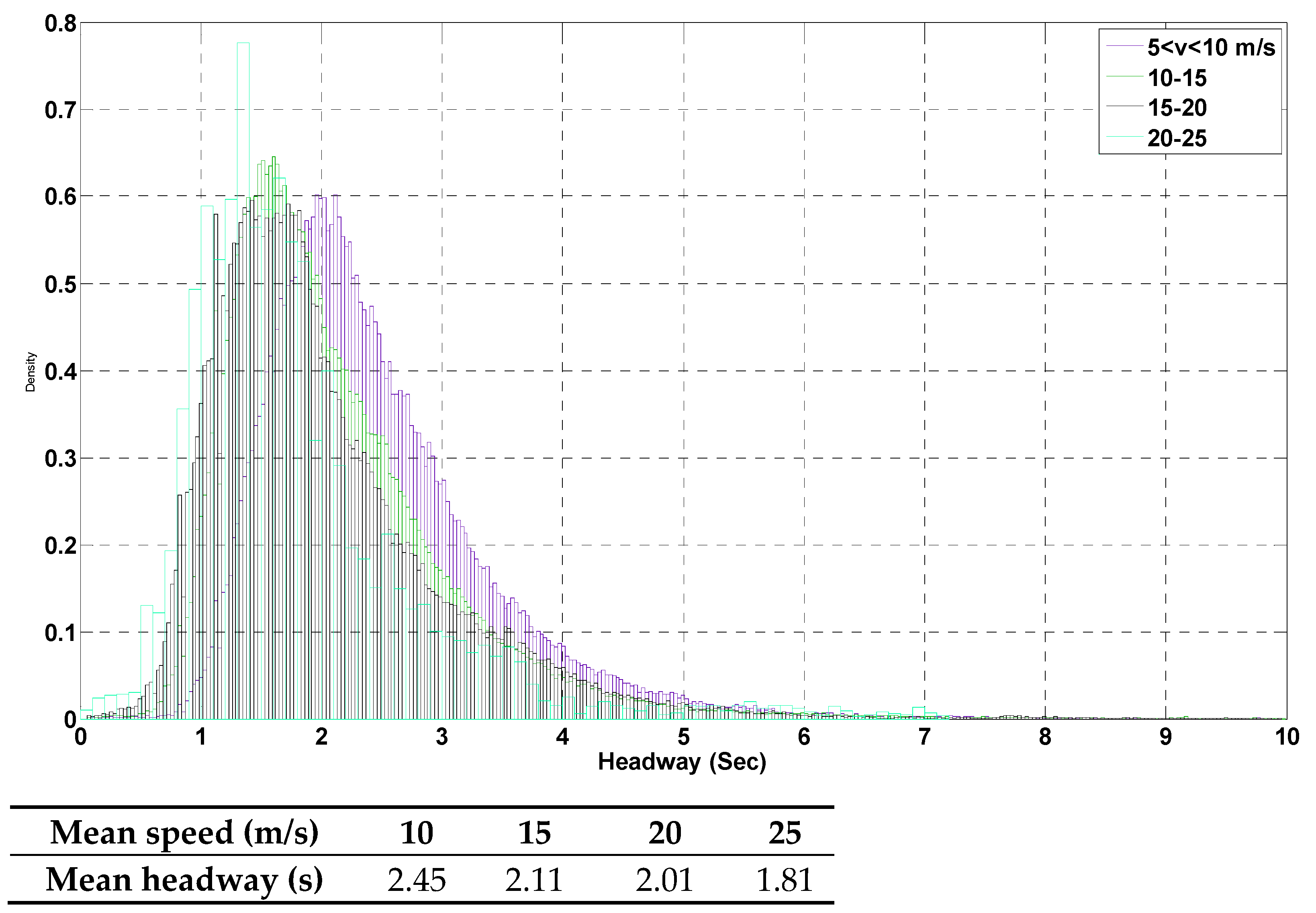
To overcome the lack of VSL data, some measures such as headways in different speed ranges can be extracted from the NGSIM data. The assumption therefore is that drivers have similar headways and TTCs, in specific ranges of speeds, regardless of whether this speed is the result of imposed speed by a VSL system. The NGSIM data is then explored in different ranges of speed. Figure 6 illustrates how headway distribution will change according to driver speed ranges. In conclusion, it is expected that once a VSL system imposes a speed limit a similar shift can be seen in traffic distributions. This fact has also been found by other researchers [43,44,45]. Minderhoud & Hansen [45] similarly found that as traffic speed increases, the average headway decreases. Therefore, it is expected that once a VSL system imposes a speed limit, a similar shift can be seen in the headway distribution. Figure 6 shows the shift in headway distribution in the observed data. The higher the speed range, the shorter the headway the driver will take. We chose relatively small speed segments of 5 m/s in order to mitigate the transitional phase error. As at the time of this research there was no access to VSL data, we were unable to track the speed transition phase of drivers. In real life, drivers need time to adjust their speed. However, Figure 6 illustrates that the headway distribution of the SBM simulation shifts due to speed changes as a result of traffic simulation flow, not VSL application. Figure 6 shows that headway distribution is affected by traffic flow average speed, as in the observed data (NGSIM).

7.1. Headway Distribution Comparison in the Aimsun Model and SBM

In the next stage of the research, it is necessary to have all complete packages of the other behavioural models such as the lane changing model simultaneously working along with the SBM CF model. Aimsun [46] provides such a platform. Moreover, Lee and Peng [47] stated that the Gipps CF model presents driver behaviour better than the other CF models. Aimsun also uses the Gipps CF model. A comparison of the headway distribution with a calibrated Aimsun motorway simulation model in Brisbane [14,48,49] was used for experiments in this next stage of the research.

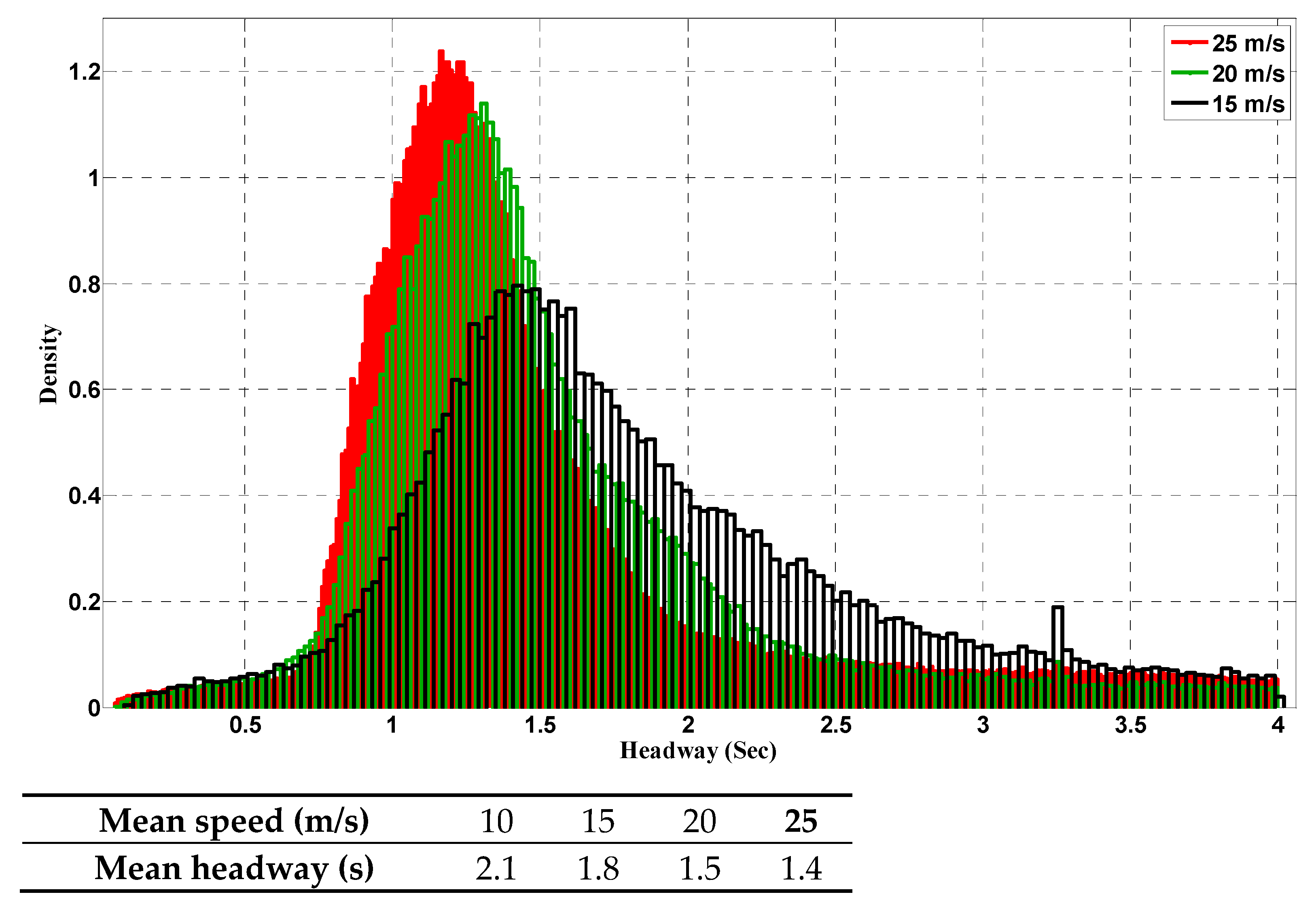
The Pacific Motorway was simulated in Aimsun (a version the Gipps CF model), and the headway distributions were acquired for different ranges of speed. Figure 7 shows headway distribution from the Gipps model for different ranges of speed. By decreasing speed, headway in the Aimsun model will not increase, and this follows almost the same distribution. This indicates that the Gipps model is not sensitive to the speed change and cannot emulate driver behaviour change as a result of speed. This indicates that the Aimsun and Gipps models are not suitable ones for the simulation of the safety effect of VSL systems.

The Space Based Model (SBM) was then selected to examine its ability to evaluate VSL. The SBM car-following was written in C++ codes and plugged into Aimsun using a Software Development Kit and substituted the Gipps CF model in Aimsun. The Aimsun CF model is a variation of the Gipps CF model. The experiments from now on use the simulated motorway in Brisbane that has three lanes on each side. By replacing the SBM car-following model in the Aimsun software, all the Aimsun behavioural models, including the lane changing model, remained the same and only the CF was replaced by the SBM. Therefore, the experiments were not only restricted to the CF model, and in the simulated three-lane motorway platform, lane changing still occurs naturally, as we had only intervened in the CF model by replacing the default CF model with the SBM. As a result, since the lane changing still occurs, the future experiments on VSL application on the motorways remain appropriate.

The SBM should be able to reflect changes in safety indicators according to speed limits imposed by VSL. The main focus though should be on the repulsion zone. One of the advantages of this model is that analyzing behaviour is more focused and easier as it has different driving zones. Since the term ${\mathrm{D}}_{\mathrm{rep}}$ is dependent on the speed of the vehicle, it is expected that the discussed shift in real data headway distribution can be seen.

Headways are slightly higher for lower speeds, as in real life. This is because at lower speeds the driver has more control over their speed and the headway they have. Figure 8 shows how headways shifted in the SBM to a higher value once the speed decreased, so this change was expected, as discussed above. Therefore, the SBM can be a more appropriate CF model to make microscopic simulation models useful for the evaluation of ITS in motorways.

7.2. The SBM Applicability for VSL Evaluation Experiment

VSL application, particularly for incident management, has increasingly gained importance for improving safety on motorways. The appropriate definition of an incident within the VSL design context could be any event that causes queues and congestion. The VSL algorithm responsible for reducing speed at the time of queue occurrence (as a result of incident or congestion) is called the queue protection (QP) algorithm. Figure 9 shows the schematic queue protection algorithm. The algorithm uses both occupancy and speed thresholds from loop detectors to identify queues. It also employs consecutive interval and consecutive detector stations to reduce false alarms. The state of the detectors can be either ‘in queue’ or ‘not in queue’ (based on predetermined thresholds).

In every calculation interval, there are three stages for determining new speed limits:

• Queue detection: update the state of all detector sites (DS) and decide if there is a queue;
• Queue information update: update queue information if there is any;
• Queue protection: set new speed limit in the queue area.

As the SBM can appropriately vary headways according to a vehicle’s speed, it can provide the right platform for testing the effectiveness of a VSL. An incident in a microscopic simulation model of the Pacific Motorway was created where two lanes were blocked. A morning peak was simulated between 6:45 and 7:00 a.m. and an incident was created at 6:50 a.m. which continued for 7 min. Figure 10 illustrates the Aimsun network running the simulation and shows the crash characteristics. The vehicle trajectories are collected and analyzed right before encountering the crash from Aimsun using an API.

Two scenarios were simulated for both the Gipps and SBM, both with and without VSL systems for the queue protection (QP) algorithm. Figure 11a shows that the Gipps model is not sensitive to the application of the VSL, and as a result cannot be used for evaluating intelligent transportation systems such as VSL. The mean TTC values for both scenarios are almost the same. The short headway frequencies have only decreased by 15% after the application of VSL.

The simulation scenarios are repeated using the SBM CF model. The box plots in Figure 11b illustrate that the SBM shows more sensitivity to the application of the VSL, and therefore can be used for the QP algorithm of the VSL system. The short headway frequencies have substantially decreased by 61% after the application of VSL. Figure 11b also illustrates that applying the VSL to protect the tail of the queue increases the mean TTC of the vehicles and shifts them to higher values. The reason for higher sensitivity of the SBM (as it is discussed in the model’s description), is that the reproduced headway depends on the driver’s speed and therefore SBM is able to reflect the driver following maneuvers more realistically.

For validation of the experiments,

Table 4. Average travel time and average speed in the section that incident occurs.

	Gipps		SBM
	No QP	QP	No QP	QP
Speed (Km/h)	72	72	68	64
Travel Time (s)	106	111	122	127

illustrates that there is no significant difference between the changes in average travel time and average speed in the simulated motorway section. Average speed is slightly lower in the SBM, and therefore it produces slightly higher travel times. Despite these slight differences between the results from the two car-following models, the SBM is much more sensitive than the Gipps model to the application of VSL in reproduction of the TTCs and Headways.

8. Conclusions

This paper has proposed an innovative CF model based on personal space and fish school modelling called the Space Based Model (SBM). SBM explains human behaviour during driving and is able to produce more accurate safety metrics for safety studies. The simulation results demonstrate that the SBM has the most robust results in terms of replication of safety metrics (that is more realistic TTCs and headways’ frequencies) for vehicles in comparison with other mainstream CF models. SBM provides the analysis of CF at a micro-level and can be applied to further understand driver behaviour. In addition, the model is simple; it allows the modeler to track the effects of any calibration on the CF parameter. The SBM is easy to calibrate for safety metrics because of its simple structure. Since SBM divides the driving phases into three, it is comparatively easy to conduct a more focused calibration.

Finally, the SBM has been applied in the safety evaluation of managed motorway systems, and the results compared with the Gipps model. For this purpose, Aimsun microscopic software was used as the testing platform, and a VSL system for queue protection was simulated for a motorway in Brisbane, Queensland, Australia. A before and after evaluation showed that the headway and TTC distribution of the proposed SBM made the simulation model sensitive to the application of the VSL, whereas the Gipps model did not. The responsiveness of the headway distribution and TTC frequency to the changes in the speed limit is similar to that found in the real world. The SBM is able to reflect the shift and changes in the headway distribution after imposing the speed limit from the VSL system, while the Gipps model could not. Further research can be conducted on other managed motorway systems such as ramp metering or lane management systems.

These research findings facilitate assessing and predicting intelligent transportation system effects on motorways using microscopic simulation. This new model is capable of reflecting changes in the headway and TTC distribution after imposing the speed limit from VSL systems, and can be applied to any other safety interventions in motorway systems.

In terms of limitations to the research, factors and parameters that can affect driver longitudinal driving behaviour are not considered, such as other vehicles in the neighbor lines or second or third leader vehicles.