From Exponential to Efficient: A Novel Matrix-Based Framework for Scalable Medical Diagnosis

Abstract

Modern diagnostic systems face computational challenges when processing exponential disease-symptom combinations, with traditional approaches requiring up to $2^n$ evaluations for n symptoms. This paper presents MARS (Matrix-Accelerated Reasoning System), a diagnostic framework combining Case-Based Reasoning with matrix representations and intelligent filtering to address these limitations. The approach encodes disease-symptom relationships as matrices enabling parallel processing, implements adaptive rule-based filtering to prioritize relevant cases, and features automatic rule generation with continuous learning through a dynamically updated Pertinence Matrix. MARS was evaluated on four diverse medical datasets (41 to 721 diseases) and compared against Decision Tree, Random Forest, KNN, SVC, Bayesian classifiers, and Neural Networks. On the most challenging dataset (721 diseases, 49,365 test cases), MARS achieved the highest accuracy (87.34%) with substantially reduced processing time. When considering differential diagnosis, accuracy reached 98.33% for top-5 suggestions. These results demonstrate that MARS effectively balances diagnostic accuracy, computational efficiency, and interpretability, three requirements critical for clinical deployment. The framework’s ability to provide ranked differential diagnoses and update incrementally positions it as a practical solution for diverse clinical settings.

1. Introduction

Medical diagnostics has undergone a remarkable transformation over the past decade. Clinicians today face an overwhelming amount of patient data, complex disease patterns, and constant pressure to make accurate decisions quickly [1]. While traditional diagnostic approaches served medicine well for decades, they now struggle to keep pace with the sheer volume and complexity of modern healthcare data [2,3]. Consider a typical scenario: when evaluating a patient with multiple symptoms, a physician must consider numerous possible disease combinations. With just n symptoms, the  evaluation potentially faces $2^n$ different combinations, a number that becomes unmanageable surprisingly quickly.

This computational challenge has sparked considerable interest in developing more sophisticated diagnostic tools. Researchers have explored numerous paths, each offering unique insights into improving medical diagnosis. For instance, Başçiftçi and colleagues took an interesting approach in 2018 when they applied Boolean function minimization to reduce the complexity of rule-based systems for cancer diagnosis [4]. Their work showed that exhaustive rule evaluation is not always necessary; clever optimization can dramatically speed up the diagnostic process without sacrificing accuracy.

Meanwhile, other researchers have focused on making diagnostic tools more accessible. Sridhara’s team recently developed a mobile application that brings machine learning-powered diagnosis to remote areas where medical expertise is scarce [5]. It serves as a reminder that sophisticated diagnostic systems mean little if they cannot reach the patients who need them most. Similarly, Singh and colleagues demonstrated in 2024 how combining machine learning association rules with rough set theory could handle the messy, incomplete data that is common in real-world medical settings [6]. Their work on neurodevelopmental diseases showed particularly promising results, suggesting that hybrid approaches might be key to handling complex diagnostic challenges.

The question of how to manage and process vast amounts of medical data efficiently has also received significant attention. Tashkandi’s group tackled this by developing methods to perform patient similarity analysis directly within database systems, rather than extracting and processing data externally [7]. This seemingly simple change led to substantial performance improvements. At a more fundamental level, Zhou and colleagues constructed comprehensive disease networks from biomedical literature, revealing surprising connections between symptoms, genetics, and protein interactions that were not apparent when looking at diseases in isolation [8]. Their network-based perspective has opened new avenues for understanding disease relationships and developing more nuanced diagnostic approaches.

Perhaps one of the most promising developments has been the emergence of hybrid reasoning systems. Traditional case-based reasoning (CBR), while powerful, exhibits several limitations when used alone [9,10]. In medical domains, conventional CBR often struggles with large and heterogeneous datasets due to the high computational cost of retrieving similar cases, limited scalability when new cases are added, and reduced accuracy when symptoms overlap or co-occur in correlated patterns. These issues make it difficult for traditional CBR to operate efficiently in real-time or complex diagnostic environments.

Recognizing these limitations, researchers have explored hybrid approaches. Sharaf-El-Deen’s team demonstrated that combining case-based reasoning with rule-based approaches could overcome many of these constraints, particularly in breast cancer and thyroid disease diagnosis [11]. Their system used rules to pre-filter candidate cases, reducing the computational burden of similarity calculations. Kumar and colleagues extended this concept into intensive care units, where the ability to adapt to rapidly changing patient conditions is crucial [12]. Their hybrid system demonstrated that flexibility and adaptability are just as important as accuracy in real-world clinical settings.

Against this backdrop of ongoing innovation, this paper presents MARS (Matrix-Accelerated Reasoning System), a diagnostic methodology that takes a different approach to managing complexity. Rather than trying to brute-force through all possible disease-symptom combinations or relying solely on black-box machine learning models, MARS combines the intuitive appeal of case-based reasoning with the computational efficiency of matrix operations. The core insight is relatively straightforward: by representing disease-symptom relationships as matrices and using intelligent filtering techniques, the  search space can be dramatically reduced without losing important diagnostic information.

What makes this approach particularly interesting is how it handles the dynamic nature of medical knowledge. New diseases emerge, understanding of existing conditions evolves, and patient populations change over time. Traditional diagnostic systems often struggle with these changes, requiring extensive retraining or manual updates. MARS, by contrast, incorporates automatic rule generation and dynamic updating mechanisms that allow seamless adaptation as new data becomes available. The Pertinence Matrix, essentially a sophisticated weighting system that captures how relevant each symptom is for different diseases, updates automatically based on encountered cases.

Careful attention has also been paid to practical deployment aspects. The  system uses set intersections to quickly narrow down the list of potential diseases for any given patient query. This might sound simple, but the effect on computational efficiency is dramatic. Where a traditional approach might need to evaluate hundreds or thousands of possibilities, this method typically considers only a handful of the most relevant cases. This efficiency does not come at the cost of accuracy; in fact, by focusing computational resources on the most promising candidates, better results are often achieved than systems that spread their analysis too thin.

To validate these claims, extensive comparative studies were conducted. The  approach was evaluated against both traditional sequential methods and modern machine learning algorithms including Decision Trees, Random Forests, K-Nearest Neighbors (KNN), Support Vector Classifiers (SVCs), Bayesian classifiers (Bernoulli Naive Bayes), and neural networks (Multi-Layer Perceptron with ReLU activation). The results were encouraging: MARS consistently delivered competitive or superior accuracy while requiring significantly less computational time. Perhaps more importantly, the system maintained its performance even when scaled up to larger datasets with more symptoms and diseases.

Recent developments in explainable AI have also influenced the design philosophy [13]. Unlike many modern diagnostic systems that operate as black boxes, the matrix-based approach provides clear insights into why particular diagnoses are suggested. Each step in the diagnostic process can be traced and understood, making it easier for clinicians to trust and validate the system’s recommendations. This transparency is crucial in medical settings where understanding the reasoning behind a diagnosis can be as important as the diagnosis itself [14].

The implications of this work extend beyond just improving diagnostic accuracy or speed. By providing a framework that is both efficient and adaptable, this research contributes to the broader goal of making sophisticated diagnostic support available wherever it is needed. Whether in a well-equipped urban hospital or a resource-constrained rural clinic, the same underlying methodology can be applied, scaled appropriately to the available computational resources.

2. Materials and Methods

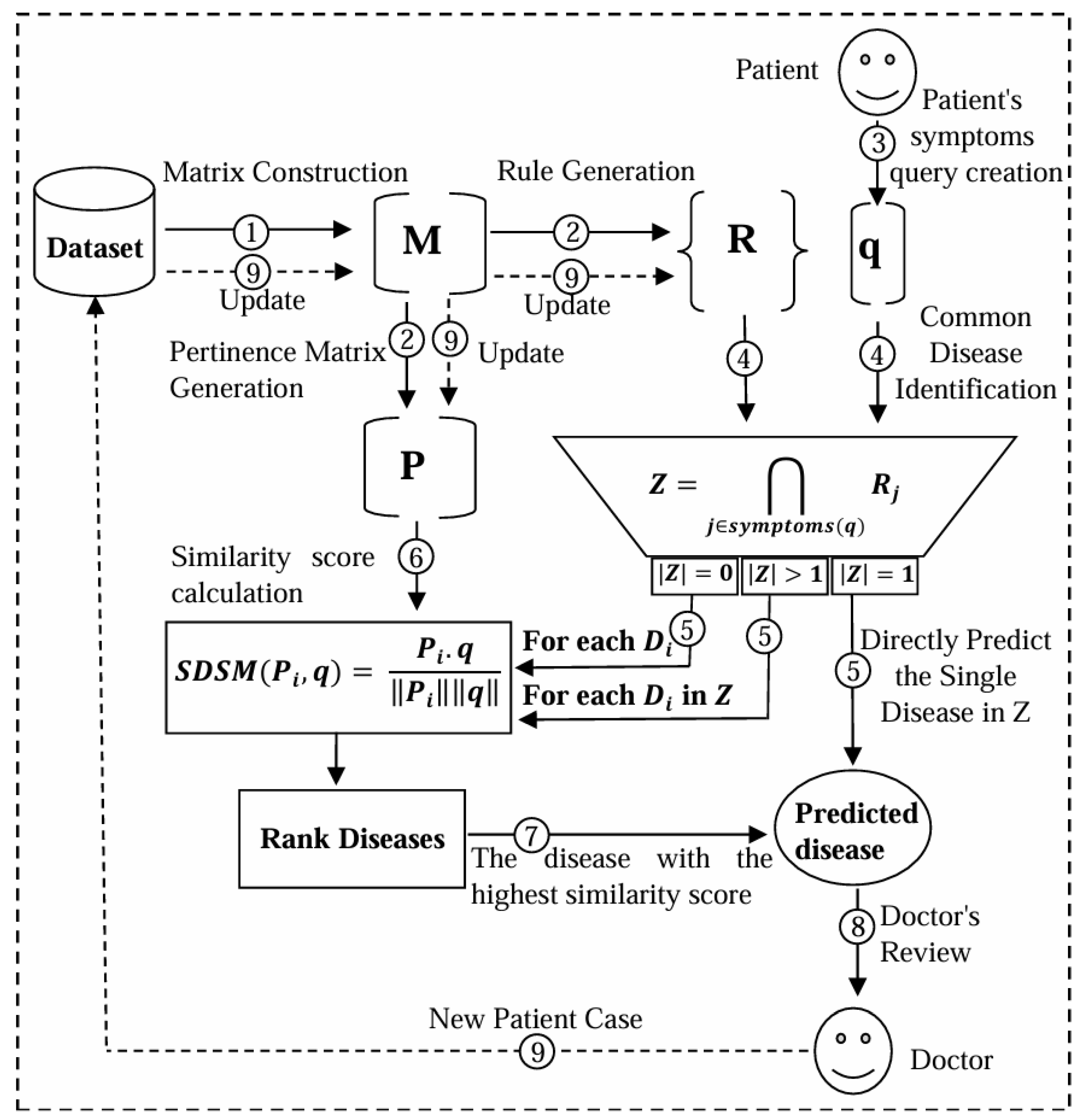
The proposed methodology integrates Case-Based Reasoning (CBR) with a matrix-based representation and rule-based filtering to predict diseases from symptoms. This combination offers a robust solution to the complexities of modern diagnostic systems by leveraging innovative matrix representations and measurement strategies. A Pertinence Matrix encodes the relationships between symptoms and diseases, while rule-based filtering refines the process by focusing on relevant cases. This approach ensures efficient handling of large datasets and high diagnostic accuracy, with dynamic updates to both the rules and the matrix for adaptability. Figure 1 provides an overview of the steps in the proposed approach, each designed to enhance the accuracy and efficiency of disease diagnosis, particularly in complex datasets. The following subsections explain these steps with examples.

2.1. Dataset Description

The datasets used in this study contain detailed information about various diseases and their associated symptoms. The data is organized as follows:

• Rows: Each row represents a single instance, which could be a patient or a case study. It provides information about the presence or absence of symptoms for a specific disease.
• Columns: Each column represents a specific symptom. The symptom columns indicate the presence or absence of symptoms in a disease, encoded using binary values (0 or 1). A value of 1 indicates that the symptom is present, while a value of 0 indicates its absence. Except the last column indicates the name of the disease corresponding to the symptoms listed in each row.

In the remainder of this section, we adopt the following notation:

• T: The training dataset.
• $T_k$: The $k^{th}$ record in T.
• $N_d$: The number of distinct diseases in T.
• $N_s$: The number of distinct symptoms in T.
• $N_t$: The number of cases in T.
• D: The set of distinct diseases in T: $D_1,D_2,\dots ,D_{N_d}$.
• S: The set of distinct symptoms in T: $S_1,S_2,\dots ,S_{N_s}$.

Table 1. Example Data.

Record	S1	S2	S3	S4	S5	Disease
T1	1	1	1	0	0	D1
T2	1	1	0	0	1	D1
T3	0	1	1	1	0	D2
T4	0	1	0	1	0	D3
T5	1	0	0	1	0	D4
T6	1	1	1	1	0	D2
T7	1	1	1	0	1	D1
T8	0	1	0	0	1	D3
T9	0	0	1	1	0	D2

presents a hypothetical record example of the data structure. Consider four diseases—$D_1$ (Flu), $D_2$ (Cold), $D_3$ (Allergy), and $D_4$ (Sinusitis)—and five symptoms: $S_1$ (Fever), $S_2$ (Cough), $S_3$ (Sore Throat), $S_4$ (Runny Nose), and $S_5$ (Headache):

In this example we have:

• $N_d=4$;
• $N_s=5$;
• $N_t=10$;
• $D=\{D_1,D_2,D_3,D_4\}=\{Flu,Cold,Allergy,Sinusitis\}$;
• $S=\{S_1,S_2,S_3,S_4,S_5\}=\{Fever,Cough,SoreThroat,RunnyNose,Headache\}$.

2.2. Matrix M Construction from Training Data

We construct a matrix M of dimension $N_d\times N_s$, where each row represents a disease and each column represents a symptom. Each element $M_{i,j}$ in this matrix represents the integer weight of symptom $S_j$ in disease $D_i$. Higher weights signify a stronger association between the symptom and the disease.

Matrix M is constructed by analyzing the training data to assign integer weights to symptoms based on their relevance to each disease. Matrix M which is initialized to null matrix is constructed as follows:

Step 1. 

Set $k=1$.

Step 2. 

Identify the disease $D_i$ associated with $T_k$.

Step 3. 

If symptom $S_j,j=1,\dots ,N_s,$ presents in $T_k$, then increment the element $M_{i,j}$ by 1.

Step 4. 

Increment k by 1 and repeat steps 2 and 3 until $k=N_t$.

The process for constructing the matrix M is expressed in Algorithm 1.

Algorithm 1: Constructing the Symptom-Disease Matrix

For example, based on the 10 records provided in Table 1, we construct the matrix M by traversing all records $T_k$. For each record, we increment its contribution to the overall matrix M.

First, the matrix is initialized as a null matrix:

$$M=\begin{array}{cccccc}& S_1& S_2& S_3& S_4& S_5\\ D_1& 0& 0& 0& 0& 0\\ D_2& 0& 0& 0& 0& 0\\ D_3& 0& 0& 0& 0& 0\\ D_4& 0& 0& 0& 0& 0\end{array}$$

Then, for $k=1,\dots ,N_t$, we proceed as follows:

$$\begin{gathered} k=1:M=\left[\begin{array}{ccccc}1& 1& 1& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right],k=2:M=\left[\begin{array}{ccccc}2& 2& 1& 0& 1\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right], \\ k=3:M=\left[\begin{array}{ccccc}2& 2& 1& 0& 1\\ 0& 1& 1& 1& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right],\dots \end{gathered}$$

After processing all records, the resulting matrix is:

$$M=\left[\begin{array}{ccccc}3& 3& 2& 0& 2\\ 1& 2& 3& 3& 0\\ 0& 2& 0& 1& 1\\ 2& 0& 0& 1& 1\end{array}\right]$$

This matrix illustrates the frequency of each symptom associated with different diseases, which can be useful for a Case-Based Reasoning system to identify and diagnose diseases based on symptom patterns. Here, $M_{1,1}=3$ indicates that Symptom $S_1$ (Fever) is associated with Disease $D_1$ (Flu) in three instances.

Next, we construct a vector C that represents the prevalence of each disease in the dataset. This vector is essential for the creation of the pertinence matrix in the following subsection. Each element $C_i$ reflects the total number of occurrences of disease $D_i$ across all records in the training dataset. For example, using the previous records, the vector C would be: $C=[3,3,2,2]$, which means that diseases $D_1$ (Flu) and $D_2$ (Cold) appear in 3 cases each, while diseases $D_3$ (Allergy) and $D_4$ (Sinusitis) each appear in 2 cases.

2.3. Pertinence Matrix Generation

The Pertinence Matrix P normalizes the integer weights of symptoms based on the occurrence frequency of each disease. Each element $P_{i,j}$ is computed as:

$$P_{i,j}={\displaystyle \frac{M_{i,j}}{C_i}}$$

(1)

For example, Pertinence Matrix P based on the matrix M and vector C from the earlier example is given by:

$$P=\left[\begin{array}{ccccc}3/3& 3/3& 2/3& 0/3& 2/3\\ 1/3& 2/3& 3/3& 3/3& 0/3\\ 0/2& 2/2& 0/2& 1/2& 1/2\\ 2/2& 0/2& 0/2& 1/2& 1/2\end{array}\right]=\left[\begin{array}{ccccc}1& 1& 2/3& 0& 2/3\\ 1/3& 2/3& 1& 1& 0\\ 0& 1& 0& 1/2& 1/2\\ 1& 0& 0& 1/2& 1/2\end{array}\right]$$

The Pertinence Matrix P enhances diagnostic accuracy by adjusting symptom relevance based on their frequency across diseases, providing a more refined comparison during the diagnostic process.

2.4. Rule Generation

In this work, the rule-based approach to disease prediction is entirely driven by automatic rule creation during the training phase. Unlike traditional systems that rely on predefined rules, this method generates rules dynamically based on the training data. For example, if three patients are present with symptom $S_1$ but have three different diseases ($D_1$, $D_3$, and $D_7$), the system automatically generates a rule associating $D_1$, $D_3$, and $D_7$ with this symptom. Similarly, if multiple patients present with Symptom $S_2$ and are diagnosed with diseases $D_2$ and $D_4$, another rule will be created linking these diseases with symptom $S_2$. These rules are not predefined but are instead generated based on patterns found in the training data. The system learns which symptoms are commonly associated with certain diseases and uses this information to create rules that will guide the diagnostic process. The number of rules corresponds to the number of symptoms in the system, and these rules are updated after each new case is processed. To enhance both accuracy and efficiency, we combine this rule-based approach with a Symptom-Disease Similarity Metric (SDSM) (Equation (2)).

The matrix M, which encodes the associations between symptoms and diseases based on the training data, is transformed into a set of ensembles $R_{S_j}$. Each $R_{S_j}$ represents a rule corresponding to a specific symptom $S_j$ and contains the diseases that are associated with that symptom. This rule-based representation is crucial for the system’s efficiency, as it allows for the quick retrieval of potential diseases based on the presence of specific symptoms. Ensembles $R_{S_j}$ are defined as follows:

• Each ensemble $R_{S_j}$ is generated by examining the non-zero entries in the column of matrix M corresponding to symptom $S_j$.
• The elements in $R_{S_j}$ indicate the diseases that have been associated with symptom $S_j$ during the training phase.
• The ensemble acts as a rule that links a particular symptom to a set of possible diseases, guiding the diagnostic process by narrowing down the list of potential diagnoses.

For example, based on the matrix M calculated in Section 2.1:

$$M=\left[\begin{array}{ccccc}3& 3& 2& 0& 2\\ 1& 2& 3& 3& 0\\ 0& 2& 0& 1& 1\\ 2& 0& 0& 1& 1\end{array}\right]$$

The rules are generated by examining this matrix to determine which diseases are linked to each symptom, see

Table 2. Rule Generation.

Symptom	Rule
$S_1$	$R_{S_1}=\{D_1,D_2,D_4\}$
$S_2$	$R_{S_2}=\{D_1,D_2,D_3\}$
$S_3$	$R_{S_3}=\{D_1,D_2\}$
$S_4$	$R_{S_4}=\{D_2,D_3,D_4\}$
$S_5$	$R_{S_5}=\{D_1,D_3,D_4\}$

.

This rule-based representation has the following properties:

Efficiency: 

It streamlines the diagnostic process. When a patient presents with a symptom $S_j$, the system can immediately refer to the corresponding ensemble $R_{S_j}$ to retrieve the most relevant diseases, significantly reducing the search space.

Dynamic Updates: 

As new cases are processed, the matrix M and the corresponding ensembles $R_{S_j},j=1,2,\dots N_s$, are updated, ensuring that the rules evolve and remain accurate over time.

Scalability: 

The approach is scalable to large datasets, as the rule creation and retrieval process remains efficient regardless of the number of symptoms or diseases involved.

This structured rule representation forms the backbone of the diagnostic system, enabling quick and accurate predictions by leveraging the associations learned during the training phase.

2.5. Test Query Representation

In this stage, the patient’s symptom query is represented as a vector $\mathbf{q}\in {\{0,1\}}^{N_s}$, where $N_s$ is the number of symptoms under consideration. Each component $q_j$ of $\mathbf{q}$ is set to 1 if the corresponding symptom $S_j$ is present in the query and 0 otherwise. For example, if a patient presents with the symptoms $S_1$ (Fever), $S_2$ (Cough), and $S_5$ (Headache), the query vector $\mathbf{q}$ would be: $\mathbf{q}=[1,1,0,0,1]$. This representation allows the system to efficiently process and compare the patient’s symptoms with the disease data stored in the Pertinence Matrix $\mathbf{P}$.

2.6. Symptom-Disease Similarity Metric (SDSM)

The Symptom-Disease Similarity Metric (SDSM) evaluates the alignment between a patient’s symptom query vector and the disease vectors represented in the Pertinence Matrix P, as described in the previous section. By utilizing cosine similarity [15,16], the SDSM provides an effective measure of compatibility between the patient’s symptom query and disease profiles. It is mathematically expressed as:

$$SDSM(d,q)={\displaystyle \frac{d·q}{\parallel d\parallel \parallel q\parallel }}$$

(2)

where:

• d: Disease vector from the Pertinence Matrix.
• q: Patient’s symptom query vector.
• $d·q$: inner product of the two vectors d and q.
• $\parallel d\parallel$ and $\parallel q\parallel$: Euclidean norms (magnitudes) of the respective vectors.

The SDSM produces a normalized score ranging from −1 to 1, where the score varies from a perfect match ($\mathrm{SDSM}=1$) to complete incompatibility ($\mathrm{SDSM}=-1$):

• The value 1 indicates a perfect match between the disease and symptom query.
• The value 0 suggests no relationship or similarity.
• The value −1 denotes complete incompatibility.

The SDSM is a powerful tool for quantifying the degree of similarity between diseases and patient symptoms, thus aiding in more precise and efficient diagnostic decision-making.

2.7. Diagnostic Process

This approach is designed to optimize computational efficiency while enhancing the accuracy of disease prediction. The proposed algorithm, as detailed in Algorithm 2, operates in a series of structured steps. It begins with the initialization of the patient’s symptom query vector, followed by the identification of common diseases through set intersections. Disease prediction is then refined by focusing on a smaller set of candidate diseases based on the intersection results. Depending on the outcome, different actions are taken to select the most probable disease. The final step returns the predicted disease based on these selection criteria.

Algorithm 2: Disease Prediction Algorithm

Input:  q: Binary symptom query vector for the patient, where each element represents the presence (1) or absence (0) of a symptom. Output:  Predicted disease based on the symptom query. Data:  R: Set of rule-based ensembles, where each rule $R_{S_j}$ is a set of diseases associated with symptom $S_j$, P:  Pertinence matrix that measures the relevance of symptoms to diseases. 1   Procedure: 2   Step 1: Common Disease Identification: Identify the indices of active symptoms in the query vector q and set: $$I=\{i\mid q[i]=1\}$$ (3) Compute the intersection of disease sets corresponding to the active symptoms: $$Z=\bigcap _{j\in I}{R}_{S_j}$$ (4) where $R_{S_j}$ is the set of diseases associated with symptom $S_j$. Step 2:  Disease Selection: Case 1: If $\left|Z\right|=1$, the predicted disease is the single disease in Z. where $\left|Z\right|$ represents the number of elements in Z. Case 2: If $\left|Z\right|>1$, the predicted disease is the one from Z that maximizes the SDSM (Equation (2)), calculated only for the diseases in Z: $$\mathrm{Predicted}\mathrm{Disease}=\underset{D_i\in Z}{argmax}\mathrm{SDSM}(P_i,q)$$ where $P_i$ is the i-th row of the pertinence matrix corresponding to the i-th disease $D_i$. Moreover, $argmax$ selects the disease with the highest SDSM score. Case 3: If $Z=\varnothing$, the predicted disease is the one that maximizes the SDSM over the entire disease set: $$\mathrm{Predicted}\mathrm{Disease}=\underset{D_i\in \mathrm{D}}{argmax}\mathrm{SDSM}(P_i,q)$$ Step 3: Output:  Return the predicted disease.

To illustrate the application of the proposed algorithm, we consider three diagnostic scenarios using the previously computed Pertinence Matrix P and Rule Matrix R.

Scenario 1: 

A patient presents with symptoms Cough ($S_2$), Sore Throat ($S_3$), and Runny Nose ($S_4$). The corresponding symptom query vector is:

$$q=[0,1,1,1,0]$$

The candidate disease set is determined as:

$$Z=R_{S_2}\cap R_{S_3}\cap R_{S_4}=\{D_1,D_2,D_3\}\cap \{D_1,D_2\}\cap \{D_2,D_3,D_4\}=\left\{D_2\right\}$$

Since $\left|Z\right|=1$, the algorithm directly predicts Cold ($D_2$) as the diagnosed disease.

Scenario 2: 

A patient presents with symptoms Fever ($S_1$), Cough ($S_2$), and Sore Throat ($S_3$). The corresponding symptom query vector is:

$$q=[1,1,1,0,0]$$

The candidate disease set is:

$$Z=R_{S_1}\cap R_{S_2}\cap R_{S_3}=\{D_1,D_2,D_4\}\cap \{D_1,D_2,D_3\}\cap \{D_1,D_2\}=\{D_1,D_2\}$$

Since $\left|Z\right|=2$ (more than one candidate), the algorithm computes the SDSM for each disease in Z:

$$SDSM(P_1,q)=SDSM([1,1,2/3,0,2/3],[1,1,1,0,0])=0.91$$

$$SDSM(P_2,q)=SDSM([1/3,2/3,1,1,0],[1,1,1,0,0])=0.72$$

Since Flu ($D_1$) has the highest cosine similarity score ($0.91$), it is selected as the predicted disease.

Scenario 3: 

A patient presents with symptoms Sore Throat ($S_3$), Runny Nose ($S_4$), and Sneezing ($S_5$). The corresponding symptom query vector is:

$$q=[0,0,1,1,1]$$

The candidate disease set is:

$$Z=R_{S_3}\cap R_{S_4}\cap R_{S_5}=\{D_1,D_2\}\cap \{D_2,D_3,D_4\}\cap \{D_1,D_3,D_4\}=\varnothing$$

Since $\left|Z\right|=0$ (no direct match), the algorithm computes the SDSM for all diseases:

$$SDSM(P_1,q)=SDSM([1,1,2/3,0,2/3],[0,0,1,1,1])=0.45$$

$$SDSM(P_2,q)=SDSM([1/3,2/3,1,1,0],[0,0,1,1,1])=0.72$$

$$SDSM(P_3,q)=SDSM([0,1,0,1/2,1/2],[0,0,1,1,1])=0.47$$

$$SDSM(P_4,q)=SDSM([1,0,0,1/2,1/2],[0,0,1,1,1])=0.47$$

Since Cold ($D_2$) has the highest similarity score ($0.72$), it is selected as the predicted disease.

2.8. Doctor’s Review and System Update

After validation by the doctor, the new patient case can be added to the dataset, enabling the automatic update of the matrices M and P, as well as the rule set R, based on this new case. This ensures that the system continuously evolves and improves its diagnostic accuracy and adaptability with each new case.

3. Results

To evaluate the effectiveness of the proposed diagnostic method, several key performance metrics were analyzed across multiple datasets. These metrics include accuracy, efficiency, and the ability to handle updates without full retraining.

3.1. Datasets

The datasets used in this study were sourced from the Kaggle repository [17,18,19,20], known for its extensive collection of open-source datasets. These datasets were selected due to their comprehensive nature, which includes a wide range of disease names and associated symptoms. The choice of Kaggle datasets ensures the availability of rich, diverse data, facilitating robust evaluation and training of the diagnostic algorithms. The data was split into two sets:

• Training Set: 80% of the data for each disease is used to train the diagnostic model. This balanced approach ensures that the model learns the relationships between symptoms and each disease effectively.
• Testing Set: 20% of the data for each disease is used to test the model’s performance.

The characteristics of the datasets used in this work are presented in

Table 3. Dataset characteristics.

Dataset	${\mathit{N}}_{\mathit{d}}$	${\mathit{N}}_{\mathit{s}}$	Number of Instances
Dataset 1 [17] (DS1)	132	400	2561
Dataset 2 [18] (DS2)	41	134	344
Dataset 3 [19] (DS3)	41	132	4920
Dataset 4 [20] (DS4)	721	328	246,823

.

3.2. Comparative Analysis with State-of-the-Art Methods

MARS was evaluated against a comprehensive range of classification approaches: traditional machine learning algorithms (Decision Tree, Random Forest, KNN, SVC), probabilistic Bayesian classifiers (Bernoulli Naive Bayes), and modern neural networks (a Multi-Layer Perceptron with two hidden layers containing 100 and 50 neurons, respectively, ReLU activation, and trained for 500 epochs). This comparison evaluates MARS against both optimization-based approaches (neural networks) and probability-based methods (Bayesian classifiers).

The primary performance metric is accuracy:

$$\mathrm{Accuracy}:={\displaystyle \frac{\mathrm{Number}\mathrm{of}\mathrm{Correct}\mathrm{Predictions}}{\mathrm{Total}\mathrm{Number}\mathrm{of}\mathrm{Predictions}}}$$

(5)

Table 4. Comprehensive Performance Comparison Across All Methods.

Method	DS1	DS2	DS3	DS4	Train (s)	Test (s)
MARS	99.22%	100%	100%	87.34%	5	2
Traditional ML Algorithms
Decision Tree	58.98%	73.53%	100%	81.46%	43	1
Random Forest	88.48%	98.53%	100%	83.60%	42	4
KNN (k = 17)	89.45%	83.82%	100%	84.90%	lazy	184
SVC (linear)	92.77%	100%	100%	86.39%	283	4043
Probabilistic Classifier
Bernoulli NB	56.64%	100%	100%	85.49%	449	1
Neural Network
NN (100, 50) ReLU	93.95%	100%	100%	85.55%	185	1

presents the comprehensive results. All experiments were conducted on an Intel Core i9-10885H CPU.

The results highlight that MARS performs exceptionally well across all datasets. It achieves perfect accuracy (100%) on DS2 and DS3, and maintains very high performance on DS1 (99.22%) and DS4 (87.34%). These results demonstrate both robustness and adaptability across varying dataset sizes. Importantly, MARS also exhibits fast execution time for the largest dataset (DS4), confirming its scalability and practicality for large-scale diagnostic applications.

In comparison, SVC achieves comparable accuracy on DS4 (86.39%) but at a much higher computational cost. Specifically, SVC requires 4043 s (over an hour) for testing, nearly 2000× slower than MARS. This dramatic increase in processing time illustrates the scalability challenge faced by optimization-based models like SVC in large datasets, which may limit their suitability for real-time clinical use.

Among all compared approaches, neural networks are the most competitive with MARS in terms of both accuracy and efficiency. Nevertheless, MARS surpasses the neural model (87.34% vs. 85.55%) due to three key distinctions:

i

Direct Calculation vs. Iterative Optimization: MARS constructs the Pertinence Matrix directly from symptom frequency data in a single pass (5 s for DS4), while neural networks require iterative training through multiple epochs (185 s). Moreover, MARS can incrementally update its matrix as new cases are introduced, unlike neural networks that typically require full retraining.

ii

Explicit Rules vs. Distributed Representations: MARS produces interpretable diagnostic rules (e.g., $R_{S_1}=\{D_1,D_2,D_4\}$) that clinicians can easily validate, ensuring transparency in decision-making. Neural networks, by contrast, distribute learned information across numerous weight matrices, making their reasoning process largely opaque.

iii

Set-Based Filtering vs. Layer-wise Transformation: MARS applies rule-based filtering, such as $Z=R_{S_1}\cap R_{S_2}\cap R_{S_3}$, to narrow down the set of possible diseases—reducing the search space in DS4 from 721 diseases to a very small subset—before computing cosine similarity (SDSM). In contrast, neural networks cannot perform such pre-filtering: the entire input is propagated through all hidden layers, and the network produces output scores for all 721 classes in the final classification layer.

Although Bayesian classifiers theoretically handle diagnostic uncertainty well, Bernoulli Naive Bayes reached only 85.49% accuracy, about 1.85 points below MARS. This is largely due to the independence assumption in Bayesian models, which rarely holds in medical contexts where symptoms are interdependent and often co-occur.

MARS’s geometric approach, leveraging cosine similarity, naturally captures these correlations via the Pertinence Matrix. When symptoms frequently appear together for a given disease, they form distinctive patterns within the disease vector, enhancing diagnostic precision.

While Decision Tree, Random Forest, and KNN achieve reasonable accuracy and fast execution times, they fall short of MARS on DS4. This suggests that although these algorithms are computationally efficient, they are less effective for large, complex diagnostic datasets.

These results validate MARS’s design: combining interpretable rule-based filtering with efficient matrix operations achieves accuracy competitive with black-box methods while maintaining transparency and computational efficiency.

3.3. Efficiency

The effectiveness of the proposed approach lies not only in its accuracy but also in the significant reduction of computational operations. This advantage is achieved through two distinct phases:

• Transformation of the Training Dataset into a Pertinence Matrix P.
• Application of Rule-Based Filtering.

To better highlight this advantage, the following subsections provide a comprehensive breakdown of each phase.

3.3.1. Computational Efficiency: Impact of the Pertinence Matrix P

In addition to enhancing accuracy, the Pertinence Matrix P offers a substantial reduction in computational complexity. To illustrate this advantage, we first review the traditional Case-Based Reasoning (CBR) approach, which compares each patient’s query against all cases in the dataset. Assuming the comparison is performed using the same SDSM as described earlier, with n patients to diagnose and m cases in the dataset, the number of SDSM evaluations required is $n\times m$.

In contrast, by using the Pertinence Matrix P, the number of evaluations is reduced to $N_d\times n$, where $N_d$ is the number of unique diseases in the training dataset.

Table 5. Comparison of SDSM evaluations for the dataset DS4.

Approach	Traditional CBR	With Pertinence Matrix P
Number of Test Cases	49,367	49,367
Number of Cases to Compare	197,456	721
Number of SDSM Evaluations	49,367 × 197,456 = 9,753,212,992	49,367 × 721 = 35,693,807
Accuracy	81.97%	83.40%

illustrates this comparison.

The results demonstrate a significant reduction in computational complexity by using the Pertinence Matrix P compared to traditional Case-Based Reasoning (CBR). While both approaches use the same number of test cases (49,367), the Pertinence Matrix reduces the number of cases to compare from 197,456 to just 721 by focusing on unique diseases. This leads to a dramatic decrease in the number of SDSM evaluations, from 9.75 billion to 35.7 million, offering a computational saving of over 270 times.

The Pertinence Matrix approach not only reduces computational complexity but also improves diagnostic accuracy, increasing it from 81.97% in traditional CBR to 83.40%. This indicates that the matrix enhances accuracy while significantly reducing computational requirements.

These findings suggest that the Pertinence Matrix approach enhances efficiency without compromising diagnostic accuracy, making it well-suited for large-scale, real-time applications.

3.3.2. Computational Efficiency: Impact of Rule-Based Filtering

The proposed approach does not stop at leveraging the Pertinence Matrix P; it further enhances this advantage by incorporating Rule-Based Filtering (RBF).

In the previous method that relied solely on the Pertinence Matrix P for diagnostics, each query test case q was compared with all diseases (rows) in P. Consequently, the number of SDSM evaluations was $N_d\times n$, where $N_d$ is the number of unique diseases in the training dataset and n is the number of test cases.

By introducing RBF, the search space is significantly reduced, thereby minimizing the number of SDSM evaluations to ${\sum }_{i=1}^n{z}_i$, where $z_i$ is computed as follows:

• If $\left|Z\right|=1$: No SDSM calculation is required, so $z_i=0$.
• If $\left|Z\right|>1$: The number of SDSM evaluations corresponds to $\left|Z\right|$, so:
  $z_i=\left|Z\right|$.
• If $\left|Z\right|=0$: All unique diseases ($N_d$) in the dataset must be evaluated using SDSM, so $z_i=N_d$.

A natural concern arises: could the reduced search space exclude the correct prediction, thus compromising accuracy and negating the computational benefits? Empirical results address this concern, demonstrating that the proposed approach consistently achieves a Complete Inclusion of the true prediction within the reduced search space provided by Z, define by (Equation (4)). Moreover, the approach improves diagnostic accuracy.

Table 6. Comparison of Pertinence Matrix Approaches for DS4: With and Without RBF.

Approach	Without RBF	With RBF
Number of Test Cases	49,367	49,367
Number of SDSM Evaluations	35,693,807	60,105
Accuracy	83.40%	87.34%

highlights this advantage by comparing the diagnostic performance of the proposed approach on the DS4 dataset, based on the Pertinence Matrix, with and without using RBF. The findings demonstrate a drastic reduction in computational complexity and an increase in diagnostic accuracy.

The integration of RBF with the Pertinence Matrix demonstrates substantial improvements in both computational efficiency and diagnostic accuracy. By narrowing the search space based on the pertinence of symptoms, the approach reduces SDSM evaluations from 35.7 million (without RBF) to 60,105, a 99.8% decrease. Accuracy also improves from 83.40% to 87.34%, ensuring that the reduced search space retains Complete Inclusion of true predictions.

This enhancement confirms the robustness and scalability of the approach, making it highly suitable for large-scale medical diagnostic systems, especially in resource-constrained environments.

3.3.3. Number of SDSM Evaluations in the Proposed Approach

In this subsection, we present a detailed analysis of the number of SDSM evaluations performed in the proposed approach, as outlined in the previous section. As noted, the number of SDSM evaluations depends on the size of the set Z, which varies according to the test case scenario.

Table 7. Experimental Results for DS4.

Case	$\left|\mathit{Z}\right|=1$	$\left|\mathit{Z}\right|>1$	$\left|\mathit{Z}\right|=0$	Overall
Number of Test Cases	37,200 (75%)	12,167 (25%)	0	49,367
Number of SDSM Evaluations	0	60,105	0	60,105
Accuracy	100%	48.62%	-	87.34%

presents the experimental results for DS4, broken down by the three cases of $\left|Z\right|$.

The results in Table 7 demonstrate the effectiveness of the proposed approach, with RBF efficiently handling the majority of test cases. It was able to classify 75% of the test cases in the scenario where $\left|Z\right|=1$, thus not requiring any SDSM evaluations. Moreover, it achieves perfect accuracy (100%) in this scenario.

This illustrates that the RBF mechanism is able to confidently identify the correct diagnosis without needing to resolve any ambiguity. However, in the remaining 25% of test cases, RBF was able to classify all of them into the scenario where $\left|Z\right|>1$. In this scenario, 60,105 SDSM evaluations were performed, resulting in a lower accuracy of 48.62%. This reflects the challenges of resolving ambiguity when multiple potential diagnoses are present. Importantly, there were no cases with $\left|Z\right|=0$, indicating that RBF effectively filters out irrelevant diseases, eliminating the need for SDSM evaluations for all diseases.

Overall, the proposed approach achieves an accuracy of 87.34%, demonstrating a strong balance between computational efficiency and diagnostic accuracy. In future work, emphasis should be placed on refining the similarity calculation function, particularly in cases with multiple potential diagnoses, to enhance both accuracy and efficiency.

3.4. Accuracy of Correct Prediction Among Top-n Suggested Diseases

Clinical diagnosis often involves uncertainty: a patient may exhibit symptoms corresponding to several possible diseases, or even present an unknown or previously unseen condition. To address this, MARS does not restrict its output to a single prediction. Instead, it ranks all potential diseases according to their SDSM scores, thereby producing a list of the most plausible candidates. This ranked output supports multi-disease and uncertain-case scenarios by allowing clinicians to interpret several likely diagnostic possibilities.

Table 8. Accuracy of Correct Prediction Among Top-n Suggested Diseases.

Dataset	# Diseases	n = 1	n = 2	n = 3	n = 4	n = 5
DS1	132	99.22%	99.80%	99.80%	100%	—
DS2	41	100%	—	—	—	—
DS3	41	100%	—	—	—	—
DS4	721	87.34%	94.11%	96.38%	97.60%	98.33%

presents how frequently the correct diagnosis appears among the top-n suggestions produced by MARS.

For DS4, the most complex dataset, accuracy increases from 87.34% for the top-1 prediction to 98.33% within the top-5 ranked diseases. This 11 percentage point gain indicates that in nearly all cases (98.33%), the correct diagnosis appears among the first few suggestions. For DS1, the correct diagnosis appears within the top-4 in 100% of cases.

These results demonstrate that MARS effectively supports differential diagnosis by offering multiple probable diseases rather than a single fixed prediction. Clinicians can then interpret the ranked list based on medical context, comorbidities, and patient history.

As a potential extension, MARS could also assign a query to an “unknown disease” category when all SDSM scores are low. This would account for new or unrepresented conditions in the training data and help prevent overconfident misclassification. Such an extension would further increase the system’s flexibility in dealing with ambiguous or previously unseen cases.

In summary, MARS aligns closely with real-world diagnostic needs by:

• Allowing multiple diseases to be suggested for complex or overlapping symptom patterns;
• Ranking diseases by their SDSM scores to guide clinical reasoning; and
• Potentially identifying uncertain or unseen cases through an “unknown disease” category.

The 98.33% top-5 accuracy confirms that MARS can reliably propose a small, clinically relevant set of candidate diseases, providing a robust foundation for multi-disease and uncertain-case diagnosis.

3.5. Other Benefits of the Proposed Method

Beyond its accuracy and efficiency, the proposed method offers several advantages over traditional approaches. One key benefit is its flexibility in handling dataset updates. Traditional diagnostic methods often require a complete retraining process when new data is introduced, which can be time-consuming and computationally expensive. In contrast, the proposed method can integrate new information incrementally, eliminating the need for extensive retraining.

This incremental update capability allows the system to remain up-to-date with evolving medical knowledge and adapt to emerging patterns or diseases, ensuring continuous high diagnostic accuracy. Moreover, the reduced computational overhead enhances the system’s scalability and long-term utility, making it particularly valuable in dynamic medical environments such as hospitals and research facilities where new data is constantly generated.

This adaptability not only improves the efficiency of the diagnostic process but also ensures that the system remains reliable and relevant over time, offering a distinct advantage over traditional methods that may struggle to keep pace with rapid medical advancements.

4. Discussion

The results presented in this study illustrate the effectiveness and robustness of MARS (Matrix-Accelerated Reasoning System) in comparison to traditional algorithms across various datasets. MARS consistently outperforms or matches other approaches in terms of accuracy, particularly in large-scale and complex datasets. This is due to its ability to maintain high accuracy while significantly reducing the search space through rule-based filtering and matrix operations.

One of the most significant strengths of MARS is its ability to efficiently manage large datasets. The method excels in reducing an initial expansive search space to a more focused set, while ensuring high accuracy. This capability is crucial in medical diagnostics, where the rapid and accurate processing of extensive patient data can directly influence clinical decision-making and outcomes.

The four datasets vary widely in size, from 41 to 721 diseases and 132 to 400 symptoms, which naturally affects diagnostic accuracy. MARS achieves perfect accuracy (100%) on the smaller datasets (DS2 and DS3) and maintains high accuracy (87.34%) on the largest dataset (DS4). This slight decrease reflects the increased diagnostic complexity when more diseases and overlapping symptoms are present. Importantly, MARS’s 98.33% top-5 accuracy on DS4 demonstrates that the correct diagnosis consistently appears within a clinically manageable differential diagnosis list.

The comparison across different algorithms further underscores MARS’s superiority. In datasets where traditional methods such as Decision Trees and K-Nearest Neighbors (KNN) faced challenges, particularly in terms of accuracy, MARS consistently delivered high accuracy. When compared to modern approaches such as neural networks (85.55%), MARS achieved the highest accuracy (87.34%) on the most challenging dataset. This demonstrates MARS’s robustness in handling the inherent complexities of medical data, which often includes significant variability and noise.

Moreover, the results from dataset DS4 highlight MARS’s capacity to manage extreme cases involving large datasets. While traditional methods like the Support Vector Classifier (SVC) faced efficiency problems such as prolonged execution time (4043 s), MARS maintained high accuracy with substantially reduced processing time (2 s), further demonstrating its robustness and suitability for large-scale applications.

By maintaining high accuracy even in these challenging scenarios, MARS proves to be not only effective across a wide range of cases but also particularly suited for complex real-world medical datasets. This reliability ensures more accurate diagnoses, reducing the likelihood of errors and enhancing patient outcomes compared to traditional approaches.

Another key advantage of MARS is its flexibility in updating the dataset without requiring complete retraining. This is particularly valuable in dynamic medical environments, where new information and research findings are continually emerging. The ability to incorporate new data seamlessly through incremental Pertinence Matrix updates ensures that the diagnostic model remains up-to-date and accurate over time, which is a significant advantage over traditional models that require extensive retraining to integrate new data.

Finally, interpretability remains one of MARS’s defining strengths. The explicit rule generation (e.g., $R_{S_1}=\{D_1,D_2,D_4\}$) and transparent SDSM calculations allow clinicians to trace and validate diagnostic reasoning, a critical requirement for clinical trust and adoption. In contrast to neural networks with opaque weight distributions, MARS achieves both high accuracy and full transparency, demonstrating that interpretability and performance are not mutually exclusive in intelligent diagnostic systems.

5. Conclusions

This paper introduces MARS (Matrix-Accelerated Reasoning System), a novel diagnostic approach that seamlessly integrates matrix-based representations with rule-based methodology and advanced similarity measures, demonstrating its efficacy across diverse medical datasets. MARS excels in both accuracy and computational efficiency, consistently identifying the correct diagnosis within a significantly reduced search space across all tested datasets. The results highlight MARS’s scalability, effectively managing large-scale data while ensuring complete inclusion of the true prediction within the reduced set. This capability is particularly crucial in real-world medical applications, where both accuracy and efficiency are paramount.

The evaluation across four datasets with varying scales (41 to 721 diseases, 132 to 400 symptoms) demonstrates MARS’s robustness across different diagnostic complexities. While accuracy naturally decreases with problem scale (100% for 41-disease datasets vs. 87.34% for 721 diseases), MARS consistently outperforms all baseline methods at each scale. The 98.33% top-5 accuracy on the most complex dataset validates MARS’s capability to provide clinically useful differential diagnoses even in challenging scenarios.

One of the key strengths of this approach is its flexibility; MARS not only delivers precise results but also allows for dynamic updates to the system as new data becomes available, without necessitating complete retraining. This adaptability ensures that the system remains current and effective in rapidly evolving medical environments, addressing one of the major limitations of traditional diagnostic algorithms.

In comparative analyses, MARS consistently outperformed established algorithms such as Decision Trees, Random Forest, and K-Nearest Neighbors in terms of accuracy, particularly in complex, large-scale datasets. Furthermore, MARS demonstrated superior performance compared to modern approaches such as neural networks (85.55%), achieving 87.34% accuracy on the most challenging dataset. Its superior performance, even when faced with efficiency challenges like the prolonged execution times encountered by other algorithms such as SVC, underscores its robustness and practicality for real-world deployment.

In conclusion, MARS represents a significant advancement in the field of medical diagnostics, combining high accuracy with operational efficiency and adaptability. Its ability to handle extensive and complex datasets with remarkable performance makes it a powerful tool for enhancing diagnostic processes in healthcare, from well-equipped urban hospitals to resource-constrained rural clinics.

Future work should focus on identifying optimal similarity calculation methods and validating unknown disease detection through datasets with out-of-distribution cases to determine appropriate SDSM thresholds. These refinements will enhance MARS’s diagnostic accuracy and expand its applicability to broader medical conditions.