Enhanced Brain Tumor Classification Using MobileNetV2: A Comprehensive Preprocessing and Fine-Tuning Approach
Abstract
1. Introduction
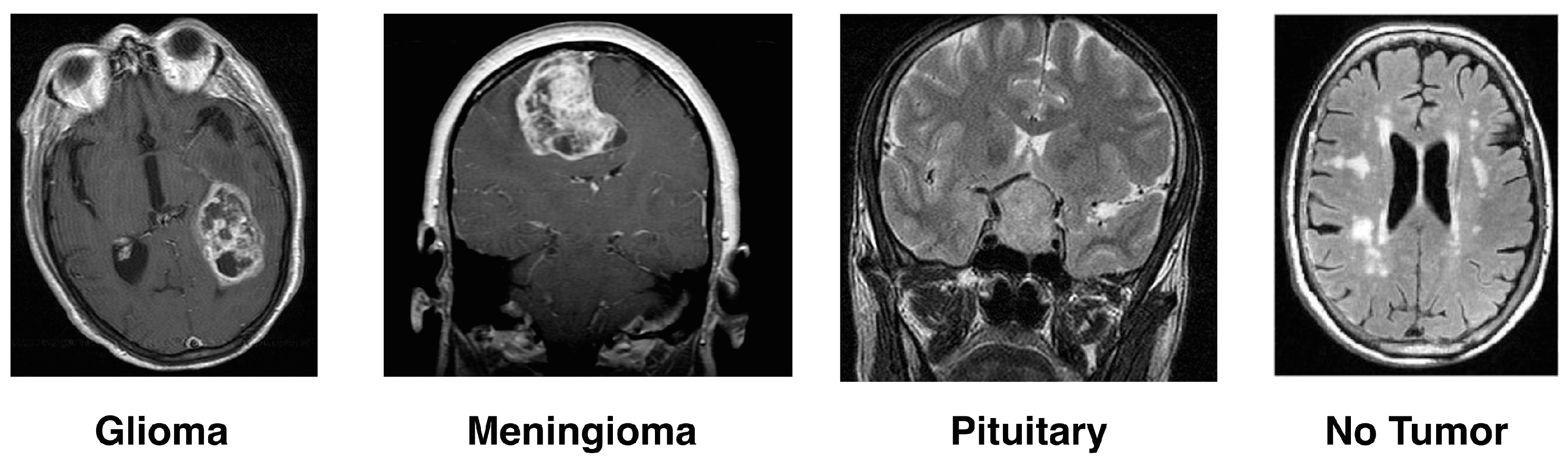
- Gliomas: One type of malignant brain tumor arises from the glial cells that help nourish and protect the brain’s sensory neurons. Glial cells are categorized according to the kind and graded into four grades by the World Health Organization (WHO). Glioblastoma multiforme (GBM) is the most fatal, and Grade IV gliomas have a poor prognosis [14,15].
- Meningioma: These are the membranes that wrap over and around a person’s brain, as well as surrounding their spinal cord, where most benign meningioma tumors usually start. They grow and pressure the brain and other nearby structures, which can cause serious health problems, even if benign. The answer to the problems, usually with surgery well removed, is how recurrence occurs [16].
- Pituitary Tumor: The pituitary gland controls the level of hormones in the body, and these tumors develop there. The vast majority of pituitary tumors (adenomas) are benign but can cause symptoms such as hormonal imbalances. Most often, the treatment involves radiation therapy, surgery, and drugs to control hormone levels [17].
- No-Tumor: Another category of MRI images is harmful, meaning they show tumors. These scans are even used as a benchmark in some research to differentiate between diseased and healthy states. It is necessary to detect and confirm that a tumor is absent for an accurate diagnosis or treatment plan.
1.1. Challenges in Brain Tumor Diagnosis and Classification
1.2. Use of Deep Learning in Classification of Brain Tumors
1.3. Importance of Preparing for Medical Image Analysis
- Implementation of Fine-Tuning Techniques: Fine-tuning was applied to pre-trained deep learning models, which were then adapted specifically for the target dataset. This approach produced substantial improvements in classification accuracy compared to traditional training or mere feature extraction.
- Comprehensive Experimental Evaluation: A systematic comparison of various fine-tuning strategies and baseline methods was conducted across multiple datasets, providing valuable benchmarks and insights into effective transfer learning practices.
- Practical Guidelines: Clear and actionable recommendations for employing fine-tuning in similar real-world applications are provided, including key optimization strategies and potential pitfalls.
2. Literature Review
3. Methodology
3.1. Dataset Description
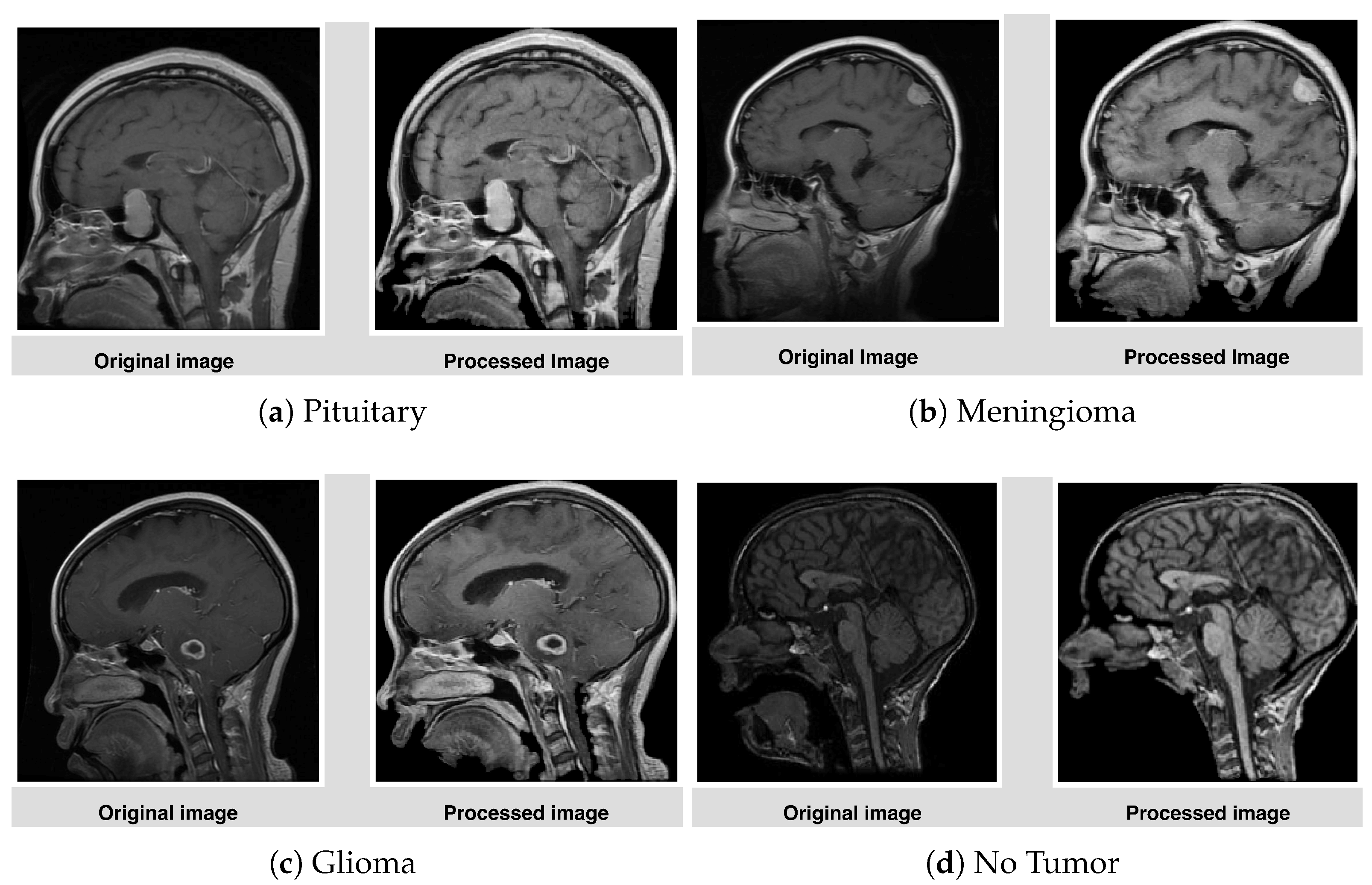
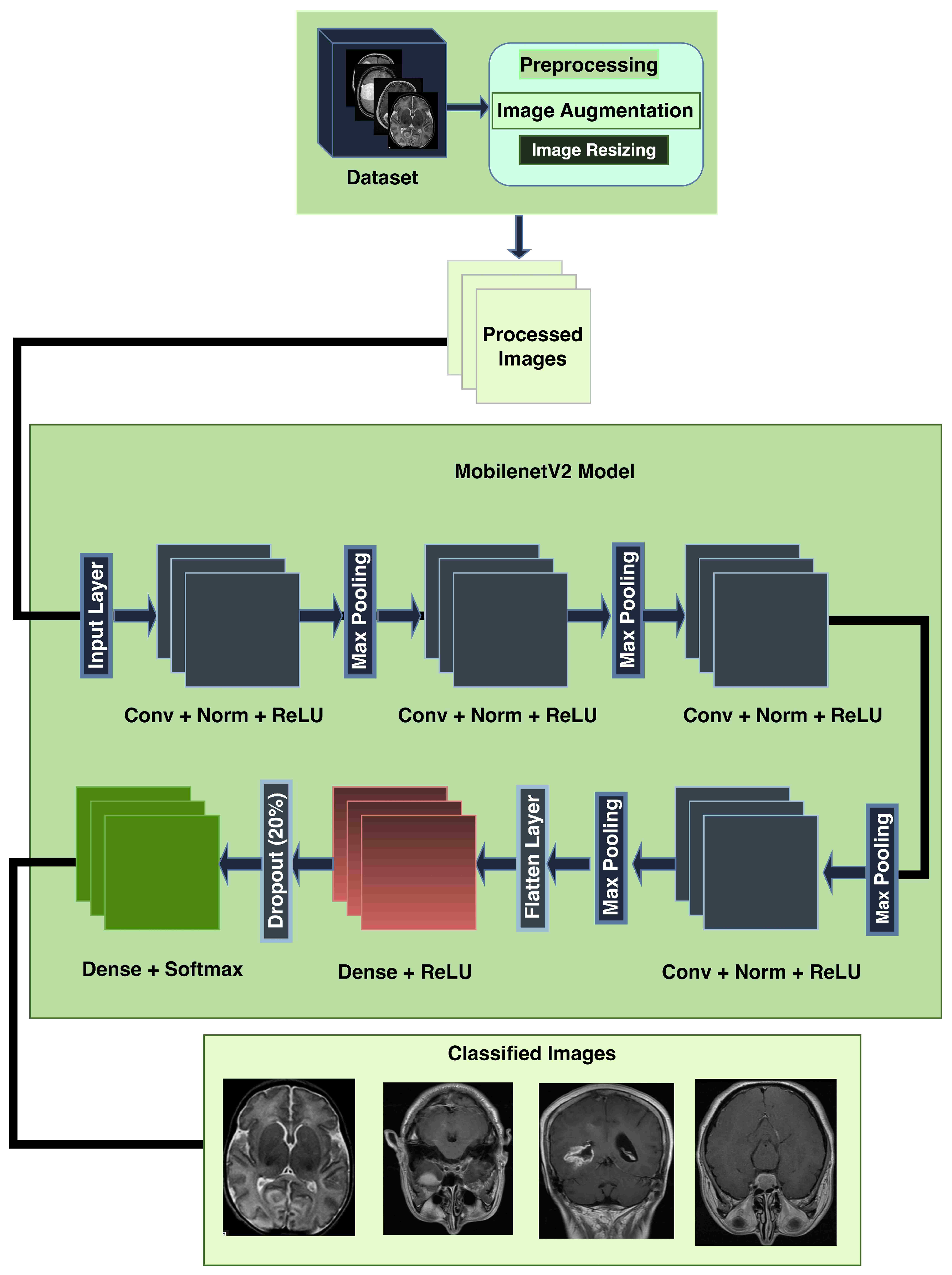
3.2. Preprocessing
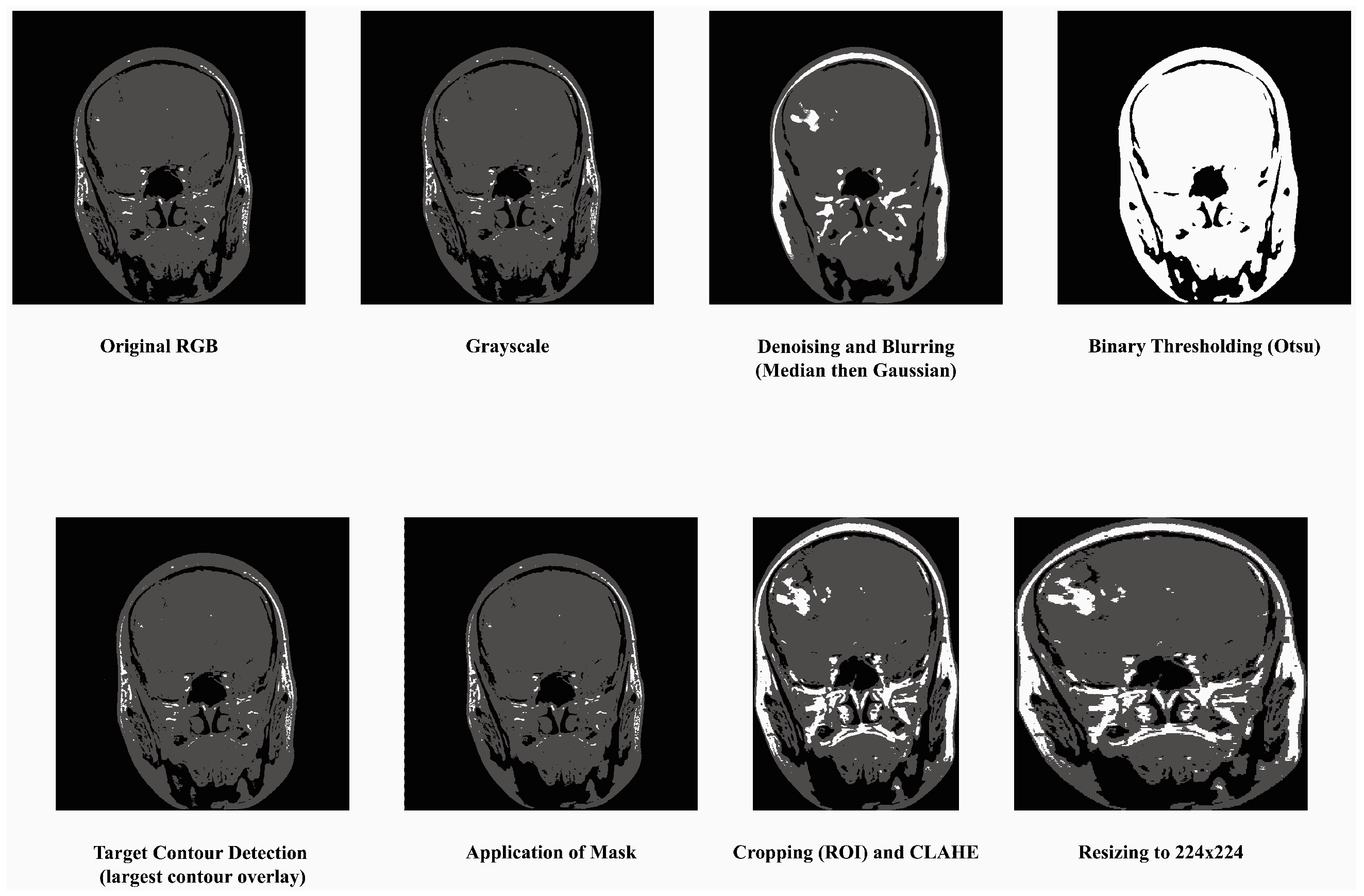
- Convert to Grayscale: Most MRI datasets are in grayscale or captured using only intensity-based information, while some datasets may also include unnecessary color channels (from RGB formats). Converting them to grayscale ensures uniformity in data representation and reduces computation by eliminating redundant information. The process has been done by grayscale using OpenCV’s cv2.cvtColor function. This step also helps focus the model on texture and contrast, which are critical for identifying tumor regions in medical imaging.
- Denoising and Blurring: MRI images often contain artifacts or noise due to acquisition methods, which can obscure key tumor features. Median filtering reduces random noise, preserving the edges and fine details critical for classification without distorting important structures like tumor contours. Blurring is applied to smooth the image and reduce high-frequency variations unrelated to tumors. It helps in suppressing minor unrelated details (e.g., scanner irregularities) and enhances the model’s ability to focus on regional features of tumors rather than noise.
- Binary Thresholding: Binary thresholding creates a clear separation of foreground (possible tumor areas) and background, which aids in isolating the tumor region. By emphasizing areas of interest based on intensity standards, this step generates a mask for tumors, facilitating structured feature extraction and segmentation. The method was applied using a fixed threshold value of 127. This process created a binary mask for tumor region selection. For normalization, pixel intensity ranges were scaled between 0 and 1 prior to thresholding.
- Target Contour Detection: After applying the binary mask, it is essential to extract the tumor region accurately. The contour detection algorithm identifies and segments the largest connected region (potential tumor) and removes non-relevant regions such as background noise or anatomical elements outside the tumor that has been done using findContours function in Python’s OpenCV library. That finds the largest contour by area greater than 500 pixels was selected as the tumor region. This ensures the model focuses on the most relevant part of the image.
- Application of Mask: The binary mask is directly applied to filter out regions irrelevant to the tumor. It allows the model to operate only on imaged regions that likely hold tumor information, improving classification accuracy and computational efficiency.
- Cropping, CLAHE: After isolating the tumor, extracting the region of interest (ROI) eliminates unnecessary background, allowing the model to focus entirely on meaningful features while standardizing input dimensions. This technique enhances the contrast of the tumor region by redistributing brightness in the image, helping highlight subtle details. CLAHE with clip limit = 2.0, grid size = (8 × 8), that reduces the inter-image variability caused by differences in MRI scanner settings, patient anatomy, or lighting conditions, which are particularly important for tumor region detection [48].
- Resizing: To ensure compatibility with the MobileNetV2 architecture, all images are resized to a fixed dimension of 224 × 224 pixels. This step provides uniformity in input size, reduces computational demands, and ensures that the model processes images efficiently without distortion.
3.3. Anatomical and Imaging Considerations in Dataset Construction
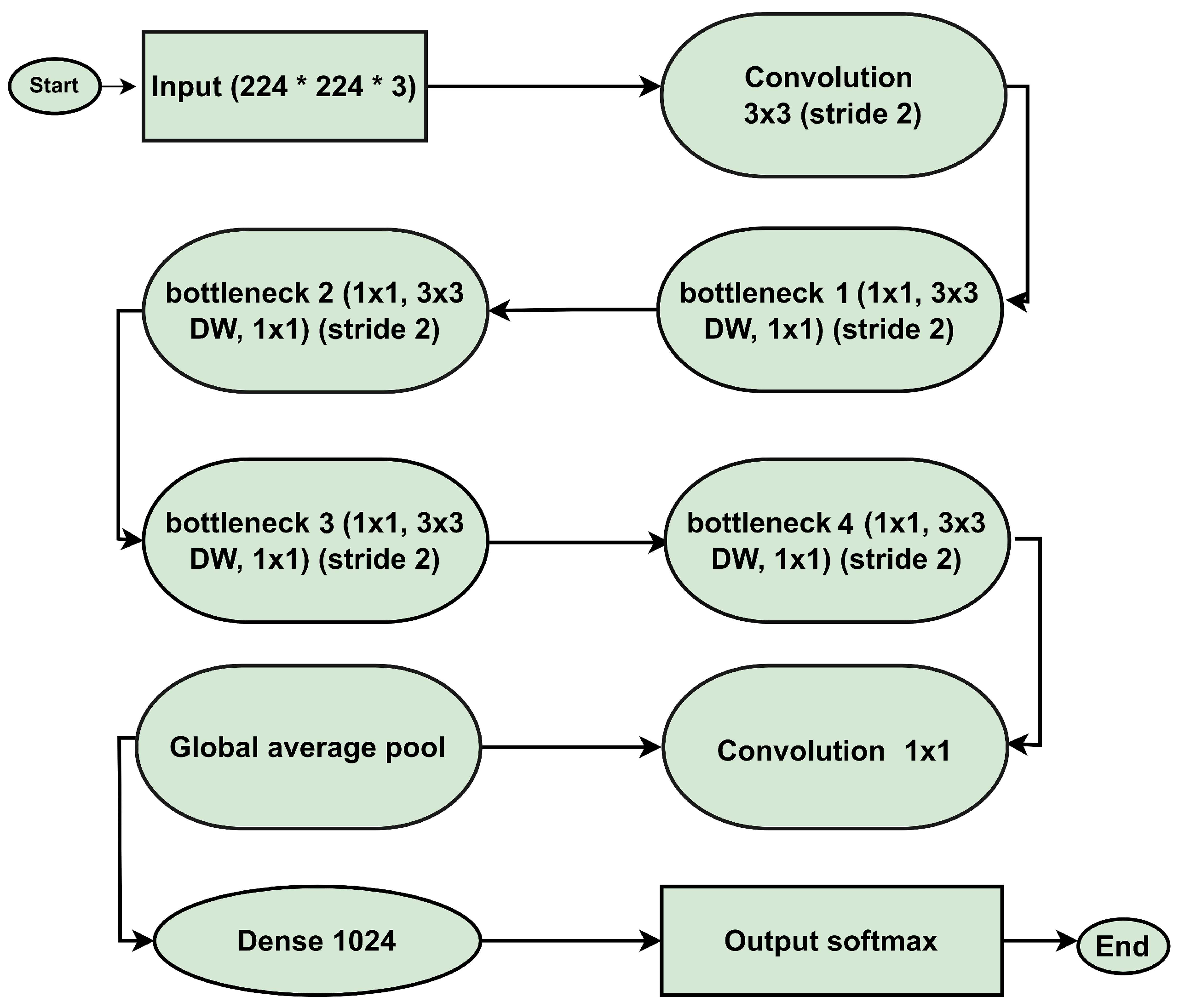
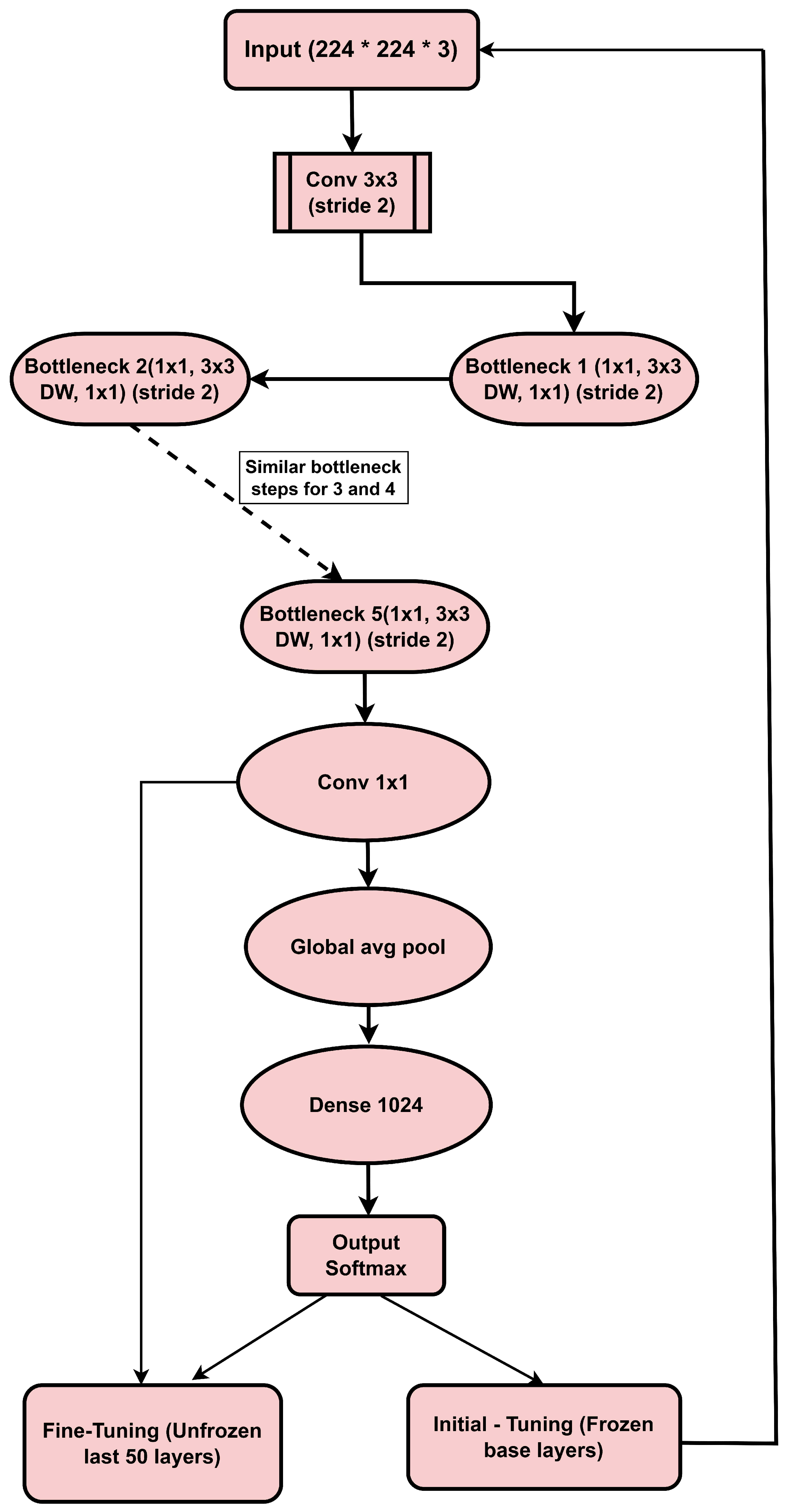
3.4. MobileNetV2 Architecture
3.4.1. Input Layer
3.4.2. Convolutional Layer (Conv 3 × 3, Stride 2)
3.4.3. Depthwise Separable Convolutions
3.4.4. Bottleneck Layers
3.4.5. ReLU6 Activation
3.4.6. Batch Normalization
3.4.7. Global Average Pooling (GAP)
3.4.8. Fully Connected Layer (Dense Layer)
3.4.9. Output Layer (Softmax)
3.5. Operational Model
- Image Augmentation: Data augmentation was applied in the training dataset to improve the generalization of the model by expanding the dataset artificially. The applied techniques included horizontal flips, vertical flips, random rotations within the range of to simulate variations in imaging position, and slight translations (up to of the image dimensions). Care was taken to ensure anatomically relevant image preservation by avoiding excessive rotations or distortions that could affect key characteristics of the brain tumor regions. These transformations were implemented in TensorFlow’s ImageDataGenerator, which automatically manages consistent application across the dataset to prevent misaligned augmentation effects. Data augmentation is very effective in boosting performance for minority classes. Despite the data imbalances, the model maintains robust performance across all classes.
- Image Resizing: All of the images are resized so that they conform to the specifications that MobileNetV2 requires for input (for example, 224 by 224 pixels).
- Normalisation: Images are normalised to ensure that the intensities of each pixel are consistent for effective learning. As input, the images that have been preprocessed are introduced into the MobileNetV2 model.
- Feature Extraction: Extracting features at multiple levels is what convolutional layers are all about.
- Batch Normalization: Batch Normalization is a process that normalizes the outputs of layers to guarantee stable and effective training.
- ReLU6 activation: The ReLU6 activation increases the amount of non-linearity while preserving the numerical predictability.
- Max Pooling: Max Pooling Layers can reduce the spatial dimensions while still preserving the essential characteristics.
- Dense layers: To pass on the features that were extracted from these layers to the dense layers, they are first flattened.
- Extraction of high-level representations from the feature space is accomplished by the Dense Layer with ReLU Activation system.
- Using a random deactivation of neurons, the Dropout Layer prevents overfitting from occurring.
- The output of the Dense Layer with Softmax Activation is a probability distribution that accounts for all of the tumour classes.
3.6. Proposed Model
3.6.1. Initial Training (Feature Extraction Stage)
- Training Base Layers: Initially, the base layers of the pre-trained model (MobileNetV2) are frozen so that they retain features learned from the large ImageNet dataset. Train only the new dense layers.
- Data Augmentation: It uses techniques like horizontal flip, longitudinal flip, and random rotations to perform Data augmentation on images used in training the model by adding variations.
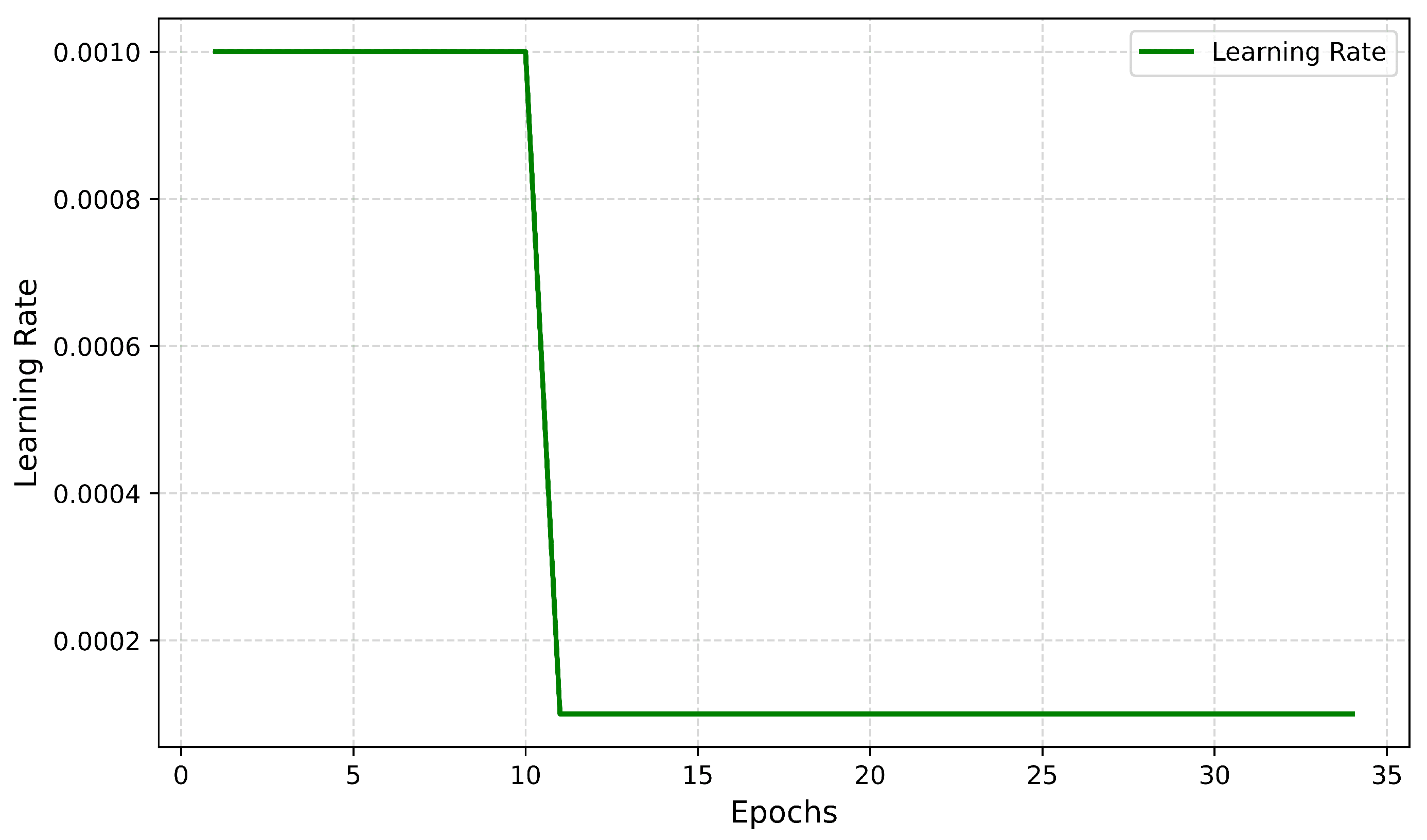
- Training: The model trains a fixed number of epochs with the optimizer set as Adam, learning rate = 0.001.
3.6.2. Fine-Tuning/Learning Weight Adjustment
- Frozen Based Last 50 Layers: Training from scratch, then unfreezing the last 50 layers of the MobilenetV2 base model for fine-tuning.
- Lower Learning Rate: The learning rate is decreased to 0.0001 to adjust the model more accurately.
- Early Stopping: This research used early stopping to avoid overfitting and maintain stable performance on new data.
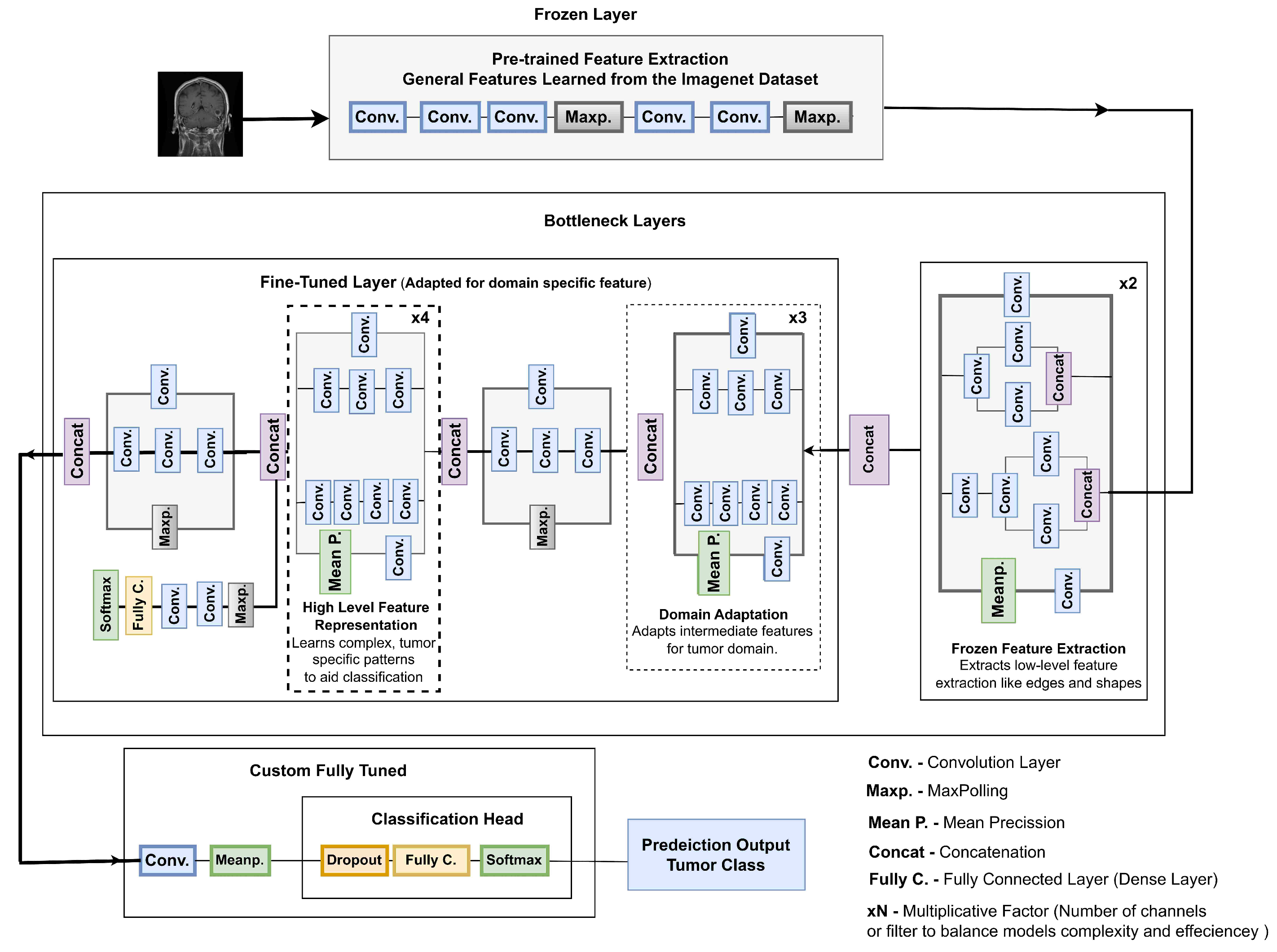
3.6.3. Frozen Layers
3.6.4. Fine-Tuned Bottleneck Layers
- ×2 Bottleneck: This initial layer utilizes pre-trained ImageNet weights and extracts low-level features such as lines, edges, and textures. By keeping this layer frozen, fundamental knowledge is preserved while avoiding overfitting to noise. As shown in Figure 6, it lays the foundation for domain-specific refinement with a minimal computational cost of 0.5 M parameters and 5.0 M FLOPs.
- ×3 Bottleneck: The intermediate ×3 bottleneck transitions from low-level to medium-level feature extraction, capturing region-level details and textural differences in MRI images. This layer bridges general features with domain-specific attributes for tumor classification. As depicted in Figure 7, it enables the model to focus on relevant sections without disrupting previously learned weights. This stage has a computational cost of 1.0 M parameters and 10.0 M FLOPs.
- ×4 Bottleneck: The ×4 bottleneck focuses on extracting high-level tumor-specific features, crucial for distinguishing between tumor classes such as gliomas, meningiomas, and pituitary tumors. Fine-tuning this layer enhances the model’s ability to identify complex patterns, ensuring accurate segmentation and classification, achieved with 1.9 M parameters and 15.0 M FLOPs.
3.6.5. Depthwise Separable Convolutions
3.6.6. Integration of Fully Tuned Layers
- Processes the features passed from the fine-tuned bottlenecks through:
- -
- A dropout layer to prevent overfitting, where the dropout rate was set to 20% in the dense layers after the ReLU activation and before the softmax layer during both initial and fine-tuning training phases.
- -
- Fully connected dense layers to aggregate and refine features into class-specific representations.
- Classifies the output into one of four classes: pituitary tumor, glioma, meningioma, and no tumor. It uses the softmax activation function to output probabilities for each class.
3.6.7. Why Fine-Tuning Is Crucial
3.7. Evaluation Metrics
3.7.1. Accuracy
3.7.2. Precision
3.7.3. Recall/Sensitivity
3.7.4. F1-Score
3.7.5. Specificity
3.7.6. Confidence Intervals and Standard Deviations
3.7.7. Matthews Correlation Coefficient (MCC)
3.7.8. Cohen’s Kappa Score
4. Results
4.1. Evaluation Metrics
Precision, Recall, F1-Score, and Support Table
4.2. Model Performance
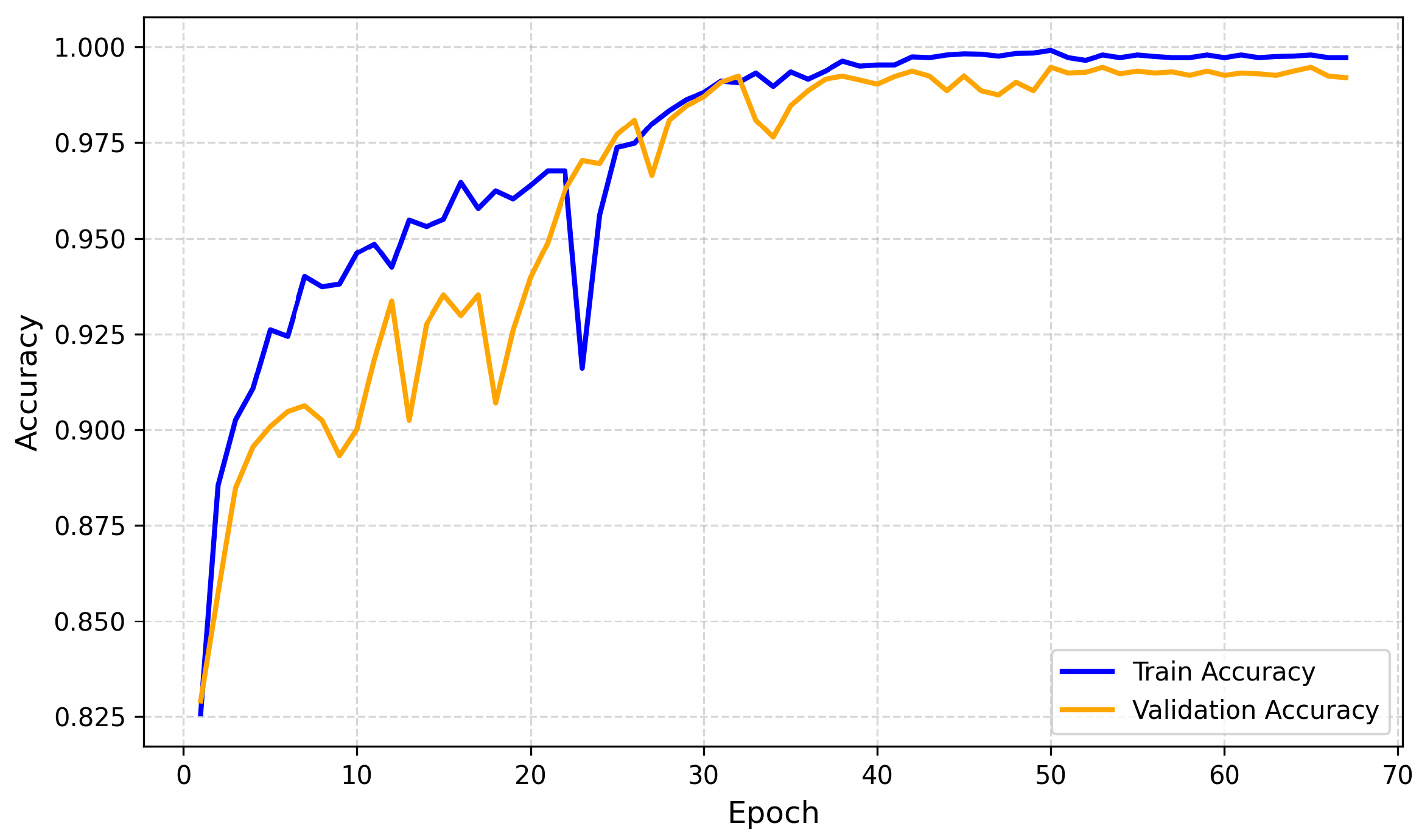
4.2.1. Training and Validation Accuracy
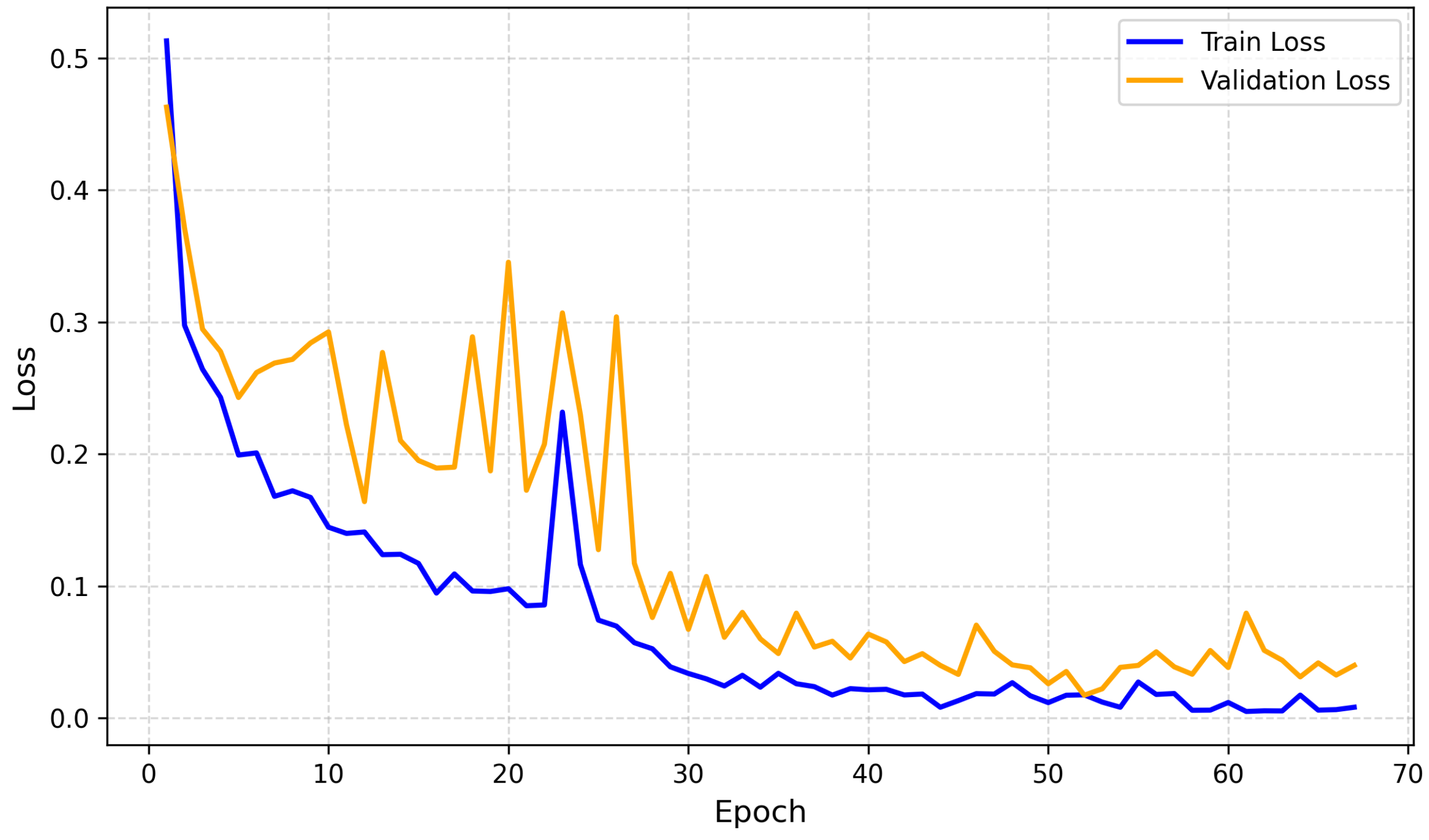
4.2.2. Training and Validation Loss
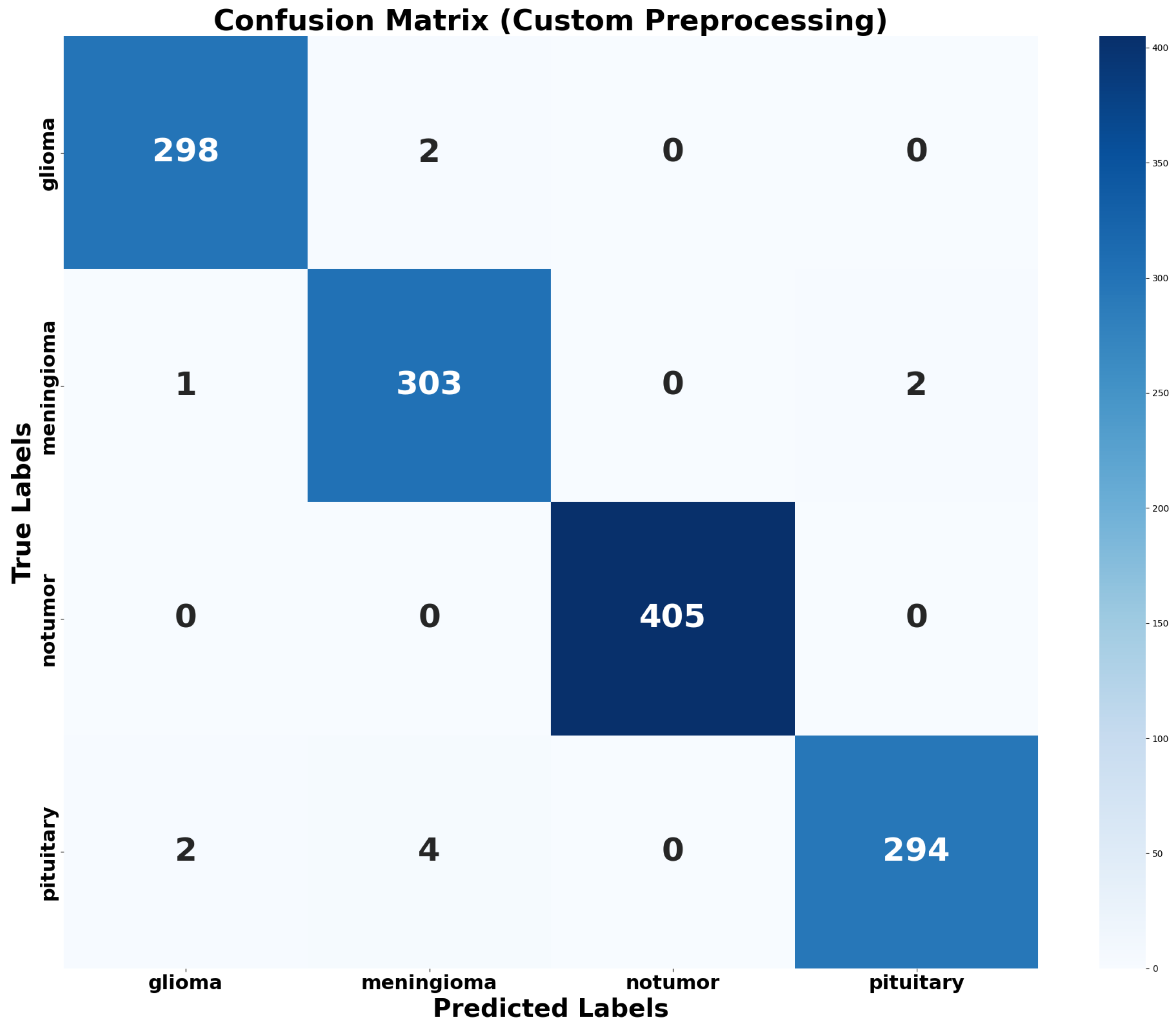
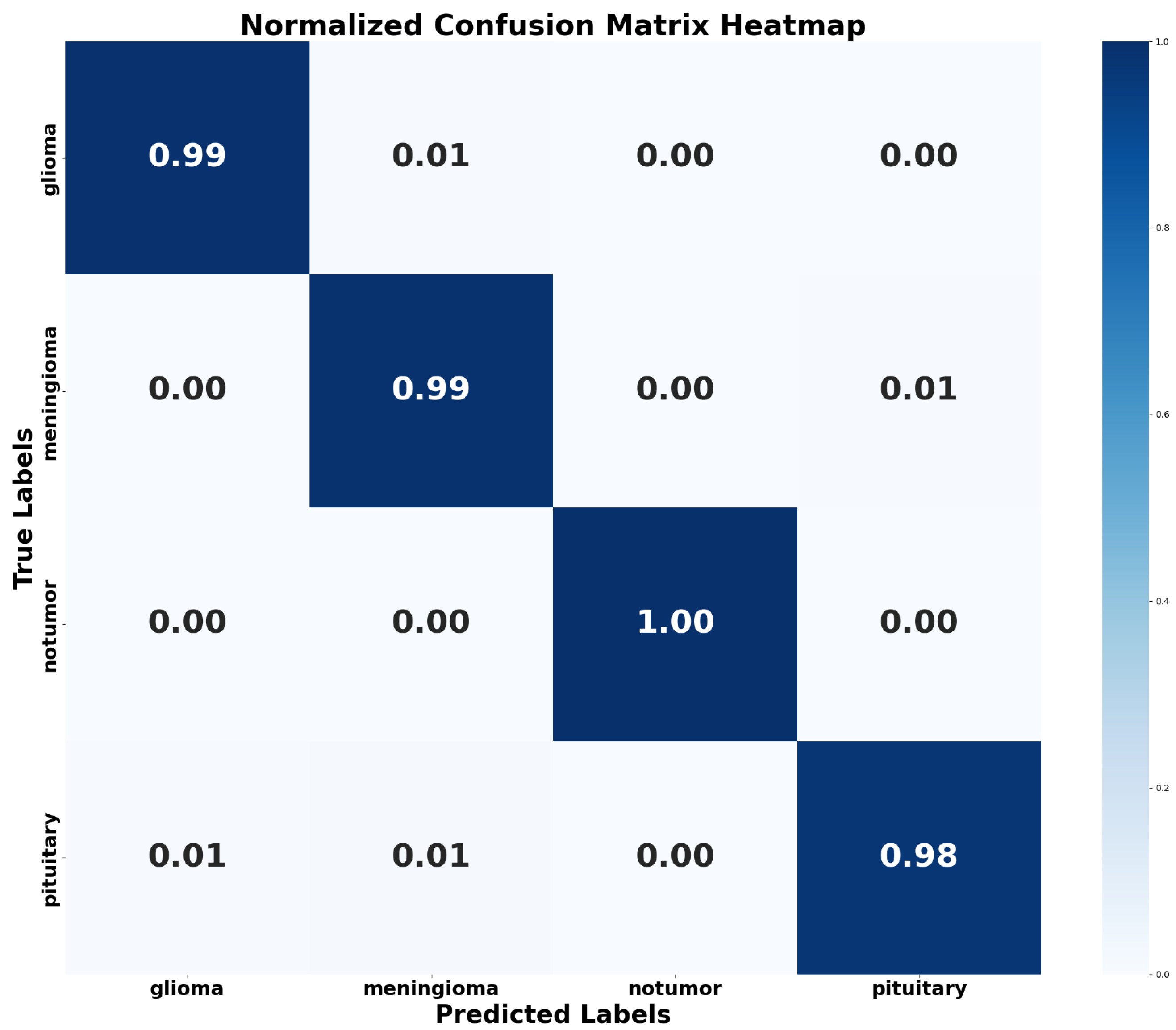
4.2.3. Confusion Matrix and Normalized Confusion Matrix Heatmap
4.2.4. Learning Rate Curve
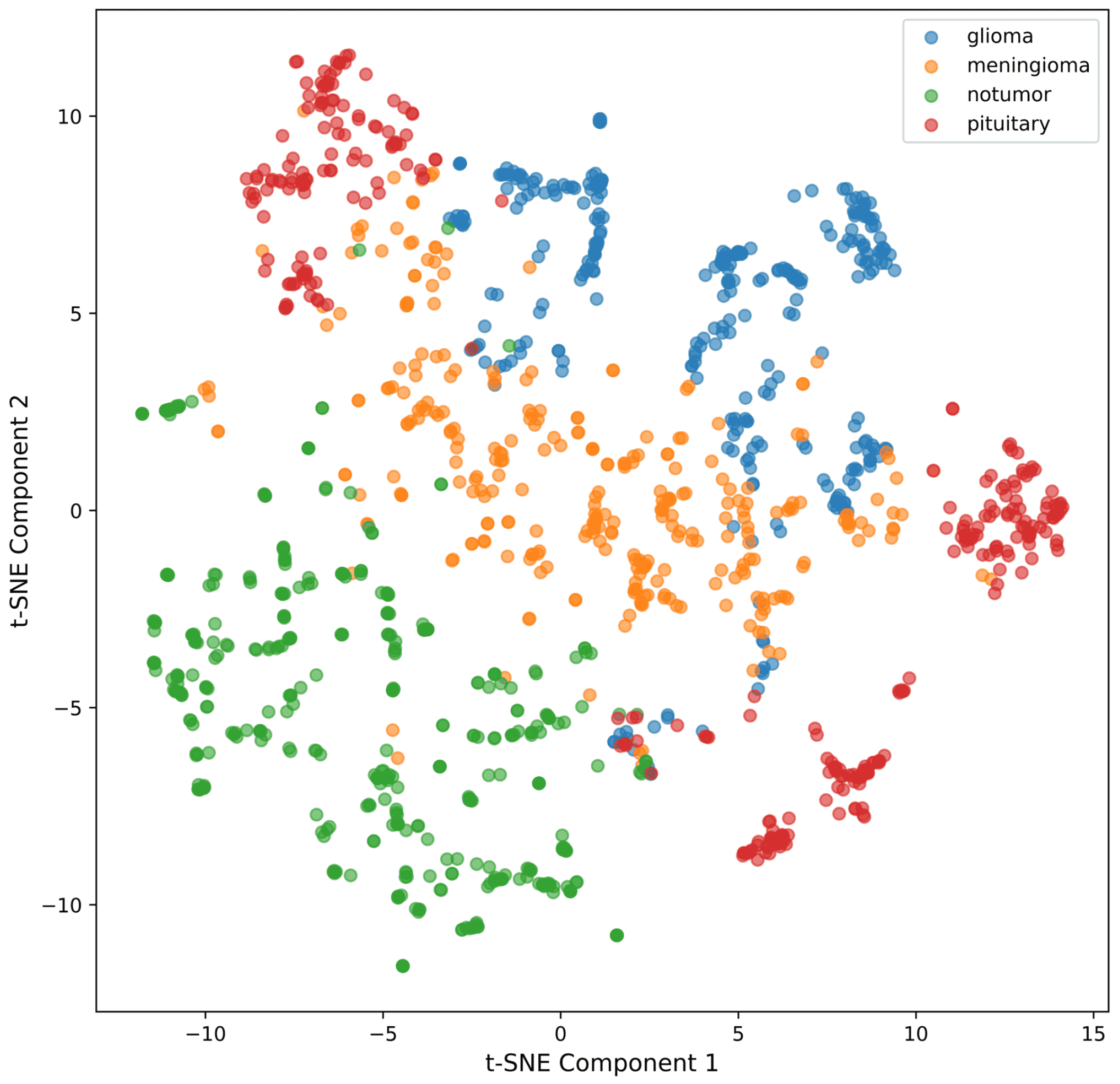
4.2.5. t-SNE for Feature Visualization
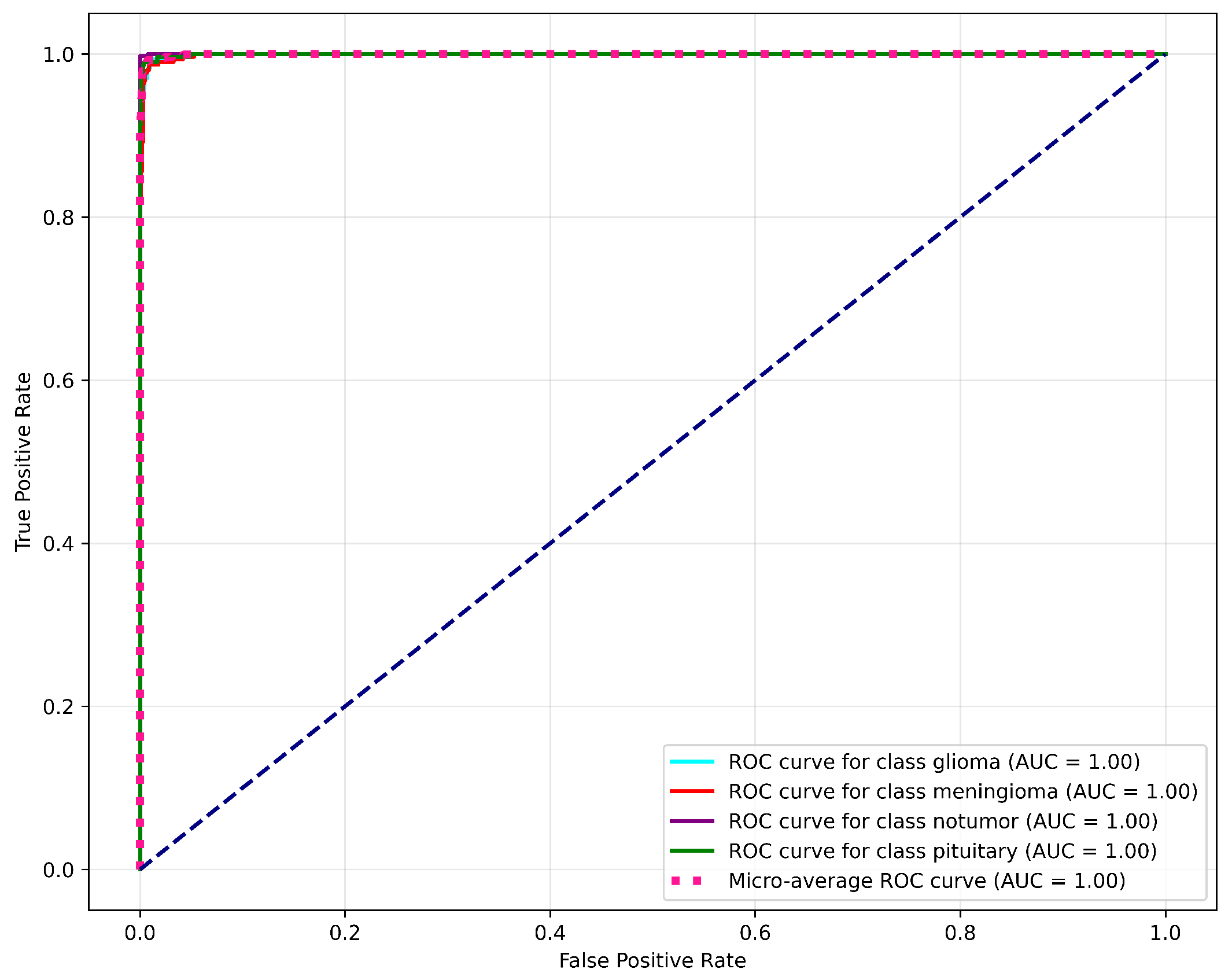
4.2.6. ROC and AUC Curve
- Specific ROC Classes: A separate sub-plot for each class, containing the ROC curve for glioma, meningioma, pituitary tumor, and no tumor, along with their respective AUC values. The model achieves an AUC of 1.00 for each tumor class, which indicates its superior performance.
- Micro-Average ROC Curve: A single curve that aggregates the performance of the model across all classes to yield a micro-average AUC of 1.00.
- Random Guessing Line: A dashed diagonal line with an AUC of 0.50, representing random guessing. The position of this line helps in understanding the model’s ability to distinguish between the different classes.
4.2.7. Model Execution Time Analysis
4.3. Error Analysis
- Glioma Misclassifications: 2 Meningioma instances were misclassified as Glioma.
- Meningioma Misclassifications: 2 samples of Pituitary Tumor were predicted to be Meningioma.
- Other Misclassifications: 1 sample of Glioma, 4 Meningioma, and 2 Pituitary Tumor samples were classified as the remaining classes.
- Class Distribution and Imbalance Analysis: The pre-partitioned distribution of the dataset reveals that the No Tumor class is a majority class, comprising 27.9% of the training data and 30.9% of the testing data. On the other hand, the Glioma and Pituitary Tumor classes have lower representation in both subsets, each contributing fewer overall images in comparison. This discrepancy created a slight class imbalance that could potentially bias the training process. 2 misclassifications as Meningioma, 4 misclassifications as Pituitary Tumor.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Conv | Convolutional Layer |
| ReLU | Rectified Linear Unit |
| Maxp. | MaxPooling |
| Meanp. | Mean Precision |
| Concat | Concatenation |
| Fully C. | Fully Connected Layer (Dense Layer) |
| xN | Multiplication Factor |
| ReLU6 | Rectified Linear Unit (version 6) |
References
- Sriharikrishnaa, S.; Suresh, P.S.; Prasada, K.S. An introduction to fundamentals of cancer biology. In Optical Polarimetric Modalities for Biomedical Research; Springer: Berlin/Heidelberg, Germany, 2023; pp. 307–330. [Google Scholar]
- Razzak, M.I.; Imran, M.; Xu, G. Efficient brain tumor segmentation with multiscale two-pathway-group conventional neural networks. IEEE J. Biomed. Health Inform. 2018, 23, 1911–1919. [Google Scholar] [CrossRef] [PubMed]
- Lei, B.; Yang, P.; Zhuo, Y.; Zhou, F.; Ni, D.; Chen, S.; Xiao, X.; Wang, T. Neuroimaging retrieval via adaptive ensemble manifold learning for brain disease diagnosis. IEEE J. Biomed. Health Inform. 2018, 23, 1661–1673. [Google Scholar] [CrossRef] [PubMed]
- Mikhno, A.; Zanderigo, F.; Ogden, R.T.; Mann, J.J.; Angelini, E.D.; Laine, A.F.; Parsey, R.V. Toward noninvasive quantification of brain radioligand binding by combining electronic health records and dynamic PET imaging data. IEEE J. Biomed. Health Inform. 2015, 19, 1271–1282. [Google Scholar] [CrossRef]
- Abiwinanda, N.; Hanif, M.; Hesaputra, S.T.; Handayani, A.; Mengko, T.R. Brain tumor classification using convolutional neural network. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering 2018, Prague, Czech Republic, 3–8 June 2018; Springer: Berlin/Heidelberg, Germany, 2019; Volume 1, pp. 183–189. [Google Scholar]
- Ghasemi, N.; Razavi, S.; Nikzad, E. Multiple sclerosis: Pathogenesis, symptoms, diagnoses and cell-based therapy. Cell J. 2017, 19, 1. [Google Scholar] [PubMed]
- ZainEldin, H.; Gamel, S.A.; El-Kenawy, E.S.M.; Alharbi, A.H.; Khafaga, D.S.; Ibrahim, A.; Talaat, F.M. Brain tumor detection and classification using deep learning and sine-cosine fitness grey wolf optimization. Bioengineering 2022, 10, 18. [Google Scholar] [CrossRef]
- Del Dosso, A.; Urenda, J.P.; Nguyen, T.; Quadrato, G. Upgrading the physiological relevance of human brain organoids. Neuron 2020, 107, 1014–1028. [Google Scholar] [CrossRef]
- Amin, J.; Sharif, M.; Haldorai, A.; Yasmin, M.; Nayak, R.S. Brain tumor detection and classification using machine learning: A comprehensive survey. Complex Intell. Syst. 2022, 8, 3161–3183. [Google Scholar] [CrossRef]
- Gritsch, S.; Batchelor, T.T.; Gonzalez Castro, L.N. Diagnostic, therapeutic, and prognostic implications of the 2021 World Health Organization classification of tumors of the central nervous system. Cancer 2022, 128, 47–58. [Google Scholar] [CrossRef]
- Louis, D.N.; Perry, A.; Wesseling, P.; Brat, D.J.; Cree, I.A.; Figarella-Branger, D.; Hawkins, C.; Ng, H.; Pfister, S.M.; Reifenberger, G.; et al. The 2021 WHO classification of tumors of the central nervous system: A summary. Neuro-oncology 2021, 23, 1231–1251. [Google Scholar] [CrossRef]
- Fountain, D.M.; Soon, W.C.; Matys, T.; Guilfoyle, M.R.; Kirollos, R.; Santarius, T. Volumetric growth rates of meningioma and its correlation with histological diagnosis and clinical outcome: A systematic review. Acta Neurochir. 2017, 159, 435–445. [Google Scholar] [CrossRef]
- Miah, M.B.A.; Kana, K.A.; Akter, A. Detection of brain cancer from MRI images using neural network. Int. J. Appl. Inf. Syst. 2016, 10, 6–11. [Google Scholar]
- Kleihues, P.; Soylemezoglu, F.; Schäuble, B.; Scheithauer, B.W.; Burger, P.C. Histopathology, classification, and grading of gliomas. Glia 1995, 15, 211–221. [Google Scholar] [CrossRef] [PubMed]
- Ohgaki, H.; Kleihues, P. Epidemiology and etiology of gliomas. Acta Neuropathol. 2005, 109, 93–108. [Google Scholar] [CrossRef] [PubMed]
- Alruwaili, A.A.; De Jesus, O. Meningioma, updated 2023 aug 23 ed.; StatPearls Publishing: Treasure Island, FL, USA, 2024. [Google Scholar]
- Melmed, S. Pathogenesis of pituitary tumors. Nat. Rev. Endocrinol. 2011, 7, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Zakareya, M.; Alam, M.B.; Ullah, M.A. Classification of cancerous skin using artificial neural network classifier. Int. J. Comput. Appl. 2018, 975, 8887. [Google Scholar] [CrossRef]
- Miah, M.B.A.; Yousuf, M.A. Detection of lung cancer from CT image using image processing and neural network. In Proceedings of the 2015 International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Savar, Dhaka, Bangladesh, 21–23 May 2015; pp. 1–6. [Google Scholar]
- Raghuvanshi, S.; Dhariwal, S. The VGG16 Method Is a Powerful Tool for Detecting Brain Tumors Using Deep Learning Techniques. Eng. Proc. 2023, 59, 46. [Google Scholar]
- Mahmud, M.I.; Mamun, M.; Abdelgawad, A. A deep analysis of brain tumor detection from mr images using deep learning networks. Algorithms 2023, 16, 176. [Google Scholar] [CrossRef]
- Chan, H.P.; Samala, R.K.; Hadjiiski, L.M.; Zhou, C. Deep learning in medical image analysis. In Deep Learning in Medical Image Analysis: Challenges and Applications; Springer Nature: Cham, Switzerland, 2020; pp. 3–21. [Google Scholar]
- Elaissaoui, K.; Ridouani, M. Application of Deep Learning in Healthcare: A Survey on Brain Tumor Detection. ITM Web Conf. 2023, 52, 02005. [Google Scholar] [CrossRef]
- Methil, A.S. Brain tumor detection using deep learning and image processing. In Proceedings of the 2021 International Conference on Artificial Intelligence and Smart Systems (ICAIS), Coimbatore, India, 25–27 March 2021; pp. 100–108. [Google Scholar]
- Kumar, P.R.; Bonthu, K.; Meghana, B.; Vani, K.S.; Chakrabarti, P. Multi-class Brain Tumor Classification and Segmentation using Hybrid Deep Learning Network Model. Scalable Comput. Pract. Exp. 2023, 24, 69–80. [Google Scholar] [CrossRef]
- Wadhwa, A.; Bhardwaj, A.; Verma, V.S. A review on brain tumor segmentation of MRI images. Magn. Reson. Imaging 2019, 61, 247–259. [Google Scholar] [CrossRef]
- Jesmin, T.; Ahmed, K.; Rahman, M.; Miah, M. Brain cancer risk prediction tool using data mining. Int. J. Comput. Appl. 2013, 61, 12. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Ma, N.; Zhang, X.; Zheng, H.T.; Sun, J. Shufflenet v2: Practical guidelines for efficient cnn architecture design. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 116–131. [Google Scholar]
- Ghadi, N.M.; Salman, N.H. Deep learning-based segmentation and classification techniques for brain tumor MRI: A review. J. Eng. 2022, 28, 93–112. [Google Scholar] [CrossRef]
- Patil, S.; Kirange, D. Ensemble of deep learning models for brain tumor detection. Procedia Comput. Sci. 2023, 218, 2468–2479. [Google Scholar] [CrossRef]
- Akkus, Z.; Galimzianova, A.; Hoogi, A.; Rubin, D.L.; Erickson, B.J. Deep learning for brain MRI segmentation: State of the art and future directions. J. Digit. Imaging 2017, 30, 449–459. [Google Scholar] [CrossRef]
- Younis, A.; Qiang, L.; Nyatega, C.O.; Adamu, M.J.; Kawuwa, H.B. Brain tumor analysis using deep learning and VGG-16 ensembling learning approaches. Appl. Sci. 2022, 12, 7282. [Google Scholar] [CrossRef]
- Jiang, Z.; Ding, C.; Liu, M.; Tao, D. Two-stage cascaded u-net: 1st place solution to brats challenge 2019 segmentation task. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the 5th International Workshop, BrainLes 2019, Held in Conjunction with MICCAI 2019, Shenzhen, China, 17 October 2019; Revised Selected Papers, Part I 5; Springer: Berlin/Heidelberg, Germany, 2020; pp. 231–241. [Google Scholar]
- Aboelenein, N.M.; Songhao, P.; Koubaa, A.; Noor, A.; Afifi, A. HTTU-Net: Hybrid Two Track U-Net for automatic brain tumor segmentation. IEEE Access 2020, 8, 101406–101415. [Google Scholar] [CrossRef]
- Kang, J.; Ullah, Z.; Gwak, J. MRI-based brain tumor classification using ensemble of deep features and machine learning classifiers. Sensors 2021, 21, 2222. [Google Scholar] [CrossRef] [PubMed]
- Sleem; Metwaly, A.A. A deep learning-based model for evaluating academic performance using student behavior patterns. Sustain. Mach. Intell. J. 2023, 3, 1–10. [Google Scholar]
- Tolba; Fathy. Chaotic metaheuristic optimization for improving text classification performance. Sustain. Mach. Intell. J. 2023, 3, 1–10. [Google Scholar]
- Celik, M.; Inik, O. Development of hybrid models based on deep learning and optimized machine learning algorithms for brain tumor Multi-Classification. Expert Syst. Appl. 2024, 238, 122159. [Google Scholar] [CrossRef]
- Srinivas, C.; KS, N.P.; Zakariah, M.; Alothaibi, Y.A.; Shaukat, K.; Partibane, B.; Awal, H. Deep transfer learning approaches in performance analysis of brain tumor classification using MRI images. J. Healthc. Eng. 2022, 2022, 3264367. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Guzmán, M.A.; Jiménez-Beristaín, L.; García-Guerrero, E.E.; López-Bonilla, O.R.; Tamayo-Perez, U.J.; Esqueda-Elizondo, J.J.; Palomino-Vizcaino, K.; Inzunza-González, E. Classifying brain tumors on magnetic resonance imaging by using convolutional neural networks. Electronics 2023, 12, 955. [Google Scholar] [CrossRef]
- Kazemi, A.; Shiri, M.E.; Sheikhahmadi, A. Classifying tumor brain images using parallel deep learning algorithms. Comput. Biol. Med. 2022, 148, 105775. [Google Scholar] [CrossRef] [PubMed]
- Akter, A.; Nosheen, N.; Ahmed, S.; Hossain, M.; Yousuf, M.A.; Almoyad, M.A.A.; Hasan, K.F.; Moni, M.A. Robust clinical applicable CNN and U-Net based algorithm for MRI classification and segmentation for brain tumor. Expert Syst. Appl. 2024, 238, 122347. [Google Scholar] [CrossRef]
- Rasheed, Z.; Ma, Y.K.; Ullah, I.; Ghadi, Y.Y.; Khan, M.Z.; Khan, M.A.; Abdusalomov, A.; Alqahtani, F.; Shehata, A.M. Brain tumor classification from MRI using image enhancement and convolutional neural network techniques. Brain Sci. 2023, 13, 1320. [Google Scholar] [CrossRef]
- Nickparvar, M. Brain Tumor MRI Dataset. 2021. Available online: https://www.kaggle.com/datasets/masoudnickparvar/brain-tumor-mri-dataset (accessed on 22 May 2025).
- Cheng, J. Brain Tumor Dataset. 2017. Available online: https://figshare.com/articles/dataset/brain_tumor_dataset/1512427/5 (accessed on 22 May 2025).
- Hamada, A. Brain Tumor Detection. 2022. Available online: https://www.kaggle.com/datasets/ahmedhamada0/brain-tumor-detection (accessed on 22 May 2025).
- Setiawan, A.W.; Mengko, T.R.; Santoso, O.S.; Suksmono, A.B. Color retinal image enhancement using CLAHE. In Proceedings of the International Conference on ICT for Smart Society, Jakarta, Indonesia, 13–14 June 2013; pp. 1–3. [Google Scholar]
- Miah, M.B.A.; Awang, S.; Azad, M.S.; Rahman, M.M. Keyphrases concentrated area identification from academic articles as feature of keyphrase extraction: A new unsupervised approach. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 789–796. [Google Scholar] [CrossRef]
- Miah, M.B.A.; Awang, S.; Rahman, M.M.; Hosen, A.S.; Ra, I.H. Keyphrases frequency analysis from research articles: A region-based unsupervised novel approach. IEEE Access 2022, 10, 120838–120849. [Google Scholar] [CrossRef]
- Xie, J.; Wu, J.; Xiao, Z. Spatio-Temporal Patterns and Sentiment Analysis of Ting, Tai, Lou, and Ge Ancient Chinese Architecture Buildings. Buildings 2025, 15, 1652. [Google Scholar] [CrossRef]
- Chicco, D.; Tötsch, N.; Jurman, G. The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation. BioData Min. 2021, 14, 19. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Matthews correlation coefficient (MCC) is more informative than Cohen’s Kappa and Brier score in binary classification assessment. IEEE Access 2021, 9, 78368–78381. [Google Scholar] [CrossRef]
- Sherif, M.M. Brain Tumor Dataset. 2022. Available online: https://www.kaggle.com/datasets/mohamedmetwalysherif/braintumordataset (accessed on 22 May 2025).
- Kumar, P. Brain MRI. 2021. Available online: https://www.kaggle.com/datasets/pradeep2665/brain-mri (accessed on 22 May 2025).
- Chakrabarty, N. Brain MRI Images for Brain Tumor Detection. Dataset Used in the Study “Brain Tumor Analysis Using Deep Learning and VGG-16 Ensembling Learning Approaches.”. 2022. Available online: https://www.kaggle.com/datasets/navoneel/brain-mri-images-for-brain-tumor-detection (accessed on 25 June 2024).
| Class | Train Images | Train Percent | Test Images | Test Percent | Test Ratio |
|---|---|---|---|---|---|
| Glioma | 1321 | 23.1 | 300 | 22.9 | 22.7 |
| Meningioma | 1339 | 23.4 | 306 | 23.3 | 22.9 |
| No tumor | 1595 | 27.9 | 405 | 30.9 | 25.4 |
| Pituitary | 1457 | 25.5 | 300 | 22.9 | 20.6 |
| Total | 5712 | 100 | 1311 | 100 | 22.95 Avg |
| Bottleneck Layer | Parameter Count | FLOPs (Millions) |
|---|---|---|
| ×2 | 0.5 | 5.0 |
| ×3 | 1.0 | 10.0 |
| ×4 | 1.9 | 15.0 |
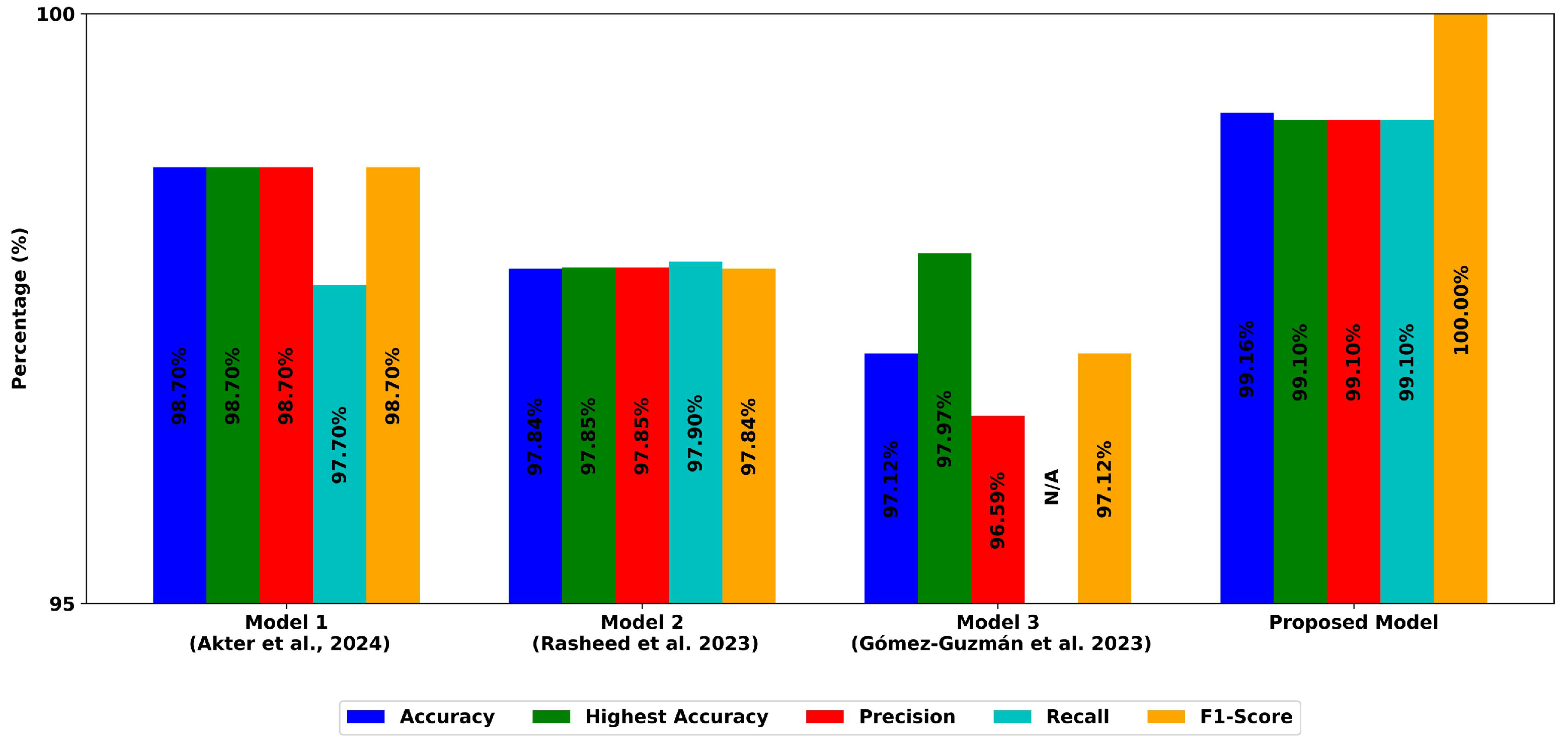
| Model | Accuracy (%) | Precision | Recall | F1-Score | MCC | Cohen’s Kappa | Dataset | Reference |
|---|---|---|---|---|---|---|---|---|
| Proposed Model (MobileNetV2) | 99.16 | 0.991 | 0.991 | 0.991 | 0.9886 | 0.980 | Kaggle (Msoud) | This Work |
| Ensemble Deep Learning (EDCNN) | 97.77 | 0.9666 | 0.9830 | 0.9747 | - | 0.9830 | Figshare | [46] |
| InceptionV3 | 97.12 | 0.9797 | 0.9659 | 0.9659 | - | - | Kaggle (Msoud) | [45] |
| VGG-16-Based Ensemble + CNN | 98.41 | 0.944 | 0.914 | 0.928 | - | - | Kaggle (Navoneel) | [56] |
| Robust CNN + U-Net (No Segmentation) | 98.70 | 0.988 | 0.987 | 0.988 | - | - | Kaggle (Msoud + Add. Datasets) | [45,47,54,55] |
| Robust CNN + U-Net (With Segmentation) | 98.80 | 0.990 | 0.988 | 0.989 | - | - | Kaggle (Msoud + Add. Datasets) | [45,47,54,55] |
| Generic CNN (Binary Classification) | 81.05 | 0.8527 | 0.7677 | 0.810 | - | - | Kaggle (Msoud) | [45] |
| Dimension | Precision | Recall | F1-Score | Support | Specificity | CI/SD for F1-Score |
|---|---|---|---|---|---|---|
| Glioma | 0.99 | 0.99 | 0.99 | 300 | 99.70 | ±0.012 (CI) |
| Meningioma | 0.98 | 0.99 | 0.99 | 306 | 99.60 | ±0.014 (CI) |
| No tumor | 1.00 | 1.00 | 1.00 | 405 | 99.89 | ±0.010 (SD) |
| Pituitary | 0.99 | 0.98 | 0.99 | 300 | 99.80 | ±0.011 (SD) |
| Accuracy | 0.99 | 1311 | ||||
| Macro avg | 0.99 | 0.99 | 0.99 | 1311 | ||
| Weighted avg | 0.99 | 0.99 | 0.99 | 1311 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.A.; Miah, M.B.A.; Hossain, M.A.; Hosen, A.S.M.S. Enhanced Brain Tumor Classification Using MobileNetV2: A Comprehensive Preprocessing and Fine-Tuning Approach. BioMedInformatics 2025, 5, 30. https://doi.org/10.3390/biomedinformatics5020030
Rahman MA, Miah MBA, Hossain MA, Hosen ASMS. Enhanced Brain Tumor Classification Using MobileNetV2: A Comprehensive Preprocessing and Fine-Tuning Approach. BioMedInformatics. 2025; 5(2):30. https://doi.org/10.3390/biomedinformatics5020030
Chicago/Turabian StyleRahman, Md Atiqur, Mohammad Badrul Alam Miah, Md. Abir Hossain, and A. S. M. Sanwar Hosen. 2025. "Enhanced Brain Tumor Classification Using MobileNetV2: A Comprehensive Preprocessing and Fine-Tuning Approach" BioMedInformatics 5, no. 2: 30. https://doi.org/10.3390/biomedinformatics5020030
APA StyleRahman, M. A., Miah, M. B. A., Hossain, M. A., & Hosen, A. S. M. S. (2025). Enhanced Brain Tumor Classification Using MobileNetV2: A Comprehensive Preprocessing and Fine-Tuning Approach. BioMedInformatics, 5(2), 30. https://doi.org/10.3390/biomedinformatics5020030









