Abstract
Background: Transforming one-dimensional (1D) biomedical signals into two-dimensional (2D) images enables the application of convolutional neural networks (CNNs) for classification tasks. In this study, we investigated the effectiveness of different 1D-to-2D transformation methods to classify electrocardiogram (ECG) and electroencephalogram (EEG) signals. Methods: We select five transformation methods: Continuous Wavelet Transform (CWT), Fast Fourier Transform (FFT), Short-Time Fourier Transform (STFT), Signal Reshaping (SR), and Recurrence Plots (RPs). We used the MIT-BIH Arrhythmia Database for ECG signals and the Epilepsy EEG Dataset from the University of Bonn for EEG signals. After converting the signals from 1D to 2D, using the aforementioned methods, we employed two types of 2D CNNs: a minimal CNN and the LeNet-5 model. Our results indicate that RPs, CWT, and STFT are the methods to achieve the highest accuracy across both CNN architectures. Results: These top-performing methods achieved accuracies of 99%, 98%, and 95%, respectively, on the minimal 2D CNN and accuracies of 99%, 99%, and 99%, respectively, on the LeNet-5 model for the ECG signals. For the EEG signals, all three methods achieved accuracies of 100% on the minimal 2D CNN and accuracies of 100%, 99%, and 99% on the LeNet-5 2D CNN model, respectively. Conclusions: This superior performance is most likely related to the methods’ capacity to capture time–frequency information and nonlinear dynamics inherent in time-dependent signals such as ECGs and EEGs. These findings underline the significance of using appropriate transformation methods, suggesting that the incorporation of time–frequency analysis and nonlinear feature extraction in the transformation process improves the effectiveness of CNN-based classification for biological data.
1. Introduction
Transforming one-dimensional (1D) biomedical signals into two-dimensional (2D) formats has significantly improved the analysis and interpretation of complex physiological data. Electrocardiograms (ECGs) and electroencephalograms (EEGs) provide critical information about cardiac and brain activity, respectively. Traditional one-dimensional analysis methods face difficulties in capturing the complex patterns and anomalies present in such signals. Converting 1D signals into 2D representations would allow for optimal use of analytical techniques such as Convolutional Neural Networks (CNNs), which have transformed image processing and pattern recognition tasks across multiple domains [1,2].
CNNs excel at handling spatial hierarchies in data, making them suitable for interpreting 2D images created from processed biological information. Because of the spatial structure inherent in 2D data, CNNs can uncover local patterns and characteristics that would otherwise go undetected in 1D analysis. This capability is especially useful for biomedical applications, where the early and accurate detection of anomalies has a major impact on patient well-being. Transforming ECG and EEG information into 2D images could enable the use of CNNs, potentially boosting diagnostic accuracy and providing deeper insights into underlying physiological problems [3].
Various methods for 1D-to-2D transformation have been employed in biomedical signal processing research, including Discrete Fourier Transform (DFT), Short-Time Fourier Transform (STFT), Fast Fourier Transform (FFT), Continuous Wavelet Transform (CWT), Signal Reshaping (SR), and Recurrence Plots (RPs). Each method provides a unique way of presenting the signal’s time–frequency information in a spatial context. While transformations like DFT, FFT, STFT, and CWT focus on representing the signal in the time–frequency domain, RPs offer a different perspective by capturing the signal’s recurrent patterns and nonlinear dynamics [4,5]. However, there is a lack of studies that systematically evaluate different transformation approaches to identify which are the most effective for CNN-based categorization.
To this end, the contribution of the current work is to fill the latter gap by evaluating multiple well-known transformation strategies to assess their effectiveness in improving the classification of ECG and EEG signals using CNNs. ECG data, which record the electrical activity of the heart, may show minor variations that indicate the presence of arrhythmia or other cardiac disorders. The aim is to improve the detection of such disorders by converting ECG signals into 2D images and extracting more relevant features. Similarly, EEG signals monitor the electrical activity of the brain and are used to diagnose neurological disorders such as epilepsy. Transforming EEG signals into 2D images would allow for the examination and evaluation of complex brain patterns, which may lead to better detection of epileptic events and other disorders.
In this work, the MIT-BIH Arrhythmia Database for ECG signals and the University of Bonn’s Epilepsy EEG Dataset for EEG signals were employed. Five well-known transformation methods were used to convert 1D signals into 2D images, tested with two types of 2D classification CNNs: a minimal CNN and the Lenet-5 model. This work not only serves as a foundation for future research but also provides practical assistance to practitioners seeking efficient transformation methodologies for several biological applications [6,7].
The results of our study indicate that Recurrence Plots (RPs), Continuous Wavelet Transform (CWT), and Short-Time Fourier Transform (STFT) are superior in capturing time–frequency information in ECG and EEG signals compared to the other methods. Our findings suggest that the choice of the transformation method significantly impacts the performance of CNN-based classification models. By identifying the most effective transformation techniques, our research (note that all the codes and materials associated with this study will be available in a GitHub repository upon acceptance of this work) contributes valuable insights to the field of biomedical signal processing, potentially leading to advancements in diagnostic methodologies and improved patient care.
2. Related Work
As far as the authors’ knowledge goes, up to the day of writing this study, there is no dedicated study in the literature to cover the comparison of different dimension transformation methods towards using 2D CNNs for either the classification of biomedical signals or a different task. However, while the classification of ECG or EEG signals is a topic well covered in the literature, each reported study in the literature uses one- or two-dimension transformation methods to achieve their objective.
One major contribution of our study lies in the broad range of 1D-to-2D transformations that we systematically investigate for ECG and EEG signals. While many prior works focus on a single transformation method, such as CWT, STFT, or RPs, for a specific dataset, we directly compare five distinct approaches (CWT, STFT, FFT, RPs, and SR) under uniform experimental conditions. By doing so, we provide a more holistic understanding of how different transformations capture various aspects of signal information, whether for time–frequency content, nonlinear dynamics, or simpler amplitude-based patterns, and how these, in turn, affect classification performance. Furthermore, we test each transformation on two different CNN architectures (a minimal CNN and the deeper LeNet-5), shedding light on how model complexity interacts with the chosen transformation.
Through this work, we address an observed gap in the literature: although extensive research has explored individual transformations for biomedical signal analysis, there has been no extensive comparison of multiple 1D-to-2D methods within a single study for both ECG and EEG data. Our analysis bridges this gap by showing how effective each transformation is in capturing the key characteristics of cardiac and neural signals and indicating the approaches best matched to particular model architectures. This comparative perspective offers practical guidance to researchers seeking to optimize the CNN-based classification of biomedical signals, highlighting the conditions under which different transformations excel or fall short.
This contribution of the scientific results can be clearly observed from the details included in Table 1, where the state-of-the-art literature is compared to the present work (ours). More specifically, in study [8], the authors utilize the CWT method to transform the 1D ECG signals into 2D images. They make use of the MIT-BIH arrhythmia [7], INCART [9] and SVDB [10] datasets. A custom VGGNet 2D CNN model, composed of eight layers and pre-trained on the ImageNet, is used in order to classify ECG signals. In study [11], the authors utilize Gramian Angular Field (GAF)-based methods, including the Gramian Angular Summation Field (GASF) and Gramian Angular Difference Field (GADF), to transform the 1D ECG signals into 2D images. They make use of the Physikalisch-Technische Bundesanstalt (PTB) [12]. A custom 2D CNN model is proposed in order to differentiate the ECG signals between healthy controls and inferior myocardial (MI) subjects. In study [13], the authors utilize the Gramian Angular Field (GAF) method to transform the 1D ECG signals into 2D images. They make use of the MIT-BIH Normal Sinus Rhythm Database [14] (subjects at a resting state) and ECG-GUDB (individuals under four specific activities) [15] dataset. A custom VGG19 2D CNN model is proposed for ECG identification. In both studies [16,17], the authors make use of the Signal Reshaping (SR) method to transform the 1D ECG signals into 2D images. They utilize the MIT-BIH arrhythmia for ECG classification by training a custom 2D CNN network. In study [18], the authors utilize the RP method to transform the 1D ECG signals into 2D images. They make use of the MIT-BIH Arrhythmia, Creighton University Ventricular Tachyarrhythmia [19], MIT-BIH Atrial Fibrillation [20], and MIT-BIH Malignant Ventricular Ectopy [21] databases. The 2D CNN networks used for ECG arrhythmia classification are AlexNet, VGG16, and VGG19. In study [22], the authors utilize the STFT method to transform the 1D ECG signals into 2D images. They make use of MIT-BIH Arrhythmia ECG. This study utilizes a custom 2D CNN for ECG arrhythmia classification. In study [23], the authors utilize the STFT method to transform the 1D ECG signals into 2D images as well. They make use of MIT-BIH Arrhythmia ECG for ECG classification and utilize the ResNet18 2D CNN model. In study [24], the CWT and STFT methods are applied to transform 1D EEG signals into 2D images. The Bonn Epilepsy EEG dataset [6] is utilized in this study. The ResNet50 model, the VGG16, and a custom 2D CNN are used for EEG classification and seizure detection. In study [25], the authors utilize the FFT method to transform the 1D EEG signals into 2D images. They make use of the Bonn Epilepsy EEG and CHB-MIT scalp EEG [26] datasets. This study utilizes the PCANet 2D CNN for EEG classification. In study [27], the authors utilize the FFT method to transform the 1D EEG signals into 2D images. They use the Bern-Barcelona EEG [28] dataset and a custom 2D CNN to classify the epileptic EEG recordings. In study [29], the authors utilize the DFT method to transform the 1D EEG signals into 2D images using the SSVEP [30] dataset for EEG classification by training a custom 2D CNN network. Finally, in study [31], the authors utilize the CWT method to transform the 1D ECG signals into 2D images. They use the MIT-BIH arrhythmia and BIDMC Congestive Heart Failure [32] databases utilizing the AlexNet 2D CNN network for ECG classification.

Table 1.
Comparative table of related works versus our study.
Table 1 includes features such as the dimension transformations, datasets, and 2D CNN architectures used. As can be observed, the present work covers a wider set of different transformations while other methods deal with only one or two methods; the present study also uses two different data types (EEG and ECG) while other methods use only one data type; and two different CNN architectures are also considered that have not been previously investigated for the problem under study.
3. Materials and Methods
In this section, the datasets, preprocessing, post-processing, transformation methods, and CNN models that were used in this work are presented. It should be noted that all algorithms were implemented in Python 3.10. For the ECG signal preprocessing, we made use of the wfdb library to load the signals and the scipy.signal library for the preprocessing functions. For EEG signal preprocessing, we used both the scipy.signal and the sklearn.preprocessing libraries for the preprocessing functions, and numpy to load the signals.
3.1. Dataset Description
In this study, two widely recognized biomedical signal datasets were used in order to evaluate the effectiveness of different 1D-to-2D transformation methods. The first dataset was the MIT-BIH Arrhythmia Database from PhysioNet, which contains a large number of electrocardiogram (ECG) recordings that have been extensively used in arrhythmia detection and cardiac signal analysis studies. The second dataset is the Epilepsy EEG Dataset from the University of Bonn, which contains electroencephalogram (EEG) recordings that are critical for studying epileptic seizure detection and neural activity patterns [33,34].
3.1.1. MIT-BIH Arrhythmia Database
The MIT-BIH Arrhythmia Database [7] is a key dataset in biomedical signal processing, and it is widely used in studies on cardiac arrhythmia detection and classification. The BIH Arrhythmia Laboratory compiled the dataset between 1975 and 1979, containing 48 half-hour excerpts of two-channel ambulatory electrocardiogram (ECG) recordings from 47 different patients. These subjects included a mix of inpatients (about 60%) and outpatients (roughly 40%) from Boston’s Beth Israel Hospital, ensuring a diversified representation of cardiac problems throughout a large patient group.
The ECG signals were digitized with outstanding accuracy at 360 samples per second per channel, resulting in high-resolution data suitable for detailed analysis. The recordings had an 11-bit resolution over a 10-millivolt range, allowing for the accurate capture of the heart’s electrical activity. This high level of detail is critical for detecting subtle anomalies and arrhythmia in cardiac signals.
The cautious annotation process is a key feature of the MIT-BIH Arrhythmia Database. Two or more expert cardiologists independently reviewed each ECG record, annotating every heartbeat and arrhythmia. In cases of disagreement, the cardiologists met to resolve the differences, resulting in a consensus annotation for each beat. This rigorous process resulted in a reliable set of annotations for approximately 110,000 heartbeats, which serves as a valuable foundation for algorithm development, validation, and benchmarking in arrhythmia detection studies.
In our study, we focus on a subset of the MIT-BIH Arrhythmia Database, specifically selecting recordings including the following basic five types of heartbeats:
- 1.
- ‘N’: Normal beat. Represents standard heartbeats with no arrhythmia deviations and serves as the control group for comparison analysis. This class includes 90,631 beat samples.
- 2.
- ‘S’: Supraventricular premature beat. Early heartbeats originate above the ventricles, usually in the atria or atrioventricular nodes, and occur earlier than expected in the cardiac cycle. This class includes 2781 beat samples.
- 3.
- ‘V’: Premature ventricular contraction. Early beats from the ventricles, commonly referred to as skipped heartbeats, can indicate underlying cardiac issues. This class includes 7236 beat samples.
- 4.
- ‘F’: Fusion between ventricular and normal beats. When a normal beat and a ventricular ectopic beat overlap, the result is a complex waveform that combines features from both beats. This class includes 803 beat samples.
- 5.
- ‘Q’: Unclassifiable beat. Beats that do not fit into standard classification classes due to noise, artifacts, or atypical morphology make them difficult but necessary for robust classification systems. This class includes 8043 beat samples.
3.1.2. Epilepsy EEG Dataset
The University of Bonn’s Epilepsy EEG Dataset [6] is an extensive resource that is widely used in neurological research, particularly for the study of epilepsy and seizure detection algorithms. This dataset is carefully organized to aid in the differentiation of normal and epileptic brain activity using EEG signal analysis.
The dataset is divided into five distinct subsets, labeled A to E, each of which contains 100 single-channel EEG recordings. Each recording is 23.6 s long, providing a significant amount of data for analysis. All EEG signals are sampled at 173.61 Hz using a standardized 128-channel amplifier system. The data are converted from 12-bit analog-to-digital values and bandpass-filtered between 0.53 Hz and 40 Hz with a 12 dB/octave roll-off to focus on the most informative frequency ranges for EEG analysis.
A detailed description of each subset is provided below:
- 1.
- Set A (Z): EEG recordings of healthy subjects with their eyes open. This represents normal, awake brain activity.
- 2.
- Set B (O): EEG recordings of healthy subjects with their eyes closed. Reflects normal brain activity in the absence of visual input.
- 3.
- Set C (N): Interictal (non-seizure) EEG recordings from areas outside the epileptogenic zone in epileptic patients. Signals are from non-epileptic areas but were recorded with people who have epilepsy.
- 4.
- Set D (F): Interictal EEG recordings from the epileptogenic zone in epileptic patients. Signals may show slight variations associated with epilepsy during seizure-free periods.
- 5.
- Set E (S): Ictal (seizure) EEG recordings taken during actual seizures in epileptic patients. Signals are strongly abnormal, with distinct seizure patterns.
3.2. Data Preprocessing
Preprocessing the ECG and EEG signals is a crucial process to enhance signal quality and reliability before transforming them into 2D images. By cleaning and standardizing the data, preprocessing ensures that the 1D-to-2D transformations are capable of producing images to accurately represent the underlying physiological signals [35]. The preprocessing steps for both types of signals are illustrated in Figure 1.
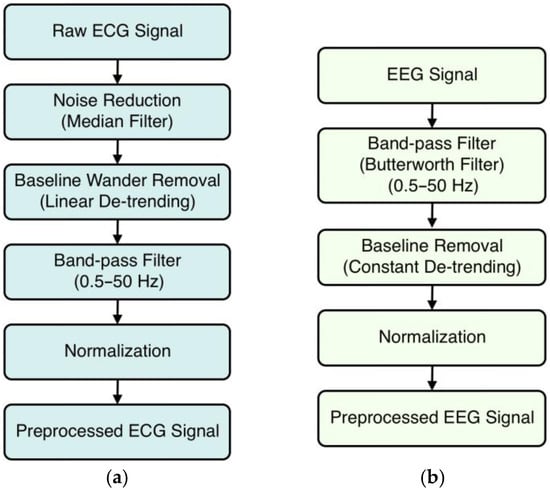
Figure 1.
Preprocessing steps for (a) ECG signals and (b) EEG signals.
3.2.1. ECG Signal Preprocessing
In our study, ECG signals went through an extensive preprocessing pipeline to improve the signals’ quality and prepare the data for accurate 1D-to-2D transformations. This preprocessing is necessary to ensure that the transformed images accurately represent the underlying physiological signals, which subsequently improves the feature extraction and classification performance of CNN models.
The first step in preprocessing is noise reduction with a median filter. ECG signals are frequently contaminated with noise, including electrical interference, muscle artifacts, and other minor fluctuations that can obscure key signal features. The median filter solves this problem by applying a sliding window across the signal and replacing each data point with the median value of the neighboring ones within that window. This procedure effectively smooths the signal by removing spikes and minor artifacts while maintaining the essential features of the ECG waveform, such as the P, QRS, and T waves. The median filter is especially good at eliminating impulsive noise without blurring sharp signal transitions, which is critical for preserving the ECG’s diagnostic features.
In the second preprocessing step, we addressed baseline wander, which is a low-frequency drift in the ECG signal caused by factors such as respiration, body movements, and electrode impedance changes. Baseline wander can cause inaccuracies in feature extraction, particularly when detecting the isoelectric line and measuring the amplitudes of different ECG components. To remove the drift, we used a detrending technique. We used linear detrending [36], which involves fitting and subtracting a straight line to the signal data to re-center the signal oscillations around a zero baseline. This method preserves the morphology of the ECG waveform while eliminating gradual changes in the baseline, ensuring that signal variations are caused by cardiac activity rather than external influences.
We also included a third step using bandpass filtering [37] to improve signal quality. The goal of bandpass filtering is to keep only the frequencies related to physiological cardiac activity while removing noise outside of this range. We applied a bandpass filter with two cutoff frequencies: 0.5 Hz and 50 Hz. Frequencies below 0.5 Hz are commonly related to baseline wander and other low-frequency noises, while frequencies above 50 Hz may include muscular artifacts and electrical interference. To implement this filter, we computed the Nyquist frequency (half of the sampling rate) and developed a fourth-order Butterworth filter [38] with a good balance of passband flatness and roll-off steepness. The used filter conducts forward and reverse filtering to reduce phase distortion while maintaining the temporal alignment of the ECG data.
Finally, we used normalization, which standardized the amplitude of the ECG signals across all samples. This is important because ECG recordings can vary significantly in amplitude due to individual physiological differences, electrode placement, and equipment calibration. We applied z-score normalization [39]. This procedure requires calculating the mean and standard deviation of the filtered ECG signal before transforming each data point by subtracting the mean and dividing it by the standard deviation. Normalization eliminates inter-subject variability and makes sure that all signals contribute equally during model training, preventing any single signal from dominating the learning process and unevenly influencing the model due to scale variations, thereby improving the stability and performance of future analyses.
Following these preprocessing steps, we segmented the ECG signals into individual beats in a manner that guarantees each segment has a uniform length. To perform this, we used annotations in the ECG. For an annotation at sample index i, we extracted a fixed window of 100 samples around i (100 samples before and 100 samples after). This method produced a consistent number of samples for each beat, thus standardizing the length of every extracted segment. By centering each segment on the annotated beat, we preserved the beat’s essential morphology while ensuring that all segments aligned in size. This windowing technique not only provides enough context around each annotated beat but also guarantees a uniform segment length for all beats.
3.2.2. EEG Signal Preprocessing
The EEG data were initially sampled at a frequency of 173.61 Hz, as specified by the dataset providers. This sampling rate accurately captures the frequency components of EEG signals, ranging from slow delta waves (<4 Hz) to faster gamma waves (>30 Hz). To focus on the most relevant neural oscillations and remove unwanted noise, we used a bandpass filter [37] to keep frequencies between 0.5 Hz and 50 Hz. High-frequency noise can be found at frequencies above 50 Hz, such as muscle artifacts (electromyographic activity), power line interference, and other electrical noises that can mask the EEG signal. The high cutoff at 50 Hz reduced the effect of these unwanted parts, increasing the signal-to-noise ratio. To create the bandpass filter, we transformed the cutoff frequencies into ratios relative to the Nyquist frequency, which is half of the sampling rate (86.805 Hz in this case). We chose a Butterworth filter [38] because of its flat response to the frequency in the passband and low-phase distortion. The filter was applied using a zero-phase filtering technique. This method avoids phase distortion, maintaining the temporal properties of the EEG signal, which is critical for precise time-domain analyses.
After the bandpass filtering, we tackled the issue of baseline drift using a process known as baseline removal or detrending. Baseline drift in EEG signals can be caused by slow fluctuations in electrode–skin impedance, breathing, or gradual movements during recording. These low-frequency shifts may mask true neural oscillations, complicating data interpretation. We used linear detrending [36] by drawing a straight line through each EEG segment and subtracting it from the signal. This method adequately centers the signal around a zero baseline while maintaining the higher-frequency components indicative of neural activity. We removed the baseline drift to ensure that the EEG signals precisely represent the brain’s electrical activity without disruption from slow-varying artifacts.
The final step in preprocessing is to normalize the EEG signals. To standardize the data across all samples and make meaningful comparisons, we used z-score normalization [39], the same as in the case of the ECG signals.
3.3. Dimension Transformation Methods
Transforming 1D signals into 2D formats is a crucial step when enabling the employment of 2D CNNs for advanced analysis towards exploiting the spatial feature extraction capabilities of CNNs, which are well-suited for image data but not directly applicable to raw 1D signals. Various transformation methods can be employed, each offering unique insights into the signal’s characteristics by emphasizing different time–frequency or spatial properties [16,40].
In this study, we utilized and compared five well-known dimension transformation methods: the Signal Reshaping (SR) method, Recurrence Plots (RPs), Fast Fourier Transform (FFT), Short-Time Fourier Transform (STFT), and Continuous Wavelet Transform (CWT). It should be noted that other methods also exist, such as the Gramian Angular Fields (GAFs), Gramian Angular Summation Fields (GASFs), Gramian Angular Difference Fields (GADFs), Markov Transition Field (MTF), Recurrence Quantification Analysis (RQA), and Dynamic Time Warping (DTW). In this work, the five more referenced transformation methods from the literature according to Scopus were selected.
The aim was to examine, among the selected transformation methods, which one yielded the optimal performance when used with the same 2D CNN model. To maintain consistency and ensure fair comparison across all processed segments, we standardized the transformed images to dimensions of 224 × 224 pixels in grayscale format. This consistency allowed the direct assessment of how each transformation method impacts CNN’s ability to learn and classify the underlying patterns in ECG and EEG signals [41,42]. Also, the preprocessed and transformed images were augmented in order to increase the quantity of our datasets and improve the robustness of the models.
For ECG signals, we used custom augmentation methods [43], including slight rotations, zooms, brightness and contrast adjustments, noise addition, and light Gaussian blurring. These augmentations introduced small, realistic variations in the images while preserving the essential features of the signals. More specifically, for each ECG beat image, we applied a set of custom augmentation functions that introduced realistic yet small alterations, preventing drastic changes that might distort important ECG features. These functions included slight rotations within ±5°, zooms fluctuating between 0.95 and 1.05 of the original size, and gentle manipulations of brightness and contrast within a narrow range (e.g., 0.95 to 1.05). We also added minimal Gaussian noise and used a light Gaussian blur filter to mimic real-world factors such as sensor variability and minor motion artifacts. By targeting each class that had fewer samples, we repeated and augmented their images until all classes reached the target number of samples (100,000 images). Through this process, the distribution of classes became balanced, helping to reduce overfitting and enabling our models, especially the minimal CNN, to generalize better. In practice, these augmented images slightly raised overall accuracy and stabilized the training process, maintaining the integrity of the signal representations while increasing the variability in the dataset, ensuring that no specific class or subtle artifact dominated the model’s learned features and that the trained models would be trained to better generalize to unseen data.
In ECG signal augmentation, our choice of methods—such as slight rotations, minimal zooming, controlled brightness and contrast adjustments, and low-level Gaussian noise—stems from the need to replicate small but realistic variations that occur naturally in clinical recordings. For instance, minor rotations simulate slight deviations in electrode placement or patient posture, while constrained zoom factors help mimic differences in signal amplitude that might arise from variations in contact pressure or minor changes in body movement. Adjusting brightness and contrast in a narrow range allows us to emulate variations in sensor calibration or subtle changes at the skin–electrode interface without distorting the fundamental morphology. Finally, adding weak Gaussian noise mirrors the background interference and minor artifacts seen in real-world environments, ensuring that the model learns to distinguish true cardiac events from incidental fluctuations.
For EEG signals, we implemented minimal rotations, zooms, brightness, contrast, and blue adjustments. More specifically, we created new EEG images by applying minor modifications to the original images, ensuring that they remained representative of real-world variability. We allowed small rotations within a range of ±3°, introduced minimal zoom fluctuations so that the image size varied by only a few percent, and adjusted brightness varied by a similarly narrow margin. These changes helped simulate realistic variations in the recording conditions without distorting the essential EEG patterns. We also slightly tweaked image contrast and introduced a very mild blur to emulate minor changes in sensor settings or environmental factors. These augmentations were primarily used to expand the smaller sets until each category reached a uniform size, mitigating class imbalance. By carefully restricting the intensity of each augmentation (e.g., limiting rotation, zoom, and brightness to small intervals), we preserved the core signal features while still providing enough diversity for the model to learn robust patterns, ultimately improving classification consistency across different EEG states.
A similar rationale to ECG applies to EEG signal augmentation. Small rotations and zooming reflect minute shifts in electrode positioning or differences in head shape across subjects. Subtle brightness and contrast changes can mimic variations in amplifier settings or electrode impedance, while minimal Gaussian blurring replicates the mild smoothing interferences that can occur due to factors like hair, minor head movements, or low-level sensor noise. Crucially, these augmentations are constrained to be slight rather than drastic, preserving the signal’s core frequency content and topographic structure essential for identifying neural dynamics. By carefully controlling the range and intensity of each augmentation, we avoided inadvertently introducing artifacts that had no physiological basis, thus helping the model learn robust patterns that genuinely correspond to normal and pathological EEG states.
In both cases, the key is that custom-applied augmentations support model robustness by exposing it to realistic variations without altering the essential nature of ECG or EEG signals. This approach strengthens the model’s generalization to clinical conditions without destroying the crucial physiological information needed for accurate classification.
For the ECG signals, we reached a target sample of 100,000 images, whereas for the EEG signals, we reached a sample of 10,000 images. Both datasets were later split into 70% for training, 15% for validation during training, and 15% for the evaluation of the 2D CNN models.
In the following section, the five transformation methods are briefly reviewed.
3.3.1. Continuous Wavelet Transform (CWT)
Continuous Wavelet Transform (CWT) [44] is a signal processing technique that converts a 1D signal to a 2D time–frequency representation, retaining both time and frequency information, and making it ideal for analyzing non-stationary signals with a changing frequency content, such as ECGs and EEGs. Mathematically, the CWT of a signal x(t) is defined by the following integral:
where C(a,b) represent the wavelet coefficients, is the scaled and translated version of the mother wavelet ψ(t), a is the scale parameter controlling the dilation or compression of the wavelet, and b is the translation parameter controlling the shift along the time axis, while the asterisk denotes the complex conjugate. The scaled and translated wavelet is given by the following equation:
By varying a and b, CWT calculates wavelet coefficients that measure the correlation between the signal and the wavelet at various scales and positions, achieving a 2D representation of how the signal’s frequency content changes over time.
For the ECG signals, the CWT method starts by analyzing each preprocessed ECG segment to capture its time–frequency features in a single 2D representation. We chose the Morlet wavelet as the mother wavelet due to its good balancing temporal and frequency localization abilities, which is necessary for recognizing transitory features in ECG signals. This magnitude matrix was scaled to a consistent dimension of 224 by 224 pixels via interpolation, guaranteeing uniformity across all images for the CNN input. The scaled matrix was then normalized to grayscale values between 0 and 255, resulting in an image format. To improve feature visibility, we used adaptive histogram equalization, which changed local contrast and light Gaussian smoothing to decrease noise.
A similar procedure was used to process the EEG signals. The Morlet wavelet was used to perform CWT on the preprocessed EEG data, which had been filtered to preserve frequencies between 0.5 Hz and 50 Hz. Appropriate scales were chosen to encompass the significant frequency bands in EEG analysis, which include delta, theta, alpha, beta, and gamma rhythms. The magnitude matrix of the EEG signals, like the ECG data, was scaled to 224 × 224 pixels, normalized to grayscale, and treated using adaptive histogram equalization and Gaussian smoothing. This resulted in clear 2D representations that represented the time–frequency properties of the EEG signals, making it easier to discern the patterns associated with various brain states, including epileptic activity.
Transformed CWT 2D images of a normal ECG and a normal EEG signal are illustrated in Figure 2.
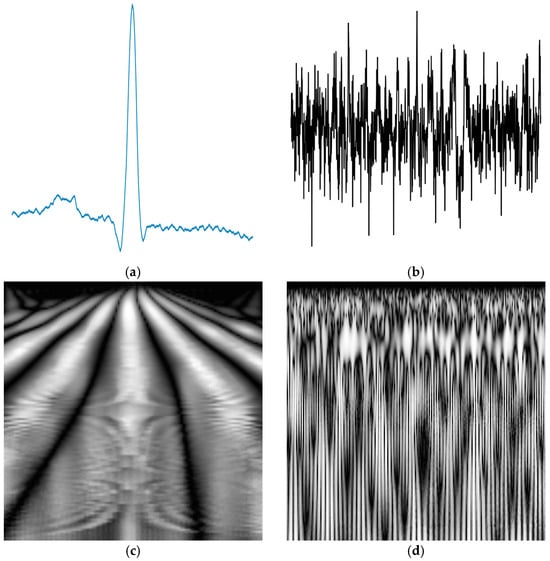
Figure 2.
A typical normal (a) ECG signal and (b) EEG signal; (c) the corresponding transformed CWT image of the ECG signal and (d) the corresponding transformed CWT image of the EEG signal.
3.3.2. Fast Fourier Transform (FFT)
Fast Fourier Transform (FFT) [45] is an efficient algorithm for computing the DFT [46] of a discrete signal. The FFT transforms a time-domain signal into its frequency-domain representation, revealing the signal’s frequency components and their amplitudes. The primary mathematical expression for the DFT, which the FFT computes, is as follows:
For the ECG signals, we transformed each preprocessed ECG beat segment into a frequency-domain representation using the FFT, revealing the strength of different frequencies within the signal. After computing the FFT, we shifted the zero-frequency component to the center of the spectrum. Centering the zero-frequency component facilitated better visualization and interpretation, as it presents the frequency components symmetrically at around zero frequency.
Then, the magnitude spectrum was calculated using the absolute values of the centered FFT data. The magnitude spectrum illustrates the amplitude of each frequency component, allowing for a clear understanding of the signal’s energy distribution throughout frequencies. To convert this 1D magnitude spectrum into a 2D image, we adjusted it to match the target image height (e.g., 224 pixels), guaranteeing consistent results across all images. The modified spectrum was then tiled horizontally to fill the target image width, resulting in a 2D image that depicted frequency variations across the signal.
The resulting 2D matrix was normalized to grayscale values ranging from 0 to 255, resulting in an image with each pixel’s intensity corresponding to the magnitude of a frequency component. This normalization ensured that all images had consistent brightness and contrast, which is required for effective CNN model training.
A similar procedure was used to process the EEG signals. Each preprocessed EEG data segment was transformed with the FFT to capture its frequency components. The FFT transformed the time-domain EEG signal into a frequency-domain representation, showing the various frequencies present and their amplitudes. The zero-frequency component was then centered, achieving a more easily interpretable symmetrical frequency spectrum.
After calculating the magnitude spectrum using the absolute values of the centered FFT data, we vertically scaled the 1D frequency data to fit the target image height. This step ensured that the image’s vertical dimension aligned consistently across all EEG samples. The scaled magnitude spectrum was then repeated horizontally to fill the target image dimensions (224 × 224 pixels), resulting in a 2D representation of the EEG frequency characteristics. The final grayscale image was normalized to values ranging from 0 to 255. The transformed FFT 2D images of a normal ECG and an EEG signal are shown in Figure 3.
3.3.3. Short-Time Fourier Transform (STFT)
The Short-Time Fourier Transform (STFT) [47] is an essential signal processing method used for examining non-stationary signals with frequency content changes over time. By dividing the signal into short, overlapping time segments and applying the Fourier Transform to each, STFT provides a time–frequency representation that reveals how spectral components evolve. Mathematically, the STFT of a continuous signal x(t) is defined as follows:
where ω(τ − t) is a window function centered at time t; f is the frequency; and j is the imaginary unit.
In the current ECG analysis, STFT is applied to each preprocessed ECG segment to capture the time-varying frequency content. We used a Hann window function with a window length that matched the ECG signal’s sampling rate. We achieved easier transitions and the more precise detection of transient events by allowing for a 50% overlap between consecutive windows.
After computing the STFT, we obtained the magnitude spectrogram by calculating the absolute value of the complex STFT coefficients. To focus on the most relevant frequency components for cardiac analysis, frequencies above 50 Hz were removed because they frequently represent noise or muscle artifacts rather than meaningful cardiac activity. The spectrogram was resized to 224 × 224 pixels using interpolation to ensure consistent input for the CNN models.
Logarithmic scaling was applied to the magnitude values to compress the dynamic range. This step increased the visibility of both low and high-amplitude components in the spectrogram. To improve image quality further, adaptive histogram equalization was performed using Contrast-Limited Adaptive Histogram Equalization (CLAHE) [48], which increases local contrast and highlights subtle data features. Finally, Gaussian smoothing was used to remove high-frequency noise and minor artifacts, resulting in a clear grayscale image that accurately depicted the ECG signal’s time–frequency characteristics.
To capture the intricate time–frequency dynamics associated with neural activity in EEG signals, a similar methodology was used. A sampling frequency of 173.61 Hz was selected and applied to the STFT with a Hann window and 50% overlap to each EEG segment. The choice of window and overlap aids in the detection of transient events, such as epileptic spikes, which are critical for accurate diagnosis.
Frequencies up to 50 Hz were maintained to cover the primary EEG frequency bands—delta, theta, alpha, beta, and gamma—that are most important for neurological analysis, while muscle artifacts or external noise were typically found at frequencies above this threshold.
The magnitude spectrogram was resized to 224 × 224 pixels to meet the input requirements of CNNs. Logarithmic scaling was used again. This scaling was necessary to identify both subtle and prominent features in EEG data. Adaptive histogram equalization was used to increase contrast and make important patterns more visible. The final step was Gaussian smoothing, which reduced noise and made the images suitable for machine learning applications. The transformed STFT 2D images of a normal ECG and a normal EEG signal are illustrated in Figure 4.
3.3.4. Recurrence Plots (RPs)
Recurrence Plots (RPs) [49] are a powerful tool in nonlinear data analysis, used to visualize the recurrent behavior of dynamic systems. Introduced by Eckmann et al. in 1987, Recurrence Plots provide a graphical representation of times at which a system revisits the same or similar states. They are particularly useful for detecting patterns, periodicities, and structural changes in complex time-series data, such as ECG and EEG signals [50].
Mathematically, a Recurrence Plot is constructed by embedding a time series x(t) into a higher-dimensional phase space using time-delay embedding. The embedded vectors xi are defined as follows:
where xi is the state vector at time ti; m is the embedding dimension; and τ is the time delay. The Recurrence Plot is then defined by the matrix Ri,j as follows:
where Θ is the Heaviside step function, ε is the threshold distance, ∥⋅∥ indicates the norm (typically Euclidean distance), and N is the number of state vectors. The matrix Ri,j contains recurrence plots where the states xi and xj are close (i.e., the system revisits a similar state), with zeros elsewhere.
In our analysis, we constructed RPs without employing time-delay embedding, simplifying the mathematical formulation. Instead of embedding the time series x(t) into a higher-dimensional phase space, we considered each data point xi as a state vector in a one-dimensional space.
The matrix Ri,j contains a value pf one where the data points xi and xj are close, i.e., when their absolute difference is less than or equal to ε, with zeros elsewhere. By comparing all pairs of data points in the time series, this approach captures both short-term and long-term recurrences without the complexities associated with phase space reconstruction.
The adaptive threshold ε is calculated by analyzing the distribution of all absolute differences ∣xi − xj∣ and selecting the value below which a certain percentage (e.g., 5%) of these differences falls.
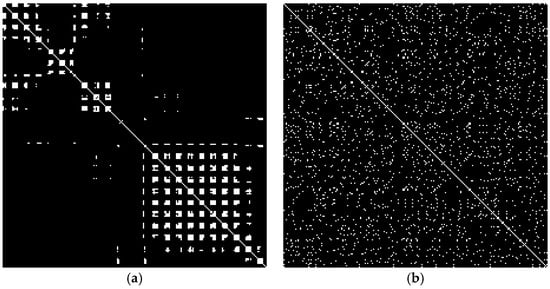
In the analysis of ECG signals, RPs were used to represent the temporal dynamics and recurring patterns found in cardiac function. We processed each ECG segment by first normalizing the data to have zero mean and unit variance. We then calculated the absolute differences between every pair of data points, represented as ∣xi − xj∣, for all indices (i,j), capturing both short-term and long-term recurrences in the cardiac signal. To determine an adaptive threshold ε, we selected the value below which a fixed percentage (e.g., 5%) of these absolute differences fell, effectively tailoring ε to the specific characteristics of each signal. Using this threshold, we constructed the recurrence matrix RR where each element was Ri,j = 1 if ∣xi − xj∣ ≤ ε, and Ri,j = 0 otherwise. The recurrence matrix was then visualized as a Recurrence Plot.
To standardize the input for deep learning models, we resized each recurrence matrix to a 224 × 224 pixels image using interpolation. The images were saved in grayscale format, where recurrent points were depicted in black (intensity 0) and non-recurrent points were depicted in white (intensity 255).
Similarly, for each EEG signal segment, the same methodology was followed. We normalized each EEG segment to have zero mean and unit variance.
The transformed RP 2D images of a normal ECG and a normal EEG signal are illustrated in Figure 5.
3.3.5. Signal Reshaping (SR)
The Signal Reshaping (SR) method [51] is a simple yet efficient technique to convert 1D signals into 2D images by reorganizing the signal data while preserving their inherent time-domain properties. This method involves scaling the signal to fit within a grayscale intensity range, resizing it to match the desired image dimensions, and placing it on a standardized image canvas.
Mathematically, given a 1D signal of x = [x1, x2, …, xN], it can be transformed into a 2D image of dimensions H × W (height H and width W) by first being normalized to the grayscale range of 0 to 255 as follows:
The scaled signal xscaled is then resized to match the image dimensions. This involves interpolating the signal to fit the height H and, if necessary, adjusting the width W by stretching or replicating the signal. The resized signal is centered within a black canvas I of size H × W, ensuring that all images have a consistent format suitable for input into the CNNs.
In the current analysis of ECG signals, the Signal Reshaping method was used to transform each 1D ECG segment into a 2D grayscale image. Each ECG segment, which represents a heartbeat or a specific time interval, was first scaled to grayscale using the normalization formula. This scaling preserved the relative amplitude variations in the ECG waveform, which are required to identify features such as the P-wave, QRS complex, and T-wave.
To fit the target image dimensions of 224 × 224 pixels, we vertically stretched the scaled signal to match the image height H = 224. The width W = 224 was achieved by either stretching the signal horizontally or by placing the vertically stretched signal in the center of the image and filling the remaining space with black pixels (intensity 0). This centering ensured that the main features of the ECG waveform were prominently displayed in a consistent location across all images.
For EEG signals, the Signal Reshaping method was similarly applied to transform 1D time-series data into 2D grayscale images. Each EEG data segment, representing brain electrical activity over time, was first normalized to the grayscale range using the same scaling equation. The final EEG signal was then resized to match the 224 × 224 pixels image dimensions. The transformed SR 2D images of a normal ECG and a normal EEG signal are illustrated in Figure 6, while the post-processing steps followed to prepare both types of images for the CNNs are illustrated in Figure 7.

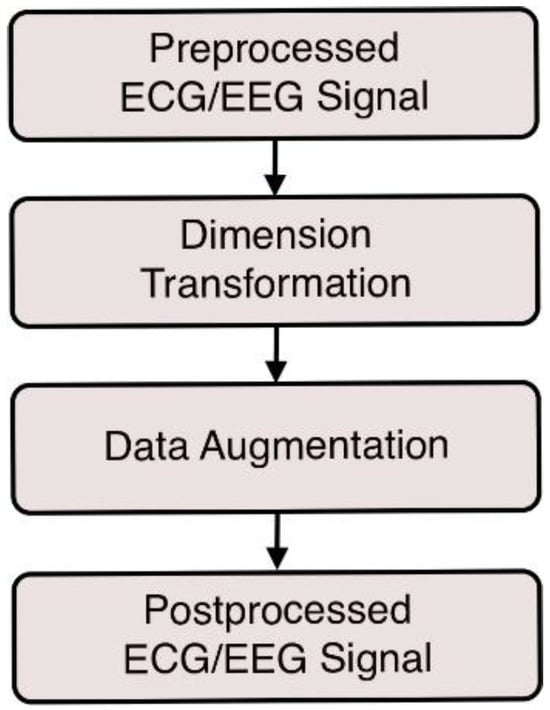
Figure 7.
Post-processing steps for both ECG and EEG signals before being fed to the CNNs.
3.4. Two-DimensionalConvolutional Neural Networks (CNNs)
Convolutional Neural Networks (CNNs) are a type of deep learning model that is designed to process data with a grid-like structure, such as two-dimensional images. By converting our one-dimensional ECG and EEG signals into two-dimensional images using methods such as CWT, STFT, FFT, RPs, and SR, we could take advantage of the powerful capabilities of 2D CNNs for analysis [52].
In this work, aiming to make the results more diverse, we decided to compare two different CNN architectures: a simple architecture of a custom minimal 2D CNN and a more complex one, that of LeNet-5 2D CNN. Note that the selection of models was made due to the fact that the minimal CNN was the simplest 2D CNN model that could be constructed, while the LeNet-5 2D CNN used is a very popular and efficient model based on the literature.
While complex models can capture intricate patterns and relationships in the data, minimal 2D CNN architectures can be proven advantageous in terms of efficiency, generalization, and practicality, especially in resource-constrained environments or when dealing with small datasets. Therefore, aiming to start with a simpler model and then increase the complexity, we intentionally incorporated two distinct CNN architectures—our custom minimal model and the more established LeNet-5—in order to better support the credibility of our findings. The minimal CNN serves as the simplest 2D architecture, highlighting how even a lightweight network can leverage effective transformations. LeNet-5, on the other hand, is both historically significant and robust, allowing us to demonstrate how more complex feature extraction capabilities influence classification outcomes. By examining each transformation technique under both a minimal and a more advanced model, we offer a more complete perspective on the generalizability and practical impact of different 1D-to-2D preprocessing approaches.
3.4.1. Custom Minimal 2D CNN
In our study, a 2D CNN was employed to analyze both ECG and EEG signals. The network began with an input layer that accepted images of dimensions of 224 × 224 pixels and a single-color channel, which corresponded to the grayscale images generated by the ECG and EEG data, as described analytically in the previous subsection. Following the input layer, this model added a convolutional layer that applied four 3 × 3 filters to the input images. This layer employed the Rectified Linear Unit (ReLU) activation function, which introduced nonlinearity into the model and aided it in learning complex patterns in the data. The convolutional layer extracted low-level spatial features from input images, such as edges and simple textures, which are critical for distinguishing different signal classes. Following the convolutional layer, a max pooling layer with a 2 × 2 window was used. Max pooling reduced the spatial dimensions of feature maps by taking the maximum value within each window, essentially downsampling the input while retaining the most important features, thus reducing the model’s computational complexity.
The output of the pooling layer was then flattened into a one-dimensional vector. This flattening process prepared the data for the next fully connected layer by converting the two-dimensional feature maps to a classification-ready format.
The final layer was a fully connected (dense) layer with five neurons, representing the number of classes related to the current classification tasks. This layer used the softmax activation function, which generated a probability distribution across the classes, enabling the model to generate probabilistic predictions of the input data.
3.4.2. LeNet-5 2D CNN
In this study, the LeNet-5 architecture was additionally used as an advanced CNN able to classify grayscale images generated from ECG and EEG signals. Yann LeCun and his colleagues developed LeNet-5, a historically significant model that performs exceptionally well in image recognition tasks [53].
The LeNet-5 architecture starts with a convolutional layer that applies six 5 × 5 filters via the tanh activation function. This layer extracts low-level spatial features from input images, such as edges and textures, which are critical for distinguishing between patterns in biomedical signals. The tanh activation function offers nonlinearity into the network, allowing it to model complex relationships in the data.
Following the first convolutional layer, an average pooling layer with a 2 × 2 window reduces the spatial dimensions by half. Average pooling smooths the feature maps, emphasizing general patterns over specific pixel intensities and reducing the sensitivity to noise.
The network then uses a second convolutional layer that applies 16 filters of size 5 × 5, again using the tanh activation function. This layer builds upon the features extracted by the previous layers, capturing more complex patterns and higher-level features from the pooled outputs. It allows the network to recognize the shapes and structures relevant to distinguishing between different classes in the ECG and EEG data.
Another average pooling layer with a 2 × 2 window follows, further reducing the spatial dimensions and enabling the network to focus on more abstract representations of the data. This is crucial for capturing the hierarchical nature of features in images, where simple patterns combine to form more complex ones.
The third convolutional layer applies 120 filters of size 5 × 5 with tanh activation. This layer performs deeper feature extraction, creating compact representations of the input data. The increased number of filters allows the network to capture a wide variety of patterns and nuances in the images, which are essential for distinguishing subtle differences in biomedical signals that may indicate different physiological or pathological conditions.
After the convolutional layers, a flattened layer converts the three-dimensional feature maps into a one-dimensional vector. The network includes a fully connected layer with 84 neurons and tanh activation. This layer learns complex relationships among the extracted features, integrating them to form a high-level representation of the input data. The choice of 84 neurons provides sufficient capacity for the model to capture intricate patterns without becoming overly complex.
The final output layer is a fully connected layer with five neurons corresponding to the number of target classes in the presented classification task (e.g., types of ECG beats or EEG states). This layer uses the softmax activation function again.
3.4.3. CNN Models’ Setup
To train both CNN models, the Adam optimizer [54] was used with a learning rate of 0.00001. Adam is an adaptive learning rate optimization algorithm that combines the advantages of two other extensions of stochastic gradient descent: the Adaptive Gradient Algorithm (AdaGrad) and Root Mean Square Propagation (RMSProp). This optimizer is well-suited for problems with sparse gradients and noisy data, providing efficient and effective convergence. Moreover, the categorical cross-entropy loss function was used, which is appropriate for multi-class classification problems where classes are mutually exclusive. This loss function measures the difference between the true class labels and the predicted probabilities, guiding the optimizer to adjust the model weights to minimize this error. Both the minimal and the LeNet-5 CNN models were trained for 20 epochs for both ECG and EEG classification.
For both CNNs, during training, the model’s performance was monitored using accuracy as the primary metric, along with the F1-score, recall, and precision. Accuracy provides a straightforward measure of the proportion of correct predictions made by the model out of all predictions, giving an intuitive understanding of its performance. Datasets were augmented, as detailed in Section 3.3, to ensure that each of the five classes in both ECG and EEG signals contained the same number of images, resulting in a well-balanced dataset. In a balanced dataset, accuracy becomes a reliable measure of overall performance since no single class dominates the data. This uniform distribution means that a model cannot achieve artificially high accuracy by favoring one class. Consequently, we used accuracy as our primary metric alongside precision, recall, and the F1-score, which remain crucial for detailed insights into each class’s classification performance. The reported metrics included in all tables in the following are the mean values of 10 runs by randomly splitting the dataset into train (70%), validation (15%), and test (15%) sets to ensure the stability of reported metrics and boost the confidence of the model’s performance.
Early stopping based on the validation loss was implemented to prevent overfitting and improve the generalization of the model. If the validation loss did not improve for three consecutive epochs, the training process was halted. Early stopping helped to avoid scenarios where the model started to learn noise and irrelevant patterns in the training data, which could negatively impact its performance on unseen data. Additionally, model checkpoints were used to save the best-performing model during training. By saving the model weights whenever the validation loss improved, we ensured that we could retain the version of the model that was most effective at generalizing new data.
The training of both CNNs was performed using an NVIDIA GeForce RTX 3080 Laptop GPU, which boasts 48 multiprocessors and a total of 6144 CUDA cores (128 cores per multiprocessor), along with 16,012 MB of total memory and a computing capability of 8.6. This powerful GPU provided substantial computational resources, enabling the efficient training and processing of our deep learning models on the transformed ECG and EEG signal images.
4. Results
In this section, the findings of the experiments conducted using two CNN architectures, the minimal 2D CNN and the LeNet-5 2D CNN, are presented, aiming to evaluate and compare the performance of the six-dimensional transformation methods applied to both ECG and EEG signals. The results reposted in this section aim to reveal how effective each transformation method is at capturing relevant features and how they affect the classification accuracy of the two CNN models. By comparing the performance of the minimal CNN and LeNet-5, we can learn about the role of model complexity in leveraging the transformed 2D representations of biomedical signals.
The exact way the ECG and EEG data are distributed between the classes is detailed in the following paragraphs.
For the ECG signals, we targeted 100,000 images per class among the five heartbeat categories (Normal (N), Supraventricular (S), Ventricular (V), Fusion (F), and Unclassifiable (Q)). Data augmentation was applied until each class reached the target number of images. This procedure ensured a balanced dataset, where each of the five classes contained exactly 100,000 samples. We then split the entire dataset into train (70%), validation (15%), and test (15%) sets, preserving class balance in each split.
For the EEG signals, we had five sets (A, B, C, D, E), which were mapped to five letters (normal with eyes open (O), normal with eyes closed (Z), seizure-free intervals in five patients from hippocampal formation in the opposite hemisphere (N), seizure-free intervals of five patients from the epileptogenic zone (F), and seizure (S)). We applied data augmentation until each set reached 10,000 images per signal type, thereby achieving a balanced distribution across the five classes. Afterward, we split these images into training (70%), validation (15%), and test (15%) portions, ensuring that each set (A/Z, B/O, C/N, D/F, E/S) contributed an equal number of samples.
Therefore, in our study, the classification task for ECG and EEG signals is a multi-class problem. For ECGs, it involves five categories (N, S, V, F, Q), each representing a different type of heartbeat or arrhythmic pattern. For EEG signals, we similarly defined five classes (O, Z, N, F, S), each corresponding to a particular EEG state or condition.
After preprocessing and segmenting the signals, we transformed these segments into 2D images and input them into our CNN models. The goal was for the CNNs to learn features that differentiated between the five classes in each dataset so that each signal segment could be correctly identified according to its characteristic cardiac or neural activity. By evaluating precision, recall, F1-score, and accuracy for each model, we assessed how effectively the transformations and CNN architectures could capture and classify the distinct classes in both ECG and EEG datasets.
4.1. ECG Signal Results
The results for the ECG signal after the evaluation of the minimal 2D CNN and the Lenet-5 2D CNN are included in Table 2 and Table 3, respectively.

Table 2.
Minimal 2D CNN on ECG signals.

Table 3.
LeNet-5 2D CNN on ECG signals.
The results of the minimal 2D CNN on the ECG dataset (Table 1) show major differences in the effectiveness of the five-dimension transformation methods. Among them, the Recurrence Plots (RPs) and the Continuous Wavelet Transform (CWT) achieved the highest performance, with precision, recall, F1-score, and accuracy at 0.99 and 0.98 across all metrics, respectively. This was followed by Signal Reshaping (SR) with scores of 0.96 and Short-Time Fourier Transform (STFT) at 0.95, both of which outperformed the remaining methods. Fast Fourier Transform (FFT) and Recurrence Plots (RPs) exhibited consistent but lower scores in the range of 0.87–0.88. The superior performance of SR compared to STFT in the minimal CNN could be attributed to the simplicity of SR’s time-domain representation, which aligns well with the limited feature extraction capabilities of this lightweight model. By contrast, STFT’s more complex time–frequency features may be underutilized by the minimal CNN, leading to slightly lower performance.
The LeNet-5 2D CNN, with its deeper architecture and more advanced feature extraction capabilities, showed significant results across all transformation methods. CWT and STFT were the best-performing methods, with near-perfect scores of 0.99 for precision, recall, F1-score, and accuracy. Interestingly, while SR maintained its effectiveness with scores of 0.96, it performed slightly worse than STFT and other advanced methods such as FFT and RP, all of which achieved scores of 0.97. The improved performance of STFT in LeNet-5 demonstrates the benefit of its richer time–frequency representations, in which the deeper architecture is better suited to handle the data. In contrast, SR’s simpler time-domain features, while effective for the minimal CNN, do not fully exploit LeNet-5’s advanced capabilities, resulting in lower performance.
These findings highlight the importance of matching the complexity of the transformation method to the capacity of the model architecture. Methods such as CWT and STFT, which retain both time and frequency information, and RPs, which transform time-series data into a two-dimensional representation that captures both linear and nonlinear patterns by mapping times at which similar states occur, consistently surpassed other methods in both models, demonstrating their ability to capture critical features for classification. The minimal CNN benefits from simpler transformations such as SR, whereas the more sophisticated LeNet-5 architecture thrives when combined with advanced transformations that provide richer and more detailed feature representations. Overall, this study shows that both transformation methods and CNN architecture are important factors in optimizing the classification performance of ECG signals.
4.2. EEG Signal Results
The results for the EEG signals after the evaluation of the minimal 2D CNN and the Lenet-5 2D CNN are presented in Table 4 and Table 5, respectively. The results of the minimal 2D CNN on the EEG dataset show a significant difference in performance between the five-dimension transformation methods. Recurrence Plots (RPs), Continuous Wavelet Transform (CWT), and the Short-Time Fourier Transform (STFT) received perfect scores across all metrics, with precision, recall, F1-score, and accuracy at a value of 1.0, indicating their efficacy in capturing the critical features of EEG signals. Other methods, such as the Fast Fourier Transform (FFT), performed moderately well, scoring 0.87. Signal Reshaping (SR) received a lower score, 0.77, across all metrics, indicating that its simple time-domain representation might not sufficiently reflect the complexity of EEG signals.

Table 4.
Minimal 2D CNN on EEG signals.

Table 5.
LeNet-5 2D CNN on EEG signals.
On the other hand, the LeNet-5 2D CNN performed consistently well for five of the five transformation methods. CWT, STFT, FFT, and SR all received perfect scores of 1.0 for precision, recall, F1-score, and accuracy, demonstrating the model’s ability to extract features from even simple transformations such as SR. However, RP continued to perform poorly, with a low F1-score of 0.17 and an accuracy of 0.2, indicating that even this more advanced architecture was unable to make full use of its representation.
These findings demonstrate the superiority of CWT and STFT in preserving the key features of EEG signals across both models. While DFT and FFT benefit from LeNet-5’s advanced capabilities, their performance is limited to simpler architectures. The large difference in Signal Reshaping results between the minimal CNN and the LeNet-5 suggests that its simplicity is better suited to advanced architectures capable of extracting deeper patterns. The consistent poor performance of the Recurrence Plot implies that its representation does not correspond well to the properties of EEG data or the classification task, regardless of model complexity. Overall, the findings once again emphasize the importance of choosing both proper transformation methods and model architectures to optimize the performance of EEG signals.
5. Discussion
In this study, we investigated the effectiveness of five-dimension transformation methods (CWT, STFT, FFT, RPs, and SR) applied to ECG and EEG signals for classification tasks using two CNN architectures: a minimal 2D CNN and the more complex LeNet-5 2D CNN. Our aim was to understand how different signal transformation techniques and the CNN architecture impact the classification performance of such signals and identify the combinations that yield the most accurate results.
On the ECG dataset, the minimal 2D CNN showed notable differences across transformation methods. RPs and CWT emerged as the most effective methods, achieving high precision, recall, F1-score, and accuracy scores of 0.99 and 0.98, respectively. This indicates that their ability to capture both linear and nonlinear patterns provides a rich feature set that even a lightweight CNN can leverage effectively. Signal Reshaping (SR) also performed well with scores around 0.96, slightly outperforming STFT at 0.95. The superior performance of SR in the minimal CNN context may be attributed to its simplicity; the time-domain representations are straightforward for a basic model to interpret without requiring complex feature extraction capabilities. In contrast, while STFT provides detailed time–frequency representations, the minimal CNN may not possess sufficient depth to fully exploit these complex features, resulting in slightly lower performance compared to SR.
FFT showed consistent but lower performance, with scores ranging to 0.88. This method may not capture the critical features necessary for accurate classification as effectively as RPs, CWT, STFT, and SR, especially when using a simpler CNN architecture.
When using the LeNet-5 2D CNN, a deeper and more sophisticated model, classification performance improved across all transformation methods on the ECG dataset. RPs, CWT, and STFT all achieved near-perfect scores of 0.99, demonstrating that the richer time–frequency and nonlinear information they provide is effectively harnessed by the advanced architecture of LeNet-5. Interestingly, while SR remained effective with scores around 0.96, it was slightly outperformed by FFT, achieving scores of approximately 0.97. This suggests that LeNet-5’s enhanced feature extraction capabilities allow it to better utilize the complex representations produced by these transformation methods, which the minimal CNN could not fully exploit the data. The improved performance of STFT and other advanced transformations with LeNet-5 highlights the advantage of aligning the complexity of the transformation method with the capacity of the model architecture.
These findings highlight the importance of selecting appropriate transformation methods based on the CNN architecture used. Simpler models like the minimal CNN benefit more from straightforward transformations like SR and RPs, which produce features that are easier for a basic model to interpret. In contrast, more complex models like LeNet-5 can take advantage of advanced transformations that provide richer and more detailed feature representations. Methods like RPs, CWT, and STFT, which preserve both time, frequency, and nonlinear information, consistently outperformed other techniques in both models, emphasizing their effectiveness in capturing critical features for classification. This demonstrates that both the transformation method and CNN architecture play critical roles in optimizing the classification performance of ECG signal analysis.
Regarding the EEG dataset, the experimental findings showed that both the minimal 2D CNN and the LeNet-5 2D CNN performed exceptionally well with certain transformation methods. RPs, CWT, and STFT achieved perfect scores across all metrics with the minimal CNN, indicating their superior ability to capture the essential features of EEG signals, which are inherently complex and non-stationary. FFT performed moderately well, with scores of around 0.87. This method provides frequency-domain representations but may lack the temporal and nonlinear resolution necessary to fully capture the dynamics of EEG signals. SR scored lower, with metrics of around 0.77, suggesting that its simple time-domain representation is insufficient for representing the intricate patterns present in EEG data when using simple CNN architecture.
Using the LeNet-5 2D CNN, the performance on the EEG dataset remained excellent for RPs, which achieved a perfect accuracy of 1.0. CWT and STFT followed closely with an accuracy of 0.99, showcasing their strong ability to extract relevant features when combined with a deeper network architecture. FFT showed improved performance compared to the minimal CNN, indicating that LeNet-5’s advanced capabilities allow it to better utilize these transformations. SR, while improved, still lagged behind the other methods, suggesting that even with a sophisticated model, the simpler time-domain features of SR are less effective for EEG classification.
These findings highlight the superior capability of RPs in representing the intricate temporal and nonlinear dynamics of EEG signals, which are crucial for accurate classification. The excellent performance of RPs across both CNN architectures suggests that they can effectively capture essential features that are readily exploited by both simple and complex models. Meanwhile, CWT and STFT also provide rich time–frequency representations that are highly effective, particularly when used with more sophisticated architectures like LeNet-5.
Several factors may have affected the outcome. The EEG dataset was initially quite small, with only 100 images per class, which we increased to 10,000 images per class using data augmentation techniques. While augmentation increases the dataset size and variability, it may not fully reproduce the diversity and complexity found in larger, more varied datasets. This may have resulted in overfitting appearing in the training of the models, thus explaining the excellent results. In contrast, the ECG dataset was larger from the start and was later expanded to 100,000 images, resulting in a more robust dataset for training and evaluation.
Our findings show that while advanced CNN architectures like LeNet-5 can significantly improve classification performance, the transformation method remains critical. Methods that capture both time, frequency, and nonlinear information—such as RPs, CWT, and STFT—perform consistently well across different models and datasets. Simpler transformations, like SR, can be effective when combined with sophisticated models capable of extracting complex patterns in data but may not match the performance of more advanced methods. Overall, RPs have played a pivotal role in our analysis of both ECG and EEG signals, offering a unique representation that highlights temporal recurrences and potential nonlinear dynamics in the data. In particular, they have proved effective for EEG classification, even when coupled with simpler CNN architectures, because they capture nonlinear and recurrent patterns that are central to EEG data. Unlike purely time–frequency approaches (e.g., STFT) or amplitude-based methods (e.g., FFT), RPs do not rely solely on frequency decomposition or simplistic representations. Instead, they highlight temporal recurrences and repeats that are naturally abundant in EEG signals, which often exhibit strong non-stationary and chaotic elements. By mapping each EEG segment into a 2D matrix reflecting these recurrences, RPs create rich visual patterns that even a basic CNN can interpret successfully without requiring complex feature extraction.
This study also emphasizes the importance of dataset size and complexity on model performance. Larger and more diverse datasets, such as ECG data, provide better opportunities for models to learn and generalize. Smaller datasets, even when augmented, may not capture the full range of variability required for robust classification, potentially limiting the effectiveness of specific transformation methods and models.
One potential limitation lies in data augmentation. While our augmentations helped balance classes and enriched the dataset with realistic variability, there was a risk that these transformations could introduce artifacts that do not genuinely reflect real-world physiological signals. Overly aggressive augmentations could cause the model to latch onto synthetic cues instead of actual biomedical features, inflating performance metrics yet reducing generalizability beyond the study conditions. This overfitting concern is particularly salient if the dataset, even after augmentation, remains relatively small or lacks critical diversity. Another possible issue that may come up is dataset bias and representativeness. Despite augmentation, certain patient subpopulations or rare clinical conditions may be underrepresented in the data, causing the model to generalize poorly in those cases. Subtle artifacts or biases in the original recordings—if not fully addressed during preprocessing—may also skew the learned features. Finally, while our findings confirmed robust classification under the conditions tested, validating the models on completely different or more heterogeneous datasets is essential to confirm their broader applicability and avoid clinical misinterpretation.
For future research, it would be beneficial to apply this approach to larger and more complex ECG and EEG datasets to evaluate the findings’ generalization. Exploring new transformation methods, such as GAF, GASF, GADF, MTF, RQA, and DTW, or combining multiple transformations, may also result in richer feature representations offering a more comprehensive assessment of how different 1D-to-2D mappings perform in CNN-based biomedical signal classification. Furthermore, experimenting with different CNN architectures, such as those with attention mechanisms or residual connections, may result in even better classification performances. To this end, this work experimentally demonstrates that understanding the relationship between signal transformation methods, dataset characteristics, and neural network architectures is critical for progressing the field of biomedical signal analysis towards creating more accurate and robust diagnostic tools.
6. Conclusions
In this work, the effectiveness of five-dimension transformation methods (CWT, STFT, FFT, RPs, and SR) applied to the ECG and EEG signals was investigated for classification tasks using two CNN architectures: a minimal 2D CNN and the more complex LeNet-5 2D CNN. Our results indicate that RPs, CWT, and STFT are the methods that achieve the highest accuracy across both CNN architectures. These top-performing methods achieved accuracies between 95 and 98% on the minimal 2D CNN, and accuracies of 99% for all three methods on the LeNet-5 model for the ECG signals. For the EEG signals, all three methods achieved an accuracy of 100% on the minimal 2D CNN and an accuracy between 99 and 100%, on the LeNet-5 2D CNN model. The research results indicated that the successful classification of ECG and EEG signals is heavily dependent on the strategic selection of the dimension transformation method and the used NN architecture.
Advanced transformations like CWT, STFT, and RPs, which effectively capture time, frequency, and nonlinear dynamics, consistently achieved superior performance across both the minimal 2D CNN and the more complex LeNet-5 model, highlighting their efficacy in preserving critical signal features essential for accurate classification. Simpler transformations such as SR showed variable results—performing well with the sophisticated LeNet-5 due to its advanced feature extraction capabilities but less effectively with the minimal CNN, especially for the EEG signals. This indicates that the complexity of the transformation must match the model’s capacity to fully leverage the features provided. The consistently superior performance of RPs, particularly with EEG signals, emphasizes the importance of selecting transformation methods that are compatible with the data’s intrinsic properties and the specific requirements of the classification task.
Our metrics for accuracy, precision, recall, and F1-score also consistently show that transformation techniques that emphasize both temporal and frequency features yield better classification results. While RPs concentrate on recurrences that highlight arrhythmic events, techniques like CWT and STFT efficiently capture the waveform’s morphology in the ECG data. These same time–frequency transformations are excellent at simulating non-stationary neural dynamics for EEG signals, and RPs once more show their worth by spotting repeating states in the midst of intricate brain activity. While simpler methods like SR can work well when combined with deeper architectures (like LeNet-5) that make up for the representation’s lack of complexity, they typically perform insufficiently with shallower networks and signals that require richer feature extraction.
Simultaneously, our studies also emphasize the function of data augmentation and how it interacts with these changes. The learning process was strengthened by mild but realistic augmentations, like slight brightness shifts or minimal rotations, especially when paired with transformations that maintain significant ECG and EEG features. By avoiding the overfitting of static or sparsely varied examples, the combination of well-chosen transformation techniques and customized augmentation allows both models to generalize more successfully. Our findings thus highlight that robust classification depends on making sure the training data accurately captures the variety and realistic variability of real physiological signals, in addition to striking a balance between transformation complexity and model depth.
Overall, our findings emphasize that the optimal classification of biomedical signals can be achieved through the careful combination of rich, informative signal transformations and appropriate neural network architectures, providing valuable insights into signal processing and deep learning techniques for biomedical applications. We advocate for future research to apply these methodologies to larger, more complex datasets to validate and extend these promising findings.
Author Contributions
Conceptualization, G.A.P.; methodology, G.A.P.; software, G.L.; validation, G.L.; formal analysis, G.L.; investigation, G.L.; resources, G.L.; data curation, G.L.; writing—original draft preparation, G.L.; writing—review and editing, E.V. and G.A.P.; visualization, G.A.P.; supervision, G.A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available at https://github.com/GeoLek/1D-to-2D-Data-Transformation (accessed on 26 January 2025).
Acknowledgments
This work was supported by the MPhil program “Advanced Technologies in Informatics and Computers”, which was hosted by the Department of Informatics, Democritus University of Thrace, Kavala, Greece.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional Neural Networks: An Overview and Application in Radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef] [PubMed]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D Convolutional Neural Networks and Applications: A Survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Saxena, A. An Introduction to Convolutional Neural Networks. Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 943–947. [Google Scholar] [CrossRef]
- Gómez-Echavarría, A.; Ugarte, J.P.; Tobón, C. The Fractional Fourier Transform as a Biomedical Signal and Image Processing Tool: A Review. Biocybern. Biomed. Eng. 2020, 40, 1081–1093. [Google Scholar] [CrossRef]
- Rangayyan, R.M.; Krishnan, S. Biomedical Signal Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of Nonlinear Deterministic and Finite-Dimensional Structures in Time Series of Brain Electrical Activity: Dependence on Recording Region and Brain State. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef]
- Al Rahhal, M.M.; Bazi, Y.; Al Zuair, M.; Othman, E.; BenJdira, B. Convolutional Neural Networks for Electrocardiogram Classification. J. Med. Biol. Eng. 2018, 38, 1014–1025. [Google Scholar] [CrossRef]
- Yakushenko, E. St Petersburg INCART 12-Lead Arrhythmia Database. Available online: https://physionet.org/content/incartdb/1.0.0/ (accessed on 2 January 2025).
- PhysioNet. MIT-BIH Supraventricular Arrhythmia Database. Available online: https://physionet.org/content/svdb/1.0.0/ (accessed on 2 January 2025).
- Yousuf, A.; Hafiz, R.; Riaz, S.; Farooq, M.; Riaz, K.; Rahman, M.M.U. Inferior Myocardial Infarction Detection From Lead II of ECG: A Gramian Angular Field-Based 2D-CNN Approach. IEEE Sens. Lett. 2024, 8, 6012104. [Google Scholar] [CrossRef]
- Bousseljot, R.-D. PTB Diagnostic ECG Database. Available online: https://physionet.org/content/ptbdb/1.0.0/ (accessed on 2 January 2025).
- Camara, C.; Peris-Lopez, P.; Safkhani, M.; Bagheri, N. ECG Identification Based on the Gramian Angular Field and Tested with Individuals in Resting and Activity States. Sensors 2023, 23, 937. [Google Scholar] [CrossRef]
- Moody, G. MIT-BIH Normal Sinus Rhythm Database. Available online: https://physionet.org/content/nsrdb/1.0.0/ (accessed on 2 January 2025).
- Howell, L.; Porr, B. High Precision ECG Database with Annotated R Peaks, Recorded and Filmed under Realistic Conditions. Available online: https://researchdata.gla.ac.uk/716/ (accessed on 2 January 2025).
- Mewada, H. 2D-Wavelet Encoded Deep CNN for Image-Based ECG Classification. Multimed. Tools Appl. 2023, 82, 20553–20569. [Google Scholar] [CrossRef]
- Degirmenci, M.; Ozdemir, M.A.; Izci, E.; Akan, A. Arrhythmic Heartbeat Classification Using 2D Convolutional Neural Networks. IRBM 2022, 43, 422–433. [Google Scholar] [CrossRef]
- Mathunjwa, B.M.; Lin, Y.-T.; Lin, C.-H.; Abbod, M.F.; Shieh, J.-S. ECG Arrhythmia Classification by Using a Recurrence Plot and Convolutional Neural Network. Biomed. Signal Process. Control 2021, 64, 102262. [Google Scholar] [CrossRef]
- PhysioNet. CU Ventricular Tachyarrhythmia Database. Available online: https://physionet.org/content/cudb/1.0.0/ (accessed on 2 January 2025).
- Moody, G. MIT-BIH Atrial Fibrillation Database. Available online: https://physionet.org/content/afdb/1.0.0/ (accessed on 2 January 2025).
- Albrecht, P.; Moody, G.; Mark, R. MIT-BIH Malignant Ventricular Ectopy Database. Available online: https://physionet.org/content/vfdb/1.0.0/ (accessed on 2 January 2025).
- Huang, J.; Chen, B.; Yao, B.; He, W. ECG Arrhythmia Classification Using STFT-Based Spectrogram and Convolutional Neural Network. IEEE Access 2019, 7, 92871–92880. [Google Scholar] [CrossRef]
- Cao, M.; Zhao, T.; Li, Y.; Zhang, W.; Benharash, P.; Ramezani, R. ECG Heartbeat Classification Using Deep Transfer Learning with Convolutional Neural Network and STFT Technique. J. Phys. Conf. Ser. 2023, 2547, 012031. [Google Scholar] [CrossRef]
- Rashed-Al-Mahfuz, M.; Moni, M.A.; Uddin, S.; Alyami, S.A.; Summers, M.A.; Eapen, V. A Deep Convolutional Neural Network Method to Detect Seizures and Characteristic Frequencies Using Epileptic Electroencephalogram (EEG) Data. IEEE J. Transl. Eng. Health Med. 2021, 9, 2000112. [Google Scholar] [CrossRef]
- Li, M.; Chen, W. FFT-Based Deep Feature Learning Method for EEG Classification. Biomed. Signal Process. Control 2021, 66, 102492. [Google Scholar] [CrossRef]
- Guttag, J. CHB-MIT Scalp EEG Database. Available online: https://physionet.org/content/chbmit/1.0.0/ (accessed on 2 January 2025).
- San-Segundo, R.; Gil-Martín, M.; D’Haro-Enríquez, L.F.; Pardo, J.M. Classification of Epileptic EEG Recordings Using Signal Transforms and Convolutional Neural Networks. Comput. Biol. Med. 2019, 109, 148–158. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, R.G.; Schindler, K.; Rummel, C. Nonrandomness, Nonlinear Dependence, and Nonstationarity of Electroencephalographic Recordings from Epilepsy Patients. Phys. Rev. E 2012, 86, 046206. [Google Scholar] [CrossRef]
- Du, H.; Riddell, R.P.; Wang, X. A Hybrid Complex-Valued Neural Network Framework with Applications to Electroencephalogram (EEG). Biomed. Signal Process. Control 2023, 85, 104862. [Google Scholar] [CrossRef]
- Nakanishi, M.; Wang, Y.; Wang, Y.-T.; Jung, T.-P. A Comparison Study of Canonical Correlation Analysis Based Methods for Detecting Steady-State Visual Evoked Potentials. PLoS ONE 2015, 10, e0140703. [Google Scholar] [CrossRef]
- Rahuja, N.; Valluru, S.K. A Deep Neural Network Approach to Automatic Multi-Class Classification of Electrocardiogram Signals. In Proceedings of the 2021 International Conference on Intelligent Technologies (CONIT), Hubli, India, 25–27 June 2021; IEEE: New York, NY, USA, 2021; pp. 1–4. [Google Scholar]
- PhysioNet. BIDMC Congestive Heart Failure Database. Available online: https://physionet.org/content/chfdb/1.0.0/ (accessed on 2 January 2025).
- Samara, C.; Vrochidou, E.; Papakostas, G.A. EEG Signal Analysis Approaches for Epileptic Seizure Event Prediction Using Deep Learning. In Proceedings of the 2023 International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 21–23 September 2023; IEEE: New York, NY, USA, 2023; pp. 1–7. [Google Scholar]
- Marinis, M.; Vrochidou, E.; Papakostas, G.A. EEG Channel Selection for Epileptic Seizure Prediction. In Proceedings of the 2024 Panhellenic Conference on Electronics & Telecommunications (PACET), Thessaloniki, Greece, 28–29 March 2024; IEEE: New York, NY, USA, 2024; pp. 1–4. [Google Scholar]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Gash, J.H.C.; Culf, A.D. Applying a Linear Detrend to Eddy Correlation Data in Realtime. Bound.-Layer Meteorol. 1996, 79, 301–306. [Google Scholar] [CrossRef]
- Christiano, L.J.; Fitzgerald, T.J. The Band Pass Filter. Int. Econ. Rev. 2003, 44, 435–465. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Burrus, C.S. Generalized Digital Butterworth Filter Design. IEEE Trans. Signal Process. 1998, 46, 1688–1694. [Google Scholar] [CrossRef]
- Patro, S.G.K.; Sahu, K.K. Normalization: A Preprocessing Stage. Int. Adv. Res. J. Sci. Eng. Technol. 2015, 2, 20–22. [Google Scholar] [CrossRef]
- Yuan, S.; Song, G.; Huang, G.; Wang, Q. Reshaping Hyperspectral Data into a Two-Dimensional Image for a CNN Model to Classify Plant Species from Reflectance. Remote Sens. 2022, 14, 3972. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, W.; Wu, J.; Zhao, W.; Chen, A. Deconvolution-and-Convolution Networks. arXiv 2021, arXiv:2103.11887. [Google Scholar]
- Gupta, V.; Mittal, M. QRS Complex Detection Using STFT, Chaos Analysis, and PCA in Standard and Real-Time ECG Databases. J. Inst. Eng. Ser. B 2019, 100, 489–497. [Google Scholar] [CrossRef]
- Alomar, K.; Aysel, H.I.; Cai, X. Data Augmentation in Classification and Segmentation: A Survey and New Strategies. J. Imaging 2023, 9, 46. [Google Scholar] [CrossRef]
- Grossmann, A.; Morlet, J. Decomposition of Hardy Functions into Square Integrable Wavelets of Constant Shape. J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Kumar, G.G.; Sahoo, S.K.; Meher, P.K. 50 Years of FFT Algorithms and Applications. Circuits Syst. Signal Process. 2019, 38, 5665–5698. [Google Scholar] [CrossRef]
- Auslander, L.; Feig, E.; Winograd, S. The Multiplicative Complexity of the Discrete Fourier Transform. Adv. Appl. Math. 1984, 5, 87–109. [Google Scholar] [CrossRef][Green Version]
- Durak, L.; Arikan, O. Short-Time Fourier Transform: Two Fundamental Properties and an Optimal Implementation. IEEE Trans. Signal Process. 2003, 51, 1231–1242. [Google Scholar] [CrossRef]
- Okuboyejo, D.A.; Olugbara, O.O.; Odunaike, S.A. CLAHE Inspired Segmentation of Dermoscopic Images Using Mixture of Methods. In Transactions on Engineering Technologies; Springer: Dordrecht, The Netherlands, 2014; pp. 355–365. ISBN 9789401791151. [Google Scholar]
- Eckmann, J.-P.; Kamphorst, S.O.; Ruelle, D. Recurrence Plots of Dynamical Systems. Europhys. Lett. 1987, 4, 973–977. [Google Scholar] [CrossRef]
- Tziridis, K.; Kalampokas, T.; Papakostas, G.A. EEG Signal Analysis for Seizure Detection Using Recurrence Plots and Tchebichef Moments. In Proceedings of the 2021 IEEE 11th Annual Computing and Communication Workshop and Conference (CCWC), Virtual, 27–30 January 2021; IEEE: New York, NY, USA, 2021; pp. 0184–0190. [Google Scholar]
- Wang, Z.; Oates, T. Imaging Time-Series to Improve Classification and Imputation. arXiv 2015, arXiv:1506.00327. [Google Scholar]
- Vakalopoulou, M.; Christodoulidis, S.; Burgos, N.; Colliot, O.; Lepetit, V. Deep Learning: Basics and Convolutional Neural Networks (CNNs). In Neuromethods; Springer: Berlin/Heidelberg, Germany, 2023; pp. 77–115. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zhang, Z. Improved Adam Optimizer for Deep Neural Networks. In Proceedings of the 2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS), Banff, AB, Canada, 4–6 June 2018; IEEE: New York, NY, USA, 2018; pp. 1–2. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).