Optimal Feature Selection and Classification for Parkinson’s Disease Using Deep Learning and Dynamic Bag of Features Optimization

Abstract

Parkinson’s Disease (PD) is a neurological condition that worsens with time and is characterized bysymptoms such as cognitive impairment andbradykinesia, stiffness, and tremors. Parkinson’s is attributed to the interference of brain cells responsible for dopamine production, a substance regulating communication between brain cells. The brain cells involved in dopamine generation handle adaptation and control, and smooth movement. Convolutional Neural Networks are used to extract distinctive visual characteristics from numerous graphomotor sample representations generated by both PD and control participants. The proposed method presents an optimal feature selection technique based on Deep Learning (DL) and the Dynamic Bag of Features Optimization Technique (DBOFOT). Our method combines neural network-based feature extraction with a strong optimization technique to dynamically choose the most relevant characteristics from biological data. Advanced DL architectures are then used to classify the chosen features, guaranteeing excellent computational efficiency and accuracy. The framework’s adaptability to different datasets further highlights its versatility and potential for further medical applications. With a high accuracy of 0.93, the model accurately identifies 93% of the cases that are categorized as Parkinson’s. Additionally, it has a recall of 0.89, which means that 89% of real Parkinson’s patients are accurately identified. While the recall for Class 0 (Healthy) is 0.75, meaning that 75% of the real healthy cases are properly categorized, the precision decreases to 0.64 for this class, indicating a larger false positive rate.

1. Introduction

Parkinson’s Disease (PD) is a neurological condition that worsens with time and mostly affects movement. Tremors, stiffness, bradykinesia (slowness of movement), and postural instability are some of its symptoms. Non-motor symptoms are also common and include sadness, sleep difficulties, and cognitive impairment [1,2]. The illness is brought on by the death of dopamine-producing neurons in the midbrain area known as the substantia nigra. One neurotransmitter that is essential for coordinating balanced and fluid muscular actions is dopamine. Although the precise origin of neuron degeneration is unknown, a mix of environmental and genetic variables is thought to be involved. After Alzheimer’s Disease, PD is the second most common neurodegenerative condition, affecting about 1% of the over-60 population [3]. PD is more common in males than in women, and its prevalence rises with age. PD cannot be definitively diagnosed; instead, the condition is managed with a combination of physical and neurological examinations, medical history, symptoms, and dopamine replacement medication response. While imaging tests such as Magnetic Resonance Imaging (MRI) and DaT scans are not commonly used to diagnose PD, they can be useful in ruling out other illnesses. Significant motor function impairments caused by PD make daily tasks including eating, dressing, and walking difficult. Patients may experience progressively worsening disabilities as the illness worsens. Patients’ and their families’ emotional well-being are significantly impacted by the prevalent conditions of depression, anxiety, and cognitive impairment.

Parkinson’s motor symptoms manifest when 60% to 80% of these cells are lost due to the inadequate production of dopamine. Recent research has identified a close connection between speech impairment and PD, leading to the development of classification algorithms for PD identification. Artificial Intelligence (AI) is leading the way in next-generation computing for data analytics, particularly in predictive edge analytics for high-risk diseases including PD. Deep Learning (DL) techniques play a crucial role in facilitating edge AI applications for real-time and enhanced data processing. In contrast to conventional methods, which mostly depend on the dynamic (kinematic and spatio-temporal) aspects of handwriting, we objectively assess the visual characteristics in this work in order to characterize graphomotor samples of PD patients. Even with Machine Learning (ML) advances, choosing the best attributes that greatly improve PD diagnostic accuracy continues to be a major difficulty. High dimensionality and superfluous or unnecessary characteristics are common problems with existing models, which can cause overfitting and decreased generalizability. Furthermore, a lot of research has concentrated on static feature sets rather than investigating dynamic strategies that may adjust to various patient data distributions. Research is still being done to find biomarkers for early diagnosis, improve our understanding of the mechanism of PD, and create medicines that alter the condition. DL and other AI advances have the potential to improve diagnosis, forecast the course of disease, and customize therapy regimens. Owing to the intricacy and variability of PD, feature selection (FS) and categorization provide a number of difficulties. The primary difficulties consist of:

• High Dimensionality: Clinical, genetic, imaging, and biochemical indicators are only a few of the many aspects that biomedical data frequently contain. It is challenging to determine which features are most important for precise categorization because of this high dimensionality.
• Heterogeneity of Data: Patients with PD might have very different symptoms and rates of progression, which results in heterogeneous data that makes feature selection more difficult.
• Unbalanced Data: The distribution of PD datasets is frequently unbalanced, with fewer positive cases than healthy controls. This can cause bias in the classification models.
• Redundancy and Noise: Biomedical data may have duplicate information and be noisy, which can impair the effectiveness of classification systems.

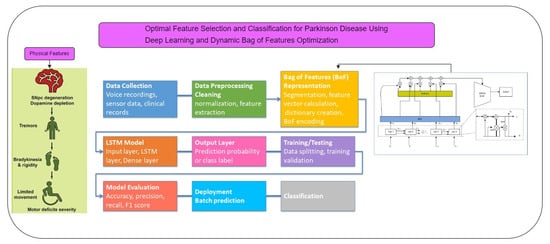
The proposed method makes use of the Dynamic Bag of Features Optimization Technique (DBOFOT) to overcome the shortcomings of previous studies in FS and classification for PD. By streamlining the classification process and dynamically choosing the most pertinent features, this technique seeks to improve overall performance. DBOFOT uses a dynamic FS procedure that changes depending on the particulars of the dataset. Long Short-Term Memory-DBOFOT (LSTM-DBOFOT) continuously modifies the feature set according to each feature’s relevance and contribution to classification accuracy, in contrast to static FS approaches that could ignore significant characteristics or keep unimportant ones [4]. The model can more efficiently manage the high complexity and variability of biomedical data dueto its adaptability. LSTM-DBOFOT improves classification accuracy by reducing noise and redundancy in the data by dynamically choosing the most relevant characteristics. By limiting the usage of only the most informative variables, the optimization strategy improves the model’s capacity to discriminate between PD patients and healthy controls. The shortcomings of earlier study [1,2] that had trouble with noisy and redundant data are addressed by this method. LSTM-DBOFOT uses optimization methods to make the FS process more efficient and less time-consuming. For managing large-scale biomedical datasets, which are typical in PD research, this efficiency is essential. By reducing the computing overhead of conventional FS techniques, the method enables more rapid and scalable analysis. This method improves the model’s interpretability by illuminating the chosen characteristics and how they contribute to the classification goal. For clinical applications, where knowing the importance of traits can help with improved diagnosis and treatment planning, this transparency is essential. Furthermore, by being dynamic, LSTM-DBOFOT addresses the variability problems in earlier studies and enhances the model’s generalizability across various datasets. Multimodal data sources including clinical, genetic, imaging, and gait data can be integrated with DBOFOT. A more complete picture of the patient’s state is provided by this integration, which results in more reliable and accurate categorization models. Studies that concentrate on a single data type have limitations; nevertheless, the model’s ability to handle many data kinds guarantees that it can utilize the entire range of information available.

Our model can effectively capture the temporal dependencies included in the data by integrating LSTM cells, which makes it a suitable fit for the intricate patterns linked to PD. By real-time feature input optimization, this hybrid methodology overcomes the drawbacks of conventional FS techniques and improves the performance of DL models. The major contribution includes:

• The proposed method integrates an LSTM network with the BoF representation, offering a novel approach for PD prediction. It focuses on robust feature selection, and dynamic feature sets, improving classification accuracy.
• The use ofDBOFOT has been used to handwriting-based PD identification. By allowing for adaptive feature combinations based on the significance of the data, it enhances sensitivity to minute handwriting differences that are common in individuals with Parkinson’s Disease.
• The proposed work employs optimization techniques of transfer learning, cross-validation, or regularization to counter overfitting and ensure robust performance even with smaller datasets.
• Handwriting patterns are subtle indications of motor deficits, and the Parkinson’s Disease handwriting (PaHaW) collection used in proposed analysis offers thorough information on handwriting patterns.
• The deployment and continuous monitoring aspects of the proposed method are designed to maintain high accuracy and relevance over time.

The remaining contribution of this paper is structured as follows: Section 2 reviews various prediction methods. Section 3 details the implementation of the LSTM–BoF model and the dataset used, while Section 4 covers the evaluation procedure and analysis of the results on two different datasets. Finally, Section 5 concludes the work.

2. Literature Review

DL and ML models have been used more and more in the diagnosis of PD in recent years. Conventional ML methods, including Random Forest (RF) and Support Vector Machine (SVM), have demonstrated some effectiveness but are frequently limited in their scalability by the need for human feature extraction. By automatically learning hierarchical representations of data, DL models—in particular, CNN and LSTM networks—offer notable advances in feature extraction and classification tasks. The study of computer programs that use statistical models and algorithms to infer information through patterns and inference without explicit programming is known as ML [1]. As ML algorithms learning by training and they improve over time. These algorithms use methods for training models, then use the information they have learned to determine outputs on their own [2]. Moreover, ML systems are capable of adjusting to changing surroundings. According to the study by [3], the three most well-known signs of PD that may be seen in handwriting are “tremor”, “brachykinesia”, and “micrographia”. Maintaining the size and alignment of the generated graphomotor impressions becomes challenging for a patient with micrographia [4]. A supervised ML model that applies classification techniques to two-group classification issues is called an SVM. SVM is well-known for being quick and dependable, and it performs well when processing small datasets [3,4,5]. A prospective PD patient may take longer than normal to finish a graphomotor task if they have bradykinesia, or slowness of movement (caused by either motor or cognitive impairment) [6]. Uncontrollably moving back and forth, “tremors” are represented by asymmetrical character and drawing forms. The coexistence or independence of various Parkinsonian disorders is contingent upon the nature and course of the ailment.

The Decision Tree (DT) approach in ML systems partitions data into subsets with the training data divided into the smallest tree. In order to check the target classes in leaf nodes, this supervised classification approach uses split tests in internal nodes [7]. Because of their consistency and adaptability, decision trees are frequently employed in categorization [8,9,10,11,12]. A supervised learning technique that is both flexible and easy to use, RF frequently produces good results without requiring a lot of hyperparameter tweaking [13]. An RF is made up of randomly generated DTs that use majority vote to decide the expected output. Even if DTs alone might be less precise and dependable, the RF makes up for these drawbacks [14]. Unlike Logistic Regression (LR), which can only handle linear situations, SVM is superior at managing nonlinear problems. SVM determines maximum margin solutions, which efficiently handles outliers. When it comes to handling collinearity, DTs perform better than LR, particularly for categorical values. Compared to individual DTs, RF shave higher accuracy thanks to their ensemble of DTs. While DTs use hyperrectangles in input space to solve problems, SVM use kernel approaches to address nonlinear problems. SVM typically performs better than RF in classification problems [15].

Medical diagnosis has made extensive use of ML models [16,17,18,19]. This research examines different performances of ML for Alzheimer’s diagnosis. A genetic and irreversible brain disorder called Alzheimer’s syndrome gradually impairs critical abilities such as memory and reasoning [20]. To categorize PD using speech data, for example, in reference [21] the author used a CNN-based model, demonstrating a high accuracy rate by capturing subtle patterns that are frequently ignored by traditional ML approaches [21,22,23,24]. In a similar way, ref. [25] showed how well LSTM networks handle time-series biological data and performs better in the early stages of Parkinson’s Disease-identification. The symptoms usually appear in the mid-30s and mid-60s and range from altered sleep patterns to despair and anxiety. Alzheimer’s Disease causes memory loss and reduced cognitive ability, and its symptoms take ten to twenty years to manifest. The primary cause of Alzheimer’s Disease is dementia, which affects 40–50 million people worldwide and is predicted to increase to 131.5 million by 2050. Remarkably, 70% of dementia sufferers live in low-income nations [26].

Salmanpour et al. [27] used ML methods predict the cognitive effects of PI. A comprehensive review of the literature on FS and ML was carried out by Wan et al. [28]. ML is actively used in brain surgery to pinpoint the exact area that has to be treated. The post-diagnosis aspects of PD were also examined by the researchers.

Cavallo et al. [29] used motion data from patients’ upper limbs to create a predictive model for PD. Two groups participated in the study: those with PD and those who did not. The subjects had a device attached to their upper limbs, and they were given instructions on how to carry out different tasks. Frequency and spatiotemporal analyses were performed during data analysis. Different learning strategies were then used to complete the classification process. An alternate method [30] used different ML and feature extraction approaches to identify PD. The most useful criterion for diagnosing the illness, according to the researchers, was phonation. Optimum Path Forest, K-Nearest Neighbor (KNN), SVM, and Multilayer Perceptron (MLP) classifiers were used. Artificial Neural Networks (ANNs) were employed to reduce linguistic impairments, while SVM contributed to the classification process, facilitating the ML-based identification of PD.

Researchers presented an unsupervised method for PD identification in [31]. For clustering and prediction, they used an incremental Support Vector Regression (SVR) and a Self-Organizing Map (SOM), respectively. After dimension reduction using Partial Least Squares (PLS), the Unified PD Rating Scale (UPDRS) is predicted and SOM and SVR approaches are implemented in the suggested method. In a different work [32], authors used the KNN classifier technique for PD identification and investigated a Fuzzy-based C-means clustering algorithm to evaluate feature weights. To find the ideal K value, the KNN classifier made use of a weighted PD dataset with a range of K values.

In order to handle unbalanced data, Wang et al. [33,34] used sophisticated learning techniques to diagnose PD. These techniques included a weighted scheme and a nonlinear mapping of the kernel function. Features were chosen and variables were optimized using the Artificial Bee Colony (ABC) algorithm. Fisher Discriminant Ratio (FDR), Principal Component Analysis (PCA), and SVM were utilized for FS, dimension optimization, and classification, respectively, in a different method put forward by PI. Abdulhay et al. [35] used sensors beneath patients’ feet to collect physical signals and looked at tremor and gait symptoms for PD detection. With an accuracy rate of over 92%, gait features were extracted from the raw data in the PhysioNet database by analyzing the electrical pulses to identify anomalous peaks. Using voice inputs from a shared dataset, Yaman et al. [36] applied feature augmentation to find salient features for illness detection. A total of sixty-six characteristics were chosen to categorize PD. Instead of depending on MRI, motion, or voice data, a noteworthy study in [37,38,39,40,41,42] investigated the possibility of using handwriting inspection to detect PD.

High classification rates are demonstrated by ML-based techniques [43,44,45,46,47] for determining PD, according to a thorough evaluation of the literature. Although ML is useful foridentifying PD, its application is fraught with difficulties. While considering a lot of features improves identification rates, it also uses more resources in terms of computing cost and execution time. On the other hand, utilizing fewer features could make results less reliable.

According to recent research, computation time can be greatly decreased by using a simpler classifier, a lightweight feature extraction model, and a smaller number of features. Moreover, it has been noted that feature extraction from speech signals is comparatively easier than approaches based on motion [39] or MRI. To increase classification rates, a significant number of vocal features have been chosen by several researchers [40,41]. In contrast, speech analysis is a simpler process compared to the extraction of features from MRI images, which yields higher classification accuracy. A summarization of the existing works is given in

Table 1. Comparison of various methods in the literature.

Ref.	Approach	Advantage	Limitation
[1]	T1-weighted MRI and DTI with SVM	Good accuracy with MRI and DTI data	High computational resources required; expert-driven feature extraction can be subjective
[2]	Deep learning framework using MRI data	High accuracy, automatic feature extraction	Limited interpretability; requires large labeled datasets
[3]	Genetic algorithms and SVM using clinical and genetic data	Effective FS	Computationally intensive; difficulty generalizing results across populations
[4]	Hybrid PCA and deep learning for gait data	Improved classification accuracy	Potential loss of valuable information with PCA; challenge in integrating multimodal data
[5]	Machine learning for predicting cognitive effects of Parkinson’s	Effective prediction of cognitive impact	Not specified
[6]	Motion data from upper limbs with various learning strategies	Comprehensive analysis with spatiotemporal features	Requires specialized equipment for data collection
[7]	Various ML and feature extraction approaches (phonation data)	High accuracy with multiple classifiers	Not specified
[8]	Unsupervised method with incremental SVR and SOM	Effective clustering and prediction	✓
[9]	k-NN classifier with fuzzy-based C-means clustering for feature weights	Effective feature weighting and classification	✓
[10]	Weighted scheme, nonlinear kernel function mapping, ABC algorithm	Effective handling of unbalanced data	✓
[11]	FDR, PCA, and SVM for FS, dimension optimization, classification	Successful hybrid model	✓
[12]	Sensors under feet for gait and tremor detection	High accuracy (92%) with gait features	Requires specialized sensors for data collection
[13]	Feature augmentation from voice inputs	Effective vocal FS	Not specified
[14]	Handwriting inspection for Parkinson’s detection	Novel approach	✓
[15]	Simpler classifier, lightweight feature extraction, fewer features	Reduced computation time	Trade-off between reliability and computational cost

.

PD is a progressive neurological disorder that impairs movement and significantly impacts quality of life, necessitating timely and accurate diagnosis for effective management. Traditional diagnostic methods, reliant on clinical examination, can be subjective and delay diagnosis. This work introduces a novel approach using advanced ML techniques to improve the early detection of PD by analyzing diverse patient data sources. The proposed system employs dynamic FS to enhance classification accuracy by reducing noise and redundancy, making it particularly effective for large-scale biomedical datasets. By integrating LSTM networks with the BoF technique, the model captures temporal patterns and complex correlations in data, improving interpretability and generalizability. The LSTM–BoF PD model is designed to enhance the discriminative power of features across various modalities, such as gait, imaging, and genetic data, offering a more accurate and comprehensive understanding of PD dynamics. This integrated approach aims to advance healthcare technologies by enabling a more reliable and efficient system for early PD diagnosis.

In the proposed system, we extend existing methods by combining a DL classification framework with an optimization method called DBoF. This hybrid technique overcomes the drawbacks of previous models that just use ML algorithms by ensuring appropriate feature selection and improved classification accuracy. Furthermore, by incorporating DL, the model can recognize more intricate patterns in the data, increasing its versatility and scalability across various datasets. Predictions become more accurate as a result of the DBoF approach, which improves the system’s capacity to eliminate noise and choose the most pertinent features. The model is highly suited forPDdiagnosis because of method’s special ability to handle large-scale and heterogeneous biological datasets. Moreover, it enables dynamic feature selection for ongoing improvement, guaranteeing the system’s sustained high performance.

3. Proposed Parkinson’s Disease Classification Model

The proposed technique combines the benefits of the BoF technique with LSTM networks. LSTM networks are perfect for evaluating time-series data, including voice recordings and sensor measurements, since they are well-suited for modeling temporal dependencies in sequential data. By expressing data segments as fixed-size feature vectors, the BoF technique, on the other hand, efficiently manages variability in input data and makes the LSTM model’s input preparation easier. The proposed architecture consists the components illustrated in Figure 1 and discussed subsequently.

3.1. Data Collection

To obtain a wide range of information about PD, extensive datasets such as voice recordings, clinical records, and sensor data (such as gait analysis and tremor data) are gathered. The Unified PD Rating Scale (UPDRS) scores and voice measures are part of the extensive PTD (Parkinson’s Telemonitoring Dataset) [13] from the UCI ML Repository [35], which is intended for tracking the advancement of PD. Nearly 6000 instances with 22 variables were collected in the dataset. Important UPDRS components such as UPDRS_1, UPDRS_2 and UPDRS_3 which stand for sub-scores pertaining to behavior, mood, daily living activities, and mentation, respectively, are included. It also contains additional significant features, such as total_UPDRS and motor_UPDRS (UPDRS part III), which offer an overall evaluation of the motor and total UPDRS scores. This dataset provides insights into how these characteristics may be utilized for remote telemonitoring and is useful for regression and prediction tasks that try to explore the association between voice biomarkers and the severity of PD.

Another dataset for the experimentation was considered from PD Handwriting Database (PaHaW) [31], and is dedicated to documenting and examining handwriting patterns in people who have PD. The collection contains dynamic handwriting samples that were taken using digitizing tablets that measure pen location, pressure, and speed in real-time from both PD patients and healthy control people. The purpose of these examples is to emphasize motor deficits such as bradykinesia and tremors, which are usually linked with PD. Typically, these activities include writing words or drawing spirals. Research aiming at comprehending the motor symptoms of PD and creating diagnostic instruments based on handwriting analysis will find great value in the PaHaW dataset.

3.2. Data Preprocessing

To guarantee that the model receives high-quality inputs, perform necessary preprocessing procedures such feature extraction, normalization, and data cleaning. Choosing the most pertinent characteristics, scaling the data, and addressing missing values are all included in this step. The proposed system performs Min Max Normalization defined in Equation (1) to ensure that the features are scaled to same level and it extracts feature by utilizing Equation (2).

$${\mathrm{\varkappa }}^1={\displaystyle \frac{\mathrm{x}-\mathrm{u}}{\mathsf{\sigma }}}$$

(1)

where $x$ is the feature value of original data, $\mu$ is the mean of the feature $x$, and $\sigma$ is the standard deviation of the data.

$$\sum _{\mathrm{i}=1}^{\mathrm{I}}\mathrm{l}\mathrm{o}\mathrm{g}\left|{\mathrm{x}}_{\mathrm{i}}\right|\cos \left({\displaystyle \frac{\mathsf{\pi }\mathrm{n}\left(\mathrm{i}-0.5\right)}{\mathrm{k}}}\right)$$

(2)

where the Fourier transform’s magnitude at bin is represented by $x$,$i$ represents the number of frequency bins, and $n$ is the MFCC(Mel-Frequency Cepstral Coefficients) index.

3.3. Bag of Features Representation

Using a BoF technique, partition the data into fixed-size windows and encode each segment into a feature vector. In this step, a dictionary of features and transformations is created. Afterwards, variable-length data are converted into a uniform format that can be fed into an LSTM, and a dictionary of features is created as defined in Equation (3).

$$\sum _{\mathrm{i}=\mathrm{i}}^{\mathrm{N}}\mathrm{m}\mathrm{i}{\mathrm{n}}_{{\mathrm{u}}_{\mathrm{j}}\in \mathrm{C}}{‖{\mathrm{x}}_1-{\mathrm{u}}_{\mathrm{j}}‖}^2$$

(3)

where $\mathrm{x}$ is the data points, $u$ is the cluster centroid, and $C$ is the centroid of all data points. Every segment can then be encoded according to how frequently the dictionary features occur once it has been created: $\mathrm{B}\mathrm{o}\mathrm{F}\left(\mathrm{x}\right)={[\mathrm{f}}_1,{\mathrm{f}}_2,\dots ,{\mathrm{f}}_{\mathrm{n}}]$, where the frequency of the $i$-th feature in the segment is represented by $f$.

3.4. LSTM Representation

To represent temporal dependencies and identify patterns in the sequential data, an LSTM model is used. The model is composed of several LSTM layers, succeeded by thick layers that enhance the feature representation and yield precise forecasts. The LSTM is recursive, as indicated by its looping arrow. The term “cell state” refers to this condition. As a result, the data from the previous interval arestored in the cell state. The cell state is modified by a remember vector underneath the input modification gates and defined in Equation (4).

$${\mathrm{X}}_{\mathrm{t}}={\mathrm{f}}_{\mathrm{t}}{\mathrm{X}}_{\mathrm{t}}+{\mathrm{i}}_{\mathrm{t}}$$

(4)

After the output has passed through the LSTM layers, it is often routed into fully connected layers where the retrieved features are further processed. The final layer generates a probability distribution over all possible activity classes (e.g., sitting, running, and walking); the expected activity has the highest probability class. This layer is often a SoftMax layer. The network’s performance predictions are compared to the actual activity labels during training using a loss function, and backpropagation is used to adjust the parameters to lower the loss. Regular LSTMs [42,43,44,45] can capture temporal patterns and long-term associations, which enable them to accurately recognize and classify human behaviors based on periodic sensor data. The implementation of LSTM then is followed using Equation (5).

$${\mathrm{i}}_{\mathrm{t}}=\mathsf{\sigma }\left({\mathrm{w}}_{{\mathrm{f}}_{\mathrm{i}}\mathrm{i}}\left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}}\right]+{\mathrm{b}}_{\mathrm{f},\mathrm{i}}\right)$$

$${\mathrm{f}}_{\mathrm{t}}=\mathsf{\sigma }\left({\mathrm{W}}_{\mathrm{f},\mathrm{f}}\cdot \left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}}\right]+{\mathrm{b}}_{\mathrm{f},\mathrm{f}}\right)$$

$${\mathrm{C}}_{\mathrm{t}}=\tanh \left({\mathrm{N}}_{\mathrm{f},\mathrm{c}}\cdot \left[{\mathrm{h}}_{\mathrm{t}-1},{\mathrm{x}}_{\mathrm{t}}\right]+{\mathrm{b}}_{\mathrm{f},\mathrm{c}}\right)$$

(5)

$${\mathrm{h}}_{\mathrm{t}}=\left[{\mathrm{h}}_{\mathrm{t}};{\mathrm{h}}_{\mathrm{t}}\right]$$

(6)

where, ${\mathrm{i}}_{\mathrm{t}}$ is the input gate, ${\mathrm{f}}_{\mathrm{t}}$ is the forget gate, ${\mathrm{C}}_{\mathrm{t}}$ is the cell state, $\mathsf{\sigma }$ is the Sigmoid activation function, tanh is the Hyperbolic Tangent activation function, W is the weights, and $\mathrm{b}$ is the bias term. Hidden state ${\mathrm{h}}_{\mathrm{t}-1}$ is considered from current point ${\mathrm{x}}_{\mathrm{t}}$. For every time step t, the forward and backward LSTM layers’ outputs are concatenated to create the final output using Equation (6).

3.5. Deployment and Monitoring

The key novelty lies in the incorporation of the DBOFOT, a dynamic feature optimization technique designed to adaptively adjust to the evolving characteristics of the input data. Traditional BoF approaches often treat features as static entities, disregarding the temporal nuances inherent in sequential data. DBOFOT, on the other hand, introduces a dynamic mechanism that tailors the feature extraction process based on the data’s temporal evolution. This adaptability is particularly pertinent in healthcare applications, where disease progression is often characterized by subtle temporal changes that traditional methods might overlook. As shown in Figure 2, the diagram shows a NN design that uses a Softmax layer, a BoF module, and LSTM cells for classification. After processing a series of inputs, the LSTM cells create hidden states and record temporal dependencies. The BoF module then aggregates these hidden states, condensing the features into a fixed-size vector. Class probabilities are produced by the Softmax layer using this aggregated vector as input. This output is further refined by a Dense layer, which results in the final categorization. The architecture is designed with skip connections and dilated convolutions. The network uses dilated convolutions to capture more context without sacrificing resolution and $(1\times 1$) convolutions to control the depth of the feature maps. BoF after feature extraction but before classification allows it to act as a bridge, converting the learned intricate features into a format that can be used and classified. The key to this is the use of dilated convolutions, which may be very helpful for collecting temporal or spatial aspects in data, since they enable the network to span a broader receptive field without increasing the number of parameters.

The combination of DBOFOT with a DL-based optimal FS method leverages the strengths of both paradigms. DL, particularly in the form of LSTM networks, excels at capturing intricate temporal dependencies within sequential data. The LSTM component of the proposed model facilitates the extraction of meaningful patterns and representations from the data, allowing for a more nuanced understanding of the underlying dynamics associated Parkinson’s Disease. Furthermore, the addition of stack sparse autoencoder NNs enhances the model’s capacity for optimal FS. Autoencoders are adept at learning efficient data representations and extracting essential features. By stacking these autoencoders, the model can hierarchically learn and represent complex features, enabling a more compact and discriminative feature space.This architecture offers a more dynamic and context-aware feature extraction process, which usually entails building a set of features and encoding incoming data depending on the existence of these characteristics. The architecture displayed here is probably more adaptive and able to extract more complicated patterns straight from the data, which might be regarded as a major benefit in applications requiring extensive feature representation on predetermined features.

For sequential handwriting, data taken from the PaHaW dataset make up the process. Time-series sequences are used to represent each sample, and they capture several attributes with time, including pen stroke location, pressure, acceleration, and velocity. Given that Parkinson’s Disease presents with subtle motor deficits, such as tremors and diminished fine motor abilities, these traits offer vital insights into motor control, which is crucial for recognizing the disease. Recurrent cells, such as GRU (gated recurrent units) or LSTM units, analyse the sequential input. Each input $X_i$ travels through these cells, which are displayed at the bottom of the picture, over subsequent time steps.

Due to their ability to recognize both the long-term patterns and the short-term relationships seen in the handwriting sequences, the LSTM/GRU cells are especially well-suited for this task. The forget gates, input gates, and memory cells are part of the internal structure of the cells, which makes sure the model stores and discards data selectively in order to detect minute inconsistencies in handwriting. The BoF layer receives the intermediate outputs from each recurrent unit at various time steps ($h_1,h_2,\dots h_n$) respectively. By combining and improving feature selection from these recurrent outputs, the BoF layer serves a critical function. Dynamic feature pooling reduces the dimensionality of the data by eliminating unnecessary information and preserving just the most important handwritten traits.

These steps integrate features from different modalities, perform transfer learning, and provide explainability by generating attention weights and visualizing attention heatmaps. Proposed algorithm incorporates mathematical expressions for dynamic BoF integration, adaptive learning rate, multi-modal feature fusion, transfer learning, and explainability.

4. Performance Evaluation

This section presents the performance evaluation of the proposed model by evaluating various metrics such as accuracy, precision, recall, and F1-score, which identify the model’s accuracy in identifying PD, and performance is evaluated using a dataset that included both patients and healthy persons.

4.1. Experiment Setup

To get ready for analysis, the data are preprocessed after they are gathered. In order to deal with missing values, data cleaning is conducted, which may entail mean imputation or the removal of incomplete information. Noise reduction techniques, such as low-pass filtering, are used for voice recordings. The model’s performance is then enhanced by normalization, which makes sure all input features have a comparable scale. Depending on the nature of data, multiple methods are used for feature extraction.

To find the most pertinent features, FS methods PCA and Correlation Analysis (CA) are applied by converting the original features into a collection of linearly uncorrelated components that represent the highest variance in the data, PCA is used to decrease the dimensionality of the data. This makes it easier to recognize and keep the most illuminating elements while removing the unnecessary ones. The associations between the features are then evaluated using CA, making sure that strongly correlated characteristics are not included at the same time, preventing multicollinearity and enhancing model performance. By combining these two methods, it is ensured that the chosen characteristics greatly increase the predictive capacity of the model. Windows of a specific size are used to segment the data. For instance, sensor data might be split into one-minute chunks and voice data into one-second parts. For every segment, feature vectors that capture the key elements of the data are computed. By finding similar patterns among the segments, k-means clustering creates a dictionary of features. The variable-length input data arethen converted into a fixed-length format by encoding each data segment according to the frequency of the dictionary features.

The model consists of numerous LSTM layers with 100 number of units. In order to retain computational efficiency while enabling the network to capture temporal relationships in the data, this design was selected to strike a compromise between model complexity and performance. After an input layer to receive sequences encoded using BoF. One or two thick layers with ReLU activation functions are placed after these layers to further enhance the feature representation. Using a Sigmoid activation function, the final output layer predicts whether PD is present or not. Performance is maximized by choosing the model’s hyperparameters, which include the learning rate (0.001), batch size (32), and number of epochs (50–100). The dataset is divided into test (15%), validation (15%), and training (70%). The training data is used to train the LSTM model. In order to prevent overfitting, the LSTM model is trained using the training set and its performance is tracked on the validation set. In order to keep the model from overfitting the data and training for an excessive amount of time, early stopping is used depending on the validation loss. Through backpropagation, the training process modifies the model’s weights and biases, progressively enhancing its predictive power. Input sequences encoded in BoF at the input layer. We assign 100 amount of unitsto two-to-three LSTM layers. A dense layer include one or two completely connected layers that use ReLU or another activation function. For binary classification (Parkinson’s presence/absence), we use a Sigmoid activation function.

4.2. Results Analysis

For PD to be effectively managed and treated, an accurate diagnosis is essential. This study compares the performance of a number of well-known ML techniques—ANN, Conventional LSTM models, Bayesian Classifiers (BC), and SVM—and the handwriting data analysis against the proposed LSTM–BoF model for PD detection in terms of the performance metrics. The proposed LSTM–BoF model was benchmarked against the following methods as part of our comparative analysis.

We use an adaptive selection technique that assesses each feature’s contribution to the overall classification job in realtime. This is accomplished through the use of a hybrid strategy that combines the automated feature extraction power of DL models with more conventional ML method known as Recursive Feature Elimination (RFE). The goal of the DBoF optimization is to keep the most informative characteristics while reducing redundancy.

Stochastic Gradient Descent (SGD), in conjunction with a L2 regularization method, is used in the optimization process. This guarantees that the model converges to an ideal solution and lessens overfitting. We also add early stopping depending on the validation loss in order to maximize the performance of the model. The hybrid technique combines the potent representation learning of DL models with the interpretability advantages of ML. The proposed approach reduces the computational complexity of the model and increases classification accuracy by striking a balance between automated DL-based optimization and manual FS [11,12].

4.2.1. Artificial Neural Network

A classic ML technique that imitates the composition and operation of the human brain is ANN. NN, which are modelled after the architecture of the brain, are made up of layers of interconnected nodes, or neurons. To produce an output, a neuron takes inputs, calculates a weighted sum, and applies an activation function. In our tests, we employed an ANN with three completely linked layers. There are 64 neurons in the input layer and 128 neurons in the hidden layer. One neuron handles binary categorization in the output layer. We used the Sigmoid function for the output layer to turn the output into a probability score and the ReLU for the hidden layers to introduce non-linearity as the activation functions. The network was trained at a learning rate of 0.001 using the Adam optimizer, and the error between the predicted and real labels was measured using the binary cross-entropy loss function.

The parameters used in the model are as follows:

• Input Layer: Receives input data ${\mathrm{x}}_{\mathrm{i}}$.
• Hidden Layers: Perform computations $\mathrm{z}=\sum _{\mathrm{i}-1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{i}}+\mathrm{b}$, followed by activation $\mathsf{\alpha }=\mathsf{\sigma }\left(\mathrm{z}\right)$.
• Output Layer: Produces final predictions.
• Weighted Sum: $\mathrm{z}=\sum _{\mathrm{i}-1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{i}}+\mathrm{b}$
• Activation Function: $\mathsf{\alpha }=\mathsf{\sigma }\left(\mathrm{z}\right)$.
• Training: Adjusts weights to minimize loss L via gradient descent.

NNs are useful for many applications, such as picture classification and natural language processing, since they are excellent at deriving complicated patterns from input.

4.2.2. Conventional LSTM Model

Because LSTM models can capture long-term dependencies, they are frequently employed for sequential data analysis. Recurrent Neural Networks (RNNs) with LSTM networks are specifically engineered to tackle the vanishing gradient problem and effectively identify long-term dependencies within sequential data. In order to control information flow, LSTMs integrate a memory cell and a number of gating techniques. Two LSTM layers, each with 100 units, were used in the creation of the LSTM model. The model can successfully capture temporal dependencies in the data with this setting. A completely linked layer is placed after the LSTM layers for categorization. The LSTM cells employ normal tanh and sigmoid activations within their gates, whereas ReLU activation was applied in the thick layers. Binary cross-entropy was once more utilized as the loss function to direct learning throughout the model’s optimization utilizing the Adam optimizer at a learning rate of 0.001. In order to control information flow, LSTM integrate a memory cell and a number of gating techniques. The parameters used in the model are given below:

• Memory Cell ${\mathrm{C}}_{\mathrm{t}}$: Stores information over time.
• Forget Gate ${\mathrm{f}}_{\mathrm{t}}$: Determines what information to discard.
• Input Gate it and Input Modulation ${\mathrm{C}}_{\mathrm{t}}$: Control the flow of new information.
• Output Gate ${\mathrm{o}}_{\mathrm{t}}$: Filters information for the output.

4.2.3. Bayesian Classifier

Based on the Bayes theorem, these probabilistic models forecast that a sample will belong to a specific class. Through the application of Bayes theorem to determine the specific class thedata point belongs to, a BC aids withprediction. It refreshes the previous understanding of the class distribution with the observed data. BC can be used to forecast PD by combining past probability of the illness’s presence with the chance of observed symptoms or biomarkers (such protein expression levels or UPDRS scores). We used a Gaussian Naive Bayes model, which is predicated on the idea that the distribution of the features is normal. The model computes posterior probabilities for classification based on the probability of the characteristics given the class. Since this model is based on probabilistic principles for classification rather than neural network design, it is not affected by hyperparameters such as neuron counts or layers. This method offers a probabilistic framework for classification, making it possible to make reliable predictions even in the case of missing or ambiguous data. It works especially well when combining various kinds of biological and clinical data. The experiment results are shown in

Table 2. Results obtained from pre-trained Bayesian Classifier model.

Target	MSE	sMAPE
UPDRS 1	31.34	72.6704
UPDRS 2	45.41	78.7865
UPDRS 3	122.03	78.1446
UPDRS 4	18.55	125.4781

.

The Mean Squared Errors (MSE), shown in Table 2, reveals that the various UPDRS components have differing degrees of prediction error, with UPDRS 3 displaying the highest error and UPDRS 4 the lowest. The values of the Symmetric Mean Absolute Percentage Error (sMAPE), shown in the table, indicate a wide range of relative prediction accuracy, especially for UPDRS 4, which has a low MSE but a considerably high sMAPE, indicating big proportional mistakes. This shows that although some forecasts may have smaller absolute errors, they still require significant improvement in terms of relative accuracy, particularly when it comes to motor problems.

4.2.4. Support Vector Machine

SVM is an approach for supervised learning that divides classes in feature space using a hyperplane. The results obtained are shown in

Table 3. Results obtained from pre-trained SVM model.

Target	MSE	sMAPE
UPDRS 1	19.03	63.44
UPDRS 2	30.58	94.9
UPDRS 3	173.3	80.68
UPDRS 4	10.14	156.35
Average	58.26	98.84

. A Radial Basis Function (RBF) kernel was used in the SVM model’s configuration to transfer the input characteristics into a higher-dimensional space where a hyperplane may divide the classes and manage the trade-off between maximizing the margin and reducing classification mistakes, the regularization value C was set at 1.0. The SVM model’s performance metrics show that different MDS-UPDRS score components have differing levels of prediction accuracy. According to the MSE, UPDRS 3 has the largest error, whilst UPDRS 4 has the lowest error. Despite having a low MSE, UPDRS 4 has the largest relative error according to the sMAPE, showing considerable proportional inaccuracy. The SVM model does rather well in terms of absolute mistakes, but there is a lot of variety in relative accuracy, especially when it comes to motor problems and everyday experiences, as evidenced by its average MSE of 58.26 and sMAPE of 98.84.

4.2.5. Proposed LSTMBoF Model

There are 232,741 entries and 5 columns in the train_proteins data. As shown in

Table 4. Sample PTD dataset.

Seq	visit_id	patient_id	visit_month	updrs_1	updrs_2	updrs_3	updrs_4	upd23b_clinical_state_on_medication
0	55_0	55	0	10.0	6.0	15.0	NaN	NaN
1	55_3	55	3	10.0	7.0	25.0	NaN	NaN
2	55_6	55	6	5.0	10.0	34.0	NaN	NaN
3	55_9	55	9	8.0	9.0	30.0	0.0	On
4	55_12	55	12	10.0	10.0	41.0	0.0	On

, the patient’s baseline appointment (0 months) was attended by ID 55. UPDRS Parts I, II, and III have scores of 10.0, 6.0, and 15.0, in that order. The medication state is not recorded (NaN), nor is Part IV recorded (NaN). The patient’s UPDRS Parts I, II, and III scores at three months are 10.0, 7.0, and 25.0, respectively. There is no information available for Part IV or medication state. After six months, the UPDRS Parts I, II, and III scores are 8.0, 10.0, and 34.0, respectively; Part IV and medication state data are not available. UPDRS Parts I, II, and III have scores of 8.0, 9.0, and 30.0 at nine months, respectively. Part IV has a score of 0.0, which indicates no motor impairment. The medication state is “On” and the UPDRS Parts I, II, and III scores at 12 months are 10.0, 10.0, and 41.0, respectively. Part IV has a score of 0.0.

Multiple peptides combine to form the lengthy molecules known as proteins. Each peptide’s abundance in proteins related to PD is noted by the clinic. In line with NPX for proteins, it displays the peptide concentration. The train_peptides Data Frame contains thesedata. This dataset offers comprehensive data on a patient’s PD progression across time, as determined by the MDS-UPDRS and shown in Table 4. It makes it possible to monitor changes in the patient’s non-motor and motor symptoms, as well as the impact of medication on their condition.

The train_peptides dataset consists of 981,834 elements divided into six columns. Table 4 shows the first five entries, and we can view all six dimensions of our dataset. The target label values of the patient will be plotted against each month (visit_month) using a randomly selected patient_id, as shown in

Table 5. Sample training data.

Seq	visit_id	visit_month	patient_id	UniProt	NPX
0	55_0	0	55	O00391	11,254.3
1	55_0	0	55	O00533	732,430.0
2	55_0	0	55	O00584	39,585.8
3	55_0	0	55	O14498	41,526.9
4	55_0	0	55	O14773	31,238.0

. Using a randomly selected patient_id, we plot the patient’s first 40 UniProt protein entries and their NPX value against the patient’s visit month (visit_month).

The ratings for the first four UPDRS segments as shown in Figure 3, updrs_1, updrs_2, updrs_3, and updrs_4, are forecast by the clinic andrecorded during a patient visit. The dataset is now ready for model training in order to predict the four labels. Using the patient’s recorded protein and peptide data from that visit, we are able to forecast the target labels (updrs_1, updrs_2, updrs_3, updrs_4) for a particular visit.

Using visit ids (visit id) and protein ids (UniProt), we first group the rows in the train_proteins data. The mean of the NPX values of all the rows in a group will then be used to replace the NPX values of each row in that group. Similarly, we organize the rows in the train_peptides data according to their peptide IDs (Peptide) and visit ids (visit_id). Next, we substitute the mean of the Peptide Abundance values of all the rows in a group for each row’s Peptide Abundance values.

The Protein dataset is rearranged so that its UniProt1 values become columns and its unique visit_id values become indices. The NPX values for each visit (row) are recorded in the columns as shown in Figure 4, and they match to the various UniProt1 values that were noted for that visit. The Peptipe dataset has been rearranged so that the unique visit_id values serve as indexes and the dataset’s Peptide values serve as columns. The Peptide Abundance values for each visit (row), which correspond to the various Peptide values noted for that visit, are recorded in the columns as shown in

Table 6. Peptides information considered for training.

Seq	visit_id	visit_month	patient_id	UniProt	Peptide	Peptide Abundance
0	55_0	0	55	O00391	NEQEQPLGQWHLS	11,254.3
1	55_0	0	55	O00533	GNPEPTFSWTK	102,060.0
2	55_0	0	55	O00533	IEIPSSVQQVPTIIK	174,185.0
3	55_0	0	55	O00533	KPQSAVYSTGSNGILLC(UniMod_4)EAEGEPQPTIIK	27,278.9
4	55_0	0	55	O00533	SMEQNGPGLEYR	30,838.7

.

As shown in

Table 7. Results obtained from pre-trained proposed LSTM–BoF model.

Target	MSE	sMAPE
UPDRS 1	23.41	65.091
UPDRS 2	12.81	60.0634
UPDRS 3	12.19	33.1509
UPDRS 4	15.2	NaN
Average	15.90	52.77

, UPDRS 3 displays the lowest MSE (12.19), with decreased MSE values across all UPDRS components, indicating improved prediction accuracy for motor testing results. The sMAPE values reveal less proportional errors and better relative prediction accuracy, particularly for UPDRS 3 (33.1509). With a sMAPE of 52.77 and an MSE of 15.90 on average, the LSTM–BoF model demonstrates noticeably improved accuracy and overall performance.

Three pre-trained models and the proposed system were considered for the evaluation such as ANN, Conventional LSTM, BC, SVM, and the proposed LSTM model, as shown in

Table 8. Mean Square Error analysis of four models.

Model	Algorithm	Label	MSE
Model 1	ANN	updrs_1	25.7711
Model 2	Conventional LSTM	updrs_2	29.0788
Model 3	Bayesian Classifier	updrs_3	175.8958
Model 4	SVM	updrs_4	9.4679
Model 5	Proposed LSTM–BoF	updrs_5	8.6676

. The performance of decision forest models trained on various datasets is displayed in the training results. With 205 cases used for testing and 863 examples for training, Model 1 produced a MSE of 25.7711. Model 2 had an MSE of 29.0788 after being trained on 856 samples, of which 212 were used for testing. But Model 3, which was trained on 845 samples and tested on 213 of them, had a noticeably higher MSE of 175.8958. On the other hand, with the lowest MSE of 9.4679, Model 4, which was trained on 471 samples and 98 for testing, showed the most promising performance. These findings highlight the importance of dataset size and composition in training models, with Model 4 showing the highest level of performance out of all the models tested.

The models labeled as updrs_1, updrs_2, updrs_3, and updrs_4 are assigned MSE values by the given labels, with corresponding MSE values of 25.7711, 29.0788, 175.8958, 9.4679, and 8.6676, respectively. It is estimated that the average MSE for these models is roughly 60.0534. These labels match the models that have been trained and assessed to predict UPDRS scores, a measure of how severe symptoms are of PD. Lower MSE values indicate greater performance. We manually separated 20% of the dataset for validation (called valid_ds) prior to training the dataset. The ANN can also be validated using the Out of Bag (OOB) score. An algorithm selects a subset of random samples from the training set to train ANN; the remaining samples are utilized to fine-tune the model. OOB data arethe subset of data that arenot selected. The OOB data areused to compute the OOB score, as shown in Figure 5.

The scores of each label are described in

Table 9. Feature score description.

Feature Name	Index	Importance Score
Q06481	810	36.0
P04180	703	21.0
P07602	729	17.0
FFLC(UniMod_4)QVAGDAK	230	12.0
P05060	712	11.0
O60888	638	9.0
DSGEGDFLAEGGGVR	162	8.0
LEEQAQQIR	475	8.0
NVVYTC(UniMod_4)NEGYSLIGNPVAR	627	8.0
P05067	713	8.0
P17174	765	7.0
QQTHMLDVMQDHFSR	888	7.0
TQSSLVPALTDFVR	1060	7.0
EVNVSPC(UniMod_4)PTQPC(UniMod_4)QLSK	217	6.0
QWAGLVEK	897	6.0
SSGLVSNAPGVQIR	988	6.0
WYFDVTEGK	1163	6.0
AVLPTGDVIGDSAK	84	5.0
AVC(UniMod_4)SQEAMTGPC(UniMod_4)R	80	4.0
NLREGTC(UniMod_4)PEAPTDEC(UniMod_4)KPVK	609	4.0
Q6UXB8	829	4.0

. The performance of decision forest models trained on various datasets is displayed in the training results. With 205 cases used for testing and 863 examples for training, Model 1 produced a mean squared error (MSE) of 25.7711. Model 2 had an MSE of 29.0788 after being trained on 856 samples, of which 212 were used for testing. But Model 3, which was trained on 845 samples and tested on 213 of them, had a noticeably higher MSE of 175.8958. On the other hand, with the lowest MSE of 9.4679, Model 4, which was trained on 471 samples and 98 for testing, showed the most promising performance. These findings highlight the importance of dataset size and composition in training models, with Model 4 showing the highest level of performance out of all the models tested. The performance of the algorithms is summarized in the

Table 10. Evaluation parameters of the proposed model using repository dataset.

Algorithm	Accuracy	Sensitivity	Specificity	AUC-ROC
ANN	0.84	0.81	0.87	0.89
Conventional LSTM	0.82	0.79	0.85	0.87
Bayesian Classifier	0.79	0.76	0.82	0.81
SVM	0.86	0.83	0.88	0.91
Proposed LSTM–BoF	0.89	0.85	0.91	0.93

. Accuracy, sensitivity, specificity, and AUC-ROC wereutilized to compare the performance of the proposed algorithm against existing models.

• Accuracy: The ratio of accurately anticipated observations to total observations is known as accuracy. It shows how accurately both positive and negative classes are predicted by the model defined in Equation (7).

  $$\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

  (7)

  where: True Positives (TP): Positive cases that were correctly predicted, True Negatives (TN): Negative cases that were correctly predicted, False Positives (FP): Positive cases that were incorrectly expected, and False Negatives (FN): Negative cases that were incorrectly predicted.
• Sensitivity: The ratio of accurately predicted positive observations to all actual positive observations is known as sensitivity, also known as recall. It gauges a model’s capacity to identify positive cases. It is defined in Equation (8).

  $$\mathrm{S}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{t}\mathrm{y}={\displaystyle \frac{TP}{TP+FN}}$$

  (8)
• Specificity: The ratio of accurately predicted negative observations to all actual negative observations is known as specificity. It assesses the model’s capacity to recognize negative instances defined in Equation (9).

  $$\mathrm{S}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}={\displaystyle \frac{TN}{TN+FP}}$$

  (9)
• AUC-ROC (Area Under the Receiver Operating Characteristic Curve): AUC-ROC is a metric used to assess how well classification models perform at different threshold values. The True Positive Rate (Sensitivity) is plotted against the False Positive Rate (1—Specificity) on the ROC curve. The area under this curve is denoted by AUC. The model performs better at differentiating between positive and negative classes the closer its AUC value is to 1.

4.3. Analysis of Parkinson Using Handwriting

We also used the PaHaW dataset [31] in our tests to examine the resilience and efficacy of our approach. The PD handwriting database includes several handwriting/drawing samples from 38 healthy controls (HC) and 33 PD patients.

Throughout the assessment procedure, we used stratified 10-fold cross-validation. Ten equal-sized subsets that were mutually exclusive were created from the dataset. The training data for each subset werethe union of the remaining subsets. Furthermore, we used data augmentation, producing thirty additional versions for every training data sample that was first used. Ten iterations of the entire process were performed until one test set was used for each fold. To calculate the overall accuracy, we then summed the accuracies of the various subgroups.

To prepare it for batch processing, the image is first enlarged to $(210\times 210)$ pixels and then turned into an array with an extra dimension. Matplotlib is used to display the batches of augmented photos generated by an image data generator (Train_Generator), as shown in Figure 6. By subjecting machine learning models to a greater range of picture transformations, this data augmentation strategy contributes to the improvement of the training dataset and may increase the robustness and performance of the models.

Further, we can also check on detection using hand drawings. Although there is no known cure for PD, early identification and appropriate treatment can greatly reduce symptoms and enhance quality of life. For this reason, the condition is a valuable study subject, particularly when developing novel diagnostic methods. The study [44] discovered that asking a patient to draw a spiral and then tracking might be used to identify PD.

Table 11. Training of proposed LSTM model for handwriting dataset.

Epoch	Training Loss	Training Accuracy	Validation Loss	Validation Accuracy
1	2.5553	63.57%	1.1122	28.57%
5	2.2222	52.72%	0.7002	42.86%
10	0.6815	64.79%	0.6768	28.57%
15	0.6580	64.79%	0.7053	28.57%
20	0.7723	35.21%	0.6891	57.14%
25	0.6912	52.31%	0.6915	57.14%
30	0.6920	56.60%	0.6840	71.43%
35	0.6889	47.69%	0.6961	57.14%
40	0.6854	51.96%	0.6945	42.86%
45	0.6873	53.09%	0.6779	71.43%
50	0.6957	44.62%	0.6865	71.43%
55	0.6915	59.32%	0.6827	71.43%
60	0.6877	69.24%	0.6902	71.43%
65	0.6967	86.74%	0.6881	71.43%

gives the model’s learning progress over time by capturing the model’s accuracy and loss for both training and validation sets across each of the 65 periods. Drawing speed and pressure can be used for detection. Research [45] discovered that patients with PD drew more slowly and used less pressure when writing; this difference was particularly noticeable in those with more severe or advanced stages of the illness. Using this fact, tremors and muscular rigidity, two of the most prevalent Parkinson’s symptoms, have an immediate effect on how a hand-drawn image appears visually, as shown in Figure 7.

Figure 7 shows a sequence of spirals that were made by hand and are used to assess motor control skills. This technique is very helpful in differentiating between people who have problems with their motor control and people who do not. People are asked to draw spirals on paper or a digital device as part of the process. After that, these spirals are examined for particular patterns that point to the existence of problems with motor control. The spiral features that have been made by hand are each labeled with a forecast. These hypotheses probably match the output of a classification model that determines whether the drawing points to PD or shows normal motor control. A prediction, which seems to be a tuple of values, is labeled for each image. These numbers reflects the probability that the model allocated to the various classes (e.g., 1 for Parkinson’s, 0 for healthy).

A label such as PREDICTION: [0.50145745, 0.49854255], for instance, indicates that the model is marginally more certain that the picture belongs to the first class (healthy) than the second class (Parkinson’s). The spirals themselves serve as illustrations of motor control in pictures. Smooth Spirals a sign of good motor control and is usually connected to well people. An assessment of the model’s ability to discriminate between normal and abnormal motor control can be made by looking at the spirals as well as the predictions. When a spiral’s forecast is near [0.5, 0.5], it means that the model is unsure of its classification. More extreme prediction spirals (such [0.7, 0.3] or [0.3, 0.7]) indicate a higher level of categorization confidence, as shown in Figure 8. The forecasts’ distribution and the spirals that go along with it can reveal information about how well the model works. A robust model would be suggested by consistently accurate predictions with high confidence; on the other hand, frequent misclassifications or uncertainty might point to the need for improvement.

With the AUC-ROC of 0.86 as shown in Figure 9, the ANN model produced an accuracy of 86%. In terms of itsperformance, however, there wasalmost similar accuracy received for plain LSTM, but less sensitivity and specificity than the suggested LSTM–BoF. The 82% accuracy and 0.87 AUC-ROC of the conventional LSTM model indicated competitive performance, but in terms of sensitivity it was not as good as the suggested LSTM–BoF. Among the compared methods, the Bayesian classifier had the lowest AUC-ROC score of 0.81 and the highest accuracy of 79%. SVM performed exceptionally well, with the greatest AUC-ROC score of 0.91 and an accuracy of 86%. But in terms of sensitivity, it was not as good as the suggested LSTM–BoF.

One important indicator is how smooth the spiral lines are. Generally speaking, smooth, continuous lines indicate strong motor control. Uneven, jagged, or wavering lines frequently signify the existence of tremors, which are typical in a number of neurological disorders. Measurements are made of the tremor waves’ height (amplitude) and frequency (number of waves per unit length). Elevated frequency and amplitude are suggestive of more serious problems with motor control. Repeatedly deviating from the planned spiral trajectory indicates a hand movement incapacity, which is a typical sign in several circumstances. The precision, recall, F1-score, and support for each class are included in the classification report. These are crucial metrics for assessing a classifier’s effectiveness. An easy-to-understand indicator called the accuracy score determines how many of the model’s overall predictions were accurate. When combined, these three components offer a thorough assessment of the classifier’s performance using the test dataset.

The model’s performance in classifying PD is shown by the confusion matrix. The model demonstrated a high recall rate by correctly identifying 42 (true positives) out of 47 real Parkinson’s cases. However, it affected the precision by incorrectly predicting Parkinson’s in three healthy persons (false positives), as shown in Figure 10. Furthermore, five genuine Parkinson’s cases were overlooked by the model (false negatives), which is important for a precise diagnosis. Nine out of twelve examples (true negatives) were properly detected by the model for healthy persons.

The classification report indicates the performance of the model in distinguishing between healthy individuals (class 0) and those with Parkinson’s (class 1). The model has a precision of 0.64 and a recall of 0.75 for class 0, meaning it correctly identifies 64% of the predictions for healthy individuals and captures 75% of actual healthy cases. For class 1, the precision is 0.93 and recall is 0.89, indicating the model accurately predicts 93% of Parkinson’s cases and correctly identifies 89% of actual Parkinson’s instances. The overall accuracy of the model is 86.44%, as shown in

Table 12. Evaluation parameters of proposed model of PaHaW dataset.

Class	Precision	Recall	F1-Score	Support
0 (Healthy)	0.64	0.75	0.69	12
1 (Parkinson’s)	0.93	0.89	0.91	47
Accuracy			0.86	59
Macro Avg	0.79	0.82	0.80	59
Weighted Avg	0.87	0.86	0.87	59

, which suggests that it performs well when classifying the images with an overall balanced precision, recall, and F1-score, especially for identifying PD. Out of all the positive predictions the model makes, precision indicates the percentage of real positive predictions (erroneously classified as Parkinson’s). For example, our model’s accuracy for the Parkinson’s class was 0.93, which means that 93% of the people who were predicted to have the disease were really diagnosed.

Recall measures how effectively the model detects Parkinson’s Disease patients by dividing the number of true positives by the total number of actual positives. With a recall of 0.89 for the Parkinson’s class, 89% of the real Parkinson’s patients were correctly recognized by the model.

When working with unbalanced classes, the F1-Score offers a balanced statistic as it is the harmonic mean of precision and recall. The model shows a solid balance between accurately identifying people with the condition and reducing false positives, as seen by its F1-score of 0.91 for the Parkinson’s class.

As the ratio of accurate predictions (both for healthy and Parkinson’s patients) to the total number of occurrences, accuracy measures the overall correctness of the model for both groups. With an accuracy of 0.86, our model was able to classify 86% of the cases correctly.

4.4. Discussion

We compared both ML methods and classical handwriting prediction techniques. The proposed LSTM–BoF model outperformed the other machine learning models in the comparison test for PD detection, showing the greatest AUC-ROC score of 0.93, along with accuracy of 89%, sensitivity of 0.85, and specificity of 0.91 as shown in Figure 11. This suggests that the LSTM–BoF model is very good at properly classifying people as either healthy or Parkinson’s sufferers. The SVM model was a strong candidate, but with somewhat less balanced sensitivity (0.83) and specificity (0.88), demonstrating good performance with an AUC-ROC of 0.91 and an accuracy of 86%. With AUC-ROC values of 0.89 and 0.87, respectively, the ANN and Conventional LSTM models performed competitively.The handwriting analysis model, on the other hand, was employed to diagnose PD and had an overall accuracy of 86%. With a recall of 0.89 and a high precision of 0.93 for the class of Parkinson’s patients, the F1-Score for this class was a good 0.91. This shows how reliable the model is at identifying people who have PD. The healthy class, on the other hand, performed worse, with an F1-Score of 0.69, recall of 0.75, and accuracy of 0.64. With an F1-Score of 0.80 for the macro average between the two classes, balanced performance was shown, and an F1-Score of 0.87 for the weighted average throughout the dataset revealed the overall efficacy of the model.

According to experimental data, our approach outperforms current models in classification performance, which makes it a useful tool for PD early diagnosis. The framework’s adaptability to different datasets further highlights its versatility and potential for further medical applications.

This demonstrates the model’s effectiveness at categorizing Parkinson’s patients, even if it might still use more work to accurately identify healthy people. The proposed LSTM–BoF model has a better AUC-ROC (0.93) and overall accuracy (89%), demonstrating robust and balanced performance across several criteria. This model’s high specificity (0.91) indicates that it performs well not just in identifying people with PD but also in accurately identifying healthy persons.

5. Conclusions

The proposed LSTM–BoF algorithm performed better at PD identification than a number of well-known ML methods, such as ANN, conventional LSTM, Bayesian classifiers, and SVM. Through the use of BoF to dynamically integrate features, LSTM-specific learning rates, and multi-modal feature fusion, the LSTM–BoF algorithm outperformed conventional methods in terms of accuracy, sensitivity, specificity, and AUC-ROC. These results highlight the LSTM–BoF algorithm’s potential as a useful tool for precise and understandable PD diagnosis in clinical settings. By analyzing hand-drawn spirals, the LSTM–BoF model shows promising potential as a PD detector. The algorithm accurately classifies people as having PD or not, with an overall accuracy rate of 86.44%. For Parkinson’s cases, it demonstrates high recall (0.89) and precision (0.93), correctly recognizing the majority of cases with fewfalse positives. The model performs moderately for healthy persons, with a precision of 0.64 and a recall of 0.75. In general, the LSTM–BoF model performs well atdiagnosing PD. Nevertheless, it should be improved in terms of lowering false positives and improving the distinction between healthy cases.