1. Introduction
Generative models have attracted much attention in the recent literature for their ability to generate realistic data [
1,
2,
3]; this is due to the nature of deep learning models in which the final performance is related to the amount of data you possess and the inner characteristics. The generative models provide the ability to enrich your dataset without the limitations that occur in real-world data campaigns. These limitations are particularly severe in the medical imaging domain. Data privacy and security can lead to significant patient data acquisition and distribution constraints. Therefore, obtaining realistic data can be crucial for easily improving the computer-aided diagnosis (CAD) systems of musculoskeletal ultrasound (MSK-US) that are heavily based on deep learning.
Generative adversarial networks (GANs) [
4] have been proposed for the generation of realistic synthetic images. Briefly, GANs are a class of deep learning models that can generate new data similar to the data on which they were trained. GANs normally consist of two deep neural networks: a generator and a discriminator network. The generator network takes random noise as input and generates a new sample of data similar to the training data. The discriminator network takes the generated and real training data as input and attempts to classify which is which. The generator network is trained to improve its ability to fool the discriminator network, while the discriminator network is trained to distinguish between the generated and real data correctly.
Several applications of GANs have been studied in ultrasound imaging. In particular, in [
5], different GAN architectures were investigated to generate realistic breast ultrasound (US) images. Afterwards, the generated images were used to train convolutional neural networks (CNNs) to classify breast ultrasound images into three categories. Their results indicated that the generated images helped to outperform the baseline model. Furthermore, at [
6], they used a GAN architecture to produce synthetic B-mode US images of bone data and their corresponding segmented bone surface masks in real time. Ref. [
7] presents a pipeline for generating medical thyroid ultrasound images with an auto-encoding generative adversarial network as a data augmentation method for performance improvement. Similarly, at [
8], a novel GAN architecture named Pix2Pix [
9] is employed for data augmentation in bone surface segmentation in ultrasound images. Finally, another similar study is [
10] in which the authors presented SpeckleGAN, a generative adversarial network with a speckle layer that can be incorporated into a neural network to add realistic and domain-dependent speckle.
Subsequently, at [
11], a pipeline for generating synthetic 2D echocardiography images is presented using the Cycle-GAN [
12]. Furthermore, at [
13], a pipeline can synthesise realistic B-mode US images with customised texture editing features. Secondly, they enhance the structural details of generated images by introducing auxiliary sketch guidance into a conditional GAN. Finally, a study that is similar to ours is [
14]. This study used Cycle-GAN to generate realistic B-mode musculoskeletal ultrasound images of longitudinal images of the gastrocnemius medialis muscle. The Cycle-GAN was fed with 100 images and a set of 100 synthetic segmented masks that featured two aponeuroses and a random number of fascicles. Their model output was a set of synthetic ultrasound images and an automated segmentation of each real input image. As a second step, they used existing software to measure muscle thickness, fascicle length, and pennation angle from the real and the generated images. The downside of their study is that they did not train a deep learning model using synthetically generated images to detect muscle architecture, so they have not evaluated how the generated images will affect the performance of such a model.
A more contemporary deep learning method that has presented exceptional results in generating synthetic images in many different applications is the denoising diffusion probabilistic model (DDPM), or simpler diffusion models [
15,
16,
17,
18]. The basic idea of diffusion models is to start with a random noise vector and then gradually transform it to produce a sample of synthetic data. The above is conducted by applying a sequence of invertible transformations to the noise vector over a series of discrete time steps. The noise vector is updated in each time step by adding a random perturbation, which helps introduce stochasticity into the model. Once the diffusion process is complete, the resulting noise vector is transformed back into a sample of synthetic data using a decoder network. Finally, the decoder network is trained to map the noise vector back to the data space, utilising a loss function that encourages the generated data to be as similar as possible to the real data. Diffusion models have several advantages over other generative models, such as GANs. They are more stable during training and do not suffer from the mode collapse problem common with GANs. They can also generate high-quality images with fine details and realistic textures.
Diffusion models have been applied in various medical imaging applications [
19,
20,
21]. In [
22], the authors propose a transformer-based UNet architecture to model the interaction between noise and semantic features. Furthermore, in [
23], a conditional latent DDPM for medical images is proposed in different medical imaging datasets. In addition, at [
24], a model which combines a synthetic diffusion-based label generator with a semantic image generator is presented and evaluated at brain magnetic resonance images. Another study worth mentioning is [
25], in which the authors achieved image quality superior to the current state-of-the-art generative models in their synthetic data. They performed conditional and unconditional image synthesis and evaluated the quality of their synthetic data on different quantitative metrics.
In this study, the DDPMs are incorporated for the first time in musculoskeletal ultrasound imaging to generate realistic muscle images. We evaluate the similarity of the real and the generated images in different scenarios. Initially, qualitative and quantitative metrics that correspond well with human judgement are used to assess the proximity of the two data types. Later, Attention-UNet [
26] is incorporated for the important clinical application of the muscle thickness measurement [
27]. In particular, similar to [
28], deep learning models are trained in various configurations to delineate the superficial and deep aponeuroses of the examined muscle. Afterwards, the muscle thickness is calculated by taking the average distance between the two aponeuroses at different muscle points.
This study aims to introduce, for the first time, the diffusion models in MSK-US imaging to generate high-quality synthetic images. Afterwards, these synthetic images would be used for training deep learning architectures in extracting muscle thickness in a novel MSK-US database. Therefore, the main contribution of this study is to present a complete methodology for reducing the amount of real data needed to be collected for achieving superior performance in the automation of clinical measurements relevant to the musculoskeletal system.
4. Discussion
This study employed state-of-the-art diffusion models to generate realistic MSK-US images of four very informative for investigating neuromuscular disorders [
40] muscles. Afterwards, the synthetic image quality was assessed both qualitatively and quantitatively compared to the real data. Specifically, a histogram analysis that demonstrates that the pixel’s intensity distribution is similar in both cases has been performed. Additionally, four qualitative metrics that correspond well with human perception were evaluated between the two types of images. In all these metrics, the results exhibited superior performance. In addition to that, features from a pretrained Attention-UNet were extracted and visualised in a two-dimensional space using PCA. Again, the results showed that a clear distinction does not exist between the two projections, another indicator of the similarity of the two sets of images. Finally, for evaluating the applicability of the synthetic data in a real-world scenario, an Attention-UNet was trained to automatically delineate the deep and superficial aponeuroses. Our results indicate that the synthetic data can be used autonomously or supplementarily for training high-performance deep-learning models for this task.
A significant advancement of this study compared to recent works presented in [
8,
14], is the use of diffusion models instead of GANs to address this problem. Generative adversarial networks have the downside that they are hard to train because they involve a complex optimisation process that requires careful tuning of hyperparameters. Additionally, GANs may suffer from mode collapse, meaning that the generator network produces a limited set of output samples, ignoring the rest of the distribution, resulting in generated images lacking diversity and quality. Apart from that, GANs are also sensitive to data quality and quantity, requiring a large and high-quality dataset to learn meaningful patterns, or the model may not generate accurate samples. Next, another limitation of the GANs is that the generation mechanism of new samples is difficult to understand and is considered a black-box model. Instead, diffusion models can be trained efficiently without excessive tuning to produce realistic results. Furthermore, unlike other deep generative models, diffusion models have an interpretable structure based on stochastic differential equations, allowing insights into the generative process and the underlying dynamics of the data. Finally, diffusion models can be used for transfer learning by fine-tuning the model on a new dataset which is useful in scenarios where labelled data are scarce or when the model needs to adapt to new domains.
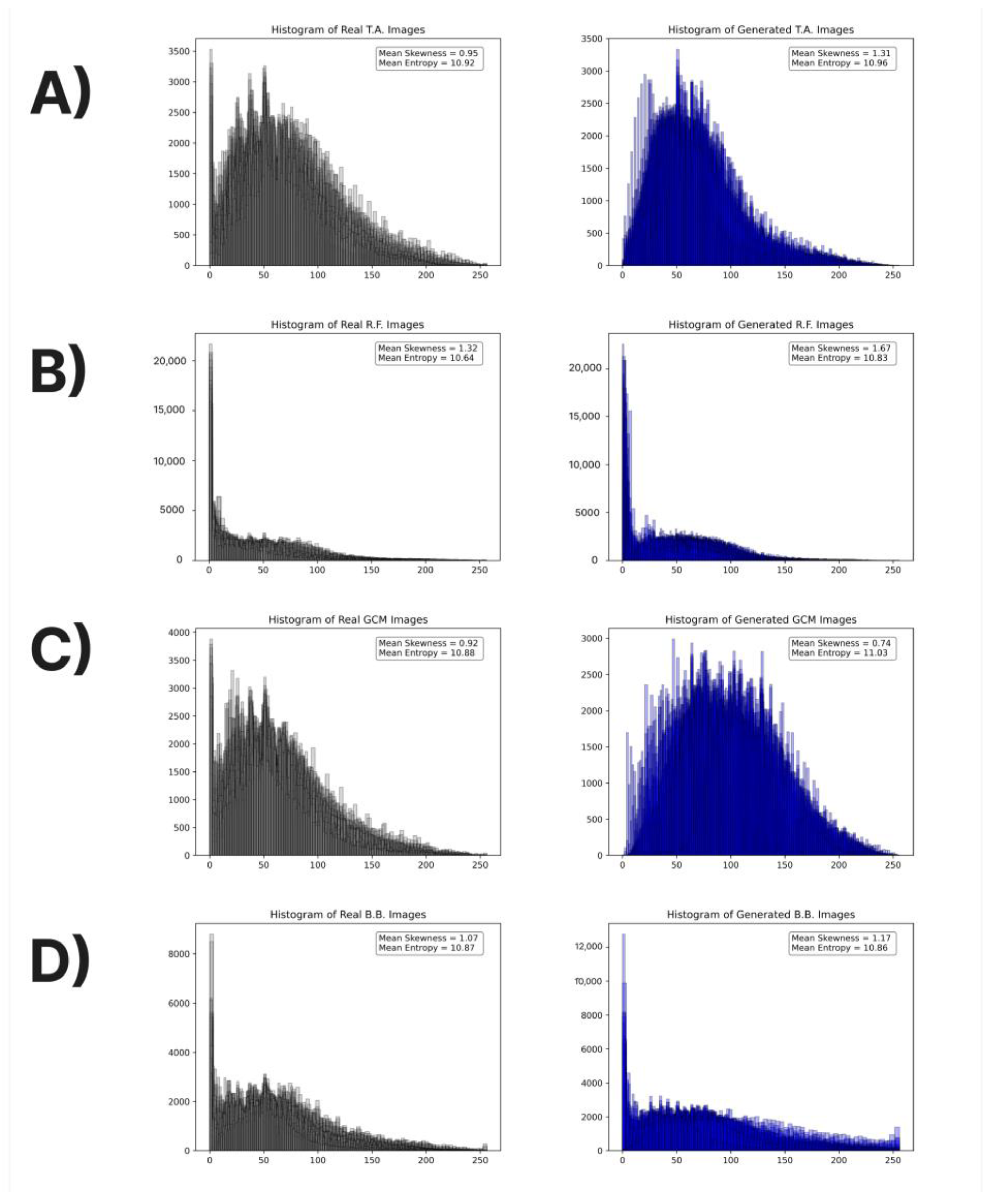
Several analyses have been performed to evaluate the quality of synthetic data properly. Initially, the histograms of the pixel intensities in 100 randomly picked generated, and real images of each muscle were extracted and compared. This analysis showed that each muscle’s distribution shape and entropy are statistically similar. In particular, a right-skewed distribution exists in every muscle with close mean skewness and entropy between the two readings. The most significant difference in the mean skewness was reported in T.A. (real: 0.95, synthetic: 1.31) and in the R.F. (real: 1.32, synthetic: 1.67, explained by the fact that the real images were darker than the synthetic in both muscles. Regarding the mean entropy values, the results were extremely close in all the examined muscles. Four metrics aligned with human judgment were used to quantify the similarity of 100 generated images for each muscle with the real dataset. In all the metrics, the results demonstrated that the quality of the synthetic data is superior. PSNR was above 60, and SSIM was close to 1 in all the examined muscles. In addition, the similarity level of the real images was analysed (inter-patient SSIM) and found almost identical to the similarity level of the synthetic images. This finding provides further evidence that the distribution of synthetic data possesses similar textural and informational characteristics to the distribution of real images. Furthermore, LPIPS and FID, which also consider textural information, were close to zero in all the muscles, another indicator of the similarity of the two sets of images. Finally, the two sets of images were visualised in a common two-dimensional space. In particular, high-level textural features were extracted from the bottleneck of a pretrained Attention-UNet for each image. Afterwards, the dimensionality of these features was reduced with PCA and visualised in a common space. The results showed that the data points of the generated and real images are not forming separate classes but are mixed between them, which is one more indicator that possesses similar textural characteristics.
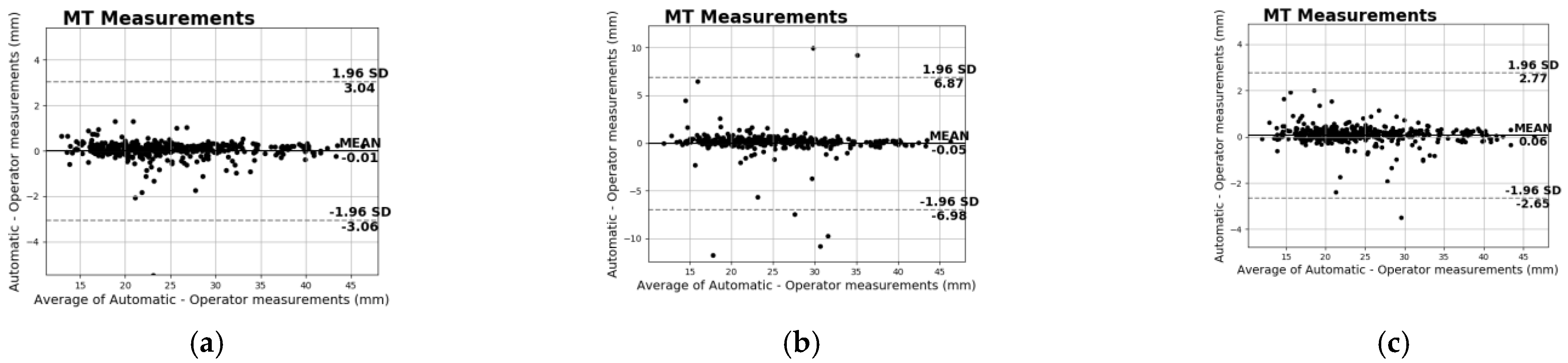
Furthermore, a system that automatically extracts the muscle thickness measurement was developed to evaluate the applicability of the generated data in a real-world clinical application. Specifically, the deep and superficial aponeuroses were segmented with the state-of-the-art Attention-UNet in a novel database of musculoskeletal ultrasound images. Afterwards, the MT is measured by computing the mean distance of the two aponeuroses at several points across the muscle. Since the main goal is to assess the generated data’s impact on the model’s final performance, different experiments were performed. From these, it is clear that the generated data are capable of producing high-performance models with (or without) the use of real images. This is a significant result that can lead to the acceleration of the integration and the improvement of the deep learning technology in MSK-US, where the acquisition process of real data is very difficult and time-consuming due to privacy restrictions. Notably, the Attention-UNet trained only with synthetic images (Gen Model) achieved over 80% with the Dice coefficient, a performance very close to the Real Model (85%) that has been trained with only real images or to the Real + Gen Model (86%) that has been trained with both types of data. In every case, these results prove that the generated data can be used autonomously or supplementarily to train high-performance models for the specific task. This also depicted the RMSE difference between the manual and automated measurements in all the different training configurations. Specifically, the average difference between the two readings for the Real Model was only 0.35 mm and for the Real + Gen model was similar at 0.38 mm. Similarly, for the model trained only with generated data, the difference is 1.05 mm, larger than before but still deviates only 4% of the manual MT measurements. Finally, an additional analysis was conducted to better demonstrate the impact of the generated data in training high-performance deep learning models. During this analysis, it was observed that all the models trained with a combination of real and generated data outperformed the baseline models. Additionally, the model that was trained with a combination of 30% of real images and generated data (30% Train + Gen) achieved almost identical performance to the model trained with more real images (50% Train). These findings provide further support for the notion that artificial data can substantially enhance the performance of deep learning models and can serve as a supplement in situations where real data are lacking.
This study has some general limitations. Firstly, the examined muscles were only four from over 200 that the human body possesses. Secondly, the number of MSK-US images was 1223 from 116 subjects, which can be considered a relatively small number. Consequently, conducting further research involving a larger sample size and more muscles would offer a clearer understanding of the diffusion models’ capability to generate MSK-US images. Another constraint is that all the actual images were obtained from a single ultrasound machine, utilizing the same software and image settings. Hence, we did not investigate multiple configuration setups that can alternate the final image. Lastly, all the recordings used in this study were acquired from young and healthy subjects, which can bias our results since the young population usually has muscles with normal echogenicity and better architectural characteristics than the elderly. However, we are confident that these challenges can be overcome with a small number of real data since the diffusion model is scalable, as we mentioned before and can be trained without excessive hyperparameter tuning.
In future work, the plan is to investigate the generation of transverse MSK-US images in these four muscles. Furthermore, we will investigate the applicability of the generated data in other clinical applications, such as the automatic extraction of the cross-sectional area (CSA) or even the extraction of the fascicle’s length and pennation angle. Finally, in the future, we will investigate the generation of data acquired from older adults with higher echogenicity since ageing leads to a reduction in muscle mass and an increase in muscle fat.
Author Contributions
Conceptualisation, S.K. and A.K; methodology, S.K., A.K., G.E. and G.P.; software, S.K. and A.K.; validation, S.K., N.B., E.P. and G.P.; data curation, S.K., N.B., P.T. and A.K.; writing—original draft preparation, S.K. and G.E.; visualisations, S.K. and A.K.; writing—review and editing, S.K., A.K., N.B., P.T., G.P., E.P. and G.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Scholarships Foundation (IKΥ), grant number MIS-5000432.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki and approved by the Ethics Committee of Patras University Hospital (protocol code 50/18-1-18).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Acknowledgments
This research was co-financed by Greece and the European Union (European Social Fund—ESF) through the Operational Programme «Human Resources Development, Education and Lifelong Learning» in the context of the project “Strengthening Human Resources Research Potential via Doctorate Research—2nd Cycle” (MIS-5000432), implemented by the State Scholarships Foundation (ΙΚΥ).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kingma, D.P.; Mohamed, S.; Jimenez Rezende, D.; Welling, M. Semi-Supervised Learning with Deep Generative Models. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Curran Associates, Inc.: Red Hook, NY, USA; Volume 27. [Google Scholar]
- Oussidi, A.; Elhassouny, A. Deep Generative Models: Survey. In Proceedings of the 2018 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 2–4 September 2018; pp. 1–8. [Google Scholar]
- Turhan, C.G.; Bilge, H.S. Recent Trends in Deep Generative Models: A Review. In Proceedings of the 2018 3rd International Conference on Computer Science and Engineering (UBMK), Sarajevo, Bosnia and Herzegovina, 20–23 September 2018; pp. 574–579. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Maack, L.; Holstein, L.; Schlaefer, A. GANs for Generation of Synthetic Ultrasound Images from Small Datasets. Curr. Dir. Biomed. Eng. 2022, 8, 17–20. [Google Scholar] [CrossRef]
- Alsinan, A.Z.; Rule, C.; Vives, M.; Patel, V.M.; Hacihaliloglu, I. GAN-Based Realistic Bone Ultrasound Image and Label Synthesis for Improved Segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2020, Lima, Peru, 4–8 October 2020; Martel, A.L., Abolmaesumi, P., Stoyanov, D., Mateus, D., Zuluaga, M.A., Zhou, S.K., Racoceanu, D., Joskowicz, L., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 795–804. [Google Scholar]
- Liang, J.; Chen, J. Data Augmentation of Thyroid Ultrasound Images Using Generative Adversarial Network. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Xi’an, China, 11–16 September 2021; pp. 1–4. [Google Scholar]
- Zaman, A.; Park, S.H.; Bang, H.; Park, C.; Park, I.; Joung, S. Generative Approach for Data Augmentation for Deep Learning-Based Bone Surface Segmentation from Ultrasound Images. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 931–941. [Google Scholar] [CrossRef] [PubMed]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks 2018. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Bargsten, L.; Schlaefer, A. SpeckleGAN: A Generative Adversarial Network with an Adaptive Speckle Layer to Augment Limited Training Data for Ultrasound Image Processing. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 1427–1436. [Google Scholar] [CrossRef]
- Gilbert, A.; Marciniak, M.; Rodero, C.; Lamata, P.; Samset, E.; Mcleod, K. Generating Synthetic Labeled Data from Existing Anatomical Models: An Example with Echocardiography Segmentation. IEEE Trans. Med. Imaging 2021, 40, 2783–2794. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.-Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks 2020. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Liang, J.; Yang, X.; Huang, Y.; Li, H.; He, S.; Hu, X.; Chen, Z.; Xue, W.; Cheng, J.; Ni, D. Sketch Guided and Progressive Growing GAN for Realistic and Editable Ultrasound Image Synthesis. Med. Image Anal. 2022, 79, 102461. [Google Scholar] [CrossRef]
- Cronin, N.J.; Finni, T.; Seynnes, O. Using Deep Learning to Generate Synthetic B-Mode Musculoskeletal Ultrasound Images. Comput. Methods Progr. Biomed. 2020, 196, 105583. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 6840–6851. [Google Scholar]
- Nichol, A.Q.; Dhariwal, P. Improved Denoising Diffusion Probabilistic Models. In Proceedings of the 38th International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 8162–8171. [Google Scholar]
- Lugmayr, A.; Danelljan, M.; Romero, A.; Yu, F.; Timofte, R.; Van Gool, L. RePaint: Inpainting Using Denoising Diffusion Probabilistic Models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2022, New Orleans, LA, USA, 18–24 June 2022; pp. 11461–11471. [Google Scholar]
- Choi, J.; Kim, S.; Jeong, Y.; Gwon, Y.; Yoon, S. ILVR: Conditioning Method for Denoising Diffusion Probabilistic Models. arXiv 2021, arXiv:2108.02938. [Google Scholar]
- Kazerouni, A.; Aghdam, E.K.; Heidari, M.; Azad, R.; Fayyaz, M.; Hacihaliloglu, I.; Merhof, D. Diffusion Models for Medical Image Analysis: A Comprehensive Survey. arXiv 2022, arXiv:2211.07804. [Google Scholar]
- Croitoru, F.-A.; Hondru, V.; Ionescu, R.T.; Shah, M. Diffusion Models in Vision: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 1–20. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Z.; Song, Y.; Hong, S.; Xu, R.; Zhao, Y.; Shao, Y.; Zhang, W.; Cui, B.; Yang, M.-H. Diffusion Models: A Comprehensive Survey of Methods and Applications. arXiv 2022, arXiv:2209.00796. [Google Scholar]
- Wu, J.; Fu, R.; Fang, H.; Zhang, Y.; Xu, Y. MedSegDiff-V2: Diffusion Based Medical Image Segmentation with Transformer. arXiv 2023, arXiv:2301.11798. [Google Scholar]
- Müller-Franzes, G.; Niehues, J.M.; Khader, F.; Arasteh, S.T.; Haarburger, C.; Kuhl, C.; Wang, T.; Han, T.; Nebelung, S.; Kather, J.N.; et al. Diffusion Probabilistic Models Beat GANs on Medical Images. arXiv 2022, arXiv:2212.07501. [Google Scholar]
- Fernandez, V.; Pinaya, W.H.L.; Borges, P.; Tudosiu, P.-D.; Graham, M.S.; Vercauteren, T.; Cardoso, M.J. Can Segmentation Models Be Trained with Fully Synthetically Generated Data? In Simulation and Synthesis in Medical Imaging. SASHIMI 2022; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion Models Beat GANs on Image Synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Oktay, O.; Schlemper, J.; Le Folgoc, L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Y Hammerla, N.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Barotsis, N.; Tsiganos, P.; Kokkalis, Z.; Panayiotakis, G.; Panagiotopoulos, E. Reliability of Muscle Thickness Measurements in Ultrasonography. Int. J. Rehabil. Res. 2020, 43, 123. [Google Scholar] [CrossRef] [PubMed]
- Katakis, S.; Barotsis, N.; Kakotaritis, A.; Economou, G.; Panagiotopoulos, E.; Panayiotakis, G. Automatic Extraction of Muscle Parameters with Attention UNet in Ultrasonography. Sensors 2022, 22, 5230. [Google Scholar] [CrossRef]
- Katakis, S.; Barotsis, N.; Kakotaritis, A.; Tsiganos, P.; Economou, G.; Panagiotopoulos, E.; Panayiotakis, G. Muscle Cross-Sectional Area Segmentation in Transverse Ultrasound Images Using Vision Transformers. Diagnostics 2023, 13, 217. [Google Scholar] [CrossRef] [PubMed]
- Katakis, S.; Barotsis, N.; Kastaniotis, D.; Theoharatos, C.; Tsiganos, P.; Economou, G.; Panagiotopoulos, E.; Fotopoulos, S.; Panayiotakis, G. Muscle Type and Gender Recognition Utilising High-Level Textural Representation in Musculoskeletal Ultrasonography. Ultrasound Med. Biol. 2019, 45, 1562–1573. [Google Scholar] [CrossRef]
- Katakis, S.; Barotsis, N.; Kastaniotis, D.; Theoharatos, C.; Tsourounis, D.; Fotopoulos, S.; Panagiotopoulos, E. Muscle Type Classification on Ultrasound Imaging Using Deep Convolutional Neural Networks. In Proceedings of the 2018 IEEE 13th Image, Video, and Multidimensional Signal Processing Workshop (IVMSP), Zagorochoria, Greece, 10–12 June 2018; pp. 1–5. [Google Scholar]
- Gagniuc, P.A. Markov Chains: From Theory to Implementation and Experimentation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Devroye, L. Random Variate Generation in One Line of Code. In Proceedings of the Winter Simulation Conference, Coronado, CA, USA, 8–11 December 1996; pp. 265–272. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Bertels, J.; Eelbode, T.; Berman, M.; Vandermeulen, D.; Maes, F.; Bisschops, R.; Blaschko, M. Optimizing the Dice Score and Jaccard Index for Medical Image Segmentation: Theory and Practice. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2019, Shenzhen, China, 13–17 October 2019; Springer: Cham, Switzerland, 2019; Volume 11765, pp. 92–100. [Google Scholar]
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Los Alamitos, CA, USA, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric 2018. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. arXiv 2018, arXiv:1706.08500. [Google Scholar]
- Barotsis, N.; Galata, A.; Hadjiconstanti, A.; Panayiotakis, G. The Ultrasonographic Measurement of Muscle Thickness in Sarcopenia. A Prediction Study. Eur. J. Phys. Rehabil. Med. 2020, 56, 427–437. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Forward process of the diffusion models.
Figure 2.
Forward and reverse process of the diffusion models.
Figure 3.
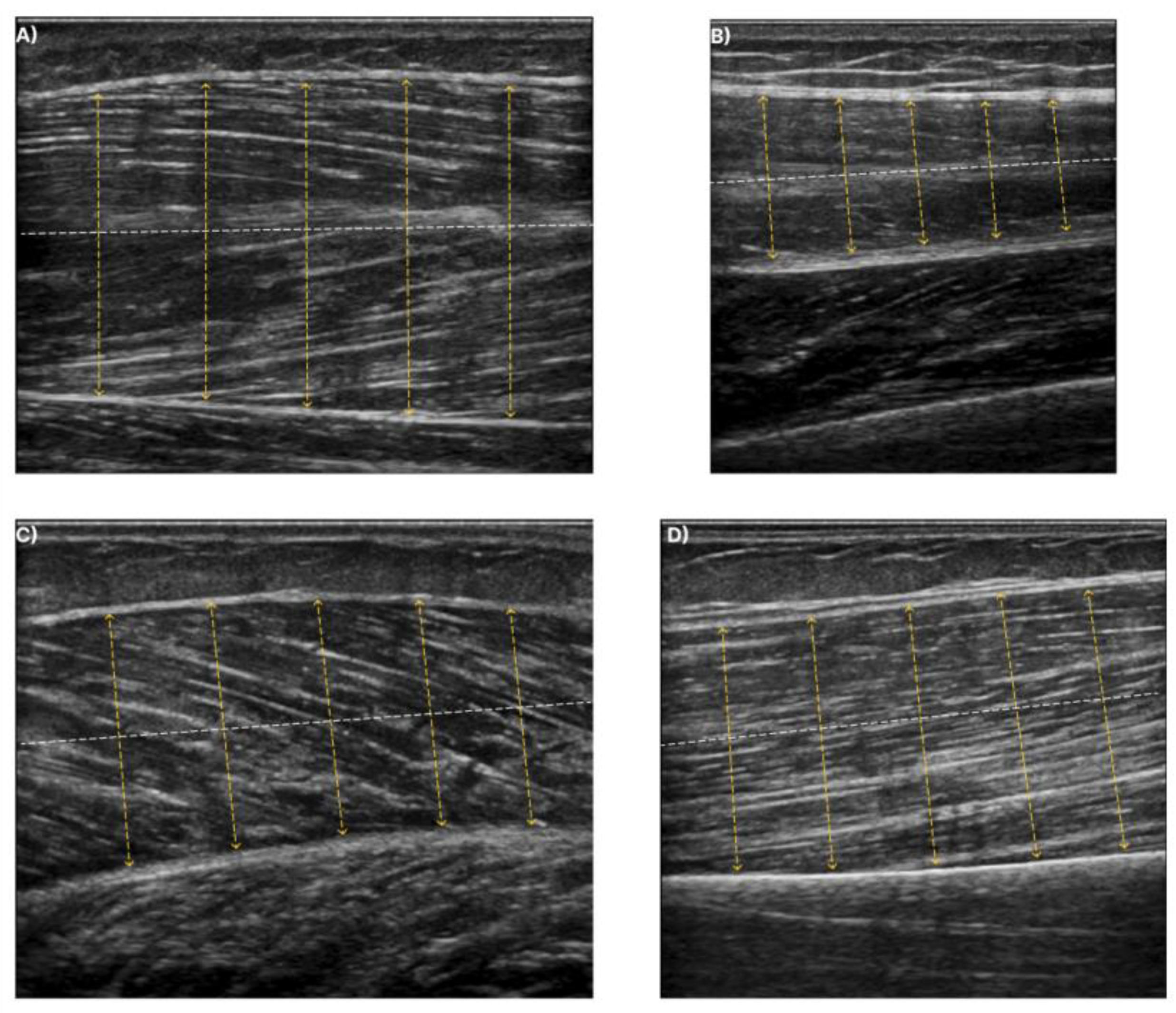
The dashed white line depicts the centreline at each muscle. The yellow lines illustrate the perpendicular chords to the centreline. Muscle thickness is measured from the average distance of the yellow dashed lines. (A) exhibits the T.A., (B) exhibits the R.F., (C) exhibits the GCM, and finally, (D) shows the B.B.
Figure 4.
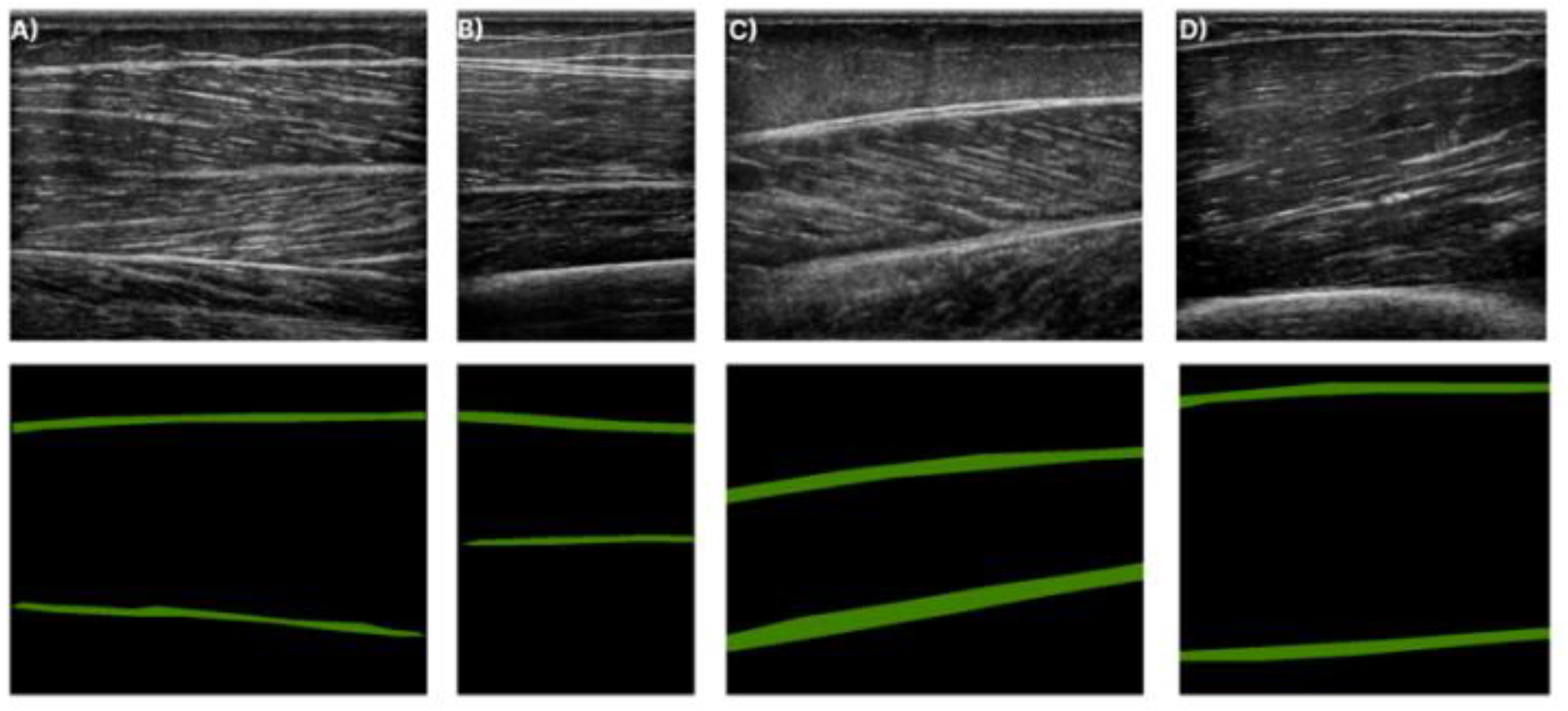
Ultrasound images for each muscle along with their corresponding annotation. The green structures in the annotation masks (second row) depict the deep and superficial aponeuroses. (A) shows T.A. muscle, (B) the R.F. muscle, (C) the GCM muscle, and finally (D) the B.B. muscle.
Figure 5.
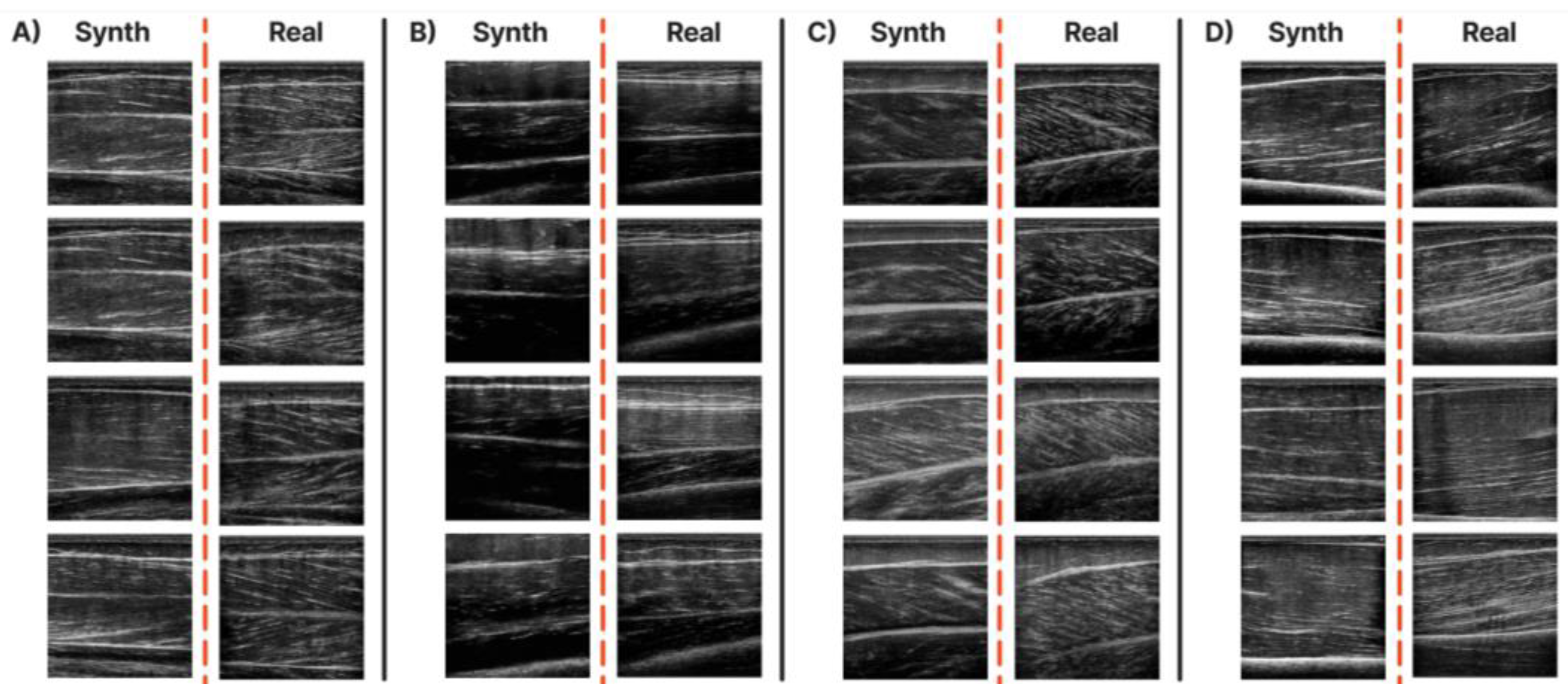
Synthetic vs. real ultrasound images from the diffusion model. (A) Samples from the T.A. muscle, (B) from the R.F. muscle, (C) the GCM muscle and (D) the B.B. muscle.
Figure 6.
Histograms for each muscle for real and generated data for the (A) T.A. muscle, (B) R.F. muscle, (C) GCM muscle, and (D) B.B. muscle.
Figure 7.
Two-dimensional visualisation for each muscle for real and synthetic data. (A) T.A. muscle, (B) R.F. muscle, (C) GCM muscle, and (D) B.B. muscle.
Figure 8.
Bland−Altman analysis of the manual vs. automatic MT measurements of the (a) Real Model, (b) Gen Model, and (c) Real + Gen Model.
Figure 9.
Qualitative results of the Gen Model in images of the four examined muscles. (A) T.A. muscle, (B) R.F. muscle, (C) GCM muscle, and (D) B.B. muscle.
Table 1.
Demographics of the dataset.
| Subjects | 116 |
|---|
| Examinations | 155 |
| Age (years) | 25.33 ± 4.92 |
| Sex (M/F) | 49/67 |
| Weight (kg) | 68.65 ± 12.32 |
| Height (cm) | 172.62 ± 9.37 |
Table 2.
Qualitative metrics between the generated and real images for each muscle.
| | | | | |
|---|
| T.A. | 61.928 | 0.996 | 0.006 | 3.395 |
| R.F. | 61.486 | 0.994 | 0.005 | 1.958 |
| GCM | 60.544 | 0.992 | 0.005 | 2.681 |
| B.B. | 60.462 | 0.993 | 0.008 | 3.819 |
Table 3.
Results of the inter-patient SSIM and synthetic SSIM.
| | | |
|---|
| T.A. | 0.995 | 0.995 |
| R.F. | 0.996 | 0.994 |
| GCM | 0.996 | 0.992 |
| B.B. | 0.995 | 0.992 |
Table 4.
Overall segmentation results for each experiment. The results are reported in mean ± std.
| | Precision | Recall | DSC | IoU |
|---|
| Real Model | 0.85 ± 0.10 | 0.87 ± 0.10 | 0.85 ± 0.07 | 0.75 ± 0.10 |
| Gen Model | 0.78 ± 0.14 | 0.85 ± 0.12 | 0.80 ± 0.10 | 0.68 ± 0.13 |
| Real + Gen Model | 0.84 ± 0.10 | 0.88 ± 0.09 | 0.86 ± 0.08 | 0.76 ± 0.10 |
Table 5.
Comparison results between the manual and automatic muscle MT measurements.
| | Manual (mm) | Automatic (mm) | RMSE (mm) |
|---|
| Real Model | 24.50 ± 6.49 | 24.51 ± 6.45 | 0.35 ± 1.52 |
| Gen Model | 24.50 ± 6.49 | 24.56 ± 6.98 | 1.05 ± 3.38 |
| Real + Gen Model | 24.50 ± 6.49 | 24.44 ± 6.51 | 0.38 ± 1.33 |
Table 6.
Comparison results of the Attention-UNet trained with different number of training data in the same validation set.
| | DSC | IoU |
|---|
| 50% Train | 0.842 | 0.735 |
| 50% Train + Gen | 0.847 | 0.743 |
| 30% Train | 0.834 | 0.724 |
| 30% Train + Gen | 0.842 | 0.735 |
| 10% Train | 0.800 | 0.680 |
| 10% Train + Gen | 0.823 | 0.710 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).