HAIMO: A Hybrid Approach to Trajectory Interaction Analysis Combining Knowledge-Driven and Data-Driven AI

Abstract

Capturing the interactions between moving objects is vital in traffic analysis, sports, and animal behavior, but remains challenging because of subtle spatiotemporal dynamics. This paper introduces HAIMO (Hybrid Analysis of the Interaction of Moving Objects), a conceptual framework that combines knowledge-driven AI for interpretable, symbolic interaction representations with data-driven models trained through self-supervised learning (SSL) on large sets of unlabeled trajectory data. In HAIMO, we propose using transformer architectures to model complex spatiotemporal dependencies while maintaining interpretability through symbolic reasoning. To illustrate the feasibility of this hybrid approach, we present a basic proof-of-concept using elite tennis rallies, where the knowledge-driven component identifies interaction patterns between players and the ball, and we outline how SSL-enhanced transformer models could support and strengthen movement prediction. By bridging symbolic reasoning and self-supervised data-driven learning, HAIMO provides a conceptual foundation for future GeoAI and spatiotemporal analytics, especially in applications where both pattern discovery and explainability are crucial.

1. Introduction

Understanding the dynamics of moving objects is crucial in various fields, such as traffic management, sports analytics, and animal behavior. However, the task of capturing the complex spatiotemporal interactions between moving objects remains a significant challenge. Interactions may occur through direct proximity (e.g., two individuals moving in tandem) or through delayed, indirect responses (e.g., an animal avoiding a location after detecting another’s presence). Capturing these nuanced relationships is fundamental to understanding movement dynamics. The foundational work by [1] formalized metrics for measuring dynamic interaction in movement data, while [2] demonstrated how asynchronous, temporally offset interactions can be detected using animal telemetry data. In this paper, we define interactions broadly as any spatiotemporal relationship between moving entities, where their presence or actions may relate to each other either through direct influence, indirect responses, or coinciding movement patterns. We present a framework that combines knowledge-driven and data-driven AI techniques for a broader, forward-looking understanding of interaction dynamics, called Hybrid Analysis of the Interaction of Moving Objects (HAIMO).

By blending symbolic reasoning (e.g., qualitative trajectory representations) with neural network-based methods, we outline a path for analyzing spatiotemporal phenomena that goes beyond the limitations of relying solely on either knowledge-driven or data-driven approaches. This integration provides a way to solve problems that neither approach could address independently, possibly enabling the capture of previously unobservable interaction dynamics. While knowledge-driven AI offers interpretability and explicit modeling of movement events, data-driven AI provides scalability and adaptability. In particular, we envision incorporating self-supervised learning (SSL) and transformer-based models, which have shown potential for capturing complex dependencies in sequence data.

Integrating these two styles of AI may yield deeper insights into the social, biological, or physical contexts in which movement occurs. Following this introduction, we first review key fundamentals of AI and GeoAI, then survey the mining of trajectory data and the core elements of HAIMO. We then illustrate a real-world example to show how merging knowledge-driven and data-driven techniques allows us to capture spatiotemporal interactions with more clarity and precision. In particular, we envision incorporating SSL and transformer-based models alongside knowledge-driven representations, such as spatiotemporal calculi, to capture complex dependencies in sequence data while preserving interpretability.

Through a stepwise presentation of concepts and examples, we illustrate how hybrid approaches may encourage new analytical angles when examining movement data. Ultimately, HAIMO is presented as a conceptual framework to provoke new perspectives and research directions, illustrating the strength of hybrid approaches in domains such as traffic, sports analytics, and wildlife behavior.

2. Artificial Intelligence and GeoAI Fundamentals

Artificial intelligence (AI) emerged within computer science in the mid-twentieth century and has steadily expanded its scope from early symbolic expert systems to today’s deep learning engines. At its core, AI builds systems that can understand language, recognize patterns, solve problems, and make decisions in ways that complement or surpass human abilities [3]. While the field largely revolves around data-driven AI, the need for more reliable reasoning in large language models (LLMs) has sparked renewed interest in integrating symbolic, knowledge-driven approaches.

Knowledge-driven AI reasons through explicit rules, ontologies, and causal models to provide transparent explanations [4,5]. Because every inference is grounded in a verifiable fact or rule, users can inspect the provenance of a conclusion, which is an important property when decisions carry legal or ethical weight.

Data-driven AI, by contrast, learns directly from observations. Fueled by the machine learning revolution [6] and ever larger datasets, these models adjust millions of parameters to extract latent structure [7]. However, their inner workings can become a “black box”, complicating trust and auditability [8].

Recent advances in SSL and attention-based transformer architectures further enrich the data-driven side. SSL dispenses with costly manual labels by exploiting intrinsic signals [9], while transformers capture long-range dependencies through sequential data [10]. Within HAIMO we envision integrating the attention weights of such models with symbolic abstractions so that the learnt patterns remain interpretable.

The contrasting strengths of the two paradigms (interpretability from knowledge-driven AI versus adaptability from data-driven models) naturally motivate hybrid approaches. In this paper, we present HAIMO as such a hybrid framework, combining symbolic reasoning with neural network-based models. This aligns with the emerging field of neuro-symbolic computing, which focuses specifically on integrating neural and symbolic AI to improve both scalability and interpretability [11].

Neuro-symbolic computing research already demonstrates this synergy in domains ranging from medical imaging to structural health monitoring. Applying similar hybrid approaches to spatial and spatiotemporal problems introduces unique challenges, particularly around interpretability and scalability. GeoAI extends mainstream AI to spatial and spatiotemporal applications, merging geographic theory with machine learning toolkits to solve problems in areas such as remote sensing, mobility analytics, and environmental modeling [12,13]. Yet location data carry privacy, fairness, and transparency risks. Hybrid, interpretable methods such as HAIMO are, therefore, essential for ensuring that spatial decision support remains accountable.

3. Data Mining and the Analysis of the Interactions of Moving Objects (AIMO)

Data mining identifies patterns in large datasets through tasks such as classification, clustering, association rule discovery, and anomaly detection [14]. These tasks underpin the analysis of spatial trajectories discussed below.

Geospatial data mining focuses on datasets containing spatial or geographic dimensions [15]. These spatial extensions are crucial when trajectories interact in space and time. This often consists of x, y (z) coordinates, plus time (t) for spatiotemporal applications. Geospatial data mining recognizes that nearby locations (both spatially and temporally) can exhibit related features—an effect known as (spatial/temporal) autocorrelation [16] Unlike ordinary data points, geospatial data bring additional layers of information, such as size, shape, and boundaries [17]. Insights from geospatial data mining can inform policies or strategies in areas such as urban planning, environmental management, transportation, and public health.

Building upon geospatial data mining, the study of moving objects introduces dynamic temporal elements into spatial analysis [18]. Objects change positions over time, meaning that time links changing spatial attributes [19]. A trajectory (like that of a thrown ball) is a continuous line in space that represents an object’s path. Some objects are georeferenced if they remain bound to specific geographic locations, whereas others move in contexts not tied to a geographic coordinate system. Analyzing moving objects aids in understanding processes in fields as diverse as physics, astronomy, geography, transportation, and sports analytics [20]. Even stationary point configurations can be considered a limiting case where velocity is effectively zero.

Advances in data mining have spurred a surge in mobility data mining, trajectory data mining, and data mining of moving objects [21]. However, research on how multiple trajectories interact remains comparatively unexplored. When two or more trajectories show a particular relationship over time, this is referred to as a trajectory interaction, whether synchronous (simultaneous proximity) or asynchronous (delayed responses). We refer to research on such interactions as AIMO (Analysis of Interactions of Moving Objects). This area is relevant in traffic analysis, sports, and body movement studies, offering insights into patterns such as recurring events in traffic flows or shared strategies in team sports. Recent self-supervised approaches, ranging from contrastive trajectory similarity learning with dual-feature attention [22] to masked autoencoder pre-training in Traj-MAE [23] show that SSL can uncover rich latent structures in movement data without manual labels. Yet applying such SSL-enhanced models specifically to detect and analyze interactions between moving objects remains, to our knowledge, largely unexplored. Our proposed HAIMO framework builds upon these developments by integrating interpretable, knowledge-driven representations with the potential future incorporation of SSL and transformer-based models for improved scalability and pattern discovery.

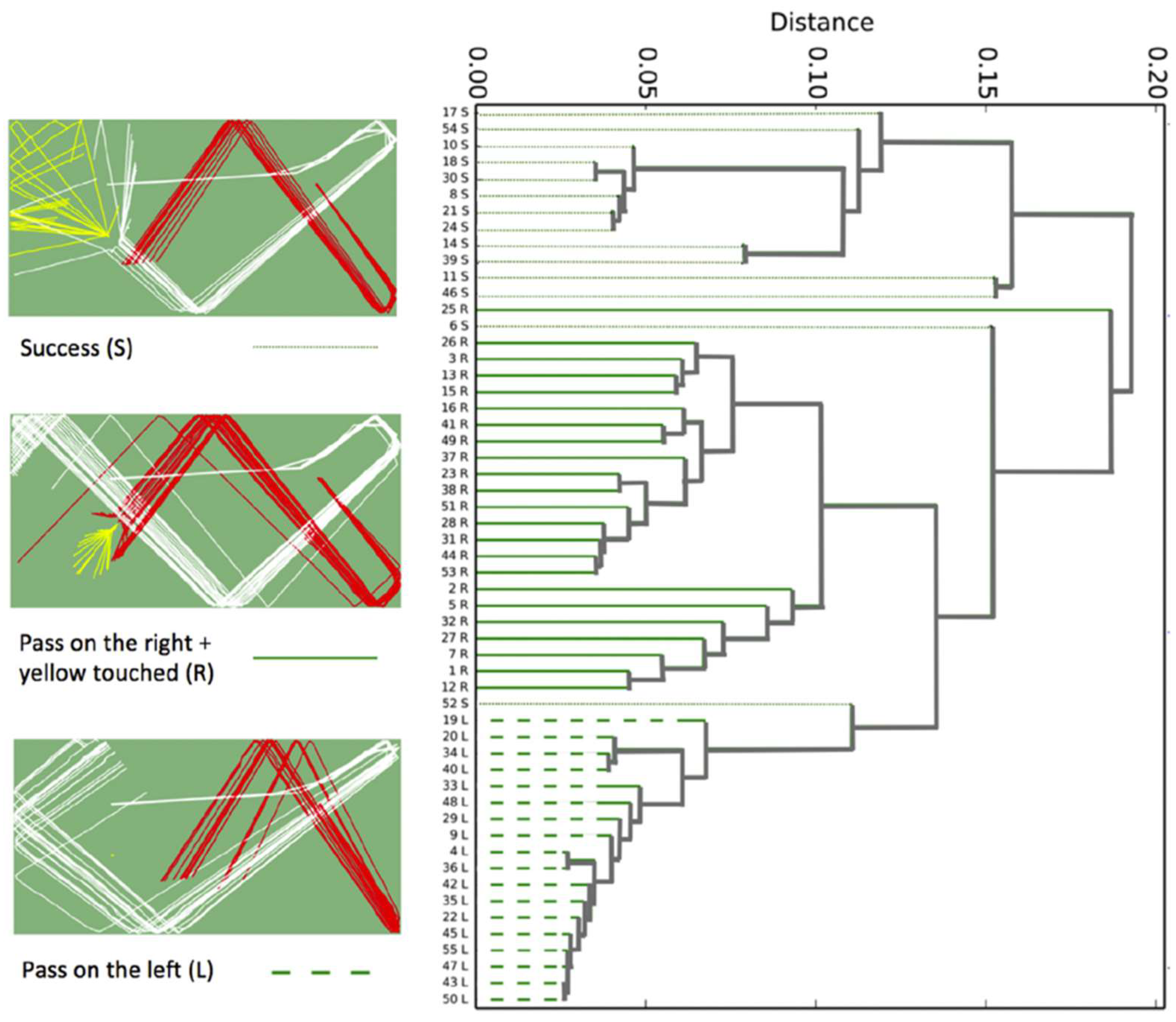
To illustrate AIMO, consider a specific application in three-cushion billiards (see Figure 1). In this game, three balls move on a pocketless table. At the start of each game, the balls are positioned as shown in Figure 2. The goal of the game is for the player to play the cue (white) ball and hit the two object balls (red and yellow) while hitting three of the sides with the cue ball before touching the last object ball. According to the success of the shot, points are given to the player. After the opening shot, the game continues with the three balls positioned as they were at the end of the opening shot. In this example, 55 opening shots were analyzed, each employing the most popular opening shot technique used by casual players [24]. By applying the Qualitative Trajectory Calculus (QTC) classification, three distinct groups of shots were identified, highlighting shared movement patterns among players. QTC, a knowledge-based method for representing and exploring the reasoning behind interactions between moving objects, was applied to classify these shots. The details of the QTC approach can be found in [25,26,27]. While this example illustrates knowledge-driven interaction analysis, HAIMO extends this foundation by integrating both symbolic reasoning and modern data-driven approaches, as outlined in the next section.

4. Towards HAIMO: A Hybrid Analysis of the Interaction of Moving Objects

The hybrid AIMO (or HAIMO) method aims to address the limitations of both knowledge-driven and data-driven approaches while offering a fresh perspective within GeoAI. By integrating these complementary approaches, HAIMO offers a pathway to analyze spatiotemporal interactions that are difficult to capture using knowledge-driven or data-driven methods in isolation. For instance, knowledge-driven AI methods like QTC allow researchers to formalize interactions as sequences of qualitative relationships, facilitating a clearer understanding of movement dynamics. Data-driven AI excels at uncovering patterns in large datasets, often revealing insights beyond purely human observation. Knowledge-driven AI, by contrast, represents movement through explicit rules that capture contextual factors that a purely statistical model may miss. In the study of moving object interactions, rule-based formalisms such as REMO (Relative Motion) [28], PDP (Point Descriptor Precedence) [29], and QTC [25] encode interactions as sequences of qualitative relationships that evolve over time, yielding interpretable descriptors of complex movement dynamics.

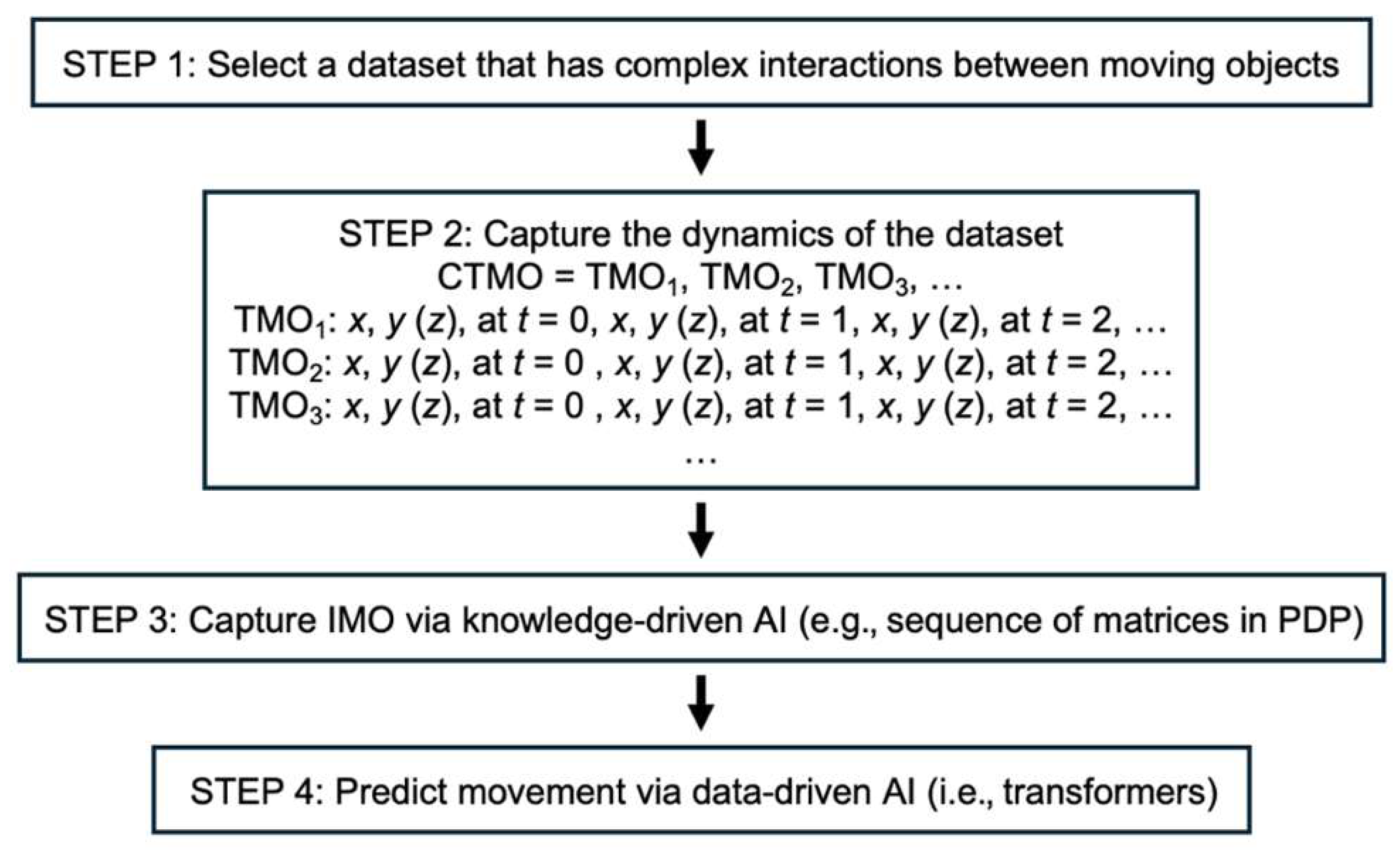
Figure 3 illustrates a conceptual outline of HAIMO. First, one selects a dataset that contains complex interactions between moving objects, such as player interactions in sports, cars in micro-traffic contexts, crowd movements, or animal interactions. The dynamics of the dataset must then be captured using x, y (z), and t coordinates. Both the individual Trajectories of Moving Objects (TMOs) and the collective configuration (CTMO) must be represented. Knowledge-driven AI approaches like QTC or PDP can capture the interactions between moving objects (IMO) as sequences of ‘characters/representations’. Examples include ball passes in soccer [30] and overtaking or lane-changing maneuvers between cars [31]. These representations enable researchers to group interactions into interpretable categories, revealing behavioral patterns that would be difficult to discern using raw data alone. In PDP, interactions are further broken down into a sequence of matrices, each corresponding to either a specific time interval or a single timestamp within the overall interaction period.

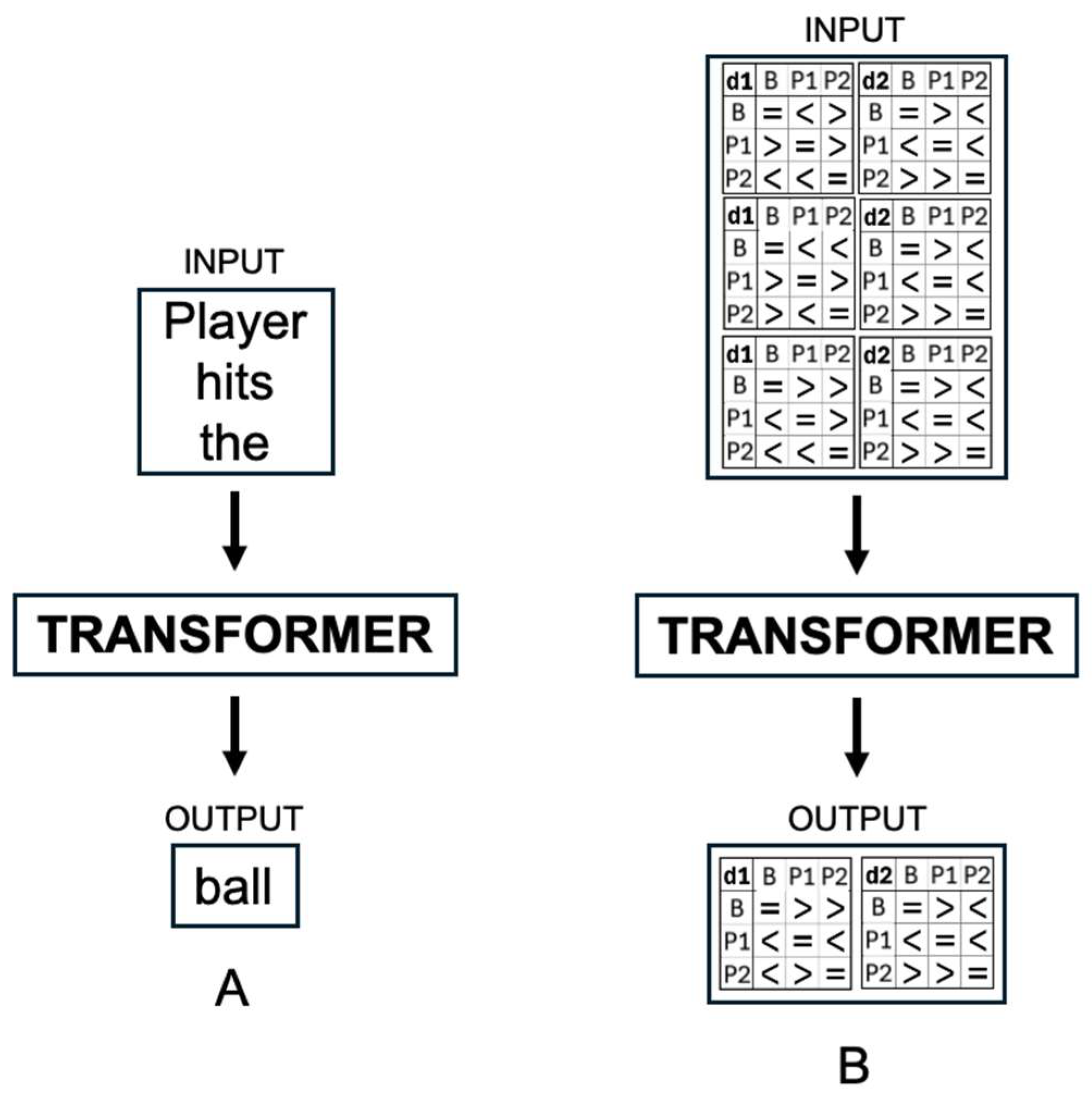
While knowledge-driven methods like PDP provide valuable insights into moving object interactions, data-driven AI has advanced dramatically across domains. Data-driven techniques now play a prominent role in generative AI, especially in large language models (LLMs). These models rely on transformer architectures [10], which process sequences of tokens, whether words, subwords, or characters. Transformers excel at capturing temporal dependencies within sequences, making them a promising tool for trajectory analysis. For example, when given the prompt “player hits the”, a transformer-based language model predicts the next token, “ball” (see Figure 4). The adaptability and efficiency of transformers extend beyond language, finding use in fields such as computer vision and bioinformatics. Within HAIMO, we propose integrating transformer architectures and SSL to analyze complex spatiotemporal interactions by combining knowledge-driven representations like PDP with data-driven predictive models. Section 5 illustrates how the PDP descriptors can be incorporated into the HAIMO workflow through a small proof-of-concept example. Although still conceptual, this hybrid approach points toward a fertile direction for future trajectory interaction research.

5. Conceptual Illustration of HAIMO

This section offers a purely conceptual walk-through of HAIMO, using a hypothetical Grand Slam tennis sequence to illustrate each step without performing any training or quantitative evaluation. Consider the four-step process involving tennis data drawn from two decades of Grand Slam finals in men’s singles tennis, beginning with Federer’s first Grand Slam win at Wimbledon in 2003. This period was shaped by Federer, Nadal, and Djokovic, each showcasing distinct styles—Federer’s precision on grass, Nadal’s clay court dominance, and Djokovic’s return game.

Step 1 involves dataset selection. We could focus on all recorded rallies during Grand Slam finals in that 20-year span, capturing a wide variety of movement patterns and match contexts. The intention is to represent each rally as a CTMO, including both players and the ball.

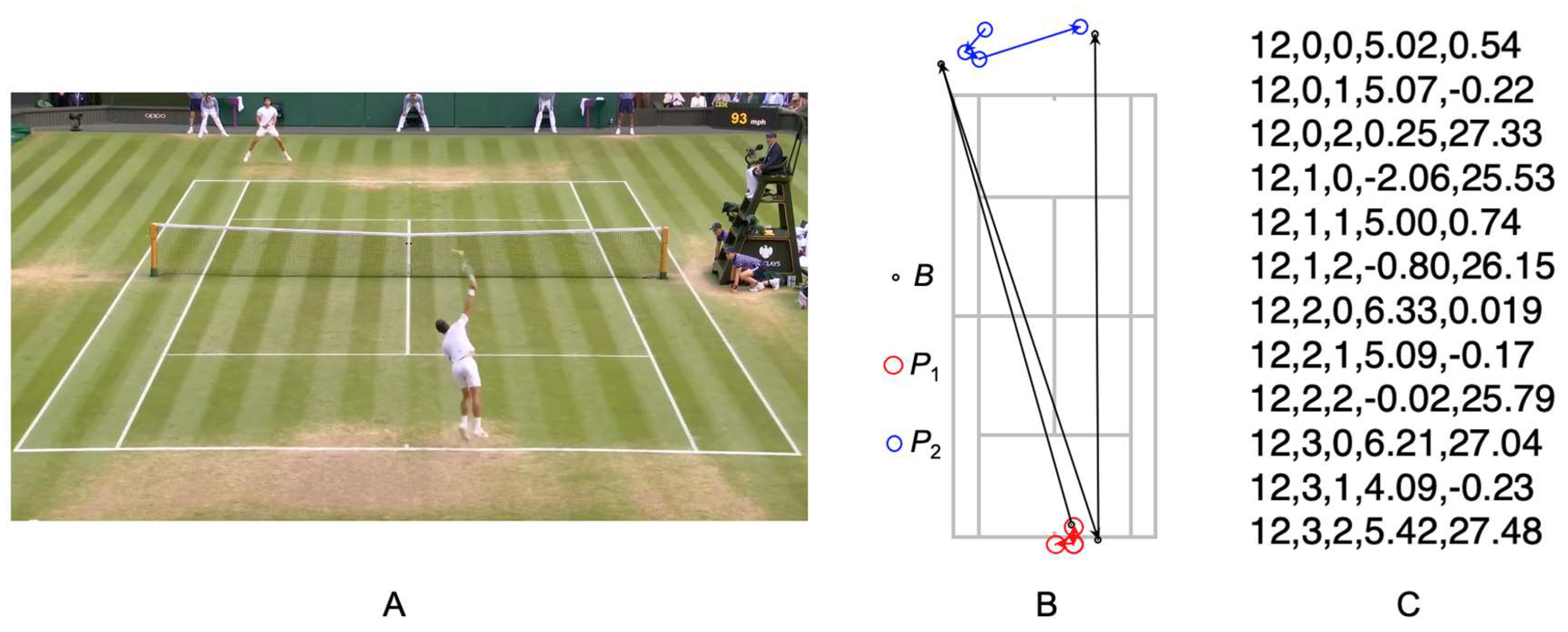
Step 2 focuses on capturing the dynamics: each rally’s x, y, and t coordinates are recorded for each timestamp. For clarity, we show a single CTMO representing a serve-and-volley rally at four discrete moments (see Figure 5). The CTMO consists of three TMOs (the ball, player 1, player 2). Each TMO is stored as a sequence of (t, x, y) points.

Beyond these spatial coordinates, rallies often exhibit complex spatiotemporal dependencies. For example, a sequence of baseline exchanges may progressively manipulate player positioning, ultimately setting up an attacking shot, such as a smash. Capturing these evolving dependencies, where actions are not isolated but built up over time, motivates the combination of symbolic representations with data-driven models within HAIMO.

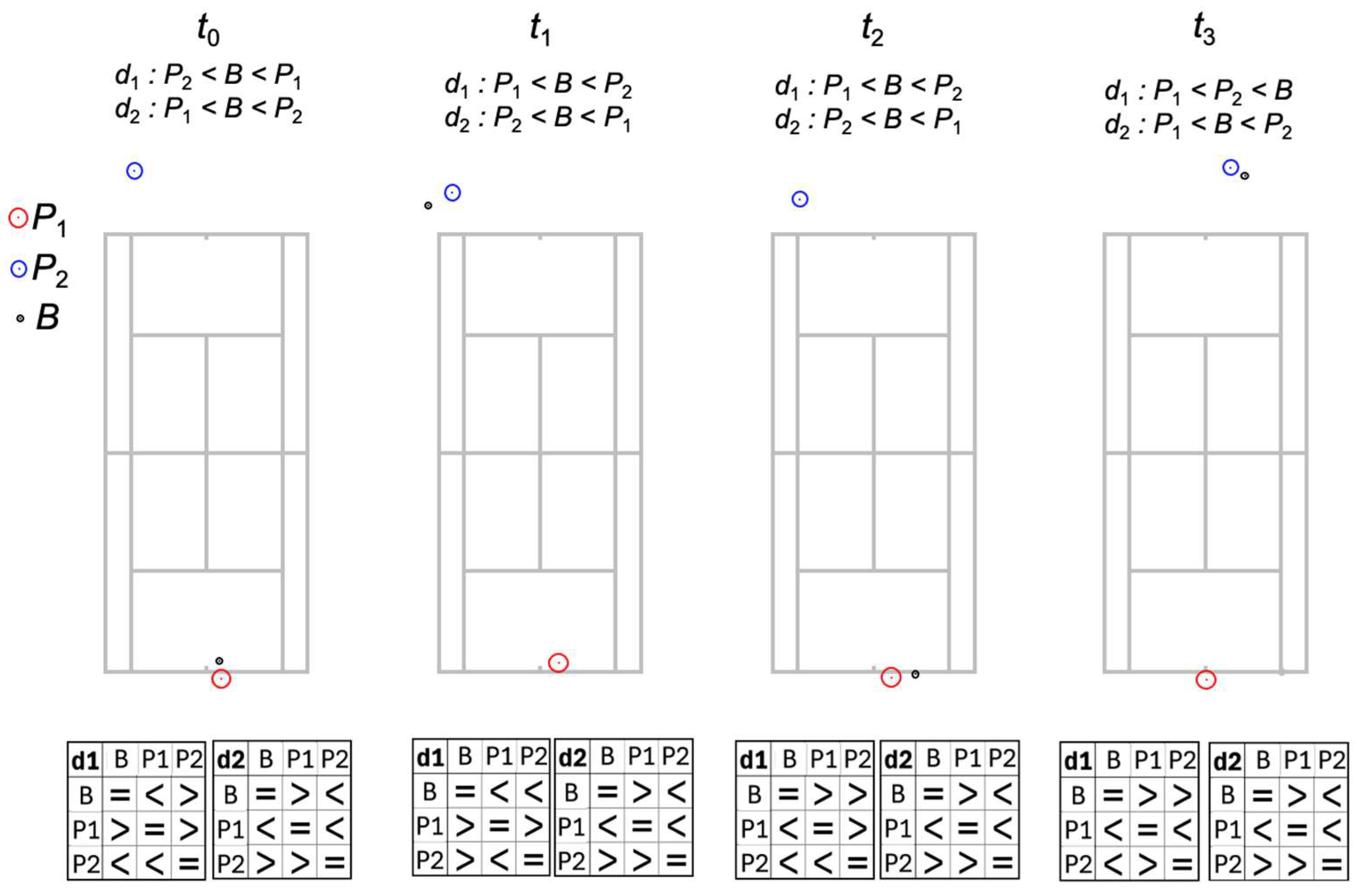
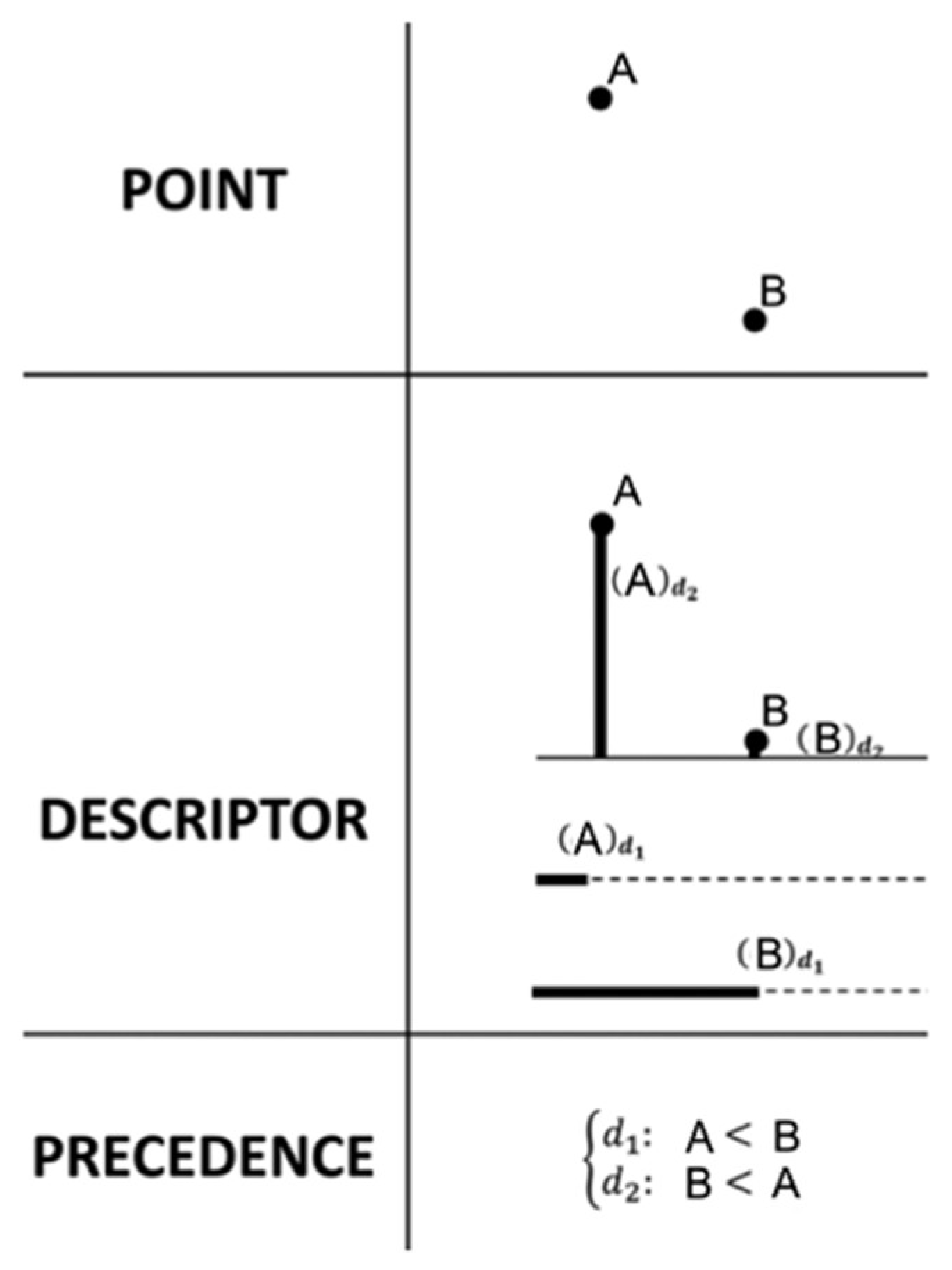
Step 3 involves representing the CTMO with knowledge-based AI, in this case PDP (see Figure 6). PDP encodes the relative positioning of points across space and time. The following three elements define PDP:

• “Point” identifies each object within the spatial framework at a given timestamp.
• “Descriptor” refers to an object’s location in each dimension.
• “Precedence” indicates how these objects are ordered or ranked based on their descriptors using relations (<, =, >).

Figure 6. A PDP representation showing the spatial configuration of points A and B, their corresponding descriptors in two dimensions, and the precedence relations (=, <, >) that define their qualitative spatial relations at a specific moment in time.

Figure 6. A PDP representation showing the spatial configuration of points A and B, their corresponding descriptors in two dimensions, and the precedence relations (=, <, >) that define their qualitative spatial relations at a specific moment in time.

Thus, for each timestamp, we create a qualitative representation of the objects’ spatial configuration, leading to a series of similarity matrices for each rally (see Figure 7). These matrices capture the temporal progression of each rally. By comparing them pairwise, it is possible to compute an overall similarity matrix that summarizes the relationships across all rallies. Conventional methods (e.g., hierarchical clustering, dimensionality reduction) can then explore trends or outliers in tennis match dynamics.

Step 4 conceptually integrates the PDP matrices into a transformer model, treating each PDP matrix as a token rather than flattening it into a sequence of symbols. Unlike traditional transformer models, where tokens represent words or subwords, our proposed approach considers entire PDP matrices at specific timestamps as input tokens (see Figure 4B). Each token, corresponding to a timestamp, provides the model with rich qualitative context about the spatial configurations at its timestamp. In an SSL setting, the transformer could be trained with objectives such as masked-matrix prediction or contrastive forecasting, allowing it to learn from raw trajectories without manual labels. Standard transformer components, including positional encoding, preserve temporal order so the model can detect patterns across timestamps. Once trained, the transformer could predict future rally configurations—for example, inferring the arrangement at t₃ from tokens t₀, t₁, and t₂—by reasoning over matrix-level patterns rather than conventional symbol sequences.

By encoding the relations of player positions and movements, we provide the transformer model with a depth of context that may translate into highly specific and nuanced sports animations. This specificity is crucial, as it enhances the interpretability of the data-driven model’s predictions and improves the quality of the generated animations, making them more realistic and informative. By grounding the transformer model in the structured understanding of sports dynamics afforded by knowledge-driven AI, we pave the way for AI systems that are not only data-driven, but also knowledge-aware. Such systems can potentially offer more accurate predictions and generate animations that are true to the complex strategies and subtleties of the sport, as well as other domains. While these design elements outline a potential implementation path, the integration of transformers within HAIMO remains a conceptual proposal at this stage.

6. Empirical Proof-of-Concept on Elite Tennis Rallies

To demonstrate HAIMO end-to-end on real data, we analyze 26 rallies manually annotated by [32] Vermeulen (2025). All rallies start with a Djokovic serve. To keep the proof-of-concept feasible and interpretable, no volleys are included, ensuring a comparable spatiotemporal structure. As this is a proof-of-concept with a low number of rallies, a short sequence is analyzed and used as basis for prediction, namely three timestamps. Additionally, only a time window length of 1 is used to ensure that each example remains highly similar to what is presented in the previous section. Of course, this approach can be extended and refined, building upon the work of [31].

This proof-of-concept focuses on the knowledge-driven component of HAIMO and illustrates how interaction representations can be extracted from real-world movement data. As described in the previous sections, such structured interaction representations could support future integration of data-driven approaches within HAIMO, including self-supervised learning (SSL) and transformer architectures. However, these elements remain conceptual at this stage, and the present example focuses solely on the knowledge-driven component. 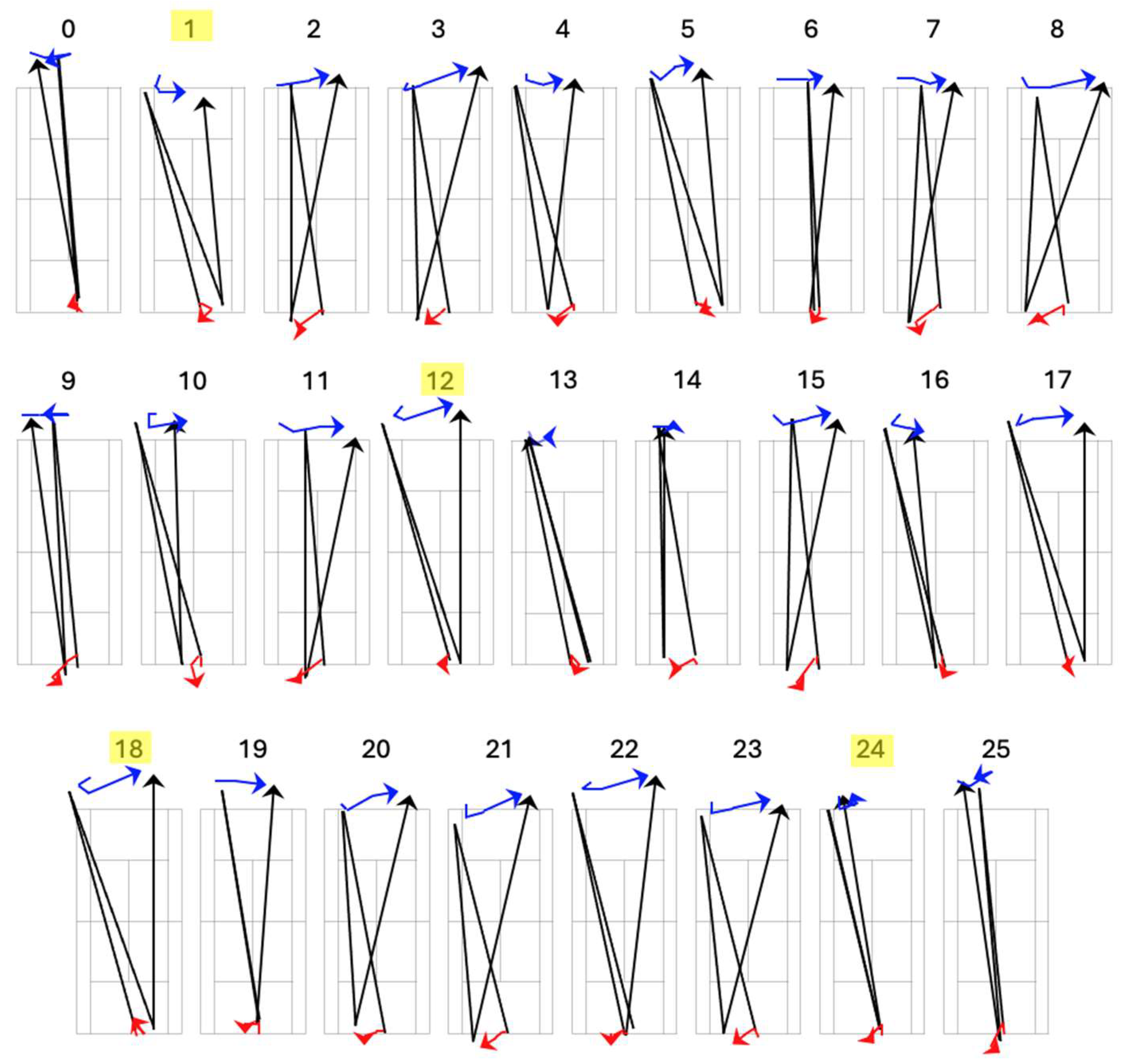Figure 8 gives an overview of the rallies used throughout this proof-of-concept.

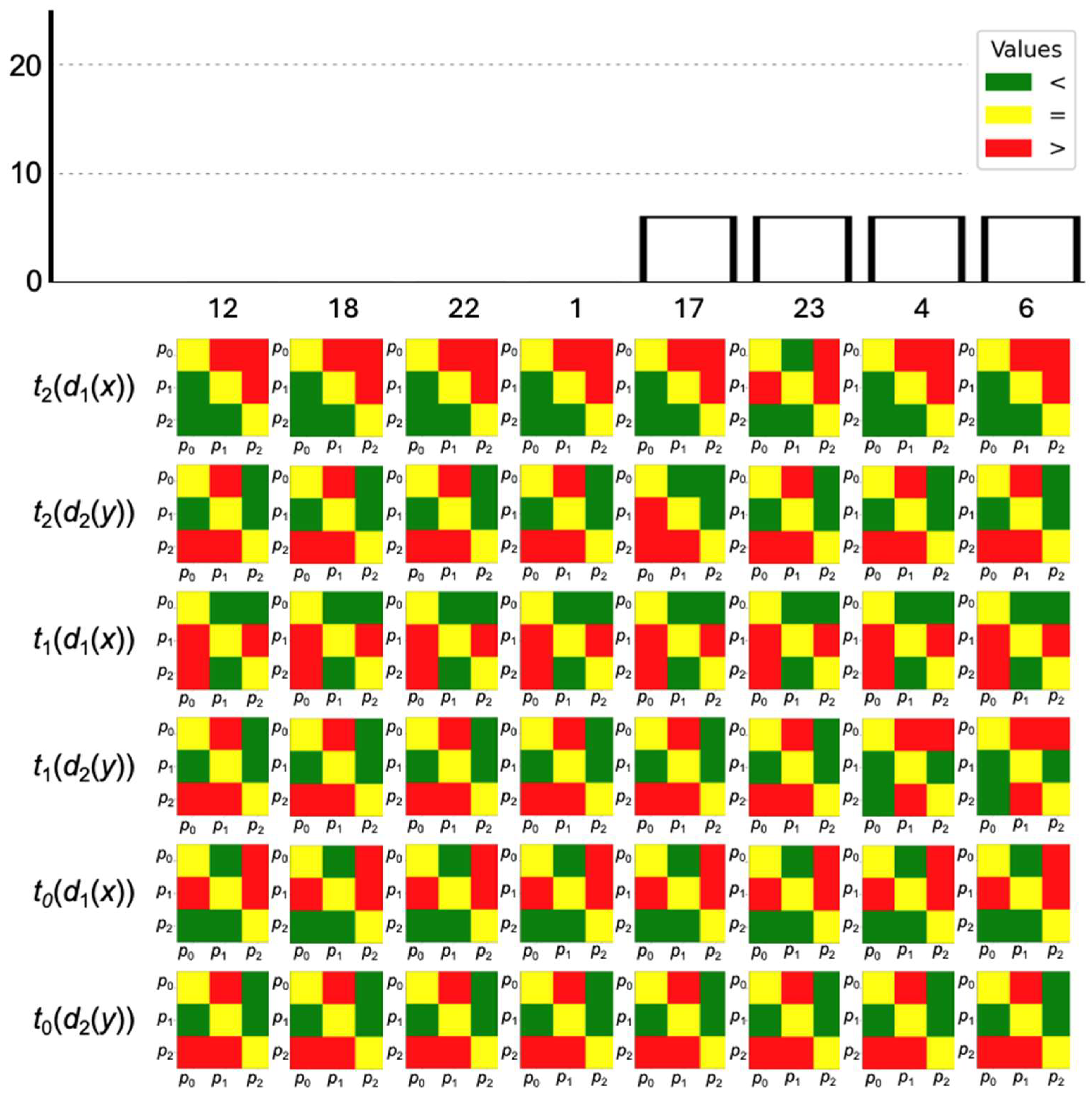
PDP processing. For each rally, x- and y-dimension inequality matrices (3 × 3) are computed, encoding the qualitative ordering (‘<’, ‘=’, ‘>’) of the players and the ball across time. Figure 9 shows representative matrices for the subset taken further into account.

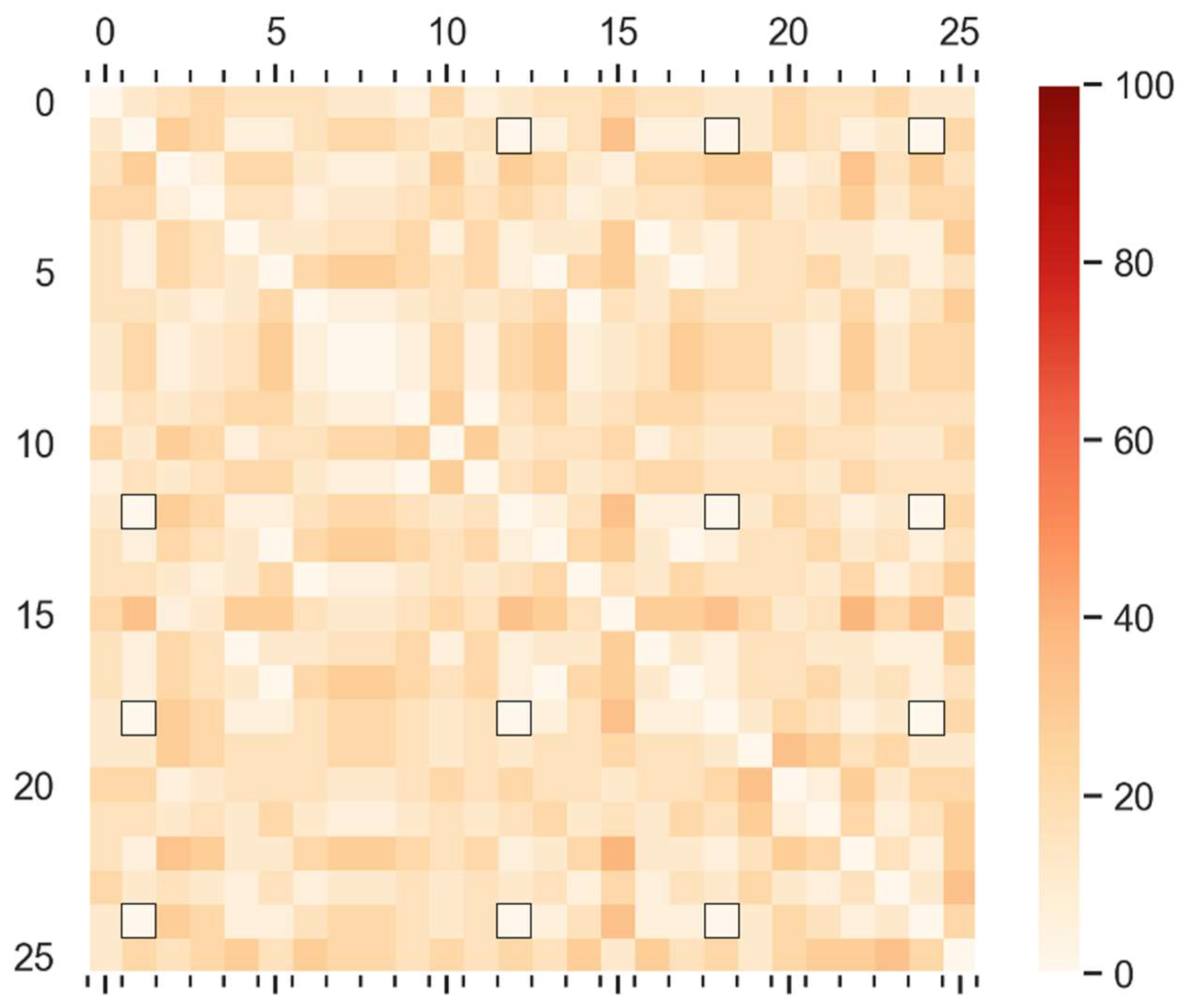
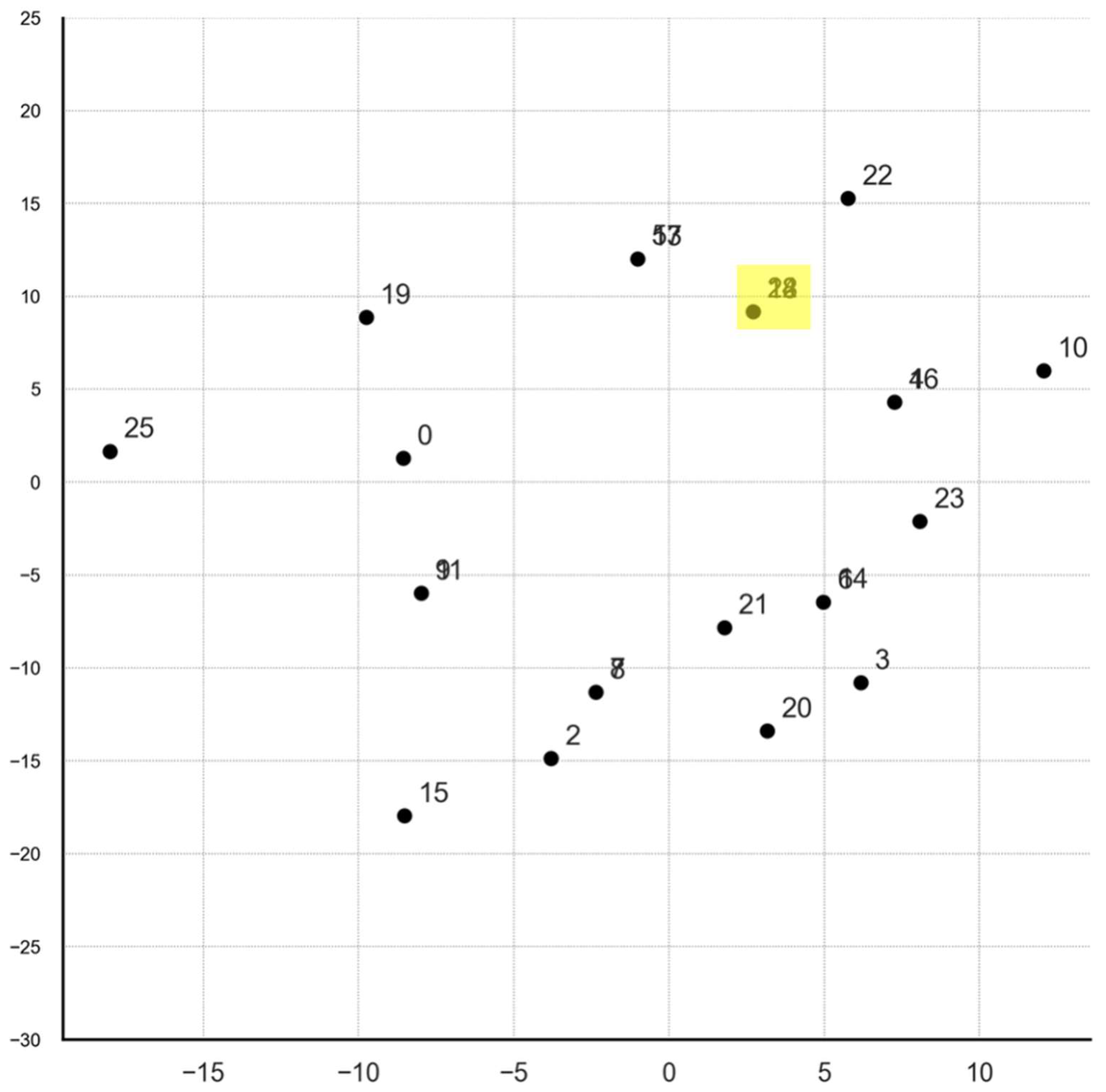
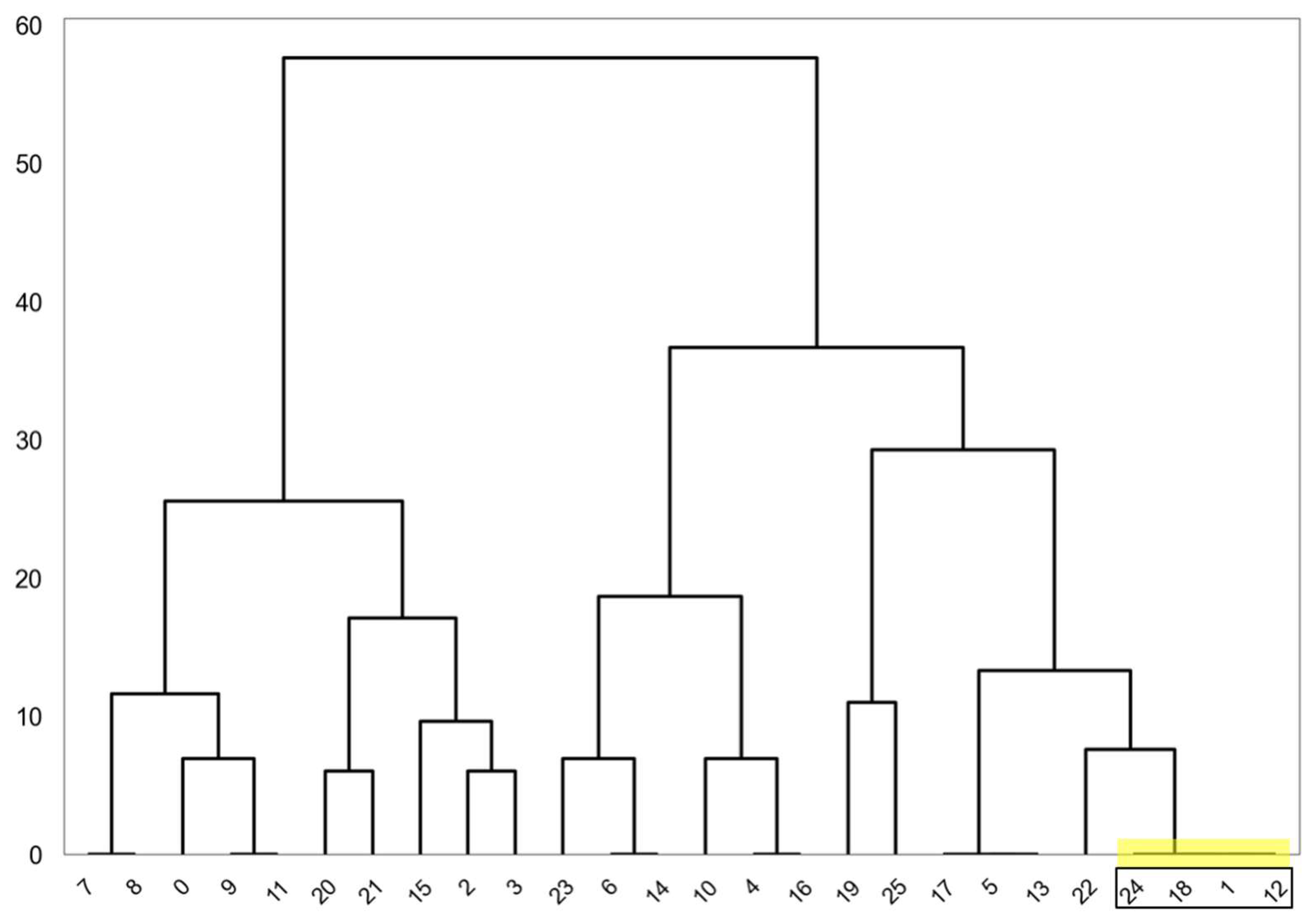
Symbolic similarity. The distances between rallies are calculated as the normalized Hamming distance between the concatenated x- and y-matrices (0 = identical, 100 = maximally different; Figure 10). A 2D multidimensional scaling projection (Figure 11) combined with hierarchical clustering (Figure 12) reveals several groups of identical matrices (distance = 0).

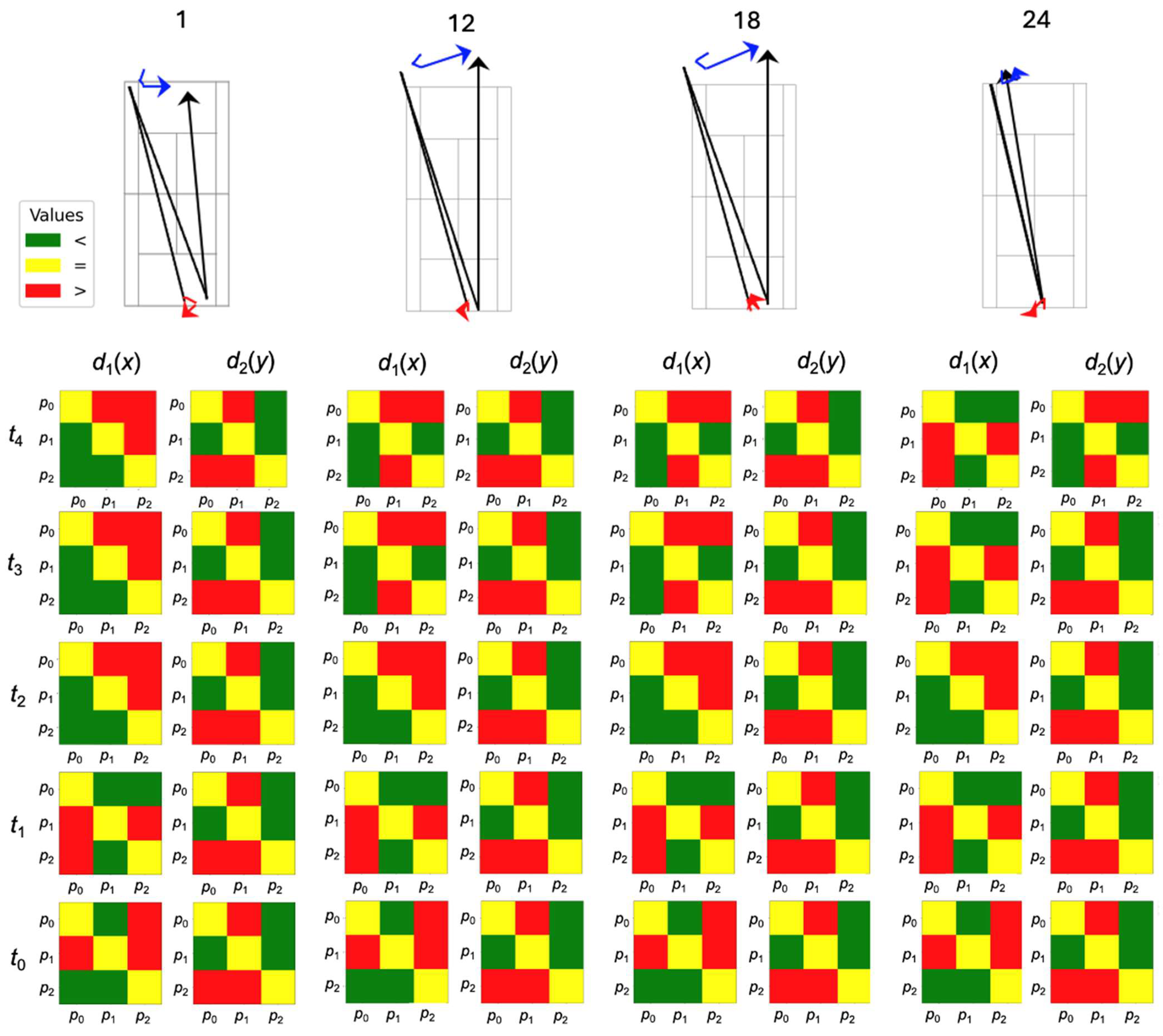
Top-K example. Using rally 12 as a query, Figure 13 lists its nearest neighbors; the matrices confirm the similarity.

Predictive outlook. Rallies 12, 18, 22, and 1 share identical matrices for t₀–t₂. The corresponding snapshots of the ground truth can be identified as t₀, t₁, and t₂ in Figure 14. In t₃ these rallies diverge: rallies 12 and 18 remain identical, while rallies 1 and 24 become different, which can be seen in Figure 9. Considering the following conditional probability $({\mathit{matrices}}_{t_0{-t}_2})\to P({\mathit{matrix}}_{t_3})$, we can, thus, say that based on this small dataset, there is a 50% chance that a rally following the sequence of 12/18/22/1 during t₀–t₂ continues as 12/18 during t₃; a 25% chance it continues as rally 1; and a 25% chance it continues as rally 22. However, robust statistical validation would require substantially larger datasets and cross-validation procedures before drawing generalizable conclusions about trajectory prediction patterns.

With a larger dataset, conditional probabilities could be modeled using transformer architectures trained with SSL, as outlined conceptually in previous sections. While these elements remain conceptual within HAIMO, this example illustrates the type of structured interaction data required to enable such data-driven approaches in future work.

Reproducibility. Further conceptual and programmatic details with respect to PDP can be found in the work of [29].

7. Conclusions

We have presented an integrated approach to trajectory analysis that merges knowledge-driven and data-driven AI to better understand interactions among moving objects. This methodology—referred to as HAIMO—can serve as a foundation for future work in AIMO and may also influence trajectory data mining, geospatial data mining, and GeoAI more broadly. The framework underscores the importance of interdisciplinary collaboration to improve and expand hybrid GeoAI strategies.

Combining the strengths of knowledge-driven and data-driven methods allows us to address complex geospatial phenomena with increased depth. Neural networks excel at finding patterns in large datasets and making predictions, while the knowledge-driven AI component provides structured, domain-specific knowledge. This integration enables the AI to tackle challenges that are difficult for either paradigm alone, such as interpreting spatiotemporal patterns in a way that is both precise and explainable. This dual perspective can yield more accurate predictions and a richer, context-informed understanding of complex movement interactions.

As part of this work, we have provided an initial empirical proof-of-concept using elite tennis rallies, focused on knowledge-driven interaction representations. This simple, real-data example illustrates HAIMO’s feasibility and highlights how structured descriptors can reveal meaningful patterns of movement. We also outlined how such representations could support future integration of SSL and transformer-based models within HAIMO, though these elements remain conceptual at this stage.

While this work establishes the conceptual foundation and demonstrates the feasibility of knowledge-driven interaction detection, several limitations must be acknowledged: (1) the empirical validation is limited to a small tennis dataset, (2) the data-driven component remains conceptual, and (3) computational scalability has not been evaluated. Future work should prioritize implementing and evaluating the complete hybrid framework using larger, diverse trajectory datasets.

Looking forward, HAIMO could be extended to hierarchical events or behaviors—for instance, grouping low-level interactions such as overtaking events in traffic to derive high-level behaviors like aggressive driving. Multiple pass sequences in soccer might combine into team tactics. In addition, future research could explore more intuitive querying of movement patterns, such as query-by-sketch or natural language interfaces. Here, users could draw or specify interaction examples, with automated grid searches optimizing the corresponding PDP or QTC signature. This would enable large-scale database exploration without the need for manual hyperparameter tuning, improving accessibility for non-technical users.

Finally, as seen in domains like language (e.g., tokenization in NLP), biology (DNA sequencing), and chemistry (material design), encoding complex patterns into meaningful, structured tokens has proven transformative. PDP and QTC signatures offer similar potential for the spatiotemporal domain, providing structured, interpretable ‘tokens’ of movement and interaction. Such formalized descriptors can enable scalable, explainable AI applications across spatiotemporal domains. By combining such representations with modern AI approaches, HAIMO may help catalyze a shift in how we analyze and understand interactions between moving objects, with wide-ranging applications across disciplines.

The evolution of hybrid GeoAI methods will hinge on continued collaboration among researchers, practitioners, and stakeholders from different domains, guiding the field toward more robust and versatile analytical tools.