Solving the Multilateration Problem without Iteration

Abstract

The process of positioning, using only distances from control stations, is called trilateration (or multilateration if the problem is over-determined). The observation equation is Pythagoras’s formula, in terms of the summed squares of coordinate differences and, thus, is nonlinear. There is one observation equation for each control station, at a minimum, which produces a system of simultaneous equations to solve. Over-determined nonlinear systems of simultaneous equations are typically solved using iterative least squares after forming the system as a truncated Taylor’s series, omitting the nonlinear terms. This paper provides a linearization of the observation equation that is not a truncated infinite series—it is exact—and, thus, is solved exactly, with full rigor, without iteration and, thus, without the need of first providing approximate coordinates to seed the iteration. However, there is a cost of requiring an additional observation beyond that required by the non-linear approach. The examples and terminology come from terrestrial land surveying, but the method is fully general: it works for, say, radio beacon positioning, as well. The approach can use slope distances directly, which avoids the possible errors introduced by atmospheric refraction into the zenith-angle observations needed to provide horizontal distances. The formulas are derived for two- and three-dimensional cases and illustrated with an example using total-station and global navigation satellite system (GNSS) data.

1. Introduction

A station’s coordinates can be determined from distances—with no angles—using a technique known as trilateration, or multilateration if there are redundant observations. The U.S. Bureau of Land Management [1] defines trilateration as, “A method of determining horizontal positions by measuring the lengths of triangle sides, usually with the use of electronic instruments.” This definition predates global navigation satellite systems (GNSSs) and is a little dated. The method is used extensively nowadays because it is how GNSSs are used to determine the coordinates of a receiver [2,3], and such positions are inherently three dimensional. For terrestrial surveying, slope distances observed with an electronic distance meter (EDM) can be used, likewise producing three-dimensional positions. The trilateration problem can be stated: given the coordinates of at least three/four control marks and the distances from the control marks to a target mark, determine the horizontal/3-d coordinates of a target mark. This is similar to the resection problem, but resection uses directions instead of distances [4].

Pythagoras’s formula is the observation equation, written with the lengths of the shorter sides are given as differences in Cartesian coordinates, Equation (3). There is one equation for each control station, so there is a set of simultaneous equations solve. The system has an analytical solution—there are three equations and three unknowns in a quadratic—however, the exact solution is somewhat unwieldy and, worse, cannot handle an over-determined system, having more observations than the minimum of three. The typical solution strategy is to linearize the system by expanding the equations in a Taylor’s series and retain only the first-order terms, then solve by iterative least squares. However, as will be shown, taking the difference of the observation equations linearizes the system without any approximations, which allows the solution to be found without iteration.

Multilateration uses mark-to-mark slope distances. If the height of the prism target above the unknown station, hr, equals the height of the optical center of the telescope in a total station, hi, then the observed slope distance $s\prime$ equals mark-to-mark slope distance $s$. Otherwise, let $\zeta \prime$ denote the observed zenith angle. Then the mark-to-mark zenith angle is [5]

$$\cot \zeta =\csc \zeta \prime \frac{hi-hr}{s\prime }+\cot \zeta \prime$$

(1)

and the mark-to-mark slope distance is

$$s=\frac{s^{\prime }\sin \zeta \prime }{\sin \zeta }$$

(2)

Hereafter, all slope distance will be assumed to be mark-to-mark.

Suppose we are to determine the coordinates of station $i=\left(e_i,n_i,u_i\right)$ given the coordinates of a set of control stations $C=\left\{\left(e_j,n_j,u_j\right),\dots \left(e_m,n_m,u_m\right)\right\}$, and $\left|C\right|=n$, i.e., there are n control stations. The slope distance from station i to station j, $s_{ij},$ is related to the stations’ Cartesian coordinates by [6].

$$s_{ij}^2={\left(e_j-e_i\right)}^2+{\left(n_j-n_i\right)}^2+{\left(u_j-u_i\right)}^2$$

(3)

Similarly, the slope distance from station i to station k, $s_{ik},$ is related to the stations’ coordinates by

$$s_{ik}^2={\left(e_k-e_i\right)}^2+{\left(n_k-n_i\right)}^2+{\left(u_k-u_i\right)}^2$$

(4)

Expanding the quadratic terms, showing only the easting terms for brevity, gives

$$\begin{gathered} s_{ij}^2=e_j^2+2e_j{e}_i+e_i^2+\cdots \\ {s}_{ik}^2=e_k^2+2e_k{e}_i+e_i^2+\cdots \end{gathered}$$

(5)

Taking $s_{ij}^2-s_{ik}^2$ eliminates the $e_i^2,n_i^2,\mathrm{and} u_i^2$ terms, leaving

$$\begin{gathered} s_{ij}^2-s_{ik}^2=e_j^2+2e_j{e}_i+e_i^2+\cdots -\left(e_k^2+2e_k{e}_i+e_i^2+\cdots \right) \\ =e_j^2-e_k^2+2e_i\left(e_j-e_k\right)+\cdots \end{gathered}$$

(6)

Putting constants on the right and factoring on the left, gives

$$\left(e_j-e_k\right)e_i+\left(n_j-n_k\right)n_i+\left(u_j-u_k\right)u_i=\frac{\left(s_{ij}^2-s_{ik}^2+e_k^2-e_j^2+n_k^2-n_j^2+u_k^2-u_j^2\right)}{2}$$

(7)

The only unknown terms are $e_i, n_i, \mathrm{and} u_i.$ If station i has been observed from stations $j\dots m,$ then these equations can be written as a matrix expression as

$$\left[\begin{array}{c}\begin{array}{ccc}{e}_j-e_k& n_j-n_k& u_j-u_k\\ e_j-e_l& n_j-n_l& u_j-u_l\\ ⋮& ⋮& ⋮\end{array}\\ \begin{array}{ccc}{e}_j-e_m& n_j-n_m& u_j-u_m\end{array}\end{array}\right]·\left[\begin{array}{c}{e}_i\\ n_i\\ u_i\end{array}\right]=\frac{1}{2}\left[\begin{array}{c}{s}_{ij}^2-s_{ik}^2+e_k^2-e_j^2+n_k^2-n_j^2+u_k^2-u_j^2\\ s_{ij}^2-s_{il}^2+e_l^2-e_j^2+n_l^2-n_j^2+u_l^2-u_j^2\\ \begin{array}{c}⋮\\ s_{ij}^2-s_{in}^2+e_n^2-e_j^2+n_n^2-n_j^2+u_n^2-u_j^2\end{array}\end{array}\right]$$

(8)

Or

$$M x=k$$

(9)

So, if M is $3\times 3$,

$$x=M^{-1}k$$

(10)

If M has more than three rows, the system is over-determined, and it is solved with a pseudo-inverse in the usual way:

$$x={\left(M^{T}M\right)}^{-1}{M}^{T}k$$

(11)

Matrix M has the differences of pairs of control coordinates for its elements. There are $n\left(n-1\right)/2$ ways to pick two items from a set of n things, and each of these could be a row in M. That would result in M having quite a few rows producing, supposedly, a lot of built-in redundancy. However, the GNSS-positioning concept of “independent baselines” applies here: many of the pairs would be trivial inverses of others, and no real additional information is added. Therefore, like with GNSS, pick one station to be a common station and form all differences with the common station. Station j is the common station in Equation (8). The constant term k in Equation (9) can be written as $(s_{ij}^2-s_{ik}^2+{\left|K\right|}^2-{\left|J\right|}^2)/2$, where ${\left|K\right|}^2=e_k^2+n_k^2+u_k^2$ is the square of distance from station k to the origin of the coordinate system; similar for station j. This suggests two things. First, picking the control station closest to the centroid of all the control stations to be the common differencing station minimizes ${\left|K\right|}^2-{\left|J\right|}^2$. Second, it is sensible to use localized coordinates to keep the coordinates themselves as small as possible so that the quadratic terms do not suffer undue truncation and round-off errors. For example, if station i is set to be a local origin, then all other stations’ coordinates become $\left(e_j-e_i,n_j-n_i,u_j-u_i\right)$.

Our method is similar to that developed by Navidi et al. [7]. Their approach depends on a special control station that they call the reference point that is required to be at the centroid of the other control stations. They then add and subtract the coordinates of the reference point from those of the other control stations to form a third type of distance that, when added to the distances from the other control stations to the unknown point, causes most of the nonlinear terms to cancel. Placing the reference point at the centroid is highly auspicious because it causes the observation matrix to become orthogonal to the parameter vector, which eliminates the remaining nonlinear term. Ignoring numerical stability issues, our method and theirs must be equivalent: they are both least squares estimators, and, since least squares is a best linear unbiased estimator, any two different approaches to the same problem using least squares must be equivalent. However, the problem formulations can differ and that can lead to implementation issues. As just stated above, we recommend that the common differencing station be near the centroid, but it is not a requirement. The method by Navidi et al. requires that the reference point be at the centroid, which could be onerous depending on how difficult it is to stake out that position, assuming that it is possible at all.

The positioning equation for GNSS uses multilateration but it includes additional terms [8], p. 410:

$$s_{ij}=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2+{\left(z_i-z_j\right)}^2}+c b_u+{ϵ}_{pi}$$

(12)

where x, y, and z are geocentric Cartesian coordinates in the reference frame of the broadcast ephemeris, c is the speed of light in a vacuum, $b_u$ is the unknown time offset of the receiver’s clock to GPS time (called a time bias), and ${ϵ}_{pi}$ is a “catch-all” error term for ionospheric and tropospheric delays, multipath, and c. Unfortunately, our scheme does not apply here because squaring the right-hand side of the equation mixes the terms together so that the quadratic terms do not cancel after differencing. Therefore, the equation is linearized by a truncated Taylor’s series and solved with iteration.

2. Stochastic Model

One can reasonably assume that the slope-distance observations are independent and normally distributed as $s_j~N({\mu }_j,{\sigma }_j^2)$ where ${\mu }_j$ is the true distance, and ${\sigma }_j$ is the EDM standard deviation given by ${\sigma }_j=c+s_j/1000\times \mathrm{ppm}$, where c is the constant term, and ppm is the “parts per million” millimeters per kilometer term. This model ignores setup uncertainty at the instrument and at the target. As such, the $n\times n$ covariance matrix of the observations $Q=diag\left({\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_n^2\right)$ is a diagonal matrix. The inverse of the covariance matrix $W=Q^{-1}=diag\left(1/{\sigma }_1^2,1/{\sigma }_2^2,\dots ,1/{\sigma }_n^2\right)$ can be used as a weight matrix, and is applied as

$$s_{ij}W M x=W k$$

(13)

which is solved by

$$\begin{array}{cc}\hfill W M x& =W k\hfill \\ \hfill M^{t}W M x& =M^{t}W k\hfill \\ \hfill {\left(M^{t}W M \right)}^{-1}{M}^{t}W M x& ={\left(M^{t}W M \right)}^{-1}{M}^{t}W k\hfill \\ \hfill x& ={\left(M^{t}W M \right)}^{-1}{M}^{t}W k\hfill \end{array}$$

(14)

The matrix ${\left(M^t{W}^{-1}M\right)}^{-1}$ is called a cofactor matrix, and it is proportional to the estimated covariance of the estimations. The constant of proportionality is called the variance of unit weight, or just “unit variance,” and the estimated covariance of the estimations is ${\sigma }_0^2{\left(M^t{Q}^{-1}M\right)}^{-1}$. The unit variance can itself be estimated as follows, [9,10]. Let $X={\left(M^{t}W M \right)}^{-1}{M}^{t}W x$ be the estimated values of the distances according to the least squares model, and let $V=M X-x$ be a column vector of the estimation residuals. Then

$${\sigma }_0^2=\frac{V^{t}W V}{n-u}$$

(15)

where, $n=\left|k\right|$ is the number of observations and $u=\left|x\right|$ is the number of coordinates to estimate (i.e., three in this case).

3. Coordinate Systems

The formulas require Cartesian coordinates for the control stations. There are three choices: geocentric Cartesian (called XYZ), topocentric Cartesian (called ENU), or grid coordinates. Grid coordinates require additional reductions be applied to the slope distances, which is thoroughly covered in standard surveying texts and an unnecessary distraction here. In fact, XYZ coordinates are well suited for this application, at least in principle.

4. Example: More Control than the Minimum

Hereafter, all linear quantities will be given in meters. In this example, we pretend to confirm the coordinates for the CTMA CORS ARP NAD 83(2011) coordinates (https://www.ngs.noaa.gov/cgi-bin/ds_cors.prl?CorsSelected=|CTMA&CorsTypeSelected=Arp, accessed on 28 June 2021), which are $x=1,456,379.711, y=-4,539,030.822, z=4,223,420.343$. Suppose there are five control stations available whose XYZ coordinates were determined using GNSS positioning as tabulated in

Table 1. Randomly generated coordinates for five control stations around CTMA.

Station	A	B	C	D	E
X	1,456,384.836	1,456,361.528	1,456,385.694	1,456,392.590	1,456,528.776
Y	−4,539,056.940	−4,539,041.958	−4,538,904.001	−4,539,083.089	−4,538,786.795
Z	4,223,384.124	4,223,414.509	4,223,553.263	4,223,358.456	4,223,631.667

. In fact, these stations’ coordinates were generated in Mathematica™ using random-number generators, such that the horizontal coordinates follow uniform distributions $\pm 300$ m from CTMA and the vertical coordinates follow a uniform distribution $\pm 5$ m from CTMA.

Inversing the control coordinates with CTMA produces exact slope distances that a perfect EDM would observe. These slope distances from the five control stations to the “unknown station” CTMA are 44.947, 22.106, 183.812, 82.023, and 355.566, to three significant digits. First, use the coordinates as given. The system of equations is

$$\begin{gathered} \left[\begin{array}{c}{x}_2-x_1\\ x_3-x_1\\ x_4-x_1\\ x_5-x_1\end{array}\begin{array}{c}{y}_2-y_1\\ y_3-y_1\\ y_4-y_1\\ y_5-y_1\end{array}{\begin{array}{c}{z}_2-z_1\\ z_3-z_1\\ z_4-z_1\\ z_5-z_1\end{array}}^{ }\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\frac{1}{2}\left[\begin{array}{c}{s}_1^2-s_2^2-x_1^2+x_2^2-y_1^2+y_2^2-z_1^2+z_2^2\\ s_1^2-s_3^2-x_1^2+x_3^2-y_1^2+y_3^2-z_1^2+z_3^2\\ s_1^2-s_4^2-x_1^2+x_4^2-y_1^2+y_4^2-z_1^2+z_4^2\\ s_1^2-s_5^2-x_1^2+x_5^2-y_1^2+y_5^2-z_1^2+z_5^2\end{array}\right] \\ \left[\begin{array}{c}-23.3078 \\ 0.85885\\ 7.755\\ 143.940\end{array}\begin{array}{c}14.9819\\ 152.939\\ -26.149\\ 270.146\end{array}{\begin{array}{c} 30.3852\\ 169.139\\ -25.668\\ 247.543\end{array}}^{ }\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}2.638\times {10}^7\\ 2.140\times {10}^7\\ 2.158\times {10}^7\\ 2.891\times {10}^7\end{array}\right] \end{gathered}$$

(16)

Using Mathematica, the solution works out to $x=1,456,379.711,y=-4,539,030.822,z=4,223,420.343$. These coordinates differ from CTMA by $-9.8\times {10}^{-6}, 0.00003,-0.00003$, which is good but it is not even machine precision. The issue is the large values in k, which involve the squares of the coordinate values, the right side of Equation (8). The solution can be improved by localizing the coordinates, which makes them much smaller numbers and, thus, improves numerical stability. For example, subtract station A’s coordinates from the other control stations, resulting in the coordinates in

Table 2. Localized XYZ control coordinates.

Station	A	B	C	D	E
local X	0	−23.308	0.859	7.755	143.940
local Y	0	14.982	152.939	−26.149	270.145
local Z	0	30.385	169.139	−25.668	247.543

.

Matrix M is unaffected by localization. The k vector’s values become much smaller: 177,359.991, 1,148,807.296, −188,483.583, and 1,758,500.670. The solution now matches CTMA’s coordinates no worse than $2\times {10}^{-9}$ m for each coordinate.

5. ENU Coordinates

If the control stations’ coordinates had been determined by radial surveying from station A using a perfect total station, we would have the control coordinates shown in

Table 3. ENU control coordinates.

Station	A	B	C	D	E
e	0	−17.616	47.543	−0.605	219.592
n	0	36.911	222.984	−37.306	326.684
u	0	4.265	4.104	3.264	5.623

.

ENU coordinates are XYZ coordinates that have been translated and rotated—no scaling or stretching—which means the distances and angles between the stations are preserved exactly in the two systems. Therefore, the ENU solution must, in principle, be identical to the XYZ solution, and would be exactly identical if exact arithmetic were available. The implication here is that, in principle, there is no need to reduce slope distances to horizontal distances.

Good strength-of-figure results from surrounding the unknown station with observations from all directions. It is unlikely, however, that the unknown station can be observed from far below or above. There might be a situation where an observation could be, say, made from a rooftop, but it will usually happen that the control stations are generally around the same height. The concepts of dilutions of precision pertain here. Borrowing from GNSS [11], the dilutions of precisions are various combinations of the diagonal elements of the estimated position’s covariance matrix, being the variances of the estimated coordinates. As with GNSS positioning, and fundamentally for the same reason, the horizontal dilution of precision will be better (lower) than the vertical dilution of precision because, for GNSS, it is impossible to observe the satellites (a.k.a. space vehicles [SVs]) below the horizon so the positioning cannot be controlled from below. If all the Up-coordinates are the same so that their differences are zero, then matrix $M=\left[\begin{array}{ccc}a& b& 0\\ c& d& 0\\ e& f& 0\end{array}\right]$ has a row echelon form of $\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right]$, which shows the matrix cannot be inverted. More generally, co-planar control stations produce an M matrix that cannot be inverted. However, M can be inverted, in principle, if the stations are not exactly coplanar, but M can become ill-conditioned [10]. For example, replacing the Up-coordinates in the previous example with normally distributed random numbers $u^{\prime }~N\left(0, 0.01\right)$ produced a $M^{T}WM$ matrix with elements differing by ten orders of magnitude, resulting in a position estimate of $\left(0.024, 0.023,-503.181\right)$ instead of (0,0,0). The accuracies of the horizontal coordinates are compromised by the ill-conditioning brought about by the vertical coordinates. Not including the vertical coordinates mitigates this, so we now re-work the problem for horizontal positioning.

6. Horizontal Positioning

The horizontal-only equations come from dropping the Up-coordinates in Equation (8) and replacing the slope distances with horizontal distances, $\overline{s}=s\cos \left(\zeta \right),$ where $\zeta$ is the mark-to-mark zenith angle. Equation (8) becomes

$$\left[\begin{array}{cc}{e}_j-e_k& n_j-n_k\\ e_j-e_l& n_j-n_l\\ ⋮& ⋮\\ e_j-e_m& n_j-n_m\end{array}\right]·\left[\begin{array}{c}{e}_i\\ n_i\end{array}\right]=\frac{1}{2}\left[\begin{array}{c}{s}_{ij}^2-s_{ik}^2+e_k^2-e_j^2+n_k^2-n_j^2\\ s_{ij}^2-s_{il}^2+e_l^2-e_j^2+n_l^2-n_j^2\\ \begin{array}{c}⋮\\ s_{ij}^2-s_{in}^2+e_n^2-e_j^2+n_n^2-n_j^2\end{array}\end{array}\right]$$

(17)

Solving Equation (17) with horizontal distances from the previous examples produces a position estimate of $\left(-1.5\times {10}^{-14}, 1.0\times {10}^{-14}\right)$, which is around machine precision for double-precision floating point arithmetic.

7. Fieldwork Example

Observations were collected on the campus of New Mexico State University in May 2020. Five stations were positioned using a static GNSS survey lasting for at least 25 min, with a 1-s sampling interval, using Topcon HiPer Lite+ GNSS receivers. The specifications of the receivers, as reported by the manufacturer, are horizontal accuracies of ±3 mm ± 0.5 ppm and vertical accuracies of ±5 mm ± 0.5 ppm for GNSS static surveys. Data were then processed using the Online Positioning User Service (OPUS) tool provided by NGS (https://geodesy.noaa.gov/OPUS/, accessed on 28 June 2021), [12]. Seven CORSs provided control, being an average of around 100 km away (DK7580, DM3997, DJ8945, DG7417, DG6517, DG5392, DG5481). The average RMS values for all coordinates was less than 3 cm, as reported by OPUS. We also measured the mark-to-mark distances using a Leica TS02 total station and accompanied Leica reflector, both erected atop a slip-leg tripod and a tribrach with an optical plummet. Leica reports the accuracy of the EDM as 1.5 mm + 2 ppm. Each distance was measured three times in both the left and right faces. The height of instrument and the height of the reflector were measured and input to the total station. We then documented the observed horizontal and slope distances (

Table 4. Total-station slope distances and horizontal distances observed from the fieldwork.

	From	To	L	R
slope_distance	A	U	35.763	35.763
slope_distance	A	U	35.767	35.767
slope_distance	A	U	35.765	35.765
slope_distance	B	U	49.618	49.618
slope_distance	B	U	49.616	49.616
slope_distance	B	U	49.620	49.620
slope_distance	C	U	44.689	44.689
slope_distance	C	U	44.691	44.691
slope_distance	C	U	44.690	44.691
slope_distance	D	U	39.547	39.548
slope_distance	D	U	39.548	39.548
slope_distance	D	U	39.550	39.549
	From	To	L	R
hz_distance	A	U	35.761	35.761
hz_distance	A	U	35.765	35.765
hz_distance	A	U	35.763	35.763
hz_distance	B	U	49.616	49.616
hz_distance	B	U	49.614	49.614
hz_distance	B	U	49.618	49.618
hz_distance	C	U	44.683	44.683
hz_distance	C	U	44.685	44.685
hz_distance	C	U	44.684	44.685
hz_distance	D	U	39.542	39.543
hz_distance	D	U	39.543	39.543
hz_distance	D	U	39.545	39.544

).

The International Terrestrial Reference Frame (ITRF) 2014 coordinates are tabulated in

Table 5. Station coordinates in ITRF 2014 in XYZ, local XYZ, and ENU coordinate systems.

Name	x	y	z	x’	y’	z’	e	n	u
A	−1,555,853.353	−5,169,686.486	3,387,031.050	−28.227	−11.773	−31.486	−23.636	−36.985	−0.405
B	−1,555,799.191	−5,169,663.062	3,387,092.663	25.935	11.651	30.127	21.478	35.421	0.337
C	−1,555,794.942	−5,169,696.699	3,387,044.381	30.184	−21.986	−18.155	35.240	−21.947	0.751
D	−1,555,853.020	−5,169,652.603	3,387,082.050	−27.894	22.110	19.514	−33.082	23.512	−0.683
CG	−1,555,825.127	−5,169,674.713	3,387,062.536	0	0	0	0	0	0
U	−1,555,832.101	−5,169,675.751	3,387,057.746	−6.975	−1.038	−4.790	−6.379	−5.654	−0.018

. Stations A, B, C, D, and U were positioned with OPUS, and station CG is the average of stations A, B, C, D. Station U is the check station, whose coordinates are to be determined using stations A, B, C, D. The XYZ coordinates were converted to geodetic longitude, latitude, and height $\left(\lambda ,\varphi ,h\right)$, and then to local topocentric ENU using CG as the origin. The direct-inverse observations where averaged to mitigate collimation error, [13] and then all corrected pairs averaged to a single value. This is not necessary: M and k can be formed from the individual collimation-corrected averages but using the single ensemble average values yielded nearly identical estimates and makes the examples below easier to read. In practice, it might be preferable to use the individual collimation-corrected averages for blunder detection.

1.

Estimate station U’s coordinates using slope distances and XYZ control coordinates (i.e., using the coordinates from OPUS directly),

$$\begin{gathered} M=X·k \\ \left[\begin{array}{ccc}54.162& 23.424& 61.613\\ 58.411& -10.213& 13.331\\ 0.333& 33.883& 51.000\end{array}\right]=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]·\left[\begin{array}{c}3,325,326.313\\ 7,073,056.703\\ -2,942,270.703\end{array}\right] \end{gathered}$$

(18)

$$\begin{gathered} X=M^{-1}·k \\ \left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}4.849& -4.453& -4.695\\ 14.831& -13.671& -14.344\\ -9.885& 9.112& 9.580\end{array}\right]·\left[\begin{array}{c}3,325,326.313\\ 7,073,056.703\\ -2,942,270.703\end{array}\right] \\ \left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}-1,555,830.328\\ -5,169,670.346\\ 3,387,054.140\end{array}\right] \end{gathered}$$

(19)

• These coordinates differ from the check coordinates by $\left(1.773, 5.405,-3.606 \right)$, which is 6.735 m in error (3-d).

2.

Estimate station U’s coordinates using slope distances and XYZ coordinates localized to their centroid, columns $x^{\prime },y^{\prime },z\prime$ in Table 5.

$$\begin{gathered} M=X·k \\ \left[\begin{array}{ccc}54.162& 23.424& 61.613\\ 58.411& -10.213& 13.331\\ 0.333& 33.883& 51.000\end{array}\right]=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]·\left[\begin{array}{c}-696.755\\ -460.340\\ -281.990\end{array}\right] \end{gathered}$$

(20)

$$\begin{gathered} X=M^{-1}·k \\ \left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}4.849& -4.453& -4.695\\ 14.831& -13.671& -14.344\\ -9.885& 9.112& 9.580\end{array}\right]·\left[\begin{array}{c}-696.755\\ -460.340\\ -281.990\end{array}\right] \\ \left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}-5.217\\ 4.317\\ -8.363\end{array}\right] \end{gathered}$$

(21)

• The XYZ coordinates are recovered by adding the coordinates of CG to the estimated coordinates.
• The estimated coordinates differ from the check coordinates by $\left(1.757, 5.356, -3.573\right)$, which is 6.674 m in error (3-d), slightly worse than using the XYZ coordinates directly.
• The matrix M is identical for both “absolute” and these relative coordinates because M is formed from the differences in coordinates.
• The k vector’s values are much smaller for the relative coordinates because the distances from the stations to the local origin (CG) are far shorter than the distances of the XYZ stations to their origin (Earth’s center of mass). These smaller values will generally lead to better numerical precision, which should have a good influence on improving the estimates, but that was not the case here.
• The XYZ coordinates yield terrible results because, although these are geometrically 3-d coordinates, the stations are nearly coplanar, topologically 2-d. As discussed above, this produces very poor strength-of-figure for the vertical coordinate, but there is no notion of the vertical in an XYZ coordinate system so the inherent weakness in the vertical direction bleeds into all three coordinates.

3.

Estimate station U’s coordinates using topocentric Cartesian ENU coordinates using station CG as the ENU coordinate system’s origin. See the e, n, u columns in Table 5.

$$\begin{gathered} M=X·k \\ \left[\begin{array}{ccc}45.114& 72.406& 0.741\\ 58.876& 15.038& 1.155\\ -9.446& 60.497& -0.278\end{array}\right]=\left[\begin{array}{c}e\\ n\\ u\end{array}\right]·\left[\begin{array}{c}-696.755\\ -460.340\\ -281.990\end{array}\right] \end{gathered}$$

(22)

$$\begin{gathered} X=M^{-1}·k \\ \left[\begin{array}{c}e\\ n\\ u\end{array}\right]=\left[\begin{array}{ccc}0.369& -0.324& -0.362\\ -0.027& 0.028& 0.042\\ -18.468& 17.018& 17.873\end{array}\right]·\left[\begin{array}{c}-696.755\\ -460.340\\ -281.990\end{array}\right] \\ \left[\begin{array}{c}e\\ n\\ u\end{array}\right]=\left[\begin{array}{c}-6.240\\ -5.666\\ -6.690\end{array}\right] \end{gathered}$$

(23)

• The errors for these coordinates are $\left(0.139,-0.012,-6.672\right)$, which is a dramatic improvement for the horizontal coordinates.
• Almost all the error is in the Up coordinate, which validates the notion that it is the vertical coordinate with poor strength-of-figure.
• The k vector is the same as the localized XYZ coordinates because (a) both coordinate systems have the same origin (station CG) and (b) ENU distances equal XYZ distances.

4.

Estimate station U’s coordinates using horizontal distances and only the East and North coordinates.

$$\begin{gathered} M=X·k \\ \left[\begin{array}{cc}45.114& 72.406\\ 58.876& 15.038\\ -9.446& 60.497\end{array}\right]·\left[\begin{array}{c}e\\ n\end{array}\right]=\left[\begin{array}{c}-696.702\\ -460.344\end{array}\right] \end{gathered}$$

(24)

$$\begin{gathered} XX={\left(M^{-1}M\right)}^{-1}{M}^T·k \\ \left[\begin{array}{c}e\\ n\end{array}\right]=\left[\begin{array}{cc}0.000239& -9.4{\mathrm{e}}^{-5}\\ -9.4{\mathrm{e}}^{-5}& 0.000146\end{array}\right]·\left[\begin{array}{c}-696.702\\ -460.344\end{array}\right] \\ \left[\begin{array}{c}e\\ n\end{array}\right]=\left[\begin{array}{c}-6.372\\ -5.654\end{array}\right] \end{gathered}$$

(25)

• The errors for these coordinates are $\left(0.0071, 0.0002\right)$, which agrees with the check values within their uncertainty.
• The numerical instability due to the ill-conditioned vertical coordinate has been removed so the estimates are very good. Notice that these EN coordinates have been estimated better than their ENU counterparts, because the deleterious effect of the Up coordinate has no effect here.
• Notice that M is almost an identity matrix, which means that k has almost solved the problem itself.

8. Discussion and Conclusions

A multilateration method for terrestrial surveying was presented using differenced observation equations, which eliminated the quadratic terms in the unknown coordinates and, thus, linearized the system to be solved. Consequently, the position can be determined with a pseudo-inverse in the usual way, an operation that is well within reach of any spreadsheet’s computational capabilities, and still provides full statistical rigor. The linearization does have a cost: using differenced observations means one additional observation set than is required by the non-linear equivalent (four instead of three).

Understanding the geometrical layout of the survey is difficult when looking at the XYZ coordinates because they impart no notion of cardinal directionality or the vertical. The ENU coordinates readily reveal that the stations are nearly at the same height and occupy the four quadrants around the check station U. Slope distances can be used with XYZ and ENU coordinates alike, and slope distances are largely unaffected by atmospheric refraction and vertical-angle pointing errors that affect horizontal distances. However, as the examples show, poor strength-of-figure can completely overwhelm these benefits when the control stations are nearly coplanar.

Standard practice is to observe all distances at least twice in independent observations. A typical protocol would be to observe in different setups, not merely observing in the direct and inverted positions of the telescope.

$M^{T}M$ is invertible, in theory, so long as the control stations are not coplanar, but $M^{T}M$ becomes ill conditioned if the stations are bunched together or if they are nearly coplanar. If $M^{T}M$ is ill conditioned, all three coordinates will have less accurate estimations because the estimates are correlated. However, as demonstrated in the example, the Up-coordinate can be especially erroneous, but perhaps sometimes not so much as to be blatantly incorrect, which is a very insidious situation. In contrast, there is no numerical stability concerns if solving for just the horizontal coordinates, provided that the control stations surround the unknown station. The best evidence for whether the Up-coordinate is trustworthy is, unsurprisingly, its standard deviation (and common sense). The covariance matrix for the above ENU example works out to be ${10}^{-6}\left[\begin{array}{ccc}2.5& -1.4& 6.8\\ -1.4& 1.1& -17\\ 6.8& -17& 769\end{array}\right]$ so the standard deviations of the E-, N-, and U-coordinates are 1.6 mm, 1.1 mm, and 27.7 mm. As with GNSS positioning, the horizontal coordinates should have similar standard deviations and the Up-coordinate’s standard deviation should be larger. However, for GNSS, the Up-coordinate is expected to be around, say, three times larger, and here, the Up-coordinate is around 20 times larger. This is because, for GNSS, one expects there to be SVs spread across the whole sky at a broad span of zenith angles, whereas for terrestrial surveying one expects the control stations to be nearly at the same height, creating a scenario equivalent for GNSS positioning in which all the SVs are within, say, $5°$ in elevation angle from one another. Thus, in general, the Up-coordinate cannot be expected to have as good precision as the horizontal coordinates in most cases.

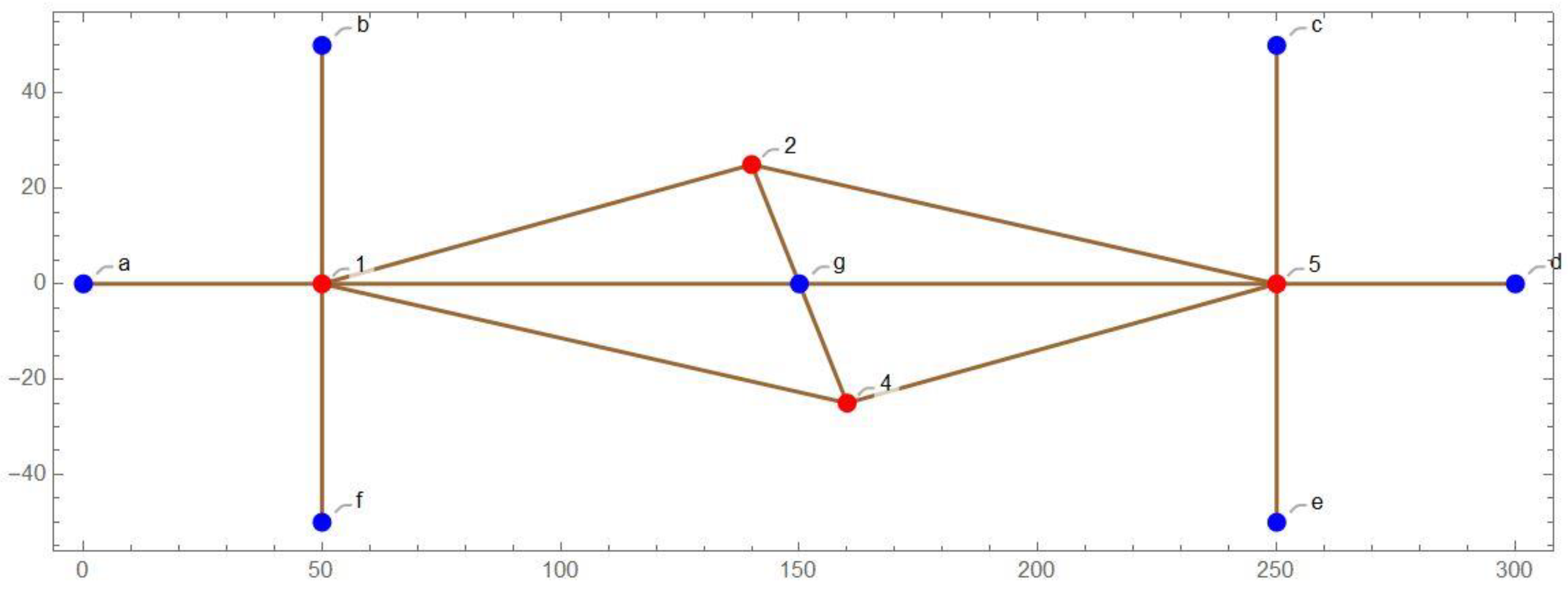
There is no limit, per se, to the number of stations that can be positioned simultaneously with this method, but every unknown station must tie to enough control stations to be positioned individually. In contrast, a typical traverse will run through “interior” stations that have no, or insufficient, direct ties to control stations, such as stations 2 and 4 in Figure 1. That is not allowed here. The reason is in the M matrix: if any of M’s elements (coordinate differences) are not unknown a priori, then M will contain variable elements, and the system becomes nonlinear. This is true for k, too: k will not be a vector of numbers only. This is not the case when solving the multilateration problem with a nonlinear system. The nonlinear solution requires a priori estimates for all the unknown coordinates, so the Jacobian matrix’s terms contain only numbers and, thus, the nonlinearity vanishes in the calculation. Nevertheless, the traverse in Figure 1 can be solved in a bootstrapping fashion by positioning stations 1 and 5, and then using those to control 2 and 4. However, if station g were unknown, nothing could be done.