A Laboratory Set-Up for Hands-On Learning of Heat Transfer Principles in Aerospace Engineering Education

Abstract

This paper describes a laboratory set-up designed to support hands-on learning of heat transfer principles in aerospace engineering education. Developed within the framework of experiential and project-based learning, the set-up enables students to experimentally characterize the convective coefficient of a cooling fan and the thermo-optical properties of aluminum plates with different surface coatings, specifically their absorptivity and emissivity. A custom-built, LED-based radiation source (the ESAT Sun simulator) and a calibrated temperature acquisition system are used to emulate and monitor radiative heating under controlled conditions. Simplified physical models are developed for both the ESAT Sun simulator and the plates that capture the dominant thermal dynamics via first-order energy balances. The laboratory workflow includes real-time data acquisition, curve fitting, and thermal model inversion to estimate the convective and thermo-optical coefficients. The results demonstrate good agreement between the model predictions and observed temperatures, which supports the suitability of the set-up for education. The proposed activities can strengthen the student’s understanding of convective and radiative heat transport in aerospace applications while also fostering skills in data analysis, physical and numerical reasoning, and system-level thinking. Opportunities exist to expand the material library, refine the physical modeling, and evaluate the long-term pedagogical impact of the educational set-up described here.

1. Introduction

In aerospace engineering education, conveying the complexity of spacecraft and other real-world systems requires more than theoretical exposition. Practical, hands-on learning has become a cornerstone of modern curricula [1,2,3], allowing students to directly engage with the behavior of the physical systems they study. From the early introduction of multifunctional tutorial platforms such as TU Berlin’s keyboard-based simulator [4] to contemporary design–build–launch projects [5], educational methodologies have increasingly prioritized experiential formats. These initiatives not only foster technical understanding, but also creativity, collaboration, and critical systems thinking.

A key pedagogical shift supporting this transformation is the integration of active learning methods, such as project-based learning (PBL) [6,7], challenge-based learning (CBL) [8,9,10,11,12,13], and research-based learning (RBL) [14,15,16]. These methods align with the CDIO framework [17]—Conceive, Design, Implement, and Operate—which is especially well suited for aerospace contexts [18]. Students exposed to these methods exhibit stronger problem solving skills and better motivation [19]. At the Universidad Politécnica de Madrid (UPM), this has led to initiatives such as participation in the ESA Concurrent Engineering Challenge [20], in which students work on the preliminary design of a space mission using industry-standard tools, developing both technical and team-based problem solving skills.

Additional examples of hands-on projects include water rockets [21], model rockets [22], and the low-cost plastic CubeSat [23], which all represent low-barrier entry points into space system design. At UPM, the development of the Educational Satellite (ESAT) platform [24]—a fully modular educational CubeSat—was a significant step forward in this area. The ESAT is used in final-year aerospace courses, bachelor’s and Master’s theses, and ESA Academy training programs. It features separable subsystems (electrical power, communications, attitude determination and control, payload, and on-board data handling) and a customizable Arduino-based software stack [25]. Combined with ground support equipment and ground segment tools, students benefit by participating in realistic satellite design, integrating sensors, testing attitude control algorithms, and simulating space operations [26]. In recent years, the ESAT platform has helped to develop several RBL projects, including three-axis control and custom testbeds, such as Helmholtz cages and air-bearing tables, which enhance the realism of the set-up. It is currently used for space-related research in the context of modern control, serving as a low-cost platform for ground laboratory testing [26,27,28].

In the context of space system design, thermal control is a topic that is often perceived by students as abstract. Thus, the combination of active learning methods and hands-on learning could be very useful from an educational point of view. Beginning with a student initiative in 2016, the “Thermocapillary Effects in Phase change materials in Microgravity” (TEPiM) experiment [29,30,31] introduced a hands-on learning experience based on RBL, with a focus on thermal and fluid physics research, and system design in the context of a parabolic flight experiment. The success of this initiative led directly to the “Marangoni in Phase Change Materials” (MarPCM) project [32,33], which is organized around the preparation of an experiment (approved by ESA and NASA) for execution on the International Space Station (ISS). These projects investigate the heat transfer enhancement in phase change materials (PCMs) that can be achieved by thermocapillary convection, as well as the relevance of this strategy for the future of passive thermal control systems in orbit; see [34,35,36] and the references therein. These educational experiences have already supported several bachelor’s and Master’s degree projects, combining numerical simulation, design and manufacturing, and experimental testing and validation on ground and in parabolic flights. Their contribution is essential to the (future) operation of the MarPCM experiment on board the ISS and a good argument for integrating undergraduate education with cutting-edge research [31]. In line with this, more recent studies have looked at the integration of PCMs in the context of lunar habitats [37,38], involving students in the development of a simple ground set-up to evaluate PCM performance [39].

Projects like these illustrate the impact of hands-on, active learning in teaching complex topics such as spacecraft thermal design [40]. Through these integrated experiences, students acquire not only conceptual knowledge, but also intuition about practical engineering, research skills, and system-level awareness. All of these are essential for modern aerospace professionals [41,42,43].

The present work is a further step in this direction. We introduce a low-cost, modular laboratory set-up designed to enhance hands-on learning of heat transfer principles in aerospace engineering education. The platform allows students to investigate the thermal behavior of materials experiencing radiative (and convective) heat exchange in conditions that simulate those relevant to spacecraft thermal control. By combining physical modeling, numerical fitting, and experimental data acquisition, students are guided through the process of estimating the convective properties of a cooling fan and the thermo-optical properties of coated aluminum plates. The manuscript is structured as follows. In Section 2 and Section 3, we describe the experimental set-up as well as the concept and planning of the hands-on laboratory session. In Section 4, the physical models used to interpret and process experimental data are presented in detail. The results are given in Section 5, including the expected outcome of the session from the student perspective. Conclusions and lines for future work are described in Section 6.

2. Experimental Set-Up

The core of the experiment is a set of three square aluminum plates with an area of 50 × 50 mm² and a thickness of 1 mm, coated with different paints. The plates are subjected to visible radiation, which is produced by the ESAT Sun simulator, a powerful LED light source commercialized by Theia Space [24]. Variable lighting conditions are achieved by placing the plates at different distances with respect to the ESAT Sun simulator. These primary elements of the set-up are mounted on a white pad that includes marks and a ruler to precisely control their relative positions. Thermocouples are installed on the rear surface of the plates to monitor their temperature and also in selected locations of the set-up to monitor the temperature of the surrounding air and laboratory. These thermocouples are connected to an analog-to-digital converter (ADC) that interfaces with a laptop, where the temperature data are stored.

The complete set-up is illustrated in Figure 1, while a more detailed description of each element is given below.

2.1. Aluminum Plates

As noted above, these plates are central to the experiment. They have a thickness of 1 mm and a surface area of 50 × 50 mm².

The plates can be coated to select the thermo-optical properties of the exposed surfaces. In the set-up of Figure 1, one plate is left in the condition it was received from the manufacturer, while the other two plates are painted black and white, respectively, using spray paints suitable for high-temperature applications. The thermo-optical properties of these surfaces are unknown beforehand, and determining them is one of the main objectives of the student laboratory session.

2.2. ESAT Sun Simulator

The ESAT Sun simulator is an in-house component, commercialized by Theia Space [24], designed to simulate the (cool white) light of the Sun. It is constructed from an LED matrix, a fan and aluminum cooling system, a conical lens, and a 3D-printed PLA front structure. The characteristics described below are used in later sections of the manuscript to model the radiative interaction between the LED matrix and the plates.

The LED matrix has a power consumption of 100 W and emits 13,000–14,000 lm of light flux over the cool white spectrum, with a correlated color temperature (CCT) of ∼6000 K. The conical lens redirects this light into a cone with semiangle $\theta ={30}^{\circ }$. The LED matrix and lens are protected by the printed PLA cover.

The ESAT Sun simulator is mounted on a dedicated 3D-printed support that keeps the axis of the emitting cone oriented in the correct direction. This support is aligned with a ruler to allow for precise positioning and alignment of the plates with respect to the light source. From this ruler to the LED matrix, there is an offset distance of $d_0\simeq 2.5$ cm.

2.3. Thermocouples

Type K welded exposed junction thermocouples are used to measure the plate and laboratory temperatures. These thermocouples have a resolution of 0.01 °C for temperatures between 60 °C and 350 °C. The exposed junction allows a fast response of less than 1 s for thermocouple measurements.

2.4. Analog-to-Digital Converter and Laptop

The thermocouples are connected to a Pico Technologies TC-08 ADC [44]. The TC-08 is connected via USB to a laptop, which provides power and data links. The temperature readings at 1 Hz are stored using the PicoLog application (version 6.2.13), which allows real-time data storage and visualization for up to 8 channels.

The raw temperature measurements have a precision of approximately 1 °C. To improve this, the thermocouples are calibrated over the temperature range 20 °C to 70 °C using the Fluke Calibration 9102S portable oven by DryWell. This oven provides a reference temperature value with a resolution of 0.1 °C. The results of the calibration, comparing reference and measured values, are introduced via software in the PicoLog application.

3. Concept and Planning of the Laboratory Session

The hands-on learning experience described here is conceived for the benefit of Master’s students enrolled in the subject “Design and Certification of Space Vehicles” (Diseño, Cálculo y Certificación de Vehículos Espaciales), which is part of the first-year program for the Máster Universitario en Ingeniería Aerospacial at UPM.

The expected duration of the session is three hours, with twelve students working in groups of two; a total of 8–10 sessions will be offered to provide sessions for all students enrolled in the subject. During the session, each group will receive safety equipment [45] including nitrile gloves and sunglasses, and detailed test procedures for each step described in the following. Once completed, each group will be asked to submit a report and supporting files for evaluation; this technical report is similar to those used in industry. The reports will be used to assess student performance and knowledge acquisition and will constitute a significant part of the grade for the subject. To evaluate the educational impact, students will fill out a pre–post survey (or similar) about their own perception of the knowledge acquired and a questionnaire to evaluate the hands-on experience itself. Similar evaluations using the “Motivational Diagnosis Instrument for Engineering Education” (MDI-EE) have been recently performed [2] in the context of PBL and the 2018 ESA Concurrent Design Challenge [20].

Considering the time constraint of the laboratory session, the convective coefficient of the cooling fan system and the absorptivity and emissivity of the plates will be estimated by performing the experimental tests outlined in the following high-level steps.

• (30 min) Introduction and preparation of set-up:
  This includes the connection of thermocouples to the associated channels of the TC-08 ADC and introduction of the associated calibration. Thermocouple readings will be calibrated beforehand so that students simply need to enter the appropriate correction in the PicoLog software.
• (30 min) Thermal characterization of ESAT Sun simulator:
  Thermocouples will be used to measure the temperature evolution of the ESAT Sun simulator and inlet air of the cooling fan. These data allow estimation of the steady-state temperature of the LED and the heat transfer coefficient that characterizes the convective cooling of the LED–fan system. In the remainder of the session, the characteristic steady-state temperature of the light source will be used as a reference to monitor its adequate functioning.
• (20 min) Radiative heating of the plates at minimum distance from ESAT Sun simulator:
  Experiments will start by heating the aluminum plates to their maximum expected temperature. In this configuration, the LED–plate radiative interaction is maximized, and the absorptivity can be estimated as well as an initial guess for the emissivity.
• (60 min) Successive experiments at increasing LED–plate distance:
  The distance between the ESAT Sun simulator and the plates will be increased, and the plate temperature will be allowed to reach a steady state each time. The evolution of the temperature across all experiments will allow for an improved estimate of the emissivity of the plates.
• (30 min) Data processing and estimate of thermo-optical properties:
  Once completed, all data will be processed to obtain estimates of the heat transfer coefficient of the cooling fan and the thermo-optical properties of the plates.
• (10 min) Wrap-up and concluding remarks.

We emphasize that the primary purpose of the laboratory experiment described here is pedagogical and that simplifications and approximations are necessary in order to keep this experiment low-cost and feasible for a three-hour session in a typical classroom environment. If performed correctly, students will obtain reasonable estimates of key thermo-optical properties, but the values they find will not have the level of accuracy or reproducibility [46,47] of a more rigorous and controlled experimental set-up. Aside from the theoretical simplifications described below, the laboratory room at UPM has no humidity or (accurate) temperature control. Temperatures will vary depending on the time of the laboratory session and the ambient conditions in the building. While the temperature will be measured so that this variation is taken into account at some level, there is no way, for example, to control for humidity or the convection generated by the movement of the students performing the activity.

4. Physical Modeling

This section describes the physical models used to interpret (and process) the results of the laboratory tests.

4.1. Simplified Model of the ESAT Sun Simulator

We consider a single-node model representing the temperature T of the ESAT Sun simulator [48]. At leading order, the temporal evolution of T is governed by the balance between the heat dissipated by the LED matrix and the heat evacuated by the fan-driven air flow between the aluminum fins of the dissipator (in contact with the matrix); see Figure 2. Note that the effects of natural convection and conduction through the surrounding air are neglected.

If the power consumption of the light is P and its light-emitting efficiency is $\eta$, then the fraction of power dissipated can be approximated as

$$\begin{array}{c}\hfill P_{\mathrm{dis}}=P(1-\eta ).\end{array}$$

(1)

This is discussed in more detail in Section 4.3.

The effect of the cooling fan is modeled using Newton’s law of cooling,

$$\begin{array}{c}\hfill q=h_{\mathrm{SS}}{A}_{\mathrm{eff}}\left(T-T_{\mathrm{inlet}}\right),\end{array}$$

(2)

where $h_{\mathrm{SS}}$ is the convective heat transfer coefficient, which, in general, depends on T and the temperature of the air at the fan inlet $T_{\mathrm{inlet}}$ via the film temperature [49]. Here, $A_{\mathrm{eff}}$ refers to the effective contact area between the aluminum fins and the air stream, which can be approximated by considering the number of fins N, their width W, and depth D:

$$\begin{array}{c}\hfill A_{\mathrm{eff}}\simeq 2NWD,\end{array}$$

(3)

where the factor of 2 accounts for the upper and lower surfaces of each fin; see Figure 2.

Under these assumptions, the energy balance is

$$\begin{array}{c}\hfill \left(m{c}_p\right){\displaystyle \frac{dT}{dt}}=P_{\mathrm{dis}}-h_{\mathrm{SS}}{A}_{\mathrm{eff}}(T-T_{\mathrm{inlet}}),\end{array}$$

(4)

where $\left(m{c}_p\right)$ is the effective thermal inertia of the LED system.

The equilibrium temperature $T_{\mathrm{eq}}$, at which $P_{\mathrm{dis}}$ is balanced by the heat extracted by the cooling air, can be easily obtained from the steady solution of Equation (4):

$$\begin{array}{c}\hfill T_{\mathrm{eq}}=T_{\mathrm{inlet}}+{\displaystyle \frac{P_{\mathrm{dis}}}{h_{\mathrm{SS}}{A}_{\mathrm{eff}}}}.\end{array}$$

(5)

Note that this simple expression reveals much of the underlying physics, predicting a linear increase in $T_{\mathrm{eq}}$ with increasing $P_{\mathrm{dis}}$ and an inverse relationship to $h_{\mathrm{SS}}{A}_{\mathrm{eff}}$.

One can use $T_{\mathrm{eq}}$ to describe the evolution of T from any initial value $T_0$ by writing:

$$\begin{array}{c}\hfill T=T_{\mathrm{eq}}(1+\mathrm{\Theta }),\end{array}$$

(6)

where $\mathrm{\Theta }$ is a dimensionless temperature. With this definition, the energy balance becomes

$$\begin{array}{c}\hfill {\displaystyle \frac{d\mathrm{\Theta }}{d\tau }}+\mathrm{\Theta }=0,\end{array}$$

(7)

where $\tau$ is the dimensionless time measured relative to the characteristic timescale $t_{\mathrm{SS}}=\left(m{c}_p\right)/\left(h_{\mathrm{SS}}{A}_{\mathrm{eff}}\right)$. Note that this assumes that $h_{\mathrm{SS}}$ depends only weakly on T and may be considered constant. Again, there is a straightforward interpretation of $t_{\mathrm{SS}}$, which increases with thermal inertia and decreases with the convective cooling factor $h_{\mathrm{SS}}{A}_{\mathrm{eff}}$.

The general solution of Equation (7) is

$$\begin{array}{c}\hfill \mathrm{\Theta }={\mathrm{\Theta }}_0{e}^{-\tau },\end{array}$$

(8)

and thus

$$\begin{array}{c}\hfill T=\left(T_{\mathrm{inlet}}+{\displaystyle \frac{P_{\mathrm{dis}}}{h_{\mathrm{SS}}{A}_{\mathrm{eff}}}}\right)\left(1+{\mathrm{\Theta }}_0{e}^{-t/t_{\mathrm{SS}}}\right).\end{array}$$

(9)

Taking into account the initial condition $T_0$, we have

$$\begin{array}{c}\hfill T=T_{\mathrm{inlet}}+{\displaystyle \frac{P_{\mathrm{dis}}}{h_{\mathrm{SS}}{A}_{\mathrm{eff}}}}+\left[T_0-\left(T_{\mathrm{inlet}}+{\displaystyle \frac{P_{\mathrm{dis}}}{h_{\mathrm{SS}}{A}_{\mathrm{eff}}}}\right)\right]e^{-t/t_{\mathrm{SS}}},\end{array}$$

(10)

or, after subtracting $T_0$ from both sides to consider the deviation from this initial condition, $\Delta T=T-T_0$:

$$\begin{array}{c}\hfill \Delta T=\left(T_{\mathrm{inlet}}+{\displaystyle \frac{P_{\mathrm{dis}}}{h_{\mathrm{SS}}{A}_{\mathrm{eff}}}}-T_0\right)\left(1-e^{-t/t_{\mathrm{SS}}}\right).\end{array}$$

(11)

In the laboratory set-up, $T_{\mathrm{inlet}}\simeq T_0$, which is approximately equal to the laboratory temperature $T_{\mathrm{lab}}$. This simplification yields the expression

$$\begin{array}{c}\hfill \Delta T={\displaystyle \frac{P_{\mathrm{dis}}}{h_{\mathrm{SS}}{A}_{\mathrm{eff}}}}\left(1-e^{-t/t_{\mathrm{SS}}}\right).\end{array}$$

(12)

Thus, experiments measuring the temperature of the ESAT Sun simulator and the inlet air (or the lab) can be performed, and the data can be fitted to the exponential relaxation function

$$\begin{array}{c}\hfill \Delta T=\Delta T_{\mathrm{eq}}\left(1-e^{-(t-t_0)/t_{\mathrm{c}}}\right),\end{array}$$

(13)

where $t_0$ is an offset for the fit (if appropriate) and $t_{\mathrm{c}}$ is the relaxation time constant, which is equal to $t_{\mathrm{SS}}$ for the ESAT Sun simulator. The fitting parameters $\Delta T_{\mathrm{eq}}$ and $t_{\mathrm{SS}}$ can then be used to estimate $h_{\mathrm{SS}}$ and $\left(m{c}_p\right)$. From $\Delta T_{\mathrm{eq}}$, it follows that

$$h_{\mathrm{SS}}={\displaystyle \frac{P_{\mathrm{dis}}}{\Delta T_{\mathrm{eq}}{A}_{\mathrm{eff}}}},$$

(14)

while from $t_{\mathrm{SS}}$, we have

$$\left(m{c}_p\right)={\displaystyle \frac{P_{\mathrm{dis}}{t}_{\mathrm{SS}}}{\Delta T_{\mathrm{eq}}}}.$$

(15)

Note that the thermal inertia increases with decreasing $\Delta T_{\mathrm{eq}}/t_{\mathrm{SS}}$, a ratio that represents the initial rate of change of T at $t=0$. Physically, this means that the faster the LED system heats up, the smaller its thermal inertia, and vice versa.

Finally, the analysis can be completed by looking at the specifications of the fan. In particular, knowing its flow rate Q and radius R, one can estimate the air velocity V at the inlet as

$$V_{\mathrm{inlet}}={\displaystyle \frac{Q}{\pi R^2}},$$

(16)

and, in accordance with mass conservation, the velocity within the aluminum dissipator is on the order of

$$V={\displaystyle \frac{Q}{2NW{e}_{\mathrm{fin}}}},$$

(17)

where $e_{\mathrm{fin}}$ refers to the air gap between fins.

This allows estimation of the associated Reynolds number,

$$\mathrm{Re}={\displaystyle \frac{V{l}_c}{\nu }},$$

(18)

where $\nu$ is the kinematic viscosity of air and $l_c\sim D/2$ is the characteristic length of the flow.

Note that the heat transfer coefficient for a set of fins is, in reality, a complex parameter influenced by multiple factors including fluid velocity, fin shape and spacing, flow channel length, and fluid properties, and it is generally determined by Re and the Nusselt number (Nu) through empirical correlations [50]. For simplicity, we use here an approximate yet illustrative relationship applicable in the case of a flat horizontal plate. Assuming laminar flow, the heat transfer coefficient for forced convection $h_{\mathrm{SS}}$ can be estimated [49] using

$$h_{\mathrm{SS}}\simeq {\displaystyle \frac{0.664{\mathrm{Re}}^{0.5}{\mathrm{Pr}}^{0.33}k}{l_c}},$$

(19)

and compared with the results obtained from Equation (14). Here, $\mathrm{Pr}$ and k are the Prandtl number and the thermal conductivity of air, respectively, evaluated at the film temperature $T_f=(T+T_{\mathrm{inlet}})/2$ [48]. We note that the expected variation of $T_f$ is on the order of 10 °C, which would lead to small variations in $\nu$ and k—on the order of 6% and 3%, respectively.

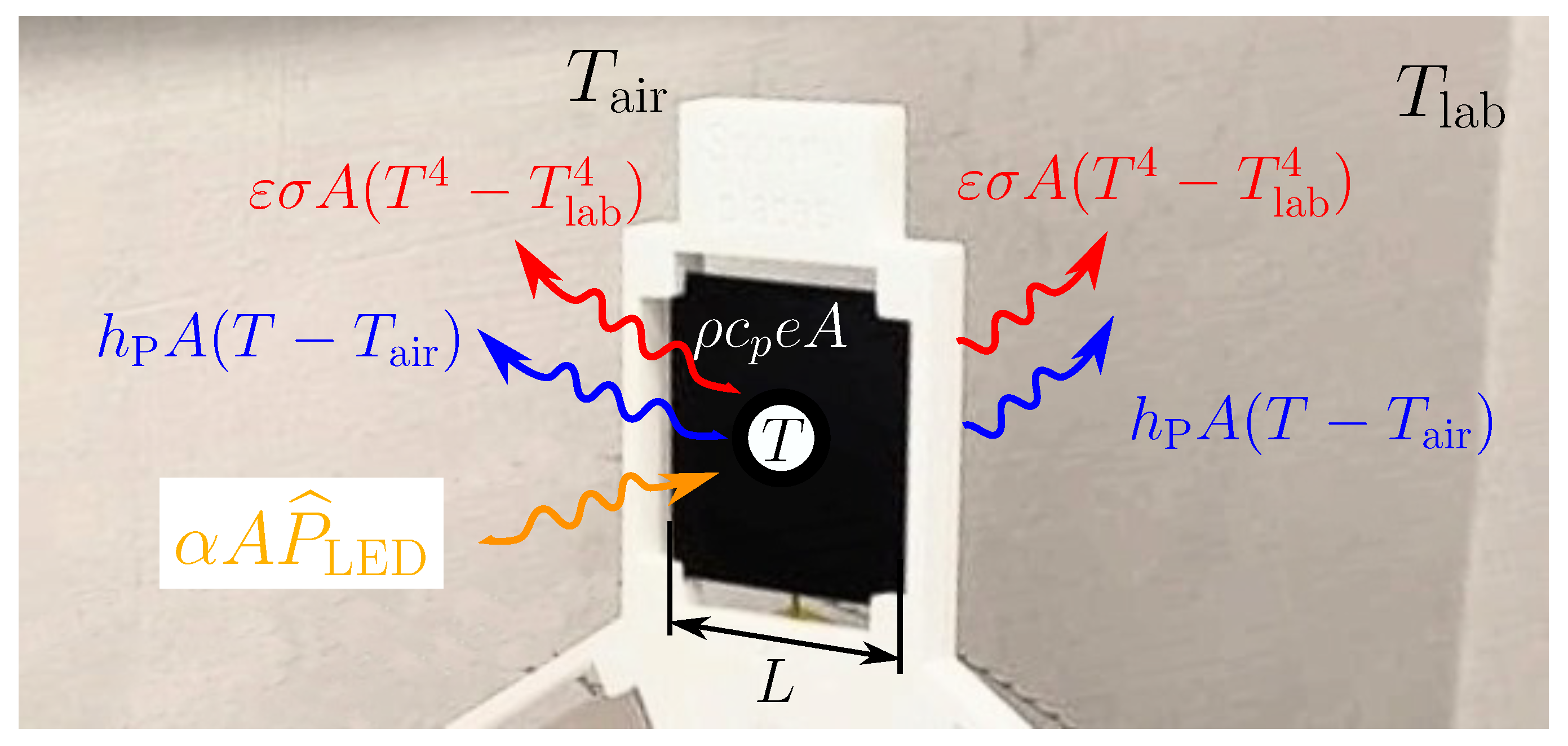
4.2. Simplified Model for the Plates Set-Up

Again, we consider a single-node model (see Figure 3), this time representing the temperature T of one plate; the validity of this simplified model will be justified in Section 5. At leading order, we can express the heat exchanged between the plate and its surroundings by summing the following terms [48]:

–

Exchange with the ESAT Sun simulator:

The ESAT Sun simulator emits radiation in the visible spectrum (with a correlated color temperature of ∼6000 K; see Section 4.3) so that the quantity of heat absorbed by the plate is

$$Q_{\mathrm{LED}}=\alpha A{\widehat{P}}_{\mathrm{LED}},$$

(20)

where $\alpha$ is the absorptivity, $A=L^2$ is the plate area, and ${\widehat{P}}_{\mathrm{LED}}$ is the average power per surface area received by the plate. The modeling of ${\widehat{P}}_{\mathrm{LED}}$ is described in Section 4.3.

–

Radiative exchange with the laboratory:

The plate, at temperature T, emits and receives radiation from its surroundings (i.e., the laboratory) primarily along its front and rear surfaces of area A. The difference in heat transferred (to the plate) is given by

$$Q_{\mathrm{rad}}=-2\epsilon \sigma A\left(T^4-T_{\mathrm{lab}}^4\right),$$

(21)

where $\epsilon$ is the infrared emissivity, $\sigma =5.67\times {10}^{-8}$ W/(m² K⁴) is the Stefan–Boltzmann constant, $T_{\mathrm{lab}}$ is the temperature of the laboratory, and the factor of 2 accounts for the front and rear plate surfaces.

Note that despite the fact that the plate is treated as a gray body with $\epsilon <1$, the radiative interaction with the laboratory can be simplified to that occurring between ideal black bodies. The surface resistance of the laboratory $R_{\mathrm{lab}}\propto A_{\mathrm{lab}}^{-1}$ is considered negligible compared with that of the plate since $A_{\mathrm{lab}}\gg A$.

–

Convective exchange with the surrounding air:

As in the case of the ESAT Sun simulator, the plate exchanges heat with the surrounding air along its front and rear surfaces. Using Newton’s law of cooling, this heat can be written as

$$Q_{\mathrm{conv}}=-2h_{\mathrm{P}}A\left(T-T_{\mathrm{air}}\right),$$

(22)

where $h_{\mathrm{P}}$ is the convective heat transfer coefficient and $T_{\mathrm{air}}$ is the temperature of the air. In Section 4.4, we describe the estimate of $h_{\mathrm{P}}$, based on empirical correlations. These correlations already account for the conductive heat exchange with the surrounding air.

Note that the effect of the air flow generated by the LED fan on the air surrounding the plates is neglected. This is justified by the fact that fan-driven convection flow exits the dissipator laterally, i.e., horizontally and parallel to the plane of the plates. Furthermore, the minimum distance between the plates and the ESAT light source is $d_{\min }=12$ cm (see Section 4.3), while the characteristic viscous length is $l_{\nu }=\nu /V$. For the air flow in the fan, we estimate $l_{\nu }\sim 5\times {10}^{-4}$ cm, which is several orders of magnitude smaller than $d_{\min }$; see Section 2.

4.2.1. Energy Balance and Equilibrium Temperature of the Plate

The energy balance equation for the plate is

$$\left(\rho c_{p}e\right){\displaystyle \frac{dT}{dt}}=\alpha {\widehat{P}}_{\mathrm{LED}}-2\epsilon \sigma \left(T^4-T_{\mathrm{lab}}^4\right)-2h_{\mathrm{P}}\left(T-T_{\mathrm{air}}\right),$$

(23)

where $\rho$, $c_p$, and e are the density, heat capacity, and thickness of the aluminum plate, respectively.

The equilibrium temperature $T_{\mathrm{eq}}$ at which the net energy exchange is zero can be obtained from the steady solution of Equation (23). Note that $T_{\mathrm{eq}}$ cannot be obtained explicitly from this nonlinear equation; numerical or perturbation methods are needed to determine it.

However, given a known value of $T_{\mathrm{eq}}$ for the plate, we can expand the solution of Equation (23) around this by writing $T=T_{\mathrm{eq}}(1+\mathrm{\Theta })$:

$$\begin{array}{cc}\hfill \left(\rho c_{p}e\right)T_{\mathrm{eq}}{\displaystyle \frac{d\mathrm{\Theta }}{dt}}=\alpha {\widehat{P}}_{\mathrm{LED}}-2\epsilon \sigma \left[T_{\mathrm{eq}}^4{(1+\mathrm{\Theta })}^4-T_{\mathrm{lab}}^4\right]-& 2h_{\mathrm{P}}\left[T_{\mathrm{eq}}(1+\mathrm{\Theta })-T_{\mathrm{air}}\right],\hfill \end{array}$$

(24)

which, keeping only terms at linear order, becomes

$$\begin{array}{c}\hfill {\displaystyle \frac{d\mathrm{\Theta }}{d\tau }}=-{\displaystyle \frac{(8\epsilon \sigma T_{\mathrm{eq}}^3+2h_{\mathrm{P}})t_{\mathrm{P}}}{\left(\rho c_{p}e\right)}}\mathrm{\Theta },\end{array}$$

(25)

where $t_{\mathrm{P}}$ is a characteristic time used to define the (new) dimensionless time $\tau$ for the plates. As in Section 4.1, $h_{\mathrm{P}}$ is assumed to be (approximately) constant, and we take $t_{\mathrm{P}}=\left(\rho c_{p}e\right)/(8\epsilon \sigma T_{\mathrm{eq}}^3+2h_{\mathrm{P}})$ to reduce Equation (25) to its canonical form. The general solution for $\Delta T=T-T_0$, where $T_0$ is the initial temperature of the plate, is thus

$$\begin{array}{c}\hfill \Delta T=(T_{\mathrm{eq}}-T_0)\left(1-e^{-t/t_{\mathrm{P}}}\right),\end{array}$$

(26)

which gives a good approximation of the temperature evolution of the plate when $T_0$ is close to $T_{\mathrm{eq}}$.

In practice, it can be expected that the laboratory set-up will depart from the initial condition $T_0\simeq T_{\mathrm{lab}}\simeq T_{\mathrm{air}}$ by tens of degrees, so that $\Delta T$ is within the range of validity for this linearized description.

As in the case of the ESAT Sun simulator, experiments measuring the temperature of the plate T, and that of the air and the laboratory, can be fitted to Equation (13) with $\Delta T_{\mathrm{eq}}$ and $t_{\mathrm{c}}$ ($t_{\mathrm{P}}$ for the plate) then being used to estimate the equilibrium temperature and thermo-optical properties of the plate. This is described in detail below.

4.2.2. Estimate of Thermo-Optical Properties

At early times when $t\ll t_{\mathrm{P}}$, $T\sim T_{\mathrm{lab}}$, Equation (23) can be reduced to

$$\left(\rho c_{p}e\right){\displaystyle \frac{dT}{dt}}=\alpha {\widehat{P}}_{\mathrm{LED}}+\dots ,$$

(27)

which indicates that the initial temperature increase of the plate is driven by the absorption of radiation emitted by the LED light source.

In experiments, however, this initial phase may be affected by three-dimensional effects, transient dynamics associated with switching on the LED, the time delay of the thermocouples, etc., which are not accounted for in the present model. For data processing, it is thus convenient to mitigate these factors by using a nonzero time offset $t_0\ll t_{\mathrm{P}}$ to obtain:

$$T=T_0+\Delta T_{\mathrm{eq}}\left(1-e^{-(t-t_0)/t_{\mathrm{P}}}\right).$$

(28)

This expression allows one to extrapolate the fit backward in time and calculate the “ideal” time $t_1$ at which $T=T_{\mathrm{lab}}$. Evaluating $dT/dt$ at $t=t_1$ gives the ideal (filtered) time derivative, which is

$${\left.{\displaystyle \frac{dT}{dt}}\right|}_{t_1}={\displaystyle \frac{\Delta T_{\mathrm{eq}}-(T_{\mathrm{lab}}-T_0)}{t_{\mathrm{P}}}}={\displaystyle \frac{T_{\mathrm{eq}}-T_{\mathrm{lab}}}{t_{\mathrm{P}}}}.$$

(29)

Taking Equation (27) into account, we then have

$$\left(\rho c_{p}e\right)\left({\displaystyle \frac{T_{\mathrm{eq}}-T_{\mathrm{lab}}}{t_{\mathrm{P}}}}\right)=\alpha {\widehat{P}}_{\mathrm{LED}},$$

(30)

which permits an estimate of the absorptivity:

$$\alpha ={\displaystyle \frac{\left(\rho c_{p}e\right)}{{\widehat{P}}_{\mathrm{LED}}}}\left({\displaystyle \frac{T_{\mathrm{eq}}-T_{\mathrm{lab}}}{t_{\mathrm{P}}}}\right).$$

(31)

The long-term dynamics for $t\gg t_{\mathrm{P}}$ then allows one to estimate the emissivity $\epsilon$. With the fitting parameter $\Delta T_{\mathrm{eq}}$ and the expression $T_{\mathrm{eq}}=T_0+\Delta T_{\mathrm{eq}}$, the steady-state solution of Equation (23),

$$0=\alpha {\widehat{P}}_{\mathrm{LED}}-2\epsilon \sigma \left(T_{\mathrm{eq}}^4-T_{\mathrm{lab}}^4\right)-2h_{\mathrm{P}}\left(T_{\mathrm{eq}}-T_{\mathrm{air}}\right),$$

(32)

can be used to determine $\epsilon$. For generality, the equation is written in terms of the equilibrium values of $T_{\mathrm{lab}}$, $T_{\mathrm{air}}$, and the associated heat transfer coefficient $h_{\mathrm{P}}$. These temperatures are assumed constant throughout the analysis. For $T_{\mathrm{lab}}$, this is consistent with the large thermal inertia of the laboratory compared with the plate. On the other hand, the smaller thermal inertia of air results in more rapid variation followed by stabilization at an equilibrium temperature, which holds during most of the time during which the plate’s temperature is evolving.

During the laboratory session, experiments will be performed with different distances d between the ESAT Sun simulator and the plates, allowing one to determine $T_{\mathrm{eq}}$ as a function of d. Given that the estimate of $\alpha$ is based on the initial part of the experiments, one can simply use the minimum value of d, for which the heat absorbed by the plate is the largest and the experimental errors are relatively smaller, to estimate the absorptivity as described above.

Considering that $\epsilon$ is calculated from the steady-state dynamics (and that this can be influenced by various experimental uncertainties), experiments at different values of d can be used to estimate it. To reduce the influence of uncertainties, optimization methods can be applied to minimize the error after evaluating Equation (32) in each of these experiments.

4.3. Modeling the LED–Plate Radiative Interaction

As described above, the ESAT Sun simulator is an in-house component created to simulate the Sun’s (cool white) light. It is composed of an LED matrix, an aluminum fan cooling system, a conical lens, and a plastic front structure.

As per the manufacturer’s data sheet, the LED matrix has a power consumption of $P=100$ W and emits ${\varphi }_{\mathrm{LED}}\simeq$ 13,000–14,000 lm of light flux over the cool white spectrum, with a correlated color temperature of ∼6000 K. This specification has been checked by measuring the lux value at several distances using the “Traceable Dual-Display Light Meter” [51] device. For this type of light source, the light efficiency (i.e., the luminous efficacy of radiation for a ∼6000 K source) is $K_m\simeq 275$ lm/W [52,53], which allows us to calculate the fraction of P that is converted into light:

$$P_{\mathrm{LED},\mathrm{light}}={\displaystyle \frac{{\varphi }_{\mathrm{LED}}}{K_m}}\simeq 47.3\mathrm{W}.$$

(33)

The LED efficiency $\eta$ is thus

$$\eta ={\displaystyle \frac{P_{\mathrm{LED},\mathrm{light}}}{P}}\simeq 0.47,$$

(34)

a value that was used in previous sections to quantify the fraction of P that is dissipated as heat: $P_{\mathrm{dis}}=(1-\eta )P$.

The lens is used to redirect the light emitted by the LED matrix into a cone of semiangle $\theta ={30}^{\circ }$. The LED and lens are covered by a PLA-printed piece, and the assembly has an optical efficiency ${\eta }_{\mathrm{opt}}$ of approximately 0.5, which means that the effective emitted power is

$$P_{\mathrm{eff}}={\eta }_{\mathrm{opt}}{P}_{\mathrm{LED},\mathrm{light}}.$$

(35)

The efficiency and uniformity of the light flux after leaving the lens has been checked with the same luxometer mentioned above [51].

Recall that the ESAT Sun simulator is mounted on a dedicated support in order to direct the axis of the emitting cone in the appropriate direction. This support is aligned with a ruler so that the plates can be positioned with respect to it, and there is an offset distance of $d_0\simeq 2.5$ cm from this ruler to the LED matrix.

The square plates used for the experiments have a thickness of $e=1$ mm and a lateral size of $L=50$ mm. The plates are mounted in a dedicated PLA structure that holds them laterally aligned with, and perpendicular to, the axis of the light cone, and with the midpoint at a constant distance $r_0$ above it. Figure 4 shows a sketch of this configuration with one plate. A value of $r_0=50$ mm is selected to reduce the thermal interaction between the plates.

The intensity of the emitted light is

$$I={\displaystyle \frac{P_{\mathrm{eff}}}{2\pi (1-\cos \theta )}},$$

(36)

where $\Omega =2\pi (1-\cos \theta )$, with $\theta ={30}^{\circ }$, is the solid angle of the ESAT Sun simulator.

Because of the cylindrical symmetry of the optics, the power received for each of the three plates is approximately equal. To calculate it, we use a reference frame with the y and z axes aligned with the vertical midline of the plate and the cone axis, respectively, with its origin in the intersection between the beam axis and the plane of the plate. In this coordinate system, the LED is located at ${\mathbf{r}}_{\mathrm{LED}}=(0,0,d+d_0)$, and a point within the plate has the coordinates $\mathbf{r}=(x,y,0)$ where $-L/2\le x,y-r_0\le L/2$.

A point within the plate receives an illuminance

$$E={\displaystyle \frac{I}{x^2+y^2+{(d+d_0)}^2}}\cos \alpha ,$$

(37)

where $\cos \alpha =(d+d_0)/\sqrt{x^2+y^2+{(d+d_0)}^2}$, and the total quantity of light received by the plate is

$$P={\displaystyle \frac{P_{\mathrm{eff}}(d+d_0)}{2\pi (1-\cos \theta )}}{\int }_{-L/2}^{L/2}{\int }_{r_0-L/2}^{r_0+L/2}{\displaystyle \frac{dxdy}{{[x^2+y^2+{(d+d_0)}^2]}^{3/2}}}.$$

(38)

Note that this expression assumes that the plate lies completely within the illuminating cone, i.e., $\theta \ge \alpha$. In the laboratory set-up described here, this sets a minimum distance between the ESAT Sun simulator and the plates, requiring $d\ge d_{\min }\simeq 12$ cm.

Consistent with the single-node model described in Section 4.2, we consider the average power ${\widehat{P}}_{\mathrm{LED}}=P/L^2$,

$$\begin{array}{cc}\hfill {\widehat{P}}_{\mathrm{LED}}=P/L^2=& {\displaystyle \frac{P_{\mathrm{eff}}(d+d_0)}{2\pi L^2(1-\cos \theta )}}{\int }_{-L/2}^{L/2}{\int }_{r_0-L/2}^{r_0+L/2}{\displaystyle \frac{dxdy}{{[x^2+y^2+{(d+d_0)}^2]}^{3/2}}},\hfill \end{array}$$

(39)

which needs to be evaluated numerically since the integral only has a closed-form expression in the limit $d+d_0\gg L$.

4.4. Heat Transfer Coefficient of Natural Convection

The Grashof number $\mathrm{Gr}$, which characterizes the ratio of buoyancy to viscous forces, is

$$\begin{array}{c}\hfill \mathrm{Gr}={\displaystyle \frac{g\beta (T-T_{\mathrm{air}})L^3}{{\nu }^2}},\end{array}$$

(40)

where $g=9.81$ m/s² is the gravitational acceleration, $\beta$ is the (ideal gas) thermal expansion coefficient

$$\begin{array}{c}\hfill \beta ={\displaystyle \frac{2}{T+T_{\mathrm{air}}}},\end{array}$$

(41)

L is the height of the plate(s), and $\nu$ is the kinematic viscosity of air; all fluid properties are evaluated at the film temperature $T_f={\beta }^{-1}$. The Rayleigh number can then be written as the product of Gr and Pr:

$$\begin{array}{c}\hfill \mathrm{Ra}=\mathrm{Gr}\mathrm{Pr}.\end{array}$$

(42)

For laminar flow on a vertical plate, valid for ${10}^4\lesssim \mathrm{Ra}\lesssim {10}^9$, the average Nusselt number can be estimated [54] using the empirical expression

$$\begin{array}{c}\hfill \mathrm{Nu}=0.59{\mathrm{Ra}}^{0.25}.\end{array}$$

(43)

Finally, $h_{\mathrm{P}}$ is related to Nu via

$$\begin{array}{c}\hfill h_{\mathrm{P}}={\displaystyle \frac{\mathrm{Nu}k}{L}},\end{array}$$

(44)

where k is the thermal conductivity of air. Recall that $T_f$ varies on the order of 10 °C, which induces only small changes in $\nu$ and k with respect to their room temperature values.

This approach provides a practical and widely used estimate for heat transfer in natural convection with vertical surfaces. More details and background on these relationships can be found in [48].

5. Results

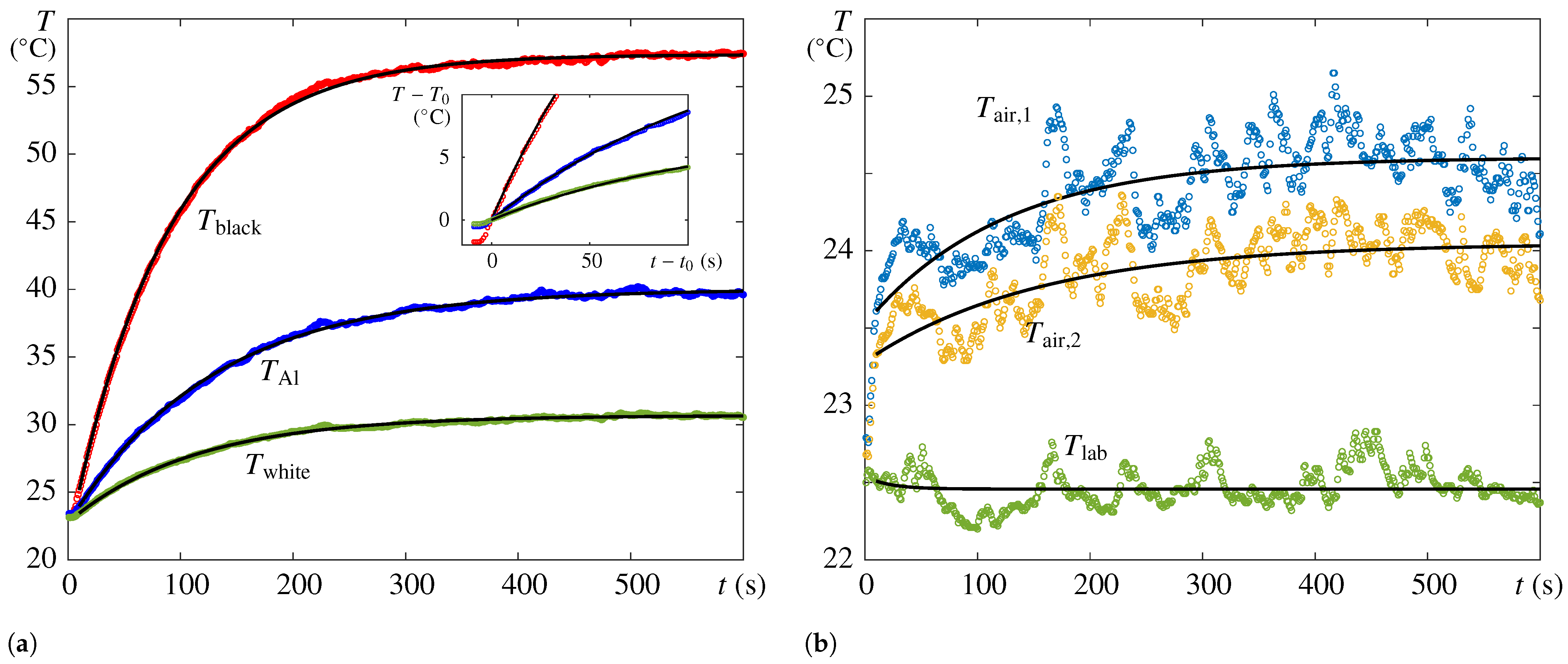
5.1. Thermal Characterization of the ESAT Sun Simulator

The results of an experiment performed for the thermal characterization of the ESAT Sun simulator are illustrated in Figure 5, which shows the temperature $T_{\mathrm{LED}}$ of the LED (red curve) and the inlet air $T_{\mathrm{inlet}}$ (blue) and the corresponding fits (black curves) to Equation (13) with $t_0=15$ s. These fits provide values for the steady-state temperatures of $45.6\pm 0.18$ °C and $22.9\pm 0.12$ °C, respectively, where the errors account for the fitting (using the 95% confidence interval) and the 0.1 °C uncertainty of the calibration.

With the model described in Section 4.1, these values can be used to estimate the convective heat transfer coefficient of the fan:

$$\begin{array}{c}\hfill h_{\mathrm{SS}}={\displaystyle \frac{P_{\mathrm{dis}}}{{(T_{\mathrm{LED}}-T_{\mathrm{inlet}})}_{\mathrm{eq}}{A}_{\mathrm{eff}}}}\simeq 21.0\pm 0.2\mathrm{W}/\left({\mathrm{m}}^2\mathrm{K}\right),\end{array}$$

(45)

where $A_{\mathrm{eff}}\simeq 0.1104$ m² and the thermal inertia of the system is

$$\begin{array}{c}\hfill \left(m{c}_p\right)={\displaystyle \frac{P_{\mathrm{dis}}{t}_{\mathrm{SS}}}{\Delta T_{\mathrm{eq}}}}\simeq 331\pm 6\mathrm{J}/\mathrm{K},\end{array}$$

(46)

where $t_{\mathrm{SS}}=142.8\pm 0.9$ s. This thermal inertial value can later be compared with that of the plates.

According to the manufacturer’s specifications, the fan generates an air flow Q of 20 cubic feet per minute ($9.34\times {10}^{-3}$ m³/s). With a radius $R\simeq 0.04$ m, the air velocity at the fan inlet is thus

$$\begin{array}{c}\hfill V_{\mathrm{inlet}}\simeq 1.85\mathrm{m}/\mathrm{s},\end{array}$$

(47)

and, as per mass conservation, the characteristic air velocity within the aluminum dissipator is

$$\begin{array}{c}\hfill V\simeq {\displaystyle \frac{Q}{2NW{e}_{\mathrm{fin}}}}\simeq 3.38\mathrm{m}/\mathrm{s}.\end{array}$$

(48)

Recall that $e_{\mathrm{fin}}\simeq 2$ mm is the air gap between the aluminum fins of the dissipator.

Taking $l_c\sim D/2\simeq 0.04$ m as the characteristic length of the flow within the dissipator and using values of $\nu =1.57\times {10}^{-5}$ m²/s, $k=0.025$ W/(m K), and $\mathrm{Pr}=0.7$ for the kinematic viscosity, thermal conductivity, and Prandtl number of air at room temperature, the Reynolds number is $\mathrm{Re}=8.96\times {10}^3$, and the estimate of the convective heat transfer coefficient from Equation (19) is $34.9\mathrm{W}/\left({\mathrm{m}}^2\mathrm{K}\right)$, which is of the same order of magnitude as that obtained from the experimental fit in Equation (45), albeit about 60% larger. Recall that Equation (19) provides the heat transfer coefficient for a horizontal plate.

Finally, considering $h_{\mathrm{SS}}\simeq 21.0\mathrm{W}/\left({\mathrm{m}}^2\mathrm{K}\right)$, one can calculate the associated Biot number for the aluminum dissipator:

$$\mathrm{Bi}={\displaystyle \frac{h_{\mathrm{SS}}{l}_c}{k_{\mathrm{Al}}}}\simeq 0.004,$$

(49)

where $k_{\mathrm{Al}}=240$ W/(m K) is the associated thermal conductivity. The fact that $\mathrm{Bi}\ll 1$ helps justify the use of a lumped mass model in this case. At the same time, Equation (49) suggests a limit on the $l_c/k$ ratio for which this simplification is a good approximation of the real thermal dynamics. For aluminum, requiring $\mathrm{Bi}\lesssim 0.01$ means that the characteristic length of the dissipator should be $l_c\lesssim 0.1$ m. Alternatively, if $l_c\simeq 0.04$ m for example, then the thermal conductivity of the material should satisfy $k\gtrsim 100$ W/(m K).

5.2. Radiative Heating of the Plates at the Minimum Distance from the ESAT Sun Simulator

The results of the experiment with $d=12.5$ cm are illustrated in Figure 6. Panel (a) shows the temporal evolution of the temperature for the three plates: one coated in black paint (temperature $T_{\mathrm{black}}$, shown in red), one left uncoated ($T_{\mathrm{Al}}$, shown in blue), and one coated in white paint ($T_{\mathrm{white}}$, shown in green). Panel (b) shows the laboratory temperature $T_{\mathrm{lab}}$ (green markers) and the surrounding air temperature $T_{\mathrm{air}}$ at two selected positions below the plates (blue and yellow markers); see Figure 1. The numerical fits performed with Equation (13) and $t_0=10$ s are superimposed (black curves).

With the model proposed in Section 4.2, the fitting parameters can be used to estimate the absorptivity of the plates and obtain an initial guess of their emissivities. Recall that the initial dynamics can be used to estimate $\alpha$ via Equation (31):

$$\begin{array}{c}\hfill \alpha ={\displaystyle \frac{\left(\rho c_{p}e\right)}{{\widehat{P}}_{\mathrm{LED}}}}\left({\displaystyle \frac{T_{\mathrm{eq}}-T_{\mathrm{lab}}}{t_{\mathrm{P}}}}\right).\end{array}$$

(50)

Here, we take $\rho \simeq 2700$ kg/m³, $c_p\simeq 900$ J/(kg K), and $e\simeq 1$ mm as the density, heat capacity, and thickness of the aluminum plates, respectively, while ${\widehat{P}}_{\mathrm{LED}}\simeq 1046$ W/m² is the average power received by the plate at $d=12.5$ cm; see Section 4.3. Note that the thermal inertia of the plates is 6.075 J/K, which is two orders of magnitude smaller than that obtained for the ESAT Sun simulator in the previous section.

The steady-state temperatures $T_{\mathrm{eq}}$ provided by the fits for the black coated, uncoated (aluminum), and white coated plates are 57.4 ± 0.13 °C, 40.0 ± 0.13 °C, and 30.7 ± 0.12 °C, respectively, while the characteristic times $t_{\mathrm{P}}$ are $87.3\pm 0.4$ s, $127.4\pm 0.9$ s, and $112.5\pm 1.0$ s. Using these values and a laboratory temperature $T_{\mathrm{lab}}\simeq 22.5\pm 0.11$ °C, the estimates for $\alpha$ for the three plates, respectively, are

$$\begin{array}{c}\hfill {\alpha }_{\mathrm{black}}\simeq 0.93\pm 0.02,{\alpha }_{\mathrm{Al}}\simeq 0.32\pm 0.01,{\alpha }_{\mathrm{white}}\simeq 0.17\pm 0.01.\end{array}$$

(51)

After obtaining these values for the absorptivity, the long-term dynamics can be used to obtain an initial estimate ${\epsilon }_0$ for $\epsilon$ according to Equation (32):

$${\epsilon }_0={\displaystyle \frac{\alpha {\widehat{P}}_{\mathrm{LED}}-2h_{\mathrm{P}}\left(T_{\mathrm{eq}}-T_{\mathrm{air}}\right)}{2\sigma \left(T_{\mathrm{eq}}^4-T_{\mathrm{lab}}^4\right)}},$$

(52)

which will be used later on as an initial guess for the data processing associated with the subsequent tests. In some cases, this initial estimate may give ${\epsilon }_0>1$, which is not a physically realistic value. This is an indication that the estimate of $h_{\mathrm{P}}$ from Equation (44) may underestimate the cooling provided by natural convection in this set-up. The estimate of ${\epsilon }_0$ is also affected by the accuracy of the measurements of $T_{\mathrm{air}}$. There is a clear benefit in using several experiments to correct for these errors.

The initial characterization of the thermo-optical properties of the plates is included (below) in panel (b) of Figure 8 using small markers (with error bars). The results for the black coated, uncoated (aluminum), and white coated plates are shown in red, blue, and green, respectively, a color coding that is preserved in all relevant figures.

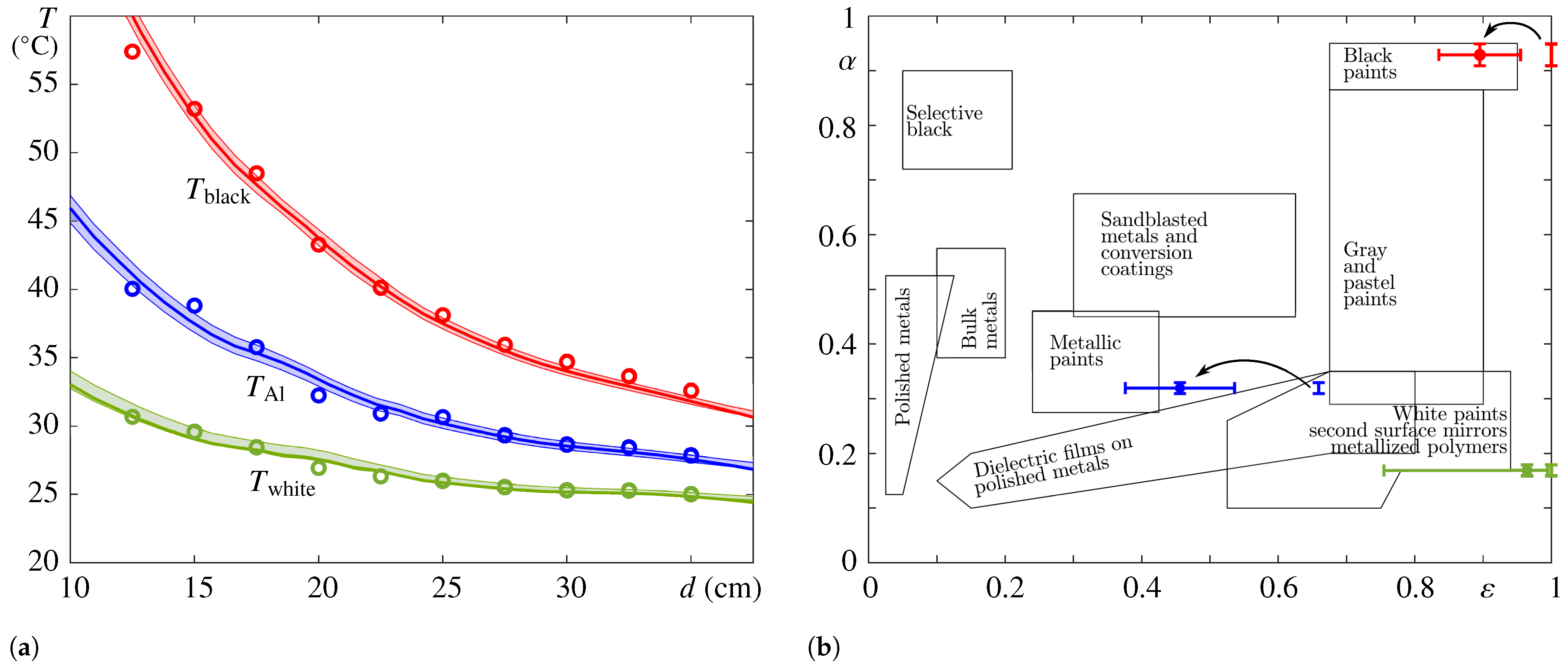
5.3. Successive Experiments at Increasing LED–Plate Distance

The laboratory session continues with back-to-back experiments conducted at increasing values of d. This series of experiments significantly improves the estimate of $\epsilon$ and, in particular, reduces the effect of any error in the estimate of $h_{\mathrm{P}}$ performed with Equation (44). An example of an experiment with $d=17.5$ cm is shown in Figure 7, where one can observe how the temperature decreases for all plates as the radiative interaction with the ESAT Sun simulator is reduced due to the increased distance. Again, the temporal evolutions of the plate temperatures and that of the air/lab (not shown in this figure) are fit to an exponential relaxation formula to obtain the steady-state values. Note that when the experiments are performed back-to-back, the time needed to reach the equilibrium is reduced to approximately 5 min.

The equilibrium temperatures $T_{\mathrm{eq}}$ and combined measurement-fitting error (with a 95% confidence interval) for the three plates, the air, and the laboratory obtained during a series of experiments at different distances d are summarized in

Table 1. Steady-state temperatures and combined measurement-fitting error (95% confidence) for increasing d.

Distance	cm	12.5	15	17.5	20	22.5	25	27.5	30	32.5	35
Black, $T_{\mathrm{black}}$	°C	57.4	53.2	48.5	43.3	40.1	38.1	35.9	34.7	33.6	32.6
Error	°C	0.13	0.12	0.12	0.14	0.14	0.12	0.12	0.11	0.11	0.11
Metal, $T_{\mathrm{Al}}$	°C	40.0	38.8	35.8	32.3	30.9	30.7	29.3	28.6	28.4	27.9
Error	°C	0.13	0.13	0.12	0.14	0.15	0.14	0.13	0.11	0.11	0.11
White, $T_{\mathrm{white}}$	°C	30.7	29.6	28.4	26.9	26.3	26.0	25.5	25.3	25.3	25.0
Error	°C	0.12	0.11	0.11	0.12	0.13	0.12	0.12	0.11	0.11	0.11
Air black	°C	24.3	25.0	25.1	24.5	24.3	24.6	24.3	24.3	24.4	24.3
Error	°C	0.23	0.13	0.13	0.15	0.14	0.14	0.13	0.12	0.12	0.12
Air aluminum, $T_{\mathrm{air},1}$	°C	24.5	25.2	25.3	24.8	24.5	24.8	24.5	24.6	24.8	24.7
Error	°C	0.13	0.13	0.13	0.16	0.15	0.14	0.15	0.12	0.12	0.12
Air white, $T_{\mathrm{air},2}$	°C	24.0	24.7	24.9	24.2	24.2	24.3	24.1	24.0	24.0	23.9
Error	°C	0.13	0.13	0.12	0.14	0.14	0.13	0.11	0.12	0.12	0.12
Lab, $T_{\mathrm{lab}}$	°C	22.5	22.4	22.5	24.9	22.6	22.7	22.6	22.7	23.1	23.0
Error	°C	0.11	0.11	0.11	0.11	0.12	0.11	0.11	0.11	0.11	0.13

. The temperature of the surrounding area is organized by considering the nearest plate: $T_{\mathrm{air},1}$ and $T_{\mathrm{air},2}$ denote the measurements taken below the aluminum and white plates, respectively, while “Air black” estimates the temperature below the black plate using the average between $T_{\mathrm{air},1}$ and $T_{\mathrm{air},2}$.

5.4. Data Processing and Estimate of Thermo-Optical Properties

After collecting the data shown in Table 1, it is possible to obtain a more precise estimate for $\epsilon$ by minimizing the error between the experimental results and the steady state balance of Equation (23):

$$\begin{array}{c}\hfill 0=\alpha {\widehat{P}}_{\mathrm{LED}}-2\epsilon \sigma \left(T_{\mathrm{eq}}^4-T_{\mathrm{lab}}^4\right)-2h_{\mathrm{P}}\left(T_{\mathrm{eq}}-T_{\mathrm{air}}\right).\end{array}$$

(53)

Recall that this equation must be solved numerically for $T_{\mathrm{eq}}$.

Figure 8a shows the experimental results for each plate using open markers, with the solution of Equation (53) being superposed on this after minimizing the error by adjusting $\epsilon$. These best-fit $\epsilon$ values are

$$\begin{array}{c}\hfill {\epsilon }_{\mathrm{black}}\simeq 0.90\pm 0.06,{\epsilon }_{\mathrm{Al}}\simeq 0.46\pm 0.08,{\epsilon }_{\mathrm{white}}\simeq 0.96\pm 0.21,\end{array}$$

(54)

for the black, aluminum, and white plates, respectively. The associated error estimates are based on Equation (53), considering the worst-case scenario for each term. Note that this fitting procedure requires that the heat transfer coefficient $h_{\mathrm{P}}$ be calculated separately at each point as described in Section 4.4. The temperatures $T_{\mathrm{air}}$ and $T_{\mathrm{lab}}$ are obtained (at intermediate points) by interpolating the measured values.

The final characterization of the thermo-optical properties is shown with large color-coded error bars in Figure 8b and summarized in

Table 2. Thermo-optical properties determined by the experiment.

	Black	Aluminum	White
$\alpha$	$0.93\pm 0.02$	$0.32\pm 0.01$	$0.17\pm 0.01$
$\epsilon$	$0.90\pm 0.06$	$0.46\pm 0.08$	$0.96\pm 0.21$

. The results are in good agreement with those found for black, metallic, and white paints in the literature [55,56,57]. These final results, obtained by fitting the measurements taken with varying d to Equation (53), are a significant improvement over the initial estimates. Panel (a) also shows the uncertainty in $T_{\mathrm{eq}}$ associated with the errors in the determination of $(\alpha ,\epsilon )$, which is in good agreement with the variance of the data.

As discussed above, it is easy to calculate an upper bound for the heat transfer coefficient $h_{\mathrm{P}}\le 4.9$ W/(m² K) and use that to estimate the associated Biot number in the plates: $\mathrm{Bi}=h_{\mathrm{P}}L/k_{\mathrm{Al}}\le 0.001$. As with the aluminum dissipator, the fact that $\mathrm{Bi}\ll 1$ for the plates supports the use of a lumped mass model and can be used to set similar bounds on L and k for alternative materials and/or dimensions.

6. Conclusions and Future Work

This article presents a modular laboratory set-up designed to enhance hands-on learning of heat transfer principles in aerospace engineering education. The designed platform allows students to investigate the thermal behavior of materials under radiative heating and simulates a basic heat transport scenario relevant to the thermal control of spacecraft. By combining physical modeling, numerical fitting, and experimental data acquisition, students are guided through the process of estimating the convective heat transfer coefficient of a cooling fan and the thermo-optical properties of coated aluminum plates.

The simplified single-node models developed for both the ESAT Sun simulator and the irradiated plates capture the dominant heat transfer mechanisms and are well suited for educational purposes. The experimental results show good agreement with the model predictions, validating the use of exponential fitting to extract thermal parameters. The final estimates for absorptivity and emissivity align with the expected values for similar types of surface coatings (black, metallic, and white).

The proposed laboratory activity not only provides a strong pedagogical foundation for teaching radiative and convective heat exchange but also promotes essential engineering skills such as data acquisition, model fitting, and system-level reasoning, while remaining accessible in terms of simplicity, cost, and implementation. The inclusion of calibration routines and numerical integration techniques adds additional educational value. Overall, this platform exemplifies how targeted hands-on experiments can be expected to significantly improve student understanding of thermal systems in aerospace environments, helping to bridge the gap between abstract concepts and real-world engineering applications. Although a number of relatively simple, low-cost heat transfer experiments for students have been proposed recently (see, e.g., [58,59]), this is the first one (to the best of our knowledge) to focus on this type of aerospace application.

Future work will focus on (but will not be limited to) the following topics. First, the introduction of additional materials and coatings (e.g., anodized aluminum, multilayer insulation, and Kapton films) would allow students to simulate a broader range of spacecraft surface conditions and thermo-optical behavior and enhance the generality of experimental results and conclusions. As a first step in this line, we have already manufactured plates covered with dielectric film (Kapton) and other paints, as well as plates with different levels of polishing, with preliminary results in agreement with the literature. Second, the refinement of physical models to include multidimensional heat conduction, transient radiative exchange, and variable or multi-material properties would allow for more advanced student investigations and would be more aligned with industry modeling practices. These refinements, as well as the addition of laboratory temperature and humidity control, would require more classroom time (and equipment) than the basic experiments and analysis described here. While accuracy and repeatability would no doubt benefit from such improvements, the current work does establish that a single-node model can provide a good starting point for thermo-optical characterization in the context of a three-hour, low-cost hands-on learning activity. Finally, in the coming years, a detailed analysis of the educational impact of the proposed hands-on experience and laboratory set-up, in terms of learning and motivation, will be performed.