Inverse Chemical Equilibrium Problem in Reacting Gaseous Mixtures: The Choice of Temperature to Maximise Product Yield

Abstract

A usual problem in chemical engineering and fuel processing is to achieve the highest possible efficiency concerning the target products. In this paper, we consider the inverse problem of chemical equilibrium and propose mathematical methods to obtain conditions under which the equilibrium state of the reacting system achieves the required characteristics. For the case of maximising the aim component yield, a new two-step algorithm is developed based on the inverse problem solution. The methods are tested using the methane reforming example.

1. Introduction

Thermodynamic analysis of chemical processes is the basis for their optimisation, including when selecting thermobaric conditions for conversion in a reactor. Depending on the conditions of interaction with the environment, the task of finding an equilibrium composition is reduced to finding the extremum of the corresponding thermodynamic function [1]. In chemical engineering, typical conditions for chemical reactions are constant temperature (T) and constant pressure (P), and equilibrium corresponds to the state with the minimum Gibbs free energy. In combustion chambers, constant enthalpy and pressure are more common, and equilibrium corresponds to a maximum of entropy [2].

Let us consider, for simplification, the first case ($T, P=\mathrm{const}$). The initial composition is required to determine the element composition of the reacting system. Then the equilibrium composition can be found as a solution of the following optimisation problem, which is further referred to as the direct equilibrium problem:

$${\mathbf{n}}^{eq}=arg \underset{\begin{array}{c}\mathbf{n}\ge \mathbf{0}\\ \mathbf{A}\mathbf{n}=\mathbf{b}\end{array}}{max}G(\mathbf{n}, T, P).$$

(1)

Here $\mathbf{n}$ is a vector of reacting component quantities (mol), G is the Gibbs free energy, $\mathbf{A}$ is a matrix of elemental composition ($a_{ij}$ is the number of i-th atoms in the j-th molecule), and vector $\mathbf{b}$ is the elemental composition of the reacting system. The material balance gives a system of linear constraints:

$$\mathbf{An}=\mathbf{A}{\mathbf{n}}^0=\mathbf{b}.$$

(2)

Here ${\mathbf{n}}^0$ denotes the initial composition of the reacting system.

To solve the problem, we need a relation between the Gibbs free energy and system composition. In ideal gaseous mixtures, the relation is as follows:

$$G(\mathbf{n}, T, P)=\sum _{j=1}^{N_s}{n}_j\left[{\mu }_j^0\left(T\right)+R_{g}Tln\left({\displaystyle \frac{P{n}_j}{\sigma }}\right)\right].$$

(3)

Here $R_g$ is the universal gas constant (8.31446 J/mol/K), ${\mu }_j^0$ is the chemical potential of the j-th component, and $\sigma$ is the sum of moles for gaseous components: $\sigma ={\displaystyle \sum _{j=1}^{N_s}}{n}_j$, where $N_s$ is a number of gas-phase components. The dependence of chemical potentials on temperature is given in handbooks [3]. The pressure under logarithm (which is a partial pressure for the j-th component) is usually considered as a relative value (reduced to the standard atmospheric pressure, 101,325 K), so the argument is non-dimensional, as it should be. In a more general case, fugacity is used instead of pressure (especially for high-pressure and low-temperature equilibria).

The usual way to solve the direct problem is to apply the Lagrange multiplier method. For a given temperature, pressure, and elemental composition, one can write the Lagrange function [4]:

$$L(\mathbf{n}, \mathsf{\lambda }, T, P)=G(\mathbf{n}, T, P)+{\mathsf{\lambda }}^T\left(\mathbf{An}-\mathbf{b}\right),$$

where $\mathsf{\lambda }$ is a vector of the Lagrange multipliers.

The stationary point of this function $\nabla L=0$ is the equilibrium point giving the constrained minimum to the Gibbs free energy. It can be shown that in ideal systems, the function $G\left(\mathbf{n}, T, P\right)$ is strictly convex, and the equilibrium solution is unique [5]. Lagrange-based methods are widely used in computational chemical thermodynamics, although mass action law methods are still used for simple systems [6,7,8] (and due to their ability to “turn off” chemical reactions [9]).

The direct problem has been intensely studied in the literature since the dawn of the computer era in chemical thermodynamics. The first methods of complex equilibria calculations were based on equilibrium constants. Immediately after the development of the first linear programming computer algorithms, the iterative methods for solving direct equilibrium problems were proposed [10]. Methods using Lagrange multipliers were presented in [11,12]. More general formulations were further proposed, taking into account real properties of fluids, and multi-phase and surface effects (including solving non-convex problems) [13,14,15,16].

The increase in computational capabilities, the refinement and expansion of databases on thermodynamic properties, universalisation, and the increased reliability of algorithms make obtaining a solution to the direct equilibrium problem fast and accurate. Thermodynamic analysis of chemical processes has become a routine procedure, and new software products make its automation possible. In the textbook [17], the search for optimal parameters of the equilibrium process of complex processes such as coal gasification is proposed as a task for students. Modern trends in thermodynamic analysis include multivariate calculations, an increase in the dimensionality of problems, an expansion of the ranges of control parameters, and a modification of the conditions of thermochemical equilibrium.

Unless considering the simplest problems, the dependence of equilibrium composition on input parameters cannot be written explicitly. The arg min is usually not a sequence of elementary functions. In complex reacting systems, the search for optimal conditions often means “brute-forcing” the parameter space.

Chemical production criteria are not directly related to thermodynamic functions. The general form of the production criterion can be written as follows:

$$F\left(\mathbf{n}\right)=\sum _{j=1}^{N_s}{c}_j{n}_j.$$

(4)

Here the coefficients $c_j$ weigh useful and harmful components. Several approaches to this kind of optimisation problem (searching for intermediate extremum states) were proposed in the works [2,4,18]. These methods, however, do not search for ordinary equilibrium states.

Given the required accuracy of 10%, one needs 10 grid points for every degree of freedom. Then, the computational work grows as ${10}^n$, where n is the number of varied parameters. Even for modern computation facilities, this could be a wearying task. When studying multi-component systems, reducing some parameters (such as temperature and pressure) would be a significant advantage.

More efficient methods to find optimal conditions for chemical conversion can be developed based on inverse optimisation theory [19,20]. It should be noted that there are several problems in reacting systems that can be called inverse problems. The first, which is the main object of the present work, is the search for the temperature and pressure that result in the required equilibrium composition. The second includes determination of thermodynamic functions (equilibrium constants, thermal effects) from equilibrium composition or temperature measurements [21]. The latter is very important to thermodynamic databases. The present work is devoted to the former one.

Inverse problems in chemical thermodynamics of the first kind were considered in [22] with application to solution equilibria. A number of specific problems were solved, including the search for conditions resulting in fixed pH, chemical potential of the solvent, or solution composition. Our study is related to gaseous mixtures, although the methods are based on the same theoretical basis. We give a more general method to find conditions with uncertainty of required equilibrium characteristics. The novelty of the study is a new algorithm for inverse problem solving using some specific properties of auxiliary thermodynamic functions that allow us to find the conditions corresponding to the required output. Instead of the difference between the variables of interest, we use the difference between thermodynamic potentials as an auxiliary function, which allows us to propose a new thermodynamic interpretation for the numerical methods for finding its zeros. Moreover, we propose a method to estimate the thermodynamic limit of chemical systems concerning the production of aim components.

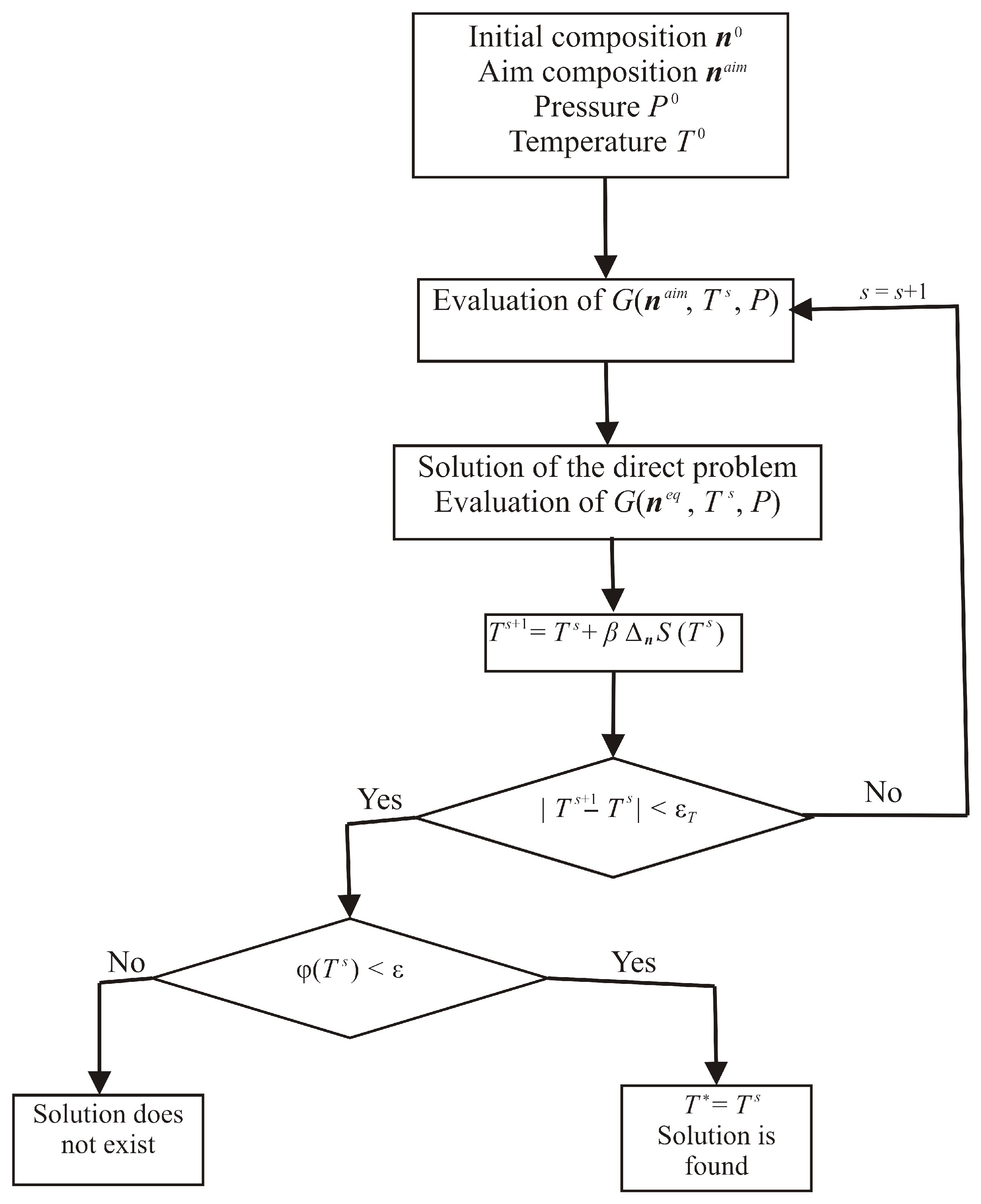
2. Inverse Problem and Auxiliary Functions

2.1. Bullseye Shot

First, let us consider the case with fixed equilibrium composition ${\mathbf{n}}^{aim}$ without knowing temperature and pressure, under which it becomes a solution of the direct problem, i.e.,

$${\mathbf{n}}^{aim}={\mathbf{n}}^{eq}.$$

(5)

The problem is then reduced to searching for parameters T and P such that

$$G({\mathbf{n}}^{aim}, T, P)=G({\mathbf{n}}^{eq}, T, P).$$

(6)

Then it is natural to consider an auxiliary function $\phi (T, P)$:

$$\phi (T, P)=G({\mathbf{n}}^{aim}, T, P)-G({\mathbf{n}}^{eq}, T, P).$$

(7)

Since problem (1) has a unique solution, function $\phi$ is differentiable. The problem is reduced to solving the equation

$$\phi (T, P)=0,$$

(8)

and zeros of the auxiliary function correspond to the conditions where Equation (5) is true.

The second term in r.h.s. (7) is implicit, i.e., the value of the equilibrium Gibbs energy can be found only after solving the optimisation problem. The first term is known for every temperature and pressure. To estimate whether the given values of T and P satisfy the Equation (6), it is necessary to solve the direct problem.

It can be shown that the auxiliary function $\phi (T, P)$ has some convenient properties, namely $\phi (P, T)\ge 0$ (i.e., equilibrium Gibbs free energy is always minimum), and $\phi (P, T)=0$ if and only if Equation (5) holds, i.e., the solution is a minimum of the auxiliary function (but not vice versa). Moreover, the general thermodynamic theory allows additional simplifications.

The fundamental Gibbs equations can be presented in the following form [1]:

$$dG=VdP-SdT+\sum _j{\mu }_{j}d{n}_j.$$

Here V is volume, and S is entropy. Maxwell relations can be deduced from here:

$${\left({\displaystyle \frac{\partial G}{\partial T}}\right)}_{P,\mathbf{n}}=-S,$$

$${\left({\displaystyle \frac{\partial G}{\partial P}}\right)}_{T,\mathbf{n}}=V.$$

If there is a pair $\{T^{\ast }, P^{\ast }\}$ such as $\phi (T^{\ast }, P^{\ast })=0$, then one can write

$${\displaystyle \frac{\partial {\phi }^{\ast }}{\partial T}}\Delta T+{\displaystyle \frac{\partial {\phi }^{\ast }}{\partial P}}\Delta P=0.$$

That is, there may be a family of solutions related through a differential equation similar to the Clapeyron–Clausius equation:

$${\displaystyle \frac{d{T}^{\ast }}{d{P}^{\ast }}}=-{\displaystyle \frac{\partial \phi /\partial P^{\ast }}{\partial \phi /\partial T^{\ast }}}={\displaystyle \frac{V^{aim}-V^{eq}}{S^{aim}-S^{eq}}}.$$

(9)

The more common problem is the determination of the optimal conversion temperature. After solving it for a fixed pressure, one can extend the solution using Equation (9). Let us fix pressure and use Newton’s method to find roots of Equation (8). The iteration procedure is as follows:

$$T^{s+1}=T^s-{\displaystyle \frac{\phi \left(T^s\right)}{{(\partial \phi /\partial T)}^s}}.$$

This equation can be rewritten using thermodynamic relations:

$$T^{s+1}=T^s+{\displaystyle \frac{{\Delta }_{n}G\left(T^s\right)}{{\Delta }_{n}S\left(T^s\right)}}={\displaystyle \frac{{\Delta }_{n}H\left(T^s\right)}{{\Delta }_{n}S\left(T^s\right)}}.$$

(10)

Here the ${\Delta }_n$ operator denotes the difference between functions estimated for ${\mathbf{n}}^{aim}$ and ${\mathbf{n}}^{eq}$. The latter is not given explicitly, so thermodynamic functions are to be calculated after the direct problem is solved. Nevertheless, Equation (10) has a form that is typical for thermal control: the temperature is corrected in such a way that it compensates for the enthalpy difference between the aim state and the equilibrium state.

It should be noted that the Newton method is considered a typical example of numerical methods applicable to this problem. Other methods would give similar iterative formulas, but with different “thermostat conditions”. In the case of the Newton method, the formula has the most physically consistent sense: $\Delta H$ can be interpreted as the overall reaction heat (up to a sign), and $T\Delta S$ is correspondingly the heat transferred between the system and the thermostat, so the temperature is chosen to balance them.

It is more convenient to search for the minimum of the auxiliary function. If the minimum value is larger than zero, then a solution does not exist. In the case of an exactly given aim state, this minimum is unique. The algorithm of the inverse problem solution for temperature is presented in Figure 1.

The results above are correct only if the aim state ${\mathbf{n}}^{aim}$ is given precisely, i.e., it is known that the solution of the inverse problem exists. More common is a situation when the existence of a solution is not known a priori, or enough is known to capture the quantities of some components, but not all of them. In this case, a modification of the inverse problem is required.

2.2. Neighbourhood of the Point

Let us start with a case where the aim state is given with errors violating material balance:

$$\mathbf{A}{\mathbf{n}}^{err}\ne \mathbf{b}.$$

A correction procedure can be proposed, similar to [23]:

$${\mathbf{n}}^{aim}=arg\underset{\mathbf{n}\ge 0}{min}\left|\right|\mathbf{n}-{\mathbf{n}}^{err}{\left|\right|}^2,$$

with constraints (2).

As mentioned before, the aim state is not necessarily available. In this case, Newton’s method does not converge. Special methods can be used to check the existence of a solution (for example, the method of support functions [24]). In most cases, exact zero is not feasible due to poor accuracy, but the practical application allows the use of the closest attempt: a permissible $\epsilon$ should be given such that $T^{\ast }$ is considered as a solution if $\phi \left(T^{\ast }\right)<\epsilon$ (see Figure 1). However, the minimum of $\phi \left(T\right)$ does not always result in a feasible solution, i.e., energy metrics are not always good for the comparison of different compositions. Moreover, the components are usually unequal with respect to researcher consideration: there are valuable and undesirable reaction products, but there are also “indifferent” components, such as solvents, diluents, side products, etc. In this regard, it is no use to solve the inverse problem with all the components specified. We propose another approach.

Along with the direct problem (1)–(3) we consider its modified version, distinguished by adding a constraint:

$$\left|\right|\mathbf{n}-{\mathbf{n}}^{aim}{\left|\right|}^2\le r^2,$$

where r is a permissible radius of neighbourhood.

If there are “indifferent” components, we can modify the norm of use, for example, by weighting the components:

$$\left|\right|\mathbf{C}(\mathbf{n}-{\mathbf{n}}^{aim}){\left|\right|}^2\le r^2,$$

(11)

where $\mathbf{C}$ is a diagonal matrix with non-negative elements, presenting weights of corresponding components. If one of these elements is zero, then the component is indifferent. Restricted thermodynamic equilibria of this kind were studied in papers [18,25,26,27].

Further, we introduce the solution of the direct problem with additional inequality (11):

$${\mathbf{n}}^{res}=arg\underset{\begin{array}{c}\mathbf{n}\ge \mathbf{0}\\ \mathbf{A}\mathbf{n}=\mathbf{b}\\ \left|\right|\mathbf{C}(\mathbf{n}-{\mathbf{n}}^{aim}){\left|\right|}^2\le r^2\end{array}}{min}G(\mathbf{n}, T, P).$$

(12)

Then, similarly to the previous subsection, we introduce a new auxiliary function:

$$\psi (T, P)=G({\mathbf{n}}^{aim}, T, P)-G({\mathbf{n}}^{res}, T, P).$$

It can be shown that the auxiliary function $\psi (T, P)$ has the same properties as $\phi (T, P)$ with respect to the restricted problem, $\psi (T, P)\ge 0$, and the equality is possible only if ${\mathbf{n}}^{aim}={\mathbf{n}}^{res}$, i.e., if the solution of the inverse problem exists. Both states (${\mathbf{n}}^{eq}$ and ${\mathbf{n}}^{res}$) are not known, and the auxiliary function requires the solution of two direct equilibrium problems with and without constraint (11). In this regard, the algorithm has twice the cost.

We have an additional parameter r, which can be varied arbitrarily. The important property of the problem (12) is that when r is large enough namely, of the effective diameter of the permissible set (2), then the solution does not differ from the unconstrained problem (1)–(3).

2.3. Optimisation over Equilibria

These facts allow for solving practically interesting problems of iterative search for optimal equilibrium states, which are the states providing extrema for a linear function (4). To this end, let us choose important components and set their weight coefficients to non-zero values. Then let us solve the following linear programming problem:

$${\mathbf{n}}^{ext}=arg \underset{\begin{array}{c}\mathbf{n}\ge \mathbf{0}\\ \mathbf{A}\mathbf{n}=\mathbf{b}\end{array}}{max}\sum _j^{N_s}{c}_j{n}_j.$$

This solution ${\mathbf{n}}^{ext}$ is an extremal stoichiometrically possible state without restriction of the second law (it does not depend on temperature or pressure). This state is usually not attainable unless it is an initial state [2]: the linear optima belong to the boundary of the permissible set, and equilibrium points in ideal gaseous mixtures are internal points.

Further, we solve the problem (12) in which ${\mathbf{n}}^{aim}={\mathbf{n}}^{ext}$. This problem has a solution if r is large enough. Then, if we contract the region of search by gradually reducing r, we obtain the solution or prove that it does not exist. The lowest permissible value of r provides the best equilibrium solution approximating ${\mathbf{n}}^{ext}$. The algorithm with bisection is presented in Figure 2. The starting value of $r_{min}$ is 0, and for the starting value of $r_{max}$, we need to estimate the effective diameter of the permissible composition space. One may choose a value larger than the maximum value of the vector ${\mathbf{n}}^{ext}$ or the sum of the vector $\mathbf{b}$. A more rigorous approach would include a radius of a sphere containing the composition space. For computational purposes, an arbitrarily large number could be a good guess.

In the next section, we will study a specific chemical process using the developed theory.

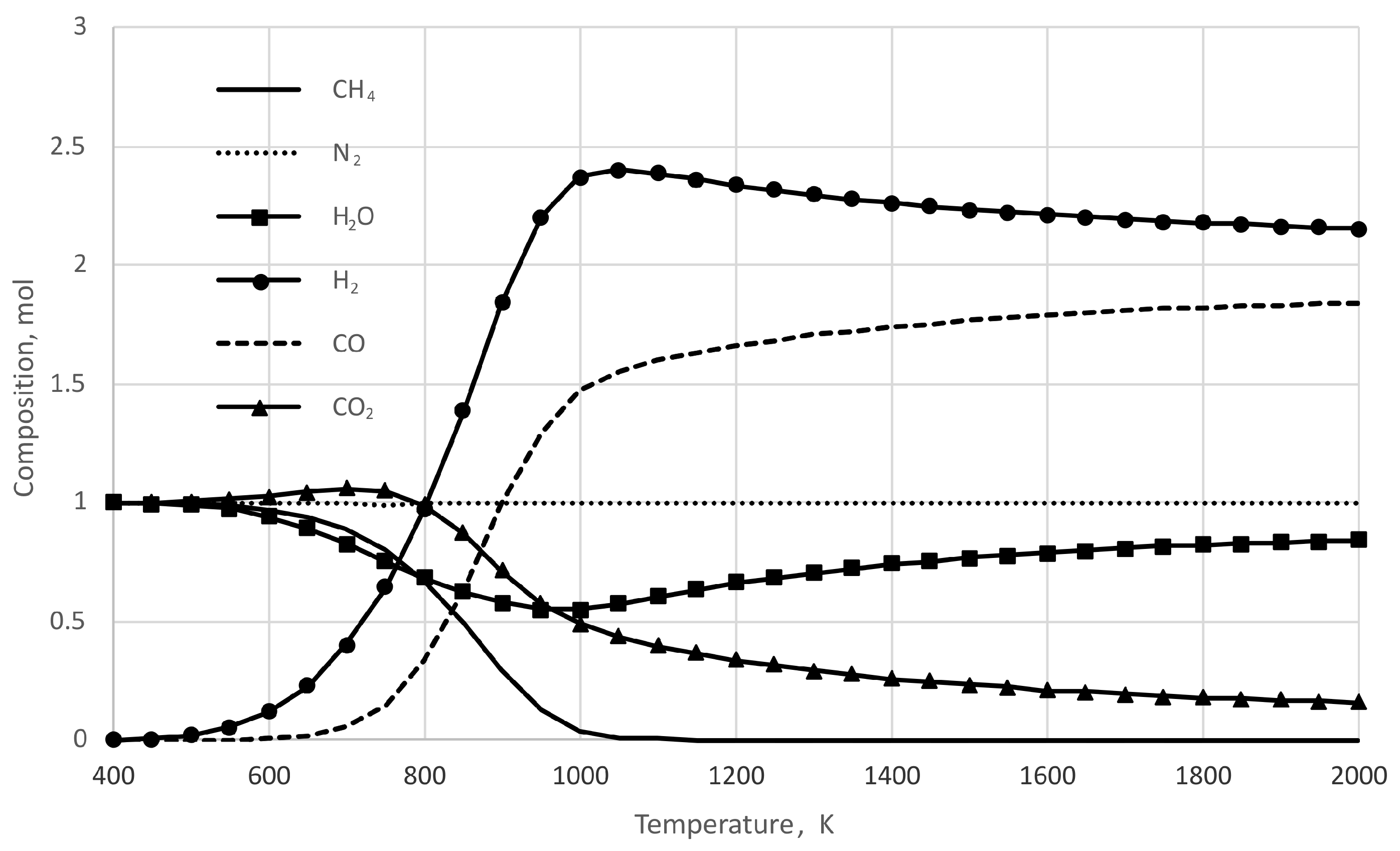
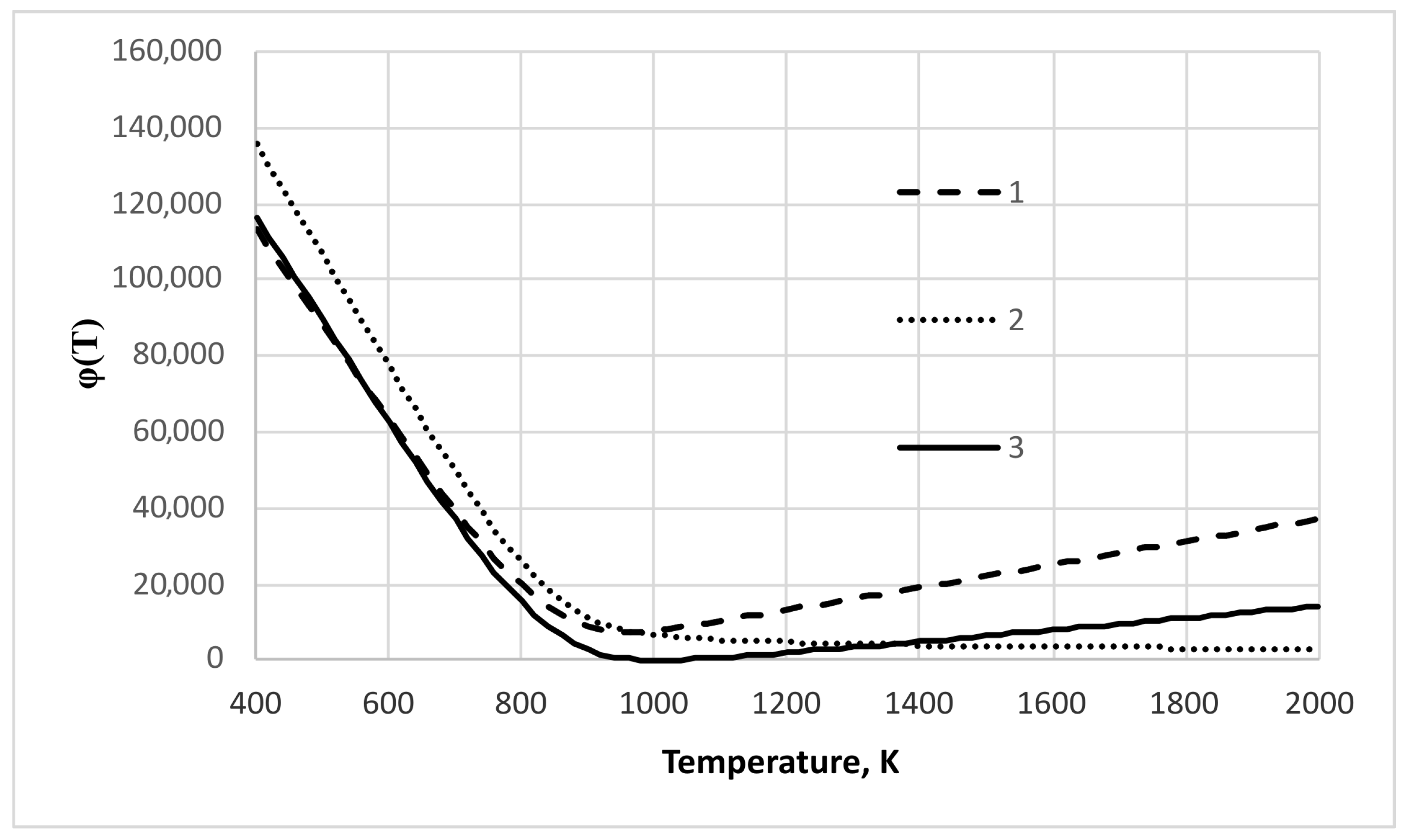
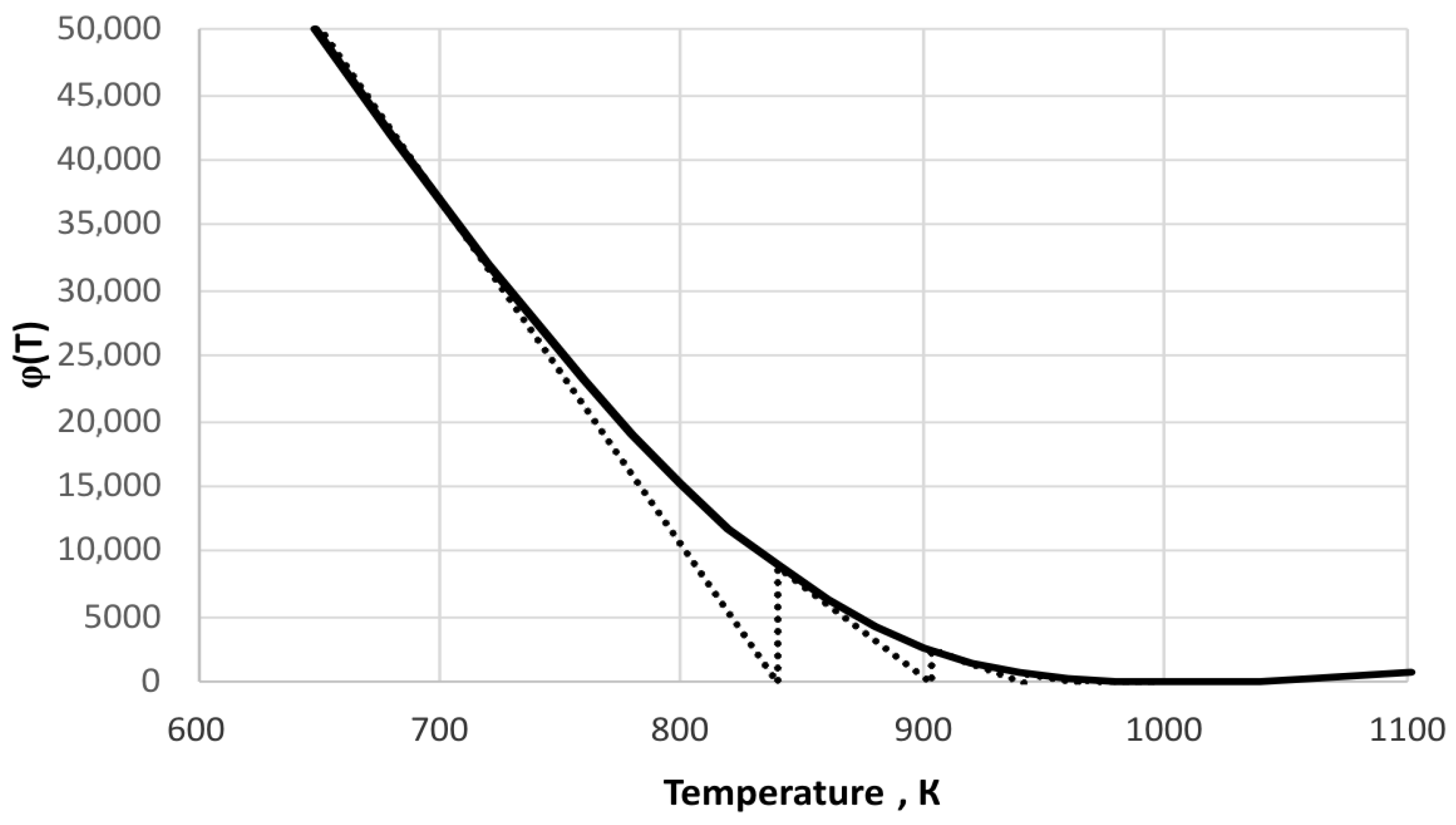
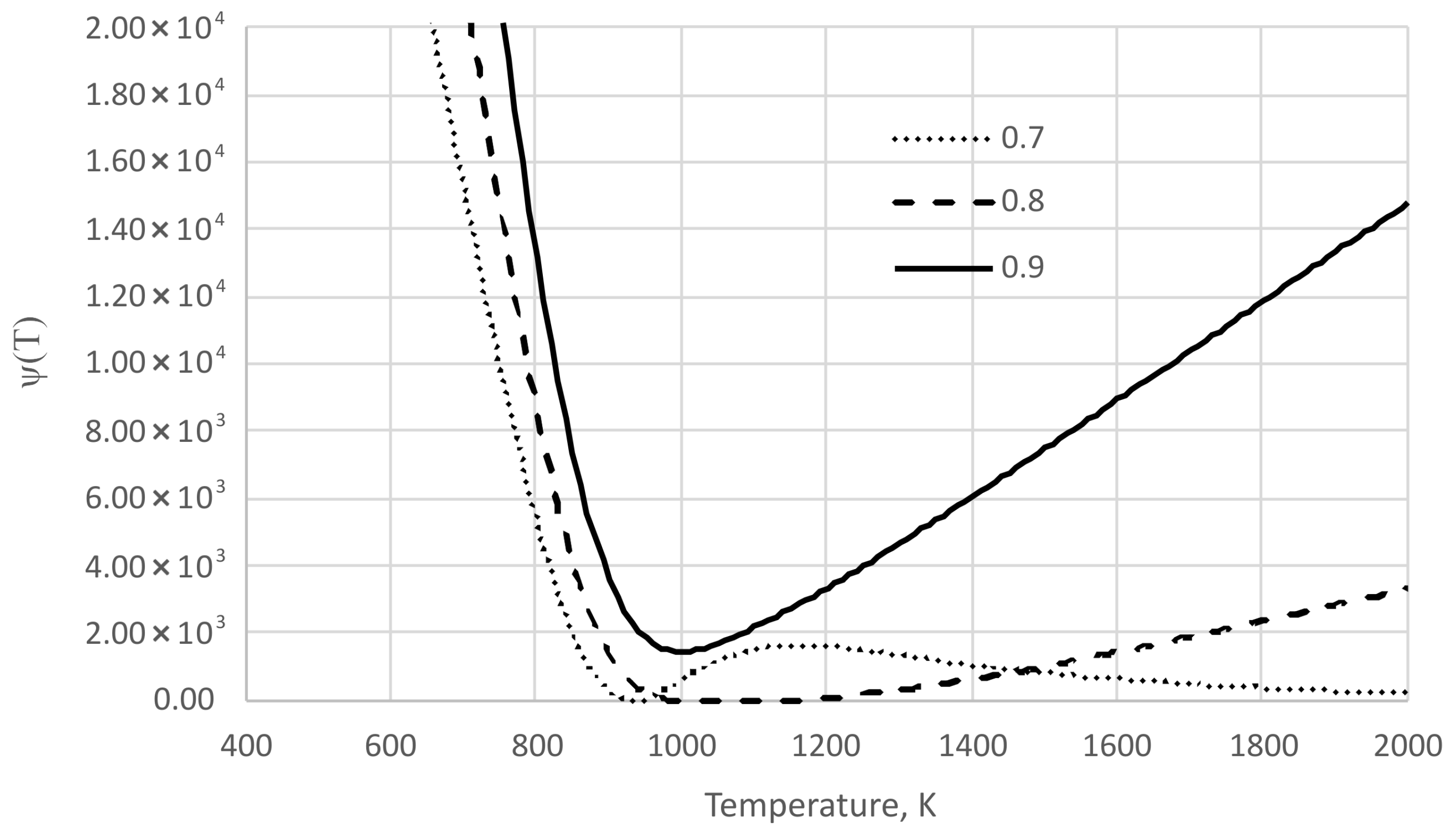
3. Results and Discussion

We consider a reacting mixture containing CO, ${\mathrm{H}}_2$, ${\mathrm{CO}}_2$, ${\mathrm{H}}_2\mathrm{O}$, ${\mathrm{CH}}_4$, and ${\mathrm{N}}_2$ as a diluent. The initial state consists of ${\mathrm{CH}}_4$, ${\mathrm{CO}}_2$, and ${\mathrm{H}}_2\mathrm{O}$, 1 mole each (the presence of inert ${\mathrm{N}}_2$ also allows us to check the material balance). The main question is how much ${\mathrm{H}}_2$ can be obtained from this mixture with varying temperatures.

This system makes it quite simple to test the methods. First, we can solve the direct problem and find the dependence of the equilibrium composition on the temperature (the pressure is 1 atm). The dependence is presented in Figure 3, which shows that the presence of ${\mathrm{H}}_2\mathrm{O}$ and ${\mathrm{CO}}_2$ results in a change in the dominant methane-reforming agent near 1000 K. At lower temperatures, the main reactant is steam, and the main product of methane conversion is syngas with high hydrogen content. At higher temperatures, the main reactant is carbon dioxide, and the hydrogen yield decreases due to the water-shift reaction. The curves were obtained using a grid with a step of 25 K.

Let us consider the values of the $\phi \left(T\right)$ function on this grid. We pick three target compositions: two of them are extremal states with a maximum of ${\mathrm{H}}_2$ (${\mathbf{n}}_1$) and CO (${\mathbf{n}}_1$), and the third (${\mathbf{n}}_3$) is the composition taken from the calculations, namely, the equilibrium composition for 1000 K. These states are listed in

Table 1. Compositions $\mathbf{n}$ for the model system.

Component	${\mathbf{n}}_1$	${\mathbf{n}}_2$	${\mathbf{n}}_3$
${\mathrm{CH}}_4$	0	0	0.04
CO	1	2	1.47
${\mathrm{H}}_2$	3	2	2.37
${\mathrm{CO}}_2$	1	0	0.49
${\mathrm{H}}_2\mathrm{O}$	0	1	0.55
${\mathrm{N}}_2$	1	1	1

. The corresponding auxiliary functions $\phi \left(T\right)$ are presented in Figure 4. For the first two states, there are no roots of the auxiliary functions: the minima of $\psi \left(T\right)$ do not touch the x-axis. For the third case, when the solution is known, the auxiliary function has a root, touching the x-axis at the temperature of 1000 K.

Let us apply the Newton method. Figure 5 shows the convergence of the iterations to the solution, which requires 10 iterations to obtain the temperature with an accuracy of 1 K. Full coverage of the temperature interval from 400 to 2000 K with the same step would require solving the direct problem 1600 times.

For the first two compositions, there are no zeros of auxiliary functions, but one can check that this is the case for the given interval using some methods [24]. As mentioned, minimum values of auxiliary functions do not always correspond to the best possible states. For example, the minimum of $\phi \left(T\right)$ for ${\mathbf{n}}_1$ is located near 960 K.

In the case of the only component of interest, a simplification is possible. Instead of using the condition (11), we will use the following linear constraint:

$$n_{{\mathrm{H}}_2}=\alpha n_{{\mathrm{H}}_2}^{ext}.$$

Here $\alpha \le 1$ is a coefficient characterising the possibility of achieving an extremum state. The rest of the procedure stays the same: we evaluate Gibbs free energy in the constrained and unconstrained problems and search for the zero of the difference between them. The corresponding curves are presented in Figure 6. Since hydrogen yield is not monotonous, the auxiliary function $\psi \left(T\right)$ is not convex. Moreover, it may have two roots in the interval of $\alpha$ corresponding to the vicinity of the maximum in Figure 1. The maximum value of $\alpha$ for which the solution of $\psi \left(T\right)=0$ exists is about 0.8. This is the thermodynamic estimate of the highest equilibrium hydrogen yield possible under given stoichiometry.

The most important thing is that this value can be found without combinatorial calculations, but using simple numerical algorithms, allowing for the localisation of the roots of the auxiliary function. These values are to be estimated by a solution of the direct equilibrium problem, but the number of points for which such evaluation is needed is drastically reduced by the proposed methods.

The important problem for future research is the optimal choice of the initial state in order to achieve a given aim state in equilibrium or to obtain better production efficiency. This problem is more complex due to the deformations of the permissible composition space (duality theory naturally becomes the main tool in this case). Nevertheless, the inverse problems have similar features that can be used to develop a more general theory of thermodynamically optimal reacting mixtures.

There are also obvious directions for the work toward multi-phase and non-ideal systems. Although this task is the subject of a separate work, one can assume that for ideal condensed phases, the algorithm would be similar. However, the phase transitions may lead to discontinuities requiring additional treatment. The presented algorithms heavily rely on the convexity and continuity of the Gibbs free energy. In some cases, weakly non-convex problems could be solved using the same techniques, but in general, we need to consider multi-phase and non-ideal systems more rigorously to develop stable and robust algorithms.

4. Conclusions

In this work, we consider the inverse equilibrium problem for an ideal reacting mixture and propose two numerical algorithms for its solution based on a new thermodynamic auxiliary function. The first algorithm allows for determining the temperature at which a given equilibrium composition is observed. The second proposed algorithm allows for estimating the limit product yield permissible by thermodynamic laws, based on the former algorithm and the bisection method. Both algorithms are tested using a model system (methane reforming by steam and carbon dioxide) and are shown to be several orders of magnitude more efficient compared to the “brute-force” approach.

The main limitation of the approach, in the present form, is the ideal homogeneous approximation for the description of the reactive mixture. Future research concerns a possible extension of the method to multi-phase and non-ideal systems.