Abstract
The evaporation/decomposition behavior of the ionic liquid 1-butyl-3-methylimidazolium chloride (BMImCl) was studied with various techniques, such as thermogravimetry (TG), Knudsen effusion mass loss (KEML), and Knudsen effusion mass spectrometry (KEMS), in order to investigate the competition between the simple evaporation of the liquid as gaseous ion pairs (NIP: neutral ion pair) and the thermal decomposition releasing volatile species. TG/DSC experiments were carried out from 293 to 823 K under both He and N2 flowing atmospheres on BMImCl as well as on BMImNTf2 (NTf2: bis(trifluoromethylsulfonyl)imide). Both ionic liquids were found undergoing a single step of mass loss in the temperature range investigated. However, while the BMImNTf2 mass loss was found to occur in different temperature ranges, depending on the inert gas used, the TG curves of BMImCl under helium and nitrogen flow were practically superimposable, thus suggesting the occurrence of thermal decomposition. Furthermore, KEML experiments on BMImCl (in the range between 398 and 481 K) indicated a clear dependence of the unit area mass loss rate on the effusion hole diameter, an effect not observed for the ILs with NTf2 anion. Finally, KEMS measurements in the 416–474 K range allowed us to identify the most abundant species in the vapor phase, which resulted in methyl chloride, butylimidazole, butyl chloride, and methylimidazole, which most probably formed from the decomposition of the liquid.
1. Introduction
The low volatility and the relatively high thermal stability are probably the properties of ionic liquids (ILs) that have aroused the greatest interest and enthusiasm for this large family of compounds in the past 20 years. For this reason, an investigation into the stability limits of the most promising classes of ILs is crucial for the assessment of their real application prospects and has been one of the subjects at the center of attention for many years [1,2,3]. The evaporation/decomposition behavior of these compounds has been the subject of a scientific debate for the past 20 years, ever since Earle et al. [4] demonstrated for the first time that many ILs could be distilled without decomposition. Today, much evidence has been gathered such that a wide gamut of cases can occur, depending on the chemical nature of the cation and anion, going from simple evaporation releasing intact gaseous ion pairs (NIP: neutral ion pair) with practically no decomposition [5,6] to severe decomposition at temperatures where simple evaporation is below any detectable level [7].
Many efforts have been made to apply experimental approaches capable of monitoring the competition between evaporation and decomposition phenomena occurring in ionic and molecular substances, based for example on the nonisothermal thermogravimetry [8,9,10,11], Knudsen effusion mass loss [12], and mass spectrometry methods [5,13,14]. Furthermore, experimental techniques such as quartz crystal microbalance (QCM) have been developed that aimed at studying the evaporation thermodynamics at temperatures low enough to limit the occurrence of degradation [15,16].
In recent years, some evidence has emerged that, in addition to temperature, the specific conditions under which the heating is performed can be decisive in moving the needle toward decomposition or evaporation. Some years ago, our group [17] reported that under effusion conditions, the competition between the evaporation and decomposition of BMImPF6 was significantly sensitive to the effusion hole diameter, with the decomposition/evaporation ratio decreasing to a significantly extent with increasing hole size. Subsequently, License et al. [18] succeeded in identifying the main decomposition products of 1-alkyl-3-methylimidazolium tetrafluoroborate and hexafluorophosphate, by combining ex situ experiments with mass spectrometry measurements. Finally, Kudin et al. [19] showed that under free surface (Langmuir) evaporation, the decomposition of 1-butyl-3-alkyl-methylimidazolium tetrafluoroborate was strongly reduced in favor of congruent evaporation into NIPs.
ILs with halide anions have long been known to be among the most prone to thermal degradation even at moderate temperatures. Long-term isothermal TG experiments on BMImCl revealed a not negligible mass loss at 433 K [20]. The degradation of EMImBr from T = 473 K was studied more than 10 years ago by Leone et al. [21], who showed the release of a number of molecular gaseous products formed from the degradation of the compound. Furthermore, mass spectrometric experiments on 1-octyl-3-methylimidazolium halides [22] revealed that in spite of the co-occurring decomposition, the evaporation process could be studied mass spectrometrically by monitoring the temperature dependence of the cation C+ peak formed by the fragmentation of the NIP. More recently, Verevkin and colleagues [23] analyzed the possible decomposition paths of various imidazolium bromide and chloride ILs and claimed that thanks to strong kinetic limitations, the degradation of the compounds should not interfere with the measurement of the vapor pressure and evaporation enthalpy with the QCM technique.
The present study is focused on three steps, the first of which is devoted to analyzing the competition between simple evaporation and the thermal decomposition of 1-buthyl-3-methylimidazolium chloride (BMImCl) on the basis of using the above mentioned nonisothermal TG method developed by Heym [9,10]. Subsequently, we present Knudsen effusion mass loss (KEML) measurements on BMImCl in the 398–481 K range to study the effect of the effusion orifice size on the specific mass loss rate, in order to demonstrate possible kinetic hindrance effects in the release of decomposition products. Finally, we report the results of Knudsen effusion mass spectrometry measurements on the same compound in the 416–474 K temperature range, giving information on the composition of the vapor phase produced and on the nature of the degradation products released under effusion conditions.
2. Materials and Methods
2.1. Theoretical Background of the Evaporation/Decomposition Competition Study with Thermogravimetry and Knudsen Effusion Techniques
A general procedure was proposed in the past by Heym and colleagues [9,10], aiming at providing a rapid and easy way to distinguish evaporation from decomposition (mainly for ionic liquid compounds) by performing nonisothermal thermogravimetry (TG) experiments under ambient pressure while using two inert carrier gases (helium and nitrogen in the present study).
The rate of thermal decomposition (TD) as well as that of evaporation (EV) increases with temperature according to an exponential function. However, when a TG experiment is carried out, there are important differences between these two processes. First, TD occurs in the whole sample volume, while the rate of EV (or sublimation, SB) is affected by the mass transport coefficient of the sample into the surrounding gas phase and to the extent of the phase boundary interface.
Heym and colleagues described in detail in previous studies [9,10] how these parameters may influence the rate of EV, so that the use of two inert carrier gases should lead to two distinct temperature ranges in the case of evaporation, while no appreciable differences should be found when using these two gases when only decomposition takes place [10].
In the KEML technique, the vapor pressure P of a sample heated in a Knudsen cell is determined at each given temperature T in the explored range by measuring the mass loss rate Δm/Δt:
where M is the molar mass of the effusing vapor species and K is a constant whose value depends on the geometry of the effusion orifice (diameter and thickness). If the vapor contains more than one gas species, M in Equation (1) is replaced by the average molar mass <M>, given by
and the pressure P derived from Equation (1) is the total pressure in the cell. If the release of gas species occurs through more than one process, the composition of the vapor phase depends on the relative contribution of the various decomposition/evaporation channels and, as a consequence, <M> is expected to be temperature dependent. Strictly speaking, owing to the presence of the effusion hole, the pressure given by Equation (1) is not equal to the equilibrium vapor pressure of the sample, which would be measured in a perfectly closed vessel. The difference between apparent pressure and thermodynamic pressure is related to the ratio between the orifice area (corrected by the transmission or Clausing coefficient) and the evaporating sample area: the smaller this ratio, the closer the measured pressure to the equilibrium value. However, even small values of this ratio may not guarantee the attainment of a close-to-equilibrium condition in the cell if the evaporation process suffers from severe kinetic limitations, as expressed by a small value (<<1) of the evaporation coefficient α.
P = K · Δm/Δt · (T/M)1/2
<M> = [∑xi,cell · (Mi)1/2]2
To take into account these effects, Equation (1) has to be corrected by a factor: [1 + (C Ahole/α Asample)], where C is the Clausing factor, α the evaporation coefficient, and Ahole and Asample are the areas of the effusion orifice and evaporating sample, respectively. The value of α can be significantly lower than 1 when the species released is particularly bulky or is formed by a decomposition process, which involves bond breaking and/or bond formation. In the simple evaporation of a liquid, α is reasonably assumed to be close to unity. In such a case, a close-to-equilibrium condition is attained inside the cell between the condensed phase and the vapor phase, so the use of orifices of different sizes is not expected to significantly affect the apparent pressure. However, if a kinetically hindered process occurs, the heterogeneous equilibrium is not attained in the cell and the orifice geometry does affect the pressure evaluated by Equation (1). Further, Equation (1) is valid only under the so-called free molecular flow conditions, i.e., when the mean free path of the molecules is larger than the orifice diameter (ideally, no smaller than 10 times larger). The KEML data collected in our experiments with the 1 mm and 0.3 mm orifices are at the limit or slightly beyond the above condition, so Equation (1) should be corrected accordingly. However, because our KEML measurements are aimed not at obtaining accurate values of the pressure but rather at investigating the dependence of the specific mass loss on the orifice size, this limitation can be overlooked for the present purposes.
Knudsen effusion mass spectrometry (KEMS) is a classic technique in which the vapors effusing from a heated Knudsen cell enter into a mass spectrometer to be analyzed. Unlike TG, KEML, QCM, and other “blind” techniques, information on the composition of the vapor phase can be obtained by KEMS, provided that the ions detected in the mass spectrum are correctly assigned to the corresponding neutral precursors. In the field of ILs, this technique was successfully applied in the past decade for identifying either the NIP or other species produced by evaporation [5,24,25] and to study the co-occurrence of evaporation and thermal decomposition/dissociation phenomena [17,19].
2.2. Material
1-Butyl-3-methylimidazolium chloride (BMImCl) was prepared according to a procedure available in the literature [26]. A solution of 1-chlorobutane (108 mmol) and 1-methylimidazole (108 mmol) in acetonitrile (60 mL) was refluxed for 48 h under inert atmosphere (Ar). Once cooled to room temperature, two layers were observed. The upper layer was removed, and the lower one was extracted with ethyl acetate three times to remove unreacted starting materials. The remaining solvent from ionic liquid was removed via rotary evaporator, and the product was dried under high vacuum at 50 °C for 24 h. The same procedure was used to synthesize BMImBr and BMImI, and all three ILs were used without any further purification. The 1H NMR spectra are reported in Figure S1 of the Supplementary Materials. BMImCl: 1H NMR (300 MHz, CD3CN) δ (ppm): 0.91 (t, J = 7.3 Hz, 3H), 1.26–1.36 (m, 2H), 1.76–1.86 (m, 2H), 3.90 (s, 3H), 4.22 (t, J = 7.2 Hz, 2H), 7.51 (m, 1H), 7.54 (m, 1H), 9.77 (s, 1H) [27]. BMImBr: 1H NMR (300 MHz, CD3CN) δ (ppm): 0.91 (t, J = 7.4 Hz, 3H), 1.24–1.37 (m, 2H), 1.76–1.86 (m, 2H), 3.88 (s, 3H), 4.21 (t, J = 7.2 Hz, 2H), 7.48 (m, 1H), 7.52 (m, 1H), 9.29 (s, 1H) [27]. BMImI: 1H NMR (300 MHz, CD3CN) δ (ppm): 0.91 (t, J = 7.3 Hz, 3H), 1.25–1.37 (m, 2H), 1.76–1.86 (m, 2H), 3.86 (s, 3H), 4.19 (t, J = 7.2 Hz, 2H), 7.43 (m, 1H), 7.49 (m, 1H), 8.93 (s, 1H). No signal from 1-methylimidazole excess or other impurities (apart from water) was observed in the spectra.
1-Butyl-3-methylimidazolium bis((trifluoromethyl)sulfonyl)imide (BMImNTf2) was supplied by Sigma-Aldrich (BASF quality over 98%). Details on any pretreatment of the sample before the measurements were reported in a previous paper [5]. Further data (molecular formulas, molar masses, CAS numbers, and diffusion coefficients) are listed in Table 1.

Table 1.
Molecular formulas, molar masses, CAS numbers, and diffusion coefficients Dig of the ILs studied by TG in two inert gases.
2.3. Thermal Analysis and Knudsen Effusion Experimental Details
Thermogravimetry experiments were carried out by using a STA 625 Stanton Redcroft simultaneous TG/DTA apparatus (Stanton Redcroft, Surrey, UK), equipped with two identical open cylindrical aluminum crucibles, using also an empty one for reference. Samples of about 10 mg were accurately weighted and analyzed at a heating rate of 10 K min−1 in the range from ambient temperature up to 673 K under nitrogen or helium carrier gases at 50 mL min−1. Very pure indium and lead wire samples were used for temperature calibration, and a final standard uncertainty of ±0.1 K can be estimated.
A Ugine-Eyraud Setaram thermobalance (B60 model) was used for KEML experiments. A graphite resistor is the heating element, containing a quartz tube with the measuring cell. The cell is inserted into a capped copper cylinder to make the sample temperature uniform. To improve the accuracy of the temperature measurement, a Pt100 platinum-resistance thermometer is inserted directly into the copper cylinder. Three pyrophyllite effusion cells with 0.3, 1 and 3 mm hole diameters were used. The calibration constants K of Equation (1) were measured for all three orifices by vaporizing pure cadmium (Sigma-Aldrich, 99.999%, purified by melting), which resulted in 92,000 (3 mm diameter), 450,000 (1 mm), and 585,000 (0.3 mm) Pa s (g mol K)−1/2, respectively. The body of the cell was 8 mm in internal diameter and 15 mm in height. The thickness of the orifices can be estimated at about 0.1 mm in all cases. Before starting each experiment, the apparatus was heated at 70 °C and kept at this temperature for approximately 12 h to remove water and other volatile substances possibly contained in the sample. Further details on the equipment and experimental conditions are available elsewhere [5]. In a typical experiment, about 100 mg of the sample was loaded in the cell, with a mass loss of about 20 mg at the end of the run. The duration of each run was in the 20–100 h range, depending on the orifice size and temperature range explored.
In our KEMS apparatus [29,30], the vapor species are positively ionized through electron impact, focused into an ion beam, and accelerated by a 6 kV voltage. The separation of ions according to their mass-to-charge ratio is accomplished through a magnetic sector and detection by using an electron multiplier. The cell is heated by irradiation from a coil-shaped tungsten resistor surrounding the Knudsen cell. An alumina Knudsen cell (1 mm effusion orifice diameter) was used and inserted into an outer tantalum container. As a rule, the energy of the ionizing electron beam was set at 40 eV, generally corresponding to the maximum of the ionization efficiency.
The ion intensity InX+ measured for a given isotope n of the species X can be converted into the partial pressure P of the corresponding neutral precursor in the cell by using Equation (3):
where Kinstr is a calibration constant, T is the absolute temperature, and a, σ, and γ are the isotope abundance, the electron impact ionization cross section, and the detector gain for the species whose intensity is measured, respectively. The calibration constant in Equation (3) was derived by vaporizing pure cadmium from the same cell used in experiments on BMImCl.
PX = (Kinstr · InX+ · T)/(σX · γnX · anX)
3. Results and Discussion
The results of the competition study between evaporation’s occurring and decomposition’s occurring in BMImCl upon heating at relatively high temperatures are presented in Section 3.1, Section 3.2 and Section 3.3. Inert purging gas atmosphere and high vacuum (under effusion regime) experimental conditions were explored by using thermal analysis and Knudsen effusion techniques, respectively.
3.1. Thermogravimetric Analysis
The TG curves of the BMIm halides are shown in Figure 1.
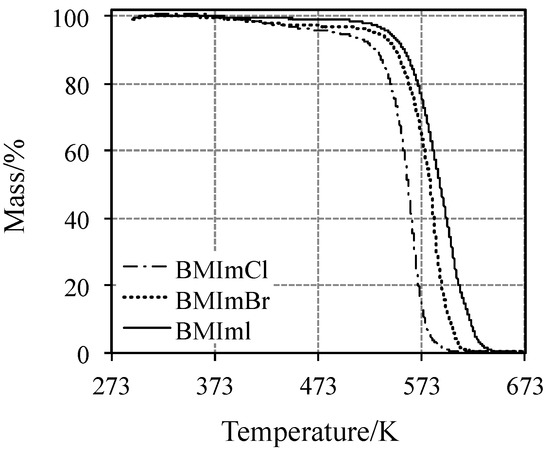
Figure 1.
TG curves for the three BMIm halide ionic liquids at 10 K min−1 under nitrogen atmosphere.
BMImBr and BMImCl undergo dehydration, accompanied by the evolution of a small amount of water between 373 and 473 K (negligible for BMImI). This process is followed by a single-step mass loss up to 673 K. The lowest onset temperature, Ton = 530.5 K, was detected for BMImCl, followed by those of bromide and iodide ILs: 540 and 550 K, respectively.
In order to evaluate the tendency of BMImCl to undergo decomposition rather than evaporation (or at least to check whether the former pathway is favored over the latter), the first-order derivatives of both the TG curves (DTG curves) of BMImCl and BMImNTf2 under identical nitrogen and helium flow were analyzed in Figure 2.
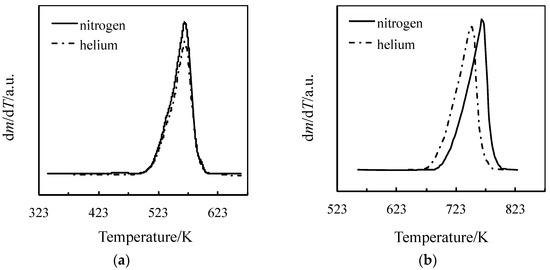
Figure 2.
DTG curves for TG experiments carried out with two inert gases at 10 K min−1 for (a) BMImCl and (b) BMImNTf2.
The DTG peaks describing the mass loss step of BMImCl (Figure 2a) are superimposed. In Heym’s approach [9,10], the authors suggest that in this case, thermal decomposition seems to prevail over evaporation. On the contrary, BMImNTf2, which is recognized as very stable (and was considered for comparison purposes), is confirmed to undergo evaporation with a negligible contribution from decomposition (Figure 2b), as revealed by the shift of the DTG peak under nitrogen compared with that under helium (thanks to the different diffusion coefficients).
3.2. Knudsen Effusion Mass Loss (KEML)
The occurrence of the thermal decomposition of BMImCl, suggested by the TG experiments, was further investigated by conducting Knudsen effusion mass loss experiments. As mentioned in the introduction, it has been recently shown that the competition between evaporation and decomposition in the BMImPF6 [17] and BMImBF4 [19] ILs is significantly affected by the degree of confinement in the sample: the greater the confinement is (e.g., effusion conditions with small orifices), the more thermal decomposition becomes important compared to evaporation, and vice versa. Therefore, under the so-called Langmuir or open-surface conditions, the decomposition is so disfavored that the simple congruent evaporation to NIPs can become the largely dominant process [19]. In spite of the fact that this behavior was observed only recently for ILs, similar evidence was previously reported for some molecular substances [31]. This phenomenon can be reasonably explained by assuming that the decomposition process is inherently slower than evaporation, and it can be more easily observed under conditions where the gas phase is allowed to persist above the liquid.
In order to gather further evidence for the occurrence of thermal decomposition processes in BMImCl, we carried out KEML experiments by using Knudsen cells with different orifice diameters. Indeed, according the abovementioned scenario, a dependence of the unit area mass loss rate from the effusion hole size would be expected because of the occurrence of thermal decomposition. Experiments were conducted with 0.3, 1, and 3 mm diameter orifices. In Table 2, we report a list of the ln(K · ∆m/∆t) vs. 1/T data points (see Equation (1)). For a given constant temperature and an average molar mass of the vapor, K · ∆m/∆t is the mass flux normalized for the different vaporizing surfaces (i.e., the orifice areas), which in turn is proportional to the vapor pressure. Therefore, this value should not depend on the orifice diameter in the absence of kinetic limitations when gaseous species are released from the solid phase.

Table 2.
Temperature dependence of the K · ∆m/∆t values according to Equation (1) for BMImCl measured by KEML with three effusion holes of diameter ϕ.
The same data are plotted in Figure 3, where the sizable increase in the mass flux with a decrease in the orifice diameter is evident. The best-fitting lines for the data reported in Figure 3 are the following:
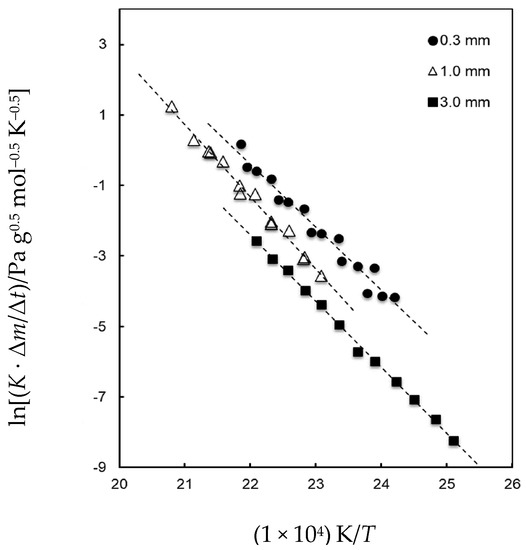
Figure 3.
Logarithmic plot of the mass loss rate multiplied by the cell constant (see Equation (1)) for BMImCl measured by KEML with three effusion holes.
- ln[(K · Δm/Δt)/Pa g0.5 mol−0.5 K−0.5] = (38.785 ± 0.636) − (18727 ± 270)/T(K) for the 3 mm orifice
- ln[(K · Δm/Δt)/Pa g0.5 mol−0.5 K−0.5] = (43.836 ± 1.216) − (20524 ± 522)/T(K) for the 1 mm orifice
- ln[(K · Δm/Δt)/Pa g0.5 mol−0.5 K−0.5] = (38.855 ± 2.065) − (17844 ± 897)/T(K) for the 0.3 mm orifice.
We point out that because the mass loss was due to the co-occurrence of several processes, the parameters of the fitting line do not lend themselves to any simple thermodynamic interpretation.
This evidence suggests that the smaller the orifice (i.e., the greater the confinement of the sample), the larger the pressure of the gas species released as a result of the decomposition. We can conclude that the outcome of KEML measurements is consistent with what we found in TG experiments. Note that the KEML data reported in Table 2 cannot be reliably converted in total pressures by using Equation (1), because the average mass of the vapor is not known, being that it is related to the various gas-releasing processes occurring in the cell and to their relative importance.
3.3. Knudsen Effusion Mass Spectrometry (KEMS)
To obtain more information on the vapor phase produced by BMImCl under decomposition/evaporation, we have performed further measurements by using KEMS. In this technique, the vapors effusing from the cell are analyzed by a mass spectrometer, as detailed in the experimental section. Two experimental runs were carried out in the overall temperature range from 416 to 474 K. Previous KEMS studies carried out on thermally stable ILs [5,6] have shown that the mass spectrum of the vapor is dominated by the peak corresponding to the cation C+ of the C+A− ionic liquid. It is assumed that this species is formed through the fragmentation of the evaporated NIP thanks to electron impact. Thus, the peak at m/e = 139 (BMIm+) is by far the most intense in the mass spectrum of BMImNTf2 [5]. On the contrary, this peak was found to have negligible intensity in the KEMS spectrum of the BMImCl vapor obtained in the present work. An extremely weak signal at m/e = 139 was detected only at the highest experimental temperature (474 K). However, many intense peaks were displayed at lower mass values. For the sake of providing an example, the spectrum registered at 474 K is reported in Figure 4. Note that the intensity of the signals in Figure 4 was background-subtracted to get rid of the contribution from molecules that did not come from the Knudsen cell.
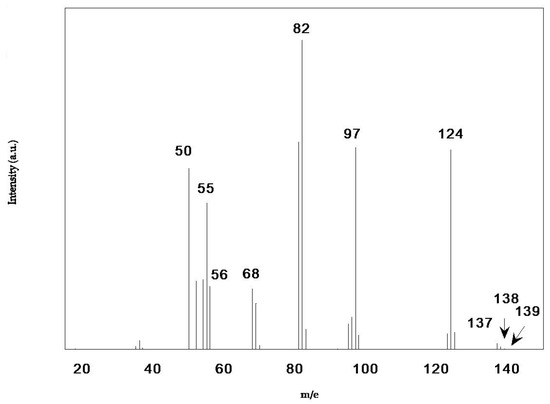
Figure 4.
KEMS spectrum of the vapor released by BMImCl at T = 474 K.
Some of the peaks in Figure 4 are easily assigned to the molecular ions of the neutral precursors corresponding to decomposition products of the BMImCl, according to the processes reported below (methyl chloride MCl (m/e = 50, 52), methylimidazole MIm (m/e = 82), and butylimidazole BIm (m/e = 124)):
BMImCl(l) → Bim(g) + MCl(g)
BMImCl(l) → Mim(g) + BCl(g)
Note that practically no peak was observed at m/e = 92 and 94, corresponding to the second product displayed in Equation (5), i.e., 1-chlorobutane BCl. This is consistent with the mass spectrum of this compound reported in the literature [32], which displays the peak at m/e = 56 as the most intense, with no appreciable signal corresponding to the molecular ion: m/e = (92, 94). The other most-intense peaks in Figure 4 (at m/e = 55, 68, 81, 82, and 97) correspond to fragment ions of butylimidazole, in agreement with the reference spectrum of this compound [32]. By analyzing the ionization efficiency curves of the CH3Cl+ and MIm+ signals, the appearance potentials were determined as (11.0 ± 0.5) and (9.2 ± 0.5) eV, respectively, which are consistent with the ionization energies reported in the literature [33], thus confirming their molecular ion nature.
Our MS results are quite consistent with the study reported by Lovelock et al. [22] on octylmethylimidazolium chloride. Unfortunately, unlike that study, in our case, the low intensity of the peak corresponding to NIP (m/e = 139) did not allow for monitoring the evaporation process as a function of temperature or for determining the associated enthalpy change. However, from the measured ion currents, it is in principle possible to estimate the partial pressures of the decomposition products that were identified from the mass spectrometric pattern. To this end, Equation (3) has to be applied, which implies that the electron impact ionization cross sections (σ) are known. In the absence of any literature data, such values have been roughly estimated by applying an additivity scheme based on the contributions of the various groups and bonds [34,35], obtaining the following values: 6.92 (methyl chloride), 14.7 (butyl chloride), 9.22 (methylimidazole), and 17.0 (butylimidazole). The partial pressures can then be estimated by taking into account the ion intensities of the most intense peaks assigned to each precursor. For the sake of providing example, the KEMS pressure of CH3Cl(g) at the mean temperature of 445 K is evaluated as 0.02 Pa. The pressure of CH3CH2CH2CH2Cl is only slightly lower. This suggests that decomposition processes (4) and (5) have roughly the same importance. In the case of alkylimidazoles, the intense peak at m/e = 82 is contributed both by methylimidazole and by the fragmentation of butylimidazole, making the estimate of the partial pressures more problematic. However, in accordance with reactions (4) and (5), the partial pressures of the imidazole species should be the same as the corresponding chloride species (after correcting for the molar mass ratio related to the different effusion rates). On this basis, from a CH3Cl partial pressure estimate of 0.02 Pa, a total pressure of the order of 0.1 Pa at 445 K can be derived. This value is in order-of-magnitude agreement with the total pressure of 0.25–0.30 Pa estimated at the same temperature from the KEML data (1 mm orifice data) by assuming from Equation (2) a mean molar mass of 85 g mol−1 (corresponding to a mole fraction of 0.25 for the four decomposition products of reactions (4) and (5)). Interestingly, the so-obtained pressure values are more than three orders of magnitude higher than the (total) evaporation pressure of the BMImCl(g) NIP derived by Verevkin et al. [23], who used the QCM technique performed under open-surface evaporation conditions. For example, at 445 K, a vapor pressure of 4.7 10−5 Pa is given in [23].
This evidence suggests that under effusion conditions, the thermal decomposition of BMImCl is strongly enhanced, whereas the release of gas is greatly reduced under open-surface evaporation. These findings confirm the outcomes of previous works on BMImPF6 [17] and BMImBF4 [19]. Moreover, the results of the KEML measurements reported above show that the KEMS-derived pressures, being obtained with an orifice of 1 mm diameter, are much more likely lower than the equilibrium values of processes displayed in Equations (4) and (5), which means that performing a thermodynamic analysis on such processes would be improper.
4. Conclusions
We carried out a multitechnique study aimed at investigating the evaporation/decomposition behavior of the BMImCl ionic liquid under different experimental conditions. Thermogravimetry experiments performed under nitrogen and helium atmospheres suggested the occurrence of thermal decomposition at temperatures above 500 K, as indicated by the TG-derivative curves, which were practically coincident regardless of the gaseous atmosphere used in the experiment. Knudsen effusion mass loss experiments performed with orifices of different geometries indicated a clear dependence of the mass loss rate per unit surface on the orifice size in the 398–481 K range, the mass flow being larger with smaller orifices, which points toward the occurrence of a kinetically limited process. Unlike the simple evaporation of neutral ion pairs from the liquid surface, a chemical decomposition inside the bulk of the liquid would be consistent with this experimental evidence. The Knudsen effusion mass spectrometry measurements carried out in the 416–474 K range confirmed this view, displaying mass spectra with strong peaks corresponding to the most plausible decomposition products of BMImCl, such as methyl chloride, butyl chloride, methylimidazole, and butylimidazole.
Furthermore, practically no signal was observed at the m/e of the integer cation (BMIm+), whose presence is usually associated with gaseous neutral ion pairs formed through the simple evaporation of the liquid. The KEML and KEMS results agreed insofar as indicating a total pressure of 0.1–0.3 Pa at 445 K (for experiments on 1 mm diameter orifices). Overall, the outcome of our work provided significant experimental evidence for the occurrence of the thermal decomposition of the compound in the temperature ranges explored. This result did not seem to be in contrast with recent studies where the simple evaporation of the liquid was actually observed under open-surface conditions at lower temperatures.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/thermo3020015/s1, Figure S1. 1H NMR spectra of (a) BMImCl, (b) BMImBr, (c) BMImI (300 MHz, CD3CN).
Author Contributions
Conceptualization, S.V.C. and A.C.; methodology, B.B., G.S., S.V.C., G.G., A.L. and A.C.; synthesis, A.L.; investigation, B.B., G.S., A.C., E.T. and S.V.C.; data curation, B.B., G.G., S.V.C. and A.C.; writing—original draft preparation, S.V.C. and A.C.; writing—review and editing, B.B., S.V.C. and A.C.; supervision, S.V.C. and A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article or Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maton, C.; De Vos, N.; Stevens, C.V. Ionic liquid thermal stabilities: Decomposition mechanisms and analysis tools. Chem. Soc. Rev. 2013, 42, 5963–5977. [Google Scholar] [CrossRef]
- Xu, C.; Cheng, Z. Thermal Stability of Ionic Liquids: Current Status and Prospects for Future Development. Processes 2021, 9, 337. [Google Scholar] [CrossRef]
- Paolone, A.; Haddad, B.; Villemin, D.; Boumediene, M.; Fetouhi, B.; Assenine, M.A. Thermal Decomposition, Low Temperature Phase Transitions and Vapor Pressure of Less Common Ionic Liquids Based on the Bis(trifuoromethanesulfonyl)imide Anion. Materials 2022, 15, 5255. [Google Scholar] [CrossRef] [PubMed]
- Earle, M.J.; Esperança, J.M.S.S.; Gilea, M.; Canongia Lopes, J.N.A. The distillation and volatility of ionic liquids. Nature 2006, 439, 831–834. [Google Scholar] [CrossRef]
- Brunetti, B.; Ciccioli, A.; Gigli, G.; Lapi, A.; Misceo, N.; Tanzi, L.; Vecchio Ciprioti, S. Vaporization of the prototypical ionic liquid BMImNTf2 under equilibrium conditions: A multitechnique study. Phys. Chem. Chem. Phys. 2014, 16, 15653–15661. [Google Scholar] [CrossRef]
- Barulli, L.; Mezzetta, A.; Brunetti, B.; Guazzelli, L.; Vecchio Ciprioti, S.; Ciccioli, A. Evaporation thermodynamics of the tetraoctylphosphonium bis(trifluoromethansulfonyl)imide([P8888]NTf2) and tetraoctylphosphonium nonafluorobutane-1-sulfonate ([P8888]NFBS) ionic liquids. J. Mol. Liq. 2021, 333, 115892. [Google Scholar] [CrossRef]
- Cao, Y.; Mu, T. Comprehensive Investigation on the Thermal Stability of 66 Ionic Liquids by Thermogravimetric Analysis. Ind. Eng. Chem. Res. 2014, 53, 8651–8664. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Zaitsau, D.H.; Schick, C.; Heym, F. Development of Direct and Indirect Methods for the Determination of Vaporization Enthalpies of Extremely Low-Volatile Compounds. In Handbook of Thermal Analysis and Calorimetry; Vyazovkin, S., Koga, N., Schick, C., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2018; Chapter 1; Volume 6, pp. 1–46. [Google Scholar] [CrossRef]
- Heym, F.; Korth, W.; Etzold, B.J.M.; Kern, C.; Jess, A. Determination of vapor pressure and thermal decomposition using thermogravimetrical analysis. Thermochim. Acta 2015, 622, 9–17. [Google Scholar] [CrossRef]
- Heym, F.; Etzold, B.J.M.; Kern, C.; Jess, A. Analysis of evaporation and thermal decomposition of ionic liquids by thermogravimetrical analysis at ambient pressure and high vacuum. Green Chem. 2011, 13, 1453–1466. [Google Scholar] [CrossRef]
- Federghini, C.; Guazzelli, L.; Pomelli, C.S.; Ciccioli, A.; Brunetti, B.; Mezzetta, A.; Vecchio Ciprioti, S. Synthesis, thermal behavior and kinetic study of N-morpholinium dicationic ionic liquids by thermogravimetry. J. Mol. Liq. 2021, 332, 115662. [Google Scholar] [CrossRef]
- Brunetti, B.; Ciccioli, A.; Lapi, A.; Buzyurov, A.V.; Nagrimanov, R.N.; Varfolomeev, M.A.; Vecchio Ciprioti, S. Sublimation Study of Six 5-Substituted-1,10-Phenanthrolines by Knudsen Effusion Mass Loss and Solution Calorimetry. Entropy 2022, 24, 192. [Google Scholar] [CrossRef] [PubMed]
- Deyko, A.; Lovelock, K.R.J.; Licence, P.; Jones, R.G. The vapour of imidazolium-based ionic liquids: A mass spectrometry study. Phys. Chem. Chem. Phys. 2011, 13, 16841–16850. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, J.P.; Hurst, C.; Jones, R.G.; Licence, P.; Lovelock, K.R.J.; Satterley, C.J.; Villar-Garcia, I.J. Vapourisation of ionic liquids. Phys. Chem. Chem. Phys. 2007, 9, 982–990. [Google Scholar] [CrossRef] [PubMed]
- Verevkin, S.P.; Zaitsau, D.H.; Emelyanenko, V.N.; Heintz, A. A New Method for the Determination of Vaporization Enthalpies of Ionic Liquids at Low Temperatures. J. Phys. Chem. B 2011, 115, 12889–12895. [Google Scholar] [CrossRef] [PubMed]
- Zaitsau, D.H.; Yermalayeu, A.V.; Emel’yanenko, V.N.; Butler, S.; Schubert, T.; Verevkin, S.P. Thermodynamics of Imidazolium-Based Ionic Liquids Containing PF6 Anions. J. Phys. Chem. B 2016, 120, 7949–7957. [Google Scholar] [CrossRef]
- Volpe, V.; Brunetti, B.; Gigli, G.; Lapi, A.; Vecchio Ciprioti, S.; Ciccioli, A. Toward the Elucidation of the Competing Role of Evaporation and Thermal Decomposition in Ionic Liquids: A Multitechnique Study of the Vaporization Behavior of 1-Butyl-3-methylimidazolium Hexafluorophosphate under Effusion Conditions. J. Phys. Chem. B 2017, 121, 10382–10393. [Google Scholar] [CrossRef]
- Clarke, C.J.; Puttick, S.; Sanderson, T.J.; Taylor, A.W.; Bourne, R.A.; Lovelock, K.R.J.; Licence, P. Thermal stability of dialkylimidazolium tetrafluoroborate and hexafluorophosphate ionic liquids: Ex situ bulk heating to complement in situ mass spectrometry. Phys. Chem. Chem. Phys. 2018, 20, 16786–16800. [Google Scholar] [CrossRef]
- Dunaev, A.M.; Motalov, V.B.; Kudin, L.S. The Composition of Saturated Vapor over 1-Butyl-3-methylimidazolium Tetrafluoroborate Ionic Liquid: A Multi-Technique Study of the Vaporization Process. Entropy 2021, 23, 1478. [Google Scholar] [CrossRef]
- Kamavaram, V.; Reddy, R.G. Thermal stabilities of di-alkylimidazolium chloride ionic liquids. Int. J. Thermal Sci. 2008, 47, 773–777. [Google Scholar] [CrossRef]
- Chambreau, S.D.; Boatz, J.A.; Vaghjiani, G.L.; Koh, C.J.; Kostko, O.; Golan, A.; Leone, S.R. Thermal Decomposition Mechanisms of 1-Ethyl-3-methylimidazolium Bromide Ionic Liquid. J. Phys. Chem. A 2012, 116, 5867–5876. [Google Scholar] [CrossRef]
- Lovelock, K.R.J.; Armostrong, J.P.; Licence, P.; Jones, R.G. Vaporisation and thermal decomposition of dialkylimidazolium halide ion ionic liquids. Phys. Chem. Chem. Phys. 2014, 16, 1339–1353. [Google Scholar] [CrossRef] [PubMed]
- Zaitsau, D.H.; Siewert, R.; Pimerzin, A.A.; Bülow, M.; Held, C.; Loor, M.; Schulz; Verevkin, S.P. From volatility to solubility: Thermodynamics of imidazolium-based ionic liquids containing chloride and bromide anions. J. Mol. Liq. 2017, 323, 114998. [Google Scholar] [CrossRef]
- Dunaev, A.M.; Motalov, V.B.; Kudin, L.S.; Butman, M.F. Thermodynamic properties of the ionic vapor species over EMImNTf2 ionic liquid studied by Knudsen effusion mass spectrometry. J. Mol. Liq. 2016, 223, 407–411. [Google Scholar] [CrossRef]
- Dunaev, A.M.; Motalov, V.B.; Kudin, L.S.; Butman, M.F. Molecular and ionic composition of saturated vapor over EMImNTf2. J. Mol. Liq. 2016, 219, 599–601. [Google Scholar] [CrossRef]
- Matsagar, B.M.; Dhepe, P.L. Effects of cations, anions and H+ concentration of acidic ionic liquids on the valorization of polysaccharides into furfural. New J. Chem. 2017, 41, 6137–6144. [Google Scholar] [CrossRef]
- Gilbert, A.; Haines, R.S.; Harper, J.B. Controlling the reactions of 1-bromogalactose acetate in methanol using ionic liquids as co-solvents. Org. Biomol. Chem. 2020, 18, 5442–5452. [Google Scholar] [CrossRef]
- Karaiskakis, G.; Gavril, D. Determination of diffusion coefficients by gas chromatography. J. Chromat. A 2004, 1037, 147–189. [Google Scholar] [CrossRef]
- Ciccioli, A.; Gigli, G. The uncertain bond energy of the NaAu molecule: Experimental redetermination and coupled cluster calculations. J. Phys. Chem. A 2013, 117, 4956–4962. [Google Scholar] [CrossRef]
- Lucci, E.; Giarrusso, S.; Gigli, G.; Ciccioli, A. Determination of the bond energies by Knudsen effusion mass spectrometry experiments combined with ab initio calculations. J. Chem. Phys. 2022, 157, 084303. [Google Scholar] [CrossRef]
- Long, G.T.; Vyazovkin, S.; Brems, B.A.; Wight, C.A. Competitive Vaporization and Decomposition of Liquid RDX. J. Phys. Chem. B 2000, 104, 2570–2574. [Google Scholar] [CrossRef]
- NIST Mass Spectrometry Data Center; Wallace, W.E. Mass Spectra. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023. [Google Scholar] [CrossRef]
- Lias, S.G.; Levin, R.D.; Kafafi, S.A. Ion Energetics Data. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023. [Google Scholar] [CrossRef]
- Bull, J.N.; Harland, P.W.; Vallance, C. Absolute Total Electron Impact Ionization Cross-Sections for Many-Atom Organic and Halocarbon Species. J. Phys. Chem. A 2012, 116, 767–777. [Google Scholar] [CrossRef] [PubMed]
- Gupta, D.; Rahla Naghma, R.; Bobby Antony, B. Electron impact total ionisation cross sections for simple bio-molecules: A theoretical approach. Mol. Phys. 2014, 112, 1201–1209. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).