Abstract
Accurate soil heat transfer models are needed to predict and adapt to a warming arctic. A numerical model to accurately predict temperatures and thaw depths in soils, both with depth and with horizontal distance from features such as cliffs, was developed in Matlab using the finite element method. The model was validated against analytical solutions to simple versions of the problem and experimental temperature data from borehole thermistor strings on the north shore of Alaska. The current model is most useful for short term (on the order of days) predictions of thaw depth and near surface temperatures in homogeneous soils with existing data to allow the calibration of soil thermal parameters. These are exactly the time scales and capabilities that would integrate well with erosional models to predict the erosion during storm events and summer thaw conditions. Comparisons with analytical solutions show the model to be fairly accurate in predictions of temperatures thaw-depth and temperatures, within about 0.25 °C and 0.02 m respectively, for reasonable arctic soil parameters. Differences between predicted temperatures and thaw-depth against borehole data from Barter Island, Alaska are within about 1 °C and 0.5 m respectively. Comparison to commercial software, which does not directly track and move the phase change boundary, shows that this moving-mesh model has much better agreement. The model developed in this work is flexible and can be modified to model a wide variety of problems, but is efficiently set up to take a surface and thaw-boundary profile (not necessarily horizontal) and use soil parameters and surface boundary conditions appropriate to Arctic regions. It has been verified to appropriately model cliffs, which are particularly vulnerable to erosion.
1. Introduction
Permafrost temperatures have increased by up to three degrees Celsius from the early 1980s to the mid-2000s in parts of northern Alaska and near-surface permafrost extent is predicted to decrease substantially in high northern latitudes by the end of the 21st century [1]. Increased coastal erosion [2,3] from higher sea levels, increased ocean temperature, and longer sea-ice-free season and infrastructure failure, as well as other environmental changes such as changes in wetlands may be expected from melting permafrost and other facets of the warming Arctic.
Soils are resistant to coastal erosion when frozen [4], thus the thermal state and evolution of the soil profile is important in understanding and predicting the erosion of these sediments. Water affects the soils it is in contact with both thermally and mechanically [5]. An added factor in the erosion of thawed soils is that frozen soils in the arctic may be predominantly ice-soils in the five-meter zone of erosion (bluffs to two meters below grade) in the Beaufort Sea coast are up to 75% ice [6].
In a warming Arctic, degradation of permafrost and increased coastal and thaw pond erosion is expected. In order to predict and mitigate the harm to infrastructure, communities, and the environment, one must develop accurate models of the thermal behavior of soils. These models can be used to investigate the effects of warming boundary conditions, the addition of active or passive soil cooling devices, or they can be paired with models of the mechanical interaction between soils and water in which they are in contact. While there exist sophisticated open source models to look at the mechanical interactions of water and soil, currently available thermal modeling software is overly complex, not easily integrated with mechanical and other models, and prohibitively expensive. A previous effort to develop an accurate soil thermal model to work with the open source sediment transport model Xbeach [5] used a one-dimensional model that would not accurately represent a cliff face or other complex geometry. To couple the thermal model to the erosional model, a highly accurate and precise depth of recently thawed soils (on short timescales of minutes to hours) is desirable to accurately predict ongoing erosion and evolution of the thermal and physical profile of the soil.
The main contribution of this work is development of a finite element model which will be useful in predicting thaw depth for short term which will be useful for erosional models to predict the erosion during storm events and summer thaw conditions.
This paper presents an experimentally verified numerical model that could accurately predict thaw depth and temperatures in arctic soils, primarily considering conduction of heat and phase change. The model developed in this work considered processes that are important such as latent heat of phase change, two-dimensional geometries, and simplified but useful boundary conditions. Because the depth to the boundary between thawed and frozen soils is the most important factor in the erodability of soils by water, the model aimed for maximum accuracy in this prediction.
The Finite Element Method (FEM) uses integral formulations instead of the difference equations from local Taylor expansions used in Finite Difference Methods [7], which allows for continuity at the boundaries of elements [8]. FEM handles problems with complex geometries or boundary conditions and non-isotropic materials better than finite difference methods.
Phase Change Modeling—Issues and Approaches to Latent Heat
Accounting for the latent heat of freezing or melting in the heat conduction problem adds complexity to the numerical modeling, and there are many ways to account for it, with different strengths and weaknesses. Voller [9] and Huy and Argyropoulos [10] both give an overview of the various approaches, as summarized below.
The phase change boundary in the case of solidification of a pure material (the Stefan Problem) is a sharp moving boundary.
The Stefan Problem is characterized by the following equations:
Heat transfer in the solid (s):
Similarly; Heat transfer in the liquid (l):
Equations (1) and (2) are essentially a 2D heat transfer equation without internal heat generation, where the dimensionality of the spatial derivatives of temperature has been generalized using the divergence of the gradient. The heat balance at the phase change boundary (known as the Stefan Condition) is:
where is the normal vector to the phase change interface, v is the velocity of the interface, and L is the volumetric latent heat.
Analytical formulations such as the Neumann solution to the Stefan problem can be used to check numerical models, with appropriate simple boundary conditions and geometries. The Neumann solution is the analytical solution to the 2-phase Stefan problem (thermal parameters c and k that are different, but constant, in each of the two phases) with a semi-infinite media and a constant temperature surface boundary condition.
Solutions to more complex geometries and boundary conditions have also been developed [10].
In numerical models, the ‘strong’ formulation of the phase change process involves locating the moving boundaries of phase change (similar to the analytical Stefan problem) and finding the temperatures at each step. Fixed grids or variable grids can be used in this numerical modeling—fixed grids are easier to formulate but break down if the boundary moves more than one grid space.
Other authors have developed numerical soil thermal models for tailored for specific applications. Ling and Zhang [11] developed a two-dimensional model in cylindrical coordinates, assuming no annular heat flow, to model thaw bulb (known as a talik) formation under thaw lakes in arctic Alaska. Borisov [12] modeled permafrost melting under heated buildings in the arcticusing the finite element method and unstructured meshes in up to three dimensions with a phase transition smoothed with linear interpolation.
Zottola [3] used SVHEAT to model soils at Drew Point, Alaska and investigate the feasibility of using thermosyphons to stabilize melting permafrost. The author develops an appropriate seasonal air temperature and n-factor function to model the air-ground boundary condition, presents appropriate soil heat capacities and conductivities from the literature for his location, and compares with borehole data to show good agreement.
Liandi [13] compares moving and non-moving mesh solutions. The paper models the use of freeze pipes circulating brine to freeze mineshaft walls in soil. The moving mesh approach is considered more accurate and flexible, but computationally more difficult and slower. The authors note that results agree with other numerical simulations and lamented the lack of experimental data to compare to.
Comparison of numerical results to experimental data (in-situ borehole soil temperature data or lab data) is rare in the literature. In general, experimental data is costly and difficult to obtain in arctic environments, and the non-ideal, heterogeneous real-world conditions are difficult to verify with tractable models. However, the Alaska DOT has used the commercial Temp/W finite element software since 2006 or earlier [14] for 2D thermal modeling of embankments on permafrost soils, and compared results to borehole temperature data. Darrow [14] has published results for such comparisons, showing agreement between measured and modeled temperatures better than about 20F and thaw depths of around one to two feet. This agreement was considered acceptable for the engineering purposes, generally slightly over-predicting embankment thaw bulbs that would allow for conservative solutions to protecting against thaw in engineering design. These were long model runs of ten-year intervals starting with simplistic initial conditions (constant temperature soil) and n-factored surface boundary conditions based on air temperature and reasonable assumptions or laboratory measurements of soil parameters.
2. Method
A moving mesh, two-dimensional finite element heat transfer model was written in Matlab R2017b that takes phase-change into account with a solution of the Stefan condition at the phase-change boundary. The physical model domain was first divided into thawed and frozen subdomains, which were separately meshed using a Delaunay triangular mesh. Initial conditions were applied to the mesh nodes of the model. At each time step, a solution of the Stefan condition along the phase-change boundary determined the distance and direction that each phase change boundary node moved, and other nodes in the model domains were moved accordingly, with the original mesh retained. ‘Mass’, ‘Stiffness’ and ‘Velocity’ matrices for a Galerkin method solution of the finite element approximation of the governing heat transfer equation were assembled, and the nodal temperature solution for the current time step was obtained from that of the last time step using simple matrix operations. Temperature or flux boundary conditions were applied at the start of the problem and at each time step, and could be a defined function of time.
2.1. Meshing
To allow for the strong formulation of the Stefan condition chosen as phase-change method the physical domain was broken into two separate sub-domains, a top (thawed) subdomain, and a bottom (frozen) subdomain. The sub-domains were individually meshed as detailed in the next paragraph, although they were designed so as to share common nodes along the phase change boundary. This boundary, also called the ‘thaw-front’, is the bottom of the top domain and the top of the bottom domain (see Figure 1 below). The model allows arbitrary piecewise-linear descriptions of the domain top, bottom and phase-change boundary. The sides are defined as linear between the top and bottom of each subdomain.

Figure 1.
A meshed domain. The phase change boundary (in blue) separates the thawed and frozen subdomains, which are meshed and modeled separately, subject to the Stefan condition at the boundary.
Two-dimensional triangular meshing was accomplished using a Matlab algorithm presented in the literature [15] and modified slightly for this application. Triangular meshing was used since built in Matlab functions for it already exist, and the robust algorithm [15] for generating and refining the triangular mesh was available in the literature. It also is easier to mesh non-rectangular geometries with triangles, and it allows for straightforward, elegant solutions to the Finite Element Method matrices given in Equations (12)–(14) below. This algorithm starts with a reasonably uniform, staggered grid of nodes of a given distance. The nodes are pruned to allow a variation of mesh size defined across the model space. After using the Matlab function for Delaunay triangulation, the algorithm moves these nodes by solving for equilibrium in a simulated truss structure to produce a mesh of high quality using a fairly simple code (see Figure 1 for example).
2.2. Phase-Change Method
Because the depth to the boundary between thawed and frozen soils is an important factor in the ability of soils to be eroded, the numerical model developed aimed for maximum accuracy in this prediction. Therefore, a strong formulation of the Stefan condition (refer to Section 2.4) was used to model latent heat, in which the Stefan equation was solved at each time step to calculate and track the phase change boundary. This was done on a moving/variable grid to allow for easy accounting of the thawed vs. frozen elements and current position of the phase change boundary. The implementation of this method was based on a one-dimensional method developed by Mori [16].
Mori’s solution divided the domain into frozen and thawed subdomains and solved the finite element matrix equations for nodal temperatures separately in each subdomain, first imposing the Stefan condition on the freeze-thaw boundary common to each subdomain for each time step [16]. The finite element solution for each subdomain was based on the standard Galerkin method, taking into account the moving node points. Mesh connectivity between the nodes (i.e., elements defined by the nodes) was maintained as the nodes move. If θi is the temperature at elemental node i, {θ} is the column vector composed of the nodal temperatures of the element, Si is the linear shape function corresponding to node i and is dependent on the position coordinates, and [S] is an array of the shape functions for an element, then temperature anywhere in the element, T, is approximated by [8]:
The one-dimensional governing equation for conduction with no heat generation within the body, and assuming isotropic conductivity and volumetric heat capacity is:
where α = k/c, or thermal conductivity divided by volumetric heat capacity.
In one dimension, using the product rule, from Equation (4) we get:
It is important to retain the time derivative of the shape functions to account for the moving nodes. If Xi is the coordinate of node i, we can expand the derivative of [S] with respect to t [17]:
Note that Equation (7) is most helpful when generalized to two-dimensions. Mori [16] does a straightforward time derivative of the linear, one-dimensional shape functions to get directly at dS/dt. The term given by Equation (7) can be seen to be a correction for the convective effects of mesh motion [17].
For the Galerkin method, we use the shape functions as the weighting functions, multiplying Equation (5) by the transposed shape function array, [S]T, and integrating over the element area. To evaluate the term involving the second spatial derivative (the Laplacian in higher dimensions), the second terms were converted into first-order terms using the chain rule, and rearranging terms (see Moaveni Ch. 9 [8]):
The area integral of the first resultant term in Equation (8) becomes an integral around the element boundary, accounting for derivative boundary conditions, using Green’s Theorem. However, we ignore domain boundaries in this part of the analysis and apply these boundary conditions later. For now, we drop this term and use the second, noting that:
Putting all of this together, pulling functions of only the nodal temperatures out of the integrals and arranging, we get:
which gives the matrix form of the moving mesh finite element equation:
where:
The matrices are commonly known as M—mass matrix, K—stiffness matrix (by analogy with mechanics problems), and N is a matrix associated with the movement of the mesh, or a velocity matrix. Note that the spatial derivatives of the shape functions are not, themselves, dependent on the spatial variables, and are pulled out of the integrals and easily evaluated from the nodal coordinates. Similarly, the derivative of Xi with respect to time also comes out of the integral and can be calculated from the difference between nodal coordinates from the current and last time step. Elemental matrices are assembled into subdomain matrices separately for each of the two subdomains, leading to an ordinary differential equation of this form for each subdomain. The remaining integrations involve only Si or SiSj terms. These are easily solved as well, either using the form of the shape function in one dimension or relationships for the area integration of triangular shape functions (S1, S2 and S3) [18]:
where m, k, and l are any integer exponents.
The Stefan condition is imposed at the interface (phase change boundary) between the two subdomains at the beginning of each time step to determine the displacement (and thus velocity) of the boundary. The general Stephan condition is, where subscript s refers to the solid, or frozen, region, and subscript l to the liquid, or thawed, region:
In one dimension, v is dSn/dt, where dSn is the change in position of the boundary, or thaw-front):
where ks is the thermal conductivity in the solid/frozen region, and kl is the thermal conductivity in the liquid/thawed region.
Mori [16] presented clearly the algorithm for solving this problem in one dimension with the freeze-thaw boundary moving as given by a numerical solution of this Stefan condition and the rest of the subdomains then equally divided into a fixed number of elements. Mori also gave the forms of the assembled matrices.
Time is discretized using an equal mesh of spacing Δt. The time derivative in the equations above are replaced by time differences, for example:
The discretization of the time derivative may be done with a mixing ratio, µ, of from fully forward to fully backward. Although the code retains this ability, all runs were done with a fully backwards difference method (µ = 1 in the equation below. µ = 0 would be fully forward).
The equation solved to give nodal temperatures at the current time step is (Equation (14) from Mori, note x = A\B is the solution to Ax = B):
Mori’s algorithms were first coded in 1-D and then generalized to two dimensions using triangular elements and barycentric coordinates (Ai/A), following a similar approach to the method of Beckett et al. [17].
Mori used the simpler, one-dimensional Stefan condition given in Equation (17) above. Equation (16) above gives the general, multi-dimensional Stefan condition. To use this equation for the two-dimensional case, the slope of the normal to the thaw-front curve was found at each node using the coordinates of neighboring nodes on the front and used to calculate a unit normal. Then the nearest nodes in the normal direction to each node on the front were found. The actual direction of the vector between these nearest nodes and the thaw-front node was found, and also their temperatures from the last time step. This allowed the magnitude and direction of movement of each thaw-front node to be determined. Then all nodes were moved (except those on the top and bottom of the domain) in the same direction and magnitude as that of the nearest thaw-front node. This helped to avoid geometry issues including triangular mesh flipping and nodes moving past other nodes.
2.3. Boundary Conditions
Temperature (Dirichlet) and flux (Neumann) boundary conditions were used at the physical boundaries of the models. Soil in contact with air (the top surface and cliff faces) was modeled using a factored seasonal sinusoid temperature boundary condition with coefficients applicable to the north coast of Alaska as determined by Zottola [3] based on seasonal average highs and lows from the temperature record. It would have been much more challenging to implement a fully physical air-ground boundary condition accounting for long and short wavelength radiation, air convection and the latent heat of evaporation. Although using this method for ocean-cliff face erosion would involve a water boundary condition as well, we did not implement this boundary condition for this paper. Soil in contact with water will generally have a convective boundary condition only, although radiative heat transfer is possible where significant radiation is able to travel through the depth of the water. However, water-soil boundary conditions could also be modeled with a suitable temperature boundary condition. The underground sides of the model domain were modeled as a no-flux boundary. For ease of modeling, and because it was reasonably consistent with the data used, a constant temperature boundary condition was used at the bottom of the domain. Nodes on the freeze-thaw boundary had an imposed temperature boundary condition (0 °C) to enhance the stability of the solution.
2.4. Initial Conditions
Initial conditions were generally set based on the depth of the node only. Depending on the problem to be solved, they are either generated by an initial analytical solution to a simple Stefan Problem or derived from borehole thermistor temperature data. In the latter case, a fit was made to the data in each of the two regions (thawed and frozen), giving an equation of temperature vs. depth for each region. Nodes in the two regions were set to an initial temperature based only on their depth in the soil profile.
3. Results
3.1. Analytical Check
An analytical check was run on the two-dimensional version of the model, comparing results to those obtained from the Neumann Analytical solution to the Stefan problem. Table 1 gives the parameters used in this comparison. First, a one-dimensional analytical solution was obtained after a time period of three days (259,200 s) to use as an initial condition to the numerical model (Figure 2). A limitation of the finite element model is that it cannot start with the phase change boundary at the surface—it must have finite thawed and frozen sub-domains to start with. From this initial solution, an initial depth of the phase-change boundary was established for the finite element model, as well as initial temperatures of nodes as a function of depth. Then the finite element model was run for one day (86,400 s) and compared to results from a purely analytical solution over the same time period.

Table 1.
Parameters used in numerical and analytical comparison.
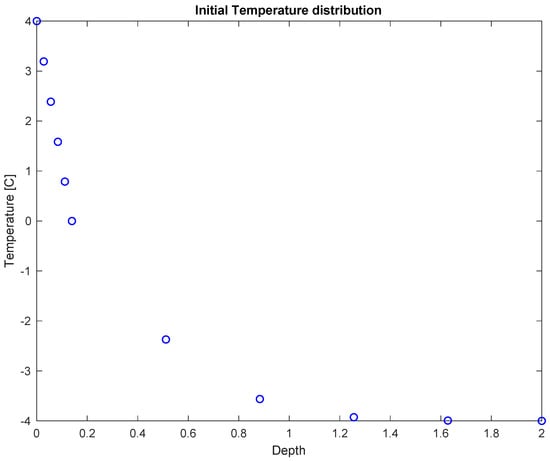
Figure 2.
Initial temperature conditions at nodes for the numerical model.
Figure 3 shows good agreement of the temperature solution for all nodes after one day of simulation.
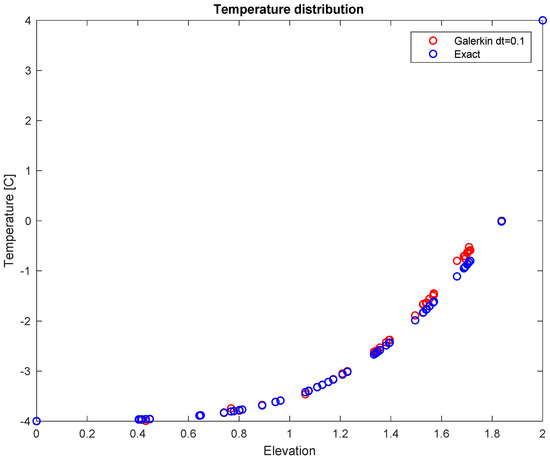
Figure 3.
Comparison of Stefan analytical solution (‘exact’) with 2-D numerical solution at end of one-day simulation.
Comparisons of the analytical results for the depth to thaw with the results of the one-day two-dimensional simulation (Figure 4 and Figure 5) show that the deviation of the analytical and numerical solution for the depth of thaw increases with time, reaching about 1.4% at one day of simulation This is a small fraction of the nodal spacing, and shows good agreement over short timescales (on the order of hours or days). However, this decrease in accuracy with time recommends this technique to these shorter timescales of modeling
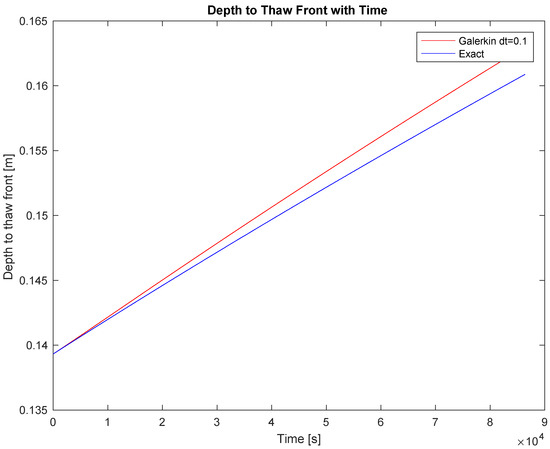
Figure 4.
Deviation of analytical solution (blue) from 2-D numerical solution (red) for thaw depth with time for one-day simulation.
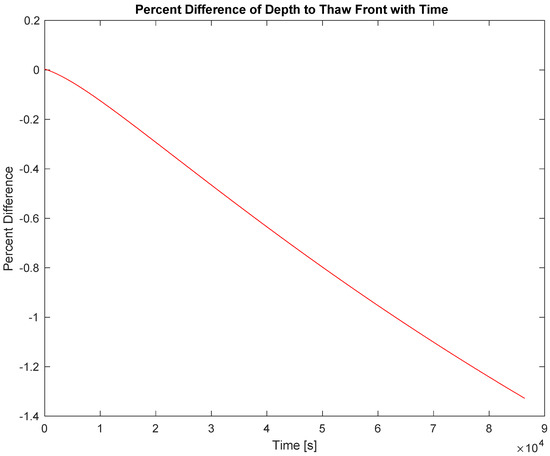
Figure 5.
Percent difference between analytical and 2-D numerical solution of thaw depth with time for one-day simulation.
As an interesting comparison, Figure 6, below, presents results of the same two-dimensional simulation as Figure 3, but without using the N matrix (the nodal-velocity matrix, correcting for the effects of the moving mesh), showing the small but helpful addition of its correction on the full temperature solution, although its effect on thaw depth solution is negligibly small for this simulation:
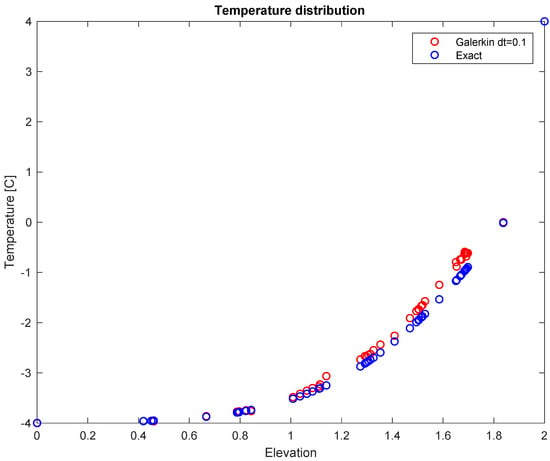
Figure 6.
Comparison of Stefan analytical solution (‘exact’) with 2-D numerical solution at end of one-day simulation neglecting the moving-mesh correction.
3.2. Check against 15 Days of Barrow Data and Finite Difference Model Results
Ravens et al. [5] used borehole temperature data from Barrow to calibrate thawed and frozen soil volumetric heat capacities, c, and thermal conductivity, k, for an earlier, one-dimensional finite difference model. Figure 7 below shows that original calibration using 15 days of available borehole thermistor-string temperature data as initial conditions and a comparison between model results and final borehole temperatures to calibrate heat capacities and conductivities. The values arrived at are reasonable values for high-moisture content soils.
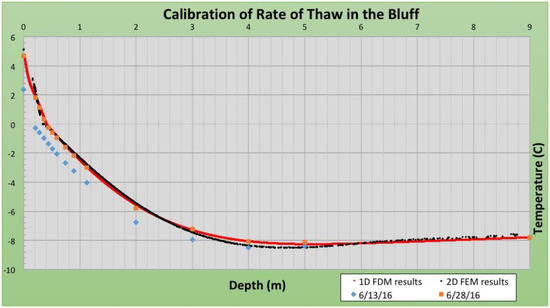
Figure 7.
Barrow borehole thermistor data compared to model results. Initial thermistor data is in blue and used as initial conditions for the models. Thermistor temperature data after 15 days is in orange and was used to calibrate soil thermal parameters for the 1D Finite difference model, in red. Results of this 2D finite element model, using these soil parameters, are in black.
The two-dimensional finite element model was run using these physical parameters (Table 2) and a sinusoidal surface boundary condition for Barter Island given in Zottola’s 2016 thesis [3]. Excel’s fit function was used to determine a polynomial fit of initial temperatures with depth in the two regimes (thawed and frozen) and those equations were used to determine initial conditions at model nodes. The results of this model are also plotted on Figure 7 and show good agreement with data and the previous finite difference model. It should be noted that, in previous work, the soil parameters were varied to give a good fit between the one-dimensional finite difference model and data, while the parameters so arrived at were used as-is in the two-dimensional FEM model. Thus, one would expect the FEM agreement to be less good. Given the real-world intricacies of the problem (non-ideally sinusoidal surface temperatures, varying soil characteristics and parameters, varying phase-change temperatures, etc.), the fit with data of the FEM model results is still considered very good.

Table 2.
Parameters used in numerical comparison to Barrow data (also used for comparison to Barter Island data with slightly modified d, t, Ts and Tb).
3.3. Check against 49 Days of Barter Island Data
Thermistor temperature data from a borehole near a shore-cliff in Barter Island (see Figure 8) was simulated with this two-dimensional FEM model using parameters given for the Barrow 15-day calibration above (Table 2).
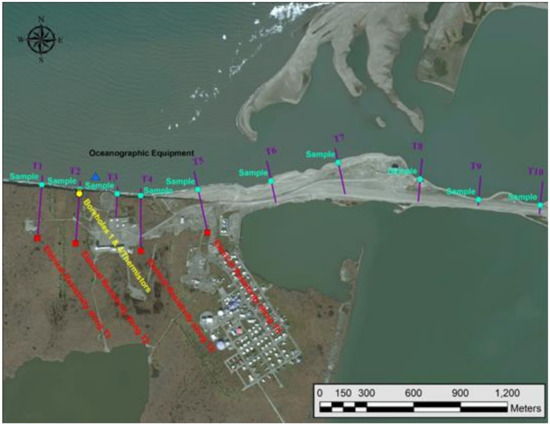
Figure 8.
Map of data location for Barter Island borehole temperature data, borehole location in yellow.
Parameters differing from those given for the Barrow calibration above were that the total depth modeled was 15 m, the constant bottom temperature condition was Tb = −5.5 C to match the Barter Island borehole data, and that the surface temperature boundary condition function was modified slightly to better match the initial and final surface temperatures in the model:
| Ts = −6.33 − 13.5(2π((i Δt/86.4 × 103) + 170 − 26)/365), for model start at Julian day 170 |
An initial simulation was run with a horizontal surface boundary condition and no-flux (infinite) side boundary conditions. This did not match well with the top part of the data near the end of the run (Figure 9), and an analysis of all of the thermistor data (Figure 10) showed daily temperature swings were strongly affecting the top five to six meters of the borehole, indicating the near-by presence of the beach-cliff. The height and distance to the cliff are within one to three meters of the cliff, and five meters is the height. Therefore, a cliff was modeled on the left side of the model by imposing the surface boundary temperature condition to a depth of five meters. As seen in Figure 10, the results of this simulation compare favorably with the data. A more exact match with thaw depth and other features could be acquired by varying soil parameters (c, k, percent moisture) and perhaps the geometry of the model. A simpler set up of the model parameters (a constant surface temperature with no ‘cliff’ in the model, as in the other Neumann analytical solution checks) agreed with an analytical solution to within about 0.02 m. This indicates that the model is working well, and parameters may not match perfectly with field conditions or actual boundary conditions. Figure 11 shows the geometry of the mesh (left) and how it changes by the end of the simulation (right).
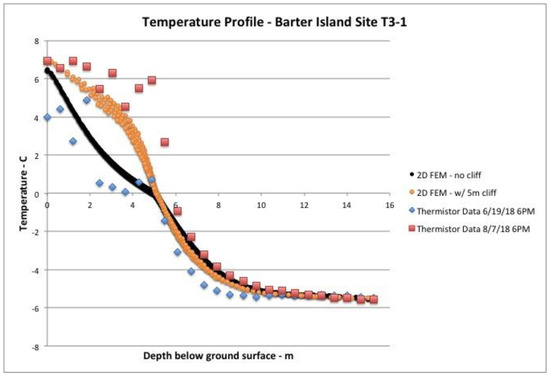
Figure 9.
Data and modeling results for Barter Island.
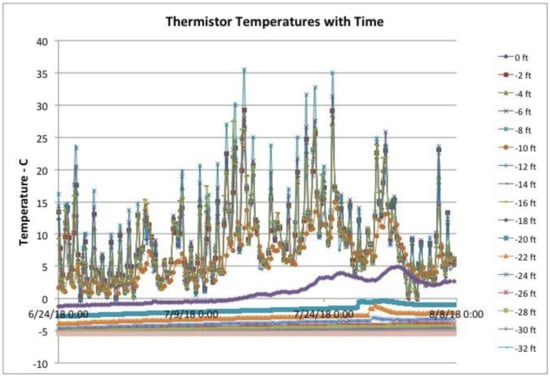
Figure 10.
Thermistor data showing daily temperature effects evident to at least 5 m in depth.

Figure 11.
Initial (left) and final (right) meshes for 49-day Barter Island Simulation. The thawed region is shown separately from, and above the frozen region in each case. The gap between the regions is not physical, the top is spatially continuous with the bottom, the discontinuity represents the phase-change boundary accounted for in the model.
3.4. ANSYS Comparison
ANSYS Mechanical is commercial software that can model heat transfer using the finite element method.
ANSYS models were set up and ran with parameters as close as possible to those used in the moving mesh models. ANSYS uses enthalpy and conductivity functions, these were made sharp (frozen values of k and c constant to −0.01 °C, thawed values constant from 0.01 °C) to match the moving mesh model. A purely backwards difference time derivative was used as in the models above for unconditional stability. ANSYS does not allow the use of linear triangular elements for 2-D thermal solutions, so linear quad elements were used. The moving mesh model used smaller elements near the phase change boundary and larger elements further away, partially to help keep geometric problems to a minimum at the domain boundaries.
As a check on the relative accuracies of ANSYS and this model, both were run with the analysis parameters in Table 1, above. The results compared with the analytical solution are plotted in Figure 12 below and show that the moving mesh model tracks the phase change boundary and temperatures near that boundary much more accurately. In the one-day run, a reasonable interpolation between nodes to find the depth to thaw would over-predict this depth by almost 0.1 m. By ten days, the depth of thaw can be more accurately inferred from the ANSYS results than it could be at one day, but the predicted temperatures are up to about 0.5 °C off of expected. For the moving mesh model, thaw depth agreement is within about 0.0025 m and temperatures within about 0.25 °C.
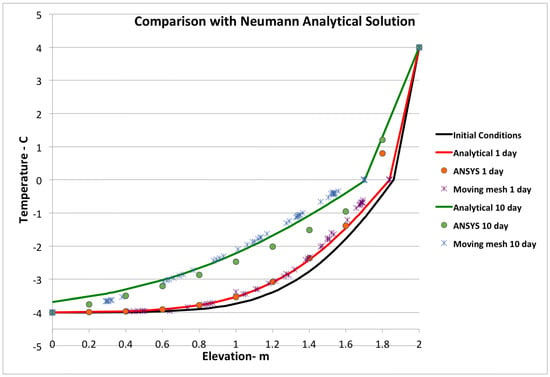
Figure 12.
Temperature with depth results for one and ten day runs of the moving mesh and ANSYS models compared with the Neumann Analytical Solutions.
4. Conclusions
In this work a numerical model was developed and verified.
- One-dimensional formulation of the models were checked and compared well with those presented in the reference used for the algorithm [16].
- One-dimensional and the two-dimensional version of the model were verified, with constant temperature boundary conditions, against the Neumann solution to the Stefan problem (a classic analytical solution to a simple two-phase phase change problem).
- Temperatures with depth agreed reasonably well, and thaw depths agreed to within a few percent at all times in simulations up to 60 days in length, or within 0.02 m, often an order of magnitude better.
- Thaw predictions of the moving mesh model agreed well with two borehole thermistor data sets collected for 15 days of from Barrow, and for 49 days from Barter Island.
Author Contributions
Conceptualization and supervision, writing—original draft preparation, writing—review and editing G.H.; methodology, validation, formal analysis, writing—review and editing M.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P., Eds.; Cambridge University Press: Cambridge, UK, 2013; 1535p. [Google Scholar] [CrossRef]
- Barnhart, K.R.; Anderson, R.S.; Overeem, I.; Wobus, C.; Clow, G.D.; Urban, F.E. Modeling erosion of ice-rich permafrost bluffs along the Alaskan Beaufort Seacoast. J. Geophys. Res. Earth Surf. 2014, 119, 1155–1179. [Google Scholar] [CrossRef]
- Zottola, J. Feasibility of Thermosyphons to Impede the Progress of Coastal Permafrost Erosion Along the Northern Coastline of Alaska. Master’s Thesis, University of Alaska, Anchorage, AK, USA, 2016. [Google Scholar]
- Reimnitz, E.; Kempema, E.; Barnes, P.W. Anchor ice, seabed freezing, and sediment dynamics in shallow Arctic Seas. J. Geophys. Res. Ocean. 1987, 92, 14671–14678. [Google Scholar] [CrossRef]
- Ravens, T.; Hailu, G.; Peng, J.; Ulmgren, M.; Wilber, M. Arctic-capable coastal geomorphic change modeling with application to Barter Island, Alaska. In Proceedings of the Oceans 17 Conference MTS/IEEE, Anchorage, AK, USA, 18–21 September 2017; Available online: http://www.oceans17mtsieeeanchorage.org (accessed on 28 September 2022).
- Reimnitz, E.; Graves, M.; Barnes, P.V. Beaufort Sea Coastal Erosion, Sediment Flux, Shoreline Evolution, and the Erosional Shelf Profile; Text to Accompany U.S. Geological Survey Series Map I-1182-G; Department of Tile Inferior, U.S. Geological Survey: Reston, VA, USA, 1988; 22p. Available online: https://pubs.usgs.gov/imap/1182g/report.pdf (accessed on 25 September 2022).
- Çengel, Y.A.; Ghajar, A.J. Heat and Mass Transfer, 5th ed.; McGraw Hill Education: New York, NY, USA, 2016. [Google Scholar]
- Moaveni, S. Finite Element Analysis: Theory and Application with ANSYS, 4th ed.; Pearson: London, UK, 2015. [Google Scholar]
- Voller, V.R. An Overview of Numerical Methods for Solving Phase Change Problems. In Advances in Numerical Heat Transfer; Minkowycz, W.J., Sparrow, E., Eds.; CRC Press: Boca Raton, FL, USA, 1996; Chapter 9; Volume 3. [Google Scholar]
- Huy, H.; Argyropoulos, S.A. Mathematical modeling of solidification and melting: A Review. Model. Simul. Mater. Sci. Eng. 1996, 4, 371–396. [Google Scholar] [CrossRef]
- Ling, F.; Zhang, T. Numerical simulation of permafrost thermal regime and talik development under shallow thaw lakes on the Alaskan Arctic Coastal Plain. J. Geophys. Res. 2003, 108, 4511. [Google Scholar] [CrossRef]
- Borisov, V. Mathematical Modeling of Underground Construction Temperature Influence on Permafrost Soils. Procedia Comput. Sci. 2015, 66, 112–121. [Google Scholar] [CrossRef]
- Liandi, F. Applications of the Finite-Element Method to the Problem of Heat Transfer in a Freezing Shaft Wall; CRREL Report 86-8; Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1986; Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/a172552.pdf (accessed on 25 September 2022).
- Darrow, M.M. Measurement of Temperature and Soil Properties for Finite Element Model Verification; Alaska Department of Transportation and Public Facilities and Alaska University Transportation Center: Juneau, AK, USA, 2010.
- Persson, P.; Strang, G. A simple mesh generator in MATLAB. SIAM Rev. 2004, 46, 329–345. [Google Scholar] [CrossRef]
- Mori, M. A finite element method for solving the two-phase Stefan problem. Publ. Res. Inst. Math. Sci. Ser. A 1977, 13, 723–753. [Google Scholar] [CrossRef]
- Beckett, G.; Mackenzie, J.; Robertson, M. A moving mesh finite element method for the solution of two-dimensional Stefan Problems. J. Comput. Phys. 2001, 168, 500–518. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.; Zhu, J. Chapter 6—Shape Functions, derivatives and integration. In The Finite Element Method: Its Basis and Fundamentals; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).