Forecasting Installation Capacity for the Top 10 Countries Utilizing Geothermal Energy by 2030
Abstract
1. Introduction
2. Material and Methods
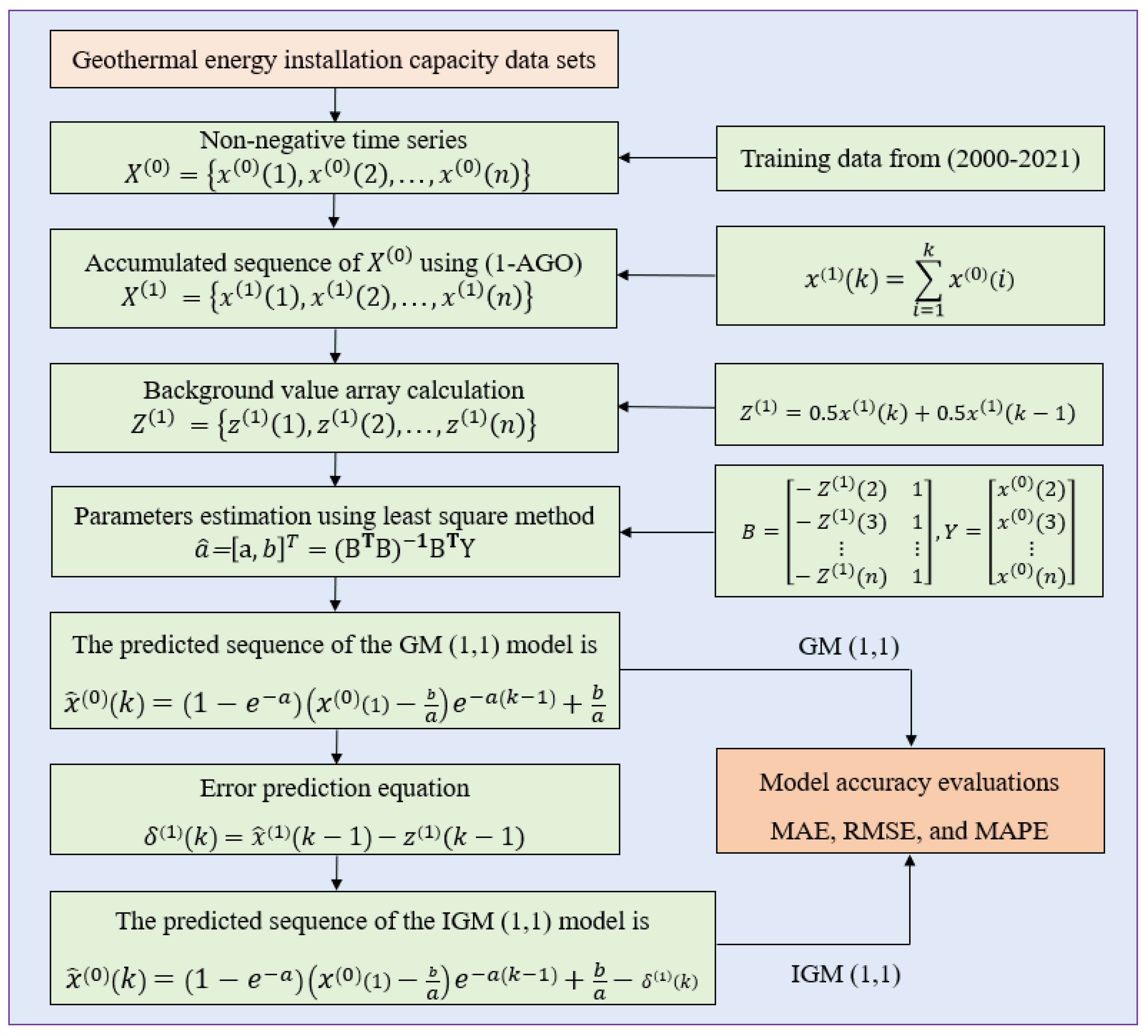
2.1. The GM (1,1) Model
2.2. The Improved IGM (1,1)
3. Data Description
4. Model Accuracy Evaluations
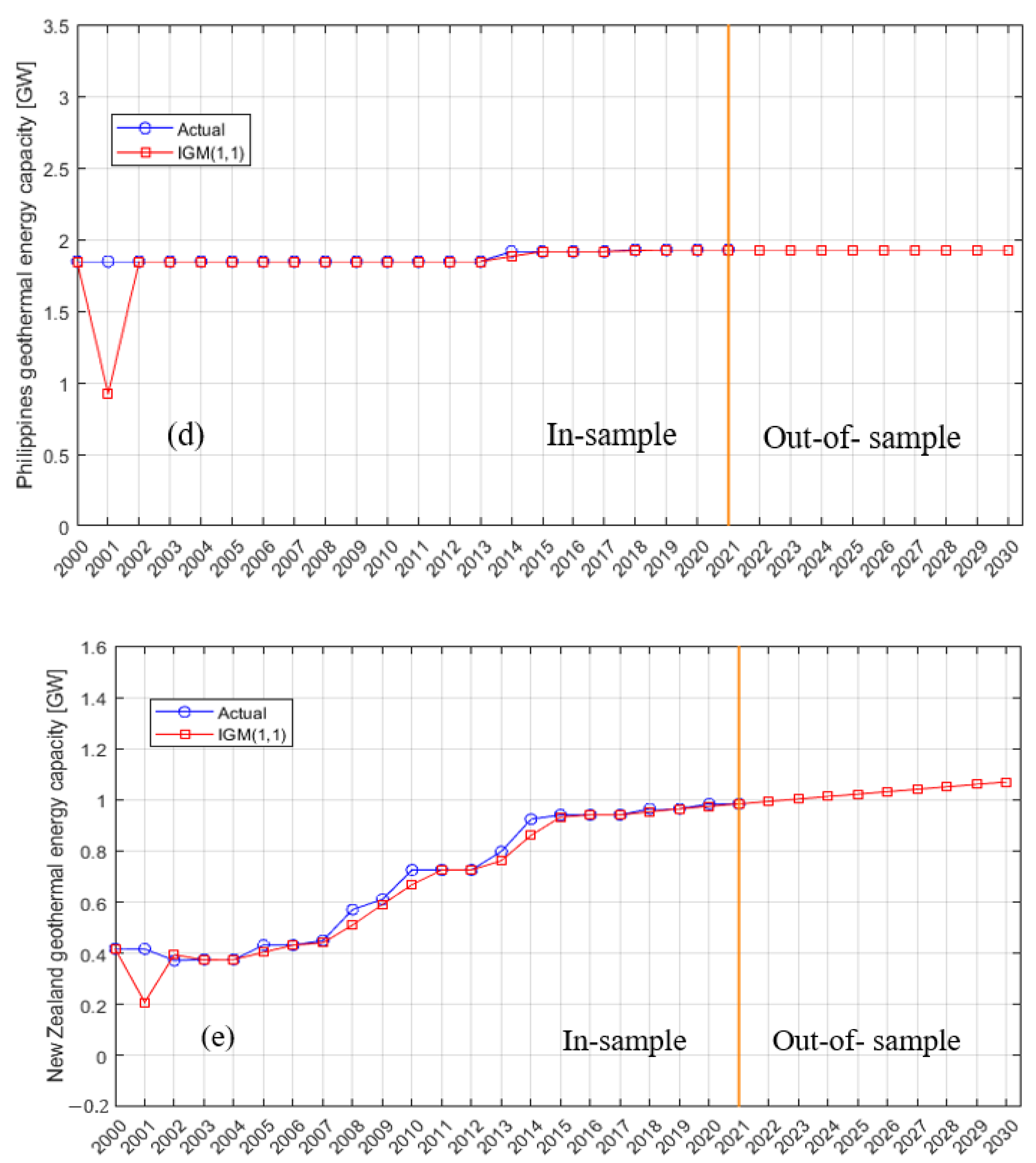
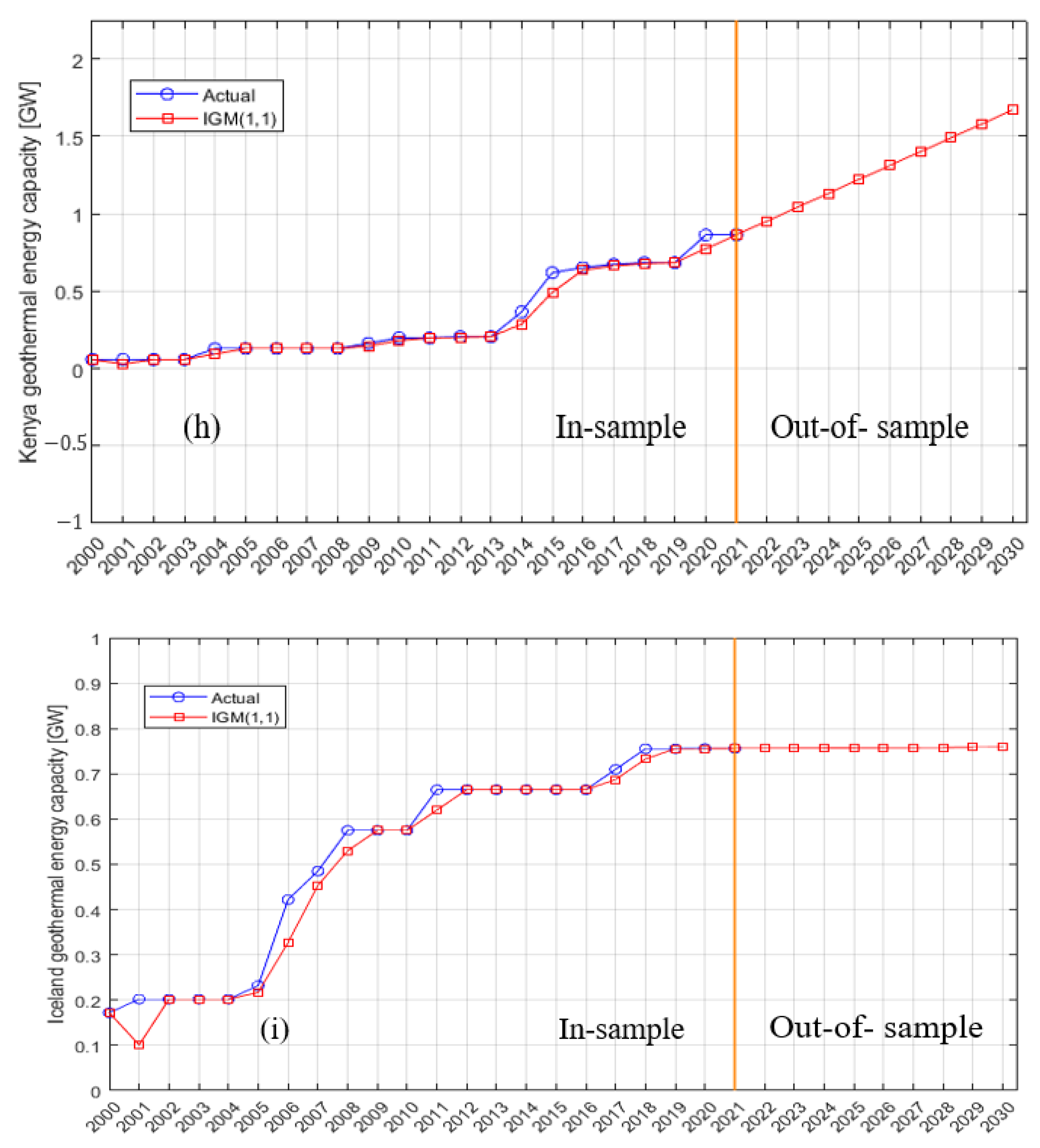
5. Results and Discussions
Annual Forecasting of the United States’ Geothermal Energy Installation Capacity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of abbreviations | |
| AGO | Accumulative generating operation |
| GM | Grey prediction model |
| GM (1,1) | GM with a first-order differential equation to predict one variable |
| IGM (1,1) | Improved grey prediction model |
| 1-AGO | First-order accumulated generating operation |
| Inverse 1-AGO | Inverse first-order accumulated generating operation |
| MAE | Mean absolute error |
| RMSE | Root mean square error |
| MAPE | Mean absolute percentage error |
| GW | Gigawatts |
| MW | Megawatts |
| List of symbols | |
| Developing coefficient | |
| Grey action quantity | |
| A non-negative original data sequence | |
| Accumulated time response of | |
| Background value array | |
| Predicted time response of grey prediction model at time | |
| Accumulated time response of grey prediction model at time | |
| Time point | |
| Number of years of observation | |
| List of greek letters | |
| Weighting factor | |
| Predicted value’s error at time k | |
References
- Geothermal Energy. 14 May 2018. Available online: https://www.encyclopedia.com/science-and-technology/technology/technology-terms-and-concepts/geothermal-energy (accessed on 1 August 2022).
- Renewable Energy World: Geothermal Electricity Production. Available online: https://www.renewableenergyworld.com/types-of-renewable-energy/tech-3/geoelectricity/#gref (accessed on 1 August 2022).
- Hyder, Z. Solar Reviews: Geothermal Energy Pros and Cons. 3 August 2022. Available online: https://www.solarreviews.com/blog/geothermal-energy-pros-and-cons (accessed on 1 August 2022).
- Hitchcock, K. 10 Geothermal Energy Facts and Statistics in 2022. 21 July 2022. Available online: https://housegrail.com/geothermal-energy-statistics/#2_Currently_27_countries_throughout_the_world_generate_geothermal_electricity (accessed on 17 August 2022).
- EIA. Geothermal Explained Use of Geothermal Energy. 18 March 2022. Available online: https://www.eia.gov/energyexplained/geothermal/use-of-geothermal-energy.php (accessed on 17 August 2022).
- Geothermal Energy Association. 2020. Available online: https://web.archive.org/web/20090419054340/http://www.geo-energy.org/publications/reports/Industry_Update_March_Final.pdf (accessed on 2 August 2022).
- Richter, A. Think GeoEnergy. 10 January 2022. Available online: https://www.thinkgeoenergy.com/thinkgeoenergys-top-10-geothermal-countries-2021-installed-power-generation-capacity-mwe/?utm_source=linkedin&utm_medium=social&utm_campaign=news (accessed on 2 August 2022).
- Madhumitha Jaganmohan. Geothermal energy capacity worldwide from 2009 to 2021. Statista. 6 May 2022. Available online: https://www.statista.com/statistics/476281/global-capacity-of-geothermal-energy/ (accessed on 2 August 2022).
- International Renewable Energy Agency (IRENA), Abu Dhabi. Available online: https://pxweb.irena.org/pxweb/en/IRENASTAT (accessed on 2 August 2022).
- Our World in Data. Available online: https://ourworldindata.org/grapher/installed-geothermal-capacity?tab=table&time=2000 (accessed on 2 August 2022).
- Bertani, R. Geothermal power generation in the world 2010–2014 update report. Geothermics 2016, 60, 31–43. [Google Scholar] [CrossRef]
- Şahin, U. Forecasting of Turkey’s electricity generation and CO2 emissions in estimating capacity factor. Environ. Prog. Sustain. Energy 2019, 38, 56–65. [Google Scholar] [CrossRef]
- Klein, C. Forecast of the Geothermal Power Generation Capacity Japan 2020–2030. 6 January 2020. Available online: https://www.statista.com/statistics/1221023/japan-geothermal-power-generation-capacity-forecast/ (accessed on 16 August 2022).
- Zheng, B.; Xu, J.; Ni, T.; Li, M. Geothermal energy utilization trends from a technological paradigm perspective. Renew. Energy 2015, 77, 430–441. [Google Scholar] [CrossRef]
- Chang, Y.; Li, Y. Power generation and cross-border grid planning for the integrated ASEAN electricity market: A dynamic linear programming model. Energy Strategy Rev. 2013, 2, 153–160. [Google Scholar] [CrossRef]
- Ju-Long, D. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar] [CrossRef]
- Talafuse, T.P.; Pohl, E.A. Small sample reliability growth modeling using a grey systems model. Qual. Eng. 2017, 29, 455–467. [Google Scholar] [CrossRef]
- Tseng, F.-M.; Yu, H.-C.; Tzeng, G.-H. Applied hybrid grey model to forecast seasonal time series. Technol. Forecast. Soc. Change 2001, 67, 291–302. [Google Scholar] [CrossRef]
- Şahin, U. Forecasting of Turkey’s electricity generation and consumption with grey prediction method. Mugla J. Sci. Technol. 2018, 4, 205–209. [Google Scholar] [CrossRef]
- Yuan, C.; Liu, S.; Fang, Z. Comparison of China’s primary energy consumption forecasting by using ARIMA (the autoregressive integrated moving average) model and GM (1, 1) model. Energy 2016, 100, 384–390. [Google Scholar] [CrossRef]
- Salhein, K.; Ashraf, J.; Zohdy, M. Output temperature predictions of the geothermal heat pump system using an improved grey prediction model. Energies 2021, 14, 5075. [Google Scholar] [CrossRef]
- Li, K.; Zhang, T. Forecasting electricity consumption using an improved grey prediction model. Information 2018, 9, 204. [Google Scholar] [CrossRef]
- Fan, G.-F.; Wang, A.; Hong, W.-C. Combining grey model and self-adapting intelligent grey model with genetic algorithm and annual share changes in natural gas demand forecasting. Energies 2018, 11, 1625. [Google Scholar] [CrossRef]
- Hsu, L.-C. Applying the grey prediction model to the global integrated circuit industry. Technol. Forecast. Soc. Change 2003, 70, 563–574. [Google Scholar] [CrossRef]
- Wang, Y.; Dang, Y.; Li, Y.; Liu, S. An approach to increase prediction precision of GM (1, 1) model based on optimization of the initial condition. Expert Syst. Appl. 2010, 37, 5640–5644. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Chen, C.-Y. Applications of improved grey prediction model for power demand forecasting. Energy Convers. Manag. 2003, 44, 2241–2249. [Google Scholar] [CrossRef]
- Yousuf, M.U.; Al-Bahadly, I.; Avci, E. A modified GM (1, 1) model to accurately predict wind speed. Sustain. Energy Technol. Assess. 2021, 43, 100905. [Google Scholar] [CrossRef]
- Yao, M.; Wang, X. Electricity consumption forecasting based on a class of new GM (1, 1) model. In Mechatronics and Automatic Control Systems; Springer: Berlin, Germany, 2014; pp. 947–953. [Google Scholar]
- Hsu, L.-C. Using improved grey forecasting models to forecast the output of opto-electronics industry. Expert Syst. Appl. 2011, 38, 13879–13885. [Google Scholar] [CrossRef]
- Akay, D.; Atak, M. Grey prediction with rolling mechanism for electricity demand forecasting of Turkey. Energy 2007, 32, 1670–1675. [Google Scholar] [CrossRef]
- Li, K.; Zhang, T. A novel grey forecasting model and its application in forecasting the energy consumption in Shanghai. Energy Syst. 2021, 12, 357–372. [Google Scholar] [CrossRef]
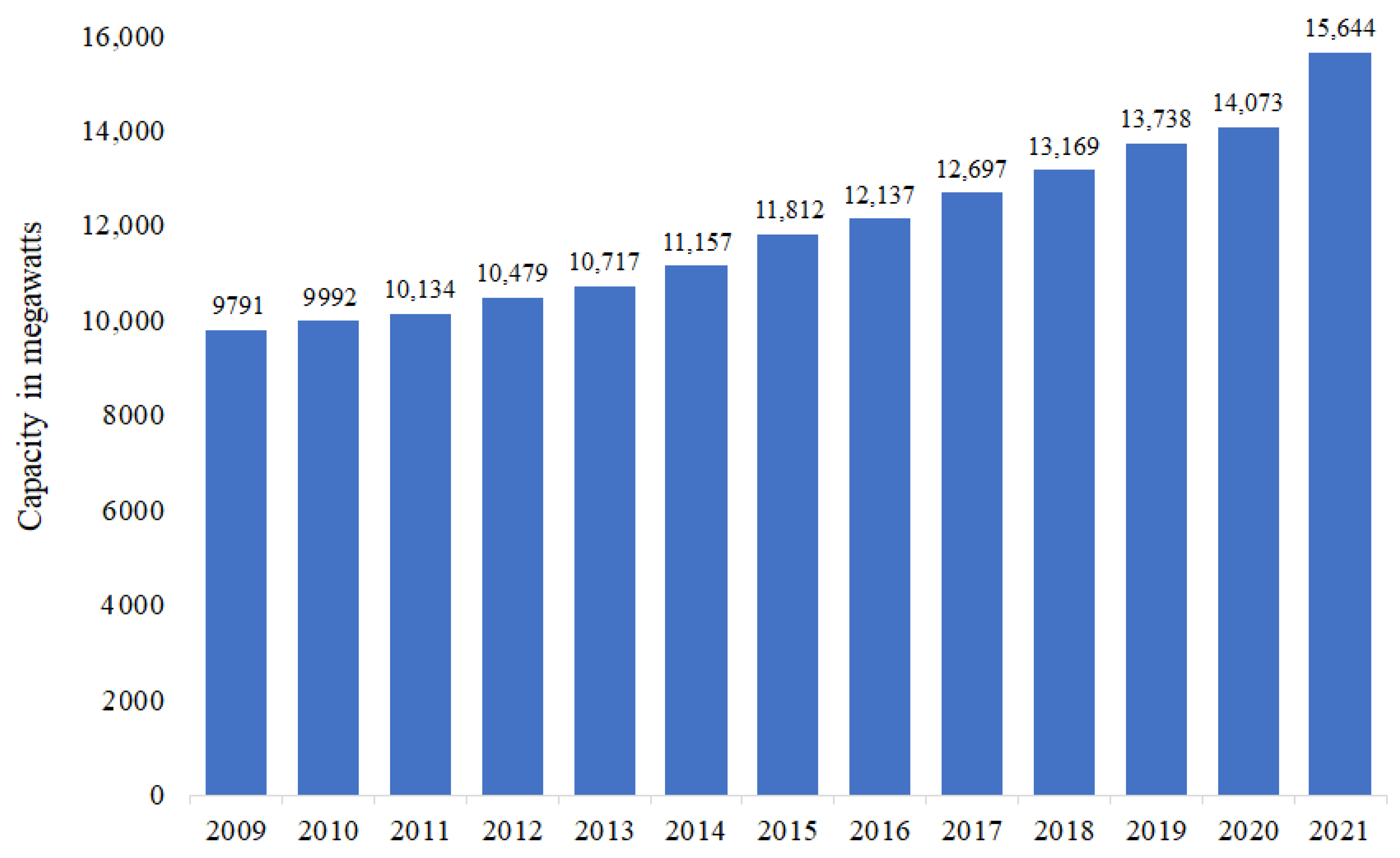



| Country | Capacity in Megawatts (MW) |
|---|---|
| United States | 3722 |
| Indonesia | 2276 |
| Philippines | 1918 |
| Turkey | 1710 |
| New Zealand | 1037 |
| Mexico | 963 |
| Italy | 944 |
| Kenya | 861 |
| Iceland | 754 |
| Japan | 603 |
| Country | Predicted Capacity (GW) | 2022 | 2023 | 2024 | 2025 | 2026 | 2027 | 2028 | 2029 | 2030 |
|---|---|---|---|---|---|---|---|---|---|---|
| United States | GM (1,1) | 3.7566 | 3.7952 | 3.8341 | 3.8735 | 3.9132 | 3.9533 | 3.9939 | 4.0349 | 4.0763 |
| IGM (1,1) | 3.741 | 3.764 | 3.787 | 3.81 | 3.833 | 3.856 | 3.879 | 3.902 | 3.925 | |
| Indonesia | GM (1,1) | 2.3824 | 2.5258 | 2.6837 | 2.8483 | 3.023 | 3.2085 | 3.4053 | 3.6143 | 3.836 |
| IGM (1,1) | 2.2769 | 2.35 | 2.4231 | 2.4962 | 2.5693 | 2.6424 | 2.7155 | 2.7886 | 2.8617 | |
| Philippines | GM (1,1) | 1.9337 | 1.9391 | 1.9446 | 1.95 | 1.9555 | 1.961 | 1.9664 | 1.972 | 1.9775 |
| IGM (1,1) | 1.9281 | 1.9281 | 1.9281 | 1.9281 | 1.9281 | 1.9281 | 1.9281 | 1.9281 | 1.9281 | |
| Turkey | GM (1,1) | 8.5189 | 10.5675 | 13.1086 | 16.2608 | 20.1709 | 25.0213 | 31.0381 | 38.5017 | 47.7601 |
| IGM (1,1) | 1.7254 | 1.8062 | 1.8869 | 1.9677 | 2.0484 | 2.1292 | 2.2099 | 2.2907 | 2.3714 | |
| New Zealand | GM (1,1) | 1.1863 | 1.2492 | 1.3154 | 1.3851 | 1.4584 | 1.5357 | 1.6171 | 1.7027 | 1.7929 |
| IGM (1,1) | 0.9935 | 1.003 | 1.0125 | 1.022 | 1.0315 | 1.041 | 1.0505 | 1.06 | 1.0695 | |
| Mexico | GM (1,1) | 0.9301 | 0.9311 | 0.9321 | 0.9331 | 0.9341 | 0.935 | 0.936 | 0.937 | 0.938 |
| IGM (1,1) | 0.9762 | 0.9889 | 1.0016 | 1.0143 | 1.027 | 1.0397 | 1.0524 | 1.0651 | 1.0778 | |
| Italy | GM (1,1) | 0.8118 | 0.8212 | 0.8307 | 0.8403 | 0.85 | 0.8599 | 0.8698 | 0.8799 | 0.8901 |
| IGM (1,1) | 0.8041 | 0.8214 | 0.8387 | 0.856 | 0.8733 | 0.8906 | 0.9079 | 0.9252 | 0.9425 | |
| Kenya | GM (1,1) | 1.2472 | 1.4273 | 1.6333 | 1.869 | 2.1388 | 2.4475 | 2.8007 | 3.205 | 3.6676 |
| IGM (1,1) | 0.9526 | 1.0422 | 1.1318 | 1.2214 | 1.311 | 1.4006 | 1.4902 | 1.5798 | 1.6694 | |
| Iceland | GM (1,1) | 0.9336 | 0.983 | 1.0349 | 1.0896 | 1.1472 | 1.2078 | 1.2717 | 1.3389 | 1.4096 |
| IGM (1,1) | 0.7565 | 0.7568 | 0.7571 | 0.7574 | 0.7577 | 0.7580 | 0.7583 | 0.7586 | 0.7589 | |
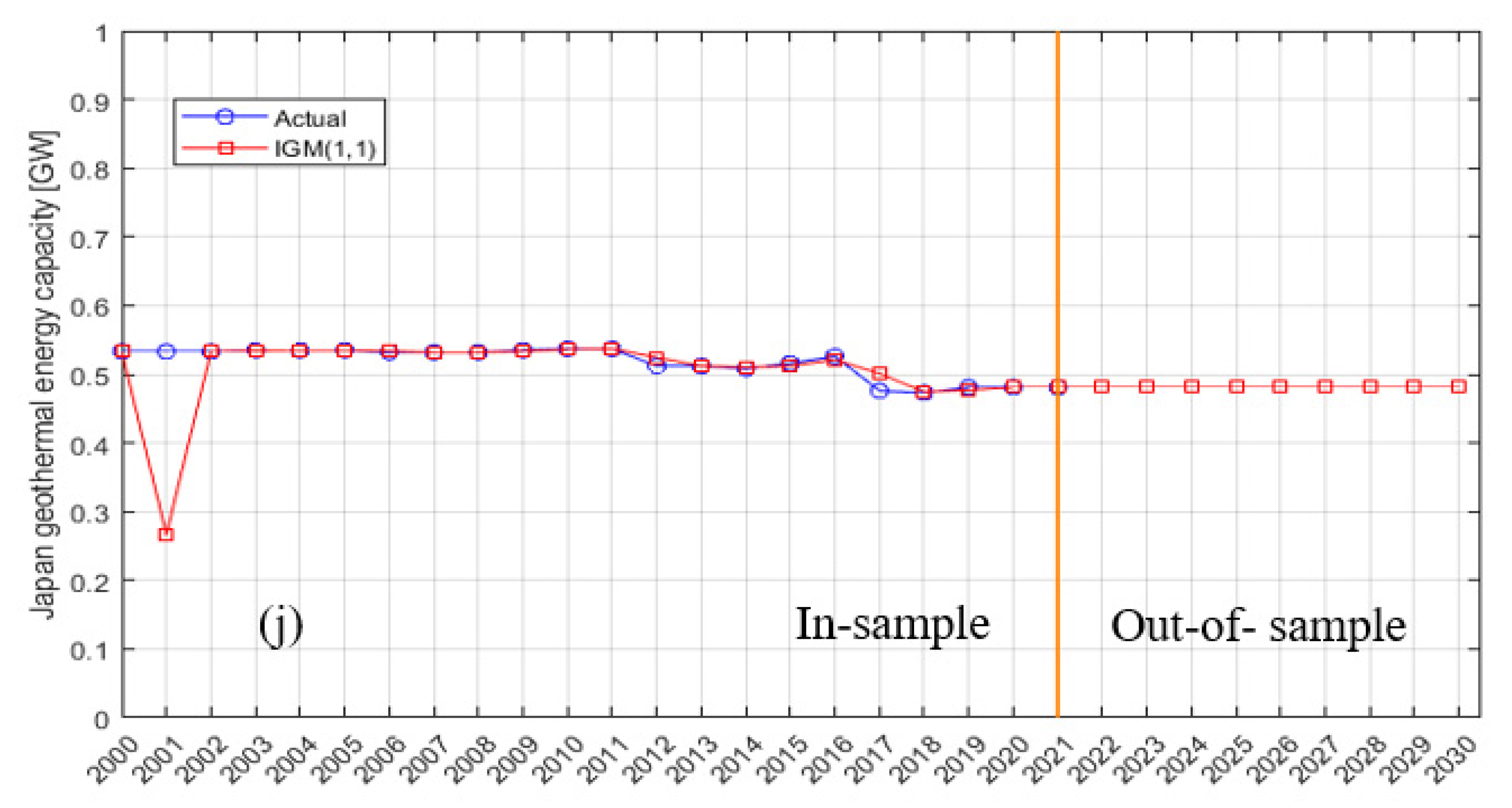
| Japan | GM (1,1) | 0.4826 | 0.4797 | 0.4768 | 0.4739 | 0.4711 | 0.4682 | 0.4654 | 0.4626 | 0.4598 |
| IGM (1,1) | 0.481 | 0.481 | 0.481 | 0.481 | 0.481 | 0.481 | 0.481 | 0.481 | 0.481 |
| Country | Accuracy Criteria | GM (1,1) | IGM (1,1) |
|---|---|---|---|
| United States | MAE | 0.026 | 0.023 |
| RMSE | 0.028 | 0.030 | |
| MAPE (%) | 0.72 | 0.64 | |
| Indonesia | MAE | 0.072 | 0.070 |
| RMSE | 0.086 | 0.081 | |
| MAPE (%) | 3.86 | 3.63 | |
| Philippines | MAE | 0.009 | 0.001 |
| RMSE | 0.011 | 0.002 | |
| MAPE (%) | 0.48 | 0.05 | |
| Turkey | MAE | 2.955 | 0.088 |
| RMSE | 3.216 | 0.094 | |
| MAPE (%) | 214.26 | 7.42 | |
| New Zealand | MAE | 0.063 | 0.004 |
| RMSE | 0.077 | 0.006 | |
| MAPE (%) | 6.44 | 0.37 | |
| Mexico | MAE | 0.020 | 0.006 |
| RMSE | 0.025 | 0.008 | |
| MAPE (%) | 2.08 | 0.62 | |
| Italy | MAE | 0.010 | 0.003 |
| RMSE | 0.012 | 0.006 | |
| MAPE (%) | 1.25 | 0.37 | |
| Kenya | MAE | 0.107 | 0.020 |
| RMSE | 0.125 | 0.038 | |
| MAPE (%) | 14.20 | 2.54 | |
| Iceland | MAE | 0.050 | 0.008 |
| RMSE | 0.067 | 0.013 | |
| MAPE (%) | 6.64 | 1.04 | |
| Japan | MAE | 0.015 | 0.006 |
| RMSE | 0.17 | 0.011 | |
| MAPE (%) | 3.10 | 1.23 |
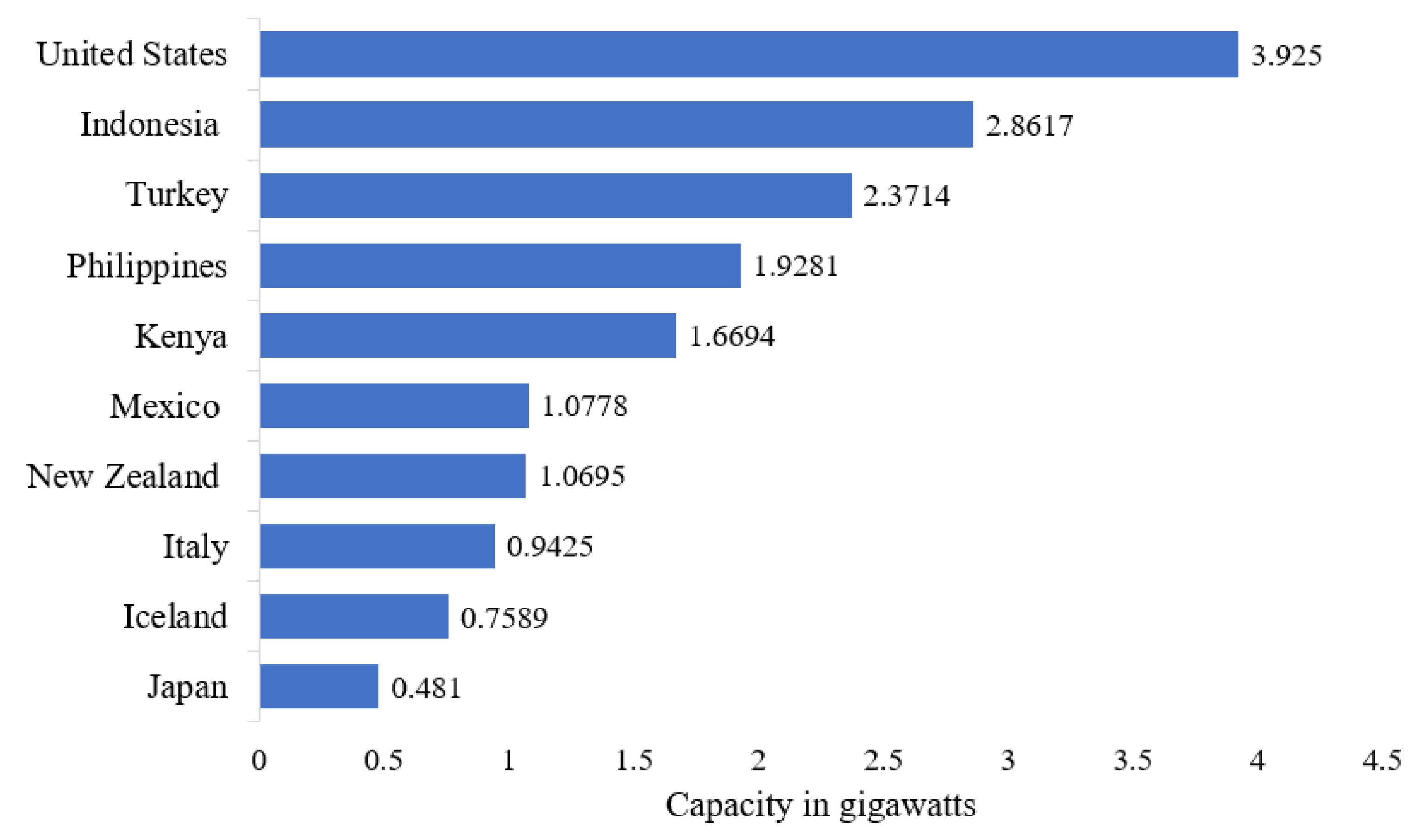
| Country | Capacity in Gigawatts (GW) |
|---|---|
| United States | 3.925 |
| Indonesia | 2.8617 |
| Turkey | 2.3714 |
| Philippines | 1.9281 |
| Kenya | 1.6694 |
| Mexico | 1.0778 |
| New Zealand | 1.0695 |
| Italy | 0.9425 |
| Iceland | 0.7589 |
| Japan | 0.481 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salhein, K.; Kobus, C.J.; Zohdy, M. Forecasting Installation Capacity for the Top 10 Countries Utilizing Geothermal Energy by 2030. Thermo 2022, 2, 334-351. https://doi.org/10.3390/thermo2040023
Salhein K, Kobus CJ, Zohdy M. Forecasting Installation Capacity for the Top 10 Countries Utilizing Geothermal Energy by 2030. Thermo. 2022; 2(4):334-351. https://doi.org/10.3390/thermo2040023
Chicago/Turabian StyleSalhein, Khaled, C. J. Kobus, and Mohamed Zohdy. 2022. "Forecasting Installation Capacity for the Top 10 Countries Utilizing Geothermal Energy by 2030" Thermo 2, no. 4: 334-351. https://doi.org/10.3390/thermo2040023
APA StyleSalhein, K., Kobus, C. J., & Zohdy, M. (2022). Forecasting Installation Capacity for the Top 10 Countries Utilizing Geothermal Energy by 2030. Thermo, 2(4), 334-351. https://doi.org/10.3390/thermo2040023







