Abstract
Physical aging deals with slow property changes over time caused by molecular rearrangements. This is relevant for non-crystalline materials such as polymers and inorganic glasses, both in production and during subsequent use. The Narayanaswamy theory from 1971 describes physical aging—an inherently nonlinear phenomenon—in terms of a linear convolution integral over the so-called material time . The resulting “Tool–Narayanaswamy (TN) formalism” is generally recognized to provide an excellent description of physical aging for small, but still highly nonlinear, temperature variations. The simplest version of the TN formalism is single-parameter aging according to which the clock rate is an exponential function of the property monitored. For temperature jumps starting from thermal equilibrium, this leads to a first-order differential equation for property monitored, involving a system-specific function. The present paper shows analytically that the solution to this equation to first order in the temperature variation has a universal expression in terms of the zeroth-order solution, . Numerical data for a binary Lennard–Jones glass former probing the potential energy confirm that, in the weakly nonlinear limit, the theory predicts aging correctly from (which by the fluctuation–dissipation theorem is the normalized equilibrium potential-energy time-autocorrelation function).
1. Introduction
The properties of non-crystalline materials, such as polymers and inorganic glasses, change slightly over time. In many cases, the aging is so slow that it cannot be observed, but sometimes it results in unwanted degradation of material properties. When aging is exclusively due to molecular rearrangements, with no chemical reactions involved, one speaks about physical aging [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. The present-day understanding of physical aging is based on the century-old observation [15] that any glass is in an out-of-equilibrium state and, as a consequence, relaxes continuously toward the equilibrium state.
During physical aging, the system’s volume decreases slightly. This reflects the fact that the equilibrium metastable liquid is denser than the glass at the same temperature. Likewise, the enthalpy decreases during aging. Both effects are extremely difficult to observe because they are minute and take place over a very long time. Defining a glass as any non-equilibrium state of a liquid resulting from a thermodynamic perturbation, a good way of studying physical aging is the following: First, equilibrate the glass-forming liquid at some “annealing” temperature just below the calorimetric glass-transition temperature. Depending on the viscosity of the liquid, this may take long time—experiments often study liquids at temperatures for which the equilibrium relaxation time is hours or days [16,17,18,19,20,21]; if the equilibrium relaxation time is one day, annealing the sample for a week ensures virtually complete thermal equilibrium. Once the sample has been equilibrated, the temperature is changed rapidly to a new value and kept there for a time long enough to allow for monitoring virtually the entire equilibration process. This defines an “ideal aging experiment” [17,22]. Such an experiment requires the ability to monitor some quantity accurately and continuously as a function of time, excellent temperature control, and the ability to change temperature rapidly [17]. Aging may be probed by measuring any property that can be monitored precisely, e.g., the electrical capacitance at a particular frequency [21,23,24,25,26]; in conjunction with a Peltier-element-based fast and accurate temperature control, this is our favorite method in Roskilde [21]. Other quantities that have been monitored during physical aging include, e.g., density [27,28], enthalpy [29,30], Young’s modulus [31], gas permeability [32], high-frequency mechanical moduli [16,33], dc conductivity [2], X-ray photon correlation spectroscopy [34], and nonlinear dielectric susceptibility [35].
The present paper develops the theory of aging by studying the so-called single-parameter aging framework, which is the simplest realization of the concept of a material time that controls aging in the Tool-–Narayanaswamy (TN) formalism [3]. An important prediction of the TN formalism is that if the aging rate is known as a function of the property monitored, knowledge of the linear limit of physical aging, e.g., following an infinitesimal temperature jump, is enough to quantitatively determine the aging that results from any time-dependent temperature variation. According to the fluctuation–dissipation (FD) theorem, any linear-response property is determined by thermal-equilibrium fluctuations quantified in terms of a time-autocorrelation function. The prospect for future experimental investigations is that one can make quantitative predictions about aging from the knowledge of equilibrium fluctuations.
Single-parameter aging results in a first-order differential equation for the normalized relaxation function following a temperature jump [18]. This equation involves an a priori unknown, system-specific function that determines the linear limit of aging. In order to predict aging, however, it is enough to know the linear-limit relaxation function that, by the FD theorem, is the relevant equilibrium time-autocorrelation function. This paper derives an explicit expression for the weakly nonlinear limit of aging based on the relevant equilibrium time-autocorrelation function. After developing the theory in Section 2, we provide an example of how to calculate a quantity similar to the fragility of glass science in Section 3; this section can be skipped in a first reading of the paper. The general first-order solution to single-parameter aging following a temperature jump is derived in Section 4. The validity of the formalism is illustrated in Section 5 by results from computer simulations of a binary Lennard–Jones system; the final section provides a brief discussion.
2. The TN Formalism and Single-Parameter Aging
The quantity probed during aging is denoted by . Following a temperature jump at , gradually approaches its equilibrium value at the new temperature . We define the normalized relaxation function by
By definition, is unity at and approaches zero as . Thus for both temperature up and down jumps, is a decreasing function of time. In practice, in experiments as well as simulations, there is always a rapid initial change of immediately after deriving from ’s dependence on the fast, vibrational degrees of freedom and/or one or more fast relaxation processes decoupled from the main and slowest () relaxation. For this reason, workers in the field often normalize the relaxation function by defining to be unity after the initial rapid change of . That is different from what is done in Equation (1) and below, which is our preference because it avoids introducing the extra parameter that comes from estimating the value of the short-time “plateau” of .
The TN material time is denoted by . This quantity, which may be thought of as the time measured on a clock with a clock rate that changes as the material ages, is related to the clock rate as follows
According to the TN formalism, the material time controls the physical aging in such a way that the variation of , denoted by
is a linear convolution integral over the temperature variation history in which is the “reference” temperature [3,29].
Single-parameter aging (SPA) is the simplest version of the TN formalism [18]. SPA assumes that the clock rate is an exponential function of the monitored property, i.e.,
Here, is the equilibrium relaxation rate at and is a constant with the same dimension as . In conjunction with the TN prediction that physical aging is linear in the temperature variation when formulated in terms of the material time, SPA may be applied to any relatively small (continuous or discontinuous) temperature variation around , not just for the discontinuous temperature jumps to which the below discussion is limited. Since by the definition of , Equation (4) may be rewritten as
For temperature jumps the TN fundamental result is that [3,29]
in which the function is the same for all temperature jumps of a given system. In view of the nonlinearity of physical aging, this is a highly nontrivial prediction. Keeping in mind the definition of (Equation (2)), Equation (6) implies . Since, according to Equation (6), is the same function of R for all jumps, defining leads to the “jump differential equation”
in which is the same function for all jumps of a given system. The negative sign in the definition of is introduced in order to make positive.
Equation (7) has been confirmed in experiments on a silicone oil and several organic liquids [18,20,21] aged to equilibrium just below their calorimetric glass transition temperature. Even though the largest temperature jumps studied were just a few percent, this is enough to exhibit a strongly nonlinear response with more than one decade of relaxation-time variation. One experimental test of Equation (7) involved rewriting it as [18,20]
and showing that the left-hand side is the same function of R for different jumps. A second test confirmed the consequence of Equation (7) that the for an arbitrary jump may be predicted from data of a single jump [18,20,21].
This paper develops the SPA formalism based on Equation (7) that, for simplicity, is rewritten by adopting the unit system in which at the temperature :
with
3. Calculation of a Generalized Fragility
Each value of leads to a unique solution denoted by of the jump differential equation, Equation (9), with the initial condition . As a first illustration of how perturbation theory may be applied whenever , we determine the dependence of the average relaxation time defined by
From , a fragility-like [36] parameter (subscript “a” for aging) may be defined by
The minus ensures that because from Equation (9) leads to a faster relaxation.
We proceed to derive the following expression in which
Note that whenever , which is usually the case [18], one has . Note also that, since from Equation (9), the equilibrium relaxation time obeys . Using this, one can transform Equation (13) into an expression for how the relative change of from its value at depends on the relative change of the equilibrium relaxation time between the two temperatures involved in the jump, i.e.,
The fact that is now intuitively obvious, since the graph of obviously falls between the equilibrium relaxation function graphs at the two temperatures.
To derive Equation (13), note that Equation (9) implies . Thus
From this we get
and
By substituting into both integrals and switching back to time as the integration variable, one finds
An alternative proof of Equation (13) makes use of an integral criterion derived in Ref. [18] (Appendix A).
For the calculation of from experimental or computer simulation data on , one proceeds as follows. Given a sequence of times at which the equilibrium normalized relaxation function is known, we have
As an example of the above, we consider the case in which the linear-limit relaxation function is a stretched exponential with exponent (for simplicity, a dimensionless time is used below),
Defining the function
we have . Since
we get
If the normalized relaxation function in the experimental time window is described by a stretched exponential with the short-time plateau , i.e., by the function , one finds
4. Solving the Jump Differential Equation to First Order in the Temperature Change
To find the solution, , of the jump differential equation in first-order perturbation theory we proceed as follows. A first-order expansion of ,
is substituted into Equation (9) where is the normalized relaxation function corresponding to an infinitesimal jump, i.e., to the linear limit of aging (this function is discussed below in Section 5.1). To first order in , one has and . This results in
which leads to the following zeroth- and first-order equations:
Due to the zero-time normalization of both and , the initial condition of is . For , one has because , as mentioned, implies a faster relaxation toward equilibrium, i.e., . Consequently, since , the function is non-monotonous.
The solution to Equation (28), obeying the initial condition , is
To derive this, we proceed as follows. First, note that the inverse of is given by
which follows by rewriting Equation (9) as and integrating. Next, we note that because , one has
in which it here and henceforth is understood that all functions are evaluated at , implying that one should put in the final evaluations. Since , using Equation (30) the numerator is evaluated as follows
For , the denominator of Equation (31) is given by
Combining these results, one arrives at Equation (29). To confirm that Equation (29) indeed solves Equation (28), one differentiates:
Since by Equation (27), we see that as required.
5. Numerical Results for a Binary Lennard–Jones Model
5.1. The Relevant Fluctuation–Dissipation Theorem
When the externally controlled variable is temperature itself, a slightly modified derivation of the FD theorem is required [37]. In the end, however, the result looks much like in the standard FD case: If is the variation of from its equilibrium value at the reference temperature, , and sharp brackets denote standard canonical averages, the variation of the potential energy is given [37] by
Following a small inverse-temperature jump of magnitude , for . Since , this leads to the well-known Einstein expression for the specific heat, .
Equation (37) implies that the response to a jump at for is given by (note that right after the temperature jump one has because of continuity). Therefore, the linear-response normalized relaxation function, , is given by
5.2. Simulation Results
We simulated the well-known Kob–Andersen binary Lennard–Jones (KA) 80/20 mixture of A and B particles [38] with the standard Nose–Hoover thermostat [39] by means of the GPU-software RUMD [40]. The pair potentials of the KA system are Lennard–Jones potentials defined by () with the following parameters: , , , , , and . All masses are set to unity. A system of N = 8000 particles was simulated. In the units based on and , the time step was = 0.0025, and the thermostat relaxation time was . The potentials were cut and shifted at = 2.5.
The potential-energy time-autocorrelation function appearing in Equation (38) was calculated at the reference temperature as follows. First, time steps were taken for equilibration, which was confirmed from two consecutive runs comparing the self-part of the intermediate scattering function. After that, a run of time steps was carried out, dumping the potential energy every 32 time steps. The potential-energy time-autocorrelation function was calculated using Fast Fourier Transform as implemented in RUMD [41].
In SPA, the constant of Equation (9) is assumed to be proportional to the change in the monitored property, in casu . was determined using the integral criterion of Ref. [18], which considers two jumps to the same temperature: an up and a down jump. For this we used the jumps from the temperatures 0.55 and 0.65 to [21], leading to
Here, is the equilibrium potential energy at the starting temperature minus the corresponding quantity at the final temperature (following the tradition in the field). The of Equation (39) was used for all predictions.
Temperature-jump simulations were carried out as follows. First, time steps were taken to ensure equilibration at the starting temperature. A total of 1000 configurations were generated from a subsequent simulation by dumping configurations every time steps. This ensures that the configurations are statistically independent at the lowest temperature studied (T = 0.50). For each of the 1000 configurations, an aging simulation of time steps was performed and the potential energy was dumped every eighth time step. The curves shown in Figure 1 represent averages over these 1000 aging simulations.
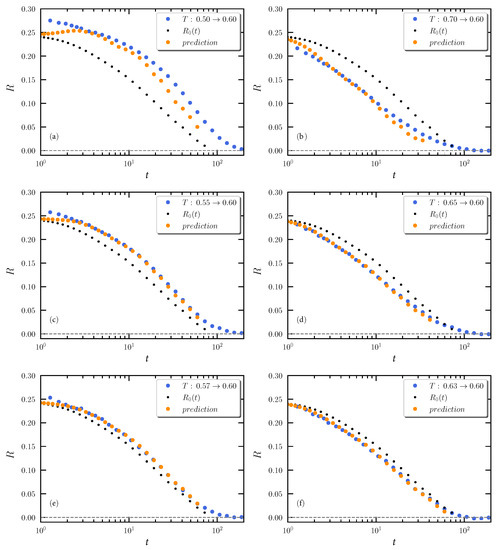
Figure 1.
Results from computer simulations of the Kob–Andersen binary Lennard–Jones model. The figures show the normalized relaxation function (Equations (25) and (29)) defined from the potential energy U after a temperature jump at starting from a state of thermal equilibrium (blue filled circles): (a,b) show results for magnitude 0.10 temperature up and down jumps to the reference temperature ; (c,d) show results for magnitude 0.05 temperature up and down jumps to ; (e,f) show results for magnitude 0.03 temperature up and down jumps to . The orange filled circles are the first-order predictions of the jump differential equation Equation (9) (given in Equation (25) in which is the normalized equilibrium potential-energy time-autocorrelation function at , is given by Equation (29), and is given by Equation (39)). For reference, in all figures is plotted as small black filled circles.
The averages were smoothed using a Gaussian function. Each point represents an average calculated over all the data points using in which is the time-step number and = 15,000. In order to reduce the number of points in Figure 1, the data were divided into 24 bins per decade.
Figure 1 shows the simulation results (blue circles) for the normalized relaxation function of the potential energy for up and down jumps to . The orange circles are the predictions of the first-order theory. In all figures the small black filled circles are the normalized equilibrium potential-energy time-autocorrelation function at , which is the linear-limit normalized relaxation function (Equation (38)). This function is faster than for up jumps and slower for down jumps. This is expected since relaxation is initially slow for the up jumps to because the fictive temperature [3] in this case is below 0.60, while the opposite happens for the down jumps to .
We see that the theory generally fits the data well, even for the fairly large temperature jumps of magnitude 0.05. Deviations between prediction and simulations is observed for larger up jumps, though. A similar pattern has been observed in experiments but there the observed relaxation function is faster than predicted, not slower [21]. In both cases, these deviations serve to emphasize that SPA is not accurate for large jumps.
The TN formalism implies that the long-time decay of the normalized relaxation function for infinitesimal jumps to different temperatures are identical except for an overall scaling of the time, i.e., it obeys time–temperature superposition (TTS) [42]. In other words, TTS is a necessary condition for TN to apply and thus, in particular, for SPA to apply. We test TTS by plotting the normalized potential-energy time-autocorrelation functions at temperatures ranging from 0.50 to 0.70 (Figure 2a) and scaling these on the time axis (Figure 2b). Except for the short-time signals that are not relevant to aging, we see that TTS indeed applies to a very good approximation.
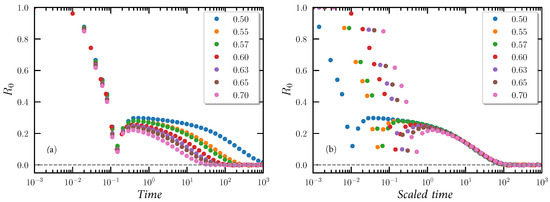
Figure 2.
Test of time–temperature superposition for the normalized potential-energy time-autocorrelation function at the temperatures indicated in the legends: (a) shows the simulation data and (b) shows the same data empirically scaled on the time axis. We conclude that TTS applies except at the shortest times.
6. Summary and Outlook
We solved the jump differential equation analytically to first order. The solution is Equation (25) in which is given by Equation (29). The solution does not explicitly involve the function ; indeed has a universal expression in terms of the zeroth-order solution, . Since the latter, by the fluctuation–dissipation theorem, is an equilibrium time-autocorrelation function, our results imply that, within the single-parameter aging scheme, knowledge of equilibrium fluctuations is enough to predict aging. The expression of relevant for the weakly nonlinear limit was confirmed by computer simulations of the Kob–Andersen binary Lennard–Jones glass former monitoring the aging of potential energy following temperature jumps of varying magnitudes.
For future development of the TN single-parameter aging formalism, it would be most interesting to monitor the equilibrium fluctuations in experiments in order to check whether aging is predicted correctly from these fluctuations. This is experimentally very challenging, but should not be impossible. It would also be interesting to monitor other quantities in simulations than the potential energy used here, although it should be mentioned that many quantities relax in a very similar way for the Kob–Andersen system [43].
Author Contributions
Conceptualization: J.C.D.; methodology and software: S.M.; writing: L.C. and J.C.D., funding acquisition: J.C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the VILLUM Foundation’s Matter grant (number 16515).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data of this study are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Equation (13) is derived here from the integral criterion of Ref. [18] that considers two jumps to the same temperature: an up and a down jump. For two small jumps of same magnitude to the temperature , denoted by a and b, one has the two normalized relaxation functions
The integral criterion [18] is
Here, is the difference in the value of jumping from above and below, implying that and . When Equation (A1) is substituted into Equation (A2), we get
Expanding to second order in leads to
This reduces to
which implies Equation (36) and, therefore, Equation (13).
References
- Mazurin, O. Relaxation phenomena in glass. J. Non-Cryst. Solids 1977, 25, 129–169. [Google Scholar] [CrossRef]
- Struik, L.C.E. Physical Aging in Amorphous Polymers and Other Materials; Elsevier: Amsterdam, The Netherland, 1978. [Google Scholar]
- Scherer, G.W. Relaxation in Glass and Composites; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Hodge, I.M. Physical aging in polymer glasses. Science 1995, 267, 1945–1947. [Google Scholar] [CrossRef] [Green Version]
- Chamon, C.; Kennett, M.P.; Castillo, H.E.; Cugliandolo, L.F. Separation of time scales and reparametrization invariance for aging systems. Phys. Rev. Lett. 2002, 89, 217201. [Google Scholar] [CrossRef] [Green Version]
- Priestley, R.D. Physical aging of confined glasses. Soft Matter 2009, 5, 919–926. [Google Scholar] [CrossRef]
- Grassia, L.; Simon, S.L. Modeling volume relaxation of amorphous polymers: Modification of the equation for the relaxation time in the KAHR model. Polymer 2012, 53, 3613–3620. [Google Scholar] [CrossRef]
- Cangialosi, D.; Boucher, V.M.; Alegria, A.; Colmenero, J. Physical aging in polymers and polymer nanocomposites: Recent results and open questions. Soft Matter 2013, 9, 8619–8630. [Google Scholar] [CrossRef]
- Dyre, J.C. Aging of CKN: Modulus versus conductivity analysis. Phys. Rev. Lett. 2013, 110, 245901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Micoulaut, M. Relaxation and physical aging in network glasses: A review. Rep. Prog. Phys. 2016, 79, 066504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McKenna, G.B.; Simon, S.L. 50th anniversary perspective: Challenges in the dynamics and kinetics of glass-forming polymers. Macromolecules 2017, 50, 6333–6361. [Google Scholar] [CrossRef]
- Roth, C.B. (Ed.) Polymer Glasses; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ruta, B.; Pineda, E.; Evenson, Z. Relaxation processes and physical aging in metallic glasses. J. Phys. Condens. Mat. 2017, 29, 503002. [Google Scholar] [CrossRef]
- Mauro, J.C. Materials Kinetics: Transport and Rate Phenomena; Elsevier: Amsterdan, The Netherlands, 2021. [Google Scholar]
- Simon, F. Über den Zustand der unterkühlten Flüssigkeiten und Gläser. Z. Anorg. Allg. Chem. 1931, 203, 219–227. [Google Scholar] [CrossRef]
- Olsen, N.B.; Dyre, J.C.; Christensen, T. Structural relaxation monitored by instantaneous shear modulus. Phys. Rev. Lett. 1998, 81, 1031–1033. [Google Scholar] [CrossRef] [Green Version]
- Hecksher, T.; Olsen, N.B.; Niss, K.; Dyre, J.C. Physical aging of molecular glasses studied by a device allowing for rapid thermal equilibration. J. Chem. Phys. 2010, 133, 174514. [Google Scholar] [CrossRef] [PubMed]
- Hecksher, T.; Olsen, N.B.; Dyre, J.C. Communication: Direct tests of single-parameter aging. Chem. Phys. 2015, 142, 241103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hecksher, T.; Olsen, N.B.; Dyre, J.C. Fast contribution to the activation energy of a glass-forming liquid. Proc. Natl. Acad. Sci. USA 2019, 116, 16736–16741. [Google Scholar] [CrossRef] [Green Version]
- Roed, L.A.; Hecksher, T.; Dyre, J.C.; Niss, K. Generalized single-parameter aging tests and their application to glycerol. J. Chem. Phys. 2019, 150, 044501. [Google Scholar] [CrossRef] [Green Version]
- Riechers, B.; Roed, L.A.; Mehri, S.; Ingebrigtsen, T.S.; Hecksher, T.; Dyre, J.C.; Niss, K. Predicting nonlinear physical aging of glasses from equilibrium relaxation via the material time. Sci. Adv. 2022, 8, eabl9809. [Google Scholar] [CrossRef] [PubMed]
- Kolla, S.; Simon, S.L. The t-effective paradox: New measurements towards a resolution. Polymer 2005, 46, 733–739. [Google Scholar] [CrossRef]
- Schlosser, E.; Schönhals, A. Dielectric relaxation during physical aging. Polymer 1991, 32, 2135–2140. [Google Scholar] [CrossRef]
- Leheny, R.L.; Nagel, S.R. Frequency-domain study of physical aging in a simple liquid. Phys. Rev. B 1998, 57, 5154–5162. [Google Scholar] [CrossRef]
- Lunkenheimer, P.; Wehn, R.; Schneider, U.; Loidl, A. Glassy aging dynamics. Phys. Rev. Lett. 2005, 95, 055702. [Google Scholar] [CrossRef]
- Richert, R. Supercooled liquids and glasses by dielectric relaxation spectroscopy. Adv. Chem. Phys. 2015, 156, 101–195. [Google Scholar]
- Kovacs, A.J. Transition vitreuse dans les polymeres amorphes. Etude phenomenologique. Fortschr. Hochpolym.-Forsch. 1963, 3, 394–507. [Google Scholar]
- Spinner, S.; Napolitano, A. Further studies in the annealing of a borosilicate glass. J. Res. NBS 1966, 70, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Narayanaswamy, O.S. A model of structural relaxation in glass. J. Amer. Ceram. Soc. 1971, 54, 491–498. [Google Scholar] [CrossRef]
- Moynihan, C.T.; Easteal, A.J.; DeBolt, M.A.; Tucker, J. Dependence of the fictive temperature of glass on cooling rate. J. Am. Ceram. Soc. 1976, 59, 12–16. [Google Scholar] [CrossRef]
- Chen, H.S. The influence of structural relaxation on the density and Young’s modulus of metallic glasses. J. Appl. Phys. 1978, 49, 3289–3291. [Google Scholar] [CrossRef]
- Huang, Y.; Paul, D.R. Physical aging of thin glassy polymer films monitored by gas permeability. Polymer 2004, 45, 8377–8393. [Google Scholar] [CrossRef]
- Leonardo, R.D.; Scopigno, T.; Ruocco, G.; Buontempo, U. Spectroscopic cell for fast pressure jumps across the glass transition line. Rev. Sci. Instrum. 2004, 75, 2631–2637. [Google Scholar] [CrossRef] [Green Version]
- Ruta, B.; Chushkin, Y.; Monaco, G.; Cipelletti, L.; Pineda, E.; Bruna, P.; Giordano, V.M.; Gonzalez-Silveira, M. Atomic-scale relaxation dynamics and aging in a metallic glass probed by x-ray photon correlation spectroscopy. Phys. Rev. Lett. 2012, 109, 165701. [Google Scholar] [CrossRef] [Green Version]
- Brun, C.; Ladieu, F.; L’Hote, D.; Biroli, G.; Bouchaud, J.-P. Evidence of growing spatial correlations during the aging of glassy glycerol. Phys. Rev. Lett. 2012, 109, 175702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Angell, C.A. Formation of glasses from liquids and biopolymers. Science 1995, 267, 1924–1935. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nielsen, J.K.; Dyre, J.C. Fluctuation-dissipation theorem for frequency-dependent specific heat. Phys. Rev. B 1996, 54, 15754–15761. [Google Scholar] [CrossRef] [PubMed]
- Kob, W.; Andersen, H.C. Testing mode-coupling theory for a supercooled binary Lennard-Jones mixture I: The van Hove correlation function. Phys. Rev. E 1995, 51, 4626–4641. [Google Scholar] [CrossRef] [Green Version]
- Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef] [Green Version]
- Bailey, N.P.; Ingebrigtsen, T.S.; Hansen, J.S.; Veldhorst, A.A.; Bøhling, L.; Lemarchand, C.A.; Olsen, A.E.; Bacher, A.K.; Costigliola, L.; Pedersen, U.R.; et al. RUMD: A general purpose molecular dynamics package optimized to utilize GPU hardware down to a few thousand particles. Scipost Phys. 2017, 3, 38. [Google Scholar] [CrossRef] [Green Version]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford Science Publications: Oxford, UK, 1987. [Google Scholar]
- Olsen, N.B.; Christensen, T.; Dyre, J.C. Time-temperature superposition in viscous liquids. Phys. Rev. Lett. 2001, 86, 1271–1274. [Google Scholar] [CrossRef] [Green Version]
- Mehri, S.; Ingebrigtsen, T.S.; Dyre, J.C. Single-parameter aging in a binary Lennard-Jones system. J. Chem. Phys. 2021, 154, 094504. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).