The Basic Theorem of Temperature-Dependent Processes
Abstract
1. Introduction
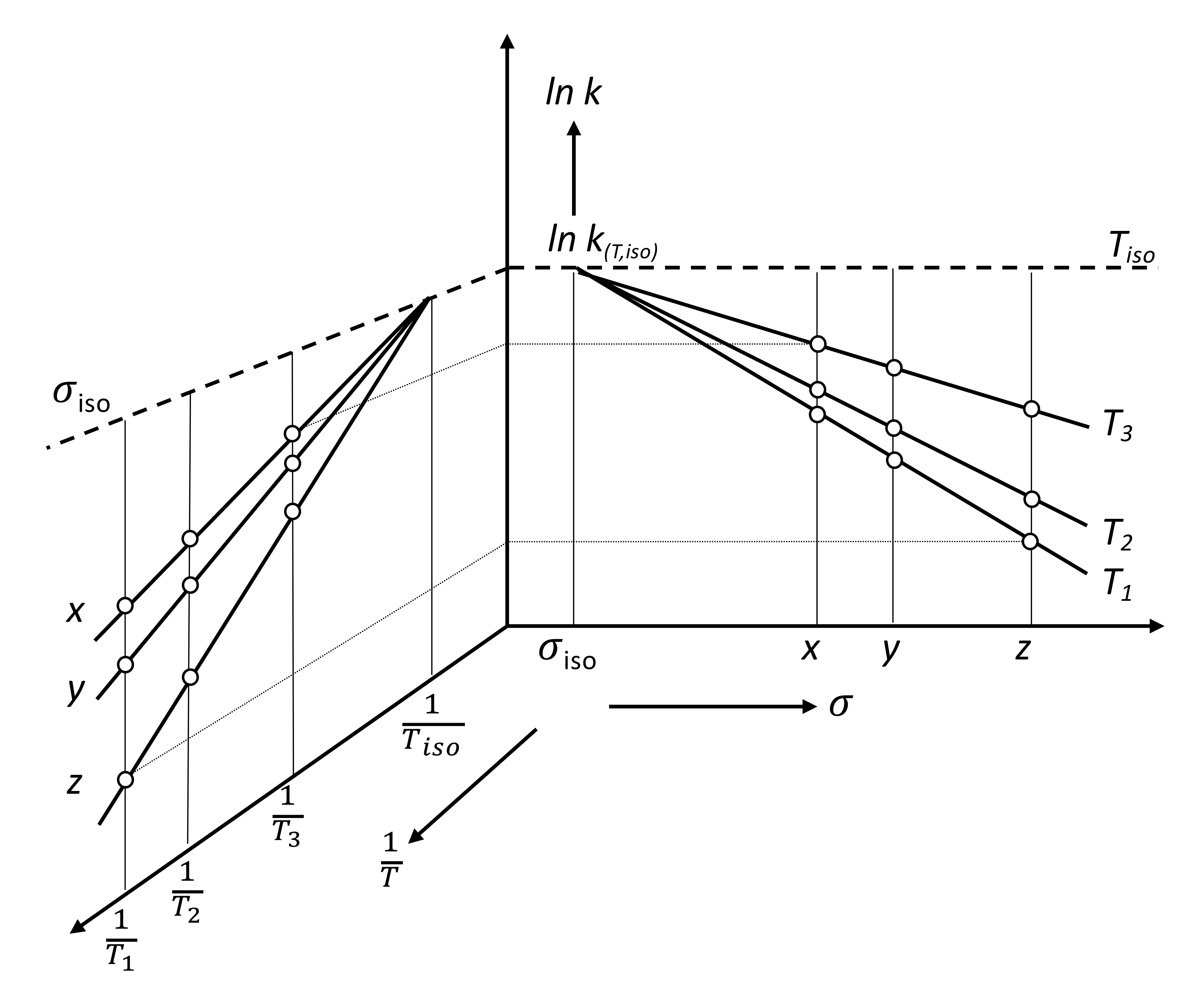
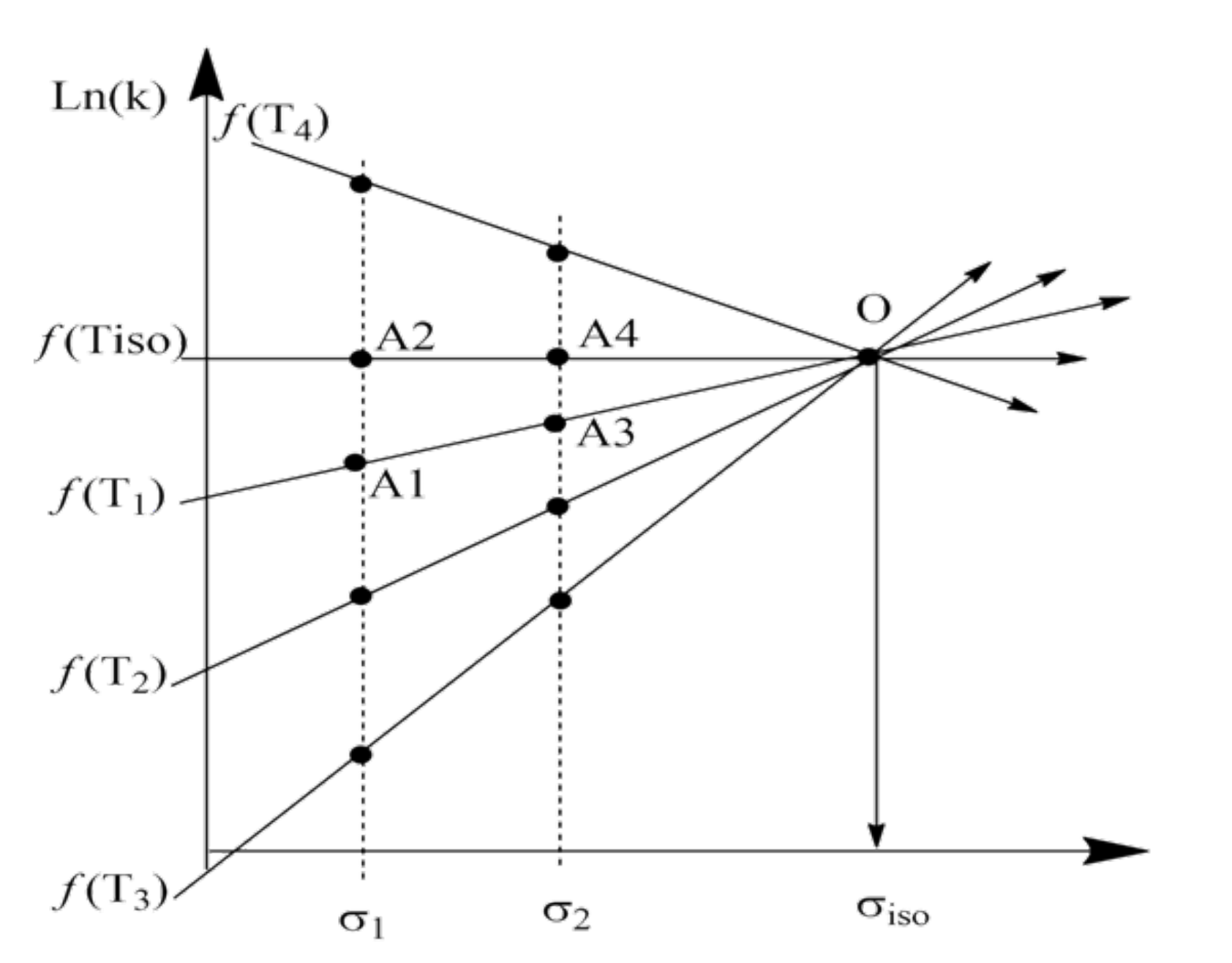
2. Discussion
3. Some Consequences of the Theorem
3.1. Interpretation of Known Empirical Regularity
3.2. The Effect of the Temperature on the Impact of Variable Parameter
3.3. The Effect of the Variable Parameter on the Free Energy of Activation
3.4. The Negative Activation Energies
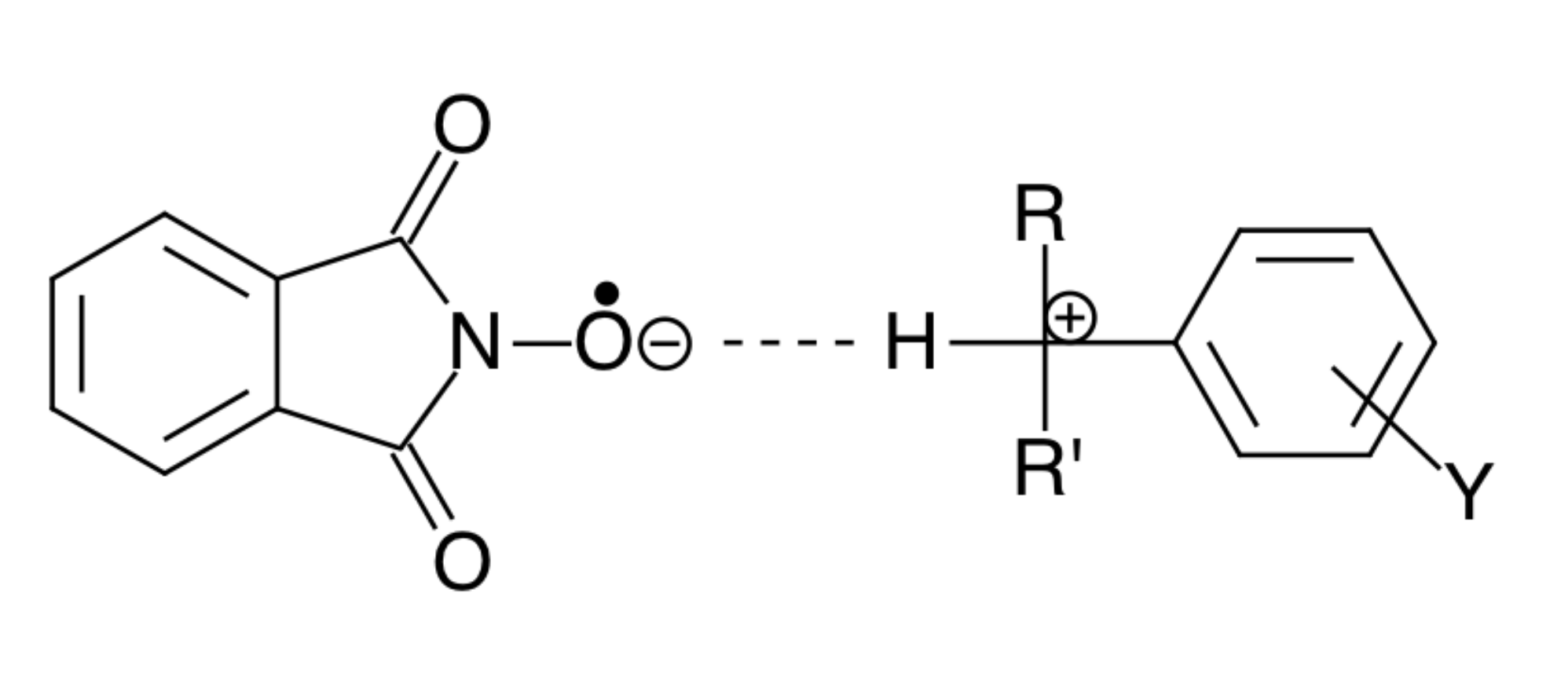
4. Outlook and Possible Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silverman, M.P. Effects of a Periodic Decay Rate on the Statistics of Radioactive Decay: New Methods to Search for Violations of the Law of Radioactive Change. J. Mod. Phys. 2015, 6, 1533–1553. [Google Scholar] [CrossRef]
- Tarvainen, V.; Hakola, H.; Hellen, H.; Back, J.; Hari, P.; Kulmala, M. Temperature and light dependence of the VOC emissions of Scots pine. Atmos. Chem. Phys. 2005, 5, 989–998. [Google Scholar] [CrossRef]
- Lubianiker, Y.; Balberg, I. A comparative study of the Meyer-Neldel rule in porous silicon and hydrogenated amorphous silicon. J. Non-Cryst. Solids 1998, 227, 180–184. [Google Scholar] [CrossRef]
- Yan, H.; Abdelhadi, M.M.; Jung, J.A.; Willemsen, B.A.; Kihlstrom, K.E. Exponential dependence of the vortex pinning potential on current density in high-T-c superconductors. Phys. Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Mehta, N.; Kushwaha, V.S.; Kumar, A. Further Meyer-Neldel Rule for Thermally Activated High Field Conduction in Thin Films of Glassy Se100-xSbx Alloys. Int. J. Appl. Glass Sci. 2010, 1, 172–179. [Google Scholar] [CrossRef]
- Widenhorn, R.; Mundermann, L.; Rest, A.; Bodegom, E. Meyer-Neldel rule for dark current in charge-coupled devices. J. Appl. Phys. 2001, 89, 8179–8182. [Google Scholar] [CrossRef][Green Version]
- Cooper, V.S.; Bennett, A.F.; Lenski, R.E. Evolution of thermal dependence of growth rate of Escherichia coli populations during 20,000 generations in a constant environment. Evolution 2001, 55, 889–896. [Google Scholar] [CrossRef]
- Englund, G.; Ohlund, G.; Hein, C.L.; Diehl, S. Temperature dependence of the functional response. Ecol. Lett. 2011, 14, 914–921. [Google Scholar] [CrossRef]
- Simon, P. Single-step kinetics approximation employing non-Arrhenius temperature functions. J. Therm. Anal. Calorim. 2005, 79, 703–708. [Google Scholar] [CrossRef]
- Šimon, P.; Thomas, P.; Dubaj, T.; Cibulková, Z.; Peller, A.; Veverka, M. The mathematical incorrectness of the integral isoconversional methods in case of variable activation energy and the consequences. J. Therm. Anal. Calorim. 2014, 115, 853–859. [Google Scholar] [CrossRef]
- Šimon, P.; Dubaj, T.; Cibulková, Z. Equivalence of the Arrhenius and non-Arrhenian temperature functions in the temperature range of measurement. J. Therm. Anal. Calorim. 2015, 120, 231–238. [Google Scholar] [CrossRef]
- Maitra, S.; Bandyopadhyay, N.; Pal, J. Application of Non-Arrhenius Method for Analyzing the Decomposition Kinetics of SrCO3 and BaCO3. J. Am. Ceram. Soc. 2008, 91, 337–341. [Google Scholar] [CrossRef]
- Chen, H.; Liu, N. Application of Non-Arrhenius Equations in Interpreting Calcium Carbonate Decomposition Kinetics: Revisited. J. Am. Ceram. Soc. 2009, 93, 548–553. [Google Scholar] [CrossRef]
- Dubaj, T.; Cibulková, Z.; Šimon, P. An incremental isoconversional method for kinetic analysis based on the orthogonal distance regression. J. Comput. Chem. 2015, 36, 392–398. [Google Scholar] [CrossRef] [PubMed]
- Li, J.V.; Johnston, S.W.; Yan, Y.; Levi, D.H. Measuring temperature-dependent activation energy in thermally activated processes: A 2D Arrhenius plot method. Rev. Sci. Instrum. 2010, 81. [Google Scholar] [CrossRef]
- Bronsted, J.N.; Pedersen, K. The catalytic disintegration of nitramide and its physical-chemical relevance. Z. Phys. Chem. Stochiom. Verwandtschaftslehre 1924, 108, 185–235. [Google Scholar]
- Hammett, L.P. Some relations between reaction rates and equilibrium constants. Chem. Rev. 1935, 17, 125–136. [Google Scholar] [CrossRef]
- Chapman, N.B.; Shorter, J. (Eds.) Advances in Linear Free Energy Relationships; Springer: New York, NY, USA, 1972. [Google Scholar] [CrossRef]
- Palm, V.A. Structure and reactivity of organic compounds (quantitative laws). Russ. Chem. Rev. 1961, 30, 471–498. [Google Scholar] [CrossRef]
- Koppel, A.; Palm, V. The Influence of the Solvent on Organic Reactivity. In Advances in Linear Free Energy Relationships; Chapman, N.B., Shorter, J., Eds.; Springer: New York, NY, USA, 1972. [Google Scholar]
- Swain, C.G.; Swain, M.S.; Powell, A.L.; Alunni, S. Solvent effects on chemical-reactivity-evaluation of anion and cation solvation components. J. Am. Chem. Soc. 1983, 105, 502–513. [Google Scholar] [CrossRef]
- Edwards, J.O. Correlation of relative rates and equilibria with a double basicity scale. J. Am. Chem. Soc. 1954, 76, 1540–1547. [Google Scholar] [CrossRef]
- Grunwald, E.; Winstein, S. The correlation of solvolysis rates. J. Am. Chem. Soc. 1948, 70, 846–859. [Google Scholar] [CrossRef]
- Winstein, S.; Grunwald, E.; Jones, H.W. The correlation of solvolysis rates and the classification of solvolysis reactions into mechanistic categories. J. Am. Chem. Soc. 1951, 73, 2700–2707. [Google Scholar] [CrossRef]
- Bronsted, J.N. Einige Bemerkungen uber den Begriff der Sauren und Basen. Recl. Trav. Chim. Pays-Bas 2010, 42, 718–728. [Google Scholar] [CrossRef]
- Taft, R.W. Linear steric energy relationships. J. Am. Chem. Soc. 1953, 75, 4538–4539. [Google Scholar] [CrossRef]
- Taft, R.W. Linear free energy relationships from rates of esterification and hydrolysis of aliphatic and ortho-substituted benzoate esters. J. Am. Chem. Soc. 1952, 74, 2729–2732. [Google Scholar] [CrossRef]
- Taft, R.W. Polar and steric substituent constants for aliphatic and o-benzoate groups from rates of esterification and hydrolysis of esters. J. Am. Chem. Soc. 1952, 74, 3120–3128. [Google Scholar] [CrossRef]
- Swain, C.G.; Lupton, E.C. Field and resonance components of substituent effects. J. Am. Chem. Soc. 1968, 90, 4328. [Google Scholar] [CrossRef]
- Yukawa, Y.; Tsuno, Y. Resonance effect in hammett relationship. 2. sigma constants in electrophilic reactions and their intercorrelation. Bull. Chem. Soc. Jpn. 1959, 32, 965–971. [Google Scholar] [CrossRef]
- Barclay, I.M.; Butler, J.A.V. The entropy of solution. Trans. Faraday Soc. 1938, 34, 1445–1454. [Google Scholar] [CrossRef]
- Schwab, G.M. About the mechanism of contact catalysis. Adv. Catal. 1950, 2, 251–267. [Google Scholar] [CrossRef]
- Manche, E.P.; Carroll, B. Compensation and the smith-topley effects. Thermochim. Acta 1979, 31, 387–390. [Google Scholar] [CrossRef]
- Bond, G.C.; Keane, M.A.; Kral, H.; Lercher, J.A. Compensation phenomena in heterogeneous catalysis: General principles and a possible explanation. Catal. Rev. Sci. Eng. 2000, 42, 323–383. [Google Scholar] [CrossRef]
- Bligaard, T.; Honkala, K.; Logadottir, A.; Norskov, J.K.; Dahl, S.; Jacobsen, C.J.H. On the compensation effect in heterogeneous catalysis. J. Phys. Chem. B 2003, 107, 9325–9331. [Google Scholar] [CrossRef]
- Meyer, W.; Neldel, H. Concerning the relationship between the energy constant epsilon and the quantum constant alpha in the conduction-temperature formula in oxydising semi-conductors. Phys. Z. 1937, 38, 1014–1019. [Google Scholar]
- Meijer, E.J.; Matters, M.; Herwig, P.T.; de Leeuw, D.M.; Klapwijk, T.M. The Meyer-Neldel rule in organic thin-film transistors. Appl. Phys. Lett. 2000, 76, 3433–3435. [Google Scholar] [CrossRef]
- Yelon, A.; Movaghar, B.; Branz, H.M. Origin and consequences of the compensation (meyer-neldel) law. Phys. Rev. B 1992, 46, 12244–12250. [Google Scholar] [CrossRef] [PubMed]
- Exner, O. Determination of isokinetic temperature. Nature 1970, 227, 366. [Google Scholar] [CrossRef]
- Wold, S.; Sjostrom, M. Linear free-energy relationships-local empirical rules-or fundamental laws of chemistry-a reply to kamlet and taft. Acta Chem. Scand. Ser. B-Org. Chem. Biochem. 1986, 40, 270–277. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Q.X. Isokinetic relationship, isoequilibrium relationship, and enthalpy-entropy compensation. Chem. Rev. 2001, 101, 673–695. [Google Scholar] [CrossRef]
- Pure, I.U. Chemical Terminology. In Gold Book, 2.3.1 ed.; IUPAC: Guaruja, Brazil, 2012; Available online: https://goldbook.iupac.org/ (accessed on 15 March 2021).
- Zsako, J. Kinetic compensation effect. J. Therm. Anal. 1976, 9, 101–108. [Google Scholar] [CrossRef]
- Zawadzki, J.; Bretsznajder, S. Some remarks on the mechanism of reactions of the type: Solid=solid + gas. Trans. Faraday Soc. 1938, 34, 951–959. [Google Scholar] [CrossRef]
- Šesták, J. Errors of kinetic data obtained from thermogravimetric curves at increasing temperature. Talanta 1966, 13, 567–579. [Google Scholar] [CrossRef]
- Koga, N. A review of the mutual dependence of Arrhenius parameters evaluated by the thermoanalytical study of solid-state reactions: The kinetic compensation effect. Thermochim. Acta 1994, 244, 1–20. [Google Scholar] [CrossRef]
- Farjas, J.; Roura, P. Exact analytical solution for the Kissinger equation: Determination of the peak temperature and general properties of thermally activated transformations. Thermochim. Acta 2014, 598, 51–58. [Google Scholar] [CrossRef]
- Holba, P. Temperature dependence of activation energy of endothermic processes and related imperfections of non-isothermal kinetic evaluations. J. Therm. Anal. Calorim. 2017, 129, 609–614. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, N. Kinetic analysis based on the kinetic compensation effect and optimization calculation. Thermochim. Acta 2020, 690, 178686. [Google Scholar] [CrossRef]
- Mianowski, A.; Radko, T.; Siudyga, T. Kinetic compensation effect of isoconversional methods. React. Kinet. Mech. Catal. 2021, 132, 37–58. [Google Scholar] [CrossRef]
- Bel’skii, V.E. Isokinetic relationships for nucleophilic substitution reactions at the saturated carbon atom. Reactions in aqueous solutions. Russ. Chem. Bull. 2000, 49, 806–811. [Google Scholar] [CrossRef]
- Freed, K.F. Entropy-Enthalpy Compensation in Chemical Reactions and Adsorption: An Exactly Solvable Model. J. Phys. Chem. B 2011, 115, 1689–1692. [Google Scholar] [CrossRef]
- Naffakh, M.; Marco, C.; Gomez, M.A.; Jimenez, I. Unique Nucleation Activity of Inorganic Fullerene-like WS2 Nanoparticles in Polyphenylene Sulfide Nanocomposites: Isokinetic and Isoconversional Study of Dynamic Crystallization Kinetics. J. Phys. Chem. B 2009, 113, 7107–7115. [Google Scholar] [CrossRef]
- Starikov, E.B.; Norden, B. Entropy-enthalpy compensation may be a useful interpretation tool for complex systems like protein-DNA complexes: An appeal to experimentalists. Appl. Phys. Lett. 2012, 100. [Google Scholar] [CrossRef]
- Perez-Galvez, A.; Jaren-Galan, M.; Minguez-Mosquera, M.I. Effect of high-temperature degradative processes on ketocarotenoids present in paprika oleoresins. J. Agric. Food Chem. 2000, 48, 2966–2971. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Ueoka, R. Studies on thermodynamics for hydrolysis. 3. isokinetic temperature related to molecular location of reactants in coaggregates. J. Org. Chem. 1990, 55, 5797–5799. [Google Scholar] [CrossRef]
- Loaiza, A.; Armstrong, K.M.; Baker, B.M.; Abu-Omar, M.M. Kinetics of thermal unfolding of phenylalanine hydroxylase variants containing different metal cofactors (Fe-II, Co-II, and Zn-II) and their lsokinetic relationship. Inorg. Chem. 2008, 47, 4877–4883. [Google Scholar] [CrossRef] [PubMed]
- McBane, G.C. Chemistry from telephone numbers: The false isokinetic relationship. J. Chem. Educ. 1998, 75, 919–922. [Google Scholar] [CrossRef]
- Barrie, P.J. The mathematical origins of the kinetic compensation effect: 1. the effect of random experimental errors. Phys. Chem. Chem. Phys. 2012, 14, 318–326. [Google Scholar] [CrossRef]
- Koudriavtsev, A.B.; Linert, W. Do Experimental Errors Really Cause Isoequilibrium and Isokinetic Relationships? Match-Commun. Math. Comput. Chem. 2013, 70, 7–28. [Google Scholar]
- Linert, W.; Yelon, A. Isokinetic relationships preface. Monatshefte Chem. 2013, 144, 1–2. [Google Scholar] [CrossRef]
- Ouvrard, C.; Berthelot, M.; Lamer, T.; Exner, O. A program for linear regression with a common point of intersection: The isokinetic relationship. J. Chem. Inf. Comput. Sci. 2001, 41, 1141–1144. [Google Scholar] [CrossRef]
- Perez-Benito, J.F.; Mulero-Raichs, M. Enthalpy-Entropy Compensation Effect in Chemical Kinetics and Experimental Errors: A Numerical Simulation Approach. J. Phys. Chem. A 2016, 120, 7598–7609. [Google Scholar] [CrossRef]
- Linert, W.; Sapunov, V.N. The isokinetic relationship. 9. connections to linear free-energy relationships. Chem. Phys. 1988, 119, 265–274. [Google Scholar] [CrossRef]
- Yelon, A.; Movaghar, B.; Crandall, R.S. Multi-excitation entropy: Its role in thermodynamics and kinetics. Rep. Prog. Phys. 2006, 69, 1145–1194. [Google Scholar] [CrossRef]
- Pinheiro, L.M.V.; Calado, A.R.T.; Reis, J.C.R. The quaternisation reaction of phosphines and amines in aliphatic alcohols. A similarity analysis using the isokinetic, isosolvent and isoselective relationships. Org. Biomol. Chem. 2004, 2, 1330–1338. [Google Scholar] [CrossRef] [PubMed]
- Larsson, R. Concluding remarks on the theory of selective energy transfer and exemplification on a zeolite kinetics study. Monatshefte Chem. 2013, 144, 21–28. [Google Scholar] [CrossRef]
- Bratlie, K.M.; Flores, L.D.; Somorjai, G.A. In situ sum frequency generation vibrational spectroscopy observation of a reactive surface intermediate during high-pressure benzene hydrogenation. J. Phys. Chem. B 2006, 110, 10051–10057. [Google Scholar] [CrossRef] [PubMed]
- Leffler, J.E. The enthalpy-entropy relationship and its implications for organic chemistry. J. Org. Chem. 1955, 20, 1202–1231. [Google Scholar] [CrossRef]
- Crandall, R.S. Defect relaxation in amorphous-silicon-stretched exponentials, the meyer-neldel rule, and the staebler-wronski effect. Phys. Rev. B 1991, 43, 4057–4070. [Google Scholar] [CrossRef]
- Wang, J.C.; Chen, Y.F. The Meyer-Neldel rule in fullerenes. Appl. Phys. Lett. 1998, 73, 948–950. [Google Scholar] [CrossRef]
- Yelon, A.; Movaghar, B. Microscopic explanation of the compensation (meyer-neldel) rule. Phys. Rev. Lett. 1990, 65, 618–620. [Google Scholar] [CrossRef]
- Dyre, J.C. A phenomenological model for the meyer-neldel rule. J. Phys. C-Solid State Phys. 1986, 19, 5655–5664. [Google Scholar] [CrossRef]
- Singh, A.K.; Singh, K. Observation of Meyer Neldel rule and crystallization rate constant stability for Se93-xZn2Te5Inx chalcogenide glasses. Eur. Phys. J. Appl. Phys. 2010, 51. [Google Scholar] [CrossRef]
- Rong, X.; Parolin, J.; Kolpak, A.M. A Fundamental Relationship between Reaction Mechanism and Stability in Metal Oxide Catalysts for Oxygen Evolution. ACS Catal. 2016, 6, 1153–1158. [Google Scholar] [CrossRef]
- Singh, K.; Mehta, N.; Sharma, S.K.; Kumar, A. Crystallization kinetics of glassy Se90In10-xAgx alloys: Observation of Mayer-Neldel rule. Process. Appl. Ceram. 2016, 10, 137–142. [Google Scholar] [CrossRef]
- Pan, A.; Biswas, T.; Rakshit, A.K.; Moulik, S.P. Enthalpy-Entropy Compensation (EEC) Effect: A Revisit. J. Phys. Chem. B 2015, 119, 15876–15884. [Google Scholar] [CrossRef]
- Laidler, K.J.; King, M.C. The development of transition-state theory. J. Phys. Chem. 1983, 87, 2657–2664. [Google Scholar] [CrossRef]
- Schmid, R.; Sapunov, V. Non-Formal Kinetics Search of Chemical Reaction Pathways. In Monographs in Modern Chemistry; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1982; Volume 14, p. 172. [Google Scholar]
- Yelon, A.; Sacher, E.; Linert, W. Multi-Excitation Entropy, Entropy-Enthalpy Relations, and their Impact on Catalysis. Catal. Lett. 2011, 141, 954–957. [Google Scholar] [CrossRef]
- Movileanu, L.; Schiff, E.A. Entropy-enthalpy compensation of biomolecular systems in aqueous phase: A dry perspective. Monatshefte Chem. 2013, 144, 59–65. [Google Scholar] [CrossRef]
- Chen, T.; Zhang, Y.; Xu, W. Single-Molecule Nanocatalysis Reveals Catalytic Activation Energy of Single Nanocatalysts. J. Am. Chem. Soc. 2016, 138, 12414–12421. [Google Scholar] [CrossRef]
- Karunakaran, C.; Chidambaranathan, V. Linear free energy relationships near isokinetic temperature. Oxidation of organic sulfides with nicotinium dichromate. Croat. Chem. Acta 2001, 74, 51–59. [Google Scholar]
- Shpan’ko, I.V.; Sadovaya, I.V. Isoparametricity paradox in the pyridine-catalyzed reaction of phenyloxirane with 3-nitrobenzoic acid. Russ. J. Phys. Chem. A 2013, 87, 1955–1959. [Google Scholar] [CrossRef]
- Shpan’ko, I.V.; Sadovaya, I.V. Phenomenon of isoparametricity in reactions of trans-2,3-diaryloxiranes with arenesulfonic acids. Mechanistic interpretation. Russ. J. Gen. Chem. 2016, 86, 2418–2422. [Google Scholar] [CrossRef]
- Ma, H.; Na, C. Isokinetic Temperature and Size-Controlled Activation of Ruthenium-Catalyzed Ammonia Borane Hydrolysis. Acs Catal. 2015, 5, 1726–1735. [Google Scholar] [CrossRef]
- Sun, D.; Wicker, L. Kinetic compensation and the role of cations in pectinesterase catalysis. J. Agric. Food Chem. 1999, 47, 1471–1475. [Google Scholar] [CrossRef] [PubMed]
- Vlasov, V.M. Energetics of bimolecular nucleophilic reactions in solution. Uspekhi Khimii 2006, 75, 851–883. [Google Scholar] [CrossRef]
- Armstrong, A.A.; Amzel, L.M. Role of entropy in increased rates of intramolecular reactions. J. Am. Chem. Soc. 2003, 125, 14596–14602. [Google Scholar] [CrossRef]
- Sohtome, Y.; Shin, B.; Horitsugi, N.; Takagi, R.; Noguchi, K.; Nagasawa, K. Entropy-Controlled Catalytic Asymmetric 1,4-Type Friedel-Crafts Reaction of Phenols Using Conformationally Flexible Guanidine/Bisthiourea Organocatalyst. Angew. Chem. Int. Ed. 2010, 49, 7299–7303. [Google Scholar] [CrossRef] [PubMed]
- Laskin, J.; Futrell, J.H. Entropy is the major driving force for fragmentation of proteins and protein-ligand complexes in the gas phase. J. Phys. Chem. A 2003, 107, 5836–5839. [Google Scholar] [CrossRef]
- Strajbl, M.; Sham, Y.Y.; Villa, J.; Chu, Z.T.; Warshel, A. Calculations of activation entropies of chemical reactions in solution. J. Phys. Chem. B 2000, 104, 4578–4584. [Google Scholar] [CrossRef]
- Van der Mynsbrugge, J.; Janda, A.; Sharada, S.M.; Lin, L.C.; Van Speybroeck, V.; Head-Gordon, M.; Bell, A.T. Theoretical Analysis of the Influence of Pore Geometry on Monomolecular Cracking and Dehydrogenation of n-Butane in Bronsted Acidic Zeolites. ACS Catal. 2017, 7, 2685–2697. [Google Scholar] [CrossRef]
- Revell, L.E.; Williamson, B.E. Why Are Some Reactions Slower at Higher Temperatures? J. Chem. Educ. 2013, 90, 1024–1027. [Google Scholar] [CrossRef]
- Hadel, L.M.; Maloney, V.M.; Platz, M.S.; McGimpsey, W.G.; Scaiano, J.C. The absolute kinetics of several reactions of substituted diphenylcarbenes. J. Phys. Chem. 1986, 90, 2488–2491. [Google Scholar] [CrossRef]
- Aquilanti, V.; Coutinho, N.D.; Carvalho-Silva, V.H. Kinetics of low-temperature transitions and a reaction rate theory from non-equilibrium distributions. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2017, 375. [Google Scholar] [CrossRef]
- Coutinho, N.D.; Silva, V.H.C.; de Oliveira, H.C.B.; Camargo, A.J.; Mundim, K.C.; Aquilanti, V. Stereodynamical Origin of Anti-Arrhenius Kinetics: Negative Activation Energy and Roaming for a Four-Atom Reaction. J. Phys. Chem. Lett. 2015, 6, 1553–1558. [Google Scholar] [CrossRef] [PubMed]
- Varlamov, V.T.; Denisov, N.N.; Nadtochenko, V.A. Negative activation energies and compensation effects for the reactions of diarylaminyl radicals with phenols. Russ. Chem. Bull. 1995, 44, 2282–2286. [Google Scholar] [CrossRef]
- Bowman, D.F.; Gillan, T.; Ingold, K.U. Kinetic applications of electron paramagnetic resonance spectroscopy. 3. self-reactions of dialkyl nitroxide radicals. J. Am. Chem. Soc. 1971, 93, 6555. [Google Scholar] [CrossRef]
- Adamic, K.; Bowman, D.F.; Gillan, T.; Ingold, K.U. Kinetic applications of electron paramagnetic resonance spectroscopy. 1. self-reactions of diethyl nitroxide radicals. J. Am. Chem. Soc. 1971, 93, 902. [Google Scholar]
- Zavitsas, A.A. Energy barriers to chemical reactions. Why, how, and how much? non-arrhenius behavior in hydrogen abstractions by radicals. J. Am. Chem. Soc. 1998, 120, 6578–6586. [Google Scholar] [CrossRef]
- Li, J.L.; Geng, C.Y.; Huang, X.R.; Sun, C.C. A barrier-free atomic radical-molecule reaction: F + propene. J. Chem. Theory Comput. 2006, 2, 1551–1564. [Google Scholar] [CrossRef]
- Ge, Y. Agreement, Complement, and Disagreement to “Why Are Some Reactions Slower at Higher Temperatures?”. J. Chem. Educ. 2017, 94, 821–823. [Google Scholar] [CrossRef]
- Kapinus, E.I.; Rau, H. Negative enthalpies of activation and isokinetic relationships in the electron transfer quenching reaction of PD-tetraphenylporphyrin by aromatic nitro compounds and quinones. J. Phys. Chem. A 1998, 102, 5569–5576. [Google Scholar] [CrossRef]
- Carlos Aledo, J.; Jimenez-Riveres, S.; Tena, M. The Effect of Temperature on the Enzyme-Catalyzed Reaction: Insights from Thermodynamics. J. Chem. Educ. 2010, 87, 296–298. [Google Scholar] [CrossRef]
- Silverstein, T. The Nuts and Bolts of Michaelis-Menten Enzyme Kinetics: Suggestions and Clarifications. J. Chem. Educ. 2011, 88, 167–168. [Google Scholar] [CrossRef]
- Zheng, W.; Andrec, M.; Gallicchio, E.; Levy, R.M. Simulating replica exchange simulations of protein folding with a kinetic network model. Proc. Natl. Acad. Sci. USA 2007, 104, 15340–15345. [Google Scholar] [CrossRef] [PubMed]
- Starikov, E.B. Valid Entropy-Enthalpy Compensation: Its True Physical-Chemical Meaning. J. Appl. Solut. Chem. Model. 2013, 2, 240–245. [Google Scholar] [CrossRef]
- Widenhorn, R.; Rest, A.; Bodegom, E. The Meyer-Neldel rule for a property determined by two transport mechanisms. J. Appl. Phys. 2002, 91, 6524–6528. [Google Scholar] [CrossRef]
- Abtew, T.A.; Zhang, M.; Pan, Y.; Drabold, D.A. Electrical conductivity and Meyer-Neldel rule: The role of localized states in hydrogenated amorphous silicon. J. Non-Cryst. Solids 2008, 354, 2909–2913. [Google Scholar] [CrossRef]
- Kushwaha, N.; Mehta, N.; Shukla, R.K.; Kumar, D.; Kumar, A. Observation of Meyer-Neldel N rule in amorphous Se100-xTex thin films. J. Optoelectron. Adv. Mater. 2005, 7, 2293–2298. [Google Scholar]
- Carvalho-Silva, V.H.; Coutinho, N.D.; Aquilanti, V. From the Kinetic Theory of Gases to the Kinetics of Rate Processes: On the Verge of the Thermodynamic and Kinetic Limits. Molecules 2020, 25, 2098. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sapunov, V.N.; Saveljev, E.A.; Voronov, M.S.; Valtiner, M.; Linert, W. The Basic Theorem of Temperature-Dependent Processes. Thermo 2021, 1, 45-60. https://doi.org/10.3390/thermo1010004
Sapunov VN, Saveljev EA, Voronov MS, Valtiner M, Linert W. The Basic Theorem of Temperature-Dependent Processes. Thermo. 2021; 1(1):45-60. https://doi.org/10.3390/thermo1010004
Chicago/Turabian StyleSapunov, Valentin N., Eugene A. Saveljev, Mikhail S. Voronov, Markus Valtiner, and Wolfgang Linert. 2021. "The Basic Theorem of Temperature-Dependent Processes" Thermo 1, no. 1: 45-60. https://doi.org/10.3390/thermo1010004
APA StyleSapunov, V. N., Saveljev, E. A., Voronov, M. S., Valtiner, M., & Linert, W. (2021). The Basic Theorem of Temperature-Dependent Processes. Thermo, 1(1), 45-60. https://doi.org/10.3390/thermo1010004







