Thermochemistry, Bond Energies and Internal Rotor Potentials of Acetic Acid Hydrazide, Acetamide, N-Methyl Acetamide (NMA) and Radicals

Abstract

Structures, thermochemical properties, bond energies, and internal rotation potentials of acetic acid hydrazide (CH₃CONHNH₂), acetamide (CH₃CONH₂), and N-methyl acetamide (CH₃CONHCH₃), and their radicals corresponding to the loss of hydrogen atom, have been studied. Gas-phase standard enthalpies of formation and bond energies were calculated using the DFT methods B3LYP/6-31G(d,p), B3LYP/6-31G(2d,2p) and the composite CBS-QB3 methods employing a series of work reactions further to improve the accuracy of the ΔH_f°(298 K). Molecular structures, vibration frequencies, and internal rotor potentials were calculated at the DFT level. The parent molecules’ standard formation enthalpies of CH₃–C=ONHNH₂, CH₃–C=ONH_2, and CH₃–C=ONHCH₃ were evaluated as −27.08, −57.40, and −56.48 kcal mol⁻¹, respectively, from the CBS–QB3 calculations. Structures, internal rotor potentials, and C–H and N–H bond dissociation energies are reported. The DFT and the CBS-QB3 enthalpy values show close agreement, and this accord is attributed to the use of isodesmic work reactions for the analysis. The agreement also suggests this combination of the B3LYP/work reaction approach is acceptable for larger molecules. Internal rotor potentials for the amides are high, ranging from 16 to 22 kcal mol⁻¹.

1. Introduction

Thermochemical and spectroscopic investigation of N-methyl Acetamide (NMA) and other substituted amides are considered as model compounds for the peptide bonds in proteins; understanding their thermochemistry can provide information about the secondary structure of proteins in the gas phase as well as inferences in solution and helpful information toward understanding kinetics. There are no studies that we are aware of that have targeted these molecules’ thermochemical properties and bond energies.

There are several reasons for interest in the structure and chemistry of these amide systems. These include: (i) clear understanding of the NMA structure is considered as the basis for understanding the geometric constraints imposed by the peptide linkages that determine, at least partly, the protein structure; (ii) detailed understanding of NMA spectroscopic features is assumed as the fundamental basis for spectroscopic methods to monitor protein structure and dynamics [1]. Both of these properties are of interest for future applications, only if both structures and spectroscopic properties of NMA are observed in the natural environment of the biological system(s).

There are many infrared (I.R.), and Raman experiments that have focused on the spectral region spanned by the three amide bands of NMA, particularly in the easily detectable I.R. amide I regime that overlaps with the C.O. stretch. In water (aq), the C.O. stretch responds to water molecules’ presence by forming hydrogen bonds, and the resulting frequency shift can be used to assess the dynamics of protein–solvent interactions [2,3,4,5,6,7,8,9]. Similarly, the amide II and amide III bands, which overlap with the N.H. in-plane wagging motion, can be used to describe the interaction between C.O. and H.N., which are part of a protein backbone. The amide hydrogen can also form a hydrogen bond with the solvent (H₂O∙HN), and the corresponding frequency shift provides further information on protein behavior in an aqueous solution [10].

The structural stability of acetohydrazide CH₃–CO–NH–NH₂ was investigated by DFT-B3LYP and ab initio MP2 calculations with a 6-311+G ** basis set. The C–N rotational barrier in the molecule was calculated to be 26 kcal mol⁻¹, which suggested the planar sp2 nature of the nitrogen atom of the central N.H. moiety with the two-fold barrier. The N atom of the terminal NH₂ group was predicted to prefer the pyramidal sp3 structure with an inversion barrier of 7–8 kcal mol⁻¹. The molecule was predicted to have a trans–syn (N–H bond is trans with respect to C=O bond and the NH₂ moiety is syn to C–N bond) conformation as the lowest energy structure. The vibrational frequencies were computed at the B3LYP/6-311+G ** level of theory and normal coordinate calculations were carried out for the trans–syn acetohydrazide. Complete vibrational assignments were made based on normal coordinate analyses and experimental infrared and Raman data [11].

The study of amide C–N rotation barriers is important because amide C–N bonds make up protein backbones. The preferred amide conformations play an important role in enzyme structure and the barrier to the rotation affects the rigidity of the structure. The rigidity of an enzyme’s structure can affect its selectivity in binding substrates. Ab initio calculations by Jasien et al. [12] have been used to determine the gas-phase rotational barrier about the C-N bond in acetamide. Their results indicate that the inclusion of polarization functions in the basis sets leads to a substantial decrease (ca. 5 kcal mol⁻¹) in the calculated barrier height at the H.F.–SCF level. Electron correlation effects decrease the barrier by less than 1 kcal mol⁻¹, while the addition of zero-point energy corrections changed the barrier height only slightly. Based upon the current (DZ + d/SCF) calculations, the 0 K rotational barrier for acetamide is predicted to be 12.5 kcal mol⁻¹. An investigation of the photolysis of acetamide was performed using light in the 250 Å regions of the spectrum, where the goal was to break down the molecule into CH₃ and CONH₂ radicals. The authors reported this was probably accompanied by a second process yielding CH₃CN and H₂O. Methyl radicals were observed to react with the parent acetamide and with the CONH₂ radical to give methane as a product and to recombine yielding ethane. The CONH₂ radicals were reported to decompose both spontaneously and thermally to give C.O. and NH₂ radicals. The subsequent reaction of the NH₂ radicals with Acetamide gives ammonia. In a separate experiment with acetone as a photo methyl radical source, the activation energy for the abstraction of hydrogen by methyl radical was found to be 9.2 kcal mol⁻¹ [13].

The importance of reliable and accessible thermochemical data (enthalpies of formation, entropies, and heat capacities) is universally accepted among scientists and engineers. This work provides thermochemical data for acetic acid hydrazide, acetamide, and N-methyl acetamide and their radicals corresponding to the loss of hydrogen atoms through the use of computational chemistry.

2. Computational Methods

Density functional theory and composite calculations via series of isodesmic reactions: the structure and thermochemical parameters of CH₃CONHNH₂, CH₃CONH_2, and CH₃CONHCH₃ are based on the density functional and composite ab initio levels using Gaussian 98 [14] and Gaussian 09 [15]. Computation levels include B3LYP/6-31G(d,p), B3LYP/6-31G(2d,2p). These methods combine the three-parameter Becke exchange functional B3 [16], with the Lee–Yang–Parr correlation functional, LYP, [17], and are used here with the 6-31G(d,p) basis set. B3LYP/6-31G(d,p) is chosen because it is computational, economical, and, thus, possibly applicable to larger molecules [18]. Energies are further refined using the procedures of the complete basis method developed by Petersson and co-workers, CBS-QB3 [19]. The CBS-QB3 method is utilized for improved energies and serves to check the DFT calculations. CBS models, a series of calculations made on a defined geometry, and a complete basis set model chemistry including corrections for basis set truncation errors. These methods show accuracy in structure and energy that requires convergence in basis set size and the degree of correlation [18].

Standard enthalpies of formation for stable species are calculated using the total energies at B3LYP/6-31G(d,p), B3LYP/6-31G(2d,2p), and CBS-QB3 levels with work reactions that are isodesmic in most cases. Isodesmic reactions conserve the number and type of bonds on both sides of an equation. The use of a work reaction with similar bonding on both sides of an equation results in a cancellation of calculation error and improves the accuracy for energy analysis [20]. The reported enthalpy values can be compared with the known enthalpies of several molecules in the system to serve as a calibration on the thermochemistry.

Contributions to S°298 and Cp°(T) of each species are calculated using the “SMCPS” (Statistical Mechanics for Heat Capacity and Entropy Cp and S) program, which incorporates the frequencies, moments of inertia, mass, symmetry, number of optical isomers, from the Gaussian calculation. It also incorporates frequency corrections. Contributions from hindered internal rotors to S°298 and Cp(T) are determined using the “VIBIR” program. The hindered rotor corrections to the S°298 and Cp(T) are obtained by adding the S and Cp values, respectively, obtained by employing the VIBIR program to those obtained from SMCPS.

3. Results and Discussion

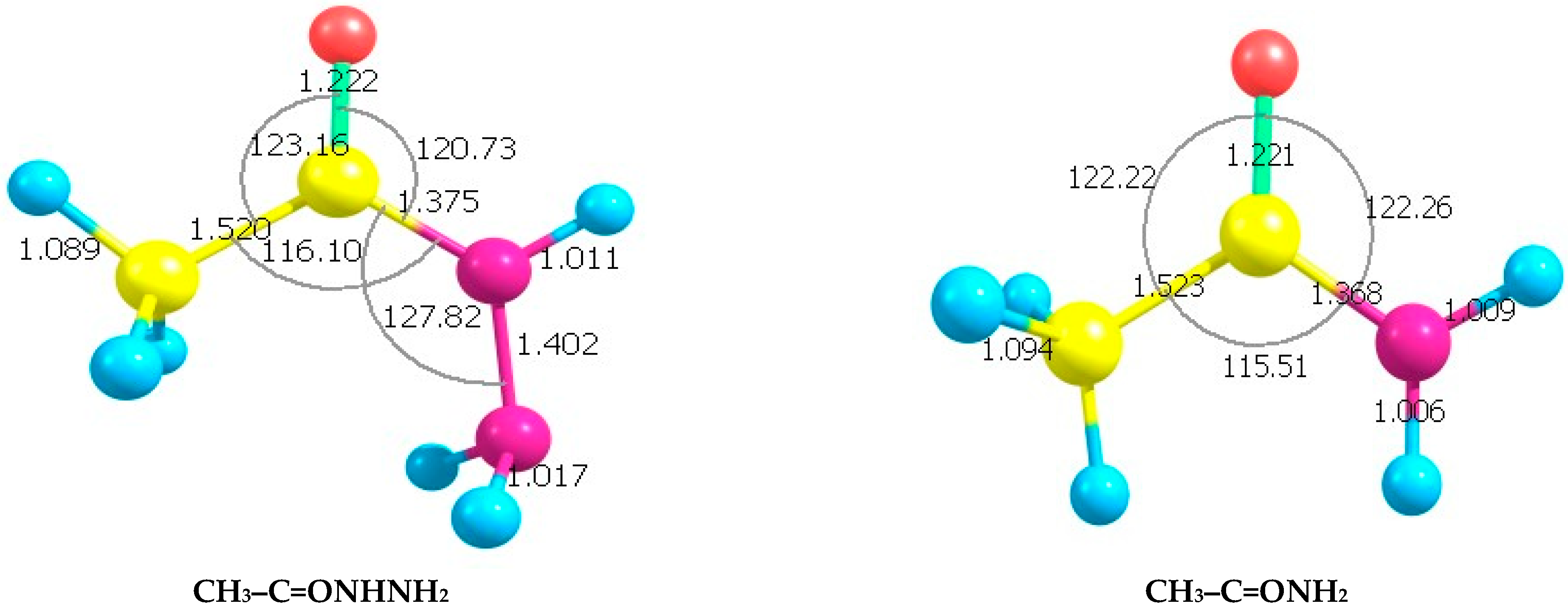
Optimized, lowest energy structures of the parent molecules—acetohydrazide, acetamide, and N-methyl acetamide are shown in Figure 1.

The torsional potentials of CH₃–C=ONHNH₂ and CH₃–C=ONHCH₃ (vide infra) show that corresponding anti- and syn-isomers respective to H₈N₇---C₅O₆ dihedral angles (see Figure 3). The anti-acetohydrazide has a near −4.86 kcal mol⁻¹ lower energy than for the syn configuration, with a 20.7 kcal mol⁻¹ barrier to the internal rotation converting the two-isomer configuration.

In contrast, the syn-N-methyl acetamide has a near −2.50 kcal mol⁻¹ lower energy than for the anti-configuration, with a 19.3 kcal mol⁻¹ barrier. The internal rotation energies for these syn–anti isomerizations are high, typically greater than 13 kcal mol⁻¹ (see below). This isomerization does not occur at standard temperature, and the isomers should be considered as different molecules in their thermochemistry and probably in their reactions.

The optimized geometries at the B3LYP/6-31G (d,p) density functional calculation level for CH₃–C=ONHNH₂, CH₃–C=ONH_2, and CH₃–C=ONHCH₃ are presented in the Supplementary Materials [SM]. The Geometric Parameters (See Section SM0, Tables S1–S3 of the SM) are listed.

3.1. Enthalpies of Formation of the Parent Molecules

Enthalpies of formation (ΔH_f°298) of the parent molecules have been determined using corresponding ΔHrxn (298) from the enthalpy of reaction in the isodesmic work reactions and calculated enthalpies of each species. The standard enthalpies of formation of the reference molecules at 298.15 K and the calculated ΔHrxn°298 are used to calculate the Δ_fHrxn°298 of the target molecule; the enthalpies are summarized in

Table 1. Standard enthalpies of formation of reference species at 298.15 K.

Species	ΔHf°298 (kcal mol−1)	Reference No.
CH3NHNH2	22.6	NIST [21]
CH3CONH2	−56.96 ± 0.19
CH3CH3	−20.04 ± 0.1
CH3CH2CH3	−25.02 ± 0.12
NH2CONH2	−56.29 ± 0.29
CH3COCH3	−52.23 ± 0.14
NH2CH2CO2H	−93.3 ± 1.1
CH3CH2OH	−56 ± 0.5
CH3CO2H	−103.5 ± 0.6
CH3C∙HCH3	22.5 ± 0.5
NH3	−10.98 ± 0.084
NH2N∙H	52.74
C∙H2NH2	36.69
CH3N∙H	44.84
NH2NH2	23.18	Dorofeeva [22]
CH3CH2NH2	−11.35 ± 0.14	Pedley [23]
N∙H2	44.5	Anderson [24]
CH3OH	−47.97 ± 3	Bozzelli [25]
C∙H2CHO	4.4 ± 0.84	ATcT [26]
CH3C∙HOH	−13.2 ± 0.61
C∙H2OH	−3.9 ± 0.33
CH3CHO	−39.9 ± 0.28
CH3C∙H2	28.6 ± 0.28
CH3NH2	−4.6

.

ΔHrxn°298 = Σ H_f products − Σ H_f reactants

The work reactions and the enthalpies obtained from three isodesmic reactions for the parent molecules are listed in

Table 2. Enthalpies of reaction at 298 K and calculated enthalpies of formation (ΔH_f°298) of parent molecules.

CH3CONHNH2 Units: (kcal mol−1)	B3LYP/631G(d,p)	B3LYP/6-31G(2d,2p)	CBS-QB3
CH3CONHNH2 + CH3NH2 → CH3NHNH2 + CH3CONH2	−29.43	−30.57	−29.51
CH3CONHNH2 + CH3CH2OH → CH3CH2NH2 + NH2CH2CO2H	−26.45	−26.10	−25.29
CH3CONHNH2 + CH3CHO → NH2CONH2 + CH3COCH3	−29.61	−29.56	−26.44
Standard Enthalpy—Average	−28.50	−28.74	−27.08
CH3CONH2
CH3CONH2+CH3CH2OH→ CH3COOH+ CH3CH2NH2	−56	−55.13	−56.63
CH3CONH2+CH3CH3→CH3COCH3+ CH3NH2	−58.46	−57.08	−55.90
CH3CONH2+CH3NH2→ CH3NHNH2 + CH3CHO	−58.72	−58.30	−59.66
Standard Enthalpy—Average	−57.73	−56.84	−57.40
CH3CONHCH3
CH3CONHCH3 + CH3NH2 → CH3CONH2 + CH3CH2NH2	−55.31	−56.04	−55.05
CH3CONHCH3 + CH3NH2 → CH3COCH3 + CH3NHNH2	−57.42	−57.53	−57.31
CH3CONHCH3 + NH2NH2 → CH3CONH2 + CH3NHNH2	−55.85	−57.22	−57.08
Standard Enthalpy—Average	−56.19	−56.93	−56.48

. Comparing the values of the enthalpies of the parent molecules calculated by two DFT and the CBS-QB3 methods shows that the values obtained by the DFT methods method are in close agreement with those obtained by CBS-QB3 calculations. We recommend the values obtained by the CBS-QB3 because it is a composite method and is known to have higher accuracy. The agreement of the DFT values suggests that the use of B3LYP calculations with the 6-31G(d,p) and 6-31G(2d,2p) basis sets coupled with work reactions results in the cancelation of error and provides reasonable results for these amide systems.

The recommended enthalpies of formation for the CH₃–C=ONHNH₂, CH₃–C=ONH_2, and CH₃–C=ONHCH₃ molecules obtained in this study are: −27.08 kcal mol⁻¹, −57.40 kcal mol^−1, and −56.48 kcal mol⁻¹ by the CBS-QB3 calculation method.

Moments of Inertia (See Section SM1, Table S4 of the SM), vibrational frequencies (Table S5 of the SM), and Mulliken Atomic Charges(Section SM2, Tables S6–S8 of the SM) of CH₃–C=ONHNH₂, CH₃–C=ONH₂, and CH₃–C=ONHCH₃ and their radicals are calculated and presented.

3.2. Radicals Corresponding to the Loss of a Hydrogen Atom

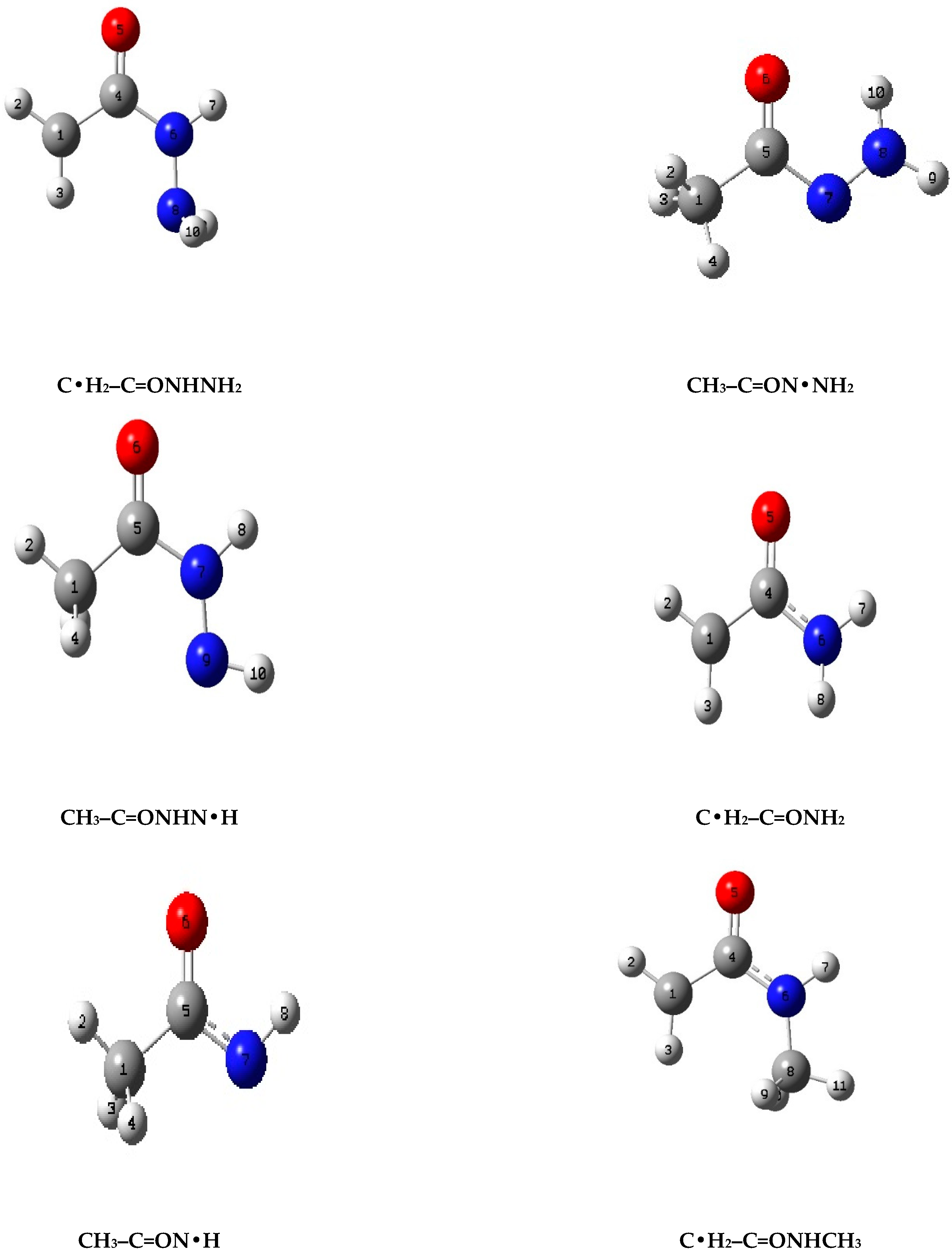
Optimized, lowest energy structures of the radicals derived from the target parent molecules are illustrated in Figure 2.

The radicals from all three parent molecules show anti-structures relative to the carbonyl group for the low energy conformation where the radical sites are on the carbons and the nitrogen, not adjacent to the carbonyl. When the radical site is on the nitrogen atom adjacent to the carbonyl, all three radicals show that the syn conformer is the lowest energy structure.

3.3. Heats of Formation, Bond Energies, and Relative Stability of the Radicals Derived from the Target Parent Molecules

Four isodesmic reactions for each radical and the calculated standard enthalpies are listed in

Table 3. Calculated standard enthalpies of formation (ΔH_f°298) of radicals and R–H bond energies.

Radical C•H2CONHNH2 Units: (kcal mol−1)	B3LYP/6-31G(d,p)	B3LYP6-31G(2d,2p)	CBS-QB3
C•H2CONHNH2 + CH3OH → CH3CONHNH2 + C•H2OH	18.96	19.14	19.13
C•H2CONHNH2 + CH3NH2 → CH3CONHNH2 + C•H2NH2	18.14	18.09	18.76
C•H2CONHNH2 + CH3CHO → CH3CONHNH2 + C•H2CHO	19.94	19.78	19.94
C•H2CONHNH2 + CH3CH2CH3 → CH3CONHNH2 + CH3C•HCH3	20.02	19.63	19.67
Standard Enthalpy—Average	19.26	19.16	19.37
Bond Energy H—CH2CONHNH2	99.50	99.40	99.61
Radical CH3CON•NH2
CH3CON•NH2 + CH3NH2 → CH3CONHNH2 + CH3N•H	−0.32	−0.06	−0.52
CH3CON•NH2 + NH2NH2 → CH3CONHNH2 + NH2N•H	−2.39	−2.71	−2.68
CH3CON•NH2 + NH3 → CH3CONHNH2 + N•H2	−2.40	−2.11	−2.02
CH3CON•NH2 + CH3CH2OH → CH3CONHNH2 + CH3C•HOH	−3.93	−3.24	−2.41
Standard Enthalpy—Average	−2.26	−2.03	−1.91
Bond Energy CH3CO(N—H)NH2	77.98	78.21	78.33
Radical CH3CONHN•H
CH3CONHN•H + CH3NH2 → CH3CONHNH2 + CH3N•H	3.63	3.18	3.28
CH3CONHN•H + NH2NH2 → CH3CONHNH2 + NH2N•H	1.56	0.53	1.12
CH3CONHN•H + NH3 → CH3CONHNH2 + N•H2	1.55	1.12	1.78
CH3CONHN•H + CH3CH2OH → CH3CONHNH2 + CH3C•HOH	0.02	0	1.40
Standard Enthalpy—Average	1.69	1.21	1.89
Bond Energy CH3CONHHNH—H	81.93	81.45	82.13
Radical C•H2CONH2
C•H2CONH2 + CH3OH → CH3CONH2 + C•H2OH	−9.48	−9.97	−10.12
C•H2CONH2 + CH3NH2 → CH3CONH2 + C•H2NH2	−10.29	−11.03	−10.49
C•H2CONH2 + CH3CHO → CH3CONH2 + C•H2CHO	−8.50	−9.33	−9.31
C•H2CONH2 + CH3CH2CH3 → CH3CONH2 + CH3C•HCH3	−8.42	−9.49	−9.57
Standard Enthalpy—Average	−9.17	−9.96	−9.87
Bond Energy H—CH2CONH2	100.21	99.43	99.52
Radical CH3CON•H
CH3CONH• + CH3NH2 → CH3CONH2 + CH3N•H	4.29	3.34	3.99
CH3CONH• + NH2NH2 → CH3CONH2 + NH2N•H	2.22	0.69	1.83
CH3CONH• + NH3 → CH3CONH2 + N•H2	2.21	1.29	2.49
CH3CONH• + CH3CH2OH → CH3CONH2 + CH3C•HOH	0.68	0.16	2.10
Standard Enthalpy—Average	2.35	1.37	2.60
Bond Energy CH3CONH—H	111.74	110.76	111.99
Radical C•H2CONHCH3
C•H2CONHCH3 + CH3OH → CH3CONHCH3 + C•H2OH	−9.40	−9.23	−9.31
C•H2CONHCH3 + CH3NH2 → CH3CONHCH3 + C•H2NH2	−10.21	−10.29	−9.69
C•H2CONHCH3 + CH3CHO → CH3CONHCH3 + C•H2CHO	−8.42	−8.59	−8.51
C•H2CONHCH3 + CH3CH2CH3 → CH3CONHCH3 + CH3C•HCH3	−8.34	−8.74	−8.77
Standard Enthalpy—Average	−9.10	−9.21	−9.07
Bond Energy H—CH2CONHCH3	99.54	99.41	99.56
Radical CH3CON•CH3
CH3CON•CH3+CH3NH2 → CH3CONHCH3 + CH3N•H	−2.81	−2.92	−2.27
CH3CON•CH3 + NH2NH2 → CH3CONHCH3 + NH2NHJ	−4.88	−5.57	−4.43
CH3CON•CH3+NH3 → CH3CONHCH3 + NH2J	−4.89	−4.97	−3.77
CH3CON•CH3 + CH3CH2OH → CH3CONHCH3 + CH3C•HOH	−6.42	−6.10	−4.15
Standard Enthalpy—Average	−4.75	−4.89	−3.65
Bond Energy CH3CON—HCH3	103.88	103.74	104.98
Radical CH3CONHC•H2
CH3CONHC•H2 + CH3OH → CH3CONHCH3 + C•H2OH	−15.58	−15.64	−15.50
CH3CONHC•H2 + CH3NH2 → CH3CONHCH3 + C•H2NH2	−16.39	−16.70	−15.88
CH3CONHC•H2 + CH3CHO → CH3CONHCH3 + C•H2CHO	−14.60	−15	−14.70
CH3CONHC•H2 + CH3CH2CH3 → CH3CONHCH3 + CH3C•HCH3	−14.52	−15.15	−14.96
Standard Enthalpy—Average	−15.27	−15.62	−15.26
Bond Energy CH3CONHCH2—H	93.36	93.01	93.37

. The data illustrate excellent agreement across the different levels of calculations and through the different reaction analyses.

The enthalpies of formation of the parent molecules averaged over three work reactions for molecules CH₃–C=ONHNH₂, CH₃–C=ONH₂ and CH₃–C=ONHCH₃ were evaluated as −28.1, −57.29, and −56.53 kcal mol⁻¹, respectively (values are average of B3LYP/6-31g(d,p), B3LYP/6-31g(2d,2p) and CBS-QB3 levels).

3.3.1. Enthalpy of Formation—Radicals

The four work reactions and calculated ΔH_f°298 for use in determining the enthalpy of formation for each radical are shown in Table 3.

The recommended enthalpies of formation, in kcal mol⁻¹, from the CBS-QB3 level calculations, averaged over four work reactions are:

(i)

Radicals from CH₃–C=ONHNH₂:

(a)

C•H₂–C=ONHNH₂ (19.27),

(b)

CH₃–C=ON•NH₂ (−2.07),

(c)

CH₃–C=ONHN•H (1.60).

(ii)

Radicals from CH₃–C=ONH₂:

• C•H₂–C=ONH₂ (−9.67),
• CH₃–C=ON•H (2.11).

(iii)

Radicals from CH₃–C=ONHCH₃

• C•H₂−C=ONHCH₃ (−9.12),
• CH₃–C=ON•CH₃ (−4.43),
• CH₃–C=ONHC•H₂ (−15.39).

3.3.2. Bond Energies

Bond energies for the formation of radicals by loss of H atom reported at 298.15 K were calculated from the standard ΔH_f°298 values of the parent molecules and of the radicals, obtained at CBS-QB3 level. ΔH_f°298 of 52.1 kcal mol⁻¹ was used for H atom enthalpy.

CH₃–C=ONHNH₂ → C•H₂–C=ONHNH₂ + H•

−28.14 19.27 52.01 kcal mol⁻¹

ΔHrxn = [19.27 + 52.1] − [−28.14] = 99.51 kcal mol⁻¹ = Bond Energy

The bond dissociation enthalpies of the radicals calculated at three different levels of theory are listed in Table 3. The largest difference in R–H bond energy for a given radical, considering the two DFT and the CBS-QB3 calculation methods and the four isodesmic reactions of each radical, was less than 1.5 kcal mol⁻¹.

The bond dissociation energies for the C–H bonds in the methyl group adjacent to the carbonyl in CH₃–C=ONHNH₂ (99.51), CH₃–C(=O)NH₂ (99.72), and CH₃–C=ONHCH₃ (99.51) kcal mol⁻¹ are in parentheses. These compare with the typical bond energy on a primary methyl site of a normal hydrocarbon of 101 kcal mol⁻¹, and are ca. 2 kcal mol⁻¹ lower. In contrast, they are ca. 3 kcal mol⁻¹ higher than a typical primary methyl C–H bond on a ketone, which is 96 kcal mol⁻¹. The C–H bond energy on the methyl group bonded to the amine to form the CH₃–C=ONHC•H₂ is 93.24 kcal mol⁻¹.

The N–H bond strengths for nitrogen atom adjacent to the carbonyl groups in CH₃–C=ONHNH₂ (78.17), CH₃–C(=O)NH₂ (111.50), and CH₃–C=ONHCH₃ (104.19) kcal mol⁻¹ are in the parenthesis. For comparison, the N–H bond in ammonia is (108), the CH₃NH–H bond in methylamine is (102.4), and the NH₂NH–H bond in hydrazine is (82) kcal mol⁻¹.

The C–H bond strength in the CH₃ group bonded to an amine in CH₃–C=ONHCH₂--H is 93.37 kcal mol⁻¹ at the CBS-QB3 level. This compares with the C–H bond energy of H–CH₂–NH₂ (~94.4) in CH₃NH₂. This C–H bond in CH₃–C=ONHC•H₂ is 1 kcal mol⁻¹ lower than on the methyl groups bonded to C=O.

The N–H bond of the N.H. group in CH₃–C=O–N•–NH₂ is the weakest in this molecule at 78.17 kcal mol⁻¹, where the C–H bond in C•H₂–C=ONHNH₂ is 99.51 kcal mol⁻¹, which is significantly higher. The N–H bond energy for acetohydrazide (CH₃–C=ONHNH•) is markedly different at only 81.84 kcal mol⁻¹. In the N–H bond cleavage of CH₃–C=ON•NH₂, the electrons from the radical site re-arrange to form a second double bond, from nitrogen to carbon. The N–H bond energy for CH₃–C=ON•CH₃ is 104.20 kcal mol⁻¹ which is much higher than the CH₃–C=ON•NH₂.

The weakening of the N–H bonds in this hydrazide is essentially independent of the nature of the β-substituent (H, RCO, CO₂Et, or PhSO₂) and the stabilizing effect on the radical is brought about entirely by the three-electron on N–NH₂ moiety [27].

3.4. Internal Rotor Potentials

Energy profiles for internal rotations about the C–C=O, O=C–N, N–C, and N–N bonds in the acetohydrazide, acetamide, and N-methyl acetamide were calculated to determine the lowest energy configurations, energies of the rotational conformers, and to identify the interconversion barriers between isomers. Torsional potentials were used to evaluate contributions to the entropy and heat capacity values when there were low barriers (less than 3.5 kcal mol⁻¹) and internal rotation occurred.

The total energies as a function of the corresponding dihedral angles were computed at the B3LYP/6-31G(d,p) level of theory by scanning the torsion angles between 0° and 360° in steps of 15°, while all remaining coordinates were fully optimized. All potentials were rescanned when a lower energy conformer, relative to the initial low-energy conformer was found. The total energy of the corresponding most stable molecular conformer was arbitrarily set to zero and used as a reference point to plot the potential barriers. The resulting potential energy barriers for internal rotations in the stable nonradical and radical molecules are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. Dihedral angles obtained for the optimized lowest energy structures are shown in parentheses.

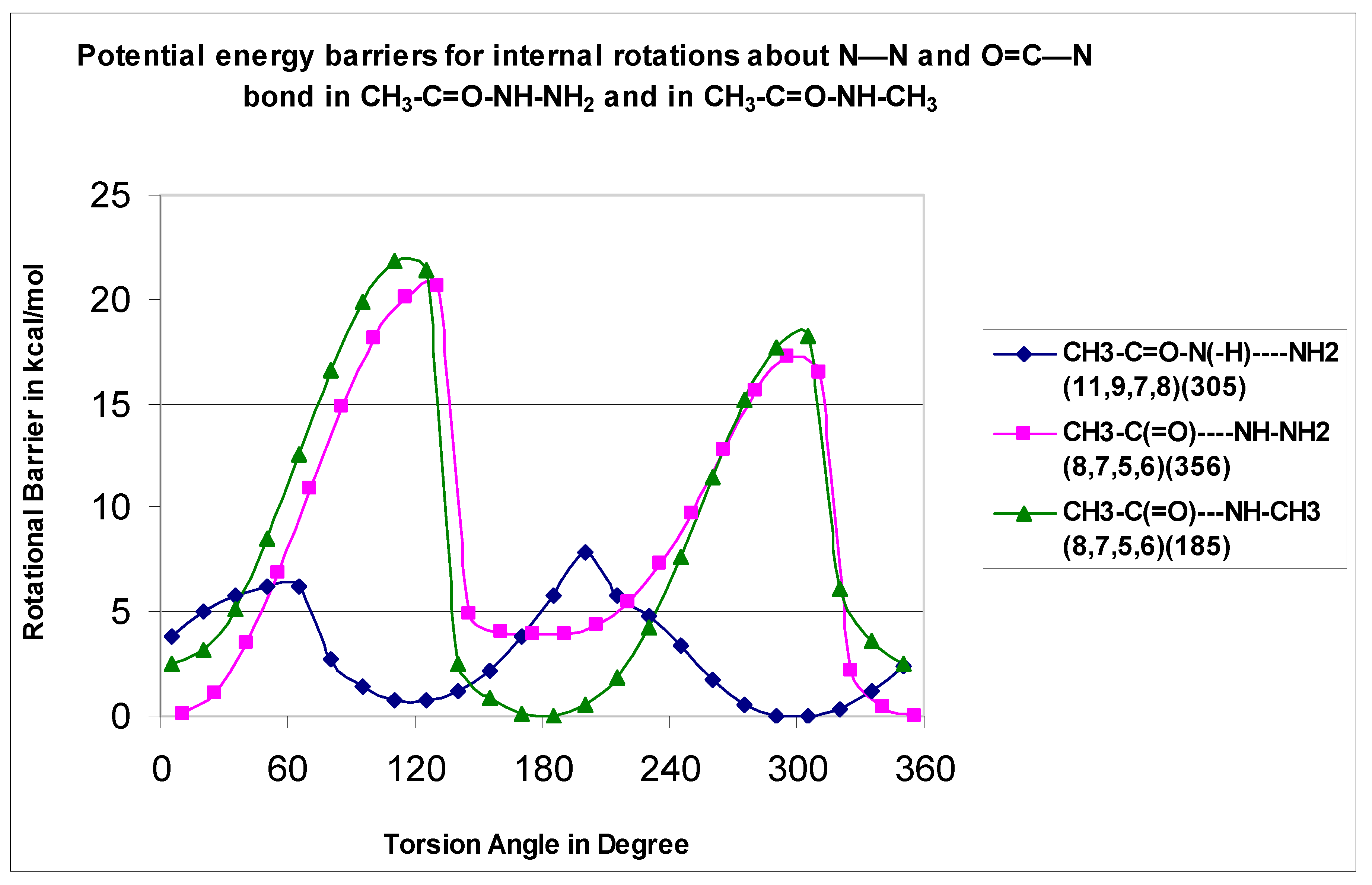
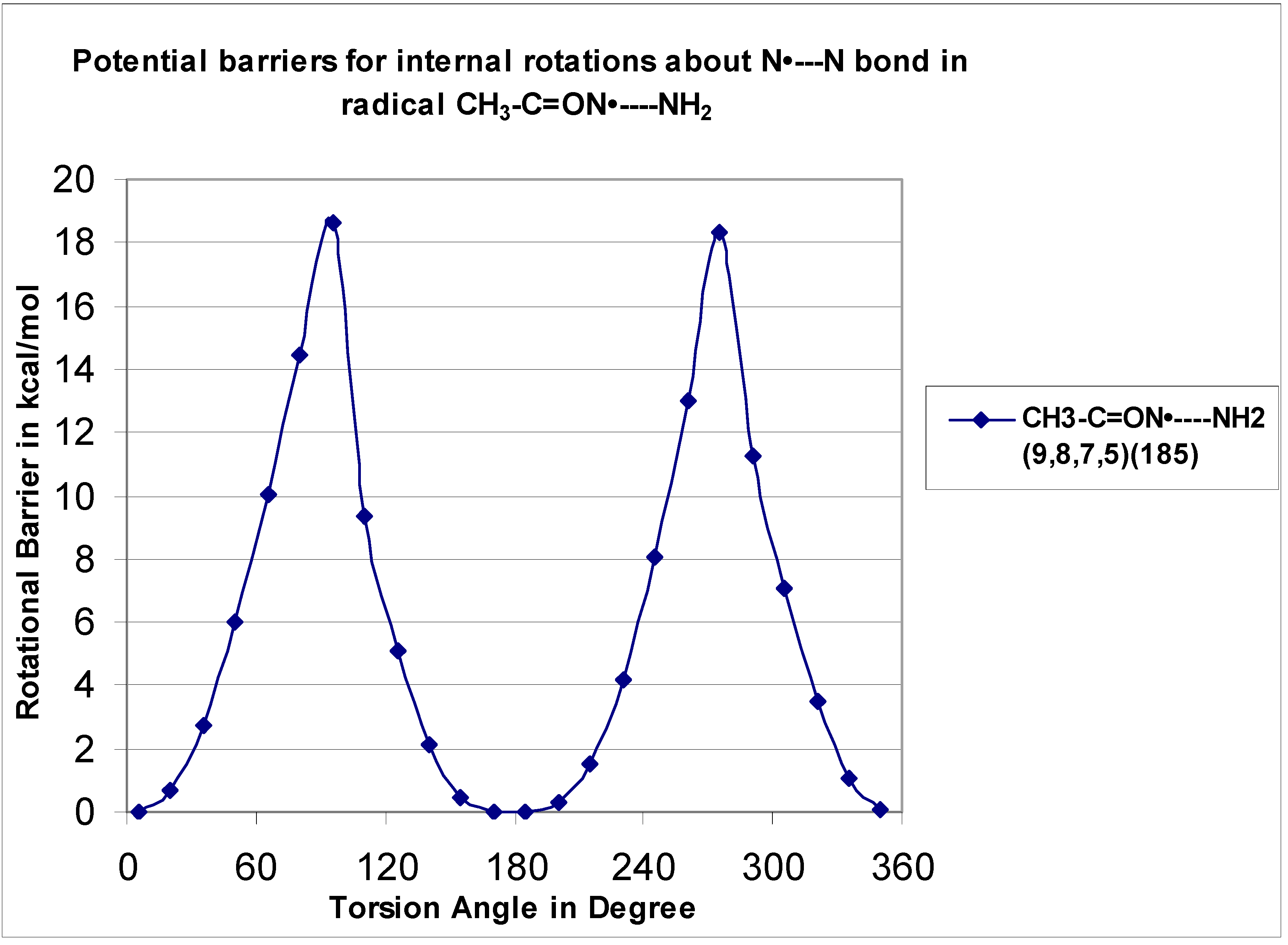
The CH₃–C=O-NH-NH₂ rotor is illustrated in Figure 3 for both the CH₃–C=O–N(–H)—NH₂ (H10–N9—N7–H8) and CH₃–C(=O)—NH–NH₂ (H8–N7—C5–O6) systems with barriers at 7.82 and 20.66 kcal mol⁻¹, respectively. The CH₃–C(=O)—NH–CH₃ (H8–N7—C5–O6) rotor shows a two-fold symmetry with a barrier at 21.7 kcal mol⁻¹. One reason for the high barriers for the rotation about the carbonyl (C=O)–NH bond involves the repulsive interaction of the carbonyl π bond with the NH lone pair.

The study of amide C–N rotation barriers is important for the evaluation of their reactivity, for input data in biochemical structure calculations other than finding the lowest energy conformer because the amide C–N bonds make up protein backbones. The amide conformations play an important role in enzyme structure and the barrier to the rotation affects the rigidity of that structure. The rigidity of an enzyme’s structure can affect its selectivity in binding substrates.

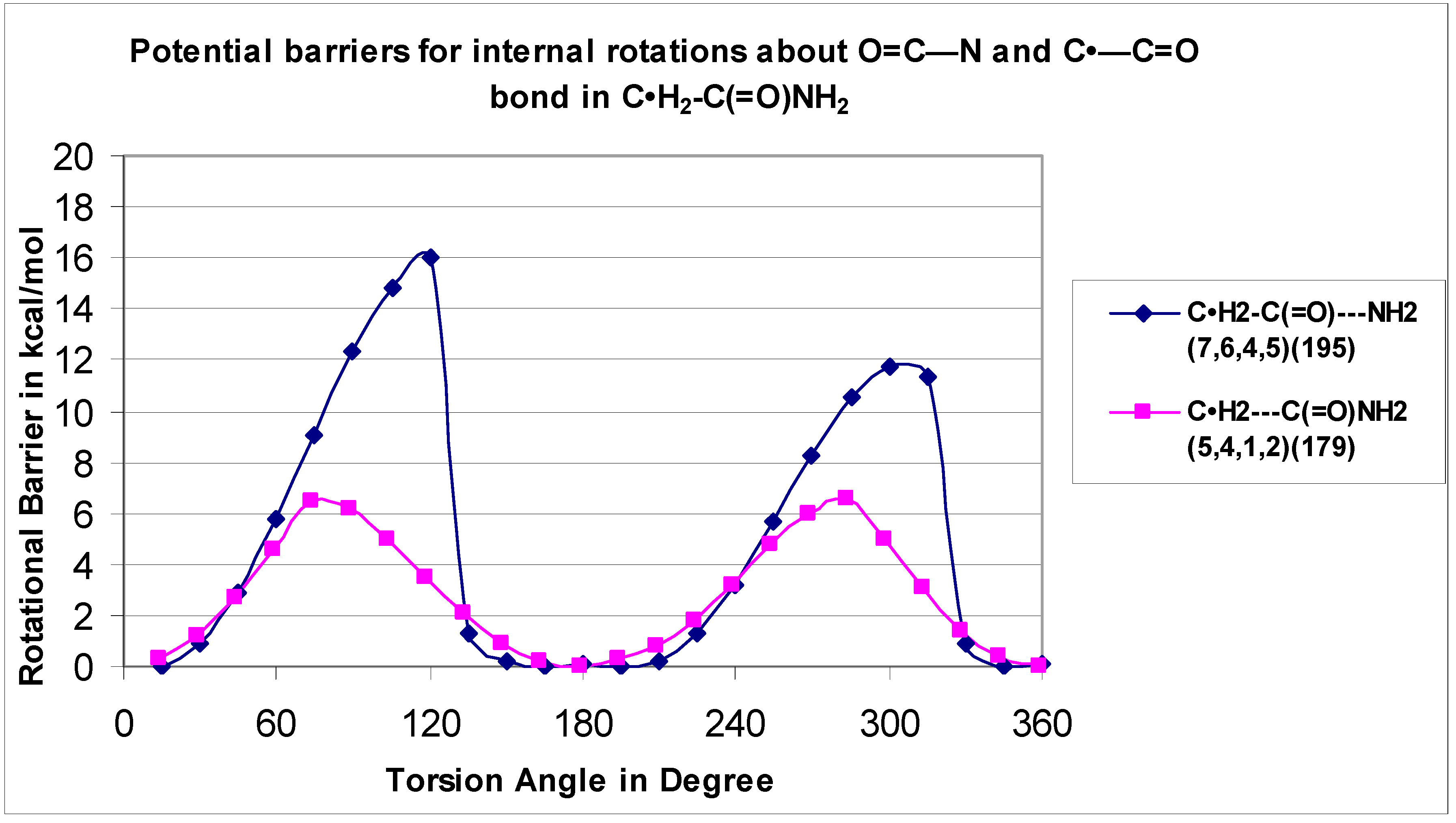
The C–N rotor for the radical C•H₂–C(=O)—NH₂ (H₇–N₆---C₄–O₅ is 15.97 kcal mol⁻¹) and the value of its parent CH₃–C(=O)—NH₂ (H₈–N₇—C₅–O₆ is 18.66 kcal mol⁻¹). According to Jasien et al. [12], based upon the current (DZ + d/SCF) calculations, the 0 K rotational barrier for acetamide between the C–N bond is predicted to be 12.5 kcal mol⁻¹.

The two protons attached to N in acetamide are inequivalent at low temperatures but become averaged by C–N rotation at higher temperatures. Typical bond rotation barriers for amides in solution are experimentally determined by NMR to be between 17 and 22 kcal/mol. However, the acetamide enolate, [CH2CONH2] has a much lower barrier; according to NMR experiments, the enolate has free rotation at all accessible temperatures [28]. The HNCO anti/trans/Z configuration is significantly more probable in proteins than the syn/cis/E geometry. The ratio is 95:5 or even higher [29].

The CH₃–C=O rotor for the CH₃—C(=O)–NH₂ (O₆–C₅—C₁–H₂) has a small barrier at 0.08 kcal mol⁻¹ and shows three-fold symmetry The data are in reasonable agreement with the previous study conducted by J.R. Bailey [30], which also reported a low, calculated barrier monosubstituted N-methyl acetamide to be 0.21 kcal mol⁻¹.

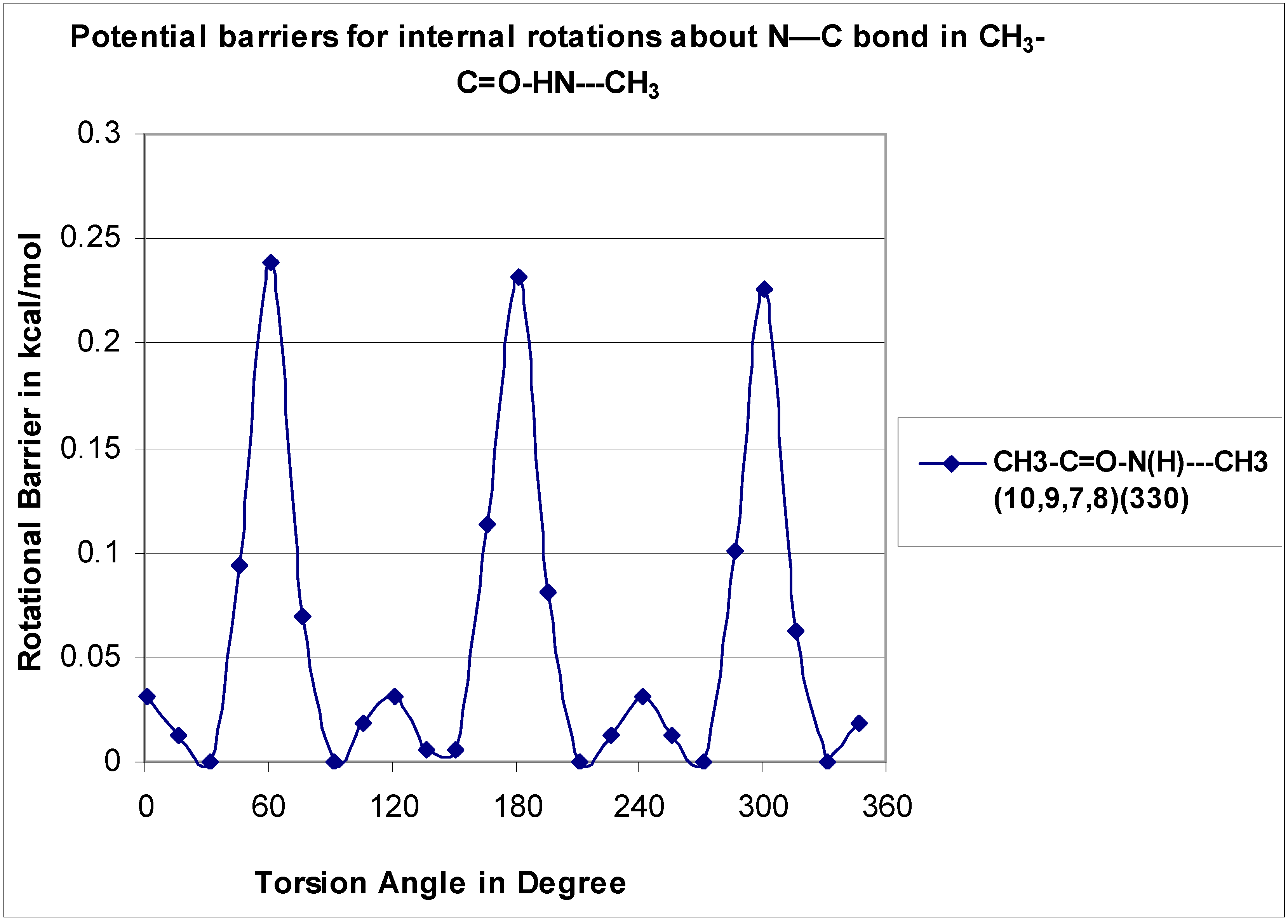
The CH₃–C=O–HN—CH₃ rotor is illustrated in Figure 6 which shows a three-fold symmetry with a barrier at 0.24 kcal mol⁻¹.

The C(=O)NH₂ rotor is illustrated in Figure 8 for both the C•H₂–C(=O)—NH₂ (H7–N6—C4–O5) and C•H2---C(=O)NH₂ (O5–C4—C1–H2) systems with a great difference in bariers at 16.0 and 6.6 kcal mol⁻¹, respectively, but with the same two-fold symmetry.

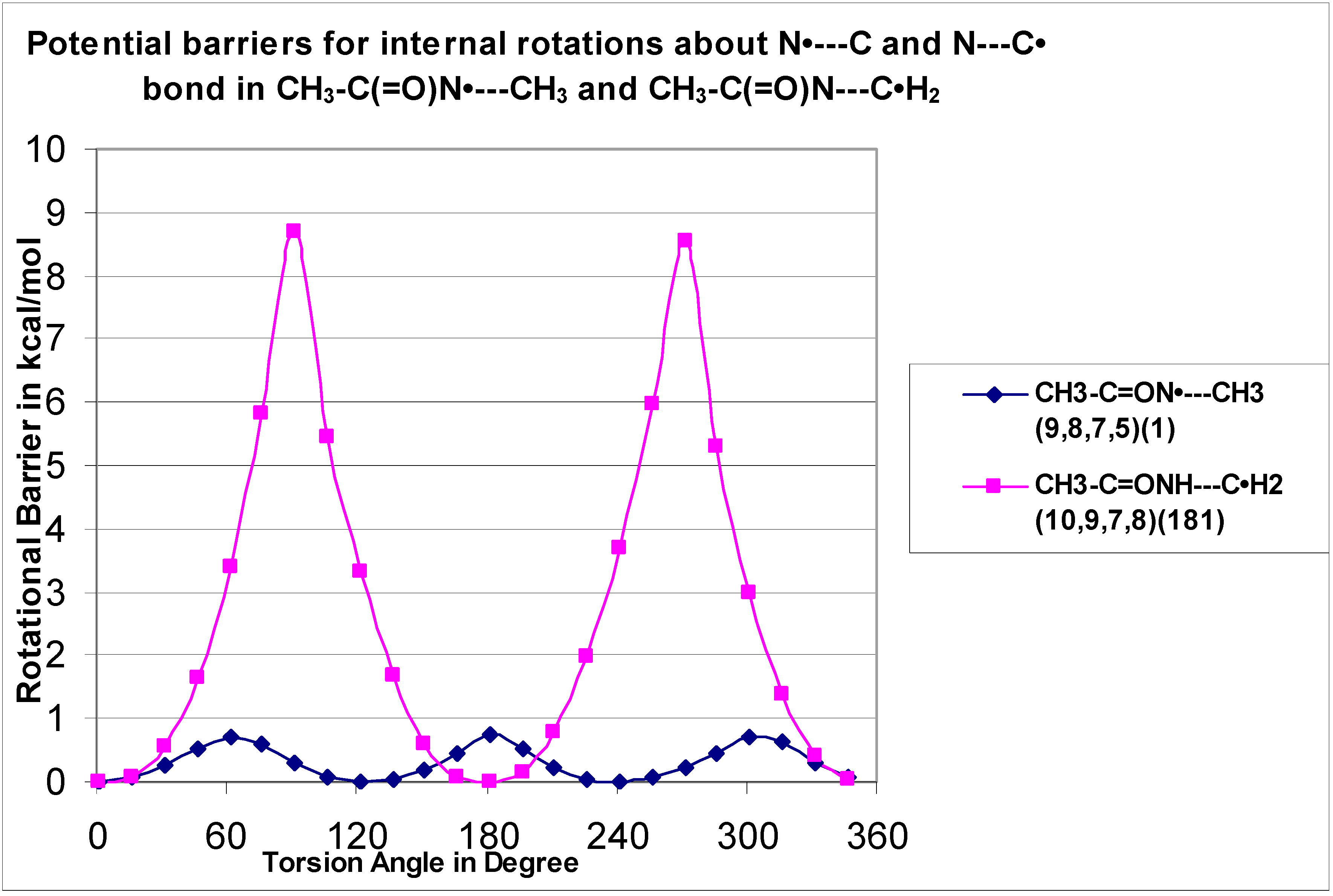
The CH₃–C(=O)N•—CH₃ (H9–C8—N₇–C5) and CH₃–C(=O)N—C•H₂ (H10–C9—N7–H8) rotors are illustrated in Figure 9 and there is a significant difference in the internal rotor barriers. CH₃–C(=O)N•—CH₃ shows extremely low three-fold symmetry at 0.7 kcal mol⁻¹, and CH₃–C(=O)N—C•H₂ shows two-fold symmetry at 8.7 kcal mol⁻¹ barrier. The low barrier in CH₃–C(=O)N•—CH₃ is a result of the overlap between the carbonyl bond and the unpaired electron of the N atom, which reduces the interaction of the methyl H atoms with the N nitrogen π orbitals. The higher barrier for CH₃–C(=O)N—C•H₂ results from overlap (resonance) between the radical and the nitrogen π bonds.

3.5. Entropy and Heat Capacity

The entropy and heat capacity data for the parent molecules and their radicals as a function of temperature were determined from the optimized structures, moments of inertia, vibrational frequencies, symmetries, the known mass of the molecules, and internal rotor contributions when barriers were low. The calculations use standard formulas from statistical mechanics for the contributions of translation, external rotation, and vibrations [31,32]. Contributions to the entropy and the heat capacity from translation, vibrations, and external rotation were calculated using the SMCPS program. This program utilizes the rigid-harmonic oscillator approximation from the optimized structures obtained at B3LYP/6-31G(d,p) level. The number of optical isomers and the spin degeneracy of unpaired electrons is also incorporated for the calculation of S°298.

Contributions from hindered internal rotors to S°298 and Cp(T) are determined using the VIBIR program. This program utilizes the method of Pitzer and Gwinn [33,34], the potential barriers, folds, and moments of inertia from the internal rotor analysis. The moments of inertia were calculated. The rotors with a barrier value greater than 3.5 kcal mol⁻¹ were treated as torsion vibrations. The internal rotor data were combined with the S(T) and Cp(T) data from frequencies, mass, moments of inertia, symmetry, and electronic degeneracy in the our statistical mechanics program SMCPS [35] and are presented in

Table 4. Ideal gas-phase thermodynamic property vs. temperature ^a of parent molecules.

T (K)	ΔHf°298 kcal mol−1	CH3CONHNH2		ΔHf°298 kcal mol−1	CH3CONH2		ΔHf°298 kcal mol−1	CH3CONHCH3
		Cp(T)	S°(T)		Cp(T)	S°(T)		Cp(T)	S°(T)
1	−28.58	7.949	16.841	−58.14	7.949	14.636	−56.54	7.949	14.677
51		8.877	48.268		8.831	46.039		8.532	45.934
101		10.851	54.999		9.835	52.512		10.155	52.332
151		13.154	59.82		11.161	56.729		12.071	56.795
201		15.609	63.932		12.866	60.163		14.237	60.555
251		18.098	67.676		14.719	63.227		16.57	63.973
298		21.575	71.052		17.539	65.962		21.065	67.078
400		26.417	77.763		21.311	71.357		26.215	73.371
500		30.648	83.881		24.613	76.245		30.961	79.271
600		34.249	89.6		27.434	80.8		35.118	84.912
700		36.275	94.949		28.832	85.054		36.677	90.28
800		39.881	99.96		31.88	89.036		41.778	95.376
900		41.108	104.665		32.663	92.774		42.417	100.209
1000		44.052	109.094		35.21	96.294		46.735	104.794
1100		44.75	113.275		35.576	99.616		46.733	109.148
1200		46.236	117.23		36.772	102.761		48.481	113.287
1300		47.54	120.98		37.824	105.744		50.005	117.225
1400		48.686	124.543		38.751	108.579		51.337	120.977
1500		50.695	127.934		40.562	111.279		54.499	124.556
2000		53.236	142.757		42.451	123.09		56.539	140.262
2500		55.241	154.866		44.091	132.751		58.785	153.137
3000		56.455	165.05		45.088	140.882		60.132	163.98
3500		57.235	173.814		45.73	147.883		60.992	173.316
4000		57.763	181.492		46.164	154.018		61.572	181.499
4500		58.135	188.317		46.471	159.473		61.979	188.775
5000		58.407	194.456		46.695	164.381		62.276	195.321

^a Thermodynamic properties refer to the standard state of an ideal gas at 1 atm. S°(T) and C°p(T) in cal mol⁻¹ K⁻¹.

for the parent molecules,

Table 5. Ideal gas-phase thermodynamic property vs. temperature ^a of radicals of parent CH₃CONHNH₂.

T (K)	ΔHf°298 kcal mol−1	C∙H2–C=ONHNH2		ΔHf°298 kcal mol−1	CH3–C=ON∙NH2		ΔHf°298 kcal mol−1	CH3–C=ONHN∙H
		Cp(T)	S°(T)		Cp(T)	S°(T)		Cp(T)	S°(T)
1	19.11	7.949	20.227	−2.08	7.949	17.901	1.58	7.949	18.037
51		9.561	52.378		8.899	49.318		8.197	49.18
101		11.599	59.551		10.976	56.109		9.838	55.307
151		14.394	64.765		13.16	60.965		12.072	59.701
201		17.265	69.294		15.366	65.047		14.494	63.498
251		20	73.436		17.568	68.707		16.912	66.986
298		22.457	77.155		21.532	71.967		20.276	70.145
400		27.093	84.422		25.642	78.367		24.789	76.43
500		30.849	90.876		29.268	84.138		28.661	82.147
600		33.906	96.772		32.372	89.496		31.919	87.474
700		36.419	102.187		33.738	94.482		33.633	92.442
800		38.53	107.186		37.219	99.135		36.954	97.082
900		40.338	111.826		37.971	103.488		37.923	101.427
1000		41.907	116.155		40.787	107.573		40.63	105.509
1100		43.28	120.212		41.12	111.419		41.111	109.353
1200		44.486	124.027		42.395	115.05		42.399	112.984
1300		45.549	127.628		43.509	118.485		43.524	116.42
1400		46.487	131.036		44.484	121.744		44.507	119.68
1500		47.315	134.27		46.4	124.84		46.368	122.778
2000		50.25	148.317		48.328	138.329		48.364	136.276
2500		51.93	159.722		50.009	149.306		50.041	147.261
3000		52.953	169.285		51.023	158.517		51.05	156.478
3500		53.614	177.5		51.674	166.433		51.696	164.398
4000		54.062	184.689		52.114	173.363		52.132	171.33
4500		54.379	191.075		52.424	179.519		52.439	177.488
5000		54.61	196.816		52.65	185.054		52.662	183.025

^a Thermodynamic properties refer to the standard state of an ideal gas at 1 atm. S°(T) and C°p(T) in cal mol⁻¹ K⁻¹.

for radicals from acetic acid hydrazide,

Table 6. Ideal gas-phase thermodynamic property vs. temperature ^a of radicals of parent CH₃CONH₂.

T (K)	ΔHf°298 kcal mol−1	C•H2–C=ONH2		ΔHf°298 kcal mol−1	CH3–C=ON•H
		Cp(T)	S°(T)		Cp(T)	S°(T)
1	−10.23	7.949	17.966	1.68	7.949	15.81
51		8.029	49.073		7.952	46.907
101		9.422	54.969		8.386	52.495
151		11.766	59.214		9.781	56.132
201		14.198	62.928		11.554	59.18
251		16.459	66.337		13.404	61.952
298		18.432	69.393		16.18	64.453
400		22.024	75.332		19.761	69.423
500		24.848	80.554		22.802	73.938
600		27.121	85.286		25.331	78.138
700		28.985	89.607		26.439	82.046
800		30.555	93.578		29.212	85.691
900		31.907	97.254		29.733	89.1
1000		33.088	100.675		32.039	92.299
1100		34.126	103.875		32.179	95.309
1200		35.043	106.882		33.167	98.15
1300		35.854	109.718		34.028	100.837
1400		36.573	112.4		34.78	103.385
1500		37.21	114.944		36.434	105.806
2000		39.482	125.985		37.724	116.342
2500		40.794	134.945		38.998	124.906
3000		41.597	142.457		39.763	132.087
3500		42.117	148.91		40.252	138.255
4000		42.47	154.557		40.582	143.652
4500		42.72	159.574		40.814	148.445
5000		42.902	164.085		40.983	152.754

^a Thermodynamic properties refer to the standard state of an ideal gas at 1 atm. S°(T) and C°p(T) in cal mol⁻¹ K⁻¹.

for radicals from acetamide, and

Table 7. Ideal gas-phase thermodynamic property vs. temperature ^a of radicals of parent CH₃CONHCH₃.

T (K)	ΔHf°298 kcal mol−1	C∙H2–C=ONHCH3		ΔHf°298 kcal mol−1	CH3–C=ON∙CH3		ΔHf°298 kcal mol−1	CH3–C=ONHC•H2
		Cp(T)	S°(T)		Cp(T)	S°(T)		Cp(T)	S°(T)
1	−8.85	7.949	18.06	−4.02	7.949	15.856	−15.11	7.949	18.072
51		8.762	49.415		8.619	47.154		9.372	49.785
101		10.951	56.118		10.268	53.62		11.973	57.054
151		13.531	61.034		12.061	58.114		14.58	62.399
201		16.137	65.279		13.97	61.837		17.073	66.931
251		18.685	69.147		16.06	65.17		19.506	70.996
298		22.115	72.628		21.367	68.168		22.907	74.613
400		26.987	79.518		25.829	74.199		27.577	81.691
500		31.217	85.77		29.988	79.812		31.654	88.051
600		34.808	91.596		33.633	85.148		35.129	93.943
700		36.841	97.034		34.446	90.202		37.056	99.42
800		40.427	102.12		39.434	94.979		40.587	104.531
900		41.654	106.89		39.552	99.493		41.755	109.315
1000		44.584	111.376		43.74	103.763		44.654	113.81
1100		45.266	115.606		43.342	107.806		45.306	118.046
1200		46.732	119.605		44.863	111.64		46.754	122.048
1300		48.014	123.394		46.182	115.281		48.023	125.838
1400		49.136	126.991		47.329	118.743		49.136	129.435
1500		51.118	130.413		50.395	122.041		51.114	132.857
2000		53.55	145.343		51.759	136.457		53.532	147.783
2500		55.472	157.513		53.646	148.224		55.455	159.949
3000		56.629	167.734		54.77	158.109		56.615	170.167
3500		57.37	176.521		55.485	166.608		57.358	178.952
4000		57.87	184.215		55.965	174.049		57.86	186.645
4500		58.221	191.052		56.302	180.66		58.214	193.48
5000		58.478	197.199		56.547	186.605		58.471	199.627

^a Thermodynamic properties refer to the standard state of an ideal gas at 1 atm. S°(T) and C°p(T) in cal mol⁻¹ K⁻¹.

for radicals from N-methyl acetamide.

Entropy and heat capacity contributions of the parent molecules and radicals using VIBIR have been calculated at temperatures ranging from 1–5000 K.

4. Summary

Thermochemical properties are presented for acetic acid hydrazide, Acetamide, N-methyl acetamide, and radicals that result from the loss of H atoms from the carbon and the nitrogen atoms. Standard enthalpies from all the work reactions and each of the calculation methods are in reasonably good agreement, suggesting that the B3LYP DFT calculations, in conjunction with the work reactions used here, are acceptable methods for larger hydrazide and amides. C–H bond energy values for the radicals C•H₂–C=ONHNH₂, C•H₂–C=ONH₂ and C•H₂–C=ONHCH₃ from the B3LYP/6-31G(d,p), B3LYP/6-31G(2d,2p) and CBS-QB3 levels of calculation were 99.50, 99.40, 99.61 and 100.22, 99.43, 99.52 and 99.54, 99.42, 99.56 kcal mol⁻¹ respectively. The N–H bond in the acetohydrazide was weak, at 78.17 kcal mol⁻¹, but strong in N-methyl acetamide at 104.20 kcal mol⁻¹. The HN–H bond energies for the formation of the radicals CH₃–C=ONHN•H and CH₃–C=ON•H from the parent molecules were also similar across the different B3LYP basis sets and CBS-QB3 level of calculations (CH₃–C=ONHN•H = 81.93, 81.45, 82.13; CH₃-C=ON•H = 111.74, 110.76, 111.99 kcal mol⁻¹) respectively.