Abstract
This paper analyzes how special relativity changes the equation for the many-body-induced current density starting from the Foldy–Wouthuysen diagonalization of the Dirac–Coulomb Hamiltonian. This current density differs from that obtained with the Gordon decomposition due to the presence of a spin-orbit coupling contribution not considered before for many-body molecular systems. This contribution diverges on atomic nuclei due to the nature of the point charges considered in the nonrelativistic approach, demonstrating that conventionally used nonrelativistic methods are not suitable for dealing with spin effects such as spin-orbit coupling or effects smaller than , with the fine structure constant, and that a fully relativistic approach with a finite charge should be used. Despite the singularity, the spin-orbit coupling current becomes an important contribution to the total current in open-shell systems with high-spin multiplicity and a high atomic number in the nuclear proximity. On long ranges, this contribution is overcome by the Coulomb potential and the derived electric field which decays very quickly for small distances from nuclear charges. An evaluation of this spin-orbit current has been performed in the linear response approach at the HF/DFT level of theory.
1. Introduction
A magnetic field induces current distributions in the electron cloud of a molecule. Some of these current distributions can be derived starting from the continuity equation by using the Schrödinger equation, but contributions that arise from electron spin cannot be obtained in this way, and a different procedure has been proposed [1,2,3,4,5,6]. Of these procedures, we recall in particular the Gordon decomposition of the Dirac four-current [1,7,8,9] that introduces a magnetization current starting from a correct, relativistic spin theory. This decomposition, however, does not allow one to obtain the spin-orbit coupling current derived by Hodge and coworkers for the hydrogen atom [6] by adopting the Landau approach [2]. The interest in the study of induced current densities comes from the fact that these kind of properties can be useful tools to rationalize the behavior of the matter caused by a perturbing electromagnetic field and as a consequence to explain chemical concepts like magnetic aromaticity [10,11,12,13], NMR chemical shifts and magnetizabilities [14,15,16,17,18,19], specific optical activities [20], electric polarizabilities [21], dynamic electric toroidizabilities [22], and other phenomena linked to the electron dynamics. The aim of this paper is to generalize the Landau approach to many-body systems and derive the total current density vector field, with the corresponding continuity equation, starting from the Foldy–Wouthuysen diagonalization of the Dirac Hamiltonian, in order to understand how the total relativistic current density can be decomposed starting with the nonrelativistic Schrödinger counterpart. The reason for this comes from the fact that Dirac’s equation not only accounted for the spin of the electron and its observed magnetic moment, but also correctly explained the fine structure of the hydrogen atom to the order Dirac had calculated it. Furthermore, starting from the Foldy–Wouthuysen diagonalization of the Dirac Hamiltonian two questions arise:
- To what extent is it possible to treat scalar relativity effects as a small correction to the nonrelativistic calculations?
- What kind of scalar corrections should be included?
To derive the total current density vector field and to answer these question, this paper is organized as follows. An outline of notation is presented in Section 2 and a short description of theoretical methods employed to derive the total current density vector field is provided in Section 3 and Section 4. In Section 5, the implementation of the spin-orbit coupling current is presented for open-shell systems, and in Section 6 the computational details of the calculations are highlighted. Concluding remarks are made in Section 7.
2. Outline of Notation and Theoretical Methods
Within the Born–Oppenheimer (BO) approximation [23], for a molecule with n electrons and N clamped nuclei, charge, mass, position, canonical and angular momentum of the k-th electron are indicated, in the configuration space, by , , , , , , using boldface letters for electronic vector operators. Analogous quantities for nuclei are , , , etc. for . Throughout this work, SI units are used and standard tensor formalism is employed, e.g., the Einstein convention of implicit summation over two repeated Greek indices is applied. The third-rank Levi–Civita skew-tensor is indicated by . The imaginary unit is represented by a Roman . Let us introduce the general definition of n-electron density functions
of electronic space-spin coordinates , where
By integrating over the spin variable , a spatial density matrix is obtained
for the reference state of the molecule. Similarly, the spin-density matrix is defined as
For the reference state the probability and charge density became
By using previous relations for any type of one-electron operators, the relation
is verified and will be used throughout the paper.
3. Many-Particle Relativistic Reduced Hamiltonian
To handle in the correct phenomenological way spin effects, our starting point is the Dirac Hamiltonian for an electron in a nonvanishing electromagnetic field:
in which the operators and are represented by 4 × 4 matrices
Here is a unit matrix and the are the Pauli spin matrices
Starting from this Hamiltonian, a practical procedure to derive the wave equation for the positive energy wave function of the Dirac equation is represented by the Foldy–Wouthuysen diagonalization [24], which requires us to put into block diagonal form:
By using this procedure and considering that for Coulomb-like potentials, or static magnetic field , the relativistic reduced Hamiltonian for an electron in an electromagnetic field can be approximated at first order considering that as
where is the representation of the spin operator on the basis of eigenstates, which can be written as the matrix
where g is the electron g-factor, and is the Bohr magneton. All terms contained in Equation (12) are one-electron operators, so the generalization of this Hamiltonian to many-body particle is straightforward in the Born–Oppenheimer (BO) approximation
where the electric field operator is defined as
Note that in this Hamiltonian we have removed the electron rest mass energy, so that the zero of our energy axis agrees with the conventional nonrelativistic one. The Darwin term is easily dealt with, indeed it can be added to the potential energy term. A different situation comes from the spin-orbit coupling and the Zeeman terms that can be neglected in a linear response approach at first insight.
4. Many-Body Current Density
In this section, we will derive the quantum expression for the many-body current density by adopting the Landau approach starting from different one-electron Hamiltonians and by using the relation
where is the expectation value of the quantum Hamiltonian. The next step is to calculate the variation , rewriting with an infinitesimally different vector potential
and then to obtain the difference of these two expressions, evaluated to the first order in the infinitesimal . It is clear by using this procedure that only terms depending on the potential vector contribute to the total current density vector field, so the Darwin terms cancel out, just as the potential energy terms and the rest energy does. They have no effect on the result for the probability current density. The results here proposed account only for the presence of a static magnetic field, so dynamic currents [25] are not considered. The one-electron Hamiltonians considered here to derive the current in spite of the previous discussion are:
- the classical kinetic energy Hamiltonian;
- the Zeeman Hamiltonian for the interaction of an electron spin with the applied magnetic field; and
- the spin-orbit coupling Hamiltonian.
4.1. Nonrelativistic Current Density
By using the relation (7), the single particle operator is
where
we can write
because
and a second order variation is not considered. From the previous equations, it follows that
Now we can use the vector identity
By using the divergence theorem, the volume integral of the first term of this equation converts to a surface integral at infinity and consequently vanishes, so
from which, by using Equation (16), it follows that
which is conventionally rewritten as
4.2. Zeeman Current Density
With the same procedure adopted before from Equation (7), we can write for this contribution
It follows that
Now considering the vector identity
and that the volume integral of the divergence term is zero, we obtain
4.3. Spin-Orbit Coupling Current Density
By using the vector identity
we obtain
Now by using Equation (16), the contribution to the total current density is for an atom
4.4. Total Electron Current Density
By summarizing the individual terms of the many-body current density obtained, it follows that the total current density is defined for an open-shell system, as
which in tensorial notation can be rewritten as
The continuity equation associated with this current that is verified is:
because the magnetization current has no divergence due to the nature of the curl and the nonrelativistic current can be obtained also with an approach that adopts the Coulomb gauge, which ensures that its divergence is zero for an exact calculation. For an open-shell molecule, as we can see from the previous equations, we have many spin-orbit coupling current densities as the number of atoms contained, but due to the presence of these currents are negligible except for very heavy atoms where spin-orbit coupling plays a fundamental role or in systems with high-spin multiplicity in the nuclear proximity. The Equation (43) for a closed-shell system reduces to
because the spin density matrices are equal and in accordance with the Wigner–Eckart theorem, the spin densities are all the same except for a proportionality constant [3], being . The current defined in Equation (42) or (43) is by definition gauge-invariant only for an exact calculation or in the limit of a complete basis set. This gauge dependence come from the nonrelativistic part of the current density [26]. The spin contributions to the total current are independent from the gauge choice also for an approximate calculation, due to the independence of spin density and the electron field operator of a point charge, from the origin of the coordinate system. If we consider the spin-orbit coupling current, a divergence should be expected in the proximity of atomic coordinates, due to the dependence of the electron field of a point charge on its origin [6]. Equation (43) does not define the total current density vector induced in a molecule by a static magnetic field because other terms in the Hamiltonian should be considered, like the Zeeman Hamiltonian of nuclei and the hyperfine interactions, but these contribution can be derived only from quantum electrodynamics, and it is not our purpose to discuss them in this paper. Moreover, these terms can be neglected at first approximation in a non-fully relativistic approach.
5. Implementation
In this section we show how it is possible to evaluate the spin-orbit coupling current for an open-shell system in the linear response approach in a Hartree–Fock or DFT calculation. In the absence of orbital degeneracy, the first term on the rhs of Equation (43) describes the system response to an external applied magnetic field. In this context, the spinless charge density can be expanded to first order in the magnetic field as
and an explicit expression for the first term on the rhs of (43) can be provided according to the well-known equations for the first order-induced current density [5,26]
where is the vector potential linked to the external magnetic field. For the Zeeman current, with the understanding that the reference frame is always chosen so that the quantization axis coincides with the direction of applied magnetic field, we can define [5]
Similarly, for the spin-orbit coupling current we have
with
As we pointed out before, we are interested only in the spin-orbit coupling current for which the tensor can be implemented, from a practical point of view, in atomic units, adopting the Szabo and Ostlund notation [27] as
with
in accordance with the Wigner–Eckart theorem. We have seen that it is possible to define a spin-orbit coupling current density tensor for all the atoms contained in an open-shell system according to
Orbital coefficients can be obtained from a Gaussian [28] calculation or generated by the SYSMOIC suite of programs. The full procedure for the calculation of total spin-orbit coupling-induced current density vector has been implemented in the freely available SYSMOIC [26] program package.
6. Computational Details
Due to the nature of the spin-orbit coupling current we have considered, as a system where it is possible to evaluate this current consistently, the Co atom with a spin multiplicity according to the high-spin electronic configuration. Owing to their small size, very accurate computations have been carried out by using the BHandHLYP functional [29], recently shown to provide good linear response properties [30], adopting the ATZP-ZORA basis set [31] of contracted functions which include terms of high angular momentum taken from BSE. The ATZP-ZORA basis set is optimized to deal with scalar relativistic effects that do not take into account the finite character of the charges, like the ZORA approach [32]. The Gaussian 16 calculation has been done by using the 6d 10f and int=dkh0 keywords to account for the 0th scalar relativistic correction to the molecular orbitals. The computational time load of this kind of calculation is about more than a standard DFT one. The spin orbit coupling current density vector field is shown in Figure 1.
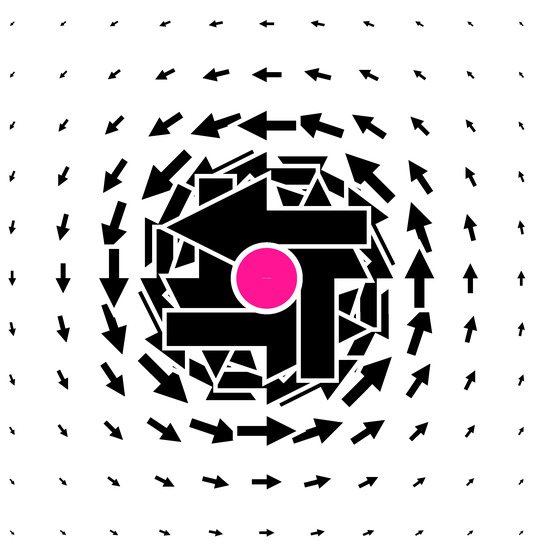
Figure 1.
Spin-orbit coupling current density vector field for the Co atom with spin multiplicity evaluated on the xy plane for a magnetic field applied in the z direction.
To answer the questions raised above, variational calculations of the energy have been done with six different Hamiltonians at the Hartree–Fock level of theory for atoms with atomic number Z that came from 1 to 20 always adopting the ATZP-ZORA basis set reported in Table 1. These Hamiltonians are

Table 1.
Variational energies in hartree, obtained with the Hartree–Fock approximation considering the different corrections to the Hamiltonian adopting the ATZP-ZORA basis set for atoms with atomic number Z that comes from 1 to 20.
- Hartree–Fock Hamiltonian;
- Hartree–Fock + mass-velocity correction Hamiltionian;
- Hartree–Fock + Darwin correction Hamiltionian;
- Hartree–Fock + Cowan–Griffin Hamiltionian;
- ZORA–Hartree–Fock Hamiltonian; and
- Douglas-Kroll-Hess 0th order–Hartree–Fock Hamiltonian (DKH0)
In particular, variational calculations, by using the mass–velocity and the Darwin Hamiltonians, have been done with the SYSMOIC software, whereas the ZORA and the DKH0 [33] variational calculations have been performed respectively with the NWCHEM [34] and Gaussian 16 [28] software packages.
For the mass–velocity corrections, a good agreement is found in the literature [35]. From the Table 1, it seems that a variational calculation with the Cowan–Griffin Hamiltonian, where it is possible, is closer to the DKH0 calculation than the ZORA approach for the basis set here adopted.
7. Conclusions
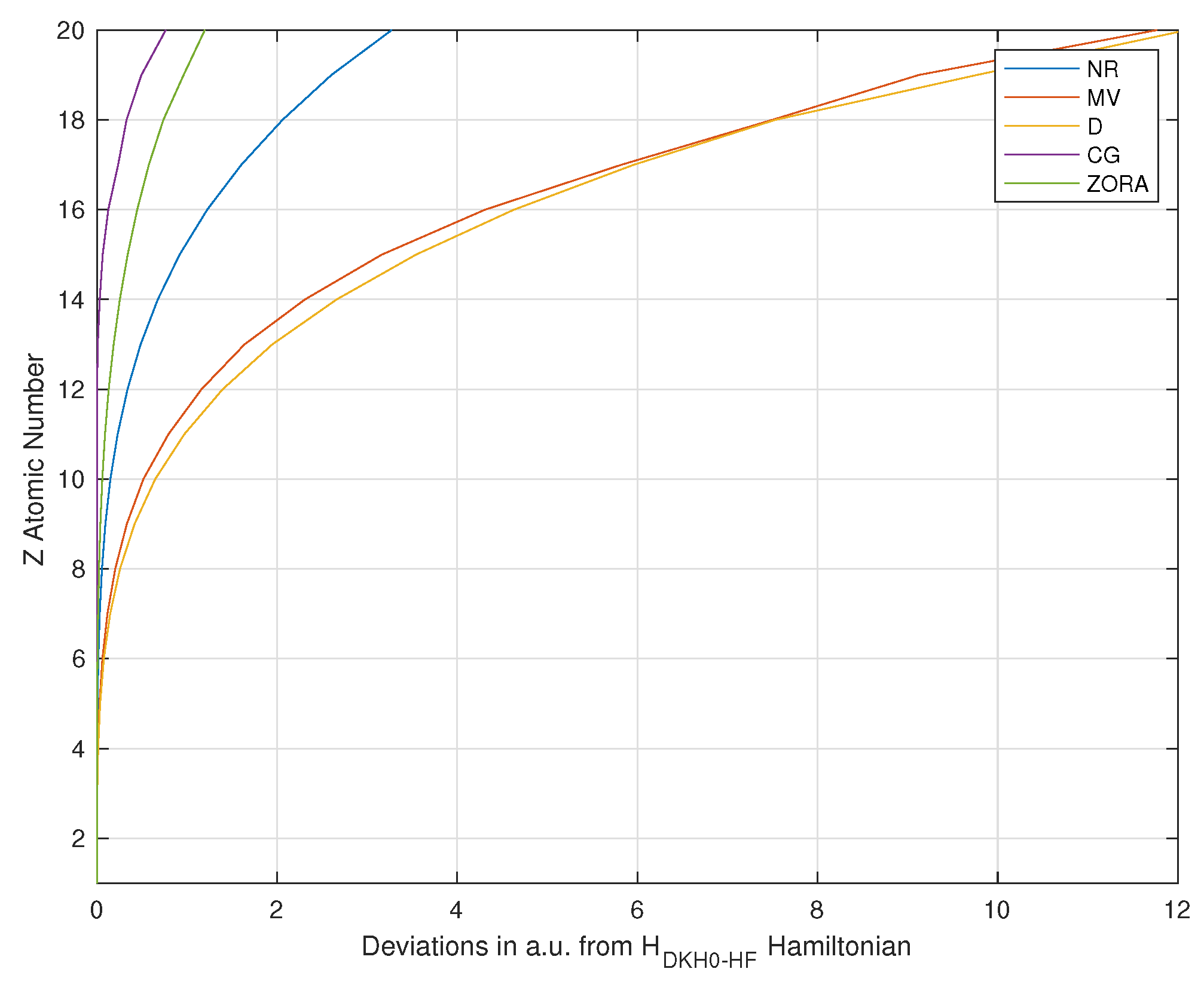
A different way to derive and calculate the total induced relativistic current density has been presented, and is focused on the different contributions that come from a relativistic picture, not presented before, if compared with standard relativistic [7,16,18,19,36] or non-relativistic ones [5,14,17,26]. Of these contributions, the spin-orbit coupling current can be neglected at first approach to deal with open-shell systems without high-spin multiplicity containing atoms of low atomic number due to the nature of the multiplicative factor. For closed-shell systems, the equations are the same obtained from a nonrelativistic picture, but molecular orbitals can be different for systems with atoms of high atomic number near nuclei if we consider scalar relativistic corrections. Based on the discussion done until now, it is clear that the quantitative description of many-body systems requires a complete relativistic treatment for systems containing atoms with atomic number Z greater than 12. Indeed a partial introduction of corrective terms, such as the mass–velocity term or the Darwin term only, leads to a greater error than that obtainable by using a non-relativistic approach, as can be seen in the Figure 2. This last approach is usable with atoms until with an error estimation of ≃1.7 kcal/mol if we consider only scalar relativistic effects. The Cowan–Griffin Hamiltonian [37] is not very useful for Z greater than 20 because it becomes unbounded from below [38,39], indeed it converges only for , whereas the spectrum of operator is [40]. The leading relativistic corrections are futile because it is well-known that the expectation values , , diverge for S states of the hydrogen atom and, in general, for the ground state of any atomic or molecular system [41,42,43].
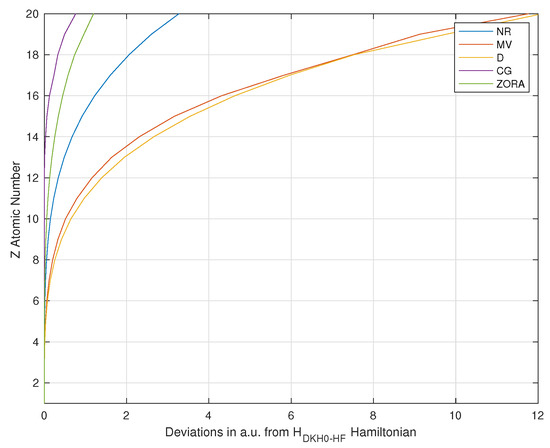
Figure 2.
Absolute deviations in a.u. from Douglas-Kroll-Hess 0th order–Hartree–Fock Hamiltonian.
Without relativistic effects it is not possible to obtain a correct description of molecular properties. This applies, in particular, for the induced current density that contains contributions arising from electron spin and that are not negligible for open-shell systems [5,44]. For closed-shell systems, only small differences in detail were found in the magnetically induced currents maps obtained at the different levels of calculations [36,45].
Author Contributions
Conceptualization, F.F.S. and R.C.; methodology, F.F.S. and R.C.; software, F.F.S.; validation, F.F.S. and R.C.; formal analysis, F.F.S. and R.C.; investigation, F.F.S. and R.C.; data curation, F.F.S.; writing—original draft preparation, F.F.S.; writing—review and editing, F.F.S. and R.C.; visualization, F.F.S.; supervision, F.F.S.; project administration, F.F.S. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support from MUR (FARB 2019) is gratefully acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank R. Zanasi, G. Monaco and P. Lazzeretti for helpful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gordon, W. Der Strom der Diracschen Elektronentheorie. Z. Physik 1928, 50, 630–632. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifšic, E.M.; Landau, L.D. Course of theoretical physics. In Quantum Mechanics: Non-Relativistic Theory, 3rd ed.; Landau, L.D., Lifshit, E.M., Eds.; Elsevier: Singapore, 2007; Volume 3. [Google Scholar]
- McWeeny, R. Methods of Molecular Quantum Mechanics, 2nd ed.; Theoretical Chemistry; Academic Press: London, UK, 1992. [Google Scholar]
- Lazzeretti, P. Gauge invariance of the nuclear spin/electron orbit interaction and NMR spectral parameters. J. Chem. Phys. 2012, 137, 074108. [Google Scholar] [CrossRef]
- Soncini, A. Charge and Spin Currents in Open-Shell Molecules: A Unified Description of NMR and EPR Observables. J. Chem. Theory Comput. 2007, 3, 2243–2257. [Google Scholar] [CrossRef] [PubMed]
- Hodge, W.B.; Migirditch, S.V.; Kerr, W.C. Electron spin and probability current density in quantum mechanics. Am. J. Phys. 2014, 82, 681–690. [Google Scholar] [CrossRef]
- Bast, R.; Jusélius, J.; Saue, T. 4-Component relativistic calculation of the magnetically induced current density in the group 15 heteroaromatic compounds. Chem. Phys. 2009, 356, 187–194. [Google Scholar] [CrossRef]
- Engel, E.; Dreizler, R.M. Density Functional Theory: An Advanced Course; Theoretical and Mathematical Physics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2011. [Google Scholar]
- Sundholm, D.; Dimitrova, M.; Berger, R.J.F. Current density and molecular magnetic properties. Chem. Commun. 2021, 57, 12362–12378. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. On the performance of some aromaticity indices: A critical assessment using a test set. J. Comput. Chem. 2008, 29, 1543–1554. [Google Scholar] [CrossRef]
- Carion, R.; Champagne, B.; Monaco, G.; Zanasi, R.; Pelloni, S.; Lazzeretti, P. Ring Current Model and Anisotropic Magnetic Response of Cyclopropane. J. Chem. Theory Comput. 2010, 6, 2002–2018. [Google Scholar] [CrossRef]
- Gershoni-Poranne, R.; Stanger, A. Magnetic criteria of aromaticity. Chem. Soc. Rev. 2015, 44, 6597–6615. [Google Scholar] [CrossRef]
- Landi, A.; Summa, F.F.; Monaco, G. Magnetic Aromaticity of Cycloporphyrin Nanorings. Chemistry 2021, 3, 991–1004. [Google Scholar] [CrossRef]
- Lazzeretti, P. Ring currents. Prog. Nucl. Magn. Reson. Spectrosc. 2000, 36, 1–88. [Google Scholar] [CrossRef]
- Helgaker, T.; Coriani, S.; Jørgensen, P.; Kristensen, K.; Olsen, J.; Ruud, K. Recent Advances in Wave Function-Based Methods of Molecular-Property Calculations. Chem. Rev. 2012, 112, 543–631. [Google Scholar] [CrossRef] [PubMed]
- Komorovsky, S.; Repisky, M.; Ruud, K.; Malkina, O.L.; Malkin, V.G. Four-Component Relativistic Density Functional Theory Calculations of NMR Shielding Tensors for Paramagnetic Systems. J. Phys. Chem. A 2013, 117, 14209–14219. [Google Scholar] [CrossRef]
- Sundholm, D.; Fliegl, H.; Berger, R.J. Calculations of magnetically induced current densities: Theory and applications. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2016, 6, 639–678. [Google Scholar] [CrossRef]
- Gillhuber, S.; Franzke, Y.J.; Weigend, F. Paramagnetic NMR Shielding Tensors and Ring Currents: Efficient Implementation and Application to Heavy Element Compounds. J. Phys. Chem. A 2021, 125, 9707–9723. [Google Scholar] [CrossRef] [PubMed]
- Franzke, Y.J.; Mack, F.; Weigend, F. NMR Indirect Spin–Spin Coupling Constants in a Modern Quasi-Relativistic Density Functional Framework. J. Chem. Theory Comput. 2021, 17, 3974–3994. [Google Scholar] [CrossRef] [PubMed]
- Summa, F.F.; Monaco, G.; Zanasi, R.; Pelloni, S.; Lazzeretti, P. Electronic Currents Induced by Optical Fields and Rotatory Power Density in Chiral Molecules. Molecules 2021, 26, 4195. [Google Scholar] [CrossRef] [PubMed]
- Summa, F.F.; Monaco, G.; Lazzeretti, P.; Zanasi, R. Origin-Independent Densities of Static and Dynamic Molecular Polarizabilities. J. Phys. Chem. Lett. 2021, 12, 8855–8864. [Google Scholar] [CrossRef]
- Summa, F.F.; Monaco, G.; Zanasi, R.; Lazzeretti, P. Dynamic toroidizability as ubiquitous property of atoms and molecules in optical electric fields. J. Chem. Phys. 2022, 156, 054106. [Google Scholar] [CrossRef]
- Born, M.; Oppenheimer, R. Zur Quantentheorie der Molekeln. Annalen der Physik 1927, 389, 457–484. [Google Scholar] [CrossRef]
- Foldy, L.L.; Wouthuysen, S.A. On the Dirac Theory of Spin 1/2 Particles and Its Non-Relativistic Limit. Phys. Rev. 1950, 78, 29–36. [Google Scholar] [CrossRef]
- Lazzeretti, P. Gauge invariance and origin independence of electronic charge density and current density induced by optical fields. J. Chem. Phys. 2018, 149, 154106. [Google Scholar] [CrossRef] [PubMed]
- Monaco, G.; Summa, F.F.; Zanasi, R. Program Package for the Calculation of Origin-Independent Electron Current Density and Derived Magnetic Properties in Molecular Systems. J. Chem. Inf. Model. 2021, 61, 270–283. [Google Scholar] [CrossRef]
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory; Dover Publications: Mineola, NY, USA, 1996. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Summa, F.F.; Monaco, G.; Lazzeretti, P.; Zanasi, R. Assessment of the Performance of DFT Functionals in the Fulfillment of Off-Diagonal Hypervirial Relationships. Phys. Chem. Chem. Phys. 2021, 23, 15268–15274. [Google Scholar] [CrossRef] [PubMed]
- Canal Neto, A.; Ferreira, I.; Jorge, F.; de Oliveira, A. All-electron triple zeta basis sets for ZORA calculations: Application in studies of atoms and molecules. Chem. Phys. Lett. 2021, 771, 138548. [Google Scholar] [CrossRef]
- van Lenthe, E.; Snijders, J.G.; Baerends, E.J. The zero-order regular approximation for relativistic effects: The effect of spin–orbit coupling in closed shell molecules. J. Chem. Phys. 1996, 105, 6505–6516. [Google Scholar] [CrossRef]
- de Jong, W.A.; Harrison, R.J.; Dixon, D.A. Parallel Douglas–Kroll energy and gradients in NWChem: Estimating scalar relativistic effects using Douglas–Kroll contracted basis sets. J. Chem. Phys. 2001, 114, 48. [Google Scholar] [CrossRef]
- Aprà, E.; Bylaska, E.J.; de Jong, W.A.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Valiev, M.; van Dam, H.J.J.; Alexeev, Y.; Anchell, J.; et al. NWChem: Past, present, and future. J. Chem. Phys. 2020, 152, 184102. [Google Scholar] [CrossRef]
- Farazdel, A.; Westgate, W.M.; Simas, A.M.; Sagar, R.P.; Smith, V.H. Validity of the mass-velocity term in the Breit-Pauli hamiltonian. Int. J. Quantum Chem. 2009, 28, 61–68. [Google Scholar] [CrossRef]
- Havenith, R.W.A.; De Proft, F.; Jenneskens, L.W.; Fowler, P.W. Relativistic ring currents in metallabenzenes: An analysis in terms of contributions of localised orbitals. Phys. Chem. Chem. Phys. 2012, 14, 9897. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cowan, R.D.; Griffin, D.C. Approximate relativistic corrections to atomic radial wave functions. J. Opt. Soc. Am. 1976, 66, 1010. [Google Scholar] [CrossRef]
- Farazdel, A.; Smith, V.H. Invalidity of the ubiquitous mass-velocity operator in quasirelativistic theories. Int. J. Quantum Chem. 1986, 29, 311–314. [Google Scholar] [CrossRef]
- Thaller, B. Normal forms of an abstract Dirac operator and applications to scattering theory. J. Math. Phys. 1988, 29, 249–257. [Google Scholar] [CrossRef]
- Almlöf, J.; Fægri, K.; Grelland, H. A variational approach to relativistic effects in LCAO calculations. Chem. Phys. Lett. 1985, 114, 53–57. [Google Scholar] [CrossRef]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Springer: Berlin/Heidelberg, Germany, 1957. [Google Scholar] [CrossRef]
- Thakkar, A.J. Relativistic kinetic energies and mass–velocity corrections in diatomic molecules. J. Chem. Phys. 1986, 85, 4509–4514. [Google Scholar] [CrossRef]
- Ketley, I.; Moss, R. On the expectation values of relativistic corrections to the Hamiltonian. Mol. Phys. 1983, 49, 1289–1295. [Google Scholar] [CrossRef]
- Lazzeretti, P. Electronic Current Densities Induced by Magnetic Fields and Nuclear Magnetic Dipoles. In Science and Technology of Atomic, Molecular, Condensed Matter & Biological Systems; Elsevier: New York, NY, USA, 2013; Volume 3, pp. 209–243. [Google Scholar] [CrossRef]
- Sulzer, D.; Olejniczak, M.; Bast, R.; Saue, T. 4-Component relativistic magnetically induced current density using London atomic orbitals. Phys. Chem. Chem. Phys. 2011, 13, 20682. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).