Advanced Machine Learning Methods for Learning from Sparse Data in High-Dimensional Spaces: A Perspective on Uses in the Upstream of Development of Novel Energy Technologies
Abstract
:1. Introduction
2. High Dimensionality and Extremely Low Data Density in the Space of Descriptors
2.1. Examples of Input—Output Mappings Used in ML for Energy Technologies
2.2. New Technologies and Challengies Require New Simulation Methods–A Large Scope for Machine Learning
2.3. The Curse of Dimensionality and Why ML Techniques Are Effective
3. Advanced Techniques for Working with Sparse Data
3.1. Brief Introduction to Neural Networks and Gaussian Process Regression
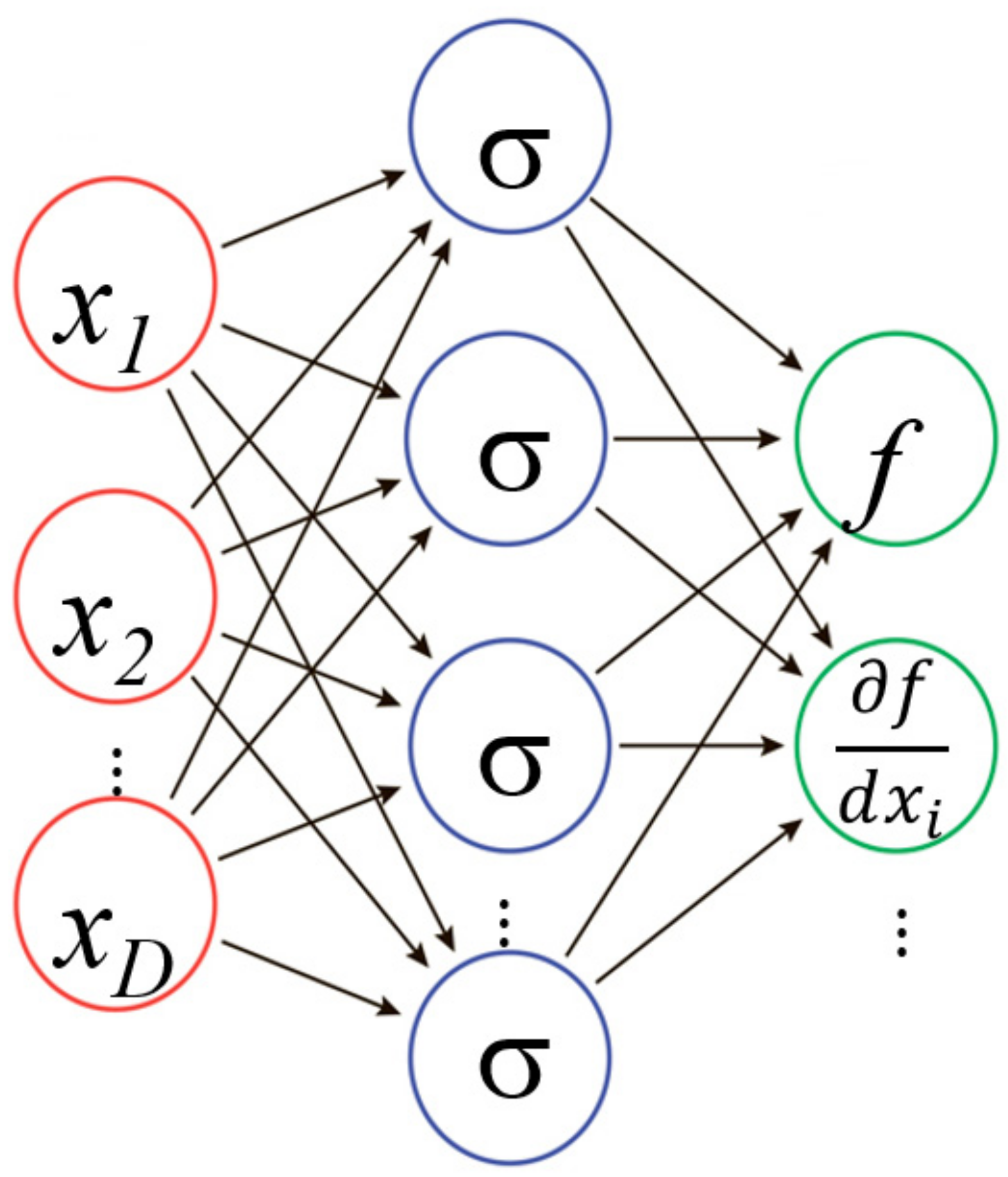
3.1.1. Neural Networks (NN)
3.1.2. Gaussian Process Regression (GPR)
3.1.3. Relative Pros and Cons of GPR vs. NN
3.2. High-Dimensional Model Representation (HDMR)
3.3. Combining HDMR with ML for Learning from Sparse Data
3.3.1. Machine Learning of HDMR Terms
3.3.2. RS-HDMR-NN (Random Sampling High-Dimensional Model Representation Neural Network)
3.3.3. RS-HDMR-GPR (Random Sampling High-Dimensional Model Representation Gaussian Process Regression)
3.4. When Are Deep NNs Useful?
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Tong, Q.; Gao, P.; Liu, H.; Xie, Y.; Lv, J.; Wang, Y.; Zhao, J. Combining Machine Learning Potential and Structure Prediction for Accelerated Materials Design and Discovery. J. Phys. Chem. Lett. 2020, 11, 8710–8720. [Google Scholar] [CrossRef]
- Walters, W.P.; Barzilay, R. Applications of Deep Learning in Molecule Generation and Molecular Property Prediction. Accounts Chem. Res. 2020, 54, 263–270. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. npj Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Wang, A.Y.-T.; Murdock, R.J.; Kauwe, S.K.; Oliynyk, A.O.; Gurlo, A.; Brgoch, J.; Persson, K.A.; Sparks, T.D. Machine Learning for Materials Scientists: An Introductory Guide toward Best Practices. Chem. Mater. 2020, 32, 4954–4965. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef] [PubMed]
- Moosavi, S.M.; Jablonka, K.M.; Smit, B. The Role of Machine Learning in the Understanding and Design of Materials. J. Am. Chem. Soc. 2020, 142, 20273–20287. [Google Scholar] [CrossRef] [PubMed]
- del Cueto, M.; Troisi, A. Determining usefulness of machine learning in materials discovery using simulated research landscapes. Phys. Chem. Chem. Phys. 2021, 23, 14156–14163. [Google Scholar] [CrossRef] [PubMed]
- Kalidindi, S.R. Feature engineering of material structure for AI-based materials knowledge systems. J. Appl. Phys. 2020, 128, 041103. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Chen, D.; Jiang, Y.; Nie, Z.; Pan, F. Encoding the atomic structure for machine learning in materials science. WIREs Comput. Mol. Sci. 2021, 12, e1558. [Google Scholar] [CrossRef]
- Im, J.; Lee, S.; Ko, T.-W.; Kim, H.W.; Hyon, Y.; Chang, H. Identifying Pb-free perovskites for solar cells by machine learning. npj Comput. Mater. 2019, 5, 37. [Google Scholar] [CrossRef] [Green Version]
- Meftahi, N.; Klymenko, M.; Christofferson, A.J.; Bach, U.; Winkler, D.A.; Russo, S.P. Machine learning property prediction for organic photovoltaic devices. npj Comput. Mater. 2020, 6, 166. [Google Scholar] [CrossRef]
- Sahu, H.; Ma, H. Unraveling Correlations between Molecular Properties and Device Parameters of Organic Solar Cells Using Machine Learning. J. Phys. Chem. Lett. 2019, 10, 7277–7284. [Google Scholar] [CrossRef] [PubMed]
- Zhuo, Y.; Brgoch, J. Opportunities for Next-Generation Luminescent Materials through Artificial Intelligence. J. Phys. Chem. Lett. 2021, 12, 764–772. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, A.; Wang, J.-L. Machine learning for high performance organic solar cells: Current scenario and future prospects. Energy Environ. Sci. 2020, 14, 90–105. [Google Scholar] [CrossRef]
- Li, F.; Peng, X.; Wang, Z.; Zhou, Y.; Wu, Y.; Jiang, M.; Xu, M. Machine Learning (ML)—Assisted Design and Fabrication for Solar Cells. Energy Environ. Mater. 2019, 2, 280–291. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.-I.; Joanito, I.; Lan, C.-F.; Hsu, C.-P. Artificial neural networks for predicting charge transfer coupling. J. Chem. Phys. 2020, 153, 214113. [Google Scholar] [CrossRef]
- An, N.G.; Kim, J.Y.; Vak, D. Machine learning-assisted development of organic photovoltaics via high-throughput in situ formulation. Energy Environ. Sci. 2021, 14, 3438–3446. [Google Scholar] [CrossRef]
- Rodríguez-Martínez, X.; Pascual-San-José, E.; Campoy-Quiles, M. Accelerating organic solar cell material’s discovery: High-throughput screening and big data. Energy Environ. Sci. 2021, 14, 3301–3322. [Google Scholar] [CrossRef]
- Priya, P.; Aluru, N.R. Accelerated design and discovery of perovskites with high conductivity for energy applications through machine learning. npj Comput. Mater. 2021, 7, 90. [Google Scholar] [CrossRef]
- Srivastava, M.; Howard, J.M.; Gong, T.; Dias, M.R.S.; Leite, M.S. Machine Learning Roadmap for Perovskite Photovoltaics. J. Phys. Chem. Lett. 2021, 12, 7866–7877. [Google Scholar] [CrossRef]
- Teunissen, J.L.; Da Pieve, F. Molecular Bond Engineering and Feature Learning for the Design of Hybrid Organic–Inorganic Perovskite Solar Cells with Strong Noncovalent Halogen–Cation Interactions. J. Phys. Chem. C 2021, 125, 25316–25326. [Google Scholar] [CrossRef]
- Miyake, Y.; Saeki, A. Machine Learning-Assisted Development of Organic Solar Cell Materials: Issues, Analyses, and Outlooks. J. Phys. Chem. Lett. 2021, 12, 12391–12401. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Liang, J.; Yu, Y.; Liu, R.; Xu, Y.; Zhu, X.; Zhao, Y. Machine Learning-Assisted Discovery of High-Voltage Organic Materials for Rechargeable Batteries. J. Phys. Chem. C 2021, 125, 21352–21358. [Google Scholar] [CrossRef]
- Moses, I.A.; Joshi, R.P.; Ozdemir, B.; Kumar, N.; Eickholt, J.; Barone, V. Machine Learning Screening of Metal-Ion Battery Electrode Materials. ACS Appl. Mater. Interfaces 2021, 13, 53355–53362. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Zhang, X.; Chen, L.; Yao, S.; Zhou, Z. A Machine Learning Model on Simple Features for CO2 Reduction Electrocatalysts. J. Phys. Chem. C 2020, 124, 22471–22478. [Google Scholar] [CrossRef]
- Lamoureux, P.S.; Winther, K.T.; Torres, J.A.G.; Streibel, V.; Zhao, M.; Bajdich, M.; Abild-Pedersen, F.; Bligaard, T. Machine Learning for Computational Heterogeneous Catalysis. ChemCatChem 2019, 11, 3581–3601. [Google Scholar] [CrossRef] [Green Version]
- Back, S.; Yoon, J.; Tian, N.; Zhong, W.; Tran, K.; Ulissi, Z.W. Convolutional Neural Network of Atomic Surface Structures To Predict Binding Energies for High-Throughput Screening of Catalysts. J. Phys. Chem. Lett. 2019, 10, 4401–4408. [Google Scholar] [CrossRef]
- Toyao, T.; Maeno, Z.; Takakusagi, S.; Kamachi, T.; Takigawa, I.; Shimizu, K.-I. Machine Learning for Catalysis Informatics: Recent Applications and Prospects. ACS Catal. 2019, 10, 2260–2297. [Google Scholar] [CrossRef]
- Li, X.; Paier, W.; Paier, J. Machine Learning in Computational Surface Science and Catalysis: Case Studies on Water and Metal–Oxide Interfaces. Front. Chem. 2020, 8, 601029. [Google Scholar] [CrossRef]
- Pablo-García, S.; García-Muelas, R.; Sabadell-Rendón, A.; López, N. Dimensionality reduction of complex reaction networks in heterogeneous catalysis: From l inear-scaling relationships to statistical learning techniques. WIREs Comput. Mol. Sci. 2021, 11, e1540. [Google Scholar] [CrossRef]
- Li, X.; Chiong, R.; Page, A.J. Group and Period-Based Representations for Improved Machine Learning Prediction of Heterogeneous Alloy Catalysts. J. Phys. Chem. Lett. 2021, 12, 5156–5162. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Zhang, J.; Cheng, M.-J.; Lu, Q.; Zhang, H. Machine Learning Investigation of Supplementary Adsorbate Influence on Copper for Enhanced Electrochemical CO2 Reduction Performance. J. Phys. Chem. C 2021, 125, 15363–15372. [Google Scholar] [CrossRef]
- Palkovits, S. A Primer about Machine Learning in Catalysis—A Tutorial with Code. ChemCatChem 2020, 12, 3995–4008. [Google Scholar] [CrossRef]
- Giordano, L.; Akkiraju, K.; Jacobs, R.; Vivona, D.; Morgan, D.; Shao-Horn, Y. Electronic Structure-Based Descriptors for Oxide Properties and Functions. Accounts Chem. Res. 2022, 55, 298–308. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; ISBN 978-0-521-82568-9. [Google Scholar]
- Jansen, A.P.J. Kinetic Monte Carlo Algorithms. In An Introduction to Kinetic Monte Carlo Simulations of Surface Reactions; Jansen, A.P.J., Ed.; Lecture Notes in Physics; Springer: Berlin, Heidelberg, 2012; pp. 37–71. ISBN 978-3-642-29488-4. [Google Scholar]
- Manzhos, S. Machine learning for the solution of the Schrödinger equation. Mach. Learn. Sci. Technol. 2020, 1, 013002. [Google Scholar] [CrossRef]
- Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 2016, 145, 170901. [Google Scholar] [CrossRef] [Green Version]
- Manzhos, S.; Golub, P. Data-driven kinetic energy density fitting for orbital-free DFT: Linear vs Gaussian process regression. J. Chem. Phys. 2020, 153, 074104. [Google Scholar] [CrossRef]
- Kulik, H.; Hammerschmidt, T.; Schmidt, J.; Botti, S.; Marques, M.A.L.; Boley, M.; Scheffler, M.; Todorović, M.; Rinke, P.; Oses, C.; et al. Roadmap on Machine Learning in Electronic Structure. Electron. Struct. 2022. [Google Scholar] [CrossRef]
- Duan, C.; Liu, F.; Nandy, A.; Kulik, H.J. Putting Density Functional Theory to the Test in Machine-Learning-Accelerated Materials Discovery. J. Phys. Chem. Lett. 2021, 12, 4628–4637. [Google Scholar] [CrossRef] [PubMed]
- Friederich, P.; Häse, F.; Proppe, J.; Aspuru-Guzik, A. Machine-learned potentials for next-generation matter simulations. Nat. Mater. 2021, 20, 750–761. [Google Scholar] [CrossRef] [PubMed]
- Statistical Review of World Energy | Energy Economics | Home. Available online: https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy.html (accessed on 7 February 2022).
- Olah, G.A.; Prakash, G.K.S.; Goeppert, A. Anthropogenic Chemical Carbon Cycle for a Sustainable Future. J. Am. Chem. Soc. 2011, 133, 12881–12898. [Google Scholar] [CrossRef] [PubMed]
- Nayak, P.K.; Mahesh, S.; Snaith, H.J.; Cahen, D. Photovoltaic solar cell technologies: Analysing the state of the art. Nat. Rev. Mater. 2019, 4, 269–285. [Google Scholar] [CrossRef]
- Herbert, G.J.; Iniyan, S.; Sreevalsan, E.; Rajapandian, S. A review of wind energy technologies. Renew. Sustain. Energy Rev. 2007, 11, 1117–1145. [Google Scholar] [CrossRef]
- Winter, M.; Brodd, R.J. What Are Batteries, Fuel Cells, and Supercapacitors? Chem. Rev. 2004, 104, 4245–4270. [Google Scholar] [CrossRef] [Green Version]
- Birdja, Y.Y.; Pérez-Gallent, E.; Figueiredo, M.C.; Göttle, A.J.; Calle-Vallejo, F.; Koper, M.T.M. Advances and challenges in understanding the electrocatalytic conversion of carbon dioxide to fuels. Nat. Energy 2019, 4, 732–745. [Google Scholar] [CrossRef]
- Detz, R.J.; Reek, J.N.H.; van der Zwaan, B.C.C. The future of solar fuels: When could they become competitive? Energy Environ. Sci. 2018, 11, 1653–1669. [Google Scholar] [CrossRef]
- Barnhart, C.J.; Benson, S.M. On the importance of reducing the energetic and material demands of electrical energy storage. Energy Environ. Sci. 2013, 6, 1083–1092. [Google Scholar] [CrossRef]
- Winter, M.; Barnett, B.; Xu, K. Before Li Ion Batteries. Chem. Rev. 2018, 118, 11433–11456. [Google Scholar] [CrossRef]
- Abram, T.; Ion, S. Generation-IV nuclear power: A review of the state of the science. Energy Policy 2008, 36, 4323–4330. [Google Scholar] [CrossRef]
- Ho, M.; Obbard, E.; A Burr, P.; Yeoh, G. A review on the development of nuclear power reactors. Energy Procedia 2019, 160, 459–466. [Google Scholar] [CrossRef]
- Suman, S. Hybrid nuclear-renewable energy systems: A review. J. Clean. Prod. 2018, 181, 166–177. [Google Scholar] [CrossRef]
- Shao, M.; Chang, Q.; Dodelet, J.-P.; Chenitz, R. Recent Advances in Electrocatalysts for Oxygen Reduction Reaction. Chem. Rev. 2016, 116, 3594–3657. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jahangiri, H.; Bennett, J.; Mahjoubi, P.; Wilson, K.; Gu, S. A review of advanced catalyst development for Fischer–Tropsch synthesis of hydrocarbons from biomass derived syn-gas. Catal. Sci. Technol. 2014, 4, 2210–2229. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.-H.; Chen, C.-Y. Water gas shift reaction for hydrogen production and carbon dioxide capture: A review. Appl. Energy 2019, 258, 114078. [Google Scholar] [CrossRef]
- Chen, L.; Qi, Z.; Zhang, S.; Su, J.; Somorjai, G.A. Catalytic Hydrogen Production from Methane: A Review on Recent Progress and Prospect. Catalysts 2020, 10, 858. [Google Scholar] [CrossRef]
- Lavoie, J.-M. Review on dry reforming of methane, a potentially more environmentally-friendly approach to the increasing natural gas exploitation. Front. Chem. 2014, 2, 81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Kitchin, J.R. SingleNN: Modified Behler–Parrinello Neural Network with Shared Weights for Atomistic Simulations with Transferability. J. Phys. Chem. C 2020, 124, 17811–17818. [Google Scholar] [CrossRef]
- Behler, J. Constructing high-dimensional neural network potentials: A tutorial review. Int. J. Quantum Chem. 2015, 115, 1032–1050. [Google Scholar] [CrossRef]
- Na, G.S.; Jang, S.; Lee, Y.-L.; Chang, H. Tuplewise Material Representation Based Machine Learning for Accurate Band Gap Prediction. J. Phys. Chem. A 2020, 124, 10616–10623. [Google Scholar] [CrossRef]
- Xu, P.; Lu, T.; Ju, L.; Tian, L.; Li, M.; Lu, W. Machine Learning Aided Design of Polymer with Targeted Band Gap Based on DFT Computation. J. Phys. Chem. B 2021, 125, 601–611. [Google Scholar] [CrossRef] [PubMed]
- Aykol, M.; Herring, P.; Anapolsky, A. Machine learning for continuous innovation in battery technologies. Nat. Rev. Mater. 2020, 5, 725–727. [Google Scholar] [CrossRef]
- Deringer, V.L. Modelling and understanding battery materials with machine-learning-driven atomistic simulations. J. Phys. Energy 2020, 2, 041003. [Google Scholar] [CrossRef]
- Thomas, J.K.; Crasta, H.R.; Kausthubha, K.; Gowda, C.; Rao, A. Battery monitoring system using machine learning. J. Energy Storage 2021, 40, 102741. [Google Scholar] [CrossRef]
- Li, W.; Cui, H.; Nemeth, T.; Jansen, J.; Ünlübayir, C.; Wei, Z.; Zhang, L.; Wang, Z.; Ruan, J.; Dai, H.; et al. Deep reinforcement learning-based energy management of hybrid battery systems in electric vehicles. J. Energy Storage 2021, 36, 102355. [Google Scholar] [CrossRef]
- Elkamel, M.; Schleider, L.; Pasiliao, E.L.; Diabat, A.; Zheng, Q.P. Long-Term Electricity Demand Prediction via Socioeconomic Factors—A Machine Learning Approach with Florida as a Case Study. Energies 2020, 13, 3996. [Google Scholar] [CrossRef]
- Krishnadas, G.; Kiprakis, A. A Machine Learning Pipeline for Demand Response Capacity Scheduling. Energies 2020, 13, 1848. [Google Scholar] [CrossRef] [Green Version]
- Nti, I.K.; Teimeh, M.; Nyarko-Boateng, O.; Adekoya, A.F. Electricity load forecasting: A systematic review. J. Electr. Syst. Inf. Technol. 2020, 7, 1–19. [Google Scholar] [CrossRef]
- Antonopoulos, I.; Robu, V.; Couraud, B.; Kirli, D.; Norbu, S.; Kiprakis, A.; Flynn, D.; Elizondo-Gonzalez, S.; Wattam, S. Artificial intelligence and machine learning approaches to energy demand-side response: A systematic review. Renew. Sustain. Energy Rev. 2020, 130, 109899. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, J.-W.; Jung, H.S.; Shin, H.; Park, N.-G. High-Efficiency Perovskite Solar Cells. Chem. Rev. 2020, 120, 7867–7918. [Google Scholar] [CrossRef] [PubMed]
- Pham, H.D.; Xianqiang, L.; Li, W.; Manzhos, S.; Kyaw, A.K.K.; Sonar, P. Organic interfacial materials for perovskite-based optoelectronic devices. Energy Environ. Sci. 2019, 12, 1177–1209. [Google Scholar] [CrossRef]
- Witt, W.C.; del Rio, B.G.; Dieterich, J.M.; Carter, E.A. Orbital-free density functional theory for materials research. J. Mater. Res. 2018, 33, 777–795. [Google Scholar] [CrossRef]
- Golub, P.; Manzhos, S. Kinetic energy densities based on the fourth order gradient expansion: Performance in different classes of materials and improvement via machine learning. Phys. Chem. Chem. Phys. 2018, 21, 378–395. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fujinami, M.; Kageyama, R.; Seino, J.; Ikabata, Y.; Nakai, H. Orbital-free density functional theory calculation applying semi-local machine-learned kinetic energy density functional and kinetic potential. Chem. Phys. Lett. 2020, 748, 137358. [Google Scholar] [CrossRef]
- Seino, J.; Kageyama, R.; Fujinami, M.; Ikabata, Y.; Nakai, H. Semi-local machine-learned kinetic energy density functional demonstrating smooth potential energy curves. Chem. Phys. Lett. 2019, 734, 136732. [Google Scholar] [CrossRef]
- Snyder, J.C.; Rupp, M.; Hansen, K.; Blooston, L.; Müller, K.-R.; Burke, K. Orbital-free bond breaking via machine learning. J. Chem. Phys. 2013, 139, 224104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, K.; Parkhill, J. Kinetic Energy of Hydrocarbons as a Function of Electron Density and Convolutional Neural Networks. J. Chem. Theory Comput. 2016, 12, 1139–1147. [Google Scholar] [CrossRef] [PubMed]
- Hausdorff, F. Dimension und äußeres Maß. Math. Ann. 1918, 79, 157–179. [Google Scholar] [CrossRef]
- Kak, S. Information theory and dimensionality of space. Sci. Rep. 2020, 10, 20733. [Google Scholar] [CrossRef] [PubMed]
- Bottou, L. Stochastic gradient descent tricks. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 421–436. ISBN 9783642352881. [Google Scholar]
- Kolmogorov, A.N.; Arnol’d, V.; Boltjanskiĭ, V.; Efimov, N.; Èskin, G.; Koteljanskiĭ, D.; Krasovskiĭ, N.; Men’šov, D.; Portnov, I.; Ryškov, S.; et al. On the representation of continuous functions of many variables by superposition of continuous functions of one variable and addition. Am. Math. Soc. Transl. Ser. 2 1963, 28, 55–59. [Google Scholar] [CrossRef]
- Sprecher, D.A. A Numerical Implementation of Kolmogorov’s Superpositions II. Neural Netw. 1997, 10, 447–457. [Google Scholar] [CrossRef]
- Sprecher, D.A. A Numerical Implementation of Kolmogorov’s Superpositions. Neural Netw. 1996, 9, 765–772. [Google Scholar] [CrossRef]
- Sprecher, D.A.; Draghici, S. Space-filling curves and Kolmogorov superposition-based neural networks. Neural Netw. 2002, 15, 57–67. [Google Scholar] [CrossRef]
- Nees, M. Approximative versions of Kolmogorov’s superposition theorem, proved constructively. J. Comput. Appl. Math. 1994, 54, 239–250. [Google Scholar] [CrossRef] [Green Version]
- Katsuura, H.; Sprecher, D.A. Computational aspects of Kolmogorov’s superposition theorem. Neural Netw. 1994, 7, 455–461. [Google Scholar] [CrossRef]
- Sprecher, D.A. A universal mapping for kolmogorov’s superposition theorem. Neural Netw. 1993, 6, 1089–1094. [Google Scholar] [CrossRef]
- Kurkova, V. Kolmogorov’s theorem and multilayer neural networks. Neural Netw. 1992, 5, 501–506. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Netw. 1990, 3, 551–560. [Google Scholar] [CrossRef]
- Gorban, A. Approximation of continuous functions of several variables by an arbitrary nonlinear continuous function of one variable, linear functions, and their superpositions. Appl. Math. Lett. 1998, 11, 45–49. [Google Scholar] [CrossRef] [Green Version]
- Manzhos, S.; Carrington, T., Jr. Using neural networks to represent potential surfaces as sums of products. J. Chem. Phys. 2006, 125, 194105. [Google Scholar] [CrossRef]
- Beck, M.; Jäckle, A.; Worth, G.; Meyer, H.-D. The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1–105. [Google Scholar] [CrossRef]
- Schmitt, M. On the Complexity of Computing and Learning with Multiplicative Neural Networks. Neural Comput. 2002, 14, 241–301. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge MA, USA, 2006; ISBN 0-262-18253-X. [Google Scholar]
- Genton, M.G. Classes of Kernels for Machine Learning: A Statistics Perspective. J. Mach. Learn. Res. 2001, 2, 299–312. [Google Scholar]
- Smola, A.; Bartlett, P. Sparse Greedy Gaussian Process Regression. In Proceedings of the Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2001; Volume 13. [Google Scholar]
- Kamath, A.; Vargas-Hernández, R.A.; Krems, R.V.; Carrington, T., Jr.; Manzhos, S. Neural networks vs Gaussian process regression for representing potential energy surfaces: A comparative study of fit quality and vibrational spectrum accuracy. J. Chem. Phys. 2018, 148, 241702. [Google Scholar] [CrossRef] [PubMed]
- Warner, B.A.; Neal, R.M. Bayesian Learning for Neural Networks (Lecture Notes in Statistical Vol. 118). J. Am. Stat. Assoc. 1997, 92, 791. [Google Scholar] [CrossRef]
- Boussaidi, M.A.; Ren, O.; Voytsekhovsky, D.; Manzhos, S. Random Sampling High Dimensional Model Representation Gaussian Process Regression (RS-HDMR-GPR) for Multivariate Function Representation: Application to Molecular Potential Energy Surfaces. J. Phys. Chem. A 2020, 124, 7598–7607. [Google Scholar] [CrossRef] [PubMed]
- Ren, O.; Boussaidi, M.A.; Voytsekhovsky, D.; Ihara, M.; Manzhos, S. Random Sampling High Dimensional Model Representation Gaussian Process Regression (RS-HDMR-GPR) for representing multidimensional functions with machine-learned lower-dimensional terms allowing insight with a general method. Comput. Phys. Commun. 2021, 271, 108220. [Google Scholar] [CrossRef]
- Manzhos, S.; Ihara, M. Rectangularization of Gaussian Process Regression for Optimization of Hyperparameters. arXiv 2021, arXiv:2112.02467. [Google Scholar]
- Li, G.; Rosenthal, C.; Rabitz, H. High Dimensional Model Representations. J. Phys. Chem. A 2001, 105, 7765–7777. [Google Scholar] [CrossRef]
- Rabitz, H.; Aliş, Ö.F. General foundations of high-dimensional model representations. J. Math. Chem. 1999, 25, 197–233. [Google Scholar] [CrossRef]
- Alış, F.; Rabitz, H. Efficient Implementation of High Dimensional Model Representations. J. Math. Chem. 2001, 29, 127–142. [Google Scholar] [CrossRef]
- Fisher, R.A. On the “Probable Error” of a Coefficient of Correlation Deduced from a Small Sample. Metron 1921, 1, 3–32. [Google Scholar]
- Sobol′, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Li, G.; Hu, J.; Wang, S.-W.; Georgopoulos, P.G.; Schoendorf, A.J.; Rabitz, H. Random Sampling-High Dimensional Model Representation (RS-HDMR) and Orthogonality of Its Different Order Component Functions. J. Phys. Chem. A 2006, 110, 2474–2485. [Google Scholar] [CrossRef]
- Wang, S.-W.; Georgopoulos, P.G.; Li, G.; Rabitz, H. Random Sampling-High Dimensional Model Representation (RS-HDMR) with Nonuniformly Distributed Variables: Application to an Integrated Multimedia/Multipathway Exposure and Dose Model for Trichloroethylene. J. Phys. Chem. A 2003, 107, 4707–4716. [Google Scholar] [CrossRef]
- Manzhos, S.; Ihara, M. On the Optimization of Hyperparameters in Gaussian Process Regression with the Help of Low-Order High-Dimensional Model Representation. arXiv 2022, arXiv:2112.01374. [Google Scholar]
- Manzhos, S.; Yamashita, K.; Carrington, T. Extracting Functional Dependence from Sparse Data Using Dimensionality Reduction: Application to Potential Energy Surface Construction. In Proceedings of the Coping with Complexity: Model Reduction and Data Analysis; Gorban, A.N., Roose, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 133–149. [Google Scholar]
- Manzhos, S.; Carrington, T., Jr. Using redundant coordinates to represent potential energy surfaces with lower-dimensional functions. J. Chem. Phys. 2007, 127, 014103. [Google Scholar] [CrossRef]
- Manzhos, S.; Yamashita, K.; Carrington, T. Fitting sparse multidimensional data with low-dimensional terms. Comput. Phys. Commun. 2009, 180, 2002–2012. [Google Scholar] [CrossRef]
- Manzhos, S.; Sasaki, E.; Ihara, M. Easy representation of multivariate functions with low-dimensional terms via Gaussian process regression kernel design: Applications to machine learning of potential energy surfaces and kinetic energy densities from sparse data. Mach. Learn. Sci. Technol. 2022, 3, 01LT02. [Google Scholar] [CrossRef]
- Manzhos, S.; Carrington, T., Jr. A random-sampling high dimensional model representation neural network for building potential energy surfaces. J. Chem. Phys. 2006, 125, 084109. [Google Scholar] [CrossRef]
- Duvenaud, D.; Nickisch, H.; Rasmussen, C.E. Additive Gaussian Processes. In Advances in Neural Information Processing Systems; Neural Information Processing Systems: San Diego, CA, USA, 2011; pp. 226–234. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
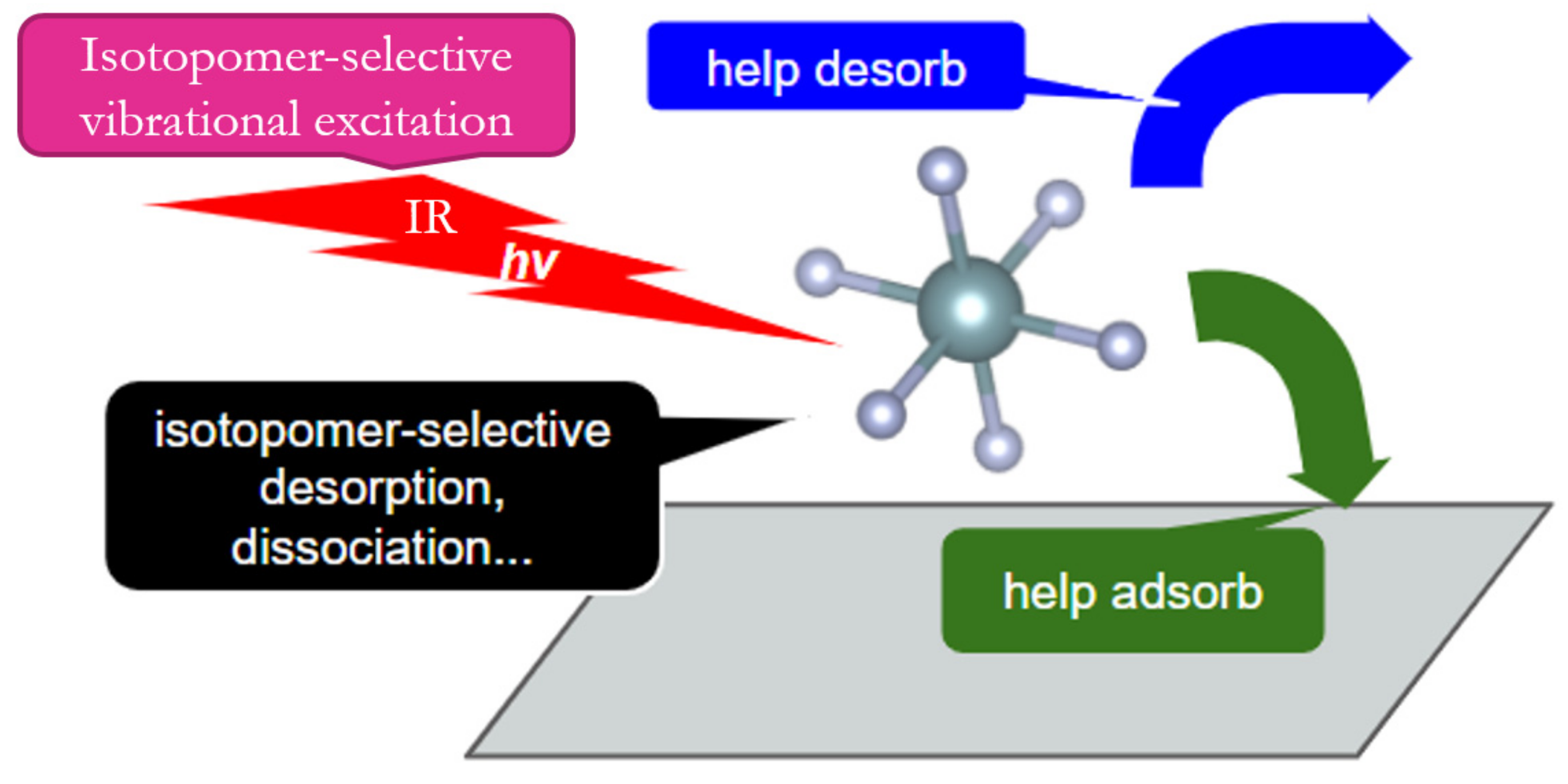
- Manzhos, S.; Yamashita, K. A model for the dissociative adsorption of N2O on Cu(100) using a continuous potential energy surface. Surf. Sci. 2010, 604, 555–561. [Google Scholar] [CrossRef]
- Wolfsberg, M.; Van Hook, A.; Paneth, P.; Rebelo, L.P.N. Isotope Effects; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Schneider, E.; Carlsen, B.; Tavrides, E.; van der Hoeven, C.; Phathanapirom, U. Measures of the environmental footprint of the front end of the nuclear fuel cycle. Energy Econ. 2013, 40, 898–910. [Google Scholar] [CrossRef] [Green Version]
- Parvin, P.; Sajad, B.; Silakhori, K.; Hooshvar, M.; Zamanipour, Z. Molecular laser isotope separation versus atomic vapor laser isotope separation. Prog. Nucl. Energy 2004, 44, 331–345. [Google Scholar] [CrossRef]
- Ronander, E.; Strydom, H.J.; Botha, L.R. High-pressure continuously tunable CO2 lasers and molecular laser isotope separation. Pramana 2014, 82, 49–58. [Google Scholar] [CrossRef]
- McDowell, R.S.; Sherman, R.J.; Asprey, L.B.; Kennedy, R.C. Vibrational spectrum and force field of molybdenum hexafluoride. J. Chem. Phys. 1975, 62, 3974–3978. [Google Scholar] [CrossRef]
- Koh, Y.W.; Westerman, K.; Manzhos, S. A computational study of adsorption and vibrations of UF6 on graphene derivatives: Conditions for 2D enrichment. Carbon 2015, 81, 800–806. [Google Scholar] [CrossRef]
- Manzhos, S.; Carrington, T.; Laverdure, L.; Mosey, N. Computing the Anharmonic Vibrational Spectrum of UF6 in 15 Dimensions with an Optimized Basis Set and Rectangular Collocation. J. Phys. Chem. A 2015, 119, 9557–9567. [Google Scholar] [CrossRef] [PubMed]
- Berezin, A.; Malyugin, S.; Nadezhdinskii, A.; Namestnikov, D.; Ponurovskii, Y.; Stavrovskii, D.; Shapovalov, Y.; Vyazov, I.; Zaslavskii, V.; Selivanov, Y.; et al. UF6 enrichment measurements using TDLS techniques. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2007, 66, 796–802. [Google Scholar] [CrossRef] [PubMed]
- Sobol’, I. On the distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Hodges, C.H. Quantum Corrections to the Thomas–Fermi Approximation—The Kirzhnits Method. Can. J. Phys. 1973, 51, 1428–1437. [Google Scholar] [CrossRef]
- Manzhos, S.; Dawes, R.; Carrington, T. Neural network-based approaches for building high dimensional and quantum dynamics-friendly potential energy surfaces. Int. J. Quantum Chem. 2014, 115, 1012–1020. [Google Scholar] [CrossRef] [Green Version]
- Manzhos, S.; Carrington, T. Neural Network Potential Energy Surfaces for Small Molecules and Reactions. Chem. Rev. 2020, 121, 10187–10217. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Ranasinghe, D.S. The power of exact conditions in electronic structure theory. Chem. Phys. Lett. 2016, 669, 54–70. [Google Scholar] [CrossRef]
- Fermi, E. Eine statistische Methode zur Bestimmung einiger Eigenschaften des Atoms und ihre Anwendung auf die Theorie des periodischen Systems der Elemente. Eur. Phys. J. A 1928, 48, 73–79. [Google Scholar] [CrossRef]
- Weizsäcker, C.F.V. Zur Theorie der Kernmassen. Eur. Phys. J. A 1935, 96, 431–458. [Google Scholar] [CrossRef]






| Rmse 1 | Ncf\Ntrain | 5000 | 3000 | 2000 |
|---|---|---|---|---|
| Full-D (d = D) | 1 | 42.2 | 75.4 | 106.7 |
| d = 1 | 15 | 234.6 | 236.4 | 237.3 |
| d = 2 | 105 | 168.1 | 178.6 | 190.3 |
| d = 3 | 455 | 65.6 | 78.0 | 97.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manzhos, S.; Ihara, M. Advanced Machine Learning Methods for Learning from Sparse Data in High-Dimensional Spaces: A Perspective on Uses in the Upstream of Development of Novel Energy Technologies. Physchem 2022, 2, 72-95. https://doi.org/10.3390/physchem2020006
Manzhos S, Ihara M. Advanced Machine Learning Methods for Learning from Sparse Data in High-Dimensional Spaces: A Perspective on Uses in the Upstream of Development of Novel Energy Technologies. Physchem. 2022; 2(2):72-95. https://doi.org/10.3390/physchem2020006
Chicago/Turabian StyleManzhos, Sergei, and Manabu Ihara. 2022. "Advanced Machine Learning Methods for Learning from Sparse Data in High-Dimensional Spaces: A Perspective on Uses in the Upstream of Development of Novel Energy Technologies" Physchem 2, no. 2: 72-95. https://doi.org/10.3390/physchem2020006
APA StyleManzhos, S., & Ihara, M. (2022). Advanced Machine Learning Methods for Learning from Sparse Data in High-Dimensional Spaces: A Perspective on Uses in the Upstream of Development of Novel Energy Technologies. Physchem, 2(2), 72-95. https://doi.org/10.3390/physchem2020006







