Influence of Ballast and Sub-Ballast Thickness on Structural Behavior of Heavy-Haul Railway Platform Determined by Using Finite Element Modeling
Abstract
1. Introduction
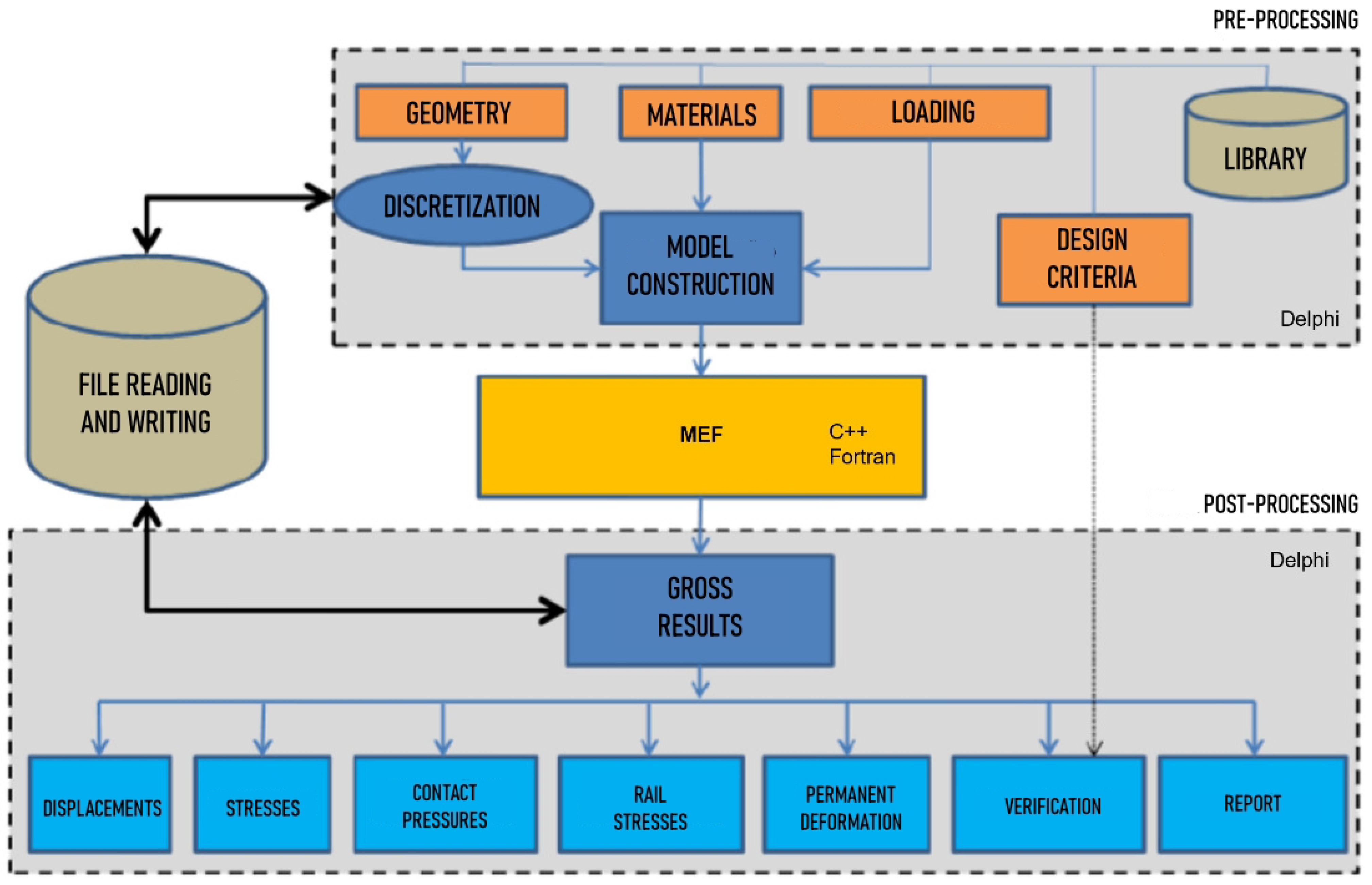
The Systrain Software
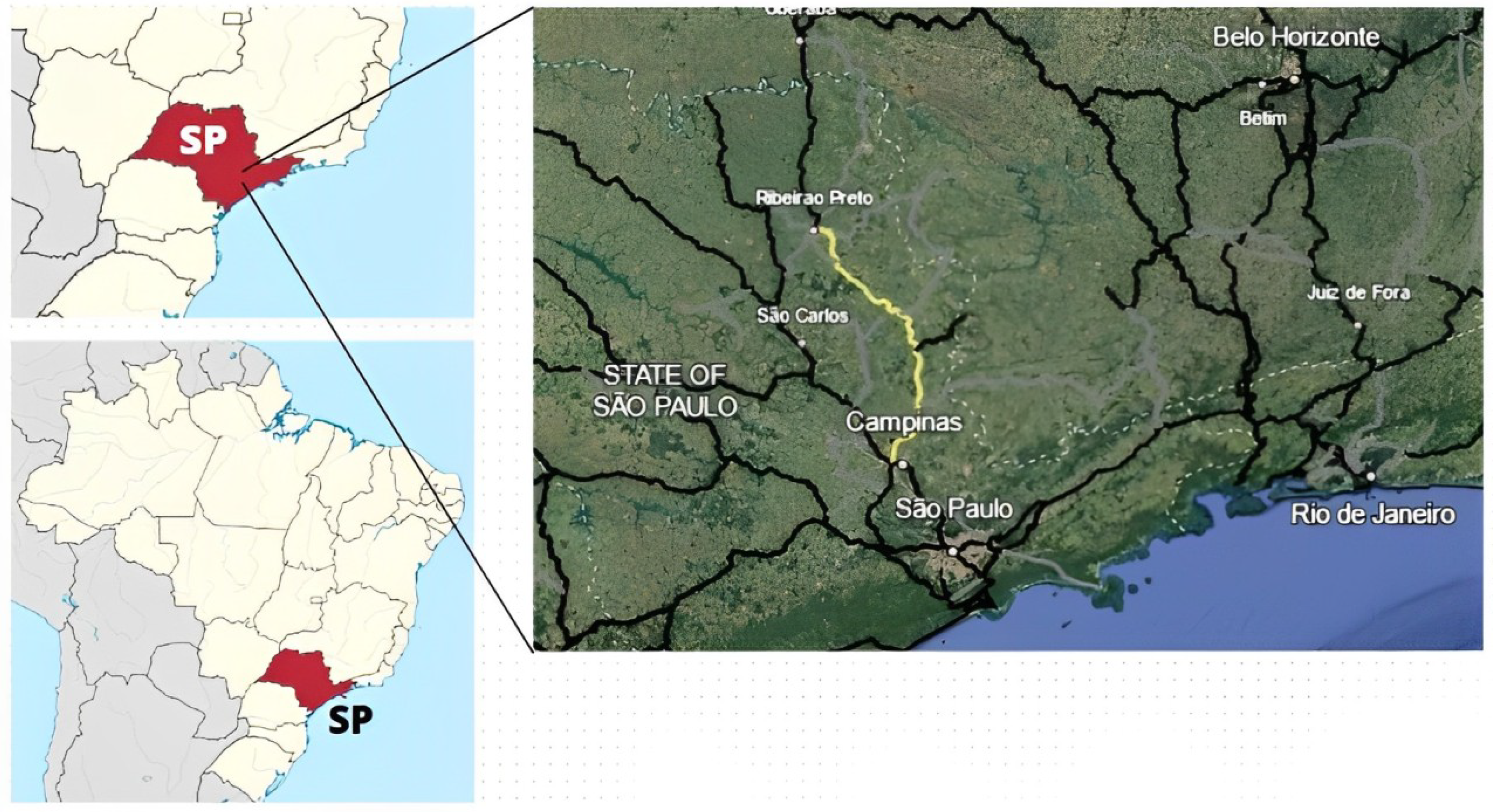
2. Methodology
2.1. Computational Modeling—SysTrain
2.1.1. Input Data
2.1.2. Simulations
2.1.3. Output Data
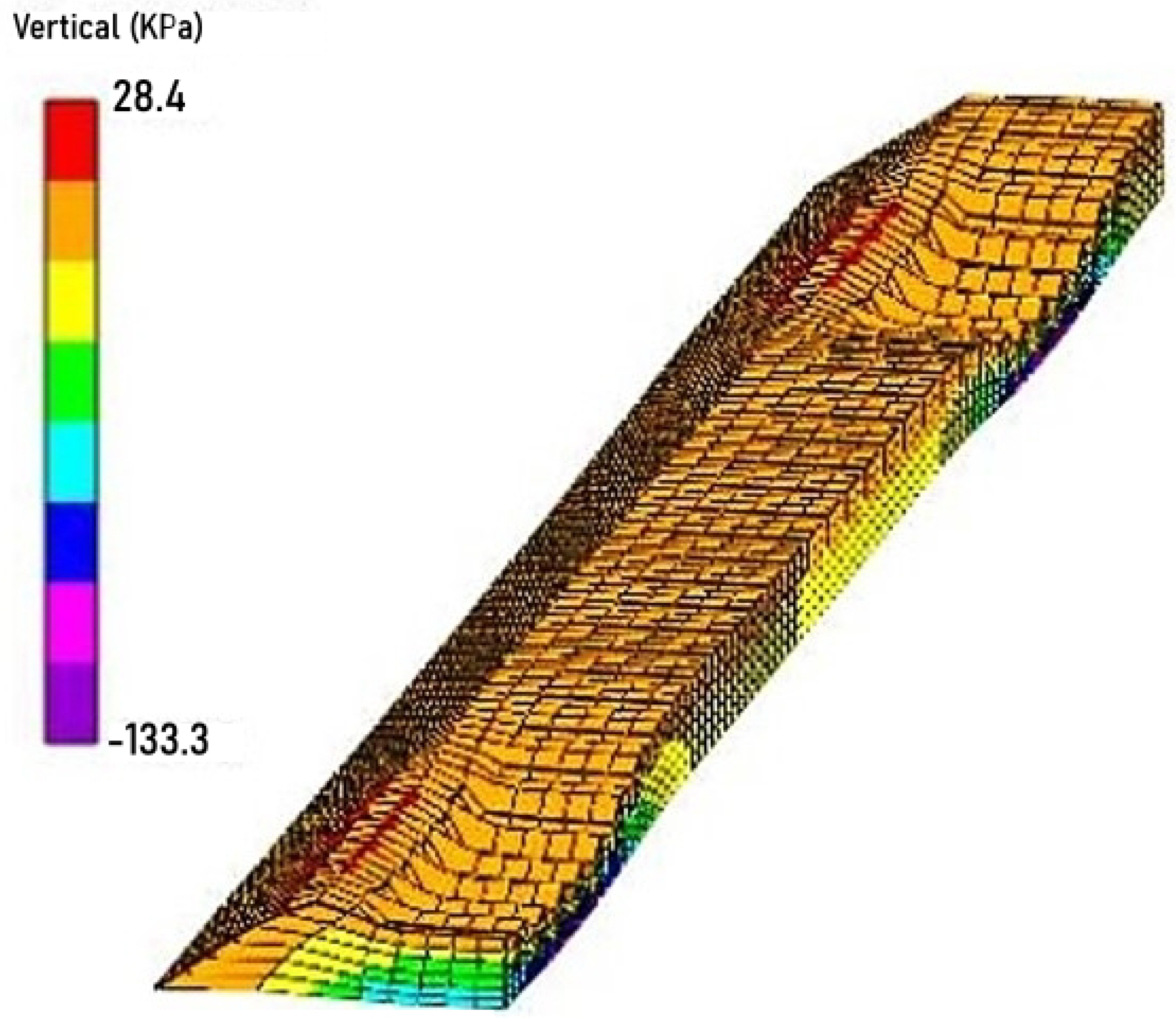
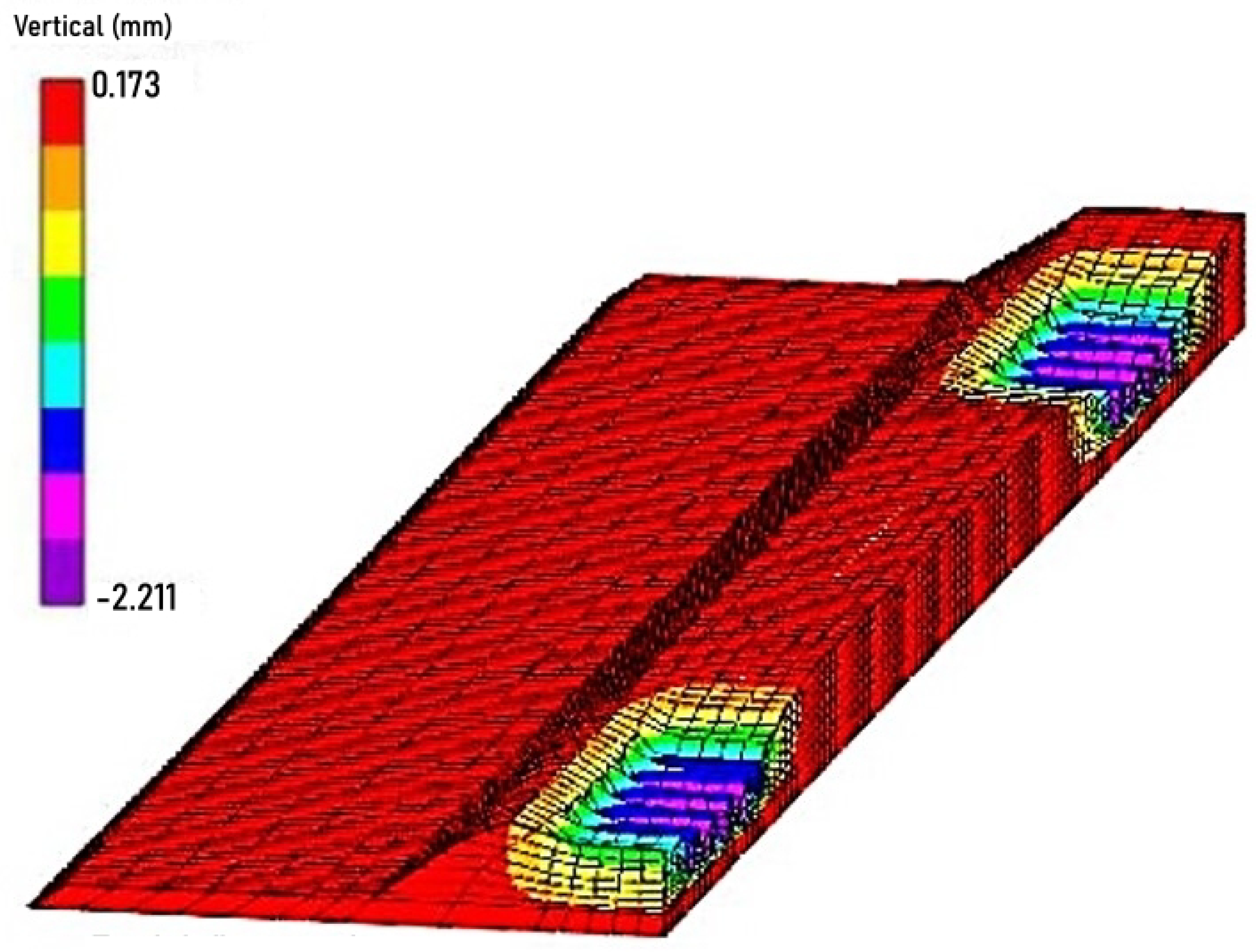
3. Results and Discussions
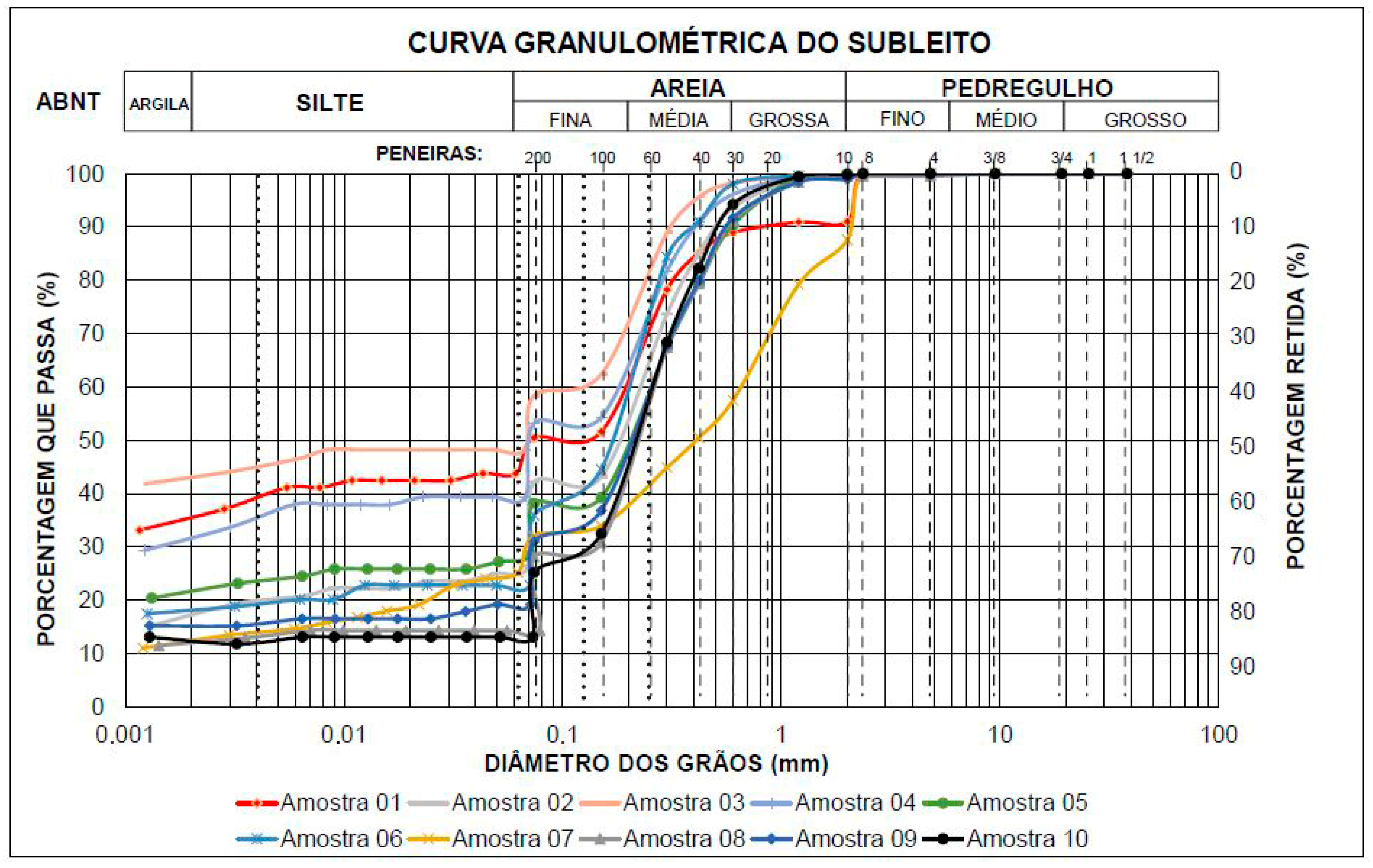
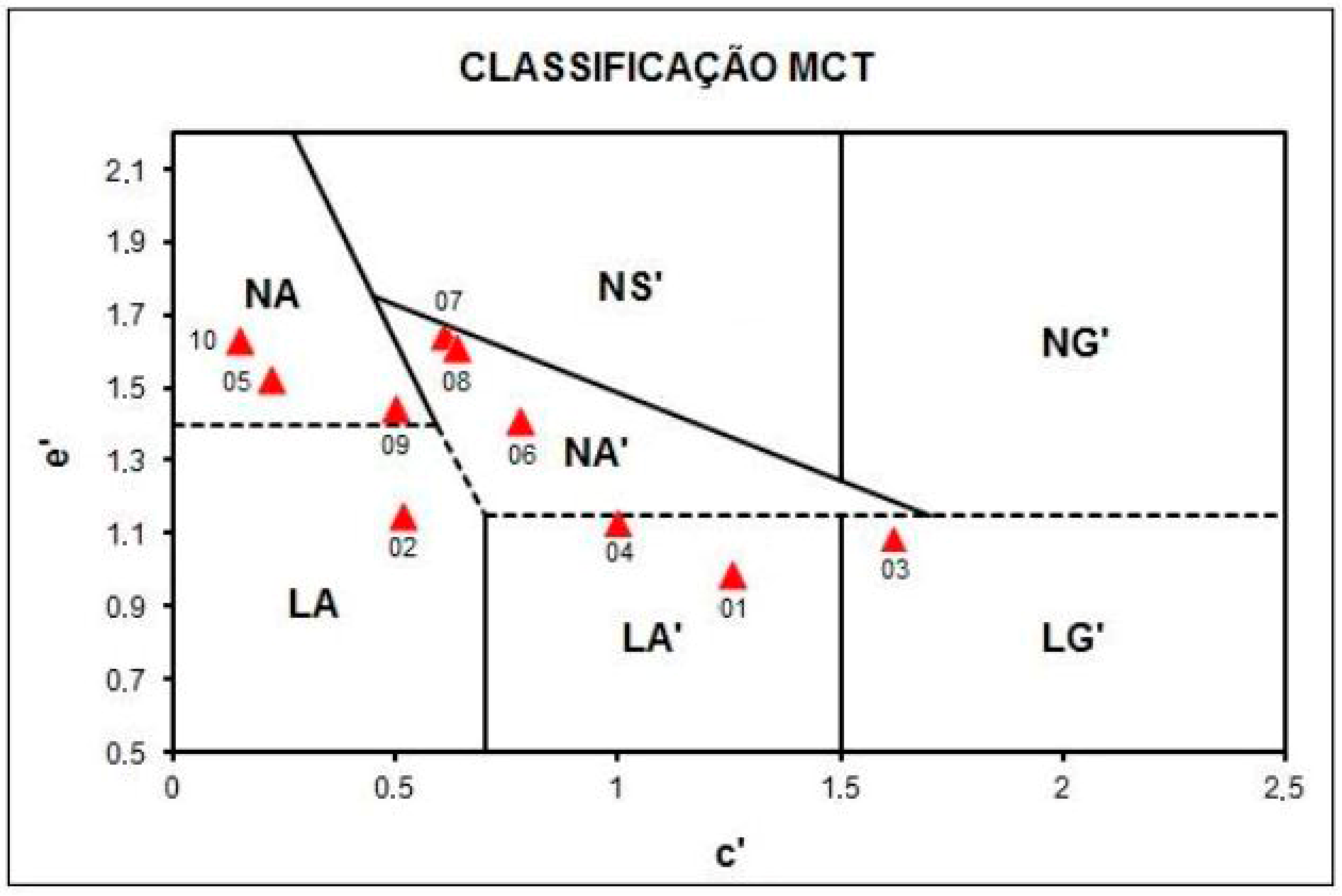
3.1. Analysis of Physical Characterization Tests
- Classes:
- -
- N—Soils with “non-lateritic” behavior
- *
- NA (Sands): Sands, Silty Sands, Silts (l)
- *
- NA’ (Sandy Soils): Silty Sands, Clayey Sands
- *
- NS (Silty Soils): Silts (k, m), Sandy Silts, and Clayey Silts
- *
- NG (Clayey Soils): Clays, Sandy Clays, Silty Clays
- -
- L—Soils with lateritic behavior
- *
- LA (Sands): Sands with low clay content
- *
- LA’ (Sandy Soils): Clayey Sands, Sandy Clays
- *
- LG (Clayey Soils): Clays, Sandy Clays
3.2. Systrain Simulations
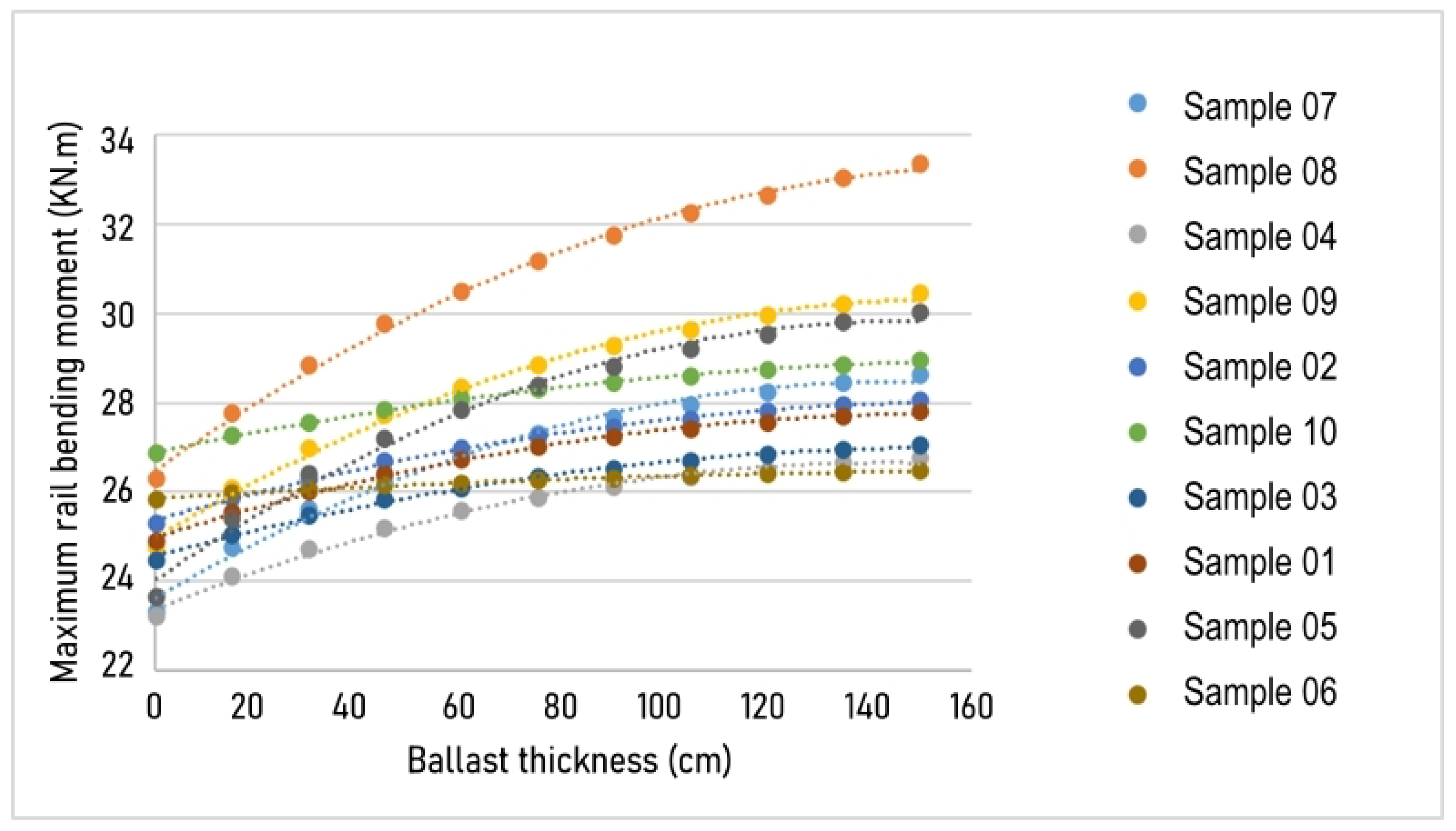
3.3. Influence of Ballast Thickness
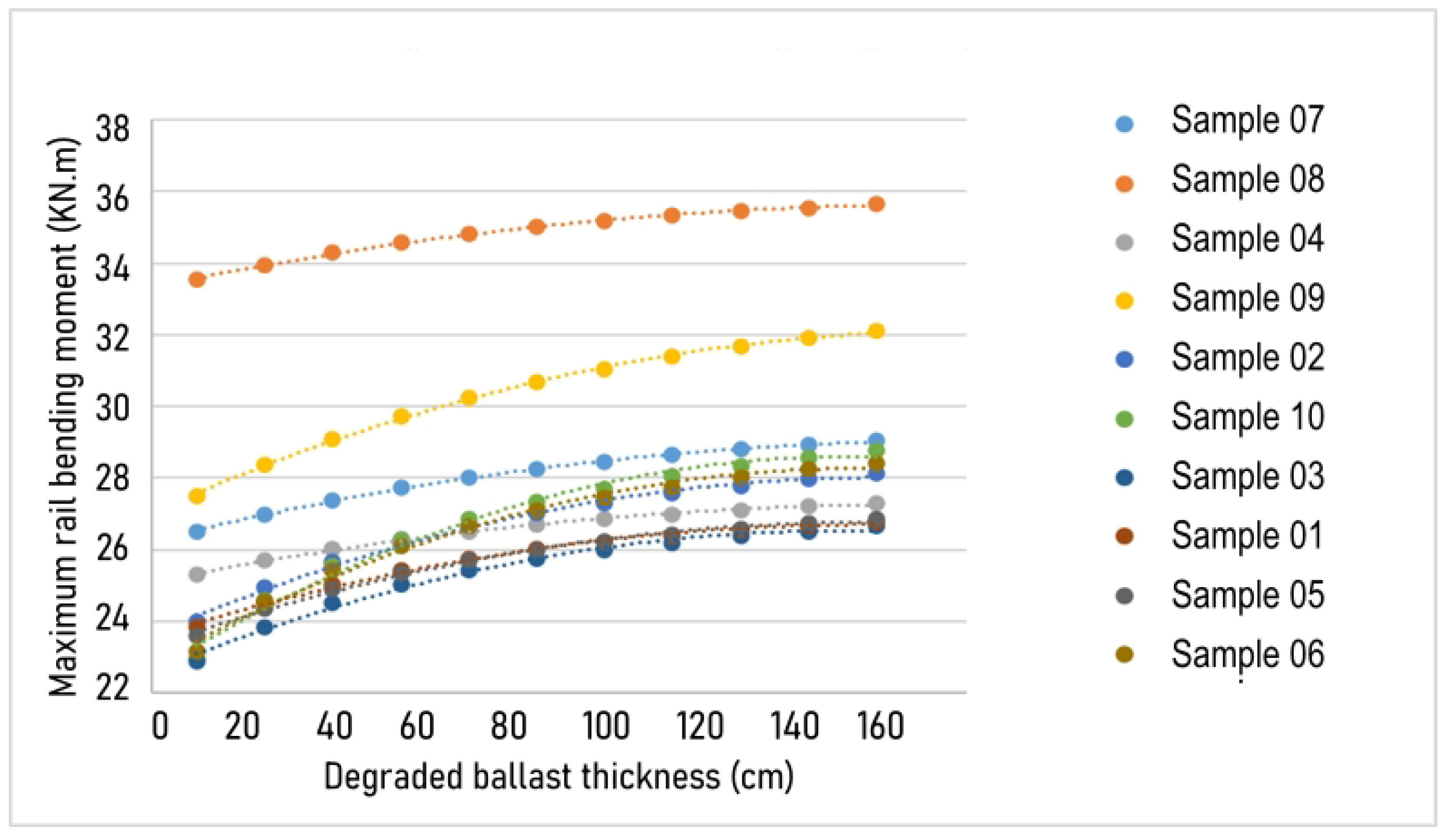
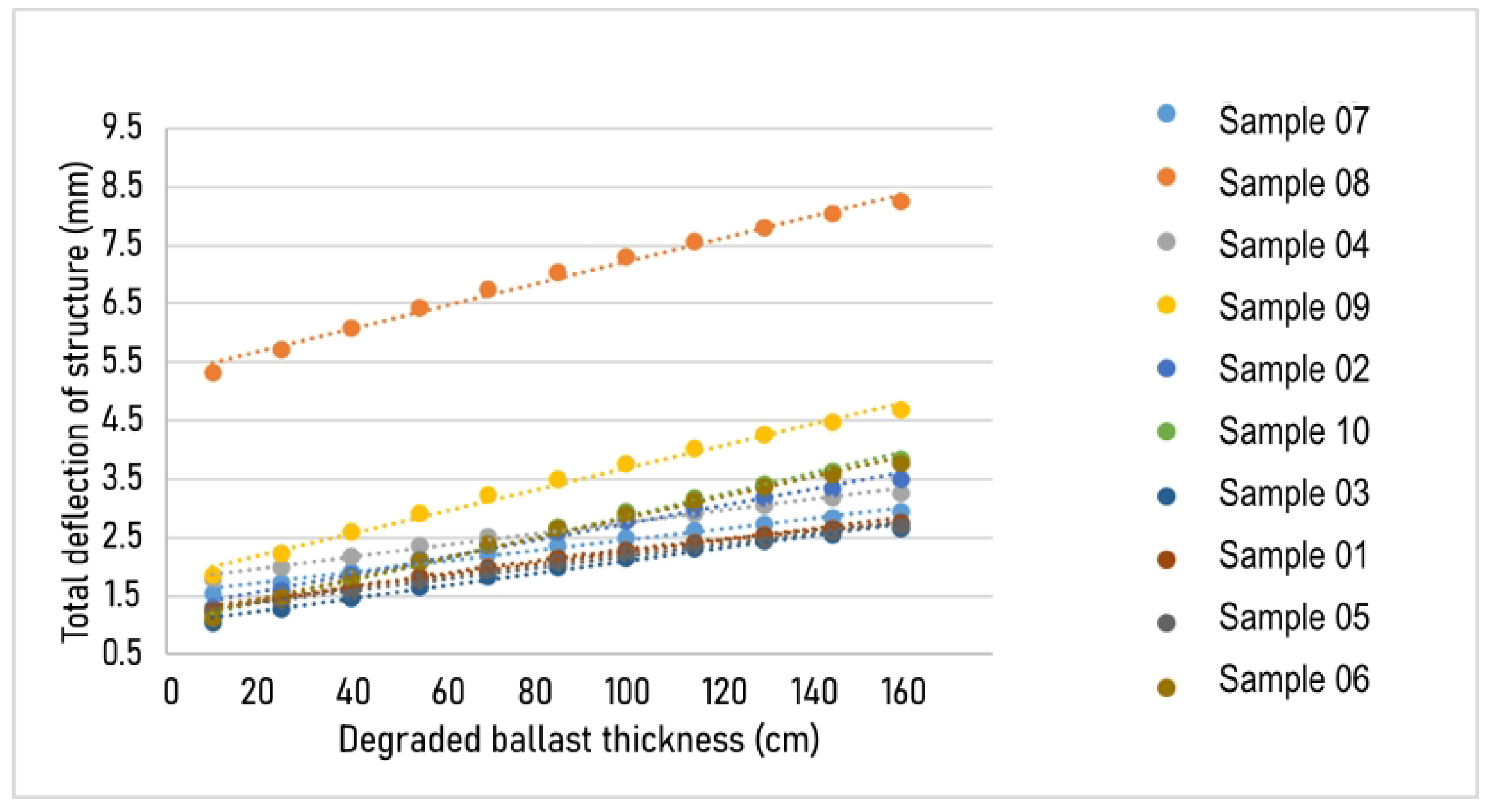
3.4. Degraded Ballast Thickness Variation
3.5. Checking Admissibility
- N = number of cycles of a composition during the design period;
- = number of locomotives;
- = number of axles per locomotive;
- = number of railcars;
- = number of axles per wagon;
- = number of daily journeys of the composition;
- = number of days in a year (365 days);
- = project period in years.
4. Conclusions
- From the results of the 10 simulations of current track conditions, it was found that even in the most critical situations, all samples proved to be admissible in terms of rail bending stress and total vertical stress in the subgrade.
- Sample 08 showed a total deflection above the admissible value (6.85 mm), which can be explained by its high ballast thickness (approximately 160 cm) resulting from indiscriminate tamping over time.
- Although most samples met the design criteria, Sample 08 indicates that the structural conditions of this specific track section may not be technically satisfactory, reinforcing the importance of monitoring ballast thickness and implementing a maintenance plan when necessary.
- The analysis of layer thickness influence generally showed that both the maximum bending moment in the rails and the total deflection of the structure were directly proportional to the ballast and sub-ballast thickness. This behavior can be attributed to the increased stress in the underlying layers due to the higher self-weight of the thicker layers.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, T.W.; Cui, Y.J.; Lamas-Lopez, F.; Calon, N.; D’Aguiar, S.C. Modelling stress distribution in substructure of French conventional railway tracks. Constr. Build. Mater. 2020, 116, 326–334. [Google Scholar] [CrossRef]
- Nielsen, J.C.O.; Li, X. Railway track geometry degradation due to differential settlement of ballast/subgrade—Numerical prediction by an iterative procedure. J. Sound Vib. 2018, 412, 441–456. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, Y.; Li, Z.; Shi, C.; Yu, Z. Three-dimensional vehicle-ballasted track-subgrade interaction: Model construction and numerical analysis. Appl. Math. Model. 2020, 86, 424–445. [Google Scholar] [CrossRef]
- Jing, G.; Wang, J.; Wang, H.; Siahkouhi, M. Numerical investigation of the behavior of stone ballast mixed by steel slag in ballasted railway track. Constr. Build. Mater. 2020, 262, 120015. [Google Scholar] [CrossRef]
- Varandas, J.N.; Paixão, A.; Fortunato, E.; Hölscher, P. A Numerical Study on the Stress Changes in the Ballast Due to Train Passages. Procedia Eng. 2016, 143, 1169–1176. [Google Scholar] [CrossRef]
- Jayasuriya, C.; Indraratna, B.; Ngo, T.N. Experimental study to examine the role of under sleeper pads for improved performance of ballast under cyclic loading. Transp. Geotech. 2019, 19, 61–73. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A.; Erp, G.V.; Aravinthan, T.; Ghabraie, K. Evaluation of an innovative composite railway sleeper for a narrow-gauge track under static load. J. Compos. Constr. 2018, 22, 04017050. [Google Scholar] [CrossRef]
- Gomes, B.; Guimarães, A.C.R.; do Nascimento, F.A.C.; Tanabe, J. Ballast with siderurgic aggregates: Variation analysis of the shape parameters of particles submitted to triaxial tests through 3D scanner. Soils Rocks 2023, 46, 3. [Google Scholar] [CrossRef]
- Andrade, G.; Dieguez, C.A.; Lima, B.T.; Guimarães, A.C.R. Evaluation of limestone aggregates for railway ballast: Particle characteristics and shear strength analysis. Soils Rocks 2024, 47, e2024011223. [Google Scholar] [CrossRef]
- Guimarães, A.C.R.; Filho, J.C.S.; Castro, C.D. Contribution to the use of alternative material in heavy haul railway sub-ballast layer. Transp. Geotech. 2021, 30, 100524. [Google Scholar] [CrossRef]
- Roshan, M.J.; A Rashid, A.S.; Abdul Wahab, N.; Tamassoki, S.; Jusoh, S.N.; Hezmi, M.A.; Nik Daud, N.N.; Mohd Apandi, N.; Azmi, M. Improved methods to prevent railway embankment failure and subgrade degradation: A review. Transp. Geotech. 2022, 37, 100834. [Google Scholar] [CrossRef]
- Scharmm, G. Technique and Economics in Permanent Way; Emma: Porto Alegre, Brazil, 1977. [Google Scholar]
- Rangel, G.W.A. A Method for Estimating Railway Pavement Deflection: Based on Numerical Simulations Using the Finite Element Method (FEM); New Academic Issues: Rio de Janeiro, Brazil, 2018. [Google Scholar]
- Queiroz, R.C. Experimental Study of Stresses and Strains in Railway Infrastructure and Superstructure Layers. Ph.D. Thesis, University of São Paulo, São Carlos, Brazil, 1990. [Google Scholar]
- Filho, J.C.S. Numerical Analysis of the Mechanical Behavior of a Railway Track for Different Types of Rail Vehicles. Master’s Thesis, NUGEO/UFOP, Ouro Preto, Brazil, 2013. [Google Scholar]
- Stopatto, S. Railway Permanent Way: Concepts and Applications; T.A.: São Paulo, Brazil, 1987. [Google Scholar]
- Indraratna, B.; Salim, W.; Rujikiatkamjorn, C. Advanced Rail Geotechnology—Ballasted Track, 1st ed.; CRC Press: London, UK, 2011. [Google Scholar] [CrossRef]
- Ji, R.; Nantung, T.; Siddiki, N.; Liao, T.; Kim, D. Field and laboratory determination of subgrade resilient modulus and its application in pavement design. J. Test. Eval. 2015, 43, 1109–1119. [Google Scholar] [CrossRef]
- Ng, K.; Henrichs, Z.; Ksaibati, K.; Wulff, S. Resilient modulus of subgrade materials for mechanistic-empirical pavement design guide. Road Mater. Pavement Des. 2018, 19, 1523–1545. [Google Scholar] [CrossRef]
- De Lima, C.; Da Motta, L.; Aragao, F.; Guimaraes, A. Mechanical characterization of fine-grained lateritic soils for mechanistic-empirical flexible pavement design. J. Test. Eval. 2019, 48, 1–17. [Google Scholar] [CrossRef]
- Kuttah, D. Determining the resilient modulus of sandy subgrade using cyclic light weight deflectometer test. Transp. Geotech. 2021, 27, 100482. [Google Scholar] [CrossRef]
- Nazzal, M.D.; Mohammad, L.N. Estimation of resilient modulus of subgrade soils using falling weight deflectometer. Transp. Res. Rec. 2010, 2186, 1–10. [Google Scholar] [CrossRef]
- Medina, J.; Motta, L. Mecânica dos Pavimentos, 3rd ed.; Editora Interciência: Rio de Janeiro, Brazil, 2015; p. 572. [Google Scholar]
- Sadrossadat, E.; Heidaripanah, A.; Osouli, S. Prediction of the resilient modulus of flexible pavement subgrade soils using adaptive neuro-fuzzy inference systems. Constr. Build. Mater. 2016, 123, 235–247. [Google Scholar] [CrossRef]
- Mazari, M.; Nazarian, S. Mechanistic approach for construction quality management of compacted geomaterials. Transp. Geotech. 2017, 13, 92–102. [Google Scholar] [CrossRef]
- Kavussi, A.; Qorbaninik, M.; Hassani, A. The influence of moisture content and compaction level on LWD modulus of unbound granular base layers. Transp. Geotech. 2019, 20, 100252. [Google Scholar] [CrossRef]
- Allah, S.; Tanyu, B.F.; Dawson, A. Reclaimed Asphalt Pavement (RAP) as an Unbound Base Course Material: A Mechanistic Design Approach Based on Multi-stage Repeated Load Triaxial Tests. Transp. Geotech. 2022, 33, 100729. [Google Scholar] [CrossRef]
- Almeida, B.D.; Coelho, L.M.; Guimarães, A.C.R.; Monteiro, S.N. Effect of Sand Addition on Laterite Soil Stabilization. Materials 2024, 17, 6033. [Google Scholar] [CrossRef] [PubMed]
- Spada, J.L.G. A Pavement Mechanics Approach Applied to Understanding the Stress-Strain Behavior Mechanism of the Railway Track. Ph.D. Thesis, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil, 2003. [Google Scholar]
- Prakoso, P.B. The basic concepts of modelling railway track systems using conventional and finite element methods. Info-Teknik 2012, 13, 57–65. [Google Scholar]
- El-kady, M.S.; Azam, A.; Yosri, A.M.; Nabil, M. Modelling of railway embankment stabilized with geotextile, geo-foam, and waste aggregates. Case Stud. Constr. Mater. 2023, 18, e01800. [Google Scholar] [CrossRef]
- Filho, J.C.S.; Guimarães, A.C.; Nascimento, G.D.C. A Comparative Study Using Traditional Method and Computational Platform for Stress Propagation Analysis in Railway Pavement. In Proceedings of the 45th Annual Pavement Meeting-RAPv, Brasília, DF, Brazil, 20 September 2016. [Google Scholar]
- Ribeiro, F.S. Contribution to the Analysis of the Life Cycle Cost of a Railway Pavement Management System. Ph.D. Thesis, Polytechnic School, University of São Paulo, São Paulo, Brazil, 2017. [Google Scholar]
- Ribeiro, F.; Nascimento, F.; Silva, M. Environmental performance analysis of railway infrastructure using life cycle assessment: Selecting pavement projects based on global warming potential impacts. J. Clean. Prod. 2022, 365, 132558. [Google Scholar] [CrossRef]
- Filho, J.C.S. Contribution to the Development of a Mechanistic-Empirical Design Method for Railway Pavements with a Focus on Tropical Soils. Ph.D. Thesis, Military Institute of Engineering, Rio de Janeiro, Brazil, 2018. [Google Scholar]
- Cruz, L.O.S.R. Procedure for Evaluation of the Structural Integrity of the Railway Platform. Master’s Thesis, Military Institute of Engineering, Rio de Janeiro, Brazil, 2019. [Google Scholar]
- Delgado, B.; Fonseca, A.; Fortunato, E.; Paixão, A.; Alves, R. Geomechanical assessment of an inert steel slag aggregate as an alternative ballast material for heavy haul rail tracks. Constr. Build. Mater. 2021, 279, 122438. [Google Scholar] [CrossRef]
- dos Santos, W.W.; Coelho, L.M.; Monteiro, S.N.; Marques, M.E.S.; Guimarães, A.C.R. Evaluation of Steel Slag as a Sustainable Alternative Aggregate for Railway Ballast: A Shakedown Theory-Based Approach. Buildings 2024, 14, 3546. [Google Scholar] [CrossRef]
- Fonte, M.S.; Donato, M.; Gouveia, B.G.; Santana, C.S.A.; Silva, M.A.V.d. Analysis of the influence of tropical soil classification methods on railway subgrades according to repeated load triaxial (RLT) and light weight deflectometer (LWD) tests. Case Stud. Constr. Mater. 2022, 17, e01301. [Google Scholar] [CrossRef]
- Silva Filho, J.; Skwarok, A.; Witiuk, R. Study of the track dynamics for optimizing the railway superstructure. In Advances in Transportation Geotechnics IV; Lecture Notes in Civil Engineering; Tutumluer, E., Nazarian, S., Al-Qadi, I., Qamhia, I., Eds.; Springer: Cham, Switzerland, 2022; Volume 165. [Google Scholar] [CrossRef]
- ABNT—Brazilian Association of Technical Standards. NBR 6459: Solo—Determinação do Limite de Liquidez; ABNT: Rio de Janeiro, Brazil, 2016. [Google Scholar]
- ABNT—Brazilian Association of Technical Standards. NBR 7180: Soil—Determination of Plasticity Limit; ABNT: Rio de Janeiro, Brazil, 1984. [Google Scholar]
- ABNT—Brazilian Association of Technical Standards. NBR 7181: Soil—Granulometric Analysis; ABNT: Rio de Janeiro, Brazil, 1984. [Google Scholar]
- DNIT—National Department of Transport Infrastructure. DNIT 259—CLA: Soil—Classification of Fine Tropical Soils for Road Purposes Using Compact Samples in Miniature Equipment—Classification; National Department of Transport Infrastructure (DNIT): Brasilia, Brazil, 2023. [Google Scholar]
- DNIT—National Department of Transport Infrastructure. DNIT-134-ME. Pavement—Soils—Determination of Resilient Modulus—Test Method; National Department of Transport Infrastructure: Brasília, Brazil, 2018. [Google Scholar]
- ABNT—Brazilian Association of Technical Standards. NBR 17091: Soils—Dynamic Cone Penetration Test; ABNT: Rio de Janeiro, Brazil, 2023. [Google Scholar]
- ASTM E2583: Standard Test Method for Measuring Deflections with a Light Weight Deflectometer (LWD); ASTM: West Conshohocken, PA, USA, 2015.
- Pezo, R.F. A General Method of Reporting Resilient Modulus Tests of Soils: A Pavement Engineer’s Point of View. In Proceedings of the 72nd Annual Meeting of the Transportation Research Board (TRB), Washington, DC, USA, 12–14 January 1993. No. 93082. [Google Scholar]
- Macêdo, J.A.G. Interpretation of Geotechnical Tests for Structural Evaluation of Flexible Pavements. Ph.D. Thesis, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil, 1996; 456p. [Google Scholar]
- Nogami, J.S.; Villibor, D.F. Low-Cost Paving with Lateritic Soils; Editora Villibor: São Paulo, Brazil, 1995. [Google Scholar]
- de Paiva, C.E.; Buck, A.P.; Ferreira, A. Sub-ballast performance in Brazilian railway infrastructures. Constr. Build. Mater. 2018, 190, 164–169. [Google Scholar] [CrossRef]
- São Paulo Metropolitan Railway Company. Material Specification for Sub-Ballast Supply for Permanent Way; Technical Report; São Paulo Metropolitan Railway Company: São Paulo, Brazil, 1979. [Google Scholar]
- Real, J.; Gómez, L.; Montalbán, L.; Real, T. Study of the influence of geometrical and mechanical parameters on ballasted railway tracks design. J. Mech. Sci. Technol. 2012, 26, 2837–2844. [Google Scholar] [CrossRef]
- Gomes, M.B.B.; Santos, J.T.A.d.; Almeida, B.D.; Serra, G.A.; Guimarães, A.C.R. Parametric Analysis of Ballast Thickness for Elastoplastic Deformations in Railway Pavement. In Proceedings of the 25th National Road Conservation Meeting (ENACOR) and 48th Annual Pavement Meeting (RAPv), Foz do Iguaçu, Brazil, 19 September 2023; Available online: https://enacorrapv.com.br/anais/2023/TT917.pdf (accessed on 3 March 2025).
- Zhuang, Y.; Wang, K. Three-dimensional shakedown analysis of ballasted railway structures under moving surface loads with different load distributions. Soil Dyn. Earthq. Eng. 2017, 100, 296–300. [Google Scholar] [CrossRef]
- AREMA—American Railway Engineering and Maintenance-of-Way Association. Manual for Railway Engineering; AREMA: Lanham, MD, USA, 2020. [Google Scholar]
- Hay, W.W. Railroad Engineering, 1st ed.; John Wiley and Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Werkmeister, S.; Dawson, A.R.; Wellner, F. Permanent Deformation Behavior of Granular Materials and the Shakedown Concept. Transp. Res. Rec. 2001, 1757, 75–81. [Google Scholar] [CrossRef]
- Brina, H.L. Railways, 1st ed.; Technical and Scientific Books: Rio de Janeiro, Brazil, 1988; Volume 2. [Google Scholar]
- Heukelom, W.; Klomp, A. Dynamic Testing as a Means of Controlling Pavement during and after Construction. In Proceedings of the 1st International Conference on the Structural Design of Asphalt Pavement, Ann Arbor, MI, USA, 20–24 August 1962; pp. 667–685. [Google Scholar]

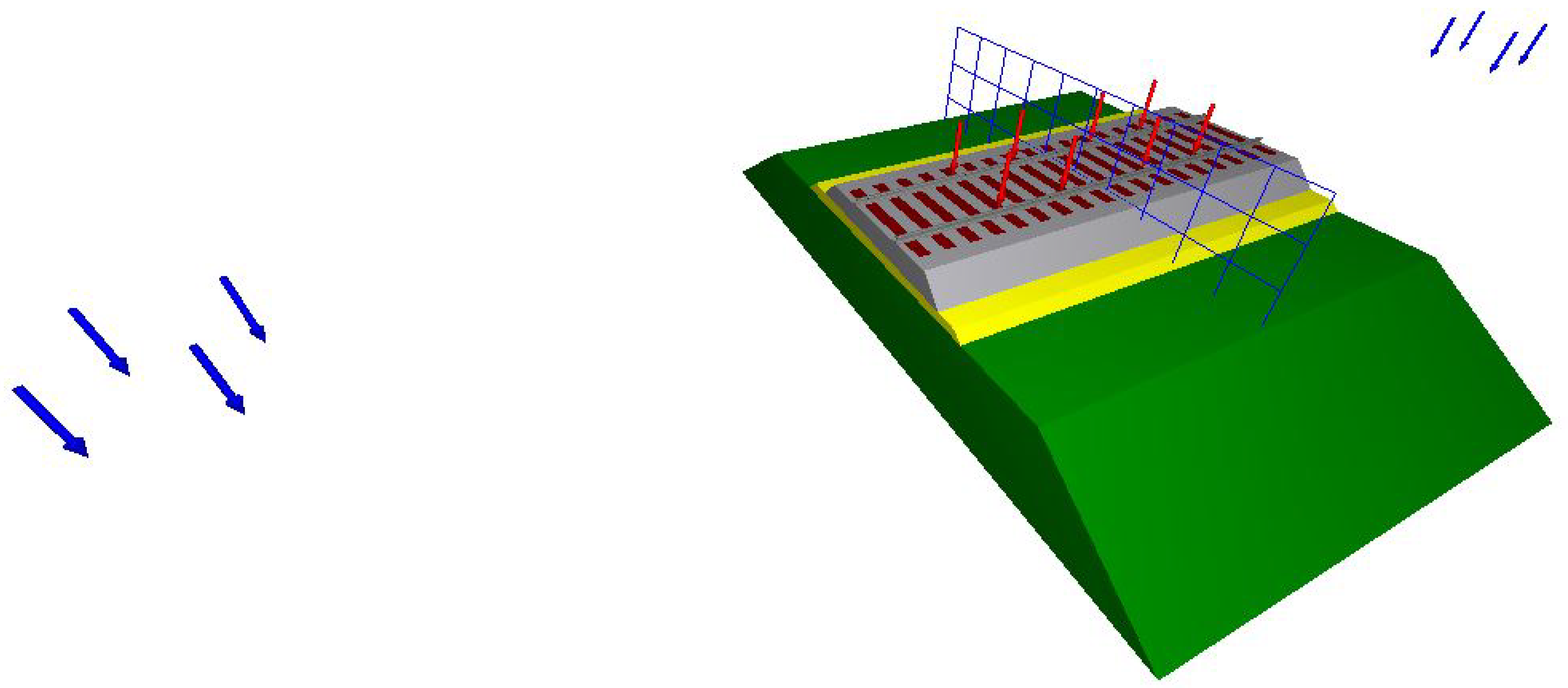

| INPUT DATA | SAMPLE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 07 | 08 | 04 | 09 | 02 | 10 | 03 | 01 | 05 | 06 | |
| GEOMETRY | ||||||||||
| Rail | ||||||||||
| Gauge of 1.00 m/Samples 07, 08, 09: Section TR-68; Others: TR-57 | ||||||||||
| Sleeper | ||||||||||
| Spacing (cm) | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 | 60 |
| Length (m) | 1.75 | 1.75 | 2.00 | 1.75 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 | 2.00 |
| Height (cm) | 19 | 19 | 16 | 19 | 16 | 16 | 16 | 16 | 16 | 16 |
| Lower Width (cm) | 20 | 20 | 22 | 20 | 22 | 22 | 22 | 22 | 22 | 22 |
| Upper Width (cm) | 16 | 16 | 22 | 16 | 22 | 22 | 22 | 22 | 22 | 22 |
| Ballast | ||||||||||
| Height (cm) | 50 | 160 | 60 | 40 | 15 | 0.1 | 10 | 15 | 5 | 10 |
| For all samples: Shoulder of 40 cm; Slope (H/V): 1.5; Bottom slope: 3%; Covering: Yes. | ||||||||||
| Degraded Ballast | ||||||||||
| Height (cm) | 10 | 10 | 20 | 10 | 45 | 70 | 50 | 60 | 25 | 50 |
| For all samples: Shoulder of 50 cm; Slope (H/V): 1.2; Bottom slope: 1% | ||||||||||
| Subgrade | ||||||||||
| For all samples: Height of 20 cm; shoulder: 2 m, slope (H/V): 1.5, bottom: 1%. | ||||||||||
| INPUT DATA | SAMPLE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 07 | 08 | 04 | 09 | 02 | 10 | 03 | 01 | 05 | 06 | |
| Rail | ||||||||||
| For all samples: name: steel; type: linear isotropic; : 7850 kg/m3; E: 210 GPa; : 0.3. | ||||||||||
| Sleeper | ||||||||||
| Name | Concrete | Concrete | Wood | Concrete | Wood | Wood | Wood | Wood | Wood | Wood |
| Type | Linear Isotropic | |||||||||
| (kg/m3) | 2400 | 2400 | 1040 | 2400 | 1040 | 1040 | 1040 | 1040 | 1040 | 1040 |
| E (GPa) | 32 | 32 | 16.583 | 32 | 16.583 | 16.583 | 16.583 | 16.583 | 16.583 | 16.583 |
| 0.3 | 0.3 | 0.23 | 0.3 | 0.23 | 0.23 | 0.23 | 0.23 | 0.23 | 0.23 | |
| INPUT DATA | SAMPLE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 07 | 08 | 04 | 09 | 02 | 10 | 03 | 01 | 05 | 06 | |
| Ballast | ||||||||||
| Type | Linear Elastic Resilient | |||||||||
| (kg/m3) | 2000 | |||||||||
| E (MPa) | 37 | 16.2 | 38.6 | 26.2 | 29.6 | 25.7 | 37.2 | 31.3 | 18.15 | 46.23 |
| 0.3 | ||||||||||
| 37 | 16.2 | 38.6 | 26.2 | 29.6 | 25.7 | 37.2 | 31.3 | 18.15 | 46.23 | |
| Degraded Ballast | ||||||||||
| Type | Linear Elastic Resilient | |||||||||
| (kg/m3) | 1900 | |||||||||
| E (MPa) | 37.6 | 9.8 | 33.3 | 18.4 | 26.9 | 22.7 | 39.2 | 42.4 | 44.06 | 22.43 |
| 0.3 | ||||||||||
| 37.6 | 9.8 | 33.3 | 18.4 | 26.9 | 22.7 | 39.2 | 42.4 | 44.06 | 22.43 | |
| Subgrade | ||||||||||
| Type | Composite Resilient | |||||||||
| (kg/m3)] | 1900 | |||||||||
| 0.3 | ||||||||||
| e min (MPa)] | 0.0207 | |||||||||
| max (MPa)] | 0.412 | |||||||||
| max (MPa)] | 0.137 | |||||||||
| 490.07 | 132.07 | 922.16 | 426.87 | 970.67 | 399.86 | 740.58 | 1045.81 | 468.25 | 833.64 | |
| 0.28 | 0.32 | 0.48 | 0.36 | 0.36 | 0.24 | 0.12 | 0.56 | 0.52 | 0.12 | |
| −0.36 | −0.68 | −0.36 | 0.36 | −0.36 | −0.36 | −0.28 | −0.2 | −0.48 | −0.32 | |
| Amostra | (g/cm3) | (g/cm3) | Wn (%) | Wo (%) | LL (%) | LP (%) | IP (%) | Class. TRB | Class. SUCS | Class. MCT |
|---|---|---|---|---|---|---|---|---|---|---|
| 01 | 2.708 | - | - | 8.50 | - | - | NP | A-4 | ML | LA’ |
| 02 | 2.628 | - | 8.10 | 6.25 | - | - | NP | A-4 | SM | LA |
| 03 | 2.626 | 1.328 | 10.50 | 10.8 | 21.8 | 14.4 | 7.4 | A-4 | CL | LG’ |
| 04 | 2.681 | - | 12.30 | 7.50 | - | - | NP | A-4 | ML | LA’ |
| 05 | 2.625 | 1.875 | 7.50 | 4.75 | - | - | NP | A-4 | SM | NA |
| 06 | 2.633 | 1.780 | 5.80 | 3.92 | - | - | NP | A-4 | SM | NA’ |
| 07 | 2.946 | - | 4.70 | 11.0 | - | - | NP | A-2-4 | SM | NA’ |
| 08 | 2.420 | 1.973 | 5.80 | 3.74 | - | - | NP | A-2-4 | SM | NA’ |
| 09 | 2.653 | 1.926 | 6.90 | 3.88 | - | - | NP | A-2-4 | SM | NA |
| 10 | 2.745 | 1.794 | 6.97 | 3.00 | - | - | NP | A-2-4 | SM | NA |
| Ballast Thickness (cm) | Sample 07 | Sample 08 | Sample 04 | Sample 09 | Sample 02 | Sample 10 | Sample 03 | Sample 01 | Sample 05 | Sample 06 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 158.1 | 144.2 | 135.2 | 149.3 | 112.8 | 112.7 | 121.1 | 124.8 | 160.3 | 100.6 |
| 15 | 117.8 | 109.1 | 115.3 | 111.9 | 102.2 | 94.6 | 107.2 | 105.6 | 110.9 | 99.3 |
| 30 | 109.0 | 106 | 107.5 | 108.3 | 97.9 | 91.3 | 99.1 | 100.4 | 98.4 | 98.1 |
| 45 | 113.9 | 111.9 | 105.2 | 114.1 | 93.4 | 90.4 | 101.0 | 98.4 | 96.8 | 98 |
| 60 | 113.7 | 111.8 | 102 | 114.1 | 93.0 | 88.4 | 98.5 | 96.5 | 92.9 | 96.5 |
| 75 | 118 | 115.9 | 100.6 | 118.5 | 93.0 | 93.0 | 100.5 | 97.5 | 90.5 | 95.6 |
| 90 | 118.3 | 118.7 | 98.4 | 121.3 | 91.4 | 92.2 | 100.1 | 97.9 | 93.1 | 95.2 |
| 105 | 121.4 | 118.7 | 97.3 | 121.6 | 94.1 | 95.2 | 99.2 | 98.5 | 96.2 | 94.7 |
| 120 | 121.4 | 118.4 | 97.3 | 121.6 | 94.1 | 95.2 | 99.2 | 99.2 | 96.2 | 94.7 |
| 135 | 123.6 | 120.4 | 100.3 | 123.5 | 97.0 | 95.0 | 101.1 | 99.9 | 99.2 | 97.1 |
| 150 | 123.3 | 119.9 | 103.5 | 123 | 100.5 | 98.8 | 101.1 | 102.8 | 103.4 | 98.2 |
| Sample | Total Displacement (mm) | Permissible Displacement (AREMA) | |
|---|---|---|---|
| (mm) | Verification | ||
| 01 | 2.14 | 6.35 | OK |
| 02 | 2.22 | 6.35 | OK |
| 03 | 1.76 | 6.35 | OK |
| 04 | 2.18 | 6.35 | OK |
| 05 | 1.52 | 6.35 | OK |
| 06 | 2.29 | 6.35 | OK |
| 07 | 1.80 | 6.35 | OK |
| 08 | 6.85 | 6.35 | NOK |
| 09 | 2.21 | 6.35 | OK |
| 10 | 2.82 | 6.35 | OK |
| Sample | Wb (cm3) | Mmáx (kN·m) | Mmáx (kgf·cm) | (kgf/cm2) | Criteria of Brina [59] | ||
|---|---|---|---|---|---|---|---|
| (kPa) | (kgf/cm2) | Verification | |||||
| 01 | 294.80 | 22.88 | 233,311.07 | 791.42 | 150,000 | 1529.57 | OK |
| 02 | 294.80 | 23.17 | 236,268.25 | 801.45 | 150,000 | 1529.57 | OK |
| 03 | 294.80 | 22.10 | 225,357.28 | 764.44 | 150,000 | 1529.57 | OK |
| 04 | 294.80 | 22.94 | 233,922.90 | 793.50 | 150,000 | 1529.57 | OK |
| 05 | 294.80 | 21.57 | 219,952.79 | 746.11 | 150,000 | 1529.57 | OK |
| 06 | 294.80 | 23.26 | 237,185.99 | 804.57 | 150,000 | 1529.57 | OK |
| 07 | 391.60 | 23.91 | 243,814.15 | 622.61 | 150,000 | 1529.57 | OK |
| 08 | 391.60 | 32.99 | 336,404.38 | 859.05 | 150,000 | 1529.57 | OK |
| 09 | 391.60 | 25.04 | 255,336.94 | 652.04 | 150,000 | 1529.57 | OK |
| 10 | 294.80 | 24.33 | 248,096.95 | 841.58 | 150,000 | 1529.57 | OK |
| Sample | Permissible Tension (kPa) | Vertical Tension (kPa) | Verification |
|---|---|---|---|
| 01 | 221.27 | 116.80 | OK |
| 02 | 727.43 | 140.90 | OK |
| 03 | 995.46 | 109.60 | OK |
| 04 | 537.54 | 151.90 | OK |
| 05 | 115.85 | 112.00 | OK |
| 06 | 756.92 | 106.90 | OK |
| 07 | 462.15 | 112.30 | OK |
| 08 | 543.60 | 143.60 | OK |
| 09 | 242.95 | 108.90 | OK |
| 10 | 471.72 | 107.00 | OK |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teixeira, M.A.d.O.; Santos, W.W.d.; Coelho, L.M.; Santana, L.H.d.S.; Ávila, F.G.d.; Monteiro, S.N.; Guimarães, A.C.R. Influence of Ballast and Sub-Ballast Thickness on Structural Behavior of Heavy-Haul Railway Platform Determined by Using Finite Element Modeling. Constr. Mater. 2025, 5, 13. https://doi.org/10.3390/constrmater5010013
Teixeira MAdO, Santos WWd, Coelho LM, Santana LHdS, Ávila FGd, Monteiro SN, Guimarães ACR. Influence of Ballast and Sub-Ballast Thickness on Structural Behavior of Heavy-Haul Railway Platform Determined by Using Finite Element Modeling. Construction Materials. 2025; 5(1):13. https://doi.org/10.3390/constrmater5010013
Chicago/Turabian StyleTeixeira, Magdiel Acaz de Oliveira, William Wilson dos Santos, Lisley Madeira Coelho, Lidiane Hellen dos Santos Santana, Fábio Grisolia de Ávila, Sergio Neves Monteiro, and Antônio Carlos Rodrigues Guimarães. 2025. "Influence of Ballast and Sub-Ballast Thickness on Structural Behavior of Heavy-Haul Railway Platform Determined by Using Finite Element Modeling" Construction Materials 5, no. 1: 13. https://doi.org/10.3390/constrmater5010013
APA StyleTeixeira, M. A. d. O., Santos, W. W. d., Coelho, L. M., Santana, L. H. d. S., Ávila, F. G. d., Monteiro, S. N., & Guimarães, A. C. R. (2025). Influence of Ballast and Sub-Ballast Thickness on Structural Behavior of Heavy-Haul Railway Platform Determined by Using Finite Element Modeling. Construction Materials, 5(1), 13. https://doi.org/10.3390/constrmater5010013






