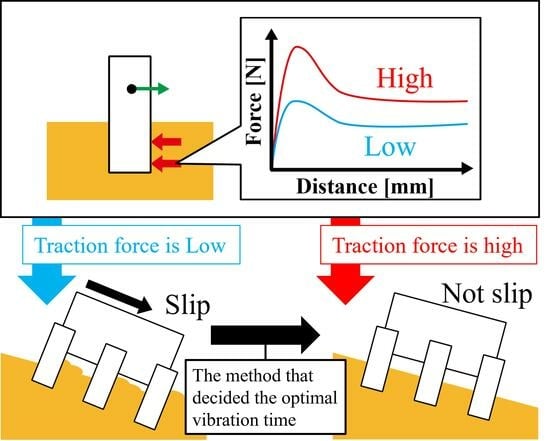
Experimental Investigation of the Relationship Between Vibration Acceleration and Bearing Capacity for Space Exploration Legged Rovers
Abstract
1. Introduction
1.1. Importance of Extraterrestrial Body Exploration
1.2. Locomotion Methods of Rovers for Extraterrestrial Body Exploration
1.3. Introduction to Our Previous Research
1.4. Research Overview
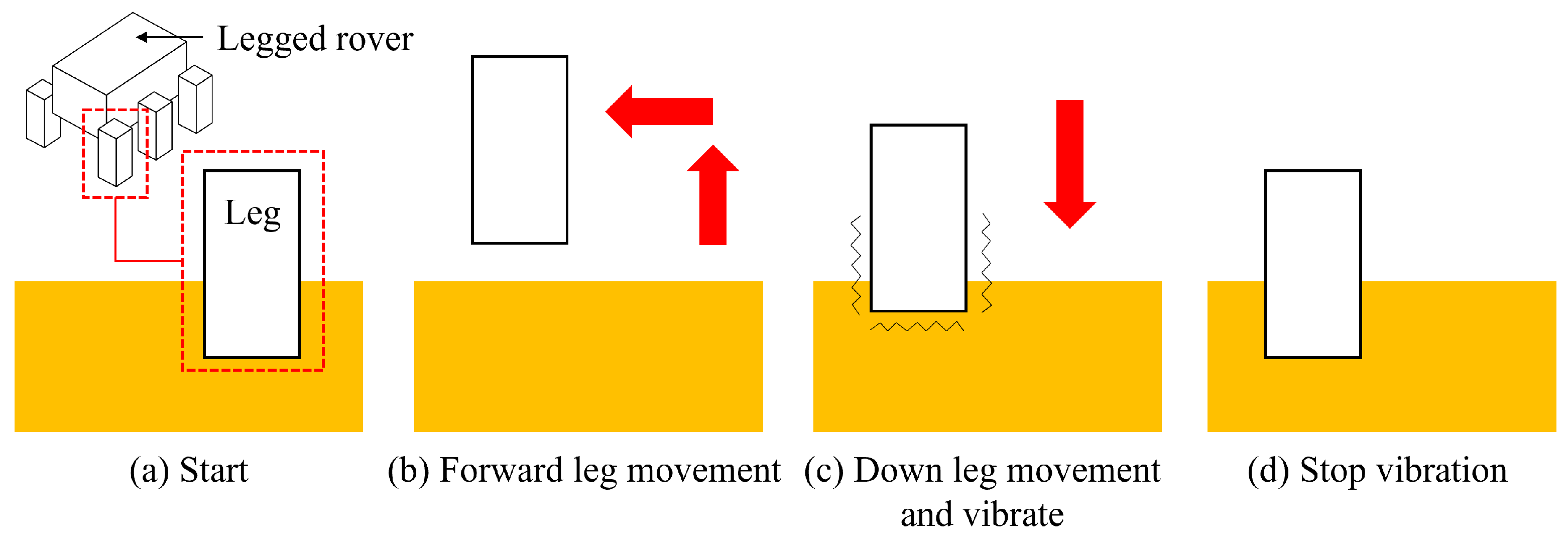
2. Methods
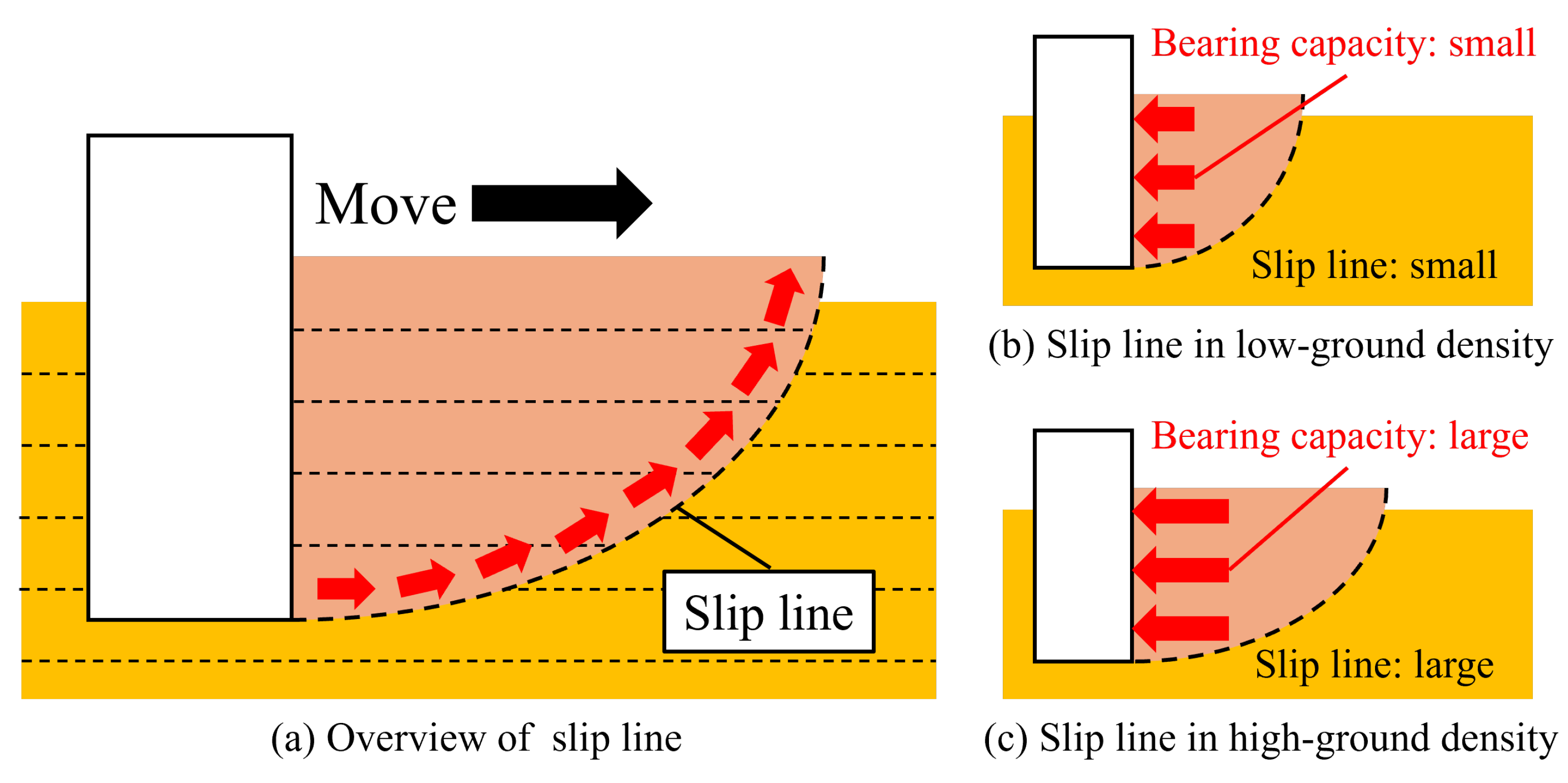
2.1. Introduction to the Related Research
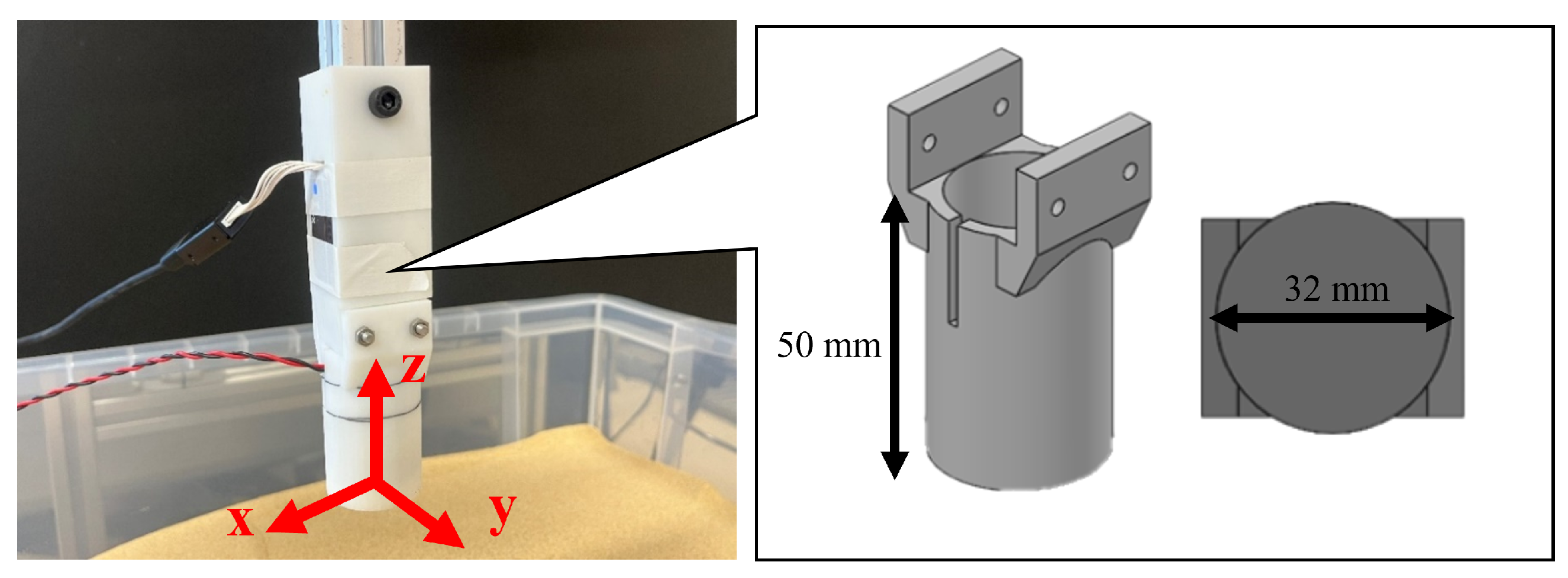
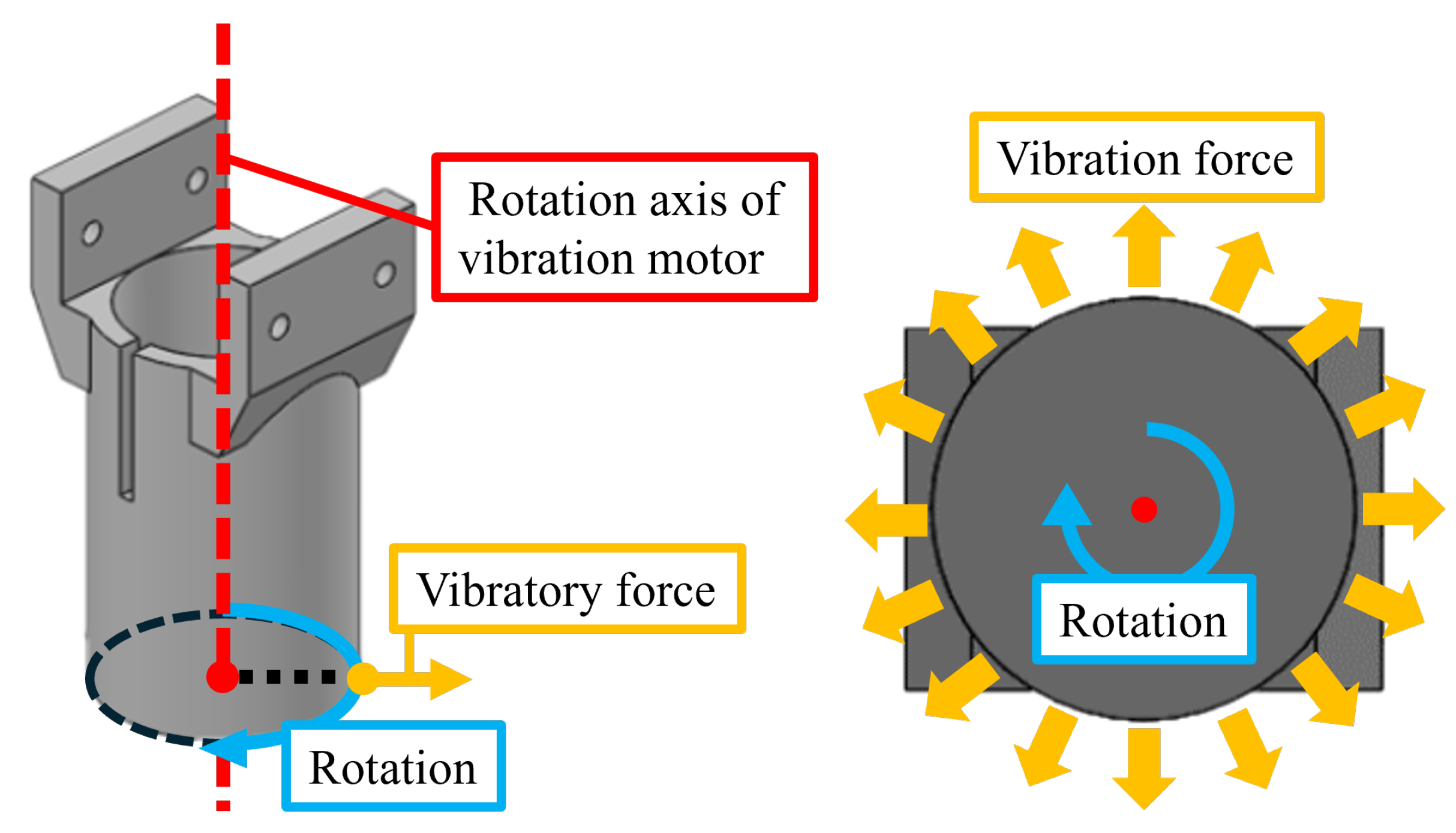
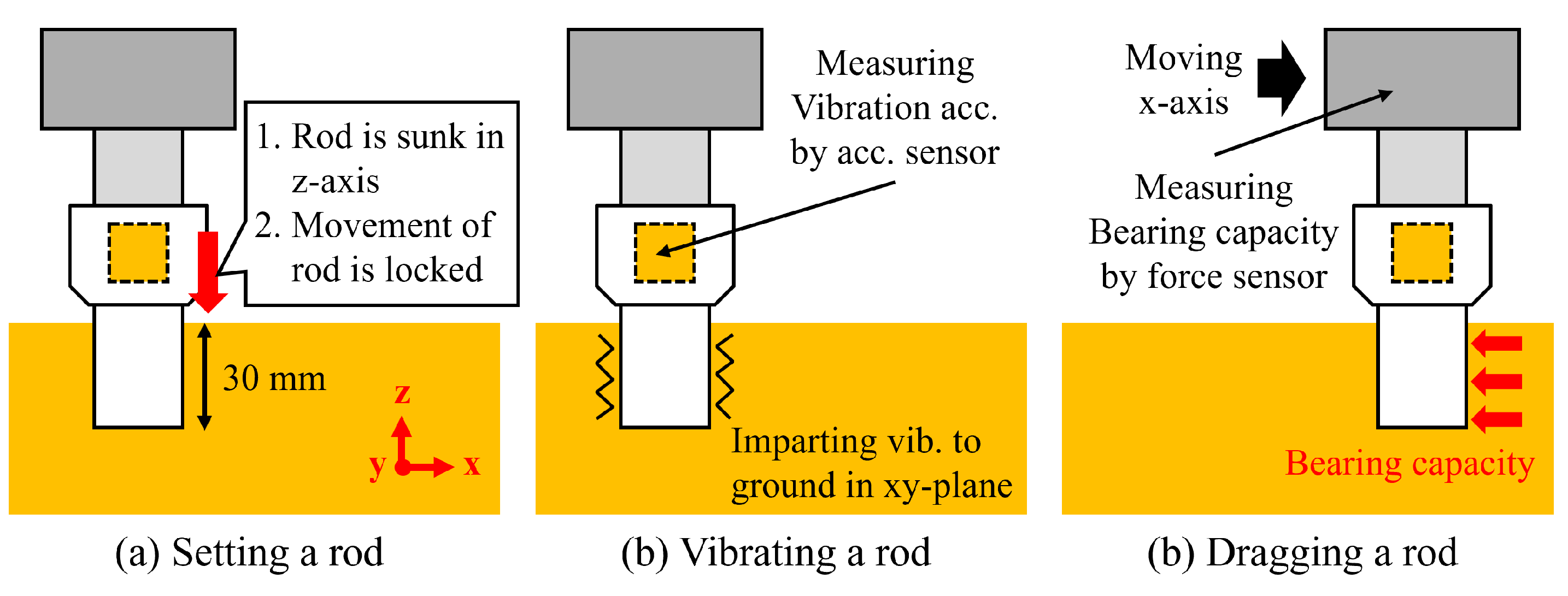
2.2. Experiments
3. Results and Discussion
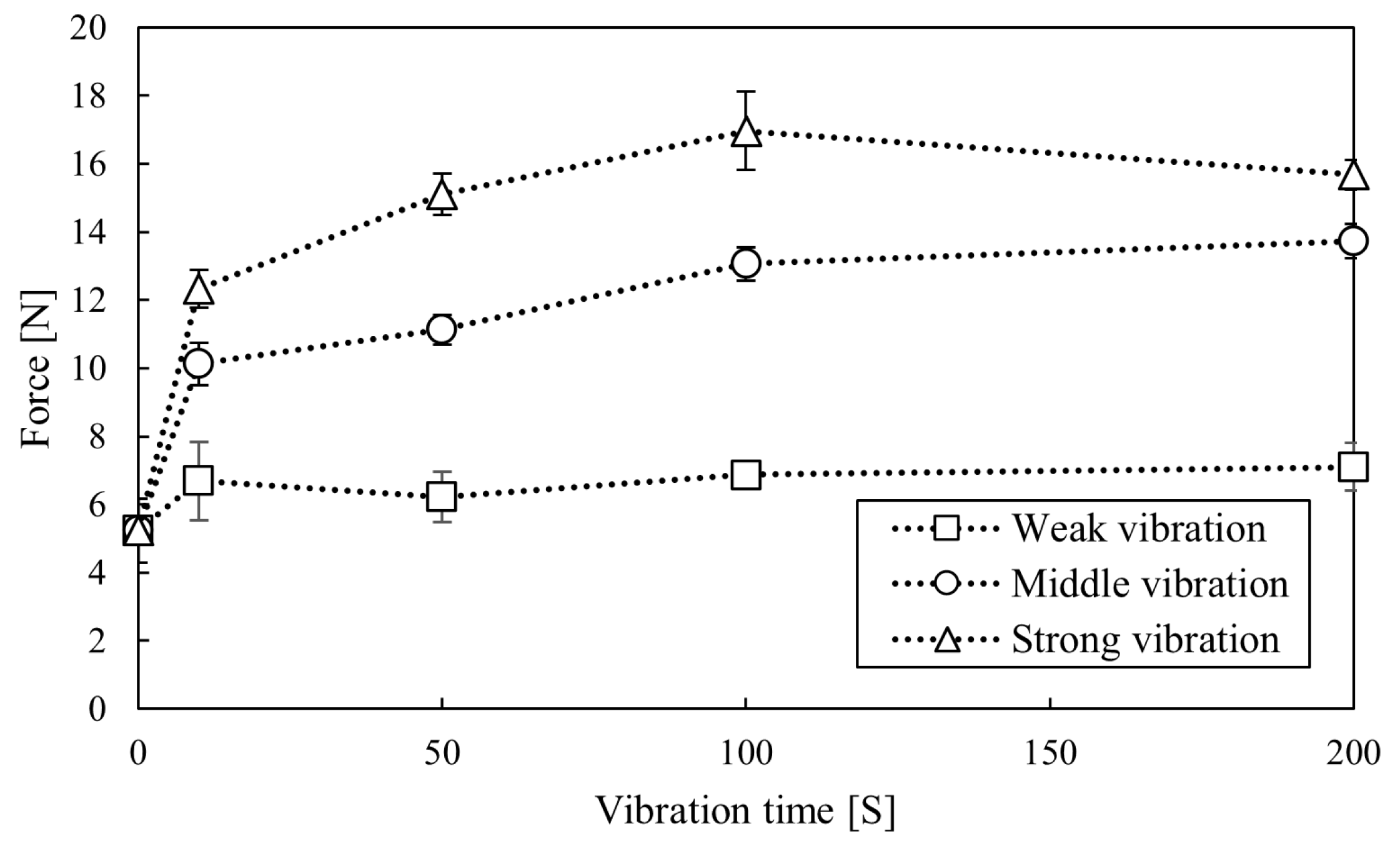
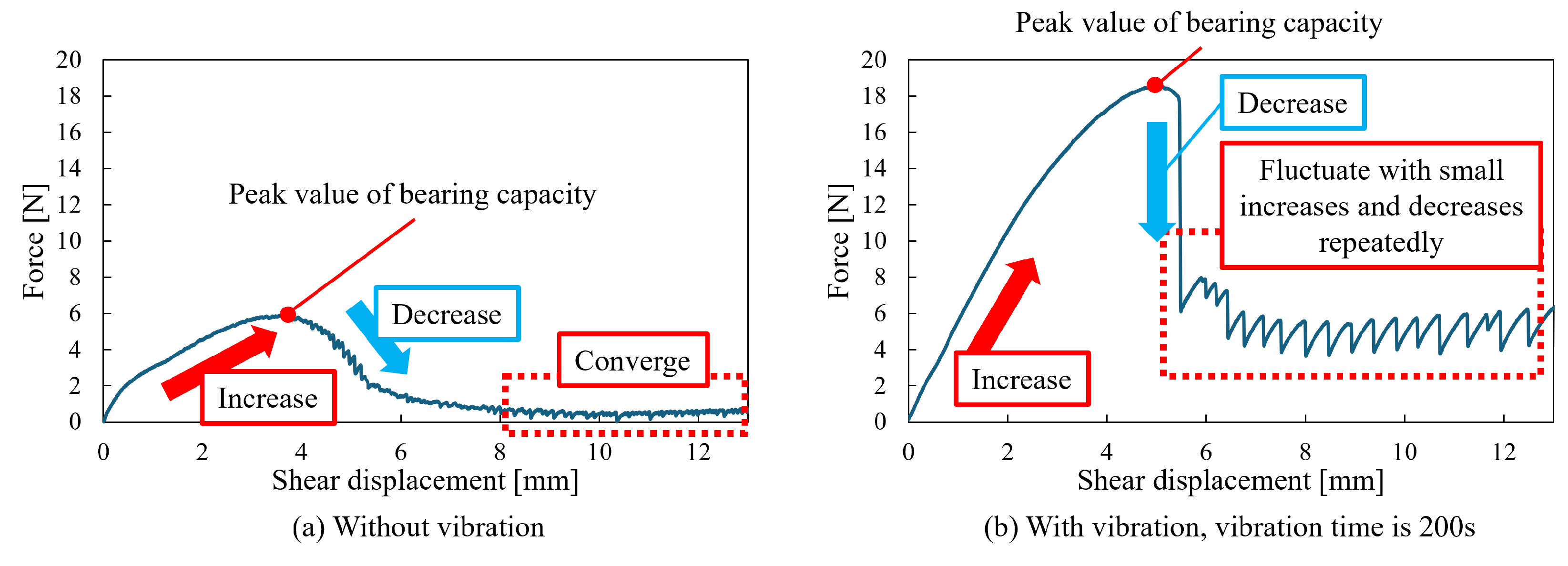
3.1. Relationship Between Vibration Time and Bearing Capacity
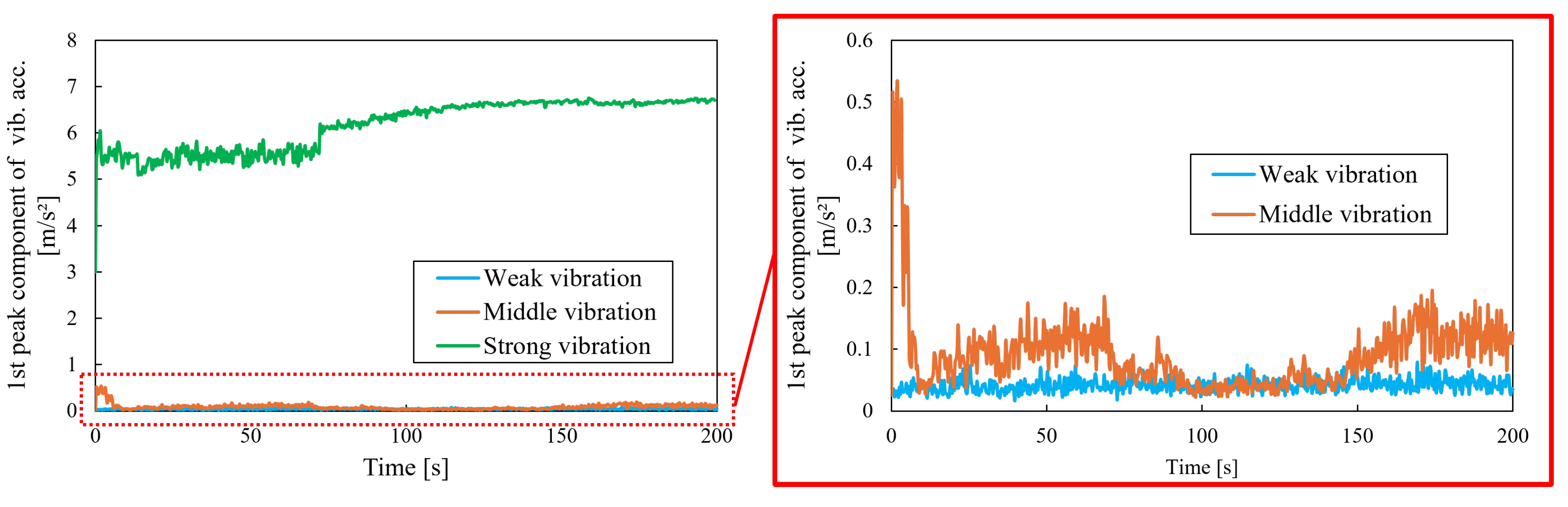
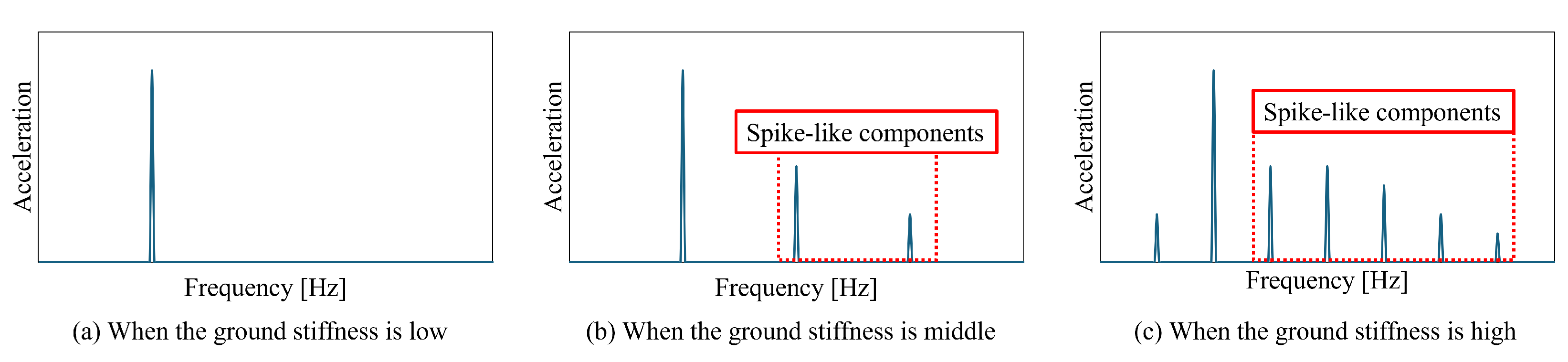
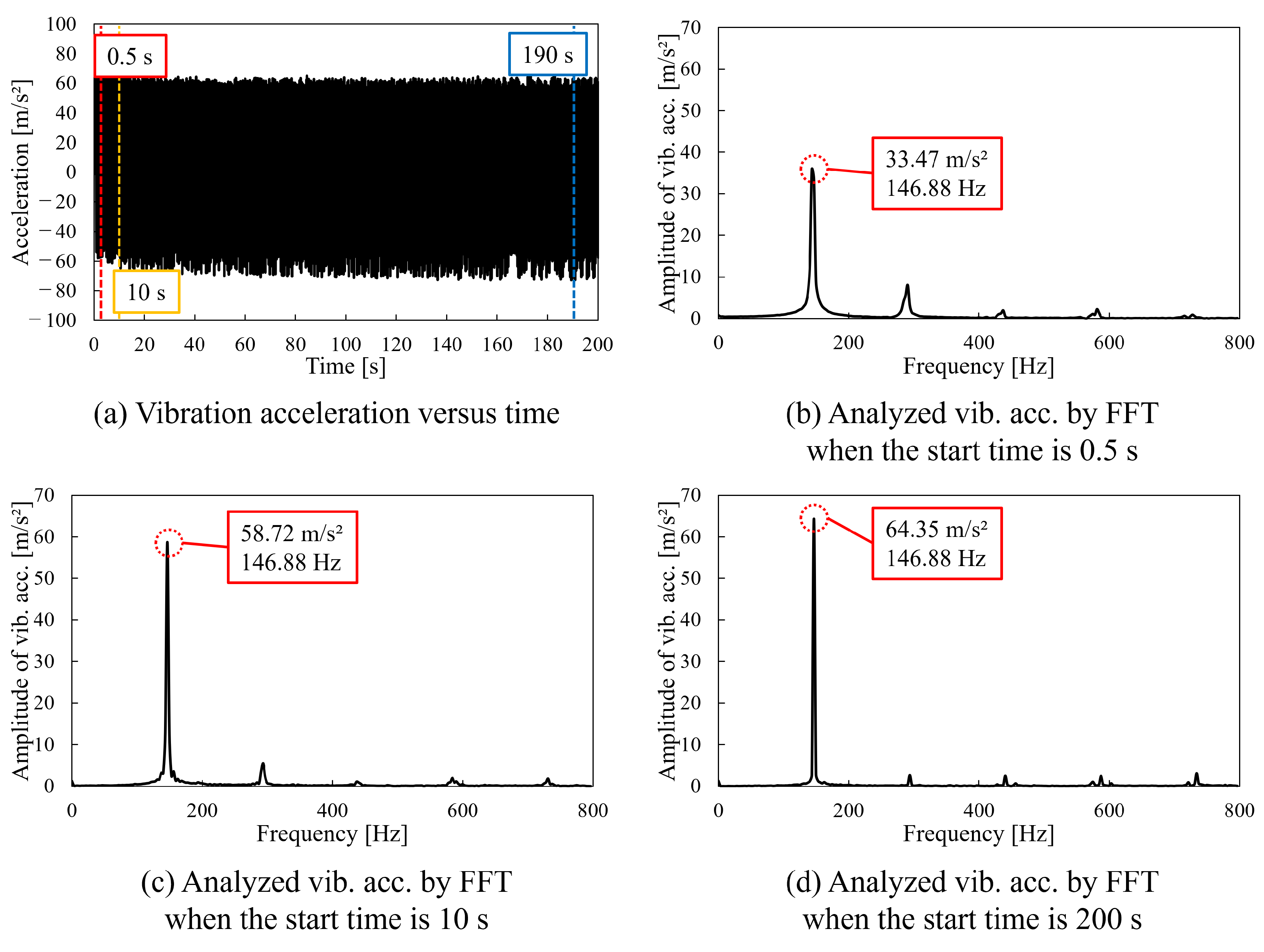
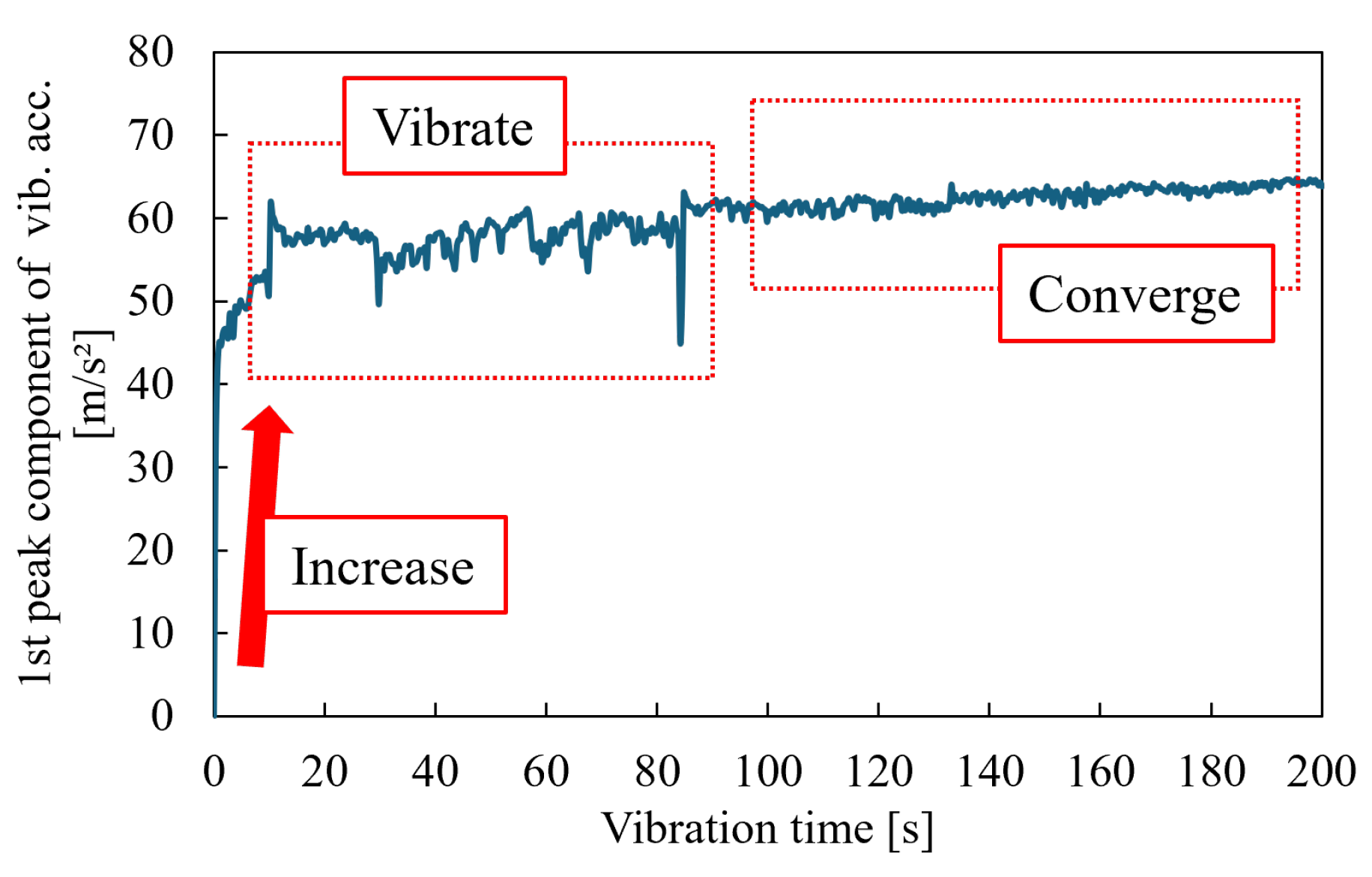
3.2. Relationship Between Vibration Time and Vibration Acceleration
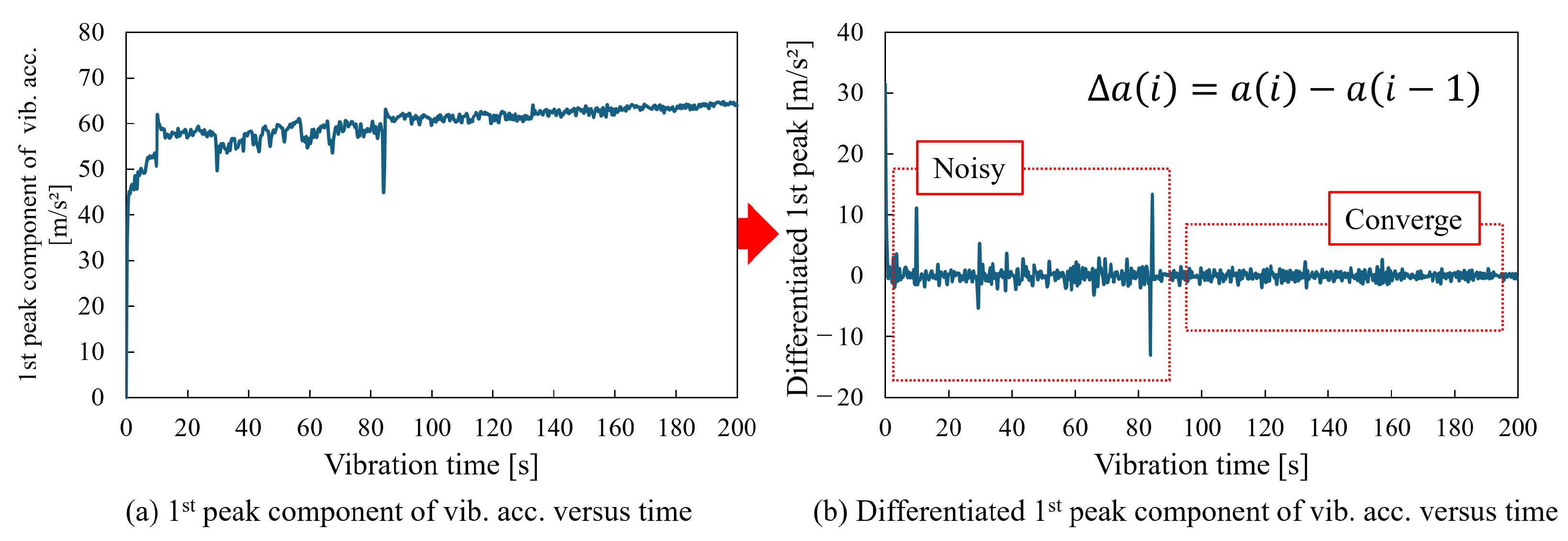
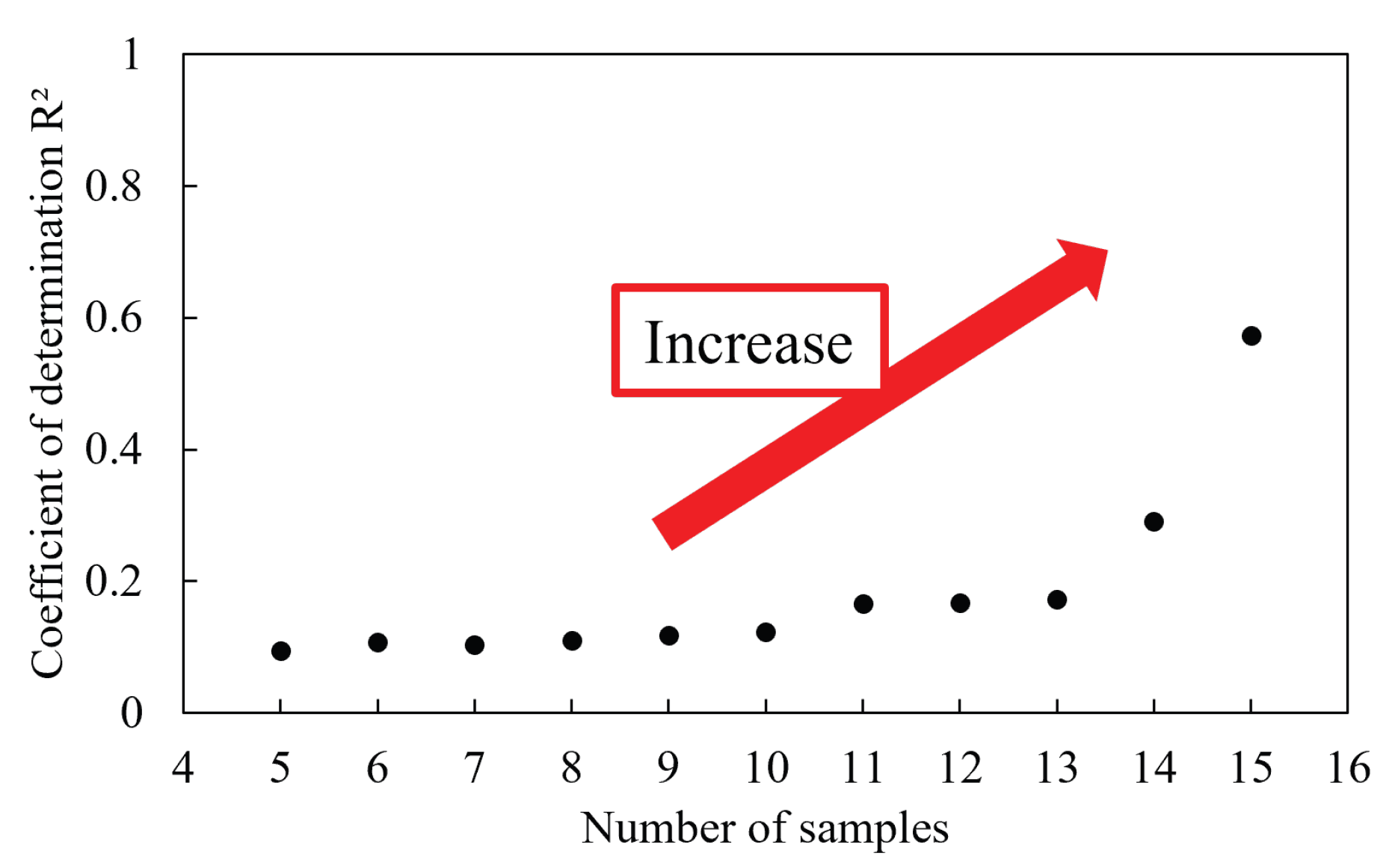
3.3. Suggestions for Correlated Indicators
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Investigation of the Effect of Experimental Condition on the Measurement Data
Appendix A.1. The Effect of the Sand Box Size on the Bearing Capacity
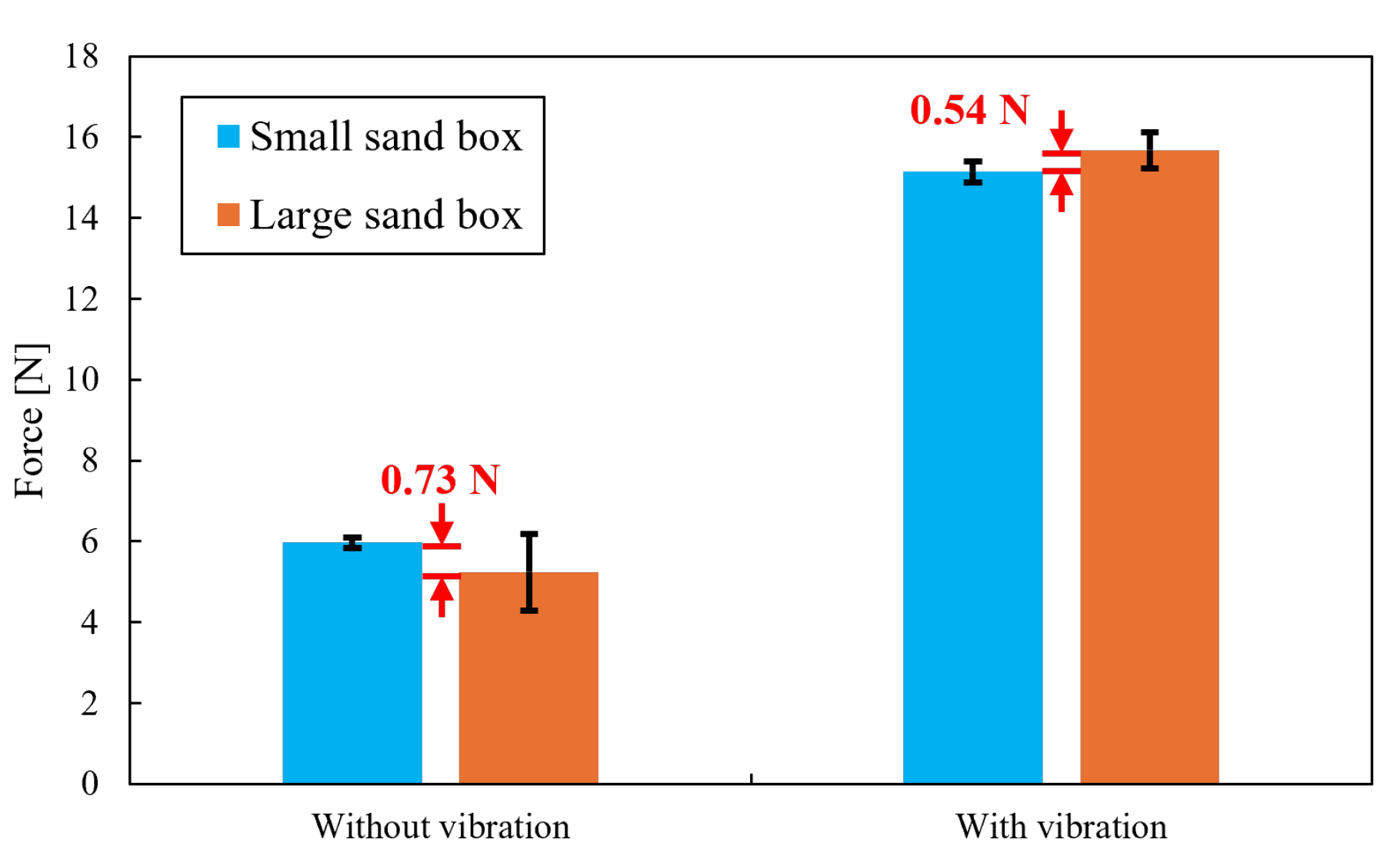
Appendix A.2. The Effect of Changing Vibrations on the Bearing Capacity and Vibration Acceleration
| Vibration | Supply Voltage [V] | Vibration Force (Error) [N] | Frequency (Error) [Hz] |
|---|---|---|---|
| Weak vibration | 10 | 1.09 () | 70 () |
| Middle vibration | 20 | 5.20 () | 154 () |
| Strong vibration | 30 | 11.9 () | 233 () |
References
- NASA, Artemis. Available online: https://www.nasa.gov/specials/artemis/ (accessed on 12 March 2025).
- NASA Gateway. Available online: https://www.nasa.gov/mission/gateway/ (accessed on 12 March 2025).
- NASA. Mars 2020 Mission Perseverance Rover. Available online: https://mars.nasa.gov/mars2020/mission/overview/ (accessed on 12 March 2025).
- Enming, J.; Changqing, L.; Jian, C.; Xiaojia, Z.; Yanqing, X.; Ping, L.; Xiaohui, F.; Zongcheng, L. Detection of allophane by the Zhurong rover indicates water-limited alteration at Utopia Planitia, Mars. Earth Planet. Sci. Lett. 2024, 639, 118769. [Google Scholar] [CrossRef]
- Fairen, A.G.; Schulze-Makuch, D.; Rodriguez, A.P.; Fink, W.; Davila, A.F.; Uceda, E.R.; Furfaro, R.; Amils, R.; McKay, C.P. Evidence for Amazonian acidic liquid water on Mars: A reinterpretation of MER mission results. Planet. Space Sci. 2009, 57, 276–287. [Google Scholar] [CrossRef]
- Golombek, M.P.; Cook, R.A.; Economou, T.; Folkner, W.M.; Haldemann, A.F.C.; Kallemeyn, P.H.; Knudsen, J.M.; Manning, R.M.; Moore, H.J.; Parker, T.J.; et al. Overview of the mars pathfinder mission and assessment of landing site predictions. Science 1997, 278, 1743–1748. [Google Scholar] [CrossRef] [PubMed]
- Witze, A. Space rovers in a record race. Nature 2013, 498, 284–285. [Google Scholar] [CrossRef] [PubMed]
- NASA Science, Spirit. Available online: https://solarsystem.nasa.gov/missions/spirit/in-depth/ (accessed on 12 March 2025).
- Wilcox, B.H. ATHLETE: A Limbed Vehicle for Solar System Exploration. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012. [Google Scholar] [CrossRef]
- Yeomans, B.; Saaj, C.M.; Winnendael, M.V. Walking planetary rovers: Experimental analysis and modelling of leg thrust in loose granular soils. J. Terramech. 2013, 50, 107–120. [Google Scholar] [CrossRef]
- Colombano, S.; Kirchner, F.; Spenneberg, D.; Hanratty, J. Exploration of planetary terrain with a legged robot as a scout adjunct to a rover. In Proceedings of the Space 2004 Conference and Exhibit, San Diego, CA, USA, 28–30 September 2004. [Google Scholar] [CrossRef]
- Seidel, D.; Hermann, M.; Gumpert, T.; Loeffl, F.C.; Albu-Schaffer, A. Using elastically actuated legged robots in rough terrain: Experiments with DLR quadrupedal bert. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020. [Google Scholar] [CrossRef]
- Kato, T.; Uno, K.; Yoshida, K. A Gripper with Pin-Array Structure for Convex and Concave Terrain Shapes. J. Robot. Soc. Jpn. 2024, 42, 177–180. [Google Scholar] [CrossRef]
- Komizunai, S.; Konno, A.; Abiko, S.; Uchiyama, M. Development of a static sinkage model for a biped robot on loose soil. In Proceedings of the 2010 IEEE/SICE International Symposium on System Integration, Sendai, Japan, 21–22 December 2010. [Google Scholar] [CrossRef]
- Watanabe, T.; Iizuka, K. Proposal of walking to reduce slipping behavior using the compaction effect of loose soil caused by propagation of vibration for small light lunar planetary exploration rovers with legs. Trans. JSME 2020, 86, 19–00263. [Google Scholar] [CrossRef]
- Watanabe, T.; Higashiyama, R.; Watanabe, D.; Iizuka, K. Analyzing bearing capacity changes due to vibration in discrete element method simulations. J. Terramech. 2025, 118, 101031. [Google Scholar] [CrossRef]
- Wada, S.; Kouda, M.; Enami, A. Experimental Study on Passive Earth Pressure Part 1: The Experimental Device and An Example of Passive Earth Pressure Tests by the Device. J. Str. Con. Eng. 1998, 63, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; Read Books Limited: Redditch, UK, 2010. [Google Scholar]
- Alqarawi, A.S.; Leo, C.J.; Liyanapathirana, D.S.; Sigdel, L.; Lu, M.; Hua, P. A spreadsheetbased technique to calculate the passive soil pressure based on the log-spiral method. Com. Geo. 2021, 130, 103926. [Google Scholar] [CrossRef]
- Fujiyama, T.; Tateyama, K. Evaluation of compacting ground stiffness by acceleration of vibratory roller. Jap. J. JSCE 2000, 652, 115–123. [Google Scholar] [CrossRef]
- Watanabe, T.; Iizuka, K. Experimental investigation of the relationship between bearing capacity and vibration parameters for planetary exploration of legged rovers. ROBOMECH J. 2023, 10, 27. [Google Scholar] [CrossRef]
- Kobayashi, T.; Fujiwara, Y.; Yamakawa, J.; Yasufuku, N.; Omine, K. Mobility performance of a rigid wheel in low-gravity environments. J. Terramech. 2010, 47, 261–274. [Google Scholar] [CrossRef]
- Ono, S.; Namikawa, S.; Yoshida, K. Analysis of soil flow and traction mechanics for lunar overs over different types of soils using particle image velocimetry. J. Terramech. 2021, 95, 89–100. [Google Scholar] [CrossRef]
- Oe, A.; Nishida, S.; Nakatani, S. Study of passive steering mechanism for small Martian surface exploration rovers. J. Terramech. 2024, 112, 35–43. [Google Scholar] [CrossRef]
- Yeomans, B.; Saaj, C.M. Towards terrain interaction prediction for bioinspired planetary exploration rovers. Bioinspir. Biomimetics 2014, 9, 016009. [Google Scholar] [CrossRef] [PubMed]







| Item | Condition (Value) |
|---|---|
| Number of trials | 5 |
| Sinkage of the rod | 30 mm |
| Dragged speed | 0.13 mm/s |
| Dragged time | 100 s |
| Type of sand | Toyoura sand |
| Vibration motor | TP-2528C-24, Three Peace Co., Ltd., Daitou-ku, Tokyo, Japan |
| Supply voltage for vibration motor | 30 V |
| Vibration force | 11.9 N |
| Vibration frequency | 233 Hz |
| Vibration time | 0, 5, 10, 20, 30, 40, 50, 60, 75, 85, 100, 125, 150, and 200 s |
| Force sensor | PFS055YA251U6, Leptrino Co., Ltd., Saku city, Nagano, Japan |
| Acceleration sensor | AccStick, Shinyei Technology Co., Ltd., Koube city, Hyougo, Japan |
| Sampling frequency of acceleration sensor | 1600 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Watanabe, T.; Fukura, Y.; Hiramoto, K.; Iizuka, K. Experimental Investigation of the Relationship Between Vibration Acceleration and Bearing Capacity for Space Exploration Legged Rovers. Geotechnics 2025, 5, 21. https://doi.org/10.3390/geotechnics5010021
Watanabe T, Fukura Y, Hiramoto K, Iizuka K. Experimental Investigation of the Relationship Between Vibration Acceleration and Bearing Capacity for Space Exploration Legged Rovers. Geotechnics. 2025; 5(1):21. https://doi.org/10.3390/geotechnics5010021
Chicago/Turabian StyleWatanabe, Tomohiro, Yutaka Fukura, Kazuhiko Hiramoto, and Kojiro Iizuka. 2025. "Experimental Investigation of the Relationship Between Vibration Acceleration and Bearing Capacity for Space Exploration Legged Rovers" Geotechnics 5, no. 1: 21. https://doi.org/10.3390/geotechnics5010021
APA StyleWatanabe, T., Fukura, Y., Hiramoto, K., & Iizuka, K. (2025). Experimental Investigation of the Relationship Between Vibration Acceleration and Bearing Capacity for Space Exploration Legged Rovers. Geotechnics, 5(1), 21. https://doi.org/10.3390/geotechnics5010021