Pore Water Pressure Generation and Energy Dissipation Characteristics of Sand–Gravel Mixtures Subjected to Cyclic Loading
Abstract
1. Introduction
2. Test Materials and Procedure
2.1. Materials
2.2. Test Procedure
3. Test Results and Discussions
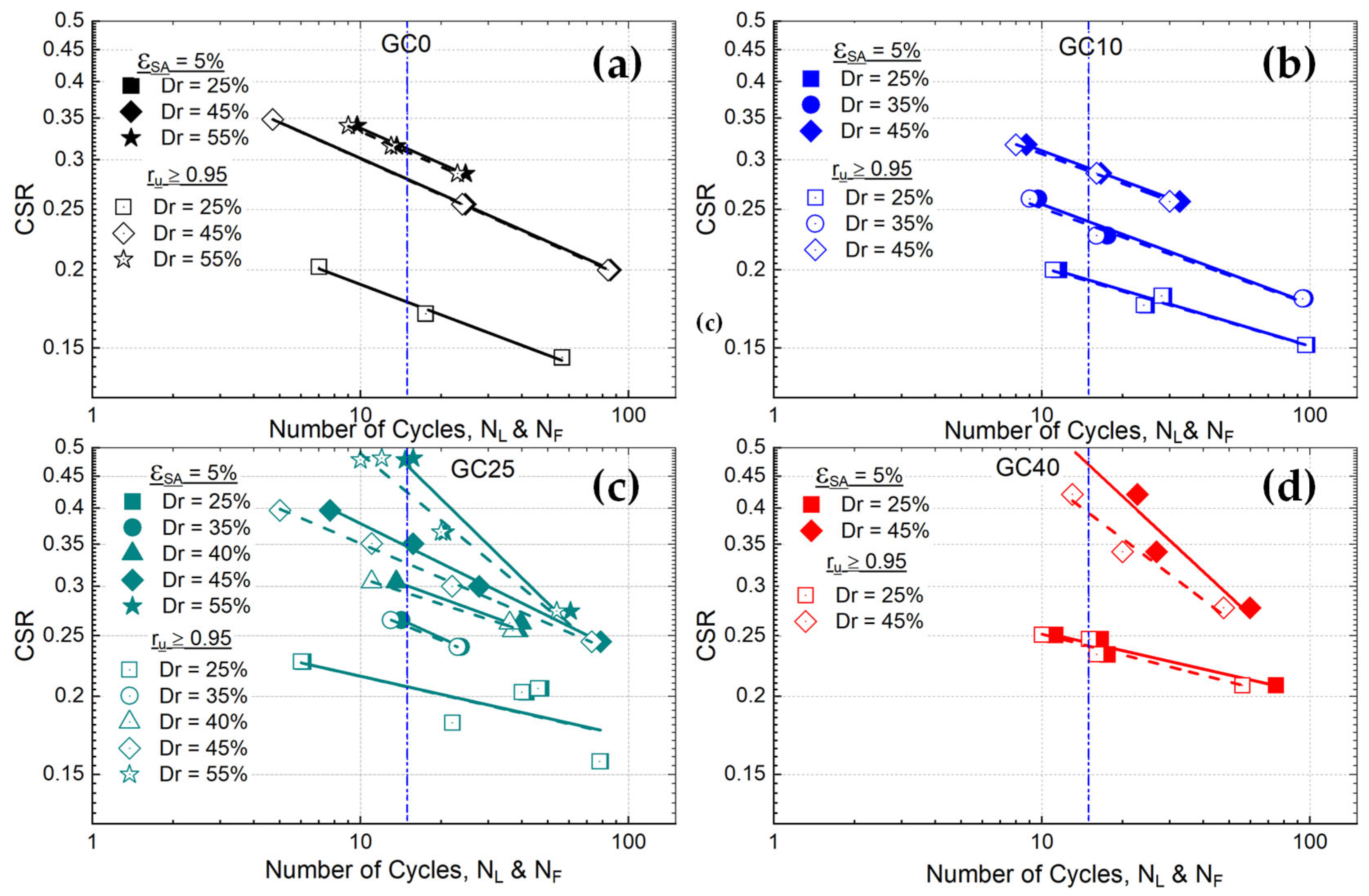
3.1. Cyclic Resistance
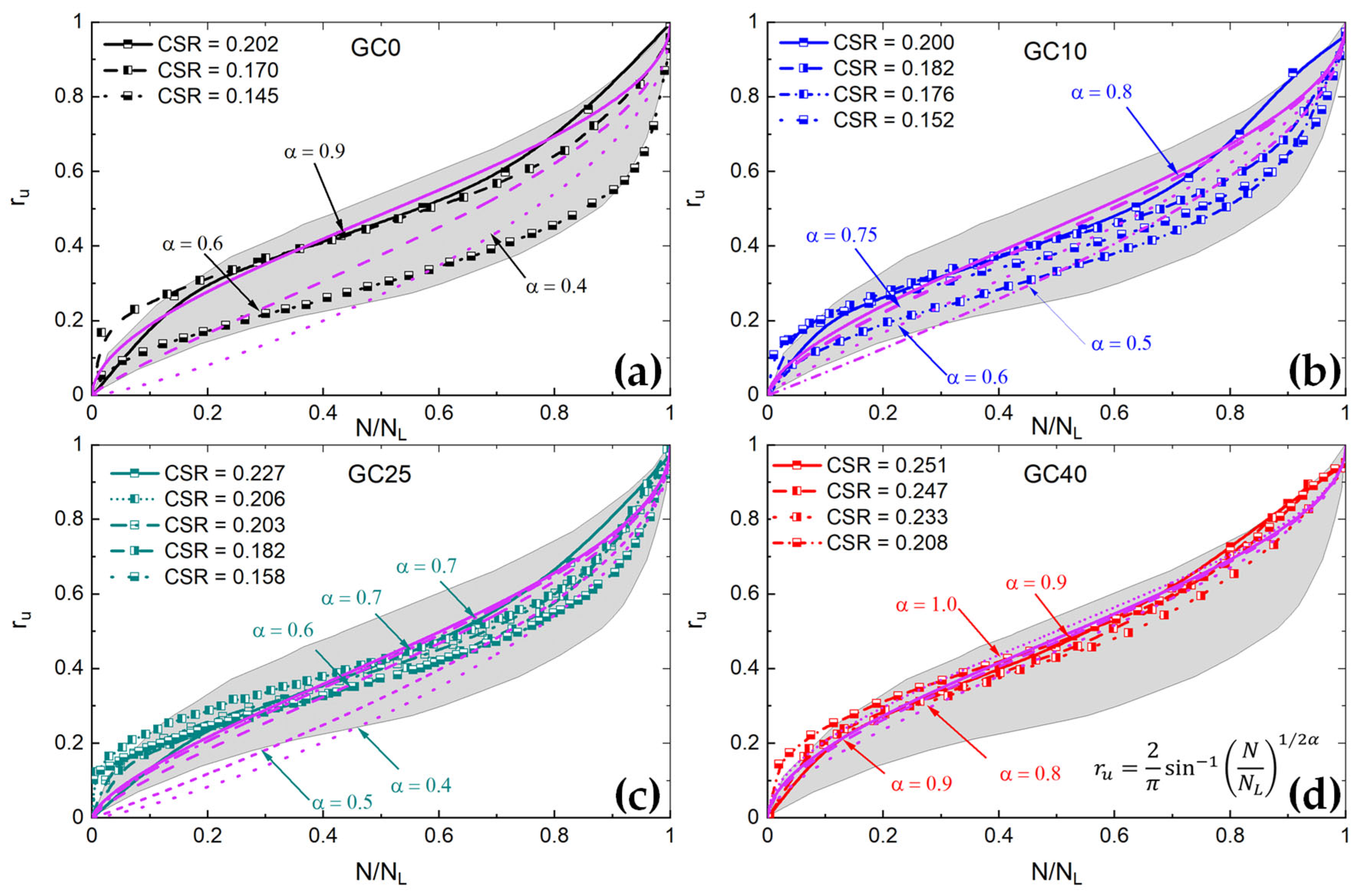
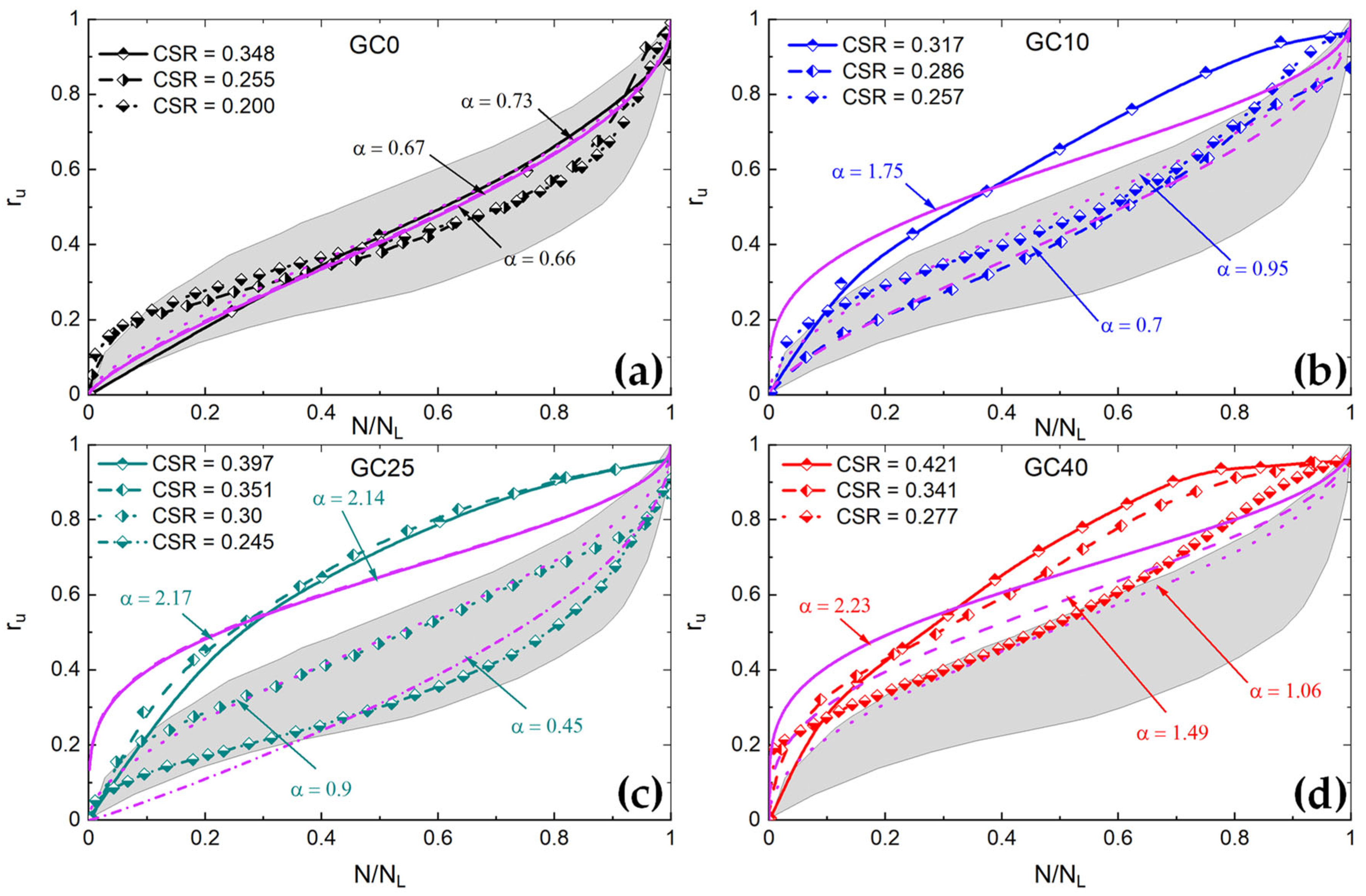
3.2. Pore Water Pressure Generation
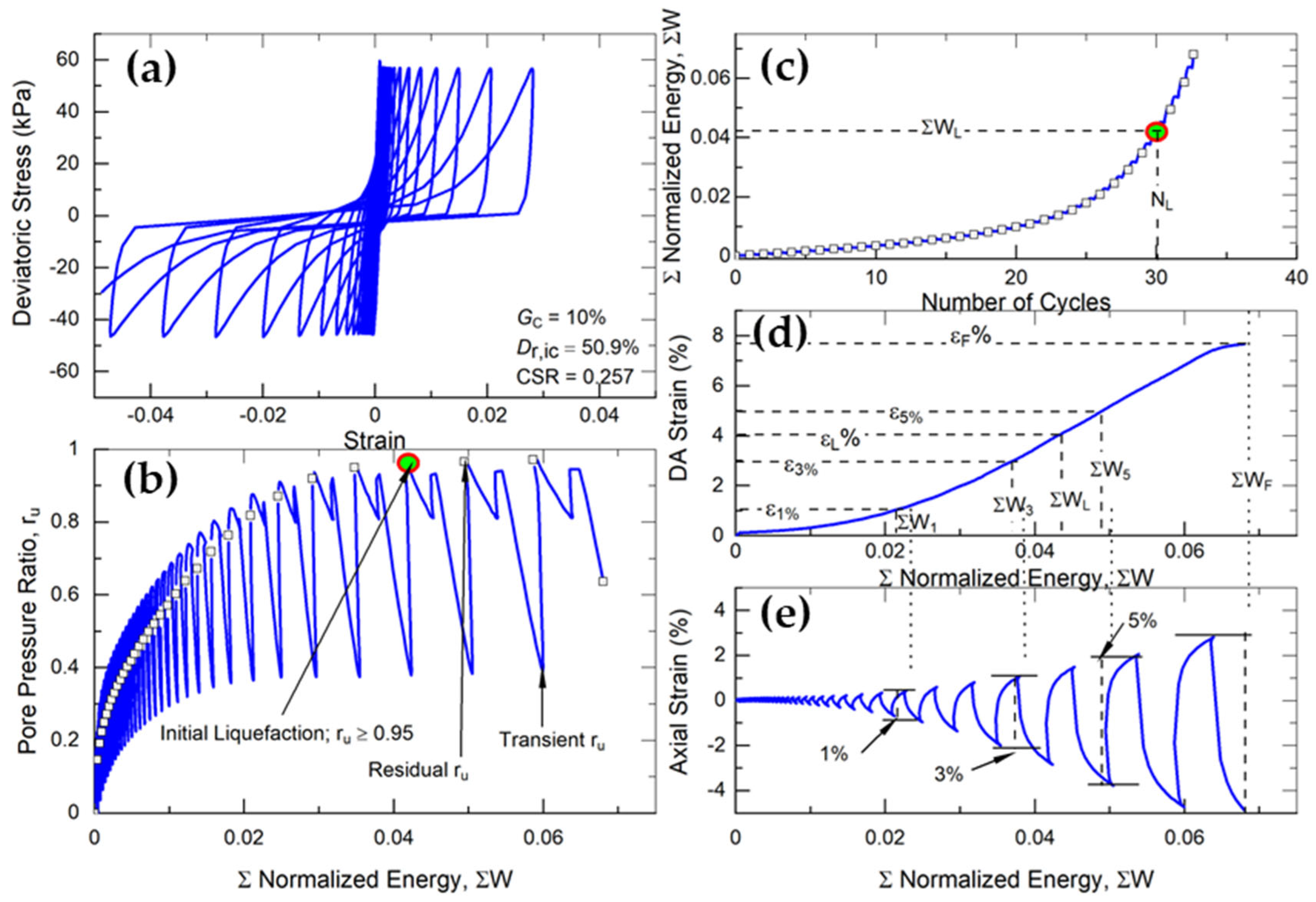
4. Energy Dissipation Approach
4.1. Theoretical Framework
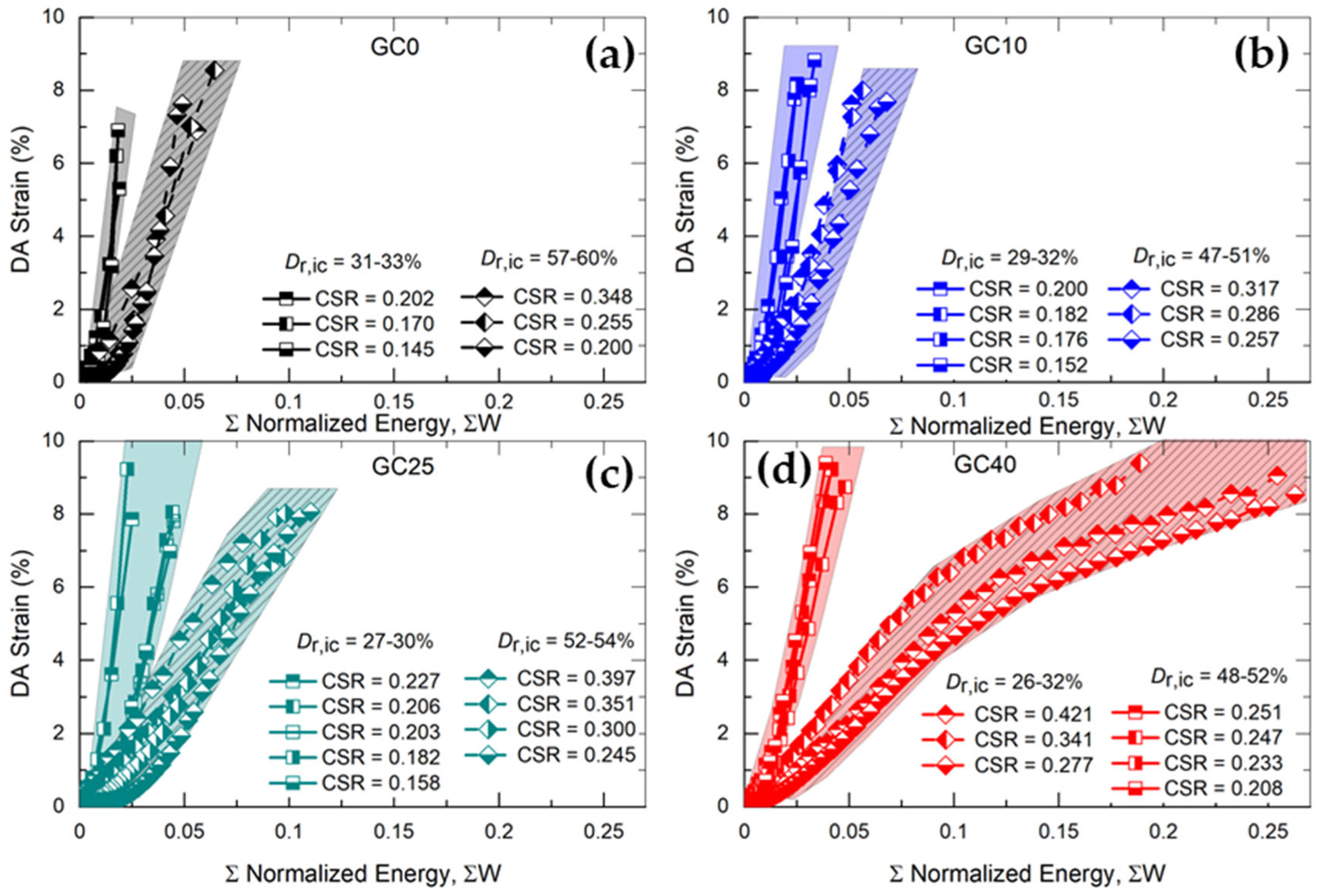
4.2. Relationship Between Energy Dissipation and Double Amplitude Axial Strain
4.3. Relationship Between Energy Dissipation and Pore Water Pressure
5. Conclusions
- It is confirmed that the liquefaction resistance (CRR) and pore water pressure generation (ru) of SGMs are influenced by the CSR, GC, and Dr; however, this study shows that it is critical to consider the combined effects of GC and Dr to properly characterize the response of SGMs subjected to undrained cyclic loading conditions;
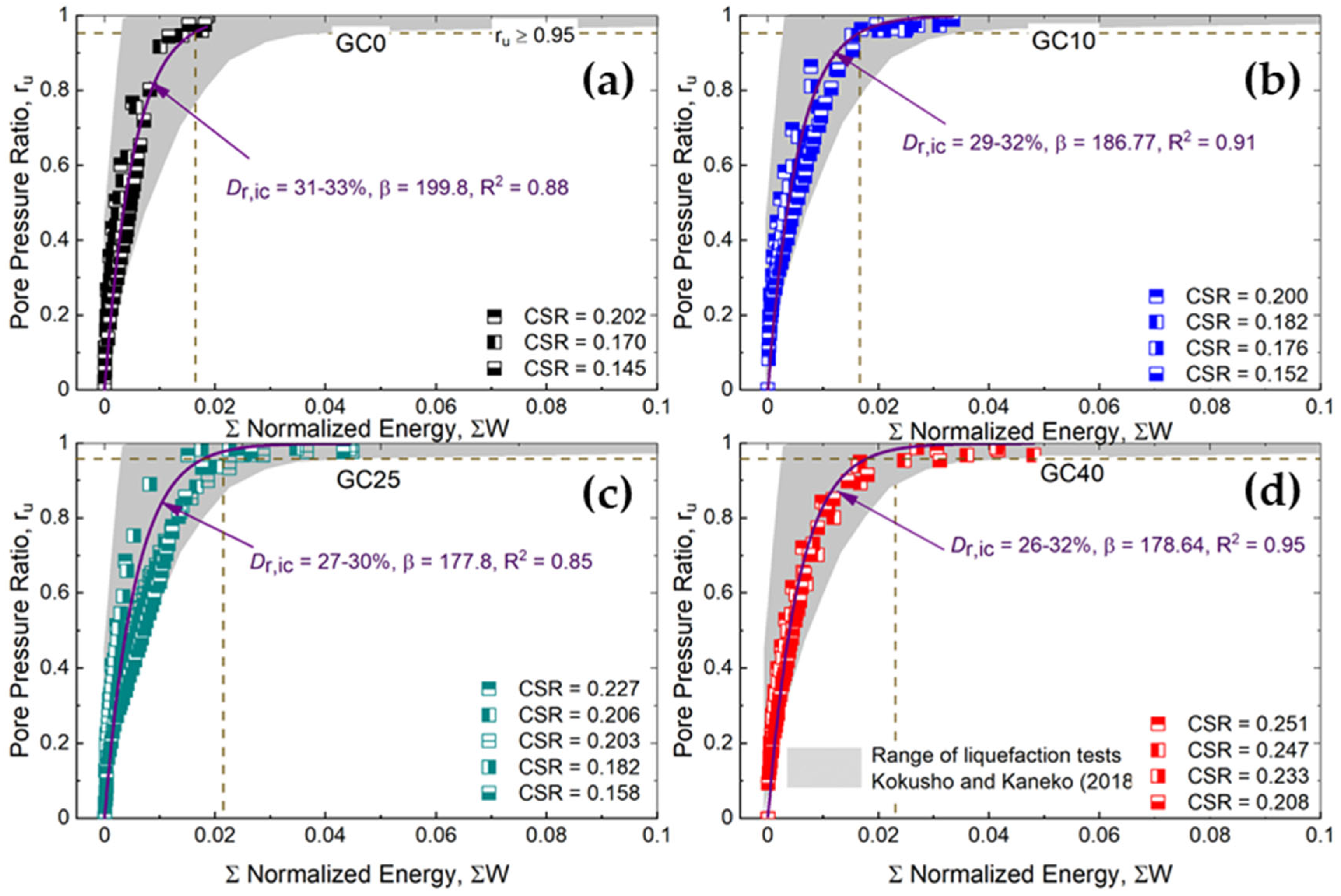
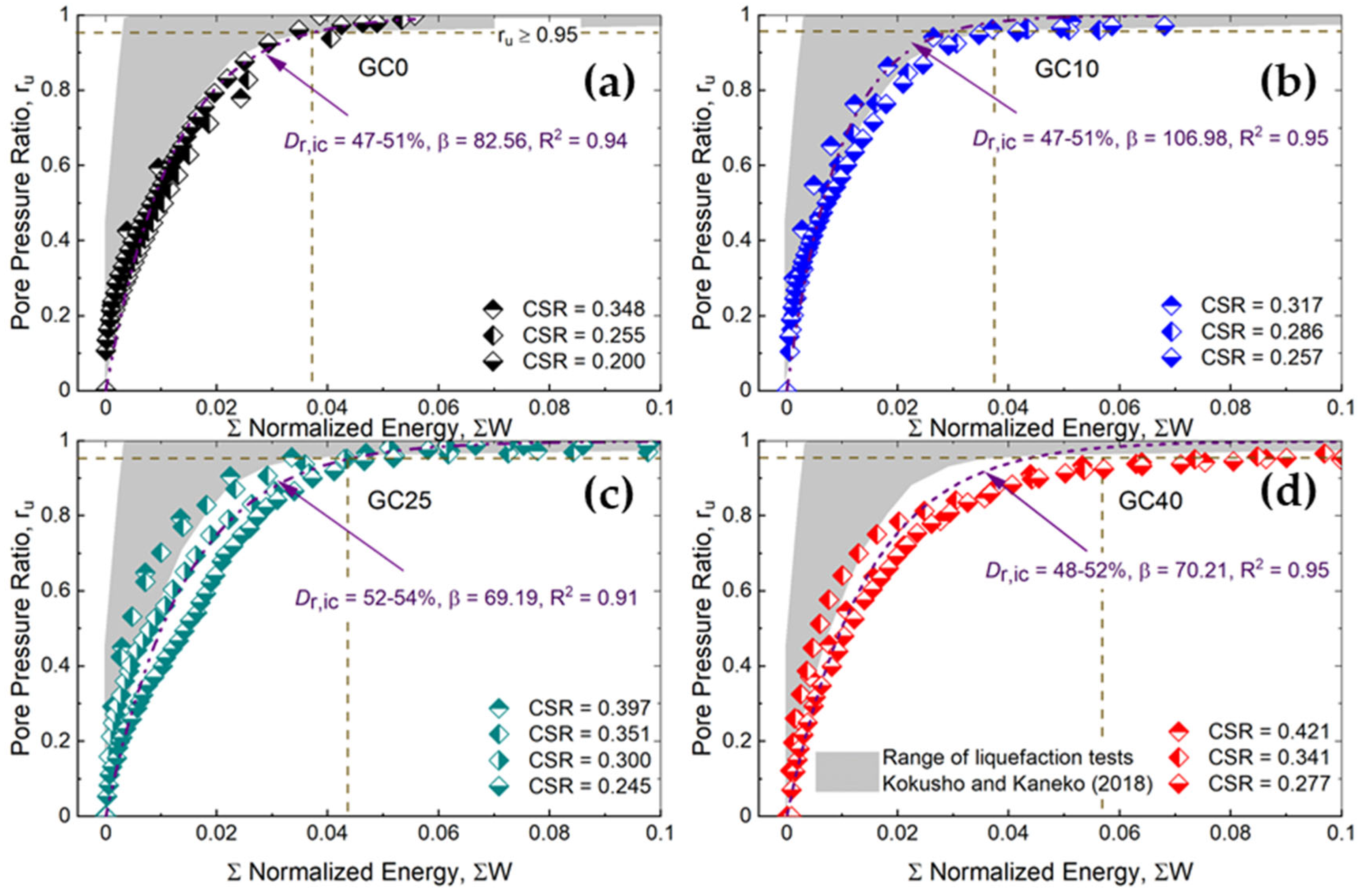
- For looser (Dr = 26–33%) SGMs, the influence of GC on the ru is marginal irrespective of the CSR level; alternatively, for denser (Dr = 47–60%) SGMs, the influence of GC on the ru becomes significant with an increasing CSR level;
- The boundary curves for ru proposed by Lee and Albaisa [25] for sand describe well the response of loose SGMs; alternatively, the response of the denser SGMs is better described by the boundary curves proposed by Haeri and Shakeri [23] for gravels. The mathematical model proposed by Booker et al. [43] is fairly applicable to all SGMs cases examined in this study (GC = 0–40%; Dr = 26–60%; CSR = 0.145–0.481);
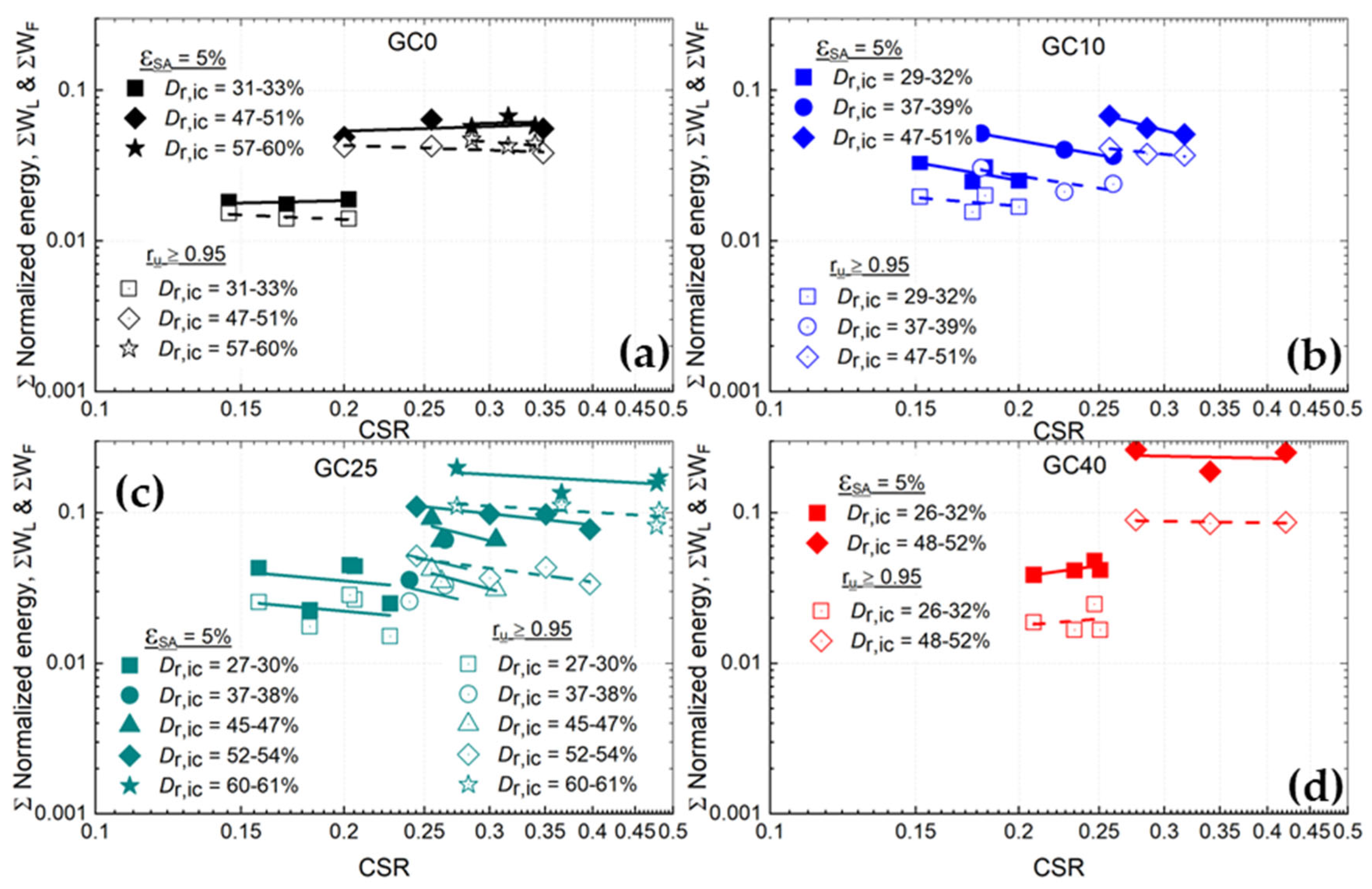
- For SGMs with GC = 0 and 10%, the normalized cumulative energy dissipation (ΣW) slightly increases with increasing Dr; in contrast, for SGMs with GC = 25 and 40%, ΣW significantly increases with increasing Dr. Irrespective of the GC and Dr combinations, the effects of CSR on ΣW are mostly marginal;
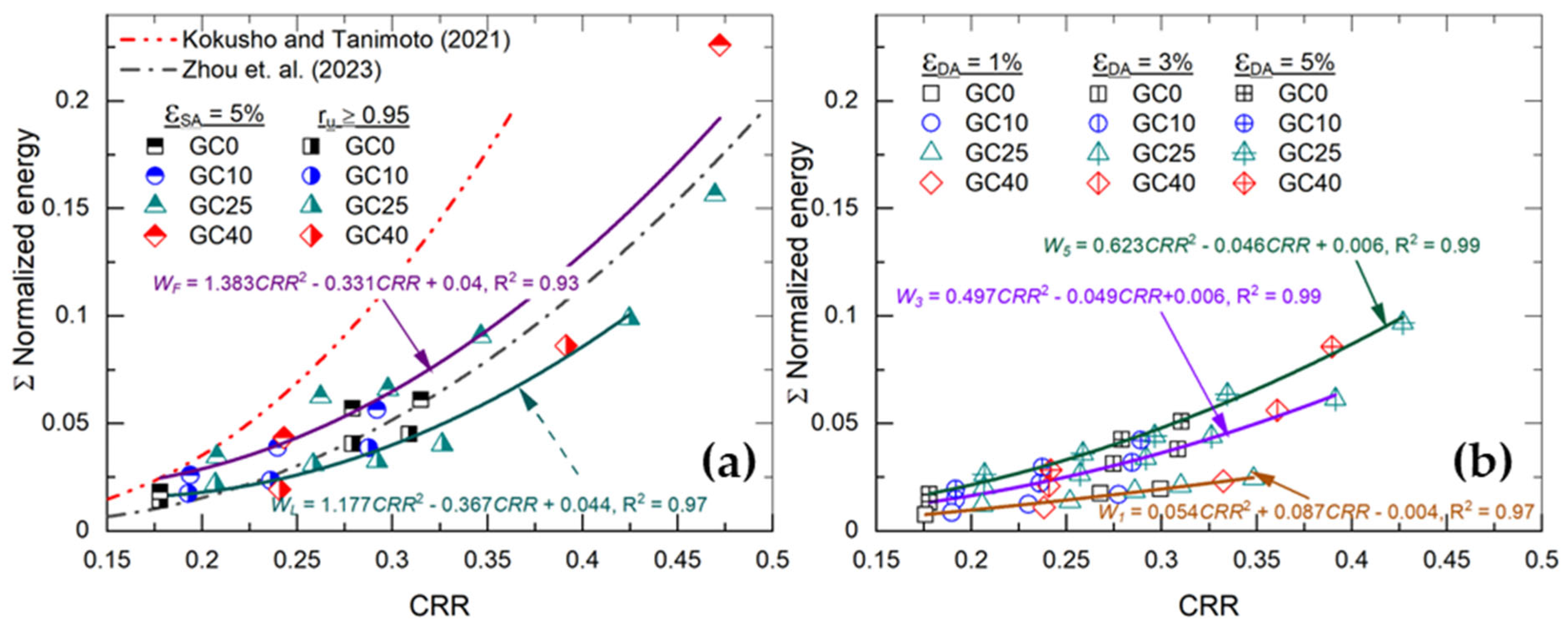
- EBM is found to be an effective approach for uniquely describing the liquefaction potential of SGMs while simultaneously capturing the effects of GC and Dr. This highlights that EBM is a promising alternative to the CSR approach, which requires additional parameters, such as the skeleton void ratio and/or equivalent void ratio, to capture the effect of GC and Dr as described and correlated with CRR in the work of Pokhrel et al. [2]. This contribution adds significant value to the existing body of literature, which primarily focuses on sand and sand–silt mixtures. Based on the existing knowledge and the findings of this study, the EBM approach has demonstrated its robustness in predicting liquefaction potential across various soil types and loading conditions.
- Both the CSR and EBM approaches demonstrate significant effectiveness in predicting the pore pressure generation of SGMs tested in this study. However, the EBM approach appears to be better suited due to the narrow band observed in the ΣW–ru. In contrast, the CSR approach shows a wider variability in the relationship between N/NL and the ru.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rollins, K.M.; Roy, J.; Athanasopoulos-Zekkos, A.; Zekkos, D.; Amoroso, S.; Cao, Z.; Milana, G.; Vassallo, M.; Di Giulio, G. A new Vs-based liquefaction-triggering procedure for gravelly soils. J. Geotech. Geoenv. Eng. 2022, 148, 04022040. [Google Scholar] [CrossRef]
- Pokhrel, A.; Chiaro, G.; Kiyota, T.; Cubrinovski, M. Liquefaction characteristics of sand-gravel mixtures: Experimental observations and its assessment based on intergranular state concept. Soils Found. 2024, 62, 101444. [Google Scholar] [CrossRef]
- Hatanaka, M.; Suzuki, Y.; Kawasaki, T.; Endo, M. Cyclic undrained shear properties of high quality undisturbed Tokyo gravel. Soils Found. 1988, 28, 57–68. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, Y.; Goto, S.; Hatanaka, M.; Tokimatsu, K. Correlation between strengths and penetration resistances for gravelly soils. Soils Found. 1993, 33, 92–101. [Google Scholar] [CrossRef]
- Flora, A.; Lirer, S.; Silvestri, F. Undrained cyclic resistance of undisturbed gravelly soils. Soil Dyn. Earthquake Eng. 2012, 43, 366–379. [Google Scholar] [CrossRef]
- Wong, R.T.; Seed, H.B.; Chan, C.K. Liquefaction of Gravelly Soils Under Cyclic Loading Conditions; Report of the Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1974; p. 92. [Google Scholar]
- Wong, R.T.; Seed, H.B.; Chan, C.K. Cyclic loading liquefaction of gravelly soils. J. Geotech. Eng. Div. 1975, 101, 571–583. [Google Scholar] [CrossRef]
- Banerjee, N.G.; Seed, H.B.; Chan, C.K. Cyclic Behavior of Dense Coarse-Grained Materials in Relation to the Seismic Stability of Dams; Report of the Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1979; p. 252. [Google Scholar]
- Lin, P.S.; Chang, C.W. Damage investigation and liquefaction potential analysis of gravelly soil. J. Chin. Inst. Eng. 2002, 25, 543–554. [Google Scholar] [CrossRef]
- Kim, J.; Athanasopoulos-Zekkos, A.; Cubrinovski, M. Monotonic and cyclic simple shear response of well-graded sandy gravel soils from Wellington, New Zealand. J. Geotech. Geoenviron. Eng. 2023, 149, 04023046. [Google Scholar] [CrossRef]
- Evans, M.D.; Zhou, S. Liquefaction behavior of sand-gravel composites. J. Geotech. Eng. 1995, 121, 287–298. [Google Scholar] [CrossRef]
- Amini, F.; Chakravrty, A. Liquefaction testing of layered sand-gravel composites. Geotech. Test. J. 2003, 27, 36–46. [Google Scholar] [CrossRef]
- Chang, W.J.; Chang, C.W.; Zeng, J.K. Liquefaction characteristics of gap-graded gravelly soils in K0 condition. Soil Dyn. Earthquake Eng. 2014, 56, 74–85. [Google Scholar] [CrossRef]
- Chang, W.J. Evaluation of liquefaction resistance for gravelly sands using gravel content–corrected shear-wave velocity. J. Geotech. Geoenviron. Eng. 2016, 142, 04016002. [Google Scholar] [CrossRef]
- Chang, W.J.; Phantachang, T. Effects of gravel content on shear resistance of gravelly soils. Eng. Geol. 2016, 207, 78–90. [Google Scholar] [CrossRef]
- Hubler, J.F.; Athanasopoulos-Zekkos, A.; Zekkos, D. Monotonic, cyclic, and postcyclic simple shear response of three uniform gravels in constant volume conditions. J. Geotech. Geoenviron. Eng. 2017, 143, 04017043. [Google Scholar] [CrossRef]
- Hubler, J.F.; Athanasopoulos-Zekkos, A.; Zekkos, D. Monotonic and cyclic simple shear response of gravel-sand mixtures. Soil Dyn. Earthquake Eng. 2018, 115, 291–304. [Google Scholar] [CrossRef]
- Toyota, H.; Takada, S. Effects of gravel content on liquefaction resistance and its assessment considering deformation characteristics in gravel—Mixed sand. Canadian Geotech. J. 2019, 56, 1743–1755. [Google Scholar] [CrossRef]
- Chen, G.; Wu, Q.; Sun, T.; Zhao, K.; Zhou, E.; Xu, L.; Zhou, Y. Cyclic behaviors of saturated sand-gravel mixtures under undrained cyclic triaxial loading. J. Earthquake Eng. 2018, 25, 756–789. [Google Scholar] [CrossRef]
- Rahman, M.M.; Lo, S.R. Equivalent granular void ratio and state parameters for loose clean sand with small amount of fines. In Proceedings of the 10th Australia New Zealand Conference on Geomechanics, Brisbane, Australia, 20–25 October 2007; pp. 674–679. [Google Scholar]
- Thevanayagam, S.; Shenthan, T.; Mohan, S.; Liang, J. Undrained fragility of clean sands, silty sands, and sandy silts. J. Geotech. Geoenviron. Eng. 2002, 128, 849–859. [Google Scholar] [CrossRef]
- Evans, M.D.; Seed, H.B. Undrained Cyclic Triaxial Testing of Gravels—The Effect of Membrane Compliance; Report No. UCB/EERC-87/0B; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1987; p. 440. [Google Scholar]
- Haeri, S.M.; Shakeri, M.R. Effects of membrane compliance on pore water pressure generation in gravelly sands under cyclic loading. Geotech. Test. J. 2010, 33, 375–384. [Google Scholar] [CrossRef]
- Hubler, J.F.; Athanasopoulos-zekkos, A.; Zekkos, D. Pore pressure generation of gravelly soils in constant volume cyclic simple shear. J. Geotech. Geoenviron. Eng. 2023, 149, 04022130. [Google Scholar] [CrossRef]
- Lee, K.L.; Albaisa, A. Earthquake induced settlements in saturated sands. J. Geotech. Eng. Div. 1974, 100, 387–406. [Google Scholar] [CrossRef]
- Polito, C.P.; Green, R.A.; Lee, J. Pore pressure generation models for sands and silty soils subjected to cyclic loading. J. Geotech. Geoenviron. Eng. 2008, 134, 1490–1500. [Google Scholar] [CrossRef]
- Porcino, D.D.; Diano, V. The influence of non-plastic fines on pore water pressure generation and undrained shear strength of sand-silt mixtures. Soil Dyn. Earthquake Eng. 2017, 101, 311–321. [Google Scholar] [CrossRef]
- Davis, R.O.; Berrill, J.B. Energy dissipation and seismic liquefaction in sands. Earthquake Eng. Struct. Dyn. 1982, 10, 59–68. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Shokooh, A. A unified approach to densification and liquefaction of cohesionless sand in cyclic shearing. Canadian Geotech. J. 1979, 16, 659–678. [Google Scholar] [CrossRef]
- Towhata, I.; Ishihara, K. Shear work and pore water pressure in undrained shear. Soils Found. 1985, 25, 73–84. [Google Scholar] [CrossRef]
- Green, R.A.; Mitchell, J.K.; Polito, C.P. An energy-based excess pore pressure generation model for cohesionless soils. In Proceedings of the John Booker Memorial Symposium—Developments in Theoretical Geomechanics, Sydney, Australia, 16–17 November 2000; pp. 1–10. [Google Scholar]
- Jafarian, Y.; Towhata, I.; Baziar, M.H.; Noorzad, A.; Bahmanpour, A. Strain energy based evaluation of liquefaction and residual pore water pressure in sands using cyclic torsional shear experiments. Soil Dyn. Earthquake Eng. 2012, 35, 13–28. [Google Scholar] [CrossRef]
- Amini, P.F.; Noorzad, R. Energy-based evaluation of liquefaction of fibre-reinforced sand using cyclic triaxial testing. Soil Dyn. Earthquake Eng. 2018, 104, 45–53. [Google Scholar] [CrossRef]
- Amini, P.F.; Huang, D.; Wang, G.; Jin, F. Effects of strain history and induced anisotropy on reliquefaction resistance of Toyoura sand. J. Geotech. Geoenviron. Eng. 2021, 147, 04021094. [Google Scholar] [CrossRef]
- Baziar, M.H.; Sharafi, H. Assessment of silty sand liquefaction potential using hollow torsional tests—An energy approach. Soil Dyn. Earthquake Eng. 2011, 31, 857–865. [Google Scholar] [CrossRef]
- Kokusho, T. Liquefaction potential evaluations: Energy-based method versus stress-based method. Canadian Geotech. J. 2013, 50, 1088–1099. [Google Scholar] [CrossRef]
- Kokusho, T. Liquefaction potential evaluations by energy-based method and stress-based method for various ground motions: Supplement. Soil Dyn. Earthquake Eng. 2017, 95, 40–47. [Google Scholar] [CrossRef]
- Kokusho, T.; Kaneko, Y. Energy evaluation for liquefaction-induced strain of loose sands by harmonic and irregular loading tests. Soil Dyn. Earthquake Eng. 2018, 114, 362–377. [Google Scholar] [CrossRef]
- Kokusho, T.; Tanimoto, S. Energy capacity versus liquefaction strength investigated by cyclic triaxial tests on intact soils. J. Geotech. Geoenviron. Eng. 2021, 147, 04021006. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Pan, K.; Yang, Z.X. Energy-based assessment of cyclic liquefaction behavior of clean and silty sand under sustained initial stress conditions. Soil Dyn. Earthquake Eng. 2023, 164, 107609. [Google Scholar] [CrossRef]
- Polito, C.P.; Moldenhauer, H.H.M. Energy dissipation and pore pressure generation in stress− and strain−controlled cyclic triaxial tests. Geotech. Test. J. 2019, 42, 1083–1089. [Google Scholar] [CrossRef]
- Yang, Z.X.; Pan, K. Energy-based approach to quantify cyclic resistance and pore pressure generation in anisotropically consolidated sand. J. Mater. Civ. Eng. 2018, 30, 04018203. [Google Scholar] [CrossRef]
- Booker, J.R.; Rahman, M.S.; Seed, H.B. GADFLEA—A Computer Program for the Analysis of Pore Pressure Generation and Dissipation During Cyclic or Earthquake Loading; Report No. EERC 76-24; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1976; p. 69. [Google Scholar]
- JGS 0111–2009; JGS 0111 Test Method for Density of Soil Particles. Japanese Geotechnical Society: Tokyo, Japan, 2009.
- JGS 0162–2009; JGS 0162 Test Method for Minimum and Maximum Densities of Gravels. Japanese Geotechnical Society: Tokyo, Japan, 2009.
- Ishihara, K. Liquefaction and flow failure during earthquakes. Geotechnique 1993, 43, 351–451. [Google Scholar] [CrossRef]
- Idriss, I.M.; Boulanger, R.W. Soil Liquefaction During Earthquake; Monograph MNO-12; Earthquake Engineering Research Institute: Oakland, CA, USA, 2008; p. 261. [Google Scholar]
- Seed, H.B.; Martin, P.P.; Lysmer, J. The Generation and Dissipation of Pore Water Pressures During Soil Liquefaction. Report No. EERC 75-26; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1975; p. 47. [Google Scholar]
- Hubler, J.F. Laboratory and In-Situ Assessment of Liquefaction of Gravelly Soils. Ph.D. Thesis, The University of Michigan, Ann Arbor, MI, USA, 2017. [Google Scholar]
- Pan, K.; Yang, Z.X. Evaluation of the liquefaction potential of sand under random loading conditions: Equivalent approach versus energy−based method. J. Earthquake Eng. 2020, 24, 59–83. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M.; Arango, I. Evaluation of liquefaction potential using field performance data. J. Geotech. Eng. 1983, 109, 458–482. [Google Scholar] [CrossRef]
- Boulanger, R.W.; Idriss, I.M. Liquefaction susceptibility criteria for silts and clays. J. Geotech. Geoenviron. Eng. 2006, 132, 1413–1426. [Google Scholar] [CrossRef]
- Simcock, K.; Davis, R.; Berrill, J.; Mullenger, G. Cyclic triaxial tests with continuous measurement of dissipated energy. Geotech. Test. J. 1983, 6, 35–39. [Google Scholar] [CrossRef]
- Berrill, J.B.; Davis, R.O. Energy dissipation and seismic liquefaction of sands: Revised model. Soils Found. 1985, 25, 106–118. [Google Scholar] [CrossRef]
- Yamazaki, F.; Towhata, I.; Ishihara, K. Numerical model for liquefaction problem under multi-directional shearing on horizontal plane. In Proceedings of the 5th International Conference on Numerical Methods in Geomechanics, Nagoya, Japan, 1–5 April 1985; pp. 399–406. [Google Scholar]
- Law, K.T.; Cao, Y.L.; He, G.N. An energy approach for assessing seismic liquefaction potential. Canadian Geotech. J. 1990, 27, 3. [Google Scholar] [CrossRef]
- Yanagisawa, E.; Sugano, T. Undrained shear behaviors of sand in view of shear work. In Proceedings of the 13th International Conference on Soil Mechanics and Foundation Engineering (Special Volume on Performance of Ground and Soil Structures during Earthquakes), New Delhi, India, 5–10 January 1994; pp. 155–158. [Google Scholar]
- Liang, L. Development of an Energy Method for Evaluating the Liquefaction Potential of a Soil Deposit. Ph.D. Thesis, Department of Civil Engineering, Case Western Reserve University, Cleveland, OH, USA, 1995. [Google Scholar]
- Wang, G.; Takemura, J.; Kuwano, J. Evaluation of excess pore water pressure of intermediate soils due to cyclic loading by energy method. In Proceedings of the Conference of Computer Methods and Advances in Geomechanics (Yuan), Morgantown, WV, USA, 22–28 May 1994; A.A. Balkema Publishers: Rotterdam, The Netherlands, 1994. [Google Scholar]
- Polito, C. The Effects of Non-Plastic and Plastic Fines on the Liquefaction of Sandy Soils. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1999. [Google Scholar]
- Davis, R.O.; Berrill, J.B. Pore pressure and dissipated energy in earthquake—Field verification. J. Geotech. Geoenviron. Eng. 2001, 127, 269–274. [Google Scholar] [CrossRef]
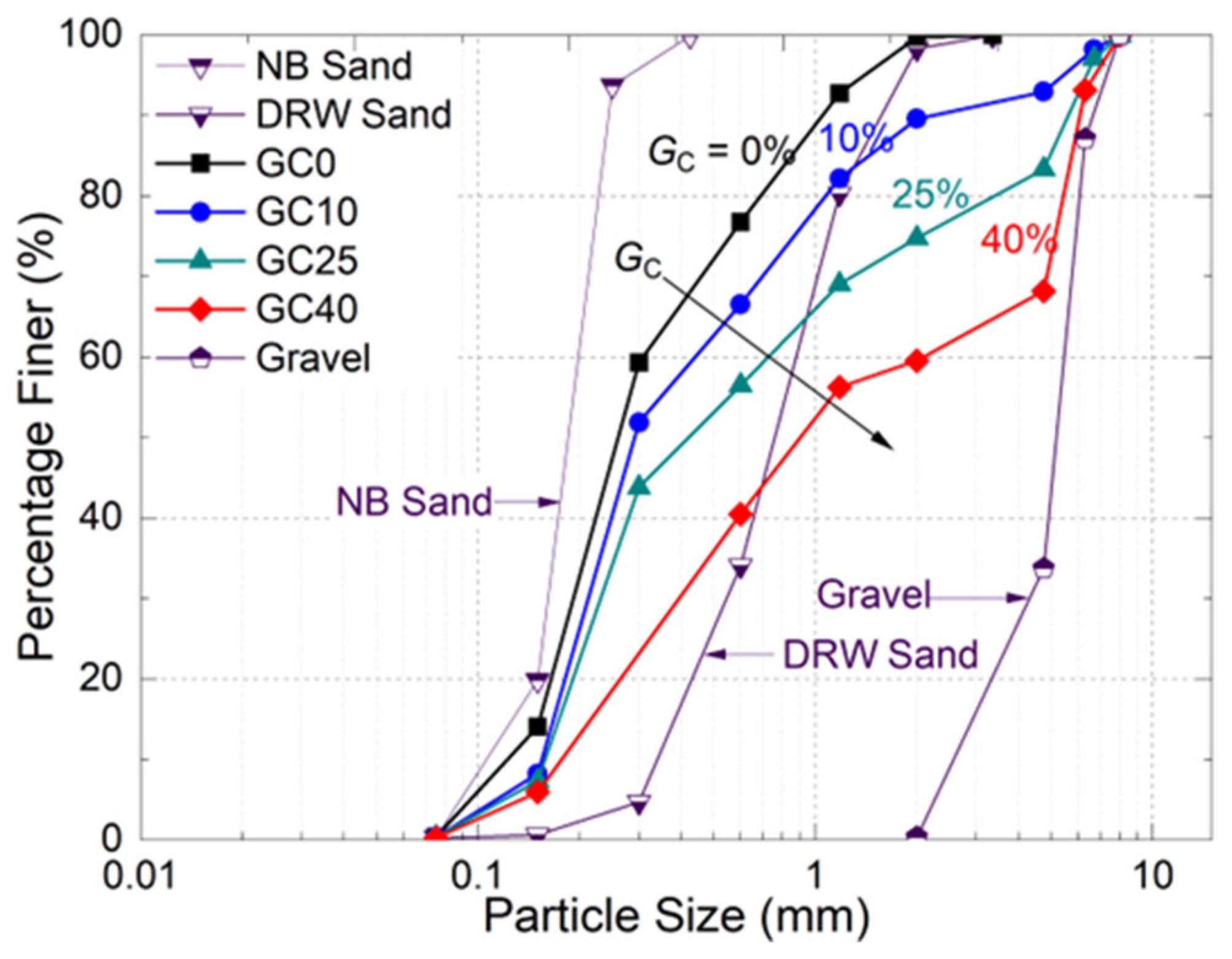





| Materials | Gc (%) | D50 (mm) | Gs | emax | emin | Cu | Cc |
|---|---|---|---|---|---|---|---|
| GC0 | 0 | 0.26 | 2.66 | 0.889 | 0.538 | 2.50 | 0.90 |
| GC10 | 10 | 0.29 | 2.66 | 0.739 | 0.494 | 2.77 | 0.66 |
| GC25 | 25 | 0.41 | 2.66 | 0.632 | 0.415 | 4.50 | 0.42 |
| GC40 | 40 | 0.90 | 2.66 | 0.520 | 0.343 | 11.76 | 0.47 |
| Test | GC (%) | Dr* (%) | Dr (%) | Dr,ic (%) | CSR | ru ≥ 0.95 | εSA = 5% | N/NL | ru = f(WF) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NL | WL | CRRL | WL* | NF | WF | CRRF | WF* | α | R2 | β | R2 | ||||||
| 1 | 0 | 25 | 29.7 | 31.5 | 0.202 | 6.7 | 0.0141 | 0.178 | 0.014 | 7.0 | 0.0189 | 0.178 | 0.018 | 0.93 | 0.99 | 360 | 0.96 |
| 2 | 28.6 | 32.4 | 0.170 | 17.5 | 0.0141 | 17.6 | 0.0175 | 0.59 | 0.96 | 269 | 0.93 | ||||||
| 3 | 31.1 | 33.1 | 0.145 | 56.3 | 0.0153 | 56.6 | 0.0182 | 0.39 | 0.85 | 147 | 0.98 | ||||||
| 4 | 45 | 46.3 | 47.2 | 0.348 | 4.6 | 0.0385 | 0.279 | 0.041 | 4.8 | 0.0558 | 0.279 | 0.057 | 0.67 | 0.91 | 104 | 0.95 | |
| 5 | 46.6 | 50.8 | 0.255 | 24.0 | 0.0428 | 24.6 | 0.0643 | 0.68 | 0.95 | 75 | 0.95 | ||||||
| 6 | 45.1 | 48.0 | 0.200 | 84.7 | 0.0424 | 85.6 | 0.0490 | 0.73 | 0.92 | 86 | 0.93 | ||||||
| 7 | 55 | 55.0 | 56.9 | 0.340 | 8.7 | 0.0443 | 0.309 | 0.045 | 9.8 | 0.0582 | 0.315 | 0.061 | 1.98 | 0.93 | 133 | 0.95 | |
| 8 | 56.0 | 59.5 | 0.316 | 13.0 | 0.0428 | 13.7 | 0.0674 | 0.60 | 0.96 | 73 | 0.98 | ||||||
| 9 | 57.0 | 60.4 | 0.285 | 23.6 | 0.0473 | 24.7 | 0.0576 | 0.54 | 0.94 | 78 | 0.98 | ||||||
| 10 | 10 | 25 | 28.6 | 31.5 | 0.200 | 11.0 | 0.0169 | 0.193 | 0.017 | 11.6 | 0.0251 | 0.194 | 0.026 | 0.80 | 0.98 | 336 | 0.96 |
| 11 | 25.9 | 28.9 | 0.182 | 28.0 | 0.0201 | 28.6 | 0.0309 | 0.75 | 0.93 | 186 | 0.92 | ||||||
| 12 | 25.9 | 30.5 | 0.176 | 24.0 | 0.0156 | 24.6 | 0.0248 | 0.49 | 0.95 | 224 | 0.97 | ||||||
| 13 | 26.7 | 28.9 | 0.152 | 96.0 | 0.0197 | 97.6 | 0.0335 | 0.60 | 0.89 | 144 | 0.95 | ||||||
| 14 | 35 | 35.5 | 38.8 | 0.260 | 8.7 | 0.0239 | 0.236 | 0.024 | 9.7 | 0.0365 | 0.239 | 0.039 | 1.19 | 0.97 | 217 | 0.95 | |
| 15 | 34.9 | 36.7 | 0.227 | 16.0 | 0.0212 | 17.6 | 0.0403 | 0.84 | 0.98 | 206 | 0.96 | ||||||
| 16 | 34.8 | 36.7 | 0.180 | 94.0 | 0.0306 | 95.6 | 0.0518 | 0.59 | 0.86 | 79 | 0.95 | ||||||
| 17 | 45 | 47.9 | 49.5 | 0.317 | 7.8 | 0.0370 | 0.288 | 0.039 | 8.8 | 0.0513 | 0.292 | 0.056 | 1.75 | 0.94 | 149 | 0.96 | |
| 18 | 45.0 | 47.4 | 0.286 | 15.6 | 0.0379 | 16.6 | 0.0563 | 0.72 | 0.99 | 107 | 0.98 | ||||||
| 19 | 50.4 | 50.9 | 0.257 | 30.0 | 0.0415 | 32.7 | 0.0680 | 0.95 | 0.98 | 99 | 0.94 | ||||||
| 20 | 25 | 25 | 25.8 | 30.0 | 0.227 | 6.0 | 0.0151 | 0.207 | 0.022 | 6.1 | 0.0250 | 0.208 | 0.035 | 0.73 | 0.99 | 360 | 0.98 |
| 21 | 23.9 | 26.7 | 0.206 | 46.0 | 0.0265 | 47.6 | 0.0442 | 0.48 | 0.94 | 129 | 0.95 | ||||||
| 22 | 26.2 | 30.2 | 0.203 | 39.8 | 0.0286 | 41.7 | 0.0448 | 0.70 | 0.97 | 147 | 0.91 | ||||||
| 23 | 24.1 | 30.2 | 0.182 | 22.0 | 0.0175 | 22.1 | 0.0226 | 0.64 | 0.96 | 302 | 0.96 | ||||||
| 24 | 26.4 | 30.0 | 0.158 | 78.0 | 0.0255 | 78.7 | 0.0431 | 0.40 | 0.89 | 108 | 0.97 | ||||||
| 25 | 35 | 35.2 | 37.8 | 0.265 | 13.0 | 0.0330 | 0.258 | 0.031 | 14.2 | 0.0661 | 0.262 | 0.062 | 1.00 | 0.99 | 146 | 0.93 | |
| 26 | 32.1 | 37.4 | 0.240 | 23.0 | 0.0258 | 23.7 | 0.0359 | 0.69 | 0.97 | 157 | 0.97 | ||||||
| 27 | 40 | 40.7 | 46.0 | 0.305 | 11.0 | 0.0310 | 0.292 | 0.032 | 13.6 | 0.0663 | 0.298 | 0.066 | 1.22 | 0.98 | 131 | 0.95 | |
| 28 | 39.4 | 45.3 | 0.262 | 37.0 | 0.0349 | 39.7 | 0.0654 | 0.38 | 0.98 | 67 | 0.99 | ||||||
| 29 | 40.3 | 47.3 | 0.255 | 36.0 | 0.0423 | 38.7 | 0.0921 | 0.64 | 0.45 | 62 | 0.95 | ||||||
| 30 | 45 | 44.7 | 52.1 | 0.397 | 5.0 | 0.0337 | 0.326 | 0.040 | 7.7 | 0.0777 | 0.346 | 0.091 | 2.14 | 0.93 | 147 | 0.97 | |
| 31 | 44.7 | 52.5 | 0.351 | 11.0 | 0.0435 | 15.7 | 0.0976 | 2.17 | 0.89 | 134 | 0.94 | ||||||
| 32 | 46.5 | 52.4 | 0.300 | 22.0 | 0.0369 | 27.7 | 0.0982 | 0.91 | 0.97 | 88 | 0.94 | ||||||
| 33 | 48.1 | 54.1 | 0.245 | 73.0 | 0.0517 | 78.7 | 0.1101 | 0.44 | 0.96 | 54 | 0.99 | ||||||
| 34 | 55 | 54.4 | 61.4 | 0.481 | 12.0 | 0.1031 | 0.425 | 0.099 | 15.7 | 0.1720 | 0.470 | 0.156 | 3.38 | 0.78 | 83 | 0.93 | |
| 35 | 55.5 | 59.8 | 0.478 | 10.0 | 0.0820 | 14.7 | 0.1575 | 3.56 | 0.77 | 94 | 0.95 | ||||||
| 36 | 55.3 | 60.0 | 0.366 | 20.0 | 0.1119 | 20.7 | 0.1361 | 0.77 | 0.98 | 57 | 0.99 | ||||||
| 37 | 56.5 | 61.1 | 0.274 | 54.0 | 0.1110 | 60.8 | 0.1992 | 0.79 | 0.99 | 67 | 0.96 | ||||||
| 38 | 40 | 25 | 24.4 | 25.6 | 0.251 | 10.0 | 0.0167 | 0.241 | 0.019 | 11.2 | 0.0417 | 0.243 | 0.044 | 0.92 | 0.99 | 243 | 0.97 |
| 39 | 25.7 | 31.5 | 0.247 | 15.0 | 0.0247 | 16.6 | 0.0480 | 0.88 | 0.98 | 167 | 0.95 | ||||||
| 40 | 25.6 | 29.4 | 0.233 | 16.0 | 0.0167 | 17.6 | 0.0414 | 0.79 | 0.98 | 199 | 0.96 | ||||||
| 41 | 25.8 | 29.4 | 0.208 | 53.0 | 0.0187 | 74.8 | 0.0387 | 1.00 | 0.99 | 163 | 0.97 | ||||||
| 42 | 45 | 47.8 | 51.5 | 0.421 | 13.0 | 0.0867 | 0.391 | 0.086 | 22.7 | 0.2523 | 0.472 | 0.226 | 2.23 | 0.9 | 68 | 0.96 | |
| 43 | 46.3 | 50.3 | 0.341 | 20.0 | 0.0851 | 26.8 | 0.1888 | 1.49 | 0.91 | 104 | 0.95 | ||||||
| 44 | 45.8 | 48.4 | 0.277 | 47.7 | 0.0898 | 59.8 | 0.2627 | 0.96 | 0.92 | 60 | 0.99 | ||||||
| Reference | CRR Criterion | A | B | C | R2 |
|---|---|---|---|---|---|
| This study | = 1%, NL = 15 | 0.054 | 0.087 | −0.004 | 0.97 |
| = 3%, NL = 15 | 0.497 | −0.049 | 0.006 | 0.99 | |
| = 5%, NL = 15 | 0.623 | −0.046 | 0.006 | 0.99 | |
| = 1, NL = 15 | 1.177 | −0.367 | 0.044 | 0.97 | |
| = 5%, NL = 15 | 1.383 | −0.331 | 0.040 | 0.93 | |
| Kokusho and Tanimoto [39] | = 5%, NL = 15 | 2.7 | −0.54 | 0.035 | 0.92 |
| Zhou et al. [40] | = 5%, NL = 20 | 1.27 | −0.272 | 0.0189 | - |
| GC (%) | 0 | 10 | 25 | 40 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dr (%) | 31–33 | 47–51 | 57–60 | 29–32 | 37–39 | 47–91 | 27–30 | 37–38 | 45–47 | 52–54 | 60–61 | 26–32 | 48–52 |
| 199.8 | 82.6 | 77.85 | 186.8 | 110.9 | 106.9 | 177.8 | 153.3 | 70.74 | 69.19 | 67.78 | 178.6 | 70.21 | |
| R2 | 0.88 | 0.94 | 0.98 | 0.91 | 0.84 | 0.95 | 0.85 | 0.95 | 0.92 | 0.91 | 0.95 | 0.95 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pokhrel, A.; Chiaro, G. Pore Water Pressure Generation and Energy Dissipation Characteristics of Sand–Gravel Mixtures Subjected to Cyclic Loading. Geotechnics 2024, 4, 1282-1303. https://doi.org/10.3390/geotechnics4040065
Pokhrel A, Chiaro G. Pore Water Pressure Generation and Energy Dissipation Characteristics of Sand–Gravel Mixtures Subjected to Cyclic Loading. Geotechnics. 2024; 4(4):1282-1303. https://doi.org/10.3390/geotechnics4040065
Chicago/Turabian StylePokhrel, Abilash, and Gabriele Chiaro. 2024. "Pore Water Pressure Generation and Energy Dissipation Characteristics of Sand–Gravel Mixtures Subjected to Cyclic Loading" Geotechnics 4, no. 4: 1282-1303. https://doi.org/10.3390/geotechnics4040065
APA StylePokhrel, A., & Chiaro, G. (2024). Pore Water Pressure Generation and Energy Dissipation Characteristics of Sand–Gravel Mixtures Subjected to Cyclic Loading. Geotechnics, 4(4), 1282-1303. https://doi.org/10.3390/geotechnics4040065









