Landslide Analysis with Incomplete Data: A Framework for Critical Parameter Estimation
Abstract
1. Introduction
- Historic landslides;
- Landslides unsafe for investigation;
- Landslide-dense areas with limited resources for individual investigation;
- Landslide studies that require interpolation between data points;
- Landslide studies lacking testing/instrumentation or exploration resources.
2. Materials and Methods
- Original slope topography and slide geometry;
- Depth to failure plane;
- Depth to water table;
- Material property parameters.
2.1. Available Data and Estimation Techniques
2.1.1. Original Slope Topography
2.1.2. Depth to Failure Plane
2.1.3. Depth to Water Table
2.1.4. Material Property Parameters
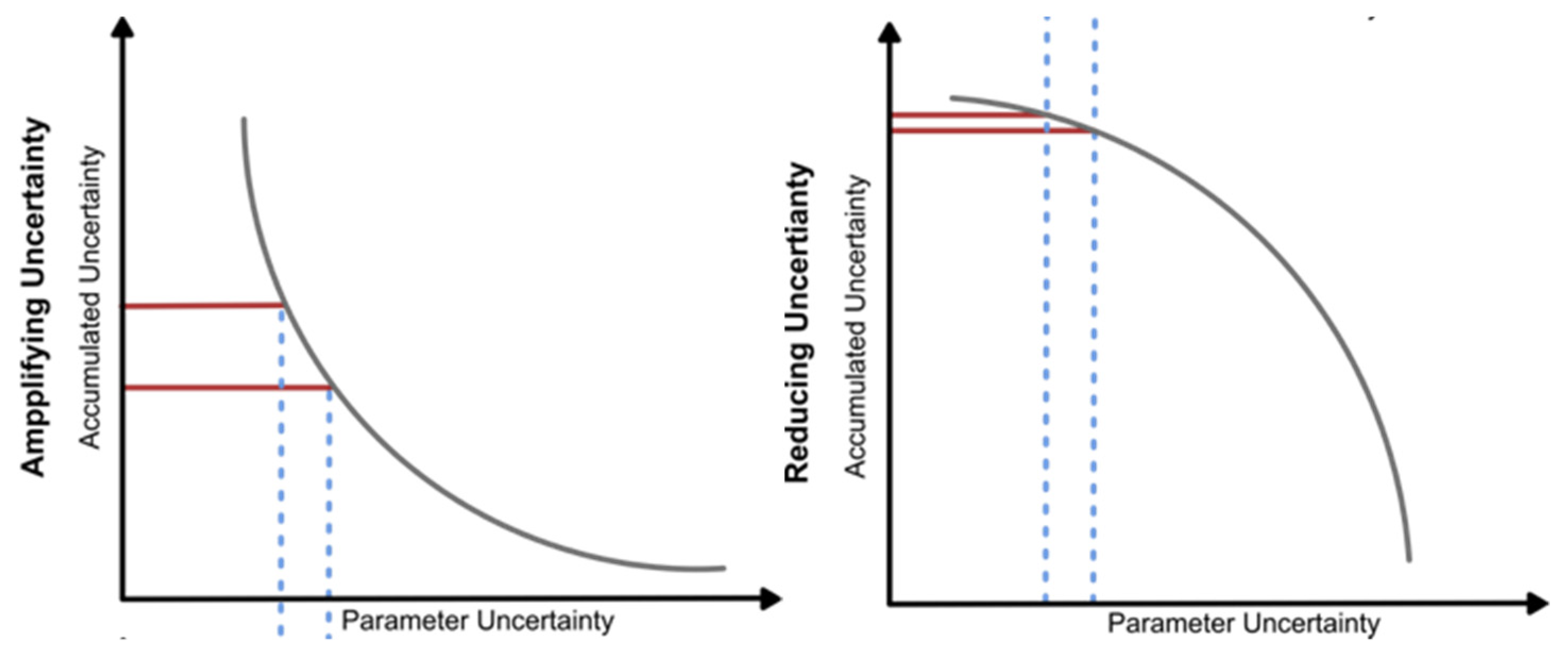
2.2. Uncertainty Relationships
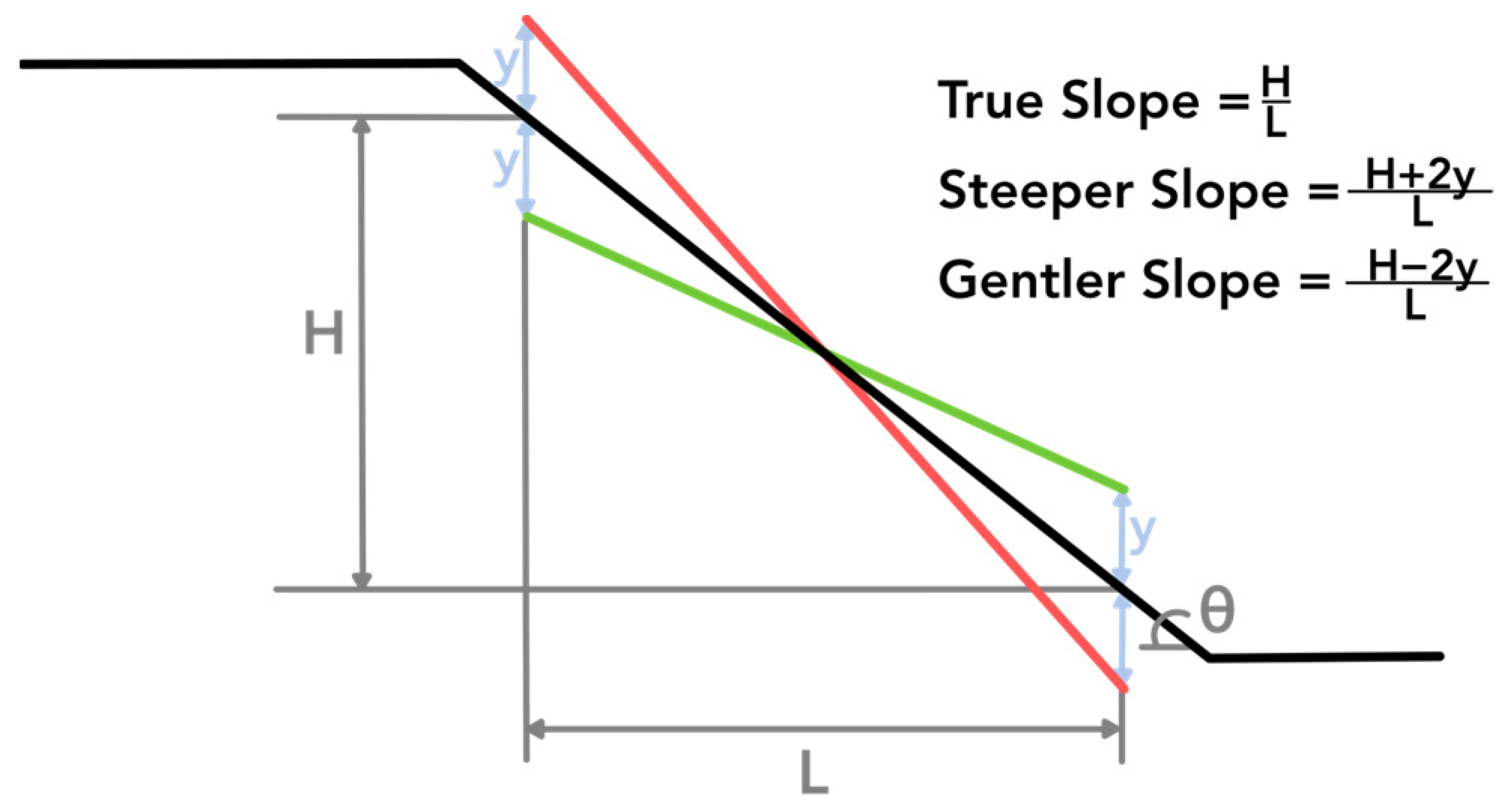
2.2.1. Original Slope Topography
2.2.2. Depth to Failure Plane
2.2.3. Depth to Water Table
2.2.4. Material Property Parameters
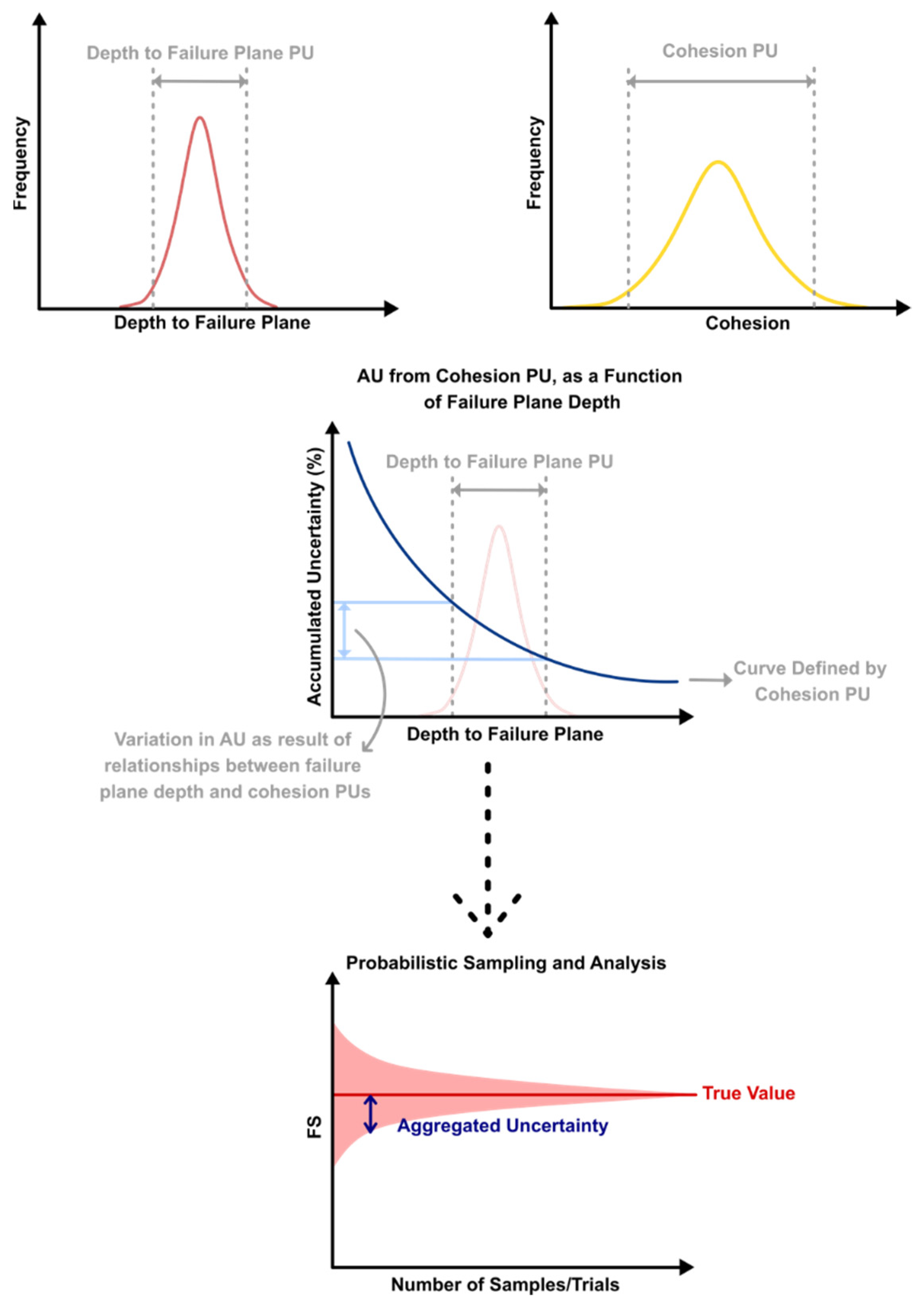
2.2.5. Critical Fields of Rapidly Accumulating Uncertainty
3. Results
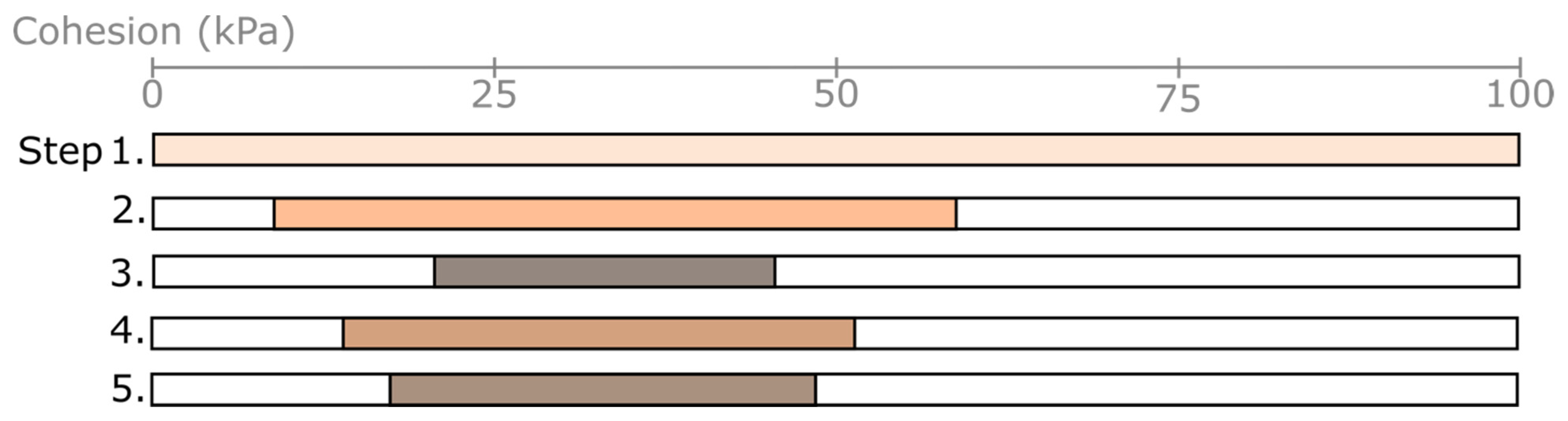
- Begin with the full range of material properties values based on data available
- Based on initial computational results, halve the length of the initial range, centered on a preferred estimated value from either literature or other available data at the site
- Based on computational results, repeat Step 2 based on engineering judgment and results of sensitivity analyses in back modeling (i.e., halve the range again if the results of Step 2 return tails far beyond FS = 1 when back modeling)
- If the range of a prior step is too narrow (does not reasonably span the values which result in an FS near 1) expand the range along the same center by fifty percent (twenty-five percent in either direction) to capture more likely values
- If it is desired, to slightly narrow the range of a prior step, final adjustments on either end of the distribution should be made.
3.1. Efficacy and Example
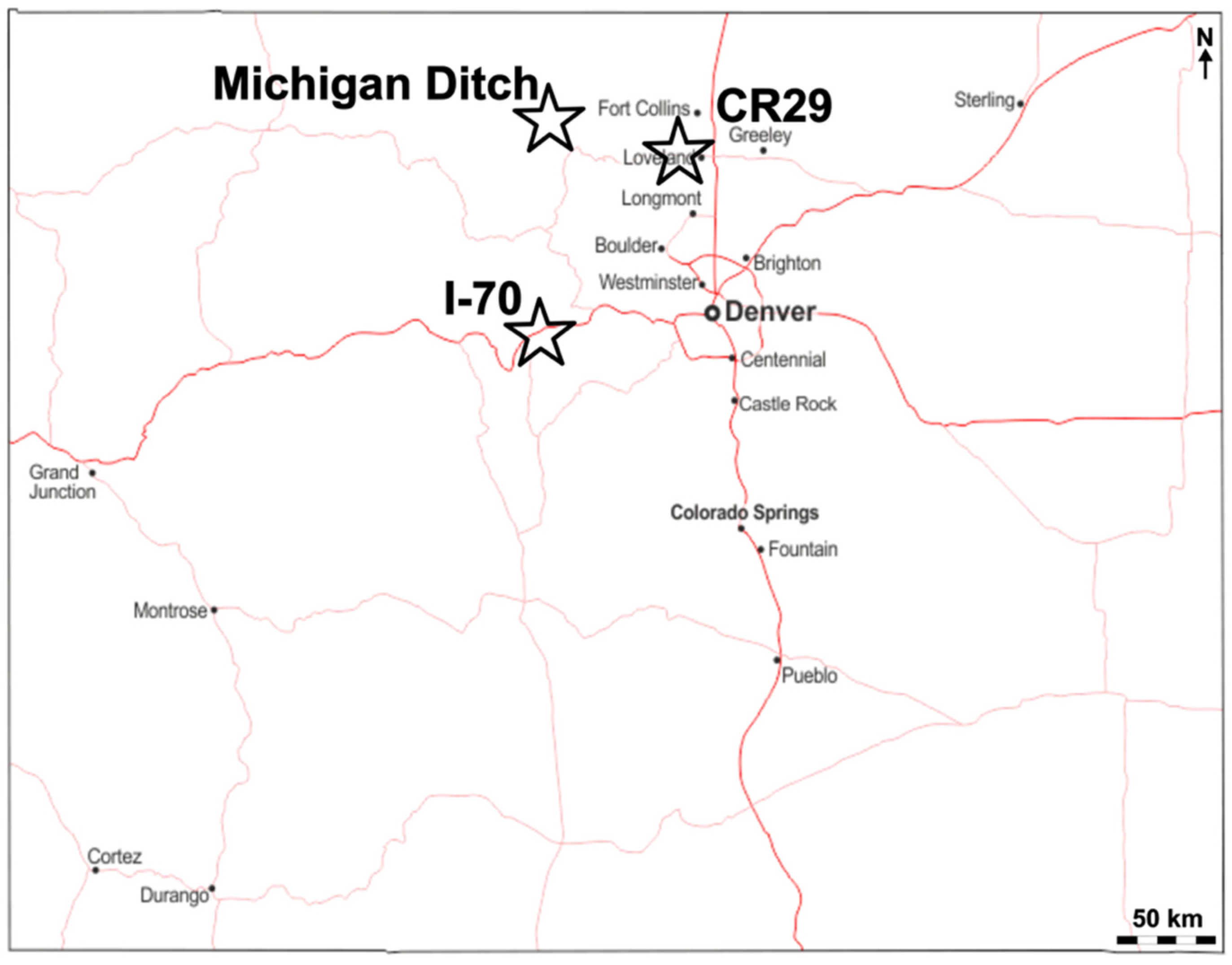
3.1.1. Test Site
3.1.2. Available Data
3.1.3. Application of the PEP Model
3.1.4. Agreement with the LT/FI Model Findings
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duncan, M. Soil Slope Stability Analysis. In Landslide Investigation and Mitigation; Transportation Resource Board Special Report 247; Turner, A., Schuster, R., Eds.; National Research Council, National Academy Press: Washington, DC, USA, 1996; pp. 337–371. [Google Scholar]
- Lee, J.; Sameen, M.; Pradhan, B.; Park, H. Modeling landslide susceptibility in data-scarce environments using optimized data mining and statistical methods. Geomorphology 2018, 303, 284–298. [Google Scholar] [CrossRef]
- Hammond, C.; Hall, D.; Miller, S.; Swetik, P. Level I Stability Analysis (LISA) Documentation for Version 2.0; General Technical Report INT-285; USDA, Forest Service, Intermountain Research Station: Ogden, UT, USA, 1992.
- Vaze, J.; Teng, J. High resolution LiDAR DEM-How good is it? In Proceedings of the MODSIM07 Conference, Virginia Beach, VA, USA, 11–13 September 2007. [Google Scholar]
- Bater, C.; Coops, N. Evaluating error associated with lidar-derived DEM interpolation. Comput. Geosci. 2009, 35, 289–300. [Google Scholar] [CrossRef]
- Mukherjee, S.; Joshi, P.; Mukherjee, S.; Gosh, A.; Garg, R.; Mukhopadhyay, A. Evaluation of vertical accuracy of open source Digital Elevation Model (DEM). Int. J. Appl. Earth Obs. Geoinf. 2012, 21, 205–217. [Google Scholar] [CrossRef]
- Schlögel, R.; Marchesini, I.; Alviolo, M.; Reichenbach, P.; Rossi, M.; Malet, J. Optimizing landslide susceptibility zonation: Effects of DEM spatial resolution and slope unit delineation on logistic regression models. Geomorphology 2018, 301, 10–20. [Google Scholar] [CrossRef]
- Smith, T.; Rheinwalt, A.; Bookhagen, B. Determining the optimal grid resolution for topographic analysis on an airborne lidar dataset. Earth Surf. Dyn. 2019, 7, 475–489. [Google Scholar] [CrossRef]
- Wechsler, S.; Kroll, C. Quantifying DEM Uncertainty and its Effect on Topographic Parameters. Photogram Eng. Remote Sens. 2006, 72, 1081–1090. [Google Scholar] [CrossRef]
- Amante, C. Estimating Coastal Digital Elevation Model Uncertainty. J. Coast. Res. 2018, 34, 1382–1397. [Google Scholar] [CrossRef]
- Chang, K.; Merghadi, A.; Yunus, A.; Pham, B.; Dou, J. Evaluating scale effects of topographic variables in landslide susceptibility models using GIS-based machine learning techniques. Sci. Rep. 2019, 9, 12296. [Google Scholar] [CrossRef]
- Chidi, C.; Zhao, W.; Chaudhary, S.; Xiong, D.; Wu, Y. Sensitivity Assessment of Spatial Resolution Difference in DEM for Soil Erosion Estimation Based on UAV Observations: An Experiment on Agriculture Terraces in the Middle Hill of Nepal. ISPRS Int. J. Geo-Inf. 2021, 10, 28. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mukherjee, S.; Bhardwaj, A.; Mukhopadhyay, A.; Garg, R.; Hazra, S. Accuracy of cartostst-1 DEM and its derived attribute at multiple scale representations. J. Earth Syst. Sci. 2015, 124, 487–495. [Google Scholar] [CrossRef][Green Version]
- ASPRS. Positional Accuracy Standards for Digital Geospatial Data. Photogramm. Eng. Remote Sens. 2015, 81, A1–A26. [Google Scholar] [CrossRef]
- Wang, T.; Liu, J.; Shi, J.; Wu, S. The influence of DEM resolution on seismic landslide hazard assessment based upon the Newmark displacement method: A case study in the loess area of Tianshui, China. Environ. Earth Sci. 2017, 76, 1–10. [Google Scholar] [CrossRef]
- Arundel, S.; Archuleta, C.; Phillips, L.; Roche, B.; Constance, E. USGS National Geospatial Program 1-Meter Digital Elevation Model Specification; Chapter 7 of Section, B. In USGS Standards, Book 11, Collection and Delineation of Spatial Data: Techniques and Methods; US Geological Survey: Reston, VA, USA, 2015. [Google Scholar] [CrossRef]
- Gesch, D.; Oimoen, M.; Evans, G. Accuracy Assessment of the U.S. Geological Survey National Elevation Dataset, and Comparison with Other Large-Area Elevation Datasets-SRTM and ASTER; USGS Open-File Report 2014-1008; US Geological Survey: Reston, VA, USA, 2014. [CrossRef]
- Santillan, J.; Makinano-Santillan, M. Vertical Accuracy Assessment of 30-m Resolution ALOS, ASTER and SRTM Global DEMs over Northeastern Mindanao, Philippines. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B4, 149–156. [Google Scholar] [CrossRef]
- Graber, A.; Santi, P.; Meza Arestegui, P. Constraining the critical groundwater conditions for initiation of large, irrigation-induced landslides, Siguas River Valley, Peru. Landslides 2021, 18, 3753–3767. [Google Scholar] [CrossRef]
- Zangerl, C.; Schneeberger, A.; Steiner, G.; Mergili, M. Geographic-information-system-based topographic reconstruction and geomechanical modelling of the Köfels rockslide. Nat. Hazard. Earth Sys. Sci. 2021, 21, 2461–2483. [Google Scholar] [CrossRef]
- Steger, S.; Schmaltz, E.; Glade, T. The (f)utility to account for pre-failure topography in data-driven landslide susceptibility modelling. Geomorphology 2020, 354, 107041. [Google Scholar] [CrossRef]
- Paulin, G.; Mickelson, K.; Contreras, T.; Galllin, W.; Jacobacci, K.; Bursik, M. Assessing landslide volume using two generic models: Application to landslides in Whatcom County, Washington, USA. Landslides 2022, 19, 901–912. [Google Scholar] [CrossRef]
- Köpfli, P.; Gräminger, L.; Moore, J.; Vockenhuber, C.; Ivy-Ochs, S. The Oeschinensee rock avalanche, Bernese Alps, Switzerland: A co-seismic failure 2300 years ago? Swiss J. Geosci. 2018, 111, 205–219. [Google Scholar] [CrossRef]
- Cruden, D.; Varnes, D. Landslide Types and Processes. In Landslide Investigation and Mitigation; Transportation Resource Board Special Report 247; Turner, A., Schuster, R., Eds.; National Research Council, National Academy Press: Washington, DC, USA, 1996; pp. 36–75. [Google Scholar]
- Hutchinson, J. Method of Locating Slip Surfaces in Landslides. Bull. Assoc. Eng. Geol. 1983, XX, 235–252. [Google Scholar] [CrossRef]
- Chiliza, S.; Hingston, E. Back analysis of an ancient rockslide at Lake Fundudzi, Limpopo Province, South Africa. Bull. Eng. Geol. Environ. 2018, 77, 29–47. [Google Scholar] [CrossRef]
- Carter, M.; Bentley, S. The geometry of slip surfaces beneath landslides: Predictions from surface measurements. Can. Geotech. J. 1985, 22, 234–238. [Google Scholar] [CrossRef]
- Guzzetti, F.; Ardizzone, F.; Cardinali, M.; Rossi, M.; Valigi, D. Landslide volumes and landslide mobilization rates in Umbria, central Italy. Earth Planet. Sci. Lett. 2009, 279, 222–229. [Google Scholar] [CrossRef]
- Booth, A.; Lamb, M.; Avouac, J.; Delacourt, C. Landslide velocity, thickness, and rheology from remote sensing: La Clapière landslide, France. Geophys. Res. Lett. 2013, 40, 4299–4304. [Google Scholar] [CrossRef]
- Jakobson, B. The Landslide at Suerte on the Göta River: Royal Swedish Geotechnical Institute Proceedings; No. 5; Royal Swedish Geotechnical Institute: Stockholm, Sweden, 1952. [Google Scholar]
- Bishop, K. Determination of translational landslide slip surface depth using balanced cross sections. Environ. Eng. Geosci. 1999, 5, 147–156. [Google Scholar] [CrossRef]
- Chase, R.; Chase, K.; Kehew, A.; Montgomery, W. Determining the kinematics of slope movements using low-cost monitoring. Environ. Eng. Geosci. 2001, 7, 193–203. [Google Scholar] [CrossRef]
- Oppikofer, T.; Böhme, M.; Nicolet, P.; Penna, I.; Hermanns, R. Metodikk for Konsekvensanalyse av Fjellskred; NGU report 2016.047; Geological Survey of Norway: Trondheim, Norway, 2016. [Google Scholar]
- Jaboyedoff, M.; Carrea, D.; Derron, M.; Oppikofer, T.; Penna, I.; Rudaz, B. A review of methods used to estimate initial landslide failure surface depths and volumes. Eng. Geol. 2020, 267, 105478. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Derron, M. Methods to estimate the surface geometry and uncertainty of landslide failure surface. Eng. Geol. Soc. Territ. 2015, 2, 339–343. [Google Scholar] [CrossRef]
- Prajapati, G.; Jaboyedoff, M. Method to estimate the initial landslide failure surface and volumes using grid points and spline curves in MATLAB. Landslides 2022, 19, 2997–3008. [Google Scholar] [CrossRef]
- Oppikofer, T.; Jaboyeoff, M.; Pedrazzini, A.; Derron, M.; Blikra, L. Detailed DEM analysis of a rockslide scar to characterize the basal sliding surface of active rockslides. J. Geophys. Res. Earth Surf. 2011, 116, 1–22. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Baillifard, F.; Couture, R.; Locat, J.; Locat, P. Toward preliminary hazard assessment using DEM topographic analysis and simple mechanic modelling by mean of the sloping local base level. In Landslides: Evaluation and Stabilization; Lacerda, W., Ehrlich, M., Fontoura, A., Sayao, A., Eds.; Taylor & Francis Group: London, UK, 2004; pp. 199–204. [Google Scholar]
- Jaboyedoff, M.; Couture, R.; Locat, P. Structural analysis of Turtle Mountain (Alberta) using digital elevation model: Toward a progressive failure. Geomorphology 2009, 103, 5–16. [Google Scholar] [CrossRef]
- Snyder, D. Estimated depth to ground water and configuration of the water table in the Portland, Oregon area: U.S. Geol. Surv. Sci. Investig. Rep. 2008, 40, 2008–5059. Available online: http://pubs.usgs.gov/sir/2008/5059/ (accessed on 28 May 2024).
- Agostini, A.; Tofanu, V.; Nolesini, T.; Gigli, G.; Tanteri, L.; Rosi, A.; Cardellini, S.; Casagli, N. A new appraisal of the Ancona landslide based on geotechnical investigations and stability modelling. Q. J. Eng. Geo Hydrogeol. 2014, 47, 29–43. [Google Scholar] [CrossRef]
- Cloutier, C.; Locat, J.; Couture, R.; Jaboyedoff, M. The anatomy of an active slide: The Gascons rockslide, Québec, Canada. Landslides 2016, 13, 241–258. [Google Scholar] [CrossRef]
- Wayllace, A.; Thunder, B.; Lu, N.; Khan, A.; Godt, J. Hydrologic behavior of an infiltration-induced landslide in Colorado, USA. Geofluids 2019, 2019, 1659303. [Google Scholar] [CrossRef]
- O’Brien, G.; Cox, S.; Townend, J. Spatially and temporally systematic hydrologic changes within large geoengineered landslides, Cromwell Gorge, New Zealand, induced by multiple regional earthquakes. J. Geophys. Res. Solid. Earth 2016, 121, 8750–8773. [Google Scholar] [CrossRef]
- Nagy-Göde, F.; Török, Á. Rainfall-Induced or Lake-Water-Level-Controlled Landslide? An Example from the Steep Slopes of Lake Balaton, Hungary. Water 2022, 14, 1169. [Google Scholar] [CrossRef]
- Coutinho, R.; Silva, M.; Santos, A.; Lacerda, W. Geotechnical Characterization and Failure Mechanism of Landslide in Granite Residual Soil. J. Geotech. Geoenviron. Eng. 2019, 145, 05019004. [Google Scholar] [CrossRef]
- Liang, X.; Gui, L.; Wang, W.; Du, J.; Ma, F.; Yin, K. Characterizing the development pattern of a colluvial landslide based on long-term monitoring in the Three Gorges Reservoir. Remote Sens. 2021, 13, 224. [Google Scholar] [CrossRef]
- Carey, J.; Moore, R.; Petley, D. Patterns of movement in the Ventnor landslide complex, Isle of Wight, southern England. Landslides 2015, 12, 1107–1118. [Google Scholar] [CrossRef]
- Macfarlane, D. Observations and predictions of the behaviour of large, slow-moving landslides in shist, Clyde Dam reservoir, New Zealand. Eng. Geol. 2009, 109, 5–15. [Google Scholar] [CrossRef]
- Clarke, D. A Phenomenal Landslide. Trans. ASCE 1904, 53, 321–411. [Google Scholar]
- Cornforth, D.C. Washington Park Reservoirs Slide. In Landslides in Practice; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 485–495. [Google Scholar]
- Cornforth, D.C. Pelton Park Slide. In Landslides in Practice; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 514–519. [Google Scholar]
- Cornforth, D.C. Pelton Upper Slide. In Landslides in Practice; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 520–528. [Google Scholar]
- Cornforth, D.C. Faraday Slide. In Landslides in Practice; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 541–547. [Google Scholar]
- Cornforth, D.C. Hagg Lake Slide. In Landslides in Practice; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 556–567. [Google Scholar]
- Fressard, M.; Maquaire, O.; Thiery, Y.; Davidson, R.; Lissak, C. Multi-method characterization of an active landslide: Case study in the Pays d’Auge plateau (Normandy, France). Geomorphology 2016, 270, 22–39. [Google Scholar] [CrossRef]
- Tohari, A.; Wibawa, S.; Koizumi, K.; Oda, K.; Komatsu, M. Effectiveness of siphon drainage method for landslide stabilization in a tropical volcanic hillslope: A case study of Cibitung landslide, West Java, Indonesia. Bull. Eng. Geol. Environ. 2021, 2021, 2101–2116. [Google Scholar] [CrossRef]
- Martínez-Carvajal, H.; Aristizábal, E.; García-Aristizábal, E. A case study on causation of the landslide on 26 October 2016 in the northern Colombian Andes. Dyna 2021, 88, 22–30. [Google Scholar] [CrossRef]
- Wang, L.; Shang, Y.; Zheng, J.; Zhang, Y. Temporary confined water-induced landslide in the binary structure of a gentle slope: A case study of the Fanshantou landslide. Water 2021, 13, 596. [Google Scholar] [CrossRef]
- Dai, X.; Schneider-Muntau, B.; Fellin, W.; Franco, A.; Gems, B. Engineering-geological analysis of a subaerial landslide in Taan Fiord, Alaska. Remote Sens. 2021, 13, 4258. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, C.; Zhang, Q.; Peng, J.; Zhu, W.; Lu, Z. Multi-temporal loess landslide inventory mapping with C-, X- and L-band SAR Datasets-A case study of Heifangtai loess landslides, China. Remote Sens. 2018, 10, 1756. [Google Scholar] [CrossRef]
- Ren, S.; Zhang, Y.; Xu, N.; Wu, R.; Liu, X.; Du, G. Mobilized strength of gravelly sliding zone soil in reactivated landslide: A case study of a giant landslide in the north-eastern margin of Tibet Plateau. Environ. Earth Sci. 2021, 80, 434. [Google Scholar] [CrossRef]
- Khorsandi, A.; Ghoreishi, S. Studying the Interaction Between Active Faults and Landslide Phenomenon: Case Study of Landslide in Latian, Northeast Tehran, Iran. Geotech. Geol. Eng. 2013, 31, 617–625. [Google Scholar] [CrossRef]
- Zhao, L.; Zuo, S.; Lin, Y.; Li, L.; Zhang, Y. Reliability back analysis of shear strength parameters of landslide with three-dimensional upper bound limit analysis theory. Landslides 2016, 13, 711–724. [Google Scholar] [CrossRef]
- Seguí, C.; Rattez, H.; Veveakis, M. On the Stability of Deep-Seated Landslides. The Cases of Vaiont (Italy) and Shuping (Three Gorges Dam, China). J. Geophys. Res. Earth Surf. 2020, 125, e2019JF005203. [Google Scholar] [CrossRef]
- Peranić, J.; Arbanas, S.; Arbanas, Ž. Importance of the unsaturated zone in landslide reactivation on flysch slopes: Observations from Valići landslide, Croatia. Landslides 2021, 18, 3737–3751. [Google Scholar] [CrossRef]
- Bian, S.; Chen, G.; Zeng, R.; Meng, X.; Jin, J.; Lin, L.; Zhang, Y.; Shi, W. Post-failure evolution analysis of an irrigation-induced loess landslide using multiple remote sensing approaches integrated with time-lapse ERT imaging: Lessons from Heifangtai, China. Landslides 2022, 19, 1179–1197. [Google Scholar] [CrossRef]
- Kang, X.; Wang, S.; Wu, W.; Xu, G.; Zhao, J.; Liu, F. Soil–water interaction affecting a deep-seated landslide: From field monitoring to experimental analysis. Bull. Eng. Geol. Environ. 2022, 81, 82. [Google Scholar] [CrossRef]
- Grelle, G.; Soriano, M.; Revellino, P.; Guerriero, L.; Anderson, M.; Diambra, A.; Fiorillo, F.; Esposito, L.; Diodate, N.; Guadagno, F. Space-time prediction of rainfall-induced shallow landslides through a combined probabilistic/deterministic approach, optimized for initial water table conditions. Bull. Eng. Geol. Environ. 2014, 73, 877–890. [Google Scholar] [CrossRef]
- Bièvre, G.; Joseph, A.; Bertrand, C. Preferential Water Infiltration Path in a Slow-Moving Clayey Earthslide Evidenced by Cross-Correlation of Hydrometeorological Time Series (Charlaix Landslide, French Western Alps). Geofluids 2018, 2018, 9593267. [Google Scholar] [CrossRef]
- Zhang, C.; Yin, Y.; Dai, Z.; Huang, B.; Zhang, A.; Jiang, X.; Tan, W.; Wang, L. Reactivation mechanism of a large-scale ancient landslide. Landslides 2021, 18, 397–407. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, D.; Xu, H.; Sun, H. Clarifying the effectiveness of drainage tunnels in landslide controls based on high-frequency in-site monitoring. Bull. Eng. Geol. Environ. 2020, 79, 3289–3305. [Google Scholar] [CrossRef]
- Jesus, C.; Oliveria, S.; Sena, C.; Marques, F. Understanding constraints and triggering factors of landslides: Regional and local perspectives on a drainage basin. Geosciences 2018, 8, 2. [Google Scholar] [CrossRef]
- Belle, P.; Aunay, B.; Lachassagne, P.; Ladouche, B.; Join, J. Control of tropical landcover and soil properties on landslides’ aquifer recharge, piezometry and dynamics. Water 2018, 10, 1491. [Google Scholar] [CrossRef]
- Xue, D.; Li, T.; Wei, Y.; Gao, M. Mechanism of reactivated Badu landslide in the Badu Mountain area, Southwest China. Environ. Earth Sci. 2015, 73, 4305–4312. [Google Scholar] [CrossRef]
- Lv, Q.; Zhou, H.; Di, S. Stability analysis and risk assessment of a landslide in southwest of China. J. Phys. Conf. Ser. 2020, 1676. [Google Scholar] [CrossRef]
- Leng, Y.; Kong, X.; He, J.; Xing, A.; Zhang, Y.; Wang, Q. The 10 July 2020, red-bed landslide was triggered by continuous rainfall in Qianxi, Guizhou, China. Landslides 2022, 19, 1421–1433. [Google Scholar] [CrossRef]
- Hare, D.; Briggs, M.; Rosenberry, D.; Boutt, D.; Lane, J. A comparison of thermal infrared to fiber-optic distributed temperature sensing for evaluation of groundwater discharge to surface water. J. Hydrol. 2015, 530, 153–166. [Google Scholar] [CrossRef]
- Doolittle, J.; Jenkinson, B.; Hopkins, D.; Ulmer, M.; Tuttle, W. Hydropedological investigations with ground-penetrating radar (GPR): Estimating water-table depths and local ground-water flow pattern in areas of coarse-textured soils. Geoderma 2006, 131, 317–329. [Google Scholar] [CrossRef]
- Johnson, D. Use of Ground-Penetrating Radar for Water Table Mapping, Brewster and Harwich, Massachusetts. U. S. Geol. Surv. Water Resour. Investig. Rep. 1992, 90, 4086. [Google Scholar]
- Tandon, R.; Gupta, V.; Venkateshwarlu, B. Geological, geotechnical, and GPR investigations along the Mansa Devi hill-bypass (MDHB) Road, Uttarakhand, India. Landslides 2021, 18, 849–863. [Google Scholar] [CrossRef]
- Ray, R.; Jacobs, J.; De Alba, P. Impacts of unsaturated zone soil moisture and groundwater table on slope instability. J. Geotech. Geoenviron. Eng. 2010, 136, 1448–1458. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.; MacMilliam, R.; Batjes, N.; Heuvelink, G.; Ribeiro, E.; Samuel-Roas, A.; Kempen, B.; Leenaars, J.; Walsh, M.; et al. SoilGrids1km—Global Soil Information Based on Automated Mapping. PLoS ONE 2014, 9, e105992. [Google Scholar] [CrossRef]
- Alberti, S.; Leshchinsky, B.; Roering, J.; Perkins, J.; Olsen, M. Inversions of landslide strength as a proxy for subsurface weathering. Nat. Commun. 2022, 13, 6049. [Google Scholar] [CrossRef]
- Schmidt, K.; Roering, J.; Stock, J.; Dietrich, W.; Montgomery, D.; Schaub, T. The variability of root cohesion as an influence on shallow landslide susceptibility in the Oregon Coast Range. Can. Geotech. J. 2001, 38, 995–1024. [Google Scholar] [CrossRef]
- Skempton, A. Residual strength of clays in landslides, folded strata and the laboratory. Geotechnique 1985, 35, 3–18. [Google Scholar] [CrossRef]
- Tian, X.; Gaamom, A.; Yin, J.; Han, W.; Xiao, J. Effects of soil structure and anisotropy on undrained shear behavior of natural clays. Arab. J. Geosci. 2022, 15, 2039. [Google Scholar] [CrossRef]
- Touch, S.; Likitlersuang, S.; Pipatpongsa, T. 3D geological modelling and geotechnical characteristics of Phnom Penh subsoils in Cambodia. Eng. Geol. 2014, 178, 58–69. [Google Scholar] [CrossRef]
- Hough, B. Basic Soils Engineering; The Ronald Press Company: New York, NY, USA, 1957. [Google Scholar]
- Lambe, T.; Whitman, R. Soil Mechanics; John Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Terzaghi, K.; Peck, B.; Mesri, G. Soil Mechanics in Engineering Practice, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Swiss Standard SN 670 010b; Characteristic Coefficients of Soils. Technical Report; Association of Swiss Road and Traffic Engineers: Geneva, Switzerland, 1999.
- Section 3.2—Subgrade Soils in Minnesota Department of Transportation’s Pavement Design Manual. 2007. Available online: https://www.dot.state.mn.us/materials/pvmtdesign/manual2007.html (accessed on 28 May 2024).
- NAVFAC. Design Manual 7.01 (DM-7.01) Soil Mechanics; Naval Facilities Engineering Command: Alexandria, VA, USA, 1986. [Google Scholar]
- Koloski, J.; Schwarz, S.; Tubbs, D. Geotechnical properties of geologic materials. Eng. Geol. Wash. Div. Geol. Earth Resour. Bull. 1989, 79, 19–26. [Google Scholar]
- Carter, M.; Bentley, S. Correlations of Soil Properties; Penetech Press Publishers: London, UK, 1991. [Google Scholar]
- Hoek, E.; Bray, J. Rock Slope Engineering, 3rd ed.; Institute of Mining and Metallurgy: London, UK, 1974. [Google Scholar]
- Bagińska, I. Estimating and verifying soil unit weight determined on the basis of SCPTu tests. Ann. Wars. Univ. Life Sci.—SGGW Land. Reclam. 2016, 48, 233–242. [Google Scholar] [CrossRef]
- BS 8002:1994; Code of Practice for Earth Retaining Structures. British Standard Institution: London, UK, 1994.
- Ortiz, J.; Serra, J.; Oteo, C. Curso Aplicado de Cimentaciones, 3rd ed.; Colegio de Arquitectos de Madrid: Madrid, Spain, 1986. [Google Scholar]
- Keystone Retaining Wall Systems Technical Information Sheets. 2021. Available online: https://www.keystonewalls.com/application/files/5116/1790/8888/All-TechnicalNotes-2021.pdf (accessed on 1 April 2023).
- Peck, R.; Hanson, W.; Thombum, T. Foundation Engineering Handbook; Wiley: London, UK, 1974. [Google Scholar]
- Hunt, R. Geotechnical Engineering Investigation Manual; McGraw-Hill: New York, NY, USA, 1984. [Google Scholar]
- Coduto, D. Foundation Design: Principles and Practices, 2nd ed.; Prentic Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Huat, B.; Kazemian, S.; Prasad, A.; Bargchi, M. State of an art review of peat: General perspective. Int. J. Phys. Sci. 2011, 6, 1988–1996. [Google Scholar] [CrossRef]
- Azhar, A.; Norhaliza, W.; Ismail, B.; Abdullah, M.; Zakaria, M. Comparison of Shear Strength Properties for Undisturbed and Reconstituted Parit Nipah Peat, Johor. Int. Eng. Res. Innov. Symp. (IRIS) IOP Conf. Ser. Mater. Sci. Eng. 2016, 160, 012058. [Google Scholar] [CrossRef]
- Santi, P.; Doyle, B. The Locations and Engineering Characteristics of Weak Rocks in the U.S. In Characterization of Weak and Weathered Rock Masses, Association of Engineering Geologists Special Publication #9; Santi, P., Shakoor, A., Eds.; Association of Engineering Geologists: Sudbury, MA, USA, 1991; pp. 1–22. [Google Scholar]
- Santi, P. Field Methods for Characterizing Weak Rock for Engineering. Environ. Eng. Geosci. 2006, 12, 1–11. [Google Scholar] [CrossRef]
- Kanji, M. Critical Issues in Soft Rocks. J. Rock. Mech. Geotech. Eng. 2014, 6, 186–195. [Google Scholar] [CrossRef]
- Marinos, V.; Marinos, P.; Hoek, E. The geological strength index: Applications and limitations. Bull. Eng. Geol. Environ. 2005, 64, 55–65. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.; Tassaka, Y.; Minami, M. Determination of residual strength parameters of jointed rock masses using the GSI system. Int. J. Rock. Mech. Min. Sci. 2007, 44, 247–265. [Google Scholar] [CrossRef]
- DeRose, R.; Trustman, N.; Blaschke, P. Geomorphic change implied by regolith — Slope relationships on steepland hillslopes, Taranaki, New Zealand. Catena 1991, 18, 489–514. [Google Scholar] [CrossRef]
- Ekinici, Y.; Türkeş, M.; Demirci, A.; Erginal, A. Shallow and deep-seated regolith slides on deforested slopes in Çanakkale, NW Turkey. Geomorphology 2013, 201, 70–79. [Google Scholar] [CrossRef]
- Leone, J.; Holbrook, W.; Riebe, C.; Chorover, J.; Ferré, T.; Carr, B.; Callahan, R. Strong slope-aspect control of regolith thickness by bedrock foliation. Earth Surf. Process. Landf. 2020, 45, 2998–3010. [Google Scholar] [CrossRef]
- Olyphant, J.; Pelletier, J.; Johnson, R. Topographic correlations with soil and regolith thickness from shallow-seismic refraction constraints across upland hillslopes in the Valles Caldera, New Mexico. Earth Surf. Process. Landf. 2016, 41, 1684–1692. [Google Scholar] [CrossRef]
- Shafique, M.; der Meijde, M.; Rossiter, D. Geophysical and remote sensing-based approach to model regolith thickness in a data-sparse environment. Catena 2011, 87, 11–19. [Google Scholar] [CrossRef]
- Comegna, L.; Picarelli, L.; Bucchignani, E.; Mercogliano, P. Potential effects of incoming climate changes on the behaviour of slow active landslides in clay. Landslides 2013, 10, 373–391. [Google Scholar] [CrossRef]
- Sun, L.; Li, C.; Shen, F. Two-surface progressive failure mechanism and stability quantitative evaluation of water-induced weakening retrogressive landslides: Case study for clay landslides, China. Bull. Eng. Geol. Environ. 2022, 81, 382. [Google Scholar] [CrossRef]
- Lumb, P. Safety factors and the probability distribution of soil strength. Can. Geotech. J. 1970, 7, 225–242. [Google Scholar] [CrossRef]
- Wolff, T. Analysis and Design of Embankment Dam Slopes: A Probabilistic Approach. Ph.D. Dissertation, Purdue University, West Lafayette, IN, USA, 1985. Available online: https://docs.lib.purdue.edu/dissertations/AAI8520092/ (accessed on 28 May 2024).
- Forrest, W.; Orr, T. Reliability of shallow foundations designed to Eurocode 7. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2010, 4, 186–207. [Google Scholar] [CrossRef]
- Di Matteo, L.; Fenton, G.; Ricco, R. Laboratory shear strength parameters of cohesive soils: Variability and potential effects on slope stability. Bull. Eng. Geol. Environ. 2013, 72, 101–106. [Google Scholar] [CrossRef]
- Galve, J.; Gutiérrez, F.; Guerrero, J.; Alonso, J.; Diego, I. Application of risk, cost-benefit and acceptability analyses to identify the most appropriate geosynthetic solution to mitigate sinkhole damage on roads. Eng. Geol. 2012, 145–146, 65–77. [Google Scholar] [CrossRef]
- Gartner, J.; Jakob, M. Debris-flow risk assessment and mitigation design for pipelines in British Columbia, Canada. In Proceedings of the 7th International Conference on Debris-Flow Hazards Mitigation, Golden, CO, USA, 10–13 June 2019. [Google Scholar]
- Liu, X.; Wang, Y. Quantifying annual occurrence probability of rainfall-induced landslide at a specific slope. Comput. Geotech. 2022, 149, 104877. [Google Scholar] [CrossRef]
- Guido, L. Landslide Analysis with Incomplete Data: Developing a Framework for Critical Parameter Estimation. Master’s Thesis, Colorado School of Mines, Golden, CO, USA, 2023. Available online: https://hdl.handle.net/11124/178463 (accessed on 28 May 2024).
- Braddock, W.; Cole, J. Geologic Map of Rocky Mountain National Park and Vicinity, Colorado; United States Geological Survey: Denver, CO, USA, 1990.
- United States Geological Survey. United States Geological Survey 3D Elevation Program 1/3 arc-second Digital Elevation Model; Distributed by OpenTopography; US Geological Survey: Reston, VA, USA, 2021. [CrossRef]
- Dornfest, R.; Lyman, T. Geologic and Geotechnical Evaluation and Mitigation “Mudslide” at Michigan Ditch Jackson County; Colorado (File No. 111150-000-005); Brierly Associates: Denver, CO, USA, 2012. [Google Scholar]
- Preisig, G. Forecasting the long-term activity of deep-seated landslides via groundwater flow and slope stability modelling. Landslides 2020, 17, 1693–1702. [Google Scholar] [CrossRef]
- Highland, L.; Bobrosky, P. The Landslide Handbook-A Guide to Understanding Landslides; United States Geological Survey Circular 1325: Reston, VA, USA, 2008.




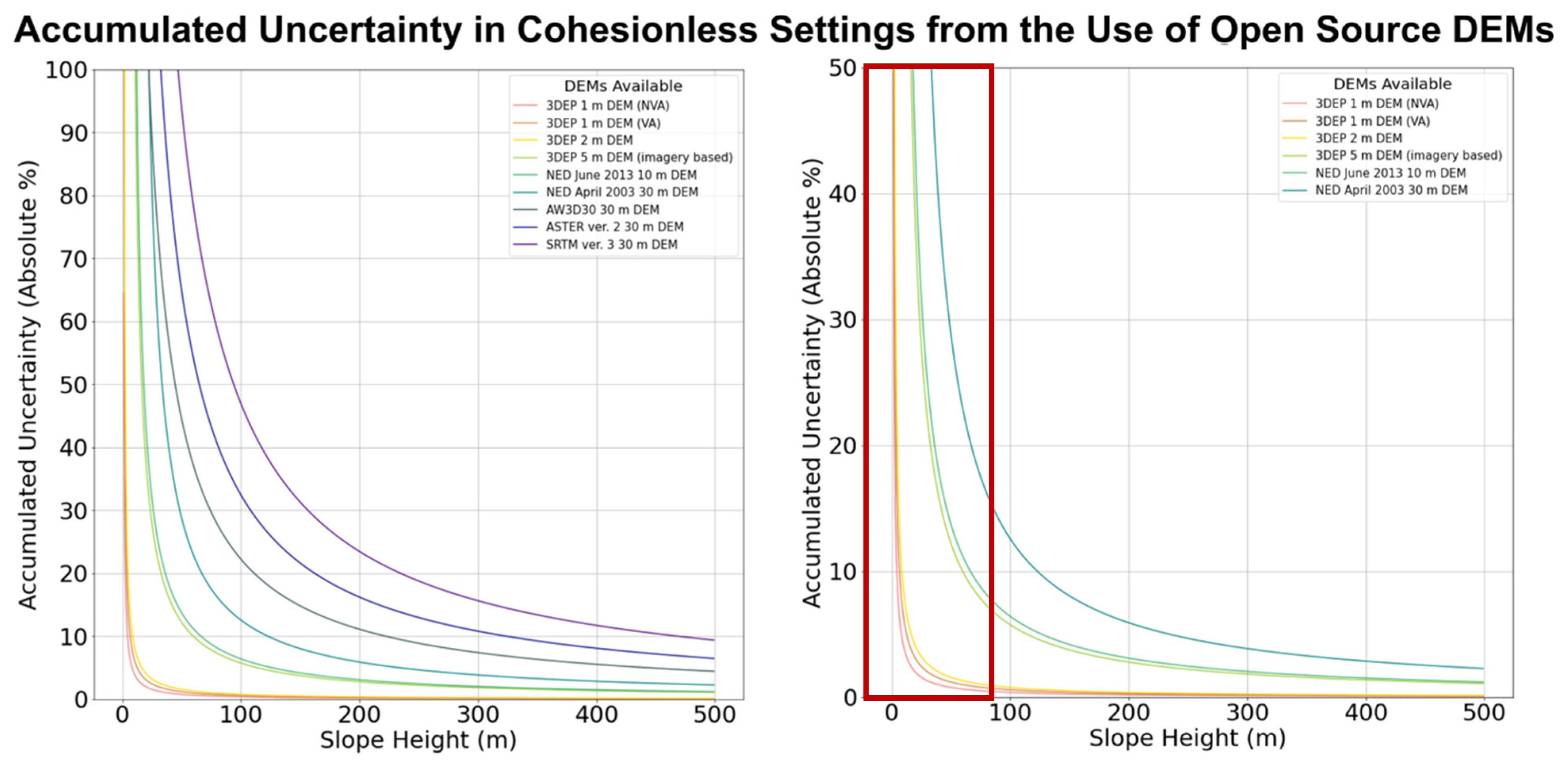
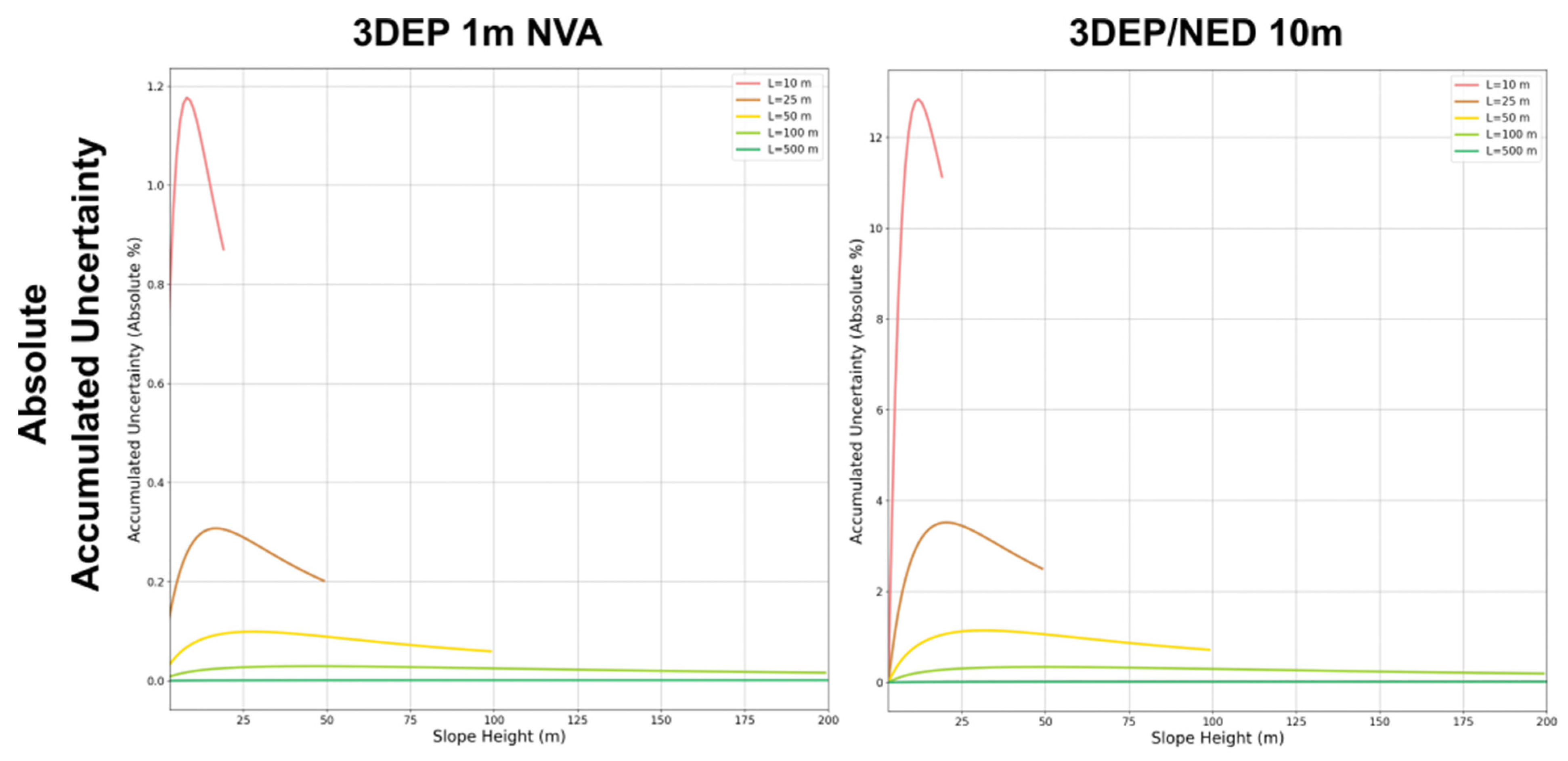

| DEM | 3DEP NVA (1 m) | 3DEP VA (1 m) | 3DEP (2 m) | 3DEP 5 m (Imagery) | NED April 2013 (10 m) | NED June 2003 (30 m) | AW3D30 (30 m) | SRTM (30 m) | ASTER ver. 2 (30 m) |
|---|---|---|---|---|---|---|---|---|---|
| 95th Percentile Vertical Error (m) | 0.196 | 0.3 | 0.392 | 2.7244 | 3.02 | 5.59 | 11.13 | 16.23 | 23.48 |
| Reference | [16] | [16] | [14] | [14] | [17] | [17] | [18] | [18] | [18] |
| Method | Landslide Type | Required Data | Description | Reference |
|---|---|---|---|---|
| Surface Area–Volume Relationship | R, T |
| Defines failure plane by empirical power function and volume to depth conversion | [28] |
| Rheological Assumptions | T (R) |
| Defines failure plane by applying rheologic relations to surface velocity and depth | [29] |
| Surface Displacement Parallel to Slip Surface | R, T |
| Defines failure plane based on parallel displacement to slip surface | [27] |
| Balanced Cross-section | T (R) |
| Defines failure plane by assuming mass balance and calculating mass transfer | [30,31,32] |
| Volumes Controlled by Discontinuities | T |
| Defines failure plane by controlling failure surfaces | [33] |
| Half Ellipsoid or Elliptic Paraboloid | R |
| Defines failure plane with geometric shape | [24] |
| Empirical Transverse Cross-section | R (T) |
| Defines failure plane by empirical graphical relationship | [34] |
| 3D Geomorphic Spline Calculation | R (T) |
| Defines failure plane using spline | [35,36] |
| Random Failure Surfaces and Probability | R, T |
| Defines failure plane by simulating stepped surfaces | [37] |
| Sloping Local Base Level (SLBL) | R (T) |
| Defines failure plane by iterative calculation of quadratic failure surface | [38,39] |
| Depth Probability Calculations | R, T |
| Defines probability of failure surface existing at a given depth | [28] |
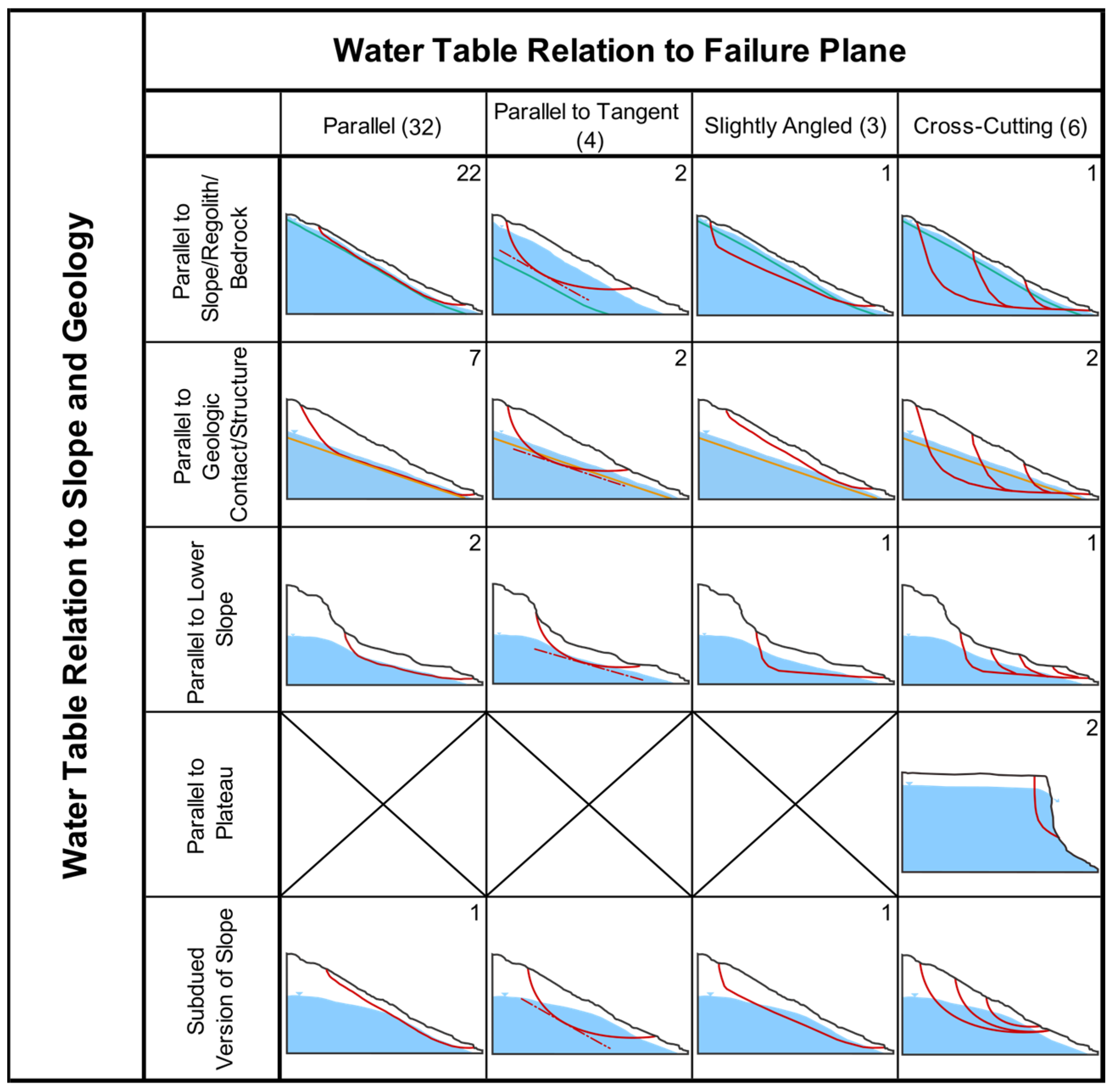
| Number | Failure Type | Groundwater Characterization | Groundwater Data Source | Groundwater Relation to Failure Plane | Reference | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parallel to Smoothed Slope | Parallel to Regolith/Bedrock Boundary | Parallel to Geologic Contact | Parallel to Lower Slope | Parallel to Plateau | Subdued Version of Slope Topography | Piezometers/ Monitoring Wells | Boreholes/ Standpipe Wells | Parallel | Parallel to Tangent | Steeper/ Shallower | Cross-cutting or complex Landslide | |||
| 1 | R-T | x | 2 | 24 | x | [41] | ||||||||
| 2 | T | x | 6 | x | [42] | |||||||||
| 3 | R | x | x | 4 | x | [43] | ||||||||
| 4 | R-T | x | x | 9 | x | [44] | ||||||||
| 5 | R | x | 4 | 1 | x | [45] | ||||||||
| 6 | T | x | x | 4 | 4 | x | [46] | |||||||
| 7 | T | x | x | 21 | x | [47] | ||||||||
| 8 | T | x | x | 9 | 7 | x | [48] | |||||||
| 9 | T | x | x | 10 | 25 | x | [49] | |||||||
| 10 | T | x | 9, and 22 shafts | x | [50,51] | |||||||||
| 11 | T | x | x | 2 | 2 | x | [52] | |||||||
| 12 | T | x | 3 | 2 | x | [53] | ||||||||
| 13 | R | x | x | 5 | x | [54] | ||||||||
| 14 | R | x | 3, and trenches | x | [55] | |||||||||
| 15 | T | x | x | 8 | x | [56] | ||||||||
| 16 | T | x | x | 13 | 4 | x | [57] | |||||||
| 17 | T | x | x | 5 | x | [58] | ||||||||
| 18 | T | x | x | 8 | x | [59] | ||||||||
| 19 | R-T | x | Back analysis | x | [60] | |||||||||
| 20 | R-T | x | x | Remote sensing and regional wells | x | [61] | ||||||||
| 21 | T | x | x | x | 12 | x | [62] | |||||||
| 22 | T | x | x | 8 | x | [63] | ||||||||
| 23 | T | x | Back analysis | x | [64] | |||||||||
| 24 | T | x | 4 | x | [65] | |||||||||
| 25 | T | x | 1 | 1 | x | [66] | ||||||||
| 26 | R | x | Remote sensing and regional wells | x | [67] | |||||||||
| 27 | T | x | x | 2 | 3 | x | [68] | |||||||
| 28 | T | x | x | Regional controls | x | [69] | ||||||||
| 29 | T | x | 2 | 3 | x | [70] | ||||||||
| 30 | T | x | x | 14 | x | [71] | ||||||||
| 31 | T | x | x | 3 | 4 | x | [72] | |||||||
| 32 | T | x | x | 4 | 38 | x | [73] | |||||||
| 33 | T | x | x | 3 | x | [74] | ||||||||
| 34 | T | x | x | 9 | x | [75] | ||||||||
| 35 | T | x | # | x | [76] | |||||||||
| 36 | T | x | x | 2 | >40 | x | [77] | |||||||
| Water Table Relationship to Slope and Geology | Description Notes | |
| Parallel to Slope/Regolith/ Bedrock |
| |
| Parallel to Geologic Contact/Structure |
| |
| Parallel to Lower Slope |
| |
| Parallel to Plateau |
| |
| Subdued Version of Slope |
|
| Category | USCS | Description | Cohesion (kPa) | Friction Angle (deg) | Unit Weight (kN/m3) | References | |||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | ||||
| Gravels | GW | Well graded gravel, sandy gravel, with little or no fines | 0 | 0 | 33 | 40 | 20 | 22 | [92,93,94,95] |
| GP | Poorly graded gravel, sandy gravel, with little or no fines | 0 | 0 | 32 | 44 | 19.5 | 21.5 | [92,93,94] | |
| GW, GP | Sandy gravels | 0 | 0 | 35 | 50 | 19 | 21 | [96,97,98,99] | |
| GM | Silty gravels, silty sandy gravels | 0 | 1 | 30 | 40 | 20.5 | 22.5 | [92,100] | |
| GC | Clayey gravels, clayey sandy gravels | 1 | 20 | 28 | 35 | 18 | 21 | [92,100] | |
| Sands | SW | Well graded sands, gravelly sands, with little or no fines | 0 | 0 | 33 | 46 | 18.5 | 22.5 | [89,92,93,94] |
| SP | Poorly graded sands, gravelly sands, with little or no fines | 0 | 0 | 27 | 39 | 17.5 | 21.5 | [89,92,93,94,95,96] | |
| SM | Silty sands | 20 | 50 | 27 | 35 | 18 | 23 | [92,94,96] | |
| SC | Clayey sands | 5 | 74 | 30 | 40 | 17 | 20 | [92,94,96] | |
| SM, SC | Sand silt clay loam with slightly plastic fines | 50 | 75 | 28 | 34 | 18 | 19 | [93,94,98,101] | |
| SM, SC | Sand silt clay loam with slightly plastic fines (saturated) | 10 | 20 | 28 | 34 | -- | -- | [93,94,101] | |
| SW, SP | Sand | 0 | 0 | 29 | 41 | 19 | 20 | [92,93,98,102] | |
| Silts | ML | Inorganic silts, silty or clayey fine sands, with slight plasticity | 2 | 67 | 25 | 41 | 12 | 17 | [89,92,94,96,100,103,104] |
| MH | Inorganic silts of high plasticity | 3 | 72 | 23 | 33 | 12 | 17 | [92,94,100,104] | |
| Clays | CL | Inorganic clays, silty clays, sandy clays of low plasticity | 4 | 86 | 27 | 35 | 12.5 | 17 | [92,94,96,100,104] |
| CH | Inorganic clays of high plasticity | 8 | 103 | 17 | 31 | 12.5 | 17 | [92,94,96,100,104] | |
| Organic Soils | OL | Inorganic clays of high plasticity | 0 | 5 | 22 | 32 | 4 | 5 | [92,104] |
| OH | Organic clays of high plasticity | 7 | 10 | 17 | 35 | 10 | 16 | [92,100,103] | |
| Pt | Peat and other highly organic soils | 10 | 21 | 0 | 10 | 8 | 14 | [95,105,106] | |
| Common Soil Mixtures | ML, OL, MH, OH | Silt loam | 10 | 90 | 25 | 32 | 4 | 17 | [93,94,103,104,105] |
| ML, OL, CL, MH, CH | Clay loam, silty clay loam | 10 | 105 | 18 | 32 | 4 | 17 | [93,94,103,104] | |
| OL, CL, OH, CH | Silty clay | 10 | 105 | 18 | 32 | 4 | 17 | [93,94,100,103,104,105] | |
| CH, MH, OH, PT | High plastic silts and clays, organics | 3 | 105 | 0 | 25 | 6 | 17 | [94,100,101,103,104,105] | |
| ML, CL, OL | Silts, low plastic clays | 3 | 105 | 25 | 30 | 12 | 17 | [94,100,101,104] | |
| GW, GP, GM, GC, SW, SP | Sand, gravel, stone | 0 | 0 | 32 | 48 | 15 | 21 | [89,99,101] | |
| GW, SW, GC, GM | Mixture of gravel and sand with fines | 1 | 3 | 15 | 28 | 18 | 22 | [92,95,100,101] | |
| ML-CL | Mixture of inorganic silt and clay | 22 | 65 | 25 | 41 | 15.5 | 19 | [89,94,96,103] | |
| Category | USCS | Description | Cohesion (kPa) | Friction Angle (deg) | References | ||
|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | ||||
| Depositional Environment | GW, GP, GM | Alluvial-high energy | 0 | 30 | 35 | [95] | |
| ML, SM, SP, SW | Alluvial-low energy | 0 | 24 | 15 | 30 | [95] | |
| SP | Eolian-dune sand | 0 | 30 | 35 | [95] | ||
| ML, SM | Eolian-loess | 24 | 48 | 20 | 30 | [95] | |
| SM, ML | Glacial-till | 48 | 192 | 35 | 45 | [95] | |
| GW, GP, SW, SP, SM | Glacial-outwash | 0 | 48 | 30 | 40 | [95] | |
| ML, SM, SP | Glacial-glaciolacustrine | 0 | 144 | 15 | 35 | [95] | |
| ML, SM, MH | Lacustrine-inorganic | 0 | 10 | 5 | 20 | [95] | |
| OL, PT | Lacustrine-organic | 0 | 10 | 0 | 10 | [95] | |
| SW, GW, SP | Marine-high energy | 0 | 25 | 35 | [95] | ||
| ML, SM, MH | Marine-low energy | 0 | 10 | 0 | 25 | [95] | |
| ML, SM | Volcanic-tephra | 0 | 48 | 20 | 35 | [95] | |
| SM, SW, GM | Volcanic-lahar | 0 | 48 | 25 | 40 | [95] | |
| Blasted/Broken Rock | Basalt | 0 | 40 | 50 | [97] | ||
| Chalk | 0 | 30 | 40 | [97] | |||
| Granite | 0 | 45 | 50 | [97] | |||
| Limestone | 0 | 35 | 40 | [97] | |||
| Sandstone | 0 | 35 | 45 | [97] | |||
| Shale | 0 | 30 | 35 | [97] | |||
| Estimation Guidance | Topography/DEM | Water Table | Material Parameters | Depth to Failure Surface |
|---|---|---|---|---|
| Highest Quality | 3DEP 1 m | Incorporate known flow patterns, nearby well data, or other unique sources with field data to assess most likely water table geometry | Lab material classification/limited testing | Well constrained depth to bedrock data from available maps, nearby borings, web soil survey data |
| Intermediate Quality | 3DEP 10 m | Use field observations to assess most likely water table geometry (with surface expressions of water) | Grain size distribution testing | Field observations of displacement and scarp development |
| 3DEP 30 m | Use field observations to assess most likely water table geometry (no surface expressions of water) | Mapping and field classification | Remote observations of displacement and scarp development | |
| Lowest Quality | AW3D30 and SRTM 30 m | Remotely assess most likely water table geometry based on slope conditions and expected failure plane characteristics | Remote classification based on bedrock/expected weathering profile | Empirical relationships to investigate a slope with no evidence of prior motion |
| Uncertainty Type | Definition | Dependent Upon |
|---|---|---|
| Parameter Uncertainty (PU) | Uncertainty in a single parameter estimation |
|
| Accumulated Uncertainty (AU) | Uncertainty is FS calculation resultant from a given parameter uncertainty |
|
| Aggregate Uncertainty | Uncertainty in FS calculation resultant from interactions of all parameter uncertainties in a Monte-Carlo or similar analysis |
|
| Parameter | Symbol | Value |
|---|---|---|
| Failure Plane Angle (deg) | q | 30 |
| Depth of Landslide (m) | z | 10 |
| Cohesion (kPa) | c | 30 |
| Friction Angle (deg) | f | 40 |
| Unit Weight (kN/m3) | g | 18 |
| Parameter | Approximate Landslide Thickness beyond Which AU Rapidly Increases (m) | AU Trends with H/L Ratio | Notes | |
|---|---|---|---|---|
| Translational | Original Slope Topography | - | Peaks around H/L ratio ~1/2 |
|
| For DEM resolution < 5 m: slope height < 25 m | ||||
| For DEM resolution > 5 m: slope height < 100 m | ||||
| Depth to Water Table | <10 [for PU <2 m] | Decreases as H/L ratio increases |
| |
| <30 [for PU >2 m] | ||||
| Depth to Failure Plane | <10 | Increases as H/L ratio increases |
| |
| Cohesion | <20 | Increases as H/L ratio increases |
| |
| Friction Angle | >10 [AU levels off high] | Decreases as H/L ratio increases |
| |
| <10 [AU rapidly decreases] | ||||
| Unit Weight | <15 | Increases as H/L ratio increases |
|
| Maximum Depth | H/L Ratio | Typical Parameters with Greatest Uncertainty Accumulation |
|---|---|---|
| Shallow | <1/2 | Water Table, Friction Angle, Failure Plane Depth |
| >1/2 | Water Table, Failure Plane Depth | |
| Medium | <1/2 | Water Table, Friction Angle, Failure Plane Depth |
| >1/2 | Water Table, Failure Plane Depth | |
| Deep | <1/2 | Water Table, Friction Angle |
| >1/2 | Water Table, Friction Angle, Unit Weight, Failure Plane Depth |
| Parameter | Considerations |
|---|---|
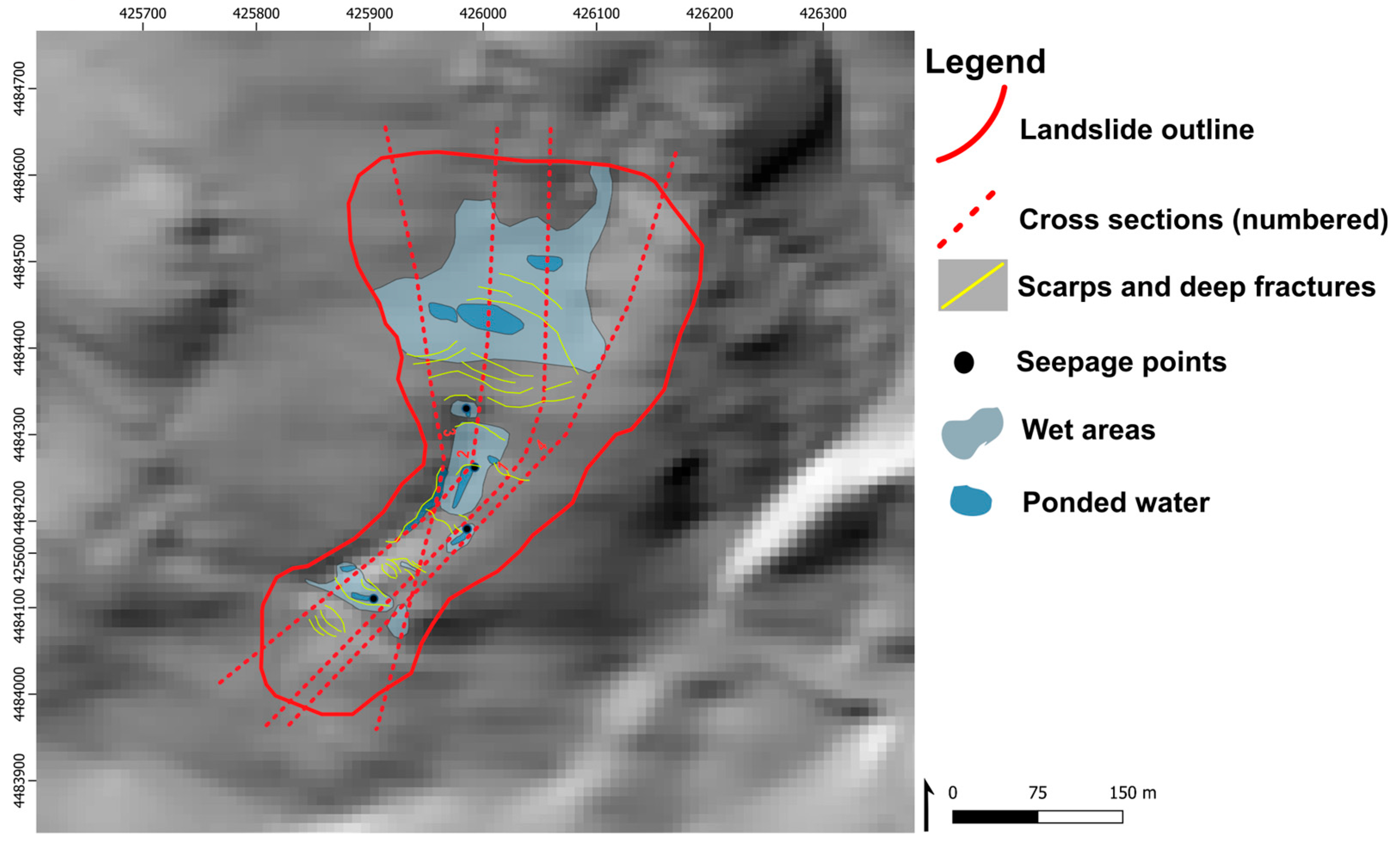
| Topography | Highest resolution DEM available is NED 10 m No pre-failure DEM topography available |
| Depth to Water Table | Frost activity expected due to elevation and location (seasonal) Ponding water, springs, and surface saturation indicative of shallow water table |
| Material Parameters | Surficial material initially classified as SP/ML in the field, with some areas having a more significant gravel component Regolith and weathered rock expected beneath soil Bedrock regionally mapped as igneous. |
| Depth to Failure Plane | Regional geology indicates crystalline bedrock below quaternary deposits, limiting failure plane depth and water table Quaternary deposits and forested location indicate translational failure |
| Cohesion (kPa) | Friction Angle (deg) | Unit Weight (kN/m3) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Min. | Max. | Mean | Min. | Max. | Mean | Min. | Max. | |
| Soil | 2 | 0 | 4 | 25 | 17 | 33 | 20 | 17.5 | 23 |
| Regolith | 0 | 0 | 0.5 | 35 | 30 | 40 | 20 | 18 | 22 |
| Bedrock | 32,300 | 27,750 | 36,850 | 55 | 53.2 | 56.8 | 21 | 20 | 22 |
| Cohesion (kPa) | Friction Angle (deg) | Unit Weight (kN/m3) | Depth to Failure Plane (m) | Depth to Water Table (m) | |||
|---|---|---|---|---|---|---|---|
| Reported Value | Soil | 0 | 25 | 18.85 | 11 | 4 | |
| Regolith | 0 | 32 | 19.632 | ||||
| Bedrock | 0 | 42 | 23.563 | ||||
| Cohesion | Friction Angle | Unit Weight | Depth to Failure Plane | Depth to Water Table | Depth to Bedrock | ||
| Parameter Uncertainty (+/−%) | Soil | 50.0 | 24.2 | 13.0 | 70.0 | 50.0 | 40.0 |
| Regolith | 50.0 | 12.5 | 9.1 | ||||
| Bedrock | 12.3 | 3.2 | 4.5 | ||||
| Deviation from LT/FI Analysis (% error) | Soil | -- | 0.0 | 6.1 | 18.2 | 0.0 | 18.2 |
| Regolith | 0.0 | 9.4 | 3.3 | ||||
| Bedrock | -- | 30.1 | 6.6 | ||||
| Cohesion | Friction Angle | Unit Weight | Depth to Failure Plane | Depth to Water Table | DEM | ||
|---|---|---|---|---|---|---|---|
| Accumulated Uncertainty (+/−%) | Soil | 15 | 20 | 1 | 30 | 25 | <0.01 |
| Regolith | 15 | 20 | 1 | ||||
| Bedrock | 4 | 2 | 0.5 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guido, L.; Santi, P. Landslide Analysis with Incomplete Data: A Framework for Critical Parameter Estimation. Geotechnics 2024, 4, 918-951. https://doi.org/10.3390/geotechnics4030047
Guido L, Santi P. Landslide Analysis with Incomplete Data: A Framework for Critical Parameter Estimation. Geotechnics. 2024; 4(3):918-951. https://doi.org/10.3390/geotechnics4030047
Chicago/Turabian StyleGuido, Lauren, and Paul Santi. 2024. "Landslide Analysis with Incomplete Data: A Framework for Critical Parameter Estimation" Geotechnics 4, no. 3: 918-951. https://doi.org/10.3390/geotechnics4030047
APA StyleGuido, L., & Santi, P. (2024). Landslide Analysis with Incomplete Data: A Framework for Critical Parameter Estimation. Geotechnics, 4(3), 918-951. https://doi.org/10.3390/geotechnics4030047






