Assessing Rainfall Variability in Jamaica Using CHIRPS: Techniques and Measures for Persistence, Long and Short-Term Trends
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data—CHIRPS
3. Methods
3.1. Serial Correlation Coefficient (SCC)
3.2. Persistence Threshold—PT
- where, is the precipitation of day i, at location j.
- and where, 1…, Number of Day observations.
- 1…, 364 Number of locations
- 1…, Number of Days exceeding Threshold
- Precipitation Threshold k
- 1…, Number of Thresholds selected.
- and,
- where, is the precipitation of day i, at location j.
- and were, 1…, Number of Day observations.
- 1…, 364 Number of locations
- 1…, Number of Days less than Threshold
- Precipitation Threshold k
- 1…, Number of Thresholds selected.
- and,
4. Results
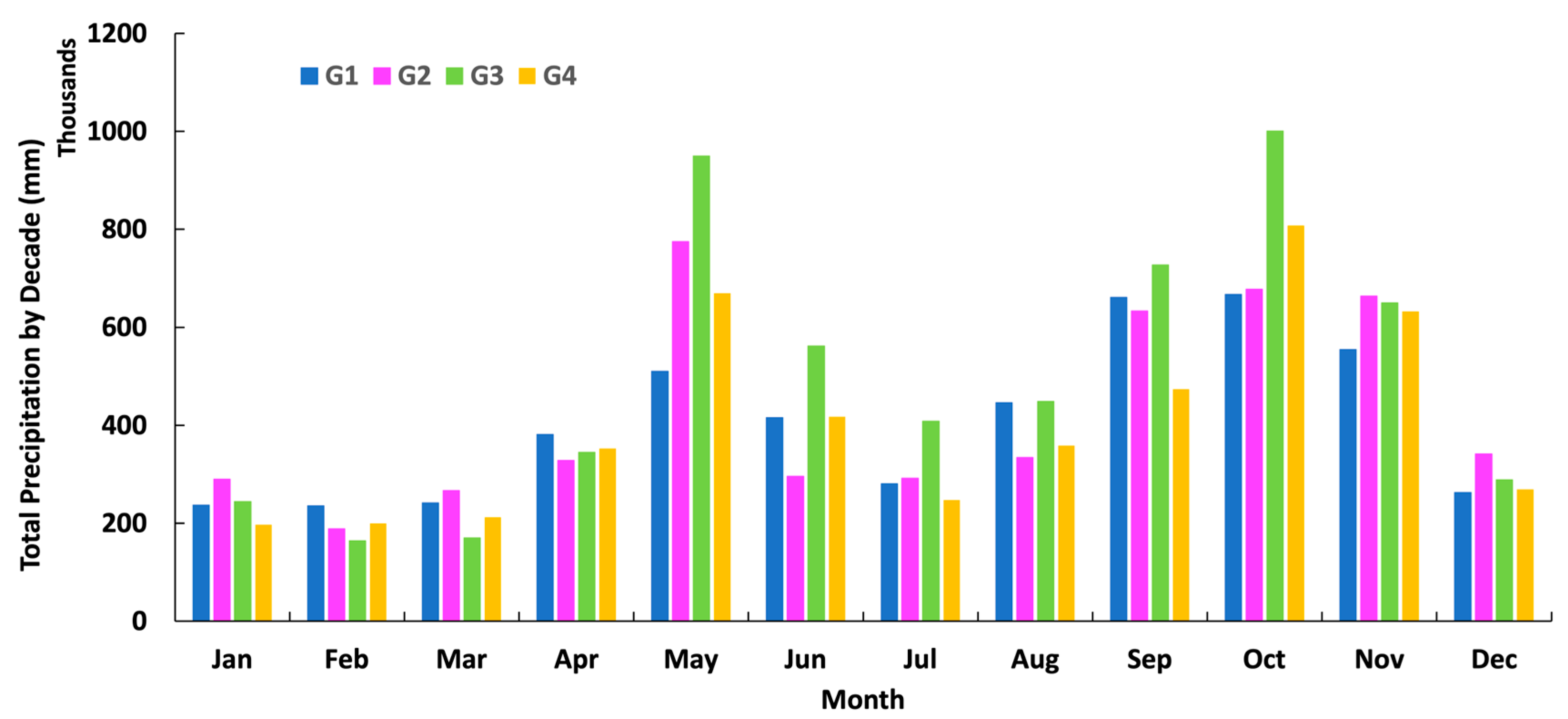
4.1. Average Temporal Rainfall Variability
Extreme Temporal Rainfall Variability
4.2. Spatial Rainfall Variability
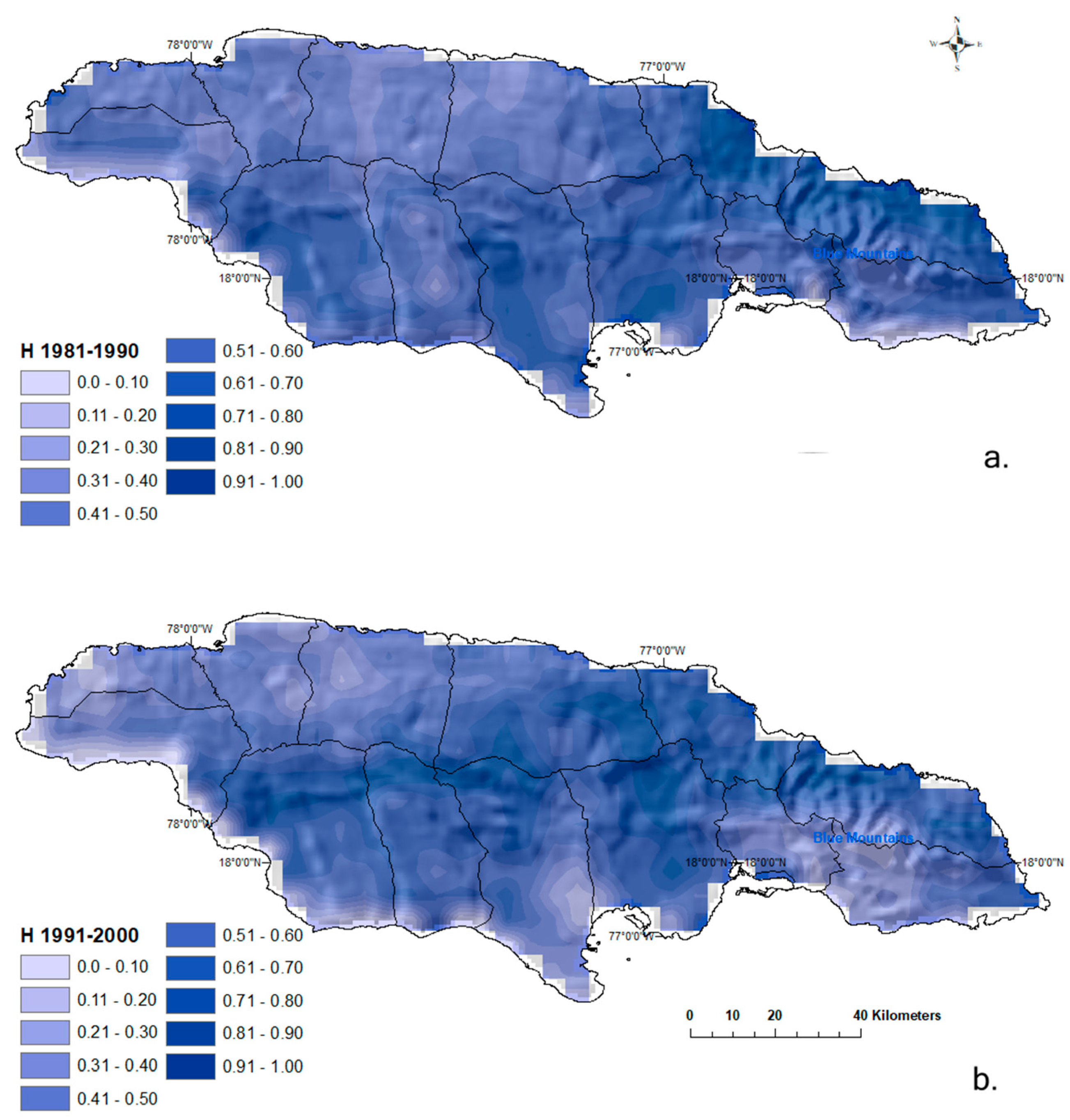
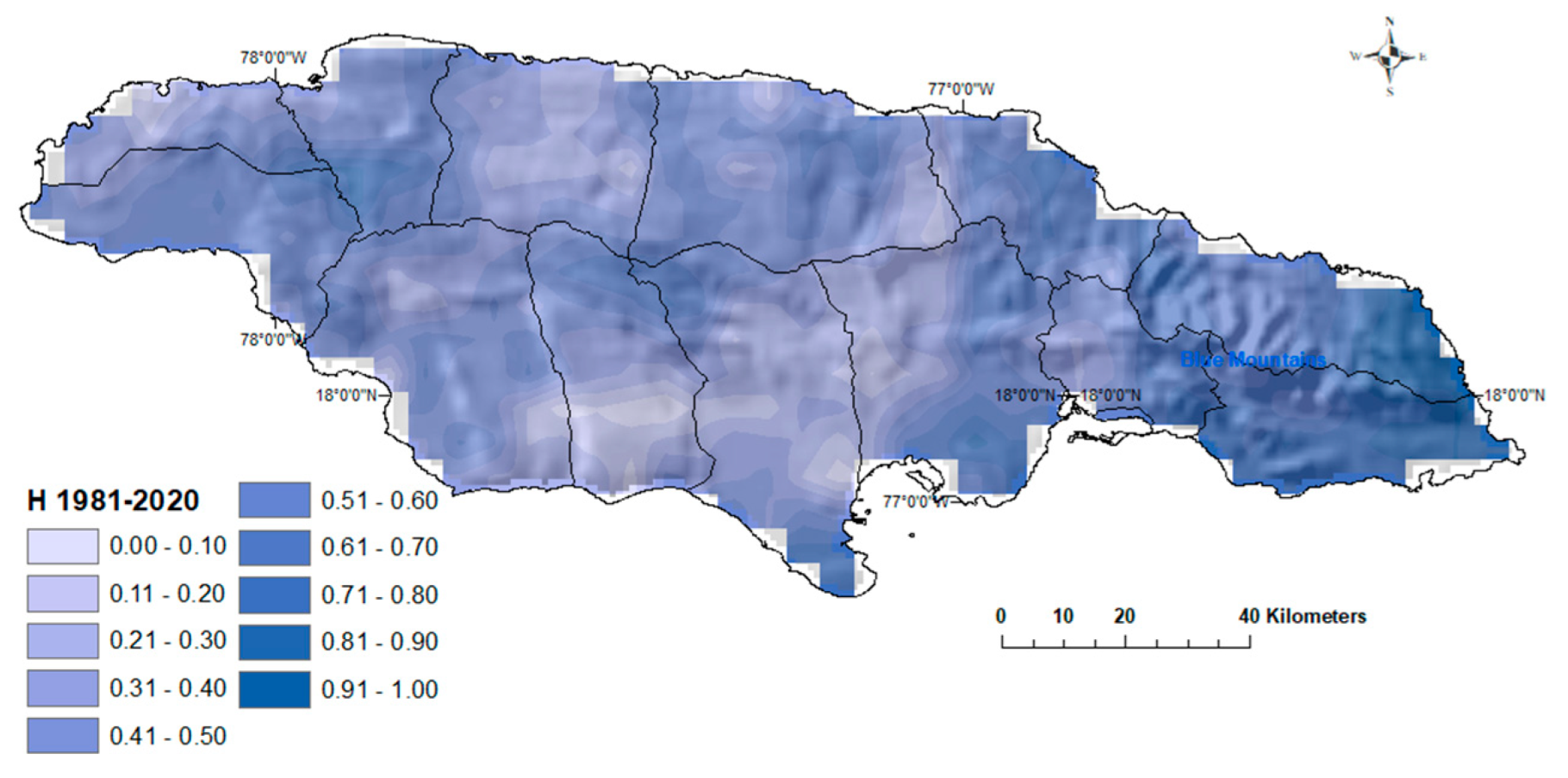
4.2.1. Hurst Exponent (H)
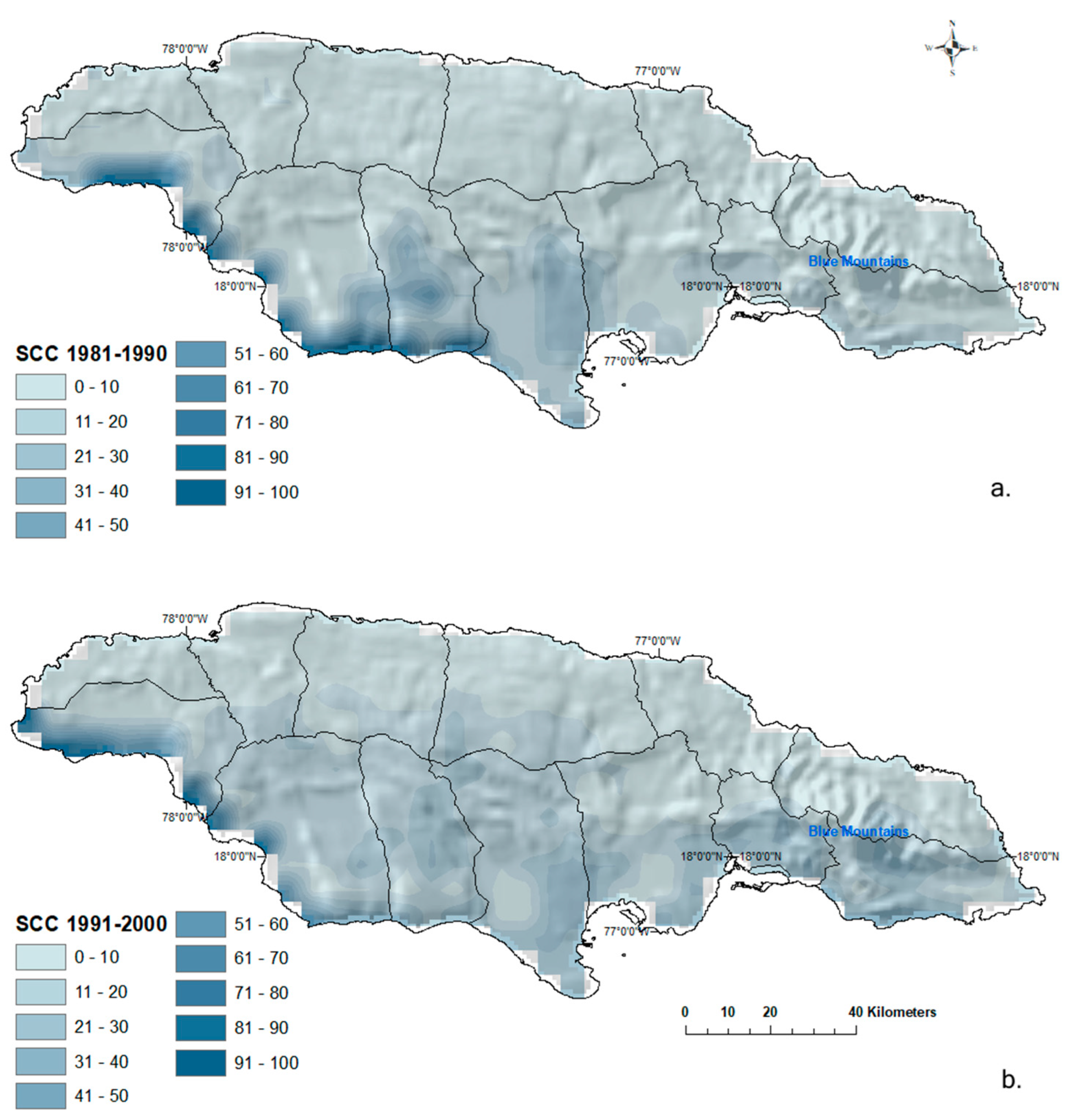
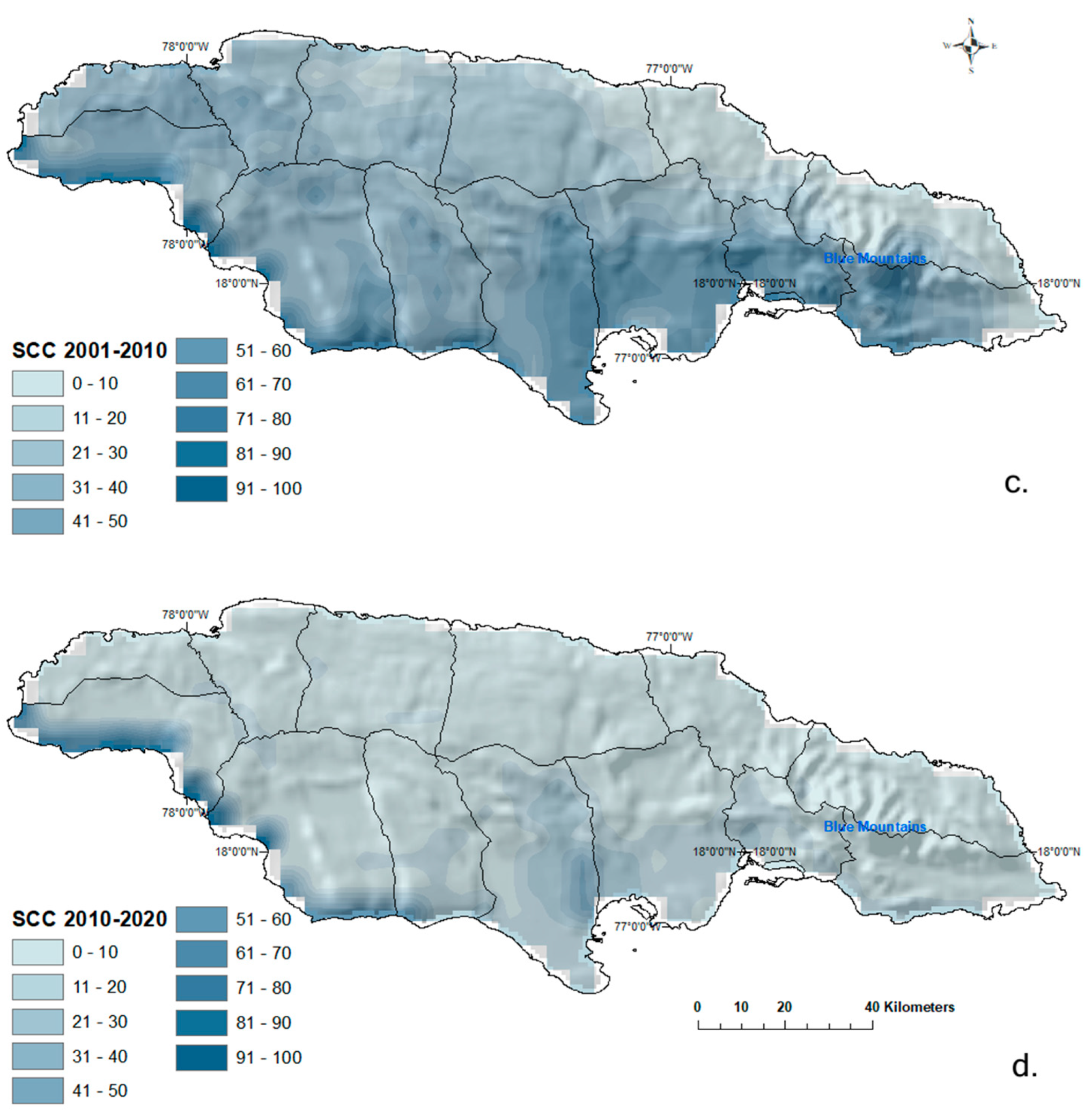
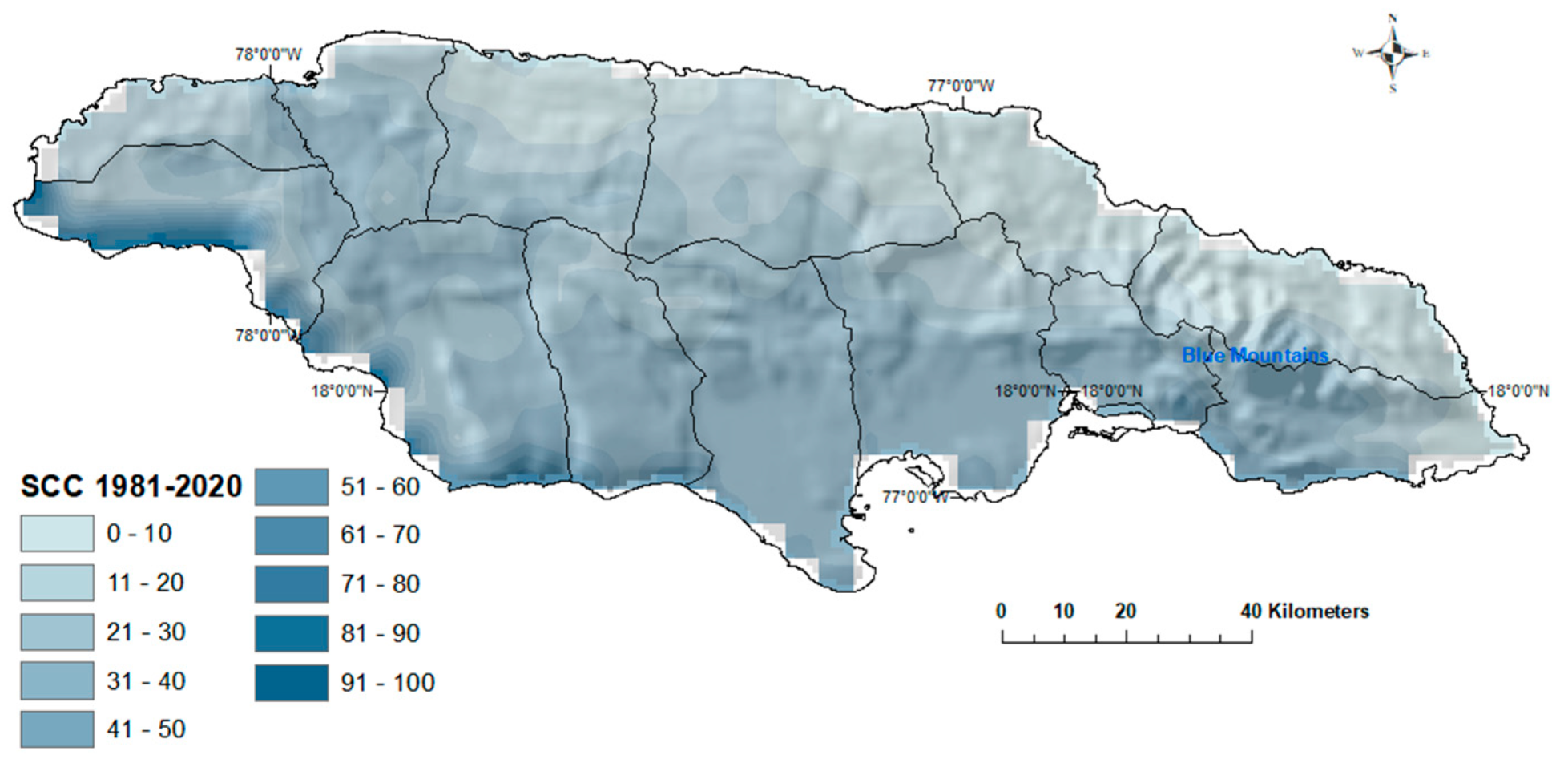
4.2.2. Serial Correlation Coefficient (SCC)
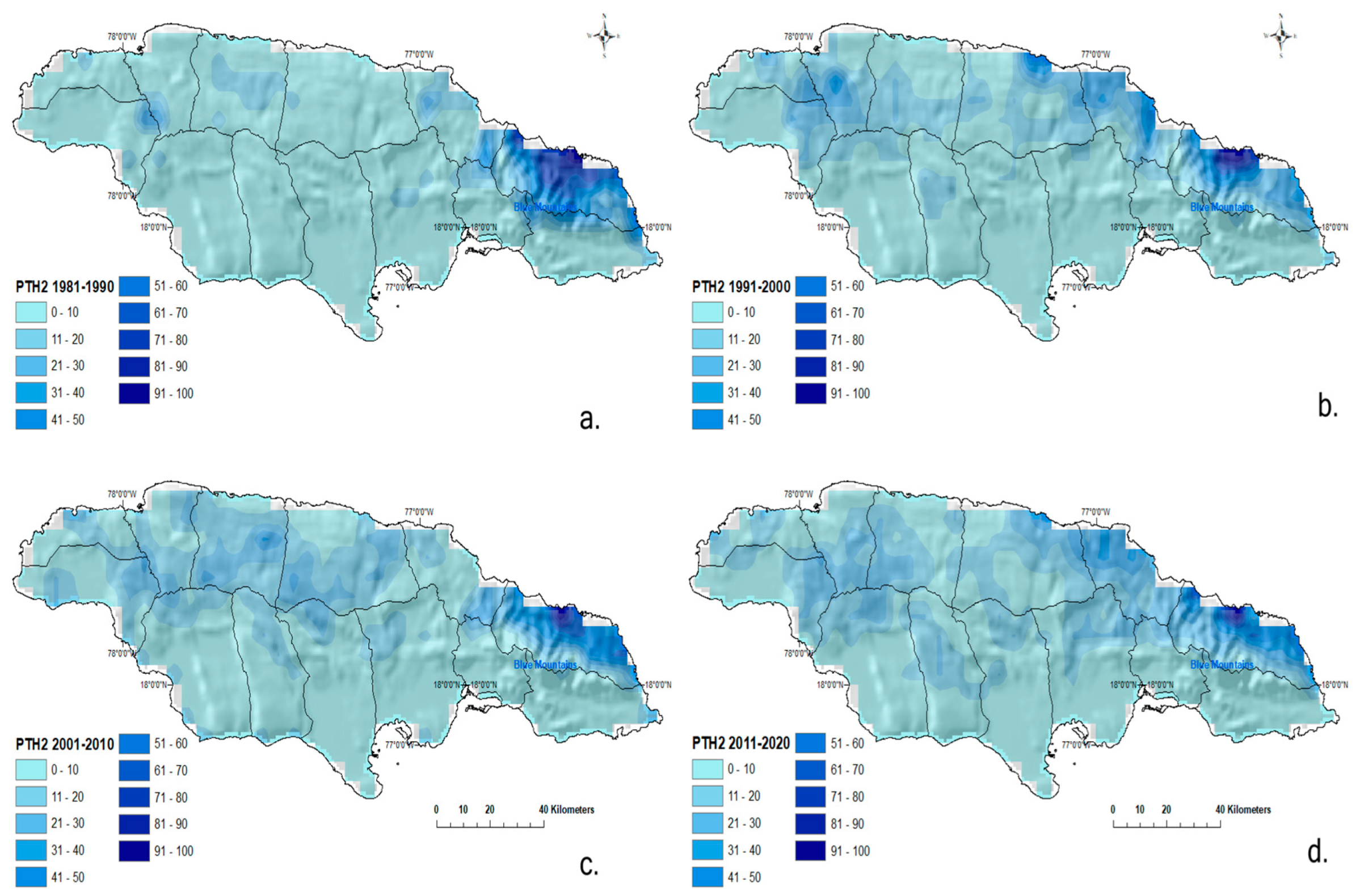
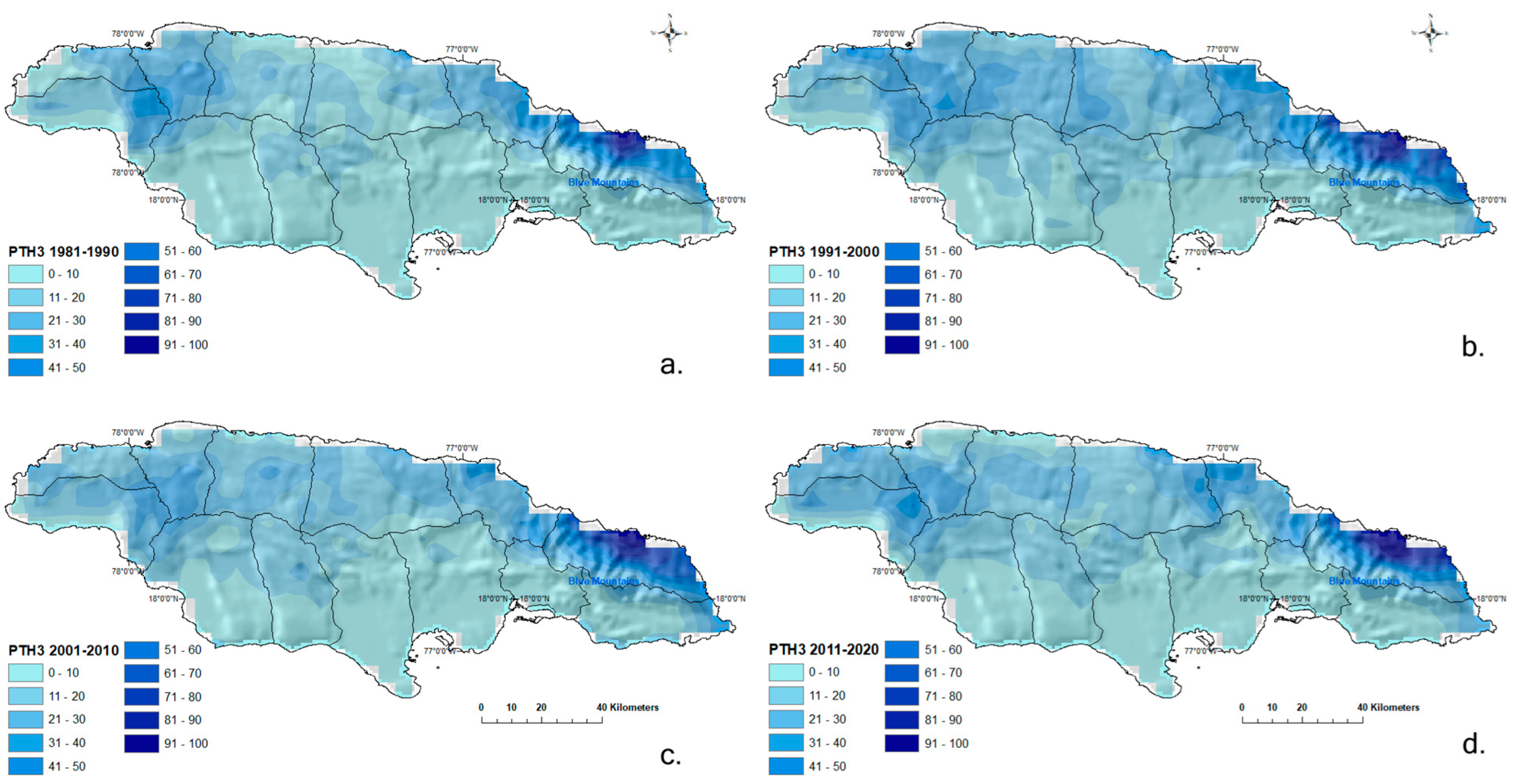
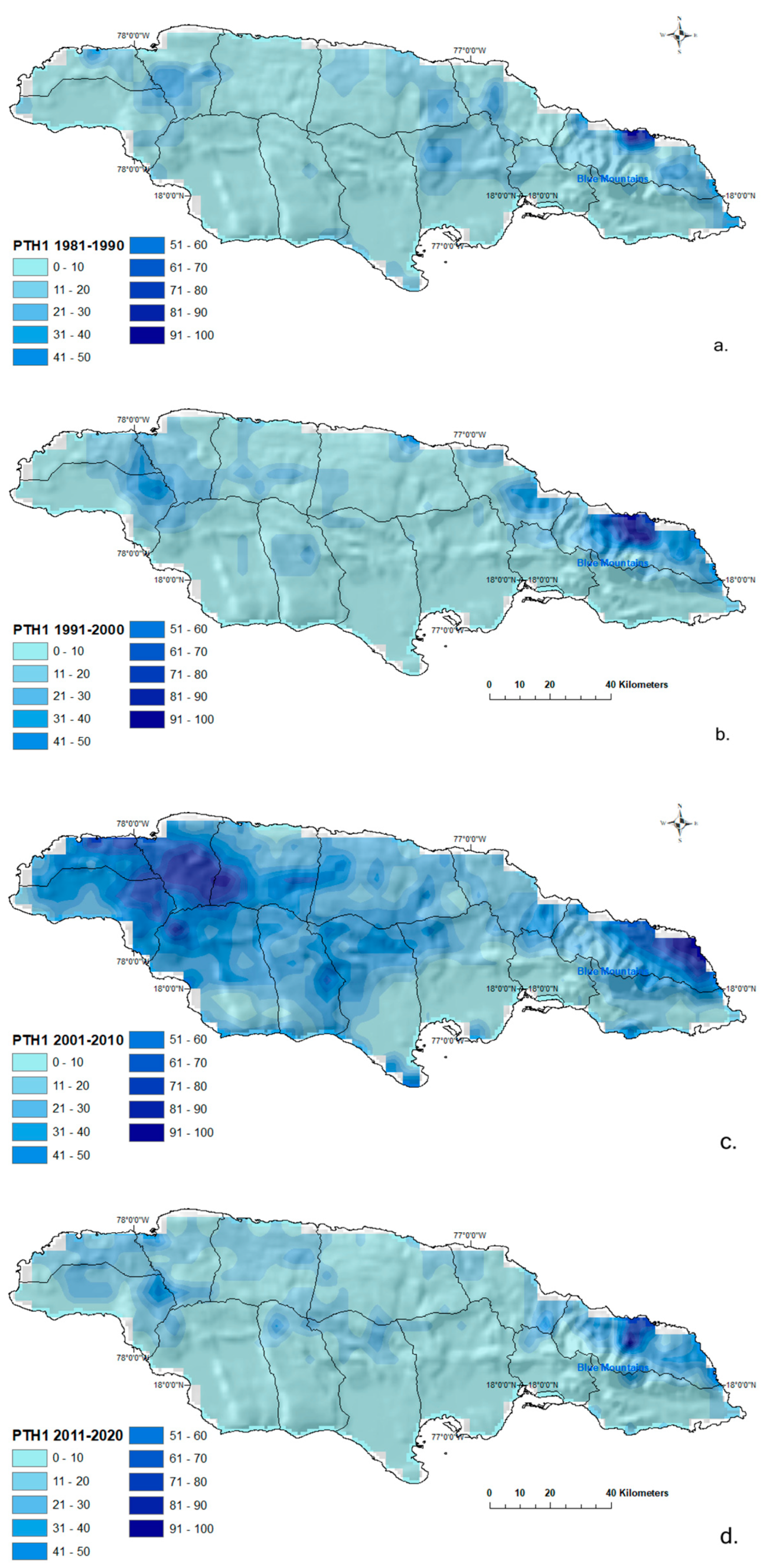
4.3. Rainfall Persistence Thresholds
4.3.1. Persistence Threshold High (PTH)
PTH1 3-Days ≥ 50 mm
PTH2 2-Days ≥ 80 mm
PTH3 1-Day ≥ 120 mm
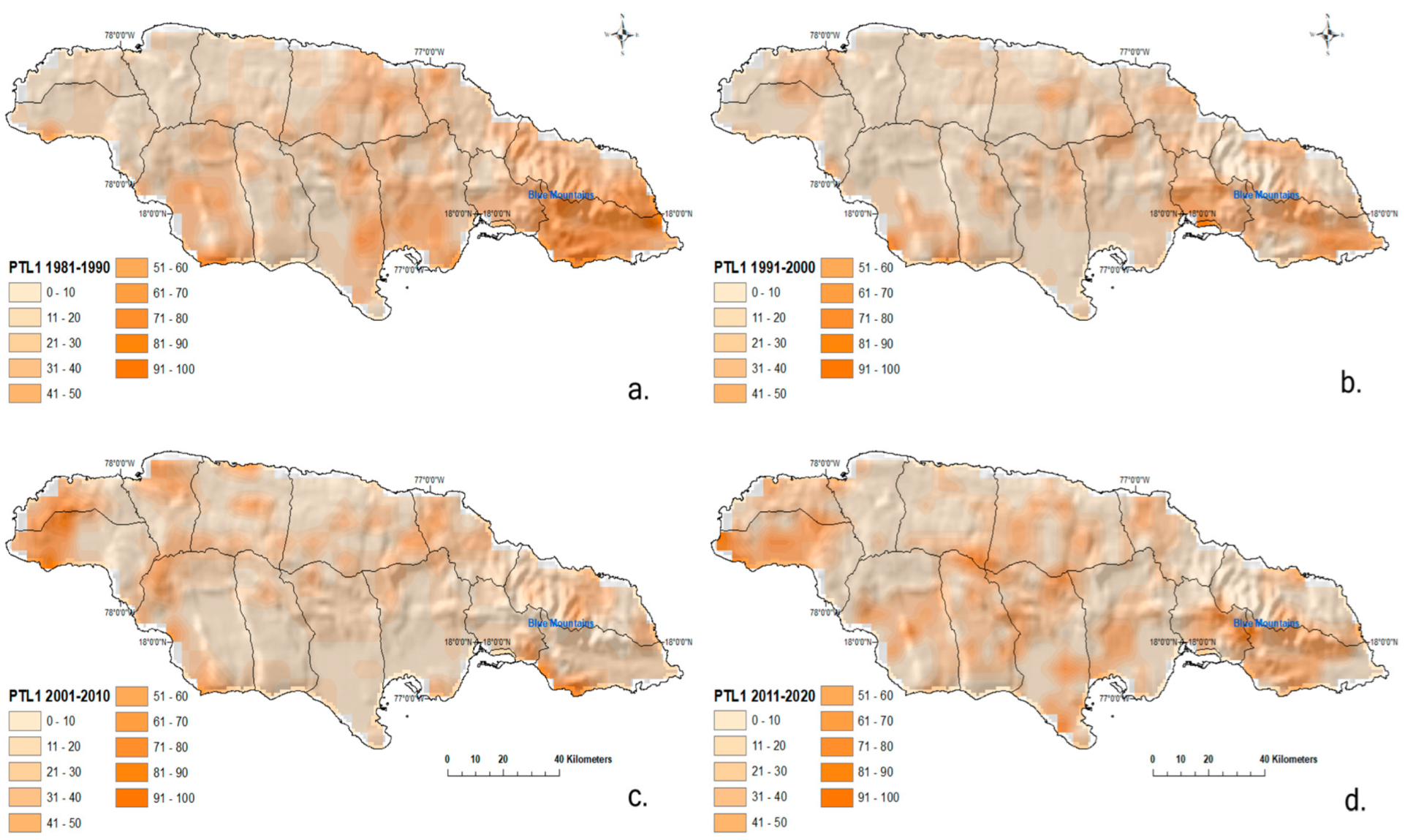
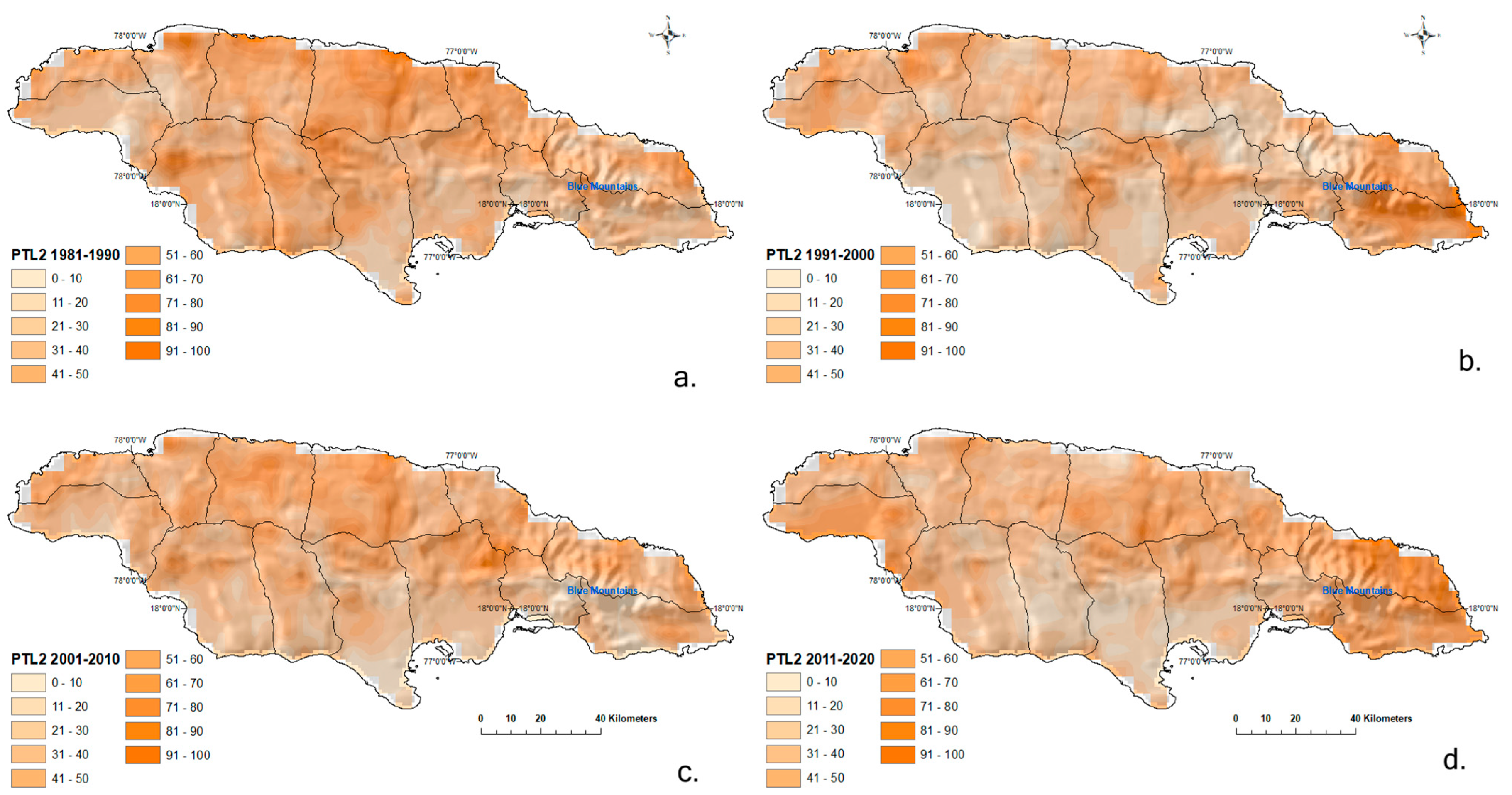
4.3.2. Persistence Threshold Low
PTL 30-Days ≤ 1 mm
PTL 10-Days ≤ 15 mm
PTL 5-Days ≤ 50 mm
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Biesbroek, R.; Bowen, K.; Lawrence, J. IPCC 2022 Summary Report; Jean: New York, NY, USA, 2022. [Google Scholar]
- Avalon-Cullen, C.; Caudill, C.; Newlands, N.K.; Enenkel, M. Big Data, Small Island: Earth Observations for Improving Flood and Landslide Risk Assessment in Jamaica. Geosciences 2023, 13, 64. [Google Scholar] [CrossRef]
- Bhalai, S. Landslide Susceptibility of Portland, Jamaica: Assessment and Zonation. Caribb. J. Earth Sci. 2010, 41, 14. [Google Scholar]
- Government of Jamaica. Climate Change Policy Framework for Jamaica Government of Jamaica. September 2015. Available online: https://www.lse.ac.uk/GranthamInstitute/wp-content/uploads/2016/05/Jamaica-Climate-Change-Policy-fwL-2015.pdf (accessed on 15 February 2022).
- Collalti, D.; Strobl, E. Economic damages due to extreme precipitation during tropical storms: Evidence from Jamaica. Nat. Hazards 2022, 110, 2059–2086. [Google Scholar] [CrossRef]
- Mandal, A.; Stephenson, T.; Campbell, J.; Taylor, M.; Watson, S.; Clarke, L.; Smith, D.; Darsan, J.; Wilson, M. An assessment of the impact of 1.5 versus 2 and 2.5 °C global temperature increase on flooding in Jamaica: A case study from the Hope watershed. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 141. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Poomalai, S.; Saminathan, B.; Suthanthiravel, S.; Sundaram, K.; Hakkim, F.F.A.; Sivapragasam, C.; Saravanan, P.; Balamurali, S.; Sumila, S.; et al. An investigation on the relationship between the Hurst exponent and the predictability of a rainfall time series. Meteorol. Appl. 2019, 26, 511–519. [Google Scholar] [CrossRef]
- Patakamuri, S.K.; Muthiah, K.; Sridhar, V. Long-Term Homogeneity, Trend, and Change-Point Analysis of Rainfall in the Arid District of Ananthapuramu, Andhra Pradesh State, India. Water 2020, 12, 211. [Google Scholar] [CrossRef]
- Moon, H.; Gudmundsson, L.; Guillod, B.P.; Venugopal, V.; Seneviratne, S.I. Intercomparison of daily precipitation persistence in multiple global observations and climate models. Environ. Res. Lett. 2019, 14, 105009. [Google Scholar] [CrossRef]
- Du, H.; Donat, M.G.; Zong, S.; Alexander, L.V.; Manzanas, R.; Kruger, A.; Choi, G.; Salinger, J.; He, H.S.; Li, M.-H.; et al. Extreme Precipitation on Consecutive Days Occurs More Often in a Warming Climate. Bull. Am. Meteorol. Soc. 2022, 103, E1130–E1145. [Google Scholar] [CrossRef]
- Matalas, N.C.; Sankarasubramanian, A. Effect of persistence on trend detection via regression. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Vogel, R.M.; Tsai, Y.; Limbrunner, J.F. The regional persistence and variability of annual streamflow in the United States. Water Resour. Res. 1998, 34, 3445–3459. [Google Scholar] [CrossRef]
- Hansen, P.R.; Lunde, A. Estimating the Persistence and the Autocorrelation Function of A Time Series That Is Measured with error. Econ. Theory 2013, 30, 60–93. [Google Scholar] [CrossRef]
- Ebisuzaki, W. A Method to Estimate the Statistical Significance of a Correlation When the Data Are Serially Correlated. J. Clim. 1997, 10, 2147–2153. [Google Scholar] [CrossRef]
- Khan, N.; Pour, S.H.; Shahid, S.; Ismail, T.; Ahmed, K.; Chung, E.; Nawaz, N.; Wang, X. Spatial distribution of secular trends in rainfall indices of Peninsular Malaysia in the presence of long-term persistence. Meteorol. Appl. 2019, 26, 655–670. [Google Scholar] [CrossRef]
- Pan, X.; Li, T.; Sun, Y.; Zhu, Z. Cause of Extreme Heavy and Persistent Rainfall over Yangtze River in Summer 2020. Adv. Atmospheric Sci. 2021, 38, 1994–2009. [Google Scholar] [CrossRef]
- Bharath, A.; Maddamsetty, R.; Manjunatha, M.; Reshma, T.V. Spatiotemporal Rainfall Variability and Trend Analysis of Shimsha River Basin, India. Environ. Sci. Pollut. Res. 2023, 1–20. [Google Scholar] [CrossRef]
- Ogunrinde, A.T.; Oguntunde, P.G.; Akinwumiju, A.S.; Fasinmirin, J.T. Analysis of recent changes in rainfall and drought indices in Nigeria, 1981–2015. Hydrol. Sci. J. 2019, 64, 1755–1768. [Google Scholar] [CrossRef]
- Iresh, A.D.S. Screening of Annual Rainfall Time-Series Data in Kala Oya Basin: Case Study in Sri Lanka. Eng. J. Inst. Eng. Sri Lanka 2020, 53, 69. [Google Scholar] [CrossRef]
- Pal, S.; Dutta, S.; Nasrin, T.; Chattopadhyay, S. Hurst exponent approach through rescaled range analysis to study the time series of summer monsoon rainfall over northeast India. Theor. Appl. Clim. 2020, 142, 581–587. [Google Scholar] [CrossRef]
- Valle, M.A.V.; García, G.M.; Cohen, I.S.; Oleschko, L.K.; Corral, J.A.R.; Korvin, G. Spatial Variability of the Hurst Exponent for the Daily Scale Rainfall Series in the State of Zacatecas, Mexico. J. Appl. Meteorol. Clim. 2013, 52, 2771–2780. [Google Scholar] [CrossRef]
- Yeşilırmak, E.; Atatanır, L. Spatiotemporal variability of precipitation concentration in western Turkey. Nat. Hazards 2015, 81, 687–704. [Google Scholar] [CrossRef]
- Xu, F.; Zhou, Y.; Zhao, L. Spatial and temporal variability in extreme precipitation in the Pearl River Basin, China from 1960 to 2018. Int. J. Clim. 2022, 42, 797–816. [Google Scholar] [CrossRef]
- Reiter, A.; Weidinger, R.; Mauser, W. Recent Climate Change at the Upper Danube—A temporal and spatial analysis of temperature and precipitation time series. Clim. Change 2011, 111, 665–696. [Google Scholar] [CrossRef]
- Casanueva, A.; Rodríguez-Puebla, C.; Frías, M.D.; González-Reviriego, N. Variability of extreme precipitation over Europe and its relationships with teleconnection patterns. Hydrol. Earth Syst. Sci. 2014, 18, 709–725. [Google Scholar] [CrossRef]
- Anderson, T.G.; Anchukaitis, K.J.; Pons, D.; Taylor, M. Multiscale trends and precipitation extremes in the Central American Midsummer Drought. Environ. Res. Lett. 2019, 14, 124016. [Google Scholar] [CrossRef]
- Nakaegawa, T.; Kitoh, A.; Murakami, H.; Kusunoki, S. Annual maximum 5-day rainfall total and maximum number of consecutive dry days over Central America and the Caribbean in the late twenty-first century projected by an atmospheric general circulation model with three different horizontal resolutions. Theor. Appl. Clim. 2014, 116, 155–168. [Google Scholar] [CrossRef]
- Bathelemy, R.; Brigode, P.; Boisson, D.; Tric, E. Rainfall in the Greater and Lesser Antilles: Performance of five gridded datasets on a daily timescale. J. Hydrol. Reg. Stud. 2022, 43, 101201. [Google Scholar] [CrossRef]
- Hsu, J.; Huang, W.-R.; Liu, P.-Y.; Li, X. Validation of CHIRPS Precipitation Estimates over Taiwan at Multiple Timescales. Remote Sens. 2021, 13, 254. [Google Scholar] [CrossRef]
- Belay, A.S.; Fenta, A.A.; Yenehun, A.; Nigate, F.; Tilahun, S.A.; Moges, M.M.; Dessie, M.; Adgo, E.; Nyssen, J.; Chen, M.; et al. Evaluation and Application of Multi-Source Satellite Rainfall Product CHIRPS to Assess Spatio-Temporal Rainfall Variability on Data-Sparse Western Margins of Ethiopian Highlands. Remote Sens. 2019, 11, 2688. [Google Scholar] [CrossRef]
- Stephenson, T.S.; Vincent, L.A.; Allen, T.L.; Van Meerbeeck, C.J.; McLean, N.; Peterson, T.C.; Taylor, M.A.; Aaron-Morrison, A.P.; Auguste, T.; Bernard, D.; et al. Changes in extreme temperature and precipitation in the Caribbean region, 1961–2010. Int. J. Climatol. 2014, 34, 2957–2971. [Google Scholar] [CrossRef]
- Population Reference Bureau. 2022 World Population Datasheet. September 2022. Available online: https://2022-wpds.prb.org/download-files/ (accessed on 20 September 2022).
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Cullen, C.A.; Al Suhili, R.; Aristizabal, E. A Landslide Numerical Factor Derived from CHIRPS for Shallow Rainfall Triggered Landslides in Colombia. Remote Sens. 2022, 14, 2239. [Google Scholar] [CrossRef]
- Lewinson. Introduction to the Hurst Exponent—With Code in Python. 2021. Available online: https://towardsdatascience.com/introduction-to-the-hurst-exponent-with-code-in-python-4da0414ca52e (accessed on 14 March 2023).
- Brockwell, J.P.; Davis, A.R. Introduction to Time Series and Forecasting, 2nd ed.; Springer: Cham, Switzerland, 2002. [Google Scholar]
- National Oceanic and Atmospheric Administration. ENSO Effects Across the Northeastern Caribbean. National Weather Service. 2023. Available online: https://www.weather.gov/sju/climo_enso (accessed on 22 March 2023).
- Curtis, S.; Gamble, D. MJO, NAO, ENSO, and Mid-Summer Rainfall in the Caribbean. US Climate Variability and Predictability Program. 2021. Available online: https://usclivar.org/2015-iasclip-abstract/mjo-nao-enso-and-mid-summer-rainfall-caribbean (accessed on 22 March 2023).
- World Meteorological Organization. The Global Climate 2001–2010: A Decade of Climate Extremes: Summary Report. 2013. Available online: https://reliefweb.int/report/world/global-climate-2001-2010-decade-climate-extremes-summary-report (accessed on 22 March 2023).




| Range | G1 | G2 | G3 | G4 | All Period | All Period % |
|---|---|---|---|---|---|---|
| 0–50 | 1,317,822 | 1,314,359 | 1,307,031 | 1,316,767 | 5,255,979 | 98.9 |
| 50–100 | 8995 | 11,693 | 17,591 | 9484 | 47,763 | 0.9 |
| 100–150 | 1694 | 1992 | 3303 | 1956 | 8945 | 0.2 |
| 150–200 | 367 | 599 | 685 | 515 | 2166 | 0 |
| 200–250 | 61 | 221 | 205 | 163 | 650 | 0 |
| 250–300 | 18 | 57 | 87 | 52 | 214 | 0 |
| 300–350 | 3 | 22 | 38 | 14 | 77 | 0 |
| 350–400 | 3 | 10 | 14 | 12 | 39 | 0 |
| 400–450 | 1 | 6 | 5 | 1 | 13 | 0 |
| 450–500 | 0 | 3 | 5 | 0 | 8 | 0 |
| 500–550 | 0 | 1 | 0 | 0 | 1 | 0 |
| 550–600 | 0 | 1 | 0 | 0 | 1 | 0 |
| Groups | t-Test for Means | p-Value |
|---|---|---|
| G1-G2 | −0.383 | 0.711 |
| G1-G3 | −1.982 | 0.072 |
| G1-G4 | 0.207 | 0.841 |
| G2-G3 | −1.465 | 0.177 |
| G2-G4 | 0.456 | 0.659 |
| G3-G4 | 2.221 | 0.053 |
| Groups | EWS | p-Value | Dry | p-Value | LWS | p-Value |
|---|---|---|---|---|---|---|
| G1–G2 | −0.57 | 0.61 | −0.03 | 0.98 | 0.14 | 0.90 |
| G1–G3 | −1.88 | 0.16 | 1.59 | 0.21 | −3.11 | 0.05 |
| G1–G4 | −0.64 | 0.57 | 1.85 | 0.16 | −0.27 | 0.80 |
| G2–G3 | −2.10 | 0.13 | 2.43 | 0.09 | −1.02 | 0.38 |
| G2–G4 | 0.30 | 0.78 | 1.74 | 0.18 | −0.40 | 0.72 |
| G3–G4 | 5.12 | 0.06 | −0.69 | 0.54 | 1.07 | 0.36 |
| Persistence | Threshold mm, Consecutive Days |
|---|---|
| low | (1,30), (5,20), (10,15), (20,10), (50,5) |
| high | (50,3), (60,2), (80,2), (100,1), (120,1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avalon Cullen, C.; Al Suhili, R. Assessing Rainfall Variability in Jamaica Using CHIRPS: Techniques and Measures for Persistence, Long and Short-Term Trends. Geographies 2023, 3, 375-397. https://doi.org/10.3390/geographies3020020
Avalon Cullen C, Al Suhili R. Assessing Rainfall Variability in Jamaica Using CHIRPS: Techniques and Measures for Persistence, Long and Short-Term Trends. Geographies. 2023; 3(2):375-397. https://doi.org/10.3390/geographies3020020
Chicago/Turabian StyleAvalon Cullen, Cheila, and Rafea Al Suhili. 2023. "Assessing Rainfall Variability in Jamaica Using CHIRPS: Techniques and Measures for Persistence, Long and Short-Term Trends" Geographies 3, no. 2: 375-397. https://doi.org/10.3390/geographies3020020
APA StyleAvalon Cullen, C., & Al Suhili, R. (2023). Assessing Rainfall Variability in Jamaica Using CHIRPS: Techniques and Measures for Persistence, Long and Short-Term Trends. Geographies, 3(2), 375-397. https://doi.org/10.3390/geographies3020020








