Forest Type Differentiation Using GLAD Phenology Metrics, Land Surface Parameters, and Machine Learning
Abstract
1. Introduction
2. Background
2.1. Remote Sensing for Forest Type Mapping
| Study | Data | Study Area | Methods | Classes | Overall Accuracy |
|---|---|---|---|---|---|
| Immitzer et al. [55] | MSI | Two small extents in Bavaria, Germany | Random Forest | 7 | 64% |
| Immitzer et al. [55] | MSI | Two small extents in Bavaria, Germany | Random Forest; GEOBIA | 7 | 66% |
| Liu et al. [50] | MSI | ~226,000 ha | Random Forest; GEOBIA | 8 | 54% |
| Liu et al. [50] | MSI; Terrain | ~226,000 ha | Random Forest; GEOBIA | 8 | 70% |
| Liu et al. [50] | MSI; OLI; SAR; Terrain | ~226,000 ha | Random Forest; GEOBIA | 8 | 83% |
| Pasquarella et al. [51] | TM; ETM+ | Western Massachusetts, United States | Random Forest; Late-Autumn | 8 | 74% |
| Pasquarella et al. [51] | TM; ETM+ | Western Massachusetts, United States | Random Forest; Multi-Date; | 8 | 79% |
| Pasquarella et al. [51] | TM; ETM+ | Western Massachusetts, United States | Random Forest; Harmonic Regression | 8 | 81% |
| Pasquarella et al. [51] | TM; ETM+; Terrain; Ancillary | Western Massachusetts, United States | Random Forest; Harmonic Regression | 8 | 83% |
| Hościło and Lewandowska [56] | MSI | ~380,000 ha | Random Forest | 8 | 76% |
| Hościło and Lewandowska [56] | MSI; Terrain | ~380,000 ha | Random Forest | 8 | 82% |
| Adams et al. [49] | Terrain | 17 Counties in Ohio, United States | Random Forest | 7 | 51% |
| Adams et al. [49] | OLI | 17 Counties in Ohio, United States | Random Forest; Seasonal Composites; Spectral Indices | 7 | 62% |
| Adams et al. [49] | OLI | 17 Counties in Ohio, United States | Random Forest; Harmonic Regression | 7 | 66% |
| Adams et al. [49] | OLI; Terrain | 17 Counties in Ohio, United States | Random Forest; Seasonal Composites; Spectral Indices | 7 | 70% |
| Adams et al. [49] | OLI; Terrain | 17 Counties in Ohio, United States | Random Forest; Harmonic Regression | 7 | 75% |
2.2. GLAD Phenology
2.3. Machine Learning
3. Materials and Methods
3.1. Study Area and Field Plots

3.2. Predictor Variables
3.3. Feature Selection, Hyperparameter Optimization, and Model Training
3.4. Model Assessment and Comparison
4. Results and Discussion
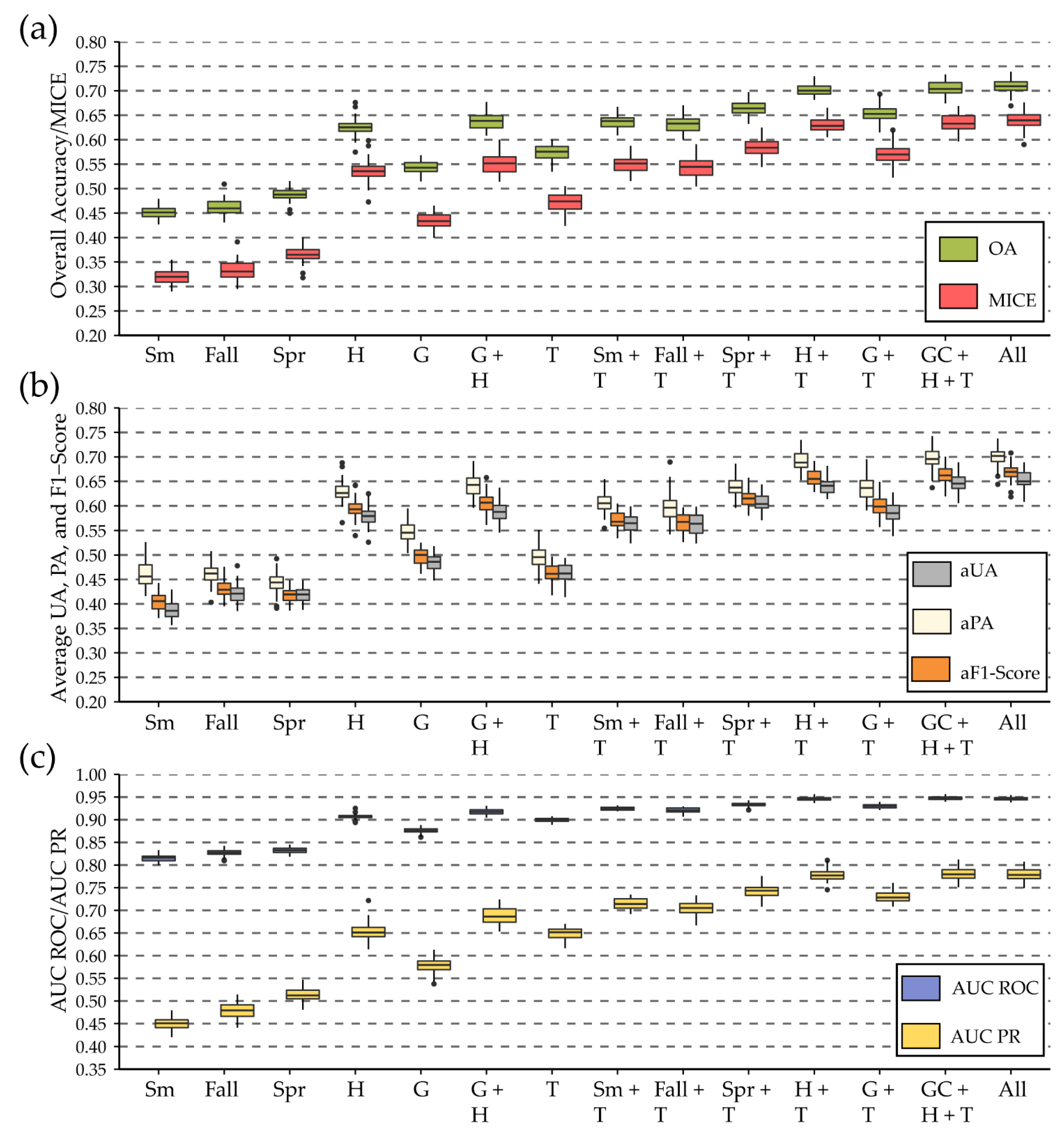
4.1. Results Using GLAD Phenology Metrics and Terrain Variables
4.2. Comparison of GLAD Phenology Metric Results with Other Methods
4.3. Summary of Key Findings and Recommendations
- Including digital terrain variables generally improved the accuracy of forest type differentiation compared to only using spectral data.
- The number of classes and class definitions can have a large impact on the accuracy of the resulting map products.
- Even if the correct class was not always predicted with the highest probability, it was generally in the top set of the highest predicted probabilities. We attribute this result to specific classes being difficult to separate, pixels not mapping well to a specific class, and/or class boundaries being gradational within the landscape. This highlights the value of supplementing “hard” classification products with associated probabilistic predictions.
- GLAD Phenology Metrics were generally of value for mapping and differentiating forest community types. However, they did not provide the level of accuracy obtained using harmonic regression coefficients.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Binkley, D. Forest Ecology: An Evidence-Based Approach; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Franklin, J.F.; Johnson, K.N.; Johnson, D.L. Ecological Forest Management; Waveland Press: Long Grove, IL, USA, 2018. [Google Scholar]
- Smail, R.A. Forest Land Conversion, Ecosystem Services, and Economic Issues for Policy: A Review; General Technical Report PNW-GTR-797; U.S. Department of Agriculture, Forest Service: Washington, DC, USA, 2009.
- Hasan, S.S.; Zhen, L.; Miah, M.G.; Ahamed, T.; Samie, A. Impact of Land Use Change on Ecosystem Services: A Review. Environ. Dev. 2020, 34, 100527. [Google Scholar] [CrossRef]
- Foley, J.A. Global Consequences of Land Use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef] [PubMed]
- Houghton, R.A.; Hackler, J.L.; Lawrence, K.T. The US Carbon Budget: Contributions from Land-Use Change. Science 1999, 285, 574–578. [Google Scholar] [CrossRef]
- Galloway, J.N. The Global Nitrogen Cycle: Changes and Consequences. Environ. Pollut. 1998, 102, 15–24. [Google Scholar] [CrossRef]
- Gruber, N.; Galloway, J.N. An Earth-System Perspective of the Global Nitrogen Cycle. Nature 2008, 451, 293–296. [Google Scholar] [CrossRef] [PubMed]
- Vitousek, P.M.; Aber, J.D.; Howarth, R.W.; Likens, G.E.; Matson, P.A.; Schindler, D.W.; Schlesinger, W.H.; Tilman, D.G. Human Alteration of the Global Nitrogen Cycle: Sources and Consequences. Ecol. Appl. 1997, 7, 737–750. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Jackson, R.B.; Randerson, J.T.; Canadell, J.G.; Anderson, R.G.; Avissar, R.; Baldocchi, D.D.; Bonan, G.B.; Caldeira, K.; Diffenbaugh, N.S.; Field, C.B.; et al. Protecting Climate with Forests. Environ. Res. Lett. 2008, 3, 044006. [Google Scholar] [CrossRef]
- Kirilenko, A.P.; Sedjo, R.A. Climate Change Impacts on Forestry. Proc. Natl. Acad. Sci. USA 2007, 104, 19697–19702. [Google Scholar] [CrossRef] [PubMed]
- Chow, J.; Kopp, R.J.; Portney, P.R. Energy Resources and Global Development. Science 2003, 302, 1528–1531. [Google Scholar] [CrossRef] [PubMed]
- Delcourt, H.R. Eastern Deciduous Forests. 2000. Available online: https://ci.nii.ac.jp/naid/10020542173/ (accessed on 11 June 2022).
- Dyer, J.M. Revisiting the Deciduous Forests of Eastern North America. BioScience 2006, 56, 341–352. [Google Scholar] [CrossRef]
- Eastern Deciduous Forest (U.S. National Park Service). Available online: https://www.nps.gov/im/ncrn/eastern-deciduous-forest.htm (accessed on 30 May 2022).
- Coddington, J.A.; Young, L.H.; Coyle, F.A. Estimating Spider Species Richness in a Southern Appalachian Cove Hardwood Forest. J. Arachnol. 1996, 24, 111–128. [Google Scholar]
- Keddy, P.A.; Drummond, C.G. Ecological Properties for the Evaluation, Management, and Restoration of Temperate Deciduous Forest Ecosystems. Ecol. Appl. 1996, 6, 748–762. [Google Scholar] [CrossRef]
- Green, N.B.; Pauley, T.K. Amphibians and Reptiles in West Virginia; University of Pittsburgh Press: Pittsburgh, PA, USA, 1987. [Google Scholar]
- Wickham, J.; Wood, P.B.; Nicholson, M.C.; Jenkins, W.; Druckenbrod, D.; Suter, G.W.; Strager, M.P.; Mazzarella, C.; Galloway, W.; Amos, J. The Overlooked Terrestrial Impacts of Mountaintop Mining. BioScience 2013, 63, 335–348. [Google Scholar] [CrossRef]
- Wickham, J.D.; Riitters, K.H.; Wade, T.; Coan, M.; Homer, C. The Effect of Appalachian Mountaintop Mining on Interior Forest. Landsc. Ecol. 2007, 22, 179–187. [Google Scholar] [CrossRef]
- Drummond, M.A.; Loveland, T.R. Land-Use Pressure and a Transition to Forest-Cover Loss in the Eastern United States. BioScience 2010, 60, 286–298. [Google Scholar] [CrossRef]
- Strausbaugh, P.; Core, E. Flora of West Virginia Ed. 2. Part 1; West Virginia University: Morgantown, VA, USA, 1970. [Google Scholar]
- Turner, M.G.; Pearson, S.M.; Bolstad, P.; Wear, D.N. Effects of Land-Cover Change on Spatial Pattern of Forest Communities in the Southern Appalachian Mountains (USA). Landsc. Ecol. 2003, 18, 449–464. [Google Scholar] [CrossRef]
- Bernhardt, E.S.; Palmer, M.A. The Environmental Costs of Mountaintop Mining Valley Fill Operations for Aquatic Ecosystems of the Central Appalachians. Ann. N. Y. Acad. Sci. 2011, 1223, 39–57. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.L.; Canham, C.D.; Murphy, L.; Donovan, T.M. Timber Harvest as the Predominant Disturbance Regime in Northeastern US Forests: Effects of Harvest Intensification. Ecosphere 2018, 9, e02062. [Google Scholar] [CrossRef]
- Cole, P.G.; Weltzin, J.F. Light Limitation Creates Patchy Distribution of an Invasive Grass in Eastern Deciduous Forests. Biol. Invasions 2005, 7, 477–488. [Google Scholar] [CrossRef]
- Flory, S.L.; Clay, K. Invasive Shrub Distribution Varies with Distance to Roads and Stand Age in Eastern Deciduous Forests in Indiana, USA. Plant Ecol. 2006, 184, 131–141. [Google Scholar] [CrossRef]
- Jo, I.; Fridley, J.D.; Frank, D.A. Linking Above-and Belowground Resource Use Strategies for Native and Invasive Species of Temperate Deciduous Forests. Biol. Invasions 2015, 17, 1545–1554. [Google Scholar] [CrossRef]
- Hubbart, J.A.; Guyette, R.; Muzika, R.-M. More than Drought: Precipitation Variance, Excessive Wetness, Pathogens and the Future of the Western Edge of the Eastern Deciduous Forest. Sci. Total Environ. 2016, 566, 463–467. [Google Scholar] [CrossRef] [PubMed]
- Havill, N.P.; Vieira, L.C.; Salom, S.M. Biology and Control of Hemlock Woolly Adelgid; FHTET-2014-05; Department of Agriculture, Forest Service, Forest Health Technology Enterprise Team: Morgantown, WV, USA, 2014; pp. 1–21.
- Vose, J.M.; Wear, D.N.; Mayfield III, A.E.; Nelson, C.D. Hemlock Woolly Adelgid in the Southern Appalachians: Control Strategies, Ecological Impacts, and Potential Management Responses. For. Ecol. Manag. 2013, 291, 209–219. [Google Scholar] [CrossRef]
- Mountaineers and Rangers: A History of Federal Forest Management in the Southern Appalachians, 1900–1981 (Chapter 1). Available online: http://npshistory.com/publications/usfs/region/8/history/chap1.htm (accessed on 30 May 2022).
- Schuler, T.M.; Gillespie, A.R. Temporal Patterns of Woody Species Diversity in a Central Appalachian Forest from 1856 to 1997. J. Torrey Bot. Soc. 2000, 127, 149–161. [Google Scholar] [CrossRef]
- Thomas-Van Gundy, M.A.; Strager, M.P. European Settlement-Era Vegetation of the Monongahela National Forest, West Virginia; General Technical Report NRS-GTR-101; US Department of Agriculture, Forest Service, Northern Research Station: Newtown Square, PA, USA, 2012; Volume 101, pp. 1–39.
- Mery, G.; Alfaro, R.; Kanninen, M.; Lobovikov, M. Changing Paradigms in Forestry: Repercussions for People and Nature. In Forests in the Global Balance-Changing Paradigms; International Union of Forest Research Organizations: Helsinki, Finland, 2005; pp. 13–20. [Google Scholar]
- Chiras, D.D.; Reganold, J.P.; Owen, O.S. Natural Resource Conservation: Management for a Sustainable Future; Benjamin Cummings: San Francisco, CA, USA, 2010. [Google Scholar]
- Lechner, A.M.; Foody, G.M.; Boyd, D.S. Applications in Remote Sensing to Forest Ecology and Management. One Earth 2020, 2, 405–412. [Google Scholar] [CrossRef]
- Wulder, M.A.; Franklin, S.E. Remote Sensing of Forest Environments: Concepts and Case Studies; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of Studies on Tree Species Classification from Remotely Sensed Data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Ruefenacht, B.; Finco, M.V.; Nelson, M.D.; Czaplewski, R.; Helmer, E.H.; Blackard, J.A.; Holden, G.R.; Lister, A.J.; Salajanu, D.; Weyermann, D.; et al. Conterminous U.S. and Alaska Forest Type Mapping Using Forest Inventory and Analysis Data. Photogramm. Eng. Remote Sens. 2008, 74, 1379–1388. [Google Scholar] [CrossRef]
- Beaubien, J. Forest Type Mapping from Landsat Digital Data. Photogramm. Eng. Remote Sens. 1979, 45, 1135–1144. [Google Scholar]
- Bryant, E.; Dodge, A.G.; Warren, S.D. Landsat for Practical Forest Type Mapping—A Test Case. Photogramm. Eng. Remote Sens. 1980, 46, 1575–1584. [Google Scholar]
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the Conterminous United States—Representing a Decade of Land Cover Change Information. Photogramm. Eng. 2015, 81, 345–354. [Google Scholar]
- Fajvan, M.A.; Grushecky, S.T.; Hassler, C.C. The Effects of Harvesting Practices on West Virginia’s Wood Supply. J. For. 1998, 96, 33–39. [Google Scholar] [CrossRef]
- Potapov, P.; Hansen, M.C.; Kommareddy, I.; Kommareddy, A.; Turubanova, S.; Pickens, A.; Adusei, B.; Tyukavina, A.; Ying, Q. Landsat Analysis Ready Data for Global Land Cover and Land Cover Change Mapping. Remote Sens. 2020, 12, 426. [Google Scholar] [CrossRef]
- Adams, B.; Iverson, L.; Matthews, S.; Peters, M.; Prasad, A.; Hix, D.M. Mapping Forest Composition with Landsat Time Series: An Evaluation of Seasonal Composites and Harmonic Regression. Remote Sens. 2020, 12, 610. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, W.; Hu, X.; Gong, J. Forest Type Identification with Random Forest Using Sentinel-1A, Sentinel-2A, Multi-Temporal Landsat-8 and DEM Data. Remote Sens. 2018, 10, 946. [Google Scholar] [CrossRef]
- Pasquarella, V.J.; Holden, C.E.; Woodcock, C.E. Improved Mapping of Forest Type Using Spectral-Temporal Landsat Features. Remote Sens. Environ. 2018, 210, 193–207. [Google Scholar] [CrossRef]
- Franklin, S.E. Interpretation and Use of Geomorphometry in Remote Sensing: A Guide and Review of Integrated Applications. Int. J. Remote Sens. 2020, 41, 7700–7733. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Shobe, C.M. Land-Surface Parameters for Spatial Predictive Mapping and Modeling. Earth-Sci. Rev. 2022, 226, 103944. [Google Scholar] [CrossRef]
- Wilson, B.T.; Knight, J.F.; McRoberts, R.E. Harmonic Regression of Landsat Time Series for Modeling Attributes from National Forest Inventory Data. ISPRS J. Photogramm. Remote Sens. 2018, 137, 29–46. [Google Scholar] [CrossRef]
- Immitzer, M.; Vuolo, F.; Atzberger, C. First Experience with Sentinel-2 Data for Crop and Tree Species Classifications in Central Europe. Remote Sens. 2016, 8, 166. [Google Scholar] [CrossRef]
- Hościło, A.; Lewandowska, A. Mapping Forest Type and Tree Species on a Regional Scale Using Multi-Temporal Sentinel-2 Data. Remote Sens. 2019, 11, 929. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping Global Forest Canopy Height through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Coulter, L.L.; Stow, D.A.; Tsai, Y.-H.; Ibanez, N.; Shih, H.; Kerr, A.; Benza, M.; Weeks, J.R.; Mensah, F. Classification and Assessment of Land Cover and Land Use Change in Southern Ghana Using Dense Stacks of Landsat 7 ETM+ Imagery. Remote Sens. Environ. 2016, 184, 396–409. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a Tasselled Cap Transformation Based on Landsat 8 At-Satellite Reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Christ, P.F.; Elshaer, M.E.A.; Ettlinger, F.; Tatavarty, S.; Bickel, M.; Bilic, P.; Rempfler, M.; Armbruster, M.; Hofmann, F.; D’Anastasi, M.; et al. Automatic Liver and Lesion Segmentation in CT Using Cascaded Fully Convolutional Neural Networks and 3D Conditional Random Fields. arXiv 2016, arXiv:1610.02177. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of Machine-Learning Classification in Remote Sensing: An Applied Review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support Vector Machines in Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Yang, L.; Jin, S.; Danielson, P.; Homer, C.; Gass, L.; Bender, S.M.; Case, A.; Costello, C.; Dewitz, J.; Fry, J.; et al. A New Generation of the United States National Land Cover Database: Requirements, Research Priorities, Design, and Implementation Strategies. ISPRS J. Photogramm. Remote Sens. 2018, 146, 108–123. [Google Scholar] [CrossRef]
- Vanderhorst, J.; Byers, E.; Streets, B. Natural Heritage Vegetation Database for West Virginia. Biodivers. Ecol. 2012, 4, 440. [Google Scholar] [CrossRef][Green Version]
- Major Land Resource Area (MLRA)|NRCS Soils. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/detail/soils/survey/geo/?cid=nrcs142p2_053624 (accessed on 28 February 2021).
- The Perl Programming Language—www.Perl.Org. Available online: https://www.perl.org/ (accessed on 25 June 2022).
- Kriegler, F.; Malila, W.; Nalepka, R.; Richardson, W. Preprocessing Transformations and Their Effects on Multispectral Recognition. Remote Sens. Environ. 1969, VI, 97. [Google Scholar]
- Philipp, M. RHarmonics 2021. Available online: https://github.com/MBalthasar/rHarmonics (accessed on 11 June 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Gesch, D.; Oimoen, M.; Greenlee, S.; Nelson, C.; Steuck, M.; Tyler, D. The National Elevation Dataset. Photogramm. Eng. Remote Sens. 2002, 68, 5–32. [Google Scholar]
- Hengl, T.; Reuter, H.I. Institute for Environment and Sustainability (European Commission. Joint Research Centre) (Eds.) Geomorphometry: Concepts, Software, Applications, 1st ed.; Developments in Soil Science; Elsevier: Amsterdam, The Netherlands; Oxford, UK; Boston, MA, USA, 2009; ISBN 978-0-12-374345-9. [Google Scholar]
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000; ISBN 978-0-471-32188-0. [Google Scholar]
- MacMillan, R.A.; Shary, P.A. Chapter 9 Landforms and Landform Elements in Geomorphometry. In Developments in Soil Science; Hengl, T., Reuter, H.I., Eds.; Geomorphometry; Elsevier: Amsterdam, The Netherlands, 2009; Volume 33, pp. 227–254. [Google Scholar]
- Evans, J.S. GradientMetrics 2022. Available online: https://github.com/jeffreyevans/GradientMetrics (accessed on 11 June 2022).
- ArcGIS Pro Python Reference—ArcGIS Pro|Documentation. Available online: https://pro.arcgis.com/en/pro-app/latest/arcpy/main/arcgis-pro-arcpy-reference.htm (accessed on 11 June 2022).
- Download ArcGIS Pro—ArcGIS Pro|Documentation. Available online: https://pro.arcgis.com/en/pro-app/latest/get-started/download-arcgis-pro.htm (accessed on 11 June 2022).
- Extract Multi Values to Points (Spatial Analyst)—ArcGIS Pro|Documentation. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/spatial-analyst/extract-multi-values-to-points.htm (accessed on 11 June 2022).
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling. Available online: https://rdrr.io/cran/raster/ (accessed on 11 June 2022).
- Liaw, A.; Wiener, M. Classification and Regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training. Available online: https://cran.r-project.org/web/packages/caret/caret.pdf (accessed on 11 June 2022).
- Hughes, G. On the Mean Accuracy of Statistical Pattern Recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Murphy, M.A.; Evans, J.S.; Storfer, A. Quantifying Bufo Boreas Connectivity in Yellowstone National Park with Landscape Genetics. Ecology 2010, 91, 252–261. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Foody, G.M. Status of Land Cover Classification Accuracy Assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Stehman, S.V.; Foody, G.M. Accuracy Assessment. In The SAGE Handbook of Remote Sensing; Sage: London, UK, 2009; pp. 297–309. [Google Scholar]
- Tharwat, A. Classification Assessment Methods. Appl. Comput. Inform. 2020. ahead-of-print. [Google Scholar] [CrossRef]
- Stehman, S.V. A Critical Evaluation of the Normalized Error Matrix in Map Accuracy Assessment. Photogramm. Eng. Remote Sens. 2004, 70, 743–751. [Google Scholar] [CrossRef]
- Stehman, S.V. Sampling Designs for Accuracy Assessment of Land Cover. Int. J. Remote Sens. 2009, 30, 5243–5272. [Google Scholar] [CrossRef]
- Stehman, S.V. Impact of Sample Size Allocation When Using Stratified Random Sampling to Estimate Accuracy and Area of Land-Cover Change. Remote Sens. Lett. 2012, 3, 111–120. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating Area from an Accuracy Assessment Error Matrix. Remote Sens. Environ. 2013, 132, 202–211. [Google Scholar] [CrossRef]
- Foody, G.M. Explaining the Unsuitability of the Kappa Coefficient in the Assessment and Comparison of the Accuracy of Thematic Maps Obtained by Image Classification. Remote Sens. Environ. 2020, 239, 111630. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Millones, M. Death to Kappa: Birth of Quantity Disagreement and Allocation Disagreement for Accuracy Assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Shao, G.; Tang, L.; Zhang, H. Introducing Image Classification Efficacies. IEEE Access 2021, 9, 134809–134816. [Google Scholar] [CrossRef]
- Fan, J.; Upadhye, S.; Worster, A. Understanding Receiver Operating Characteristic (ROC) Curves. CJEM 2006, 8, 19–20. [Google Scholar] [CrossRef]
- Saito, T.; Rehmsmeier, M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef]
- Wandishin, M.S.; Mullen, S.J. Multiclass ROC Analysis. Weather. Forecast. 2009, 24, 530–547. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Guillén, L.A. Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 1: Literature Review. Remote Sens. 2021, 13, 2450. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Guillén, L.A. Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 2: Recommendations and Best Practices. Remote Sens. 2021, 13, 2591. [Google Scholar] [CrossRef]
- Wei, R.; Wang, J. MultiROC: Calculating and Visualizing ROC and PR Curves across Multi-Class Classifications. 2018. Available online: https://github.com/WandeRum/multiROC (accessed on 11 June 2022).
- Wright, C.; Gallant, A. Improved Wetland Remote Sensing in Yellowstone National Park Using Classification Trees to Combine TM Imagery and Ancillary Environmental Data. Remote Sens. Environ. 2007, 107, 582–605. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; Volume 26. [Google Scholar]
| Metrics Based on Ranking of 16-Day Observation Time Series | ||
| Spectral | Indices | Statistics |
| Blue Green Red NIR SWIR1 SWIR2 | (NIR-Green)/(NIR + Green) (GN) (NIR-Red)/(NIR + Red) (RN) (NIR-SWIR1)/(NIR + SWIR1) (NS1) (NIR-SWIR2)/(NIR + SWIR2) (NS2) (SWIR1-SWIR2)/(SWIR1 + SWIR2) (SWSW) SVVI Tasseled Cap Greenness (TCG) | Minimum (min) Maximum (max) Median (median) Average between min and Q1 (avgminQ1) Average between Q3 and max (avQ3max) Average between Q1 and Q3 (avQ1Q3) Average of all values (avg) Standard deviation (sd) Total absolute difference (tad) Amplitude min to max (avgminmax) Amplitude Q1 to Q3 (ampQ1Q3) Amplitude Q2 to max (amp Q2max) |
| Metrics Based on Ranking of 16-Day Observation Time Series by Value of Corresponding Variable | ||
| Bands | Corresponding Variables | Statistics |
| Blue Green Red NIR SWIR1 SWIR2 | (NIR-Red)/(NIR + Red) (RN) (NIR-SWIR2)/(NIR + SWIR2) (NS2) Brightness Temperature (LST) | Minimum (min) Maximum (max) Average between min and Q1 (avgminQ1) Average between Q3 and max (avQ3max) Amplitude min to max (avgminmax) Amplitude Q1 to Q3 (ampQ1Q3) |
| NDVI-Based Phenology Metrics | ||
| Index | Phenology Metrics | |
| (NIR-Red)/(NIR + Red) (RN) | Start of season value (RNph_sos) End of season value (RNph_eos) Start of season slope (RNph_sos_slope) End of season slope (RNph_eos_slope) Start of season amplitude (RNph_sos_amp) End of season amplitude (RNph_eos_amp) Growing season average (RNph_ave) Growing season total (RNph_sum) | |
| Community Type | Plot Count |
|---|---|
| Floodplain | 495 |
| Hemlock | 167 |
| Mixed Mesophytic | 249 |
| Northern Hardwoods | 153 |
| Oak/Hickory | 648 |
| Oak/Pine | 396 |
| Red Spruce | 108 |
| Total | 2216 |
| Feature Set | Abbreviation | Number of Variables |
|---|---|---|
| GLAD Phenology Type C | G | 188 |
| Digital Terrain Variables | T | 17 |
| Harmonic Regression Coefficients | H | 32 |
| Summer | Sm | 10 |
| Fall | Fall | 10 |
| Spring | Spr | 10 |
| Variable | Abbreviation | Description/Equation |
|---|---|---|
| Linear Aspect | AspLn | |
| Cosine Aspect Transformation | AspCos | Cos(Aspect); measure of eastwardness |
| Sine Aspect Transformation | AspSin | Sin(Aspect); measure of northwardness |
| Topographic Radiation Aspect Index | TRASP | |
| Elevation | Elev | Bare-ground surface height |
| Slope (Degrees) | Slp | |
| Mean Slope | SlpMn | Calculates slope within a moving window |
| Mean Curvature | CrvMn | Average of minimum and maximum curvatures |
| Profile Curvature | CrvPro | Curvature in direction of maximum slope |
| Tangential Curvature | CrvTan | Curvature in direction tangent to contour line |
| Topographic Position Index | TPI | z − zmean |
| Topographic Dissection Index | TDI | |
| Topographic Roughness Index | TRI | σ2(z) |
| Surface Area Ratio | SAR | |
| Surface Relief Ratio | SRR | |
| Heat Load Index | HLI | Index for annual direct incoming solar radiation based on latitude, slope, and aspect |
| Site Exposure Index | SEI |
| Set | Number of Classes | OA | MICE | Top 3 | aUA | aPA | aFS | AUC ROC | AUC PR |
|---|---|---|---|---|---|---|---|---|---|
| G | 7 | 0.543 | 0.433 | 0.886 | 0.484 | 0.547 | 0.497 | 0.875 | 0.579 |
| G + T | 7 | 0.653 | 0.570 | 0.938 | 0.587 | 0.637 | 0.601 | 0.930 | 0.730 |
| G | 6 | 0.648 | 0.496 | 0.933 | 0.501 | 0.601 | 0.527 | 0.906 | 0.698 |
| G + T | 6 | 0.762 | 0.660 | 0.966 | 0.615 | 0.673 | 0.631 | 0.953 | 0.837 |
| Reference | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Floodplain | Hemlock | Mix. Meso | North. Hard. | Oak/Hick. | Oak/Pine | Red Spruce | Totals | UA | ||
| Prediction | Floodplain | 137 | 3 | 1 | 1 | 4 | 7 | 1 | 154 | 0.890 |
| Hemlock | 2 | 15 | 3 | 1 | 2 | 5 | 1 | 29 | 0.517 | |
| Mix. Meso. | 0 | 17 | 40 | 5 | 18 | 2 | 0 | 82 | 0.488 | |
| North. Hard. | 0 | 1 | 2 | 16 | 4 | 0 | 6 | 29 | 0.552 | |
| Oak/Hick. | 1 | 7 | 28 | 15 | 140 | 51 | 0 | 242 | 0.579 | |
| Oak/Pine | 0 | 7 | 0 | 2 | 26 | 51 | 0 | 86 | 0.593 | |
| Red Spruce | 0 | 0 | 0 | 4 | 0 | 3 | 24 | 31 | 0.774 | |
| Totals | 140 | 50 | 74 | 44 | 194 | 119 | 32 | |||
| PA | 0.979 | 0.300 | 0.541 | 0.364 | 0.722 | 0.429 | 0.750 | |||
| Reference | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Floodplain | Hemlock | Mix. Meso | North. Hard. | Oak/Hick. | Oak/Pine | Red Spruce | Totals | UA | ||
| Prediction | Floodplain | 108 | 3 | 8 | 3 | 30 | 11 | 2 | 165 | 0.655 |
| Hemlock | 4 | 16 | 5 | 0 | 4 | 7 | 2 | 38 | 0.421 | |
| Mix. Meso. | 0 | 9 | 12 | 4 | 17 | 4 | 0 | 46 | 0.261 | |
| North. Hard. | 0 | 2 | 1 | 14 | 7 | 0 | 3 | 27 | 0.519 | |
| Oak/Hick. | 18 | 10 | 45 | 19 | 119 | 43 | 1 | 255 | 0.467 | |
| Oak/Pine | 10 | 8 | 3 | 1 | 17 | 52 | 0 | 91 | 0.571 | |
| Red Spruce | 0 | 2 | 0 | 3 | 0 | 2 | 24 | 31 | 0.774 | |
| Totals | 140 | 50 | 74 | 44 | 194 | 119 | 32 | |||
| PA | 0.771 | 0.320 | 0.162 | 0.318 | 0.613 | 0.437 | 0.750 | |||
| Reference | |||||||||
| Floodplain | Hemlock | Mix. Meso | North. Hard. | Oak Dominant | Red Spruce | Totals | UA | ||
| Prediction | Floodplain | 135 | 4 | 2 | 2 | 8 | 1 | 152 | 0.888 |
| Hemlock | 1 | 10 | 1 | 1 | 5 | 1 | 19 | 0.526 | |
| Mix. Meso. | 1 | 11 | 36 | 2 | 13 | 0 | 63 | 0.571 | |
| North. Hard. | 0 | 1 | 2 | 13 | 3 | 7 | 26 | 0.500 | |
| Oak/Hick. | 3 | 24 | 33 | 22 | 280 | 0 | 362 | 0.773 | |
| Red Spruce | 0 | 0 | 0 | 4 | 4 | 23 | 31 | 0.742 | |
| Totals | 140 | 50 | 74 | 44 | 313 | 32 | |||
| PA | 0.964 | 0.200 | 0.486 | 0.295 | 0.895 | 0.719 | |||
| Set | OA | MICE | Top 3 | aUA | aPA | aFS | AUR ROC | AUC PR |
|---|---|---|---|---|---|---|---|---|
| T | 0.574 | 0.471 | 0.891 | 0.463 | 0.495 | 0.462 | 0.899 | 0.649 |
| Sm + T | 0.636 | 0.549 | 0.928 | 0.564 | 0.607 | 0.571 | 0.925 | 0.715 |
| Fall + T | 0.632 | 0.544 | 0.918 | 0.563 | 0.597 | 0.564 | 0.921 | 0.705 |
| Spr + T | 0.665 | 0.584 | 0.933 | 0.606 | 0.639 | 0.615 | 0.933 | 0.742 |
| H + T | 0.702 | 0.631 | 0.950 | 0.641 | 0.691 | 0.657 | 0.946 | 0.779 |
| G + T | 0.653 | 0.570 | 0.938 | 0.587 | 0.637 | 0.601 | 0.930 | 0.730 |
| G + H + T | 0.705 | 0.634 | 0.952 | 0.647 | 0.697 | 0.663 | 0.947 | 0.780 |
| All | 0.709 | 0.640 | 0.953 | 0.652 | 0.701 | 0.669 | 0.946 | 0.778 |
| Sm | 0.451 | 0.320 | 0.808 | 0.387 | 0.462 | 0.405 | 0.815 | 0.450 |
| Fall | 0.463 | 0.334 | 0.820 | 0.421 | 0.463 | 0.431 | 0.828 | 0.478 |
| Spr | 0.487 | 0.364 | 0.809 | 0.419 | 0.443 | 0.417 | 0.833 | 0.513 |
| H | 0.626 | 0.537 | 0.910 | 0.579 | 0.630 | 0.595 | 0.907 | 0.654 |
| G | 0.543 | 0.433 | 0.886 | 0.484 | 0.547 | 0.497 | 0.875 | 0.579 |
| G + H | 0.637 | 0.550 | 0.924 | 0.588 | 0.643 | 0.606 | 0.918 | 0.687 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hartley, F.M.; Maxwell, A.E.; Landenberger, R.E.; Bortolot, Z.J. Forest Type Differentiation Using GLAD Phenology Metrics, Land Surface Parameters, and Machine Learning. Geographies 2022, 2, 491-515. https://doi.org/10.3390/geographies2030030
Hartley FM, Maxwell AE, Landenberger RE, Bortolot ZJ. Forest Type Differentiation Using GLAD Phenology Metrics, Land Surface Parameters, and Machine Learning. Geographies. 2022; 2(3):491-515. https://doi.org/10.3390/geographies2030030
Chicago/Turabian StyleHartley, Faith M., Aaron E. Maxwell, Rick E. Landenberger, and Zachary J. Bortolot. 2022. "Forest Type Differentiation Using GLAD Phenology Metrics, Land Surface Parameters, and Machine Learning" Geographies 2, no. 3: 491-515. https://doi.org/10.3390/geographies2030030
APA StyleHartley, F. M., Maxwell, A. E., Landenberger, R. E., & Bortolot, Z. J. (2022). Forest Type Differentiation Using GLAD Phenology Metrics, Land Surface Parameters, and Machine Learning. Geographies, 2(3), 491-515. https://doi.org/10.3390/geographies2030030






