Spatial Modelling and Geovisualization of House Prices in the Greater Athens Region, Greece
Abstract
:1. Introduction
2. Materials and Methods
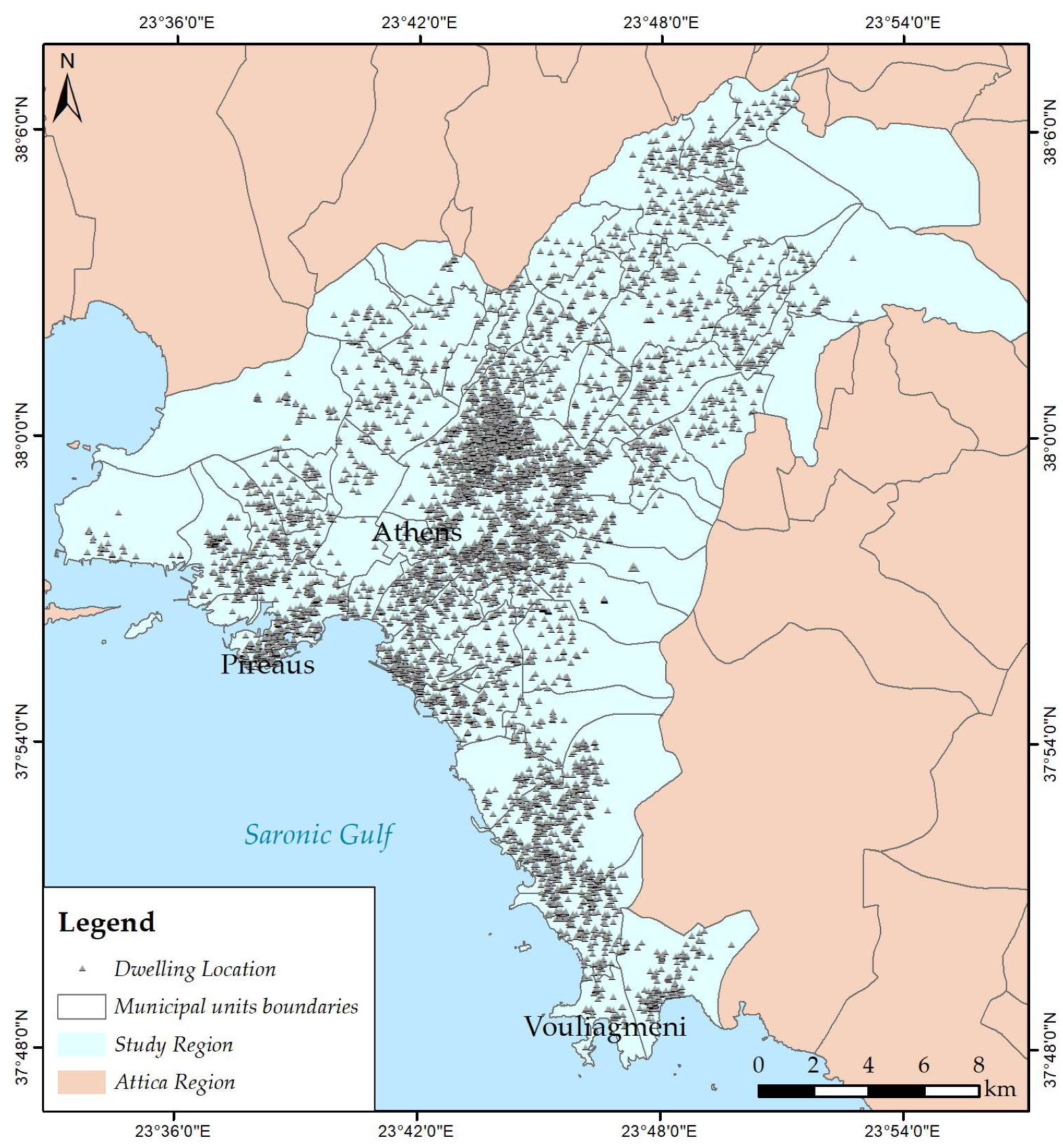
2.1. The Study Region and the Data
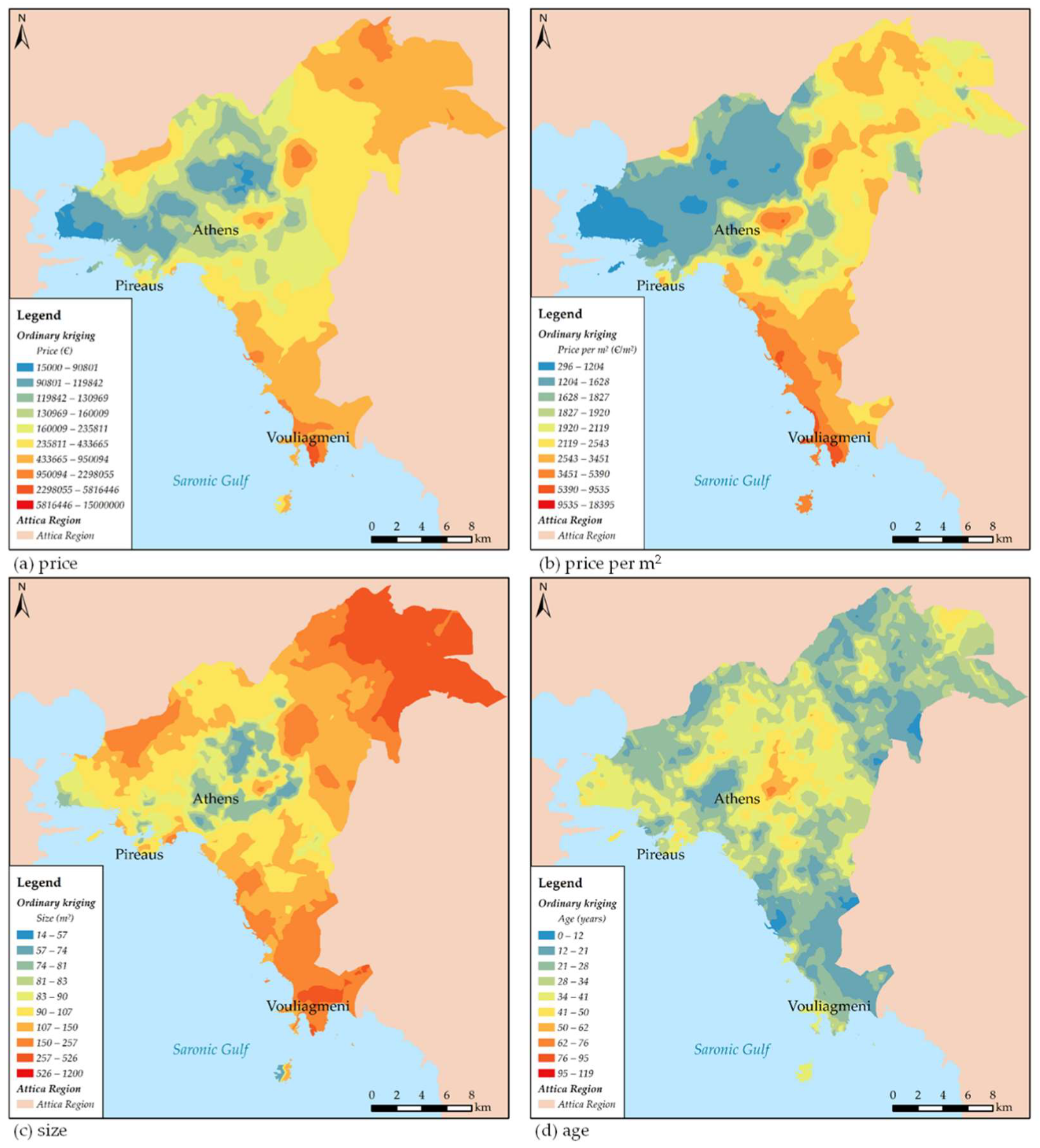
2.2. Geovisualization of the Data with Kriging Analysis
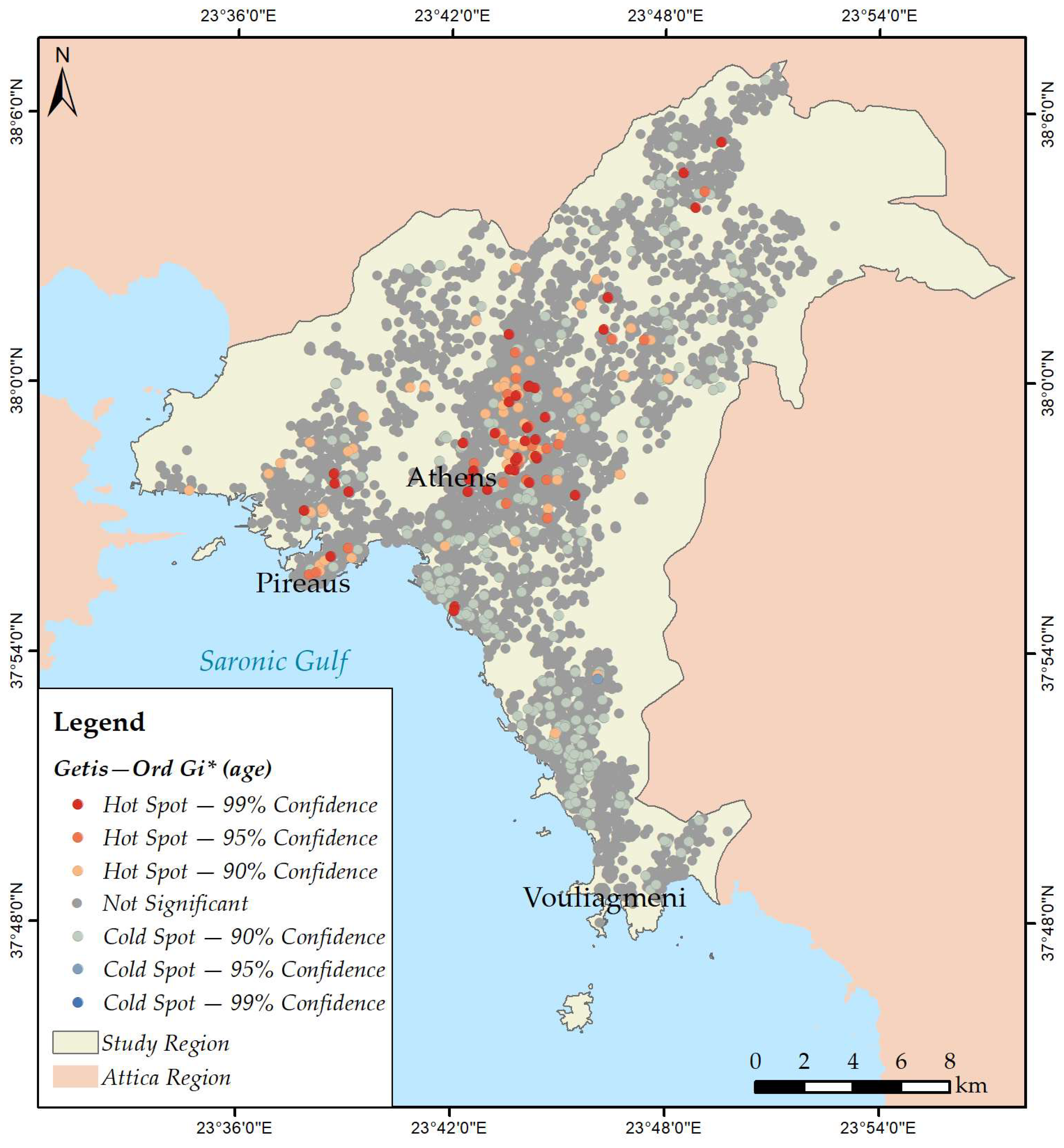
2.3. Mapping Spatial Clusters
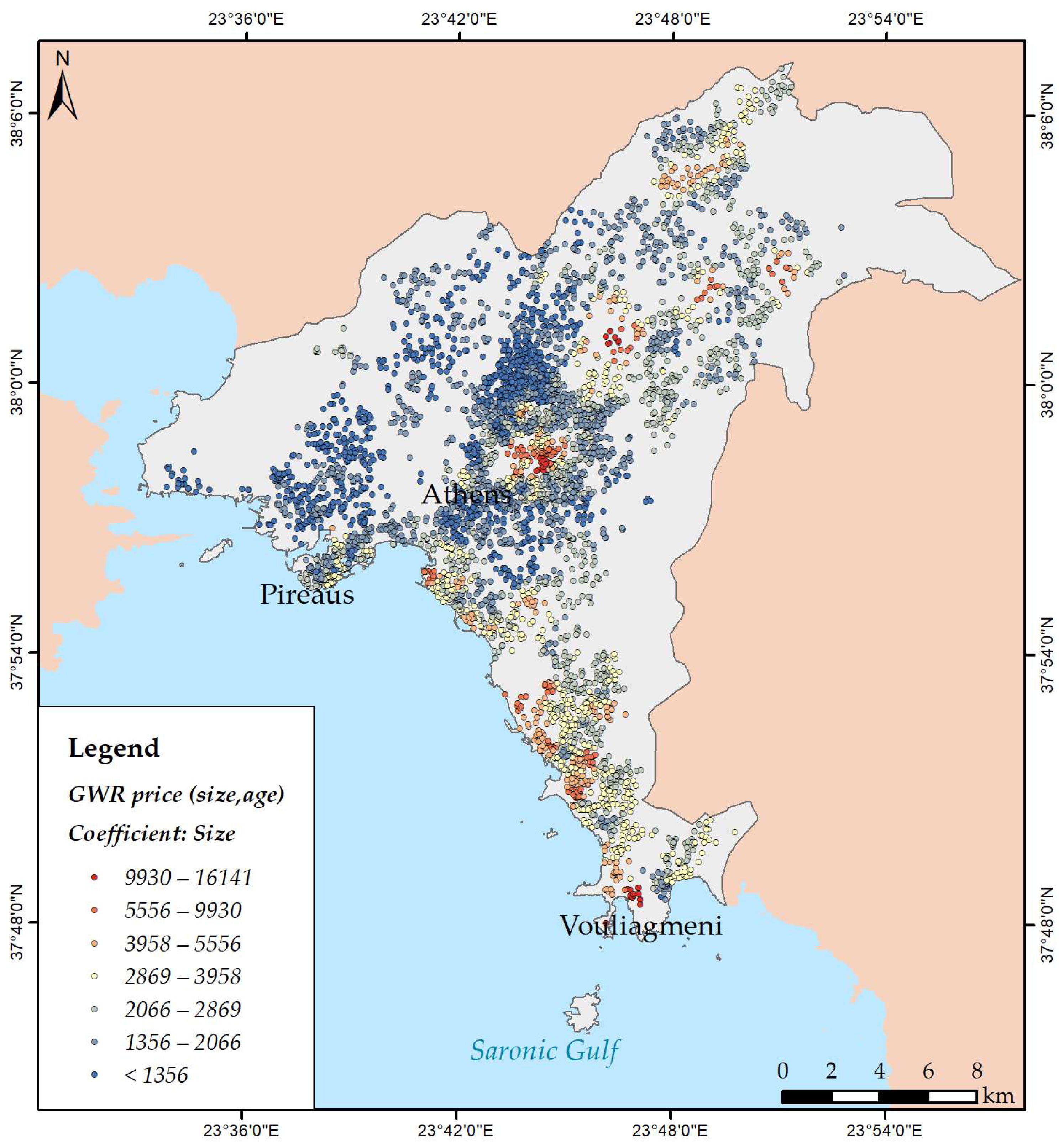
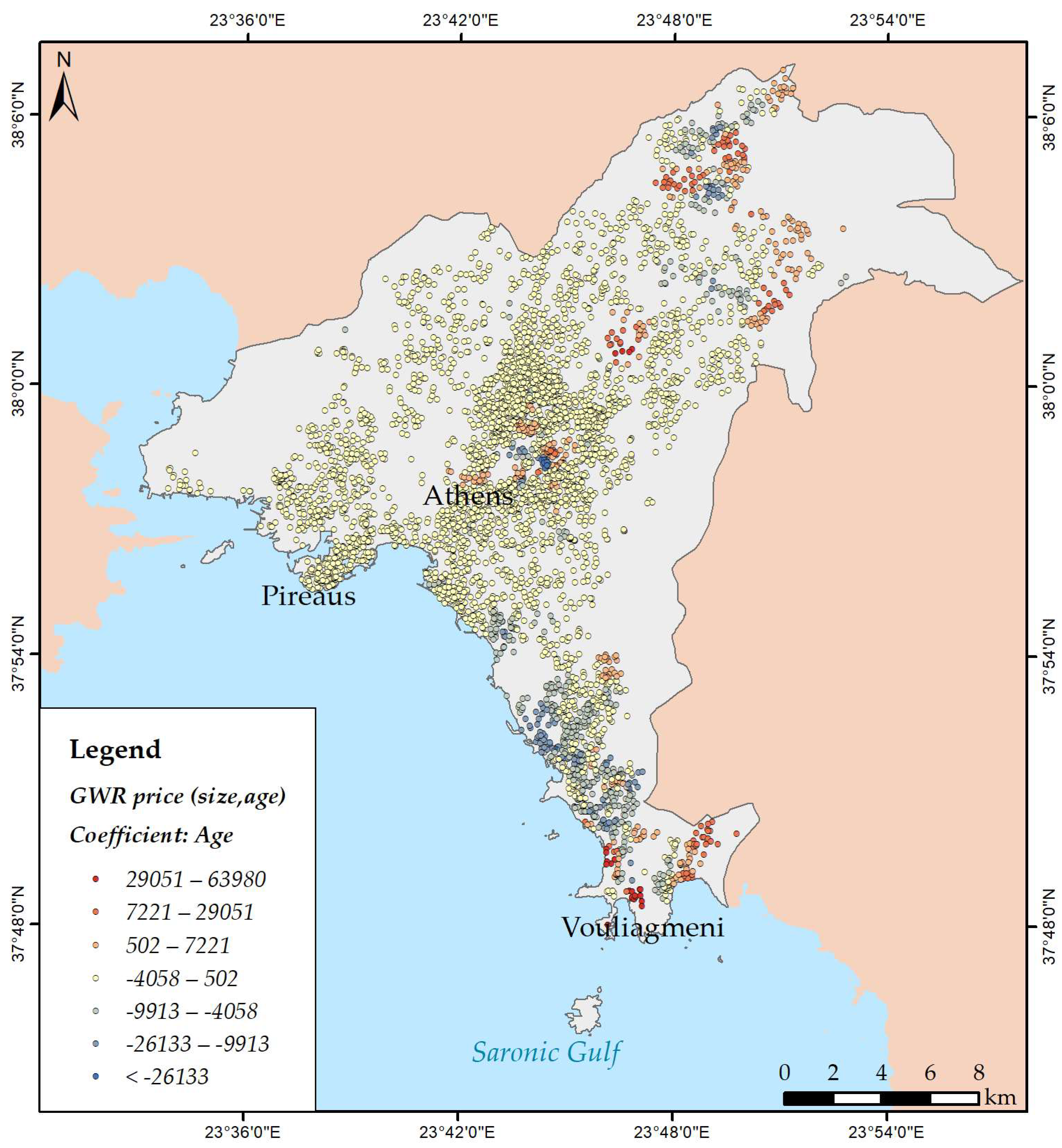
2.4. Regression Models
3. Results
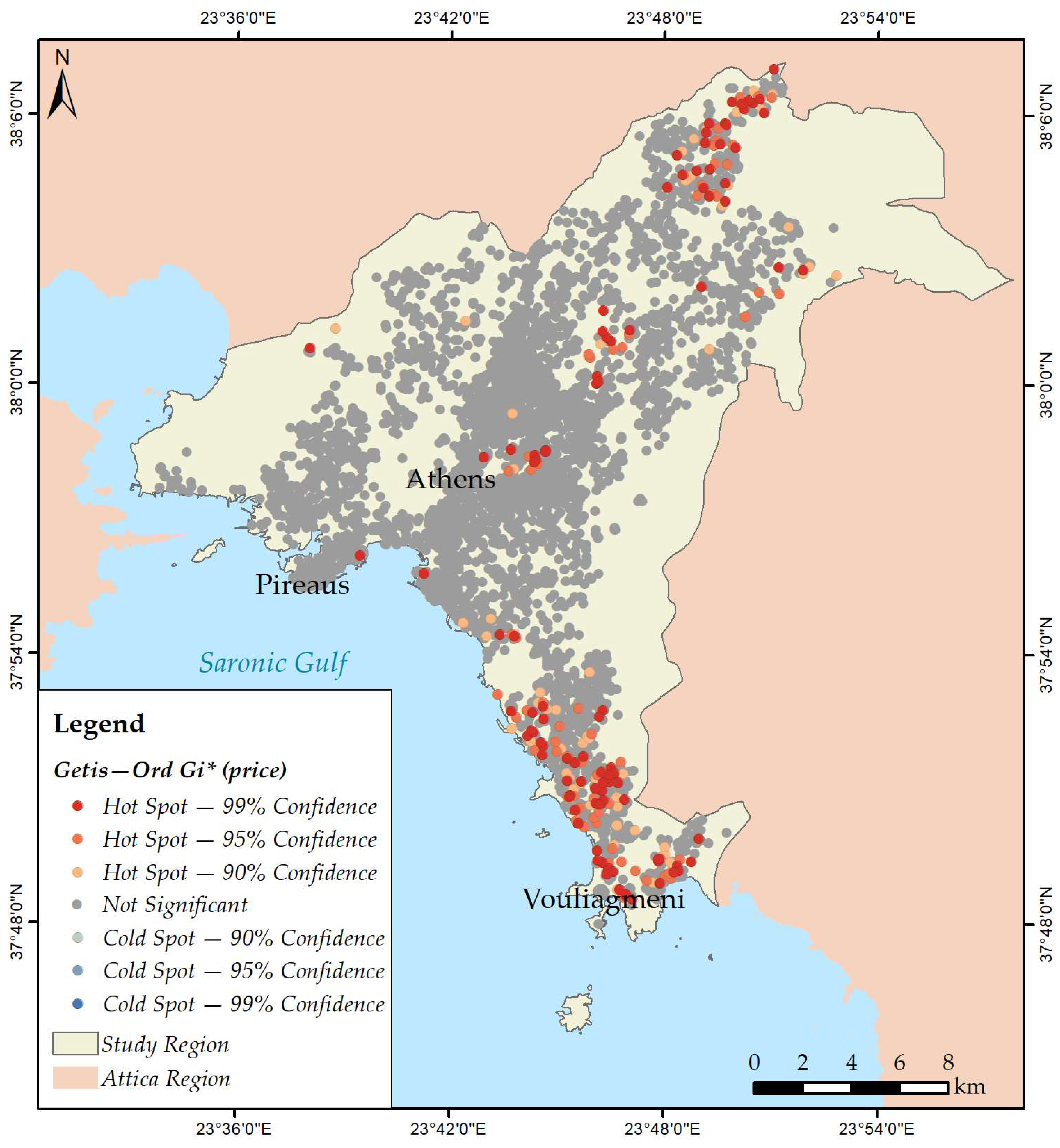
- Price;
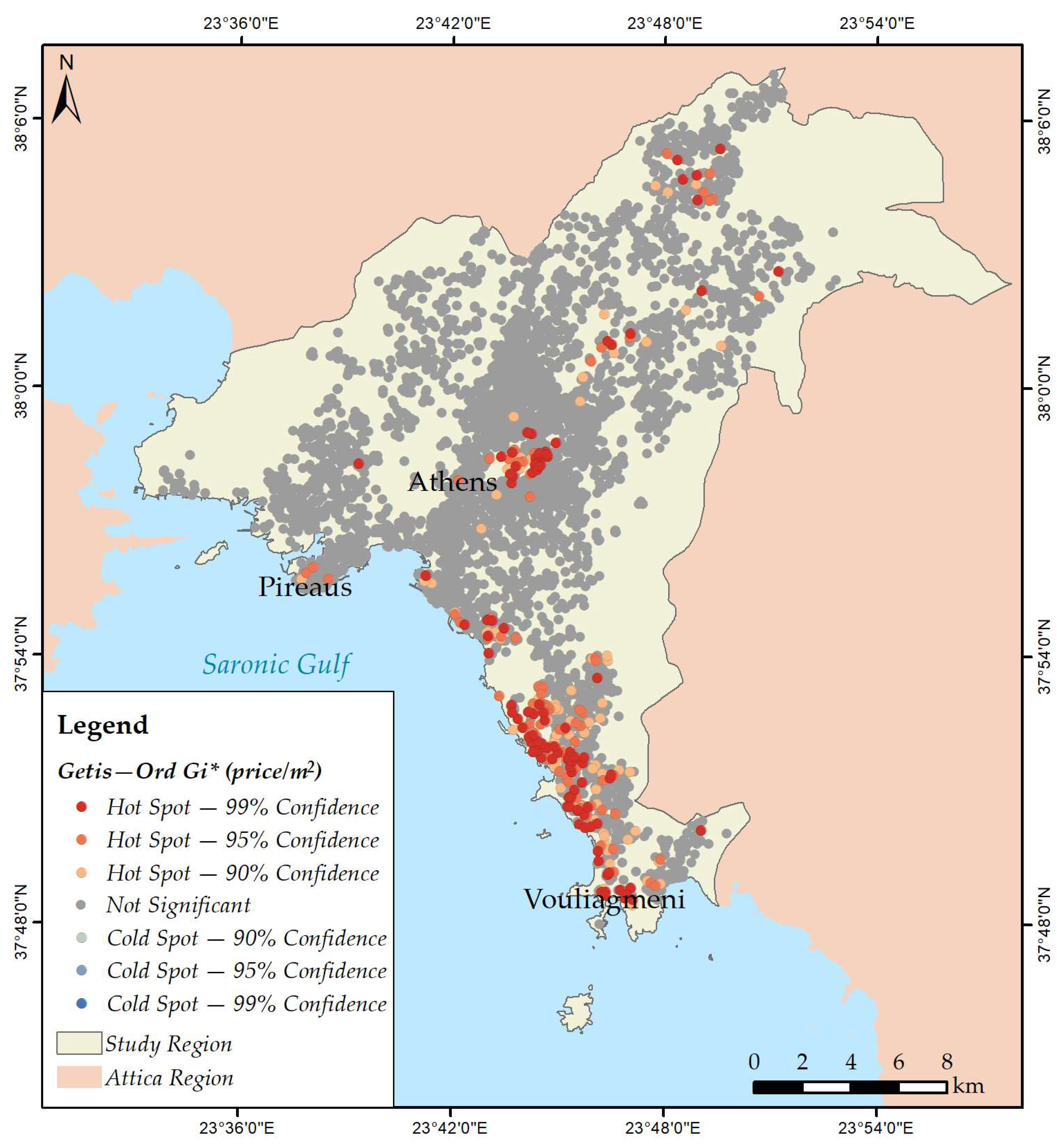
- Price per m2;
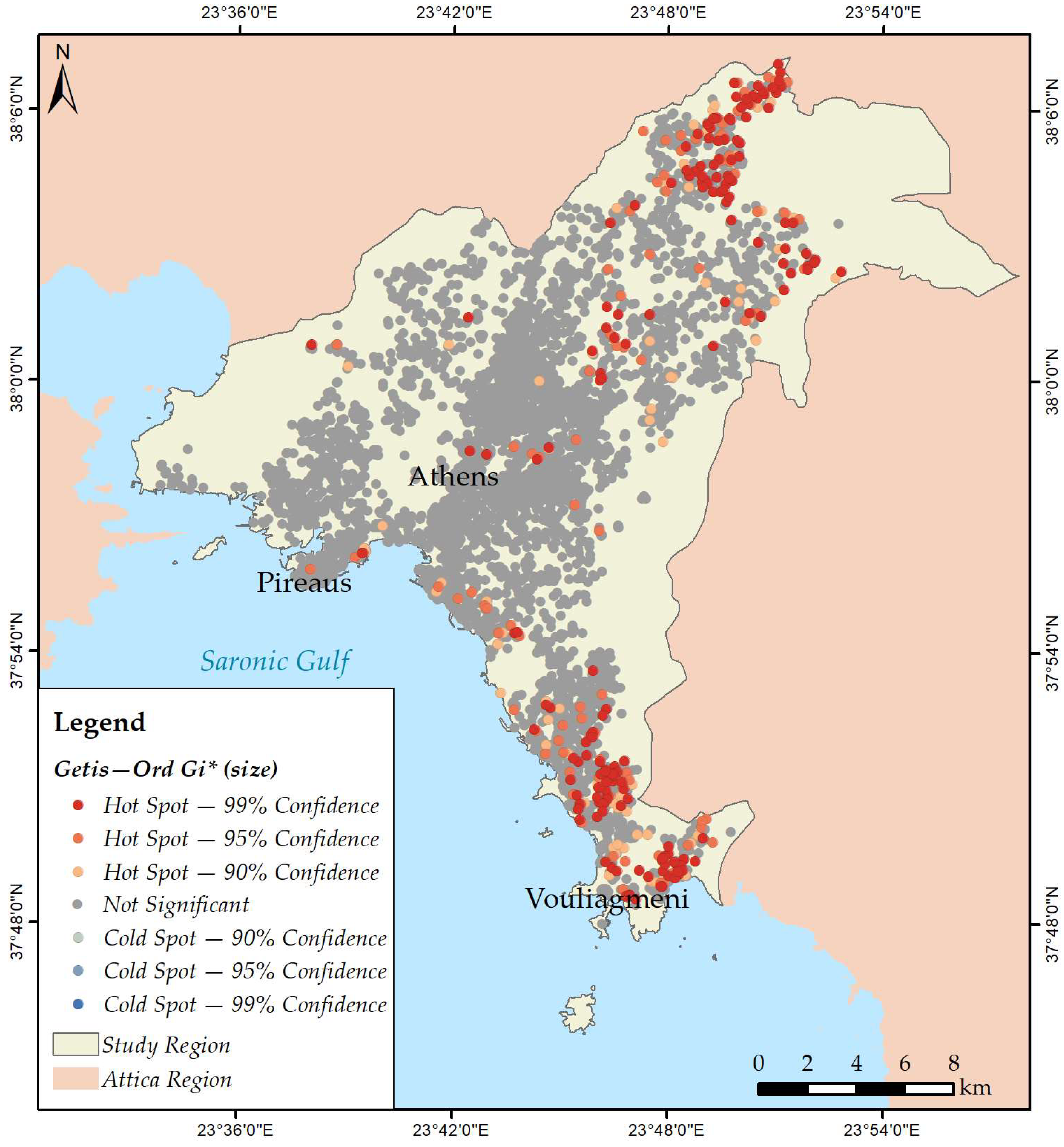
- Size;
- Age;
- Floor number;
- Number of rooms;
- Number of bathrooms;
- Existence of parking;
- Existence of view;
- Existence of fireplace;
- Distance from the center;
- Distance from the nearest metro station;
- Distance from the beach.
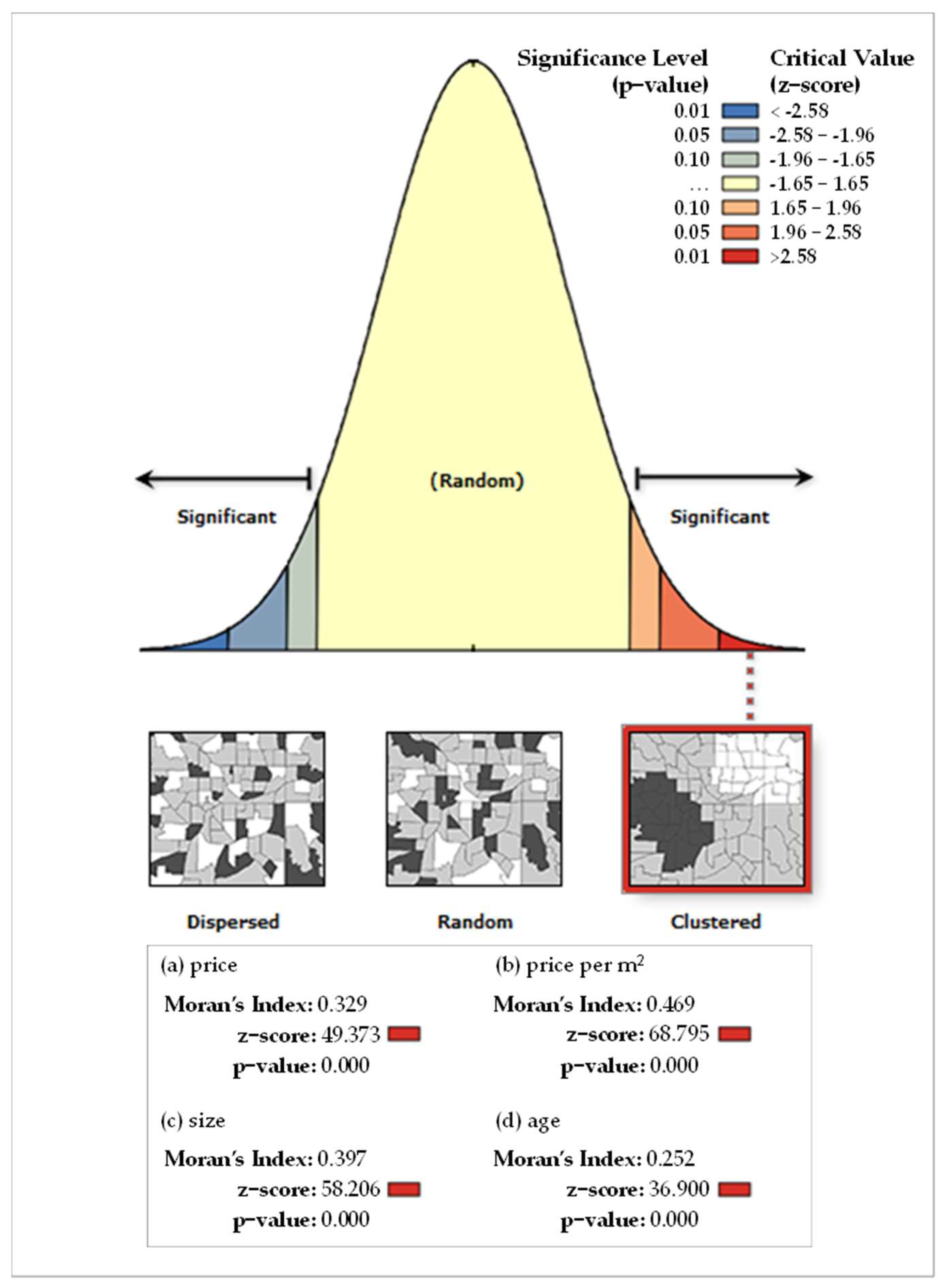
3.1. Kriging Analysis and Measures of Spatial Autocorrelation
3.2. Mapping Spatial Clusters
3.3. Modelling Spatial Relationships
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Iliopoulou, P.; Stratakis, P. The geography of housing prices in the Greater Athens Region, Greece: Patterns, Correlations and trends. In Innovative Geographies: Understanding and Connecting Our World, Proceedings of the 11th International Conference of the Hellenic Geographical Society, Lavrion, Greece, 12–15 April, 2018; Govostis Publisher Co.: Athens, Greece, 2018; Available online: http://www.geochoros.survey.ntua.gr/hgs/el/11th-conference-proceedings?field_topic_tid=All&title=&title_field_value_1=iliopoulou (accessed on 8 December 2021).
- Stamou, M.; Mimis, A.; Rovolis, A. House Price Determinants in Athens: A Spatial Econometric Approach. J. Prop. Res. 2017, 34, 269–284. [Google Scholar] [CrossRef]
- Iliopoulou, P.; Stratakis, P. Spatial Analysis of Housing Prices in the Athens Region, Greece. RELAND Int. J. Real Estate Land Plan. 2018, 1, 304–313. [Google Scholar]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Exploring, Modelling and Predicting Spatiotemporal Variations in House Prices. Ann. Reg. Sci. 2015, 54, 417–436. [Google Scholar] [CrossRef]
- O’Sullivan, D.; Unwin, D. Geographic Information Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 978-0-471-21176-1. [Google Scholar]
- Baranzini, A.; Ramirez, J.; Schaerer, C.; Thalmann, P. Hedonic Methods in Housing Markets: Pricing Environmental Amenities and Segregation; Springer Science & Business Media: New York, NY, USA, 2008; ISBN 978-0-387-76815-1. [Google Scholar]
- Bhattacharjee, A.; Castro, E.; Marques, J. Spatial Interactions in Hedonic Pricing Models: The Urban Housing Market of Aveiro, Portugal. Spat. Econ. Anal. 2012, 7, 133–167. [Google Scholar] [CrossRef]
- Xiao, Y. Urban Morphology and Housing Market; Springer Geography: Singapore, 2017; ISBN 978-981-10-2761-1. [Google Scholar]
- Anderson, S.T.; West, S.E. Open Space, Residential Property Values, and Spatial Context. Reg. Sci. Urban Econ. 2006, 36, 773–789. [Google Scholar] [CrossRef] [Green Version]
- Cho, S.-H.; Poudyal, N.C.; Roberts, R.K. Spatial Analysis of the Amenity Value of Green Open Space. Ecol. Econ. 2008, 66, 403–416. [Google Scholar] [CrossRef]
- Efthymiou, D.; Antoniou, C. How Do Transport Infrastructure and Policies Affect House Prices and Rents? Evidence from Athens, Greece. Transp. Res. Part A Policy Pract. 2013, 52, 1–22. [Google Scholar] [CrossRef]
- Luttik, J. The Value of Trees, Water and Open Space as Reflected by House Prices in the Netherlands. Landsc. Urban Plan. 2000, 48, 161–167. [Google Scholar] [CrossRef]
- McMillen, D.P.; McDonald, J. Reaction of House Prices to a New Rapid Transit Line: Chicago’s Midway Line, 1983–1999. Real Estate Econ. 2004, 32, 463–486. [Google Scholar] [CrossRef]
- Sander, H.A.; Polasky, S. The Value of Views and Open Space: Estimates from a Hedonic Pricing Model for Ramsey County, Minnesota, USA. Land Use Policy 2009, 26, 837–845. [Google Scholar] [CrossRef]
- Raslanas, S.; Tupenaite, L.; Šteinbergas, T. Research on the Prices of Flats in the South East London and Vilnius. Int. J. Strateg. Prop. Manag. 2006, 10, 51–63. [Google Scholar] [CrossRef]
- Pek, J.; Wong, O.; Wong, A. Data Transformations for Inference with Linear Regression: Clarifications and Recommendations. Pract. Assess. Res. Eval. 2019, 22, 9. [Google Scholar] [CrossRef]
- De Bruyne, K.; Van Hove, J. Explaining the Spatial Variation in Housing Prices: An Economic Geography Approach. Appl. Econ. 2013, 45, 1673–1689. [Google Scholar] [CrossRef]
- Lake, I.R.; Lovett, A.A.; Bateman, I.J.; Day, B. Using GIS and Large-Scale Digital Data to Implement Hedonic Pricing Studies. Int. J. Geogr. Inf. Sci. 2000, 14, 521–541. [Google Scholar] [CrossRef]
- Mimis, A.; Rovolis, A.; Stamou, M. Property Valuation with Artificial Neural Network: The Case of Athens. J. Prop. Res. 2013, 30, 128–143. [Google Scholar] [CrossRef]
- Pace, R.K.; Barry, R.; Sirmans, C.F. Spatial Statistics and Real Estate. J. Real Estate Financ. Econ. 1998, 17, 5–13. [Google Scholar] [CrossRef]
- Anselin, L.; Rey, S.J. Modern Spatial Econometrics in Practice: A Guide to GeoDa, GeoDaSpace and PySAL; GeoDa Press LLC: Chicago, IL, USA, 2014. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships Wiley Wiltshire; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Herath, S.; Choumert, J.; Maier, G. The Value of the Greenbelt in Vienna: A Spatial Hedonic Analysis. Ann. Reg. Sci. 2015, 54, 349–374. [Google Scholar] [CrossRef] [Green Version]
- Iliopoulou, P.; Kitsos, C. Kriging Analysis for Atmosphere Pollutants and House Prices: The case of Athens. In Economics of Natural Resources & the Environment, Proceedings of the 6th ENVECON Conference, Volos, Greece, 11–12 June 2021; Springer Science & Business Media: New York, NY, USA, 2012; pp. 233–247. Available online: http://envecon.econ.uth.gr/main/eng/images/6th_conference/6th_Conference_Proceedings.pdf (accessed on 12 December 2021).
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Kuntz, M.; Helbich, M. Geostatistical Mapping of Real Estate Prices: An Empirical Comparison of Kriging and Cokriging. Int. J. Geogr. Inf. Sci. 2014, 28, 1904–1921. [Google Scholar] [CrossRef]
- Chica-Olmo, J.; Cano-Guervos, R.; Chica-Rivas, M. Estimation of Housing Price Variations Using Spatio-Temporal Data. Sustainability 2019, 11, 1551. [Google Scholar] [CrossRef] [Green Version]
- Cressie, N.A. Statistics for Spatial Data; John Willey & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford Univ. Press: New York, NY, USA, 1989. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C. Some Thoughts on Inference in the Analysis of Spatial Data. Int. J. Geogr. Inf. Sci. 2004, 18, 447–457. [Google Scholar] [CrossRef]
- Rogerson, P.A. Statistical Methods for Geography: A Student’s Guide; SAGE: Southern Oaks, CA, USA, 2019; ISBN 978-1-5297-0023-7. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: New York, NY, USA, 1998; ISBN 978-0-471-17082-2. [Google Scholar]
- Jenks, G.F. The Data Model Concept in Statistical Mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Osborne, J. Improving Your Data Transformations: Applying the Box-Cox Transformation. Pract. Assess. Res. Eval. 2019, 15, 12. [Google Scholar] [CrossRef]
- Mankad, M.D. Analysis of Impact of Accessibility on Residential Property Values in Gotri Area of Vadodara City, India Using OLS and GWR. Int. J. Sci. Res. Sci. Eng. Technol. 2018, 4, 1118–1127. [Google Scholar] [CrossRef]
- Wheeler, D.C. Diagnostic Tools and a Remedial Method for Collinearity in Geographically Weighted Regression. Environ. Plan. A 2007, 39, 2464–2481. [Google Scholar] [CrossRef]
- Brunsdon, C.; Charlton, M.; Harris, P. Living with Collinearity in Local Regression Models. In Proceedings of the 10th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Florianópolis, Brazil, 10–13 July 2012. [Google Scholar]
- Portet, S. A Primer on Model Selection Using the Akaike Information Criterion. Infect. Dis. Model. 2020, 5, 111–128. [Google Scholar] [CrossRef]
- Rodriguez, M.; Sirmans, C.F. Quantifying the value of a view in single family housing markets. Apprais. J. 1994, 62, 600–603. [Google Scholar]
- Ozgur, C.; Hughes, Z.; Rogers, G.; Parveen, S. Multiple Linear Regression Applications in Real Estate Pricing. Int. J. Math. Stat. Invent. 2016, 4, 39–50. [Google Scholar]
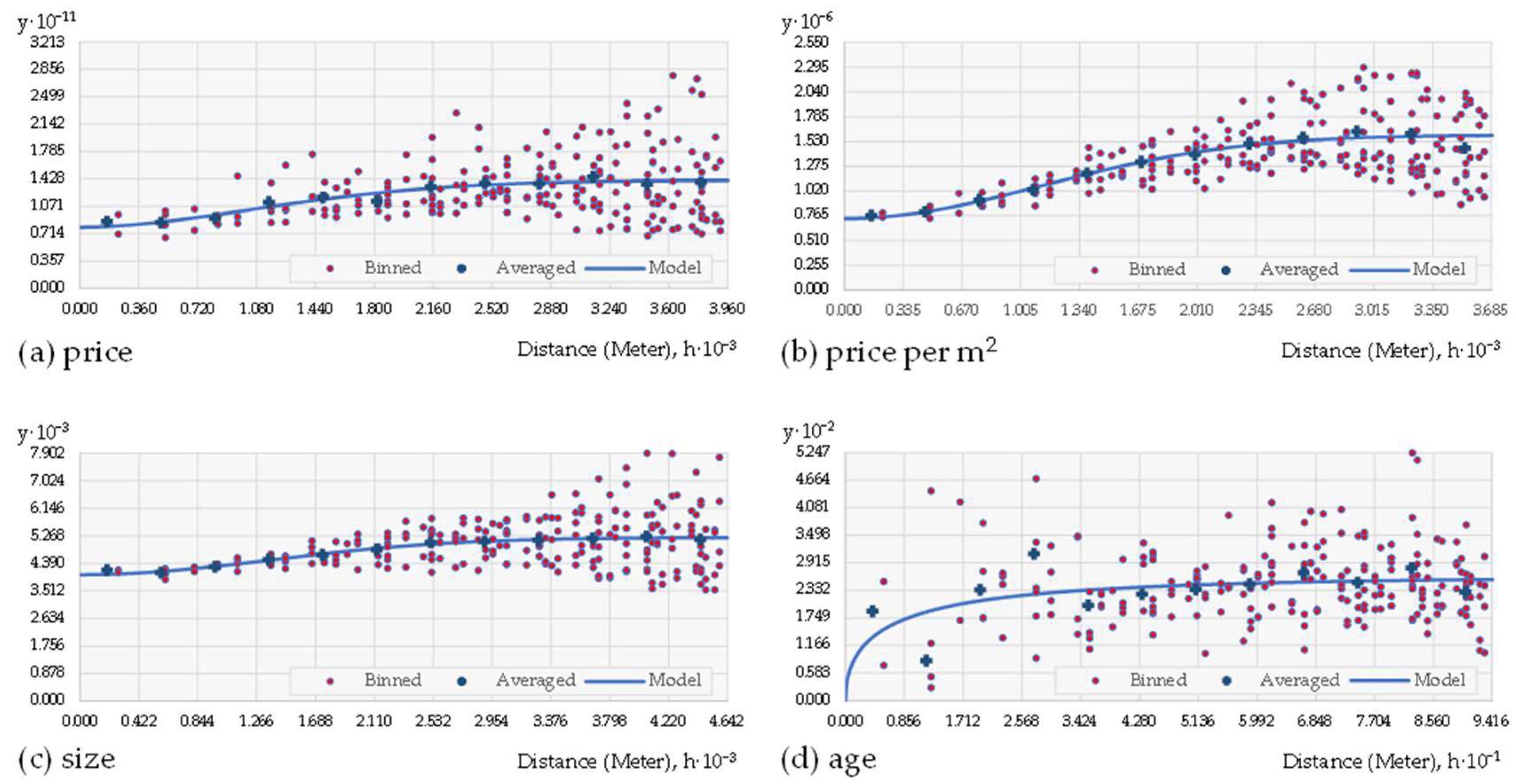
| Price | Price Per m2 | Size | Age | |
|---|---|---|---|---|
| Mean | 418.34 | 1.75 | −0.02 | −0.04 |
| Root Mean Square | 393,947.31 | 974.07 | 81.16 | 17.03 |
| Mean Standardized | 0.001 | 0.002 | −0.000 | −0.002 |
| Root Mean Square Standardized | 1.335 | 1.094 | 1.241 | 1.016 |
| Average Standard Error | 292,605.18 | 889.11 | 65.24 | 16.76 |
| Variables | Coefficients | Sig. | Standardized Coefficients (Beta) |
|---|---|---|---|
| Constant | −39,796.64 | 0.008 | - |
| Size | 3349.71 | 0.000 | 0.725 |
| Age | −695.80 | 0.014 | −0.028 |
| Distance from the beach | −9.80 | 0.000 | −0.098 |
| Parking | 34,899.72 | 0.003 | 0.037 |
| View | 54,540.50 | 0.000 | 0.053 |
| Variables | Adj. R2 |
|---|---|
| Size | 0.812 |
| Size–age | 0.848 |
| Size–distance from the beach | 0.652 |
| Size–view | 0.812 |
| Size–parking | 0.761 |
| Size–age–view | 0.411 |
| Size–age–parking | 0.799 |
| Size –age–distance from the beach | error |
| Size–age–view–parking | 0.776 |
| Size–age–view–parking–distance from the beach | error |
| Model | Adj.R2 | AIC |
|---|---|---|
| OLS | 0.583 | 140,247.45 |
| GWR | 0.848 | 136,454.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iliopoulou, P.; Feloni, E. Spatial Modelling and Geovisualization of House Prices in the Greater Athens Region, Greece. Geographies 2022, 2, 111-131. https://doi.org/10.3390/geographies2010008
Iliopoulou P, Feloni E. Spatial Modelling and Geovisualization of House Prices in the Greater Athens Region, Greece. Geographies. 2022; 2(1):111-131. https://doi.org/10.3390/geographies2010008
Chicago/Turabian StyleIliopoulou, Polixeni, and Elissavet Feloni. 2022. "Spatial Modelling and Geovisualization of House Prices in the Greater Athens Region, Greece" Geographies 2, no. 1: 111-131. https://doi.org/10.3390/geographies2010008
APA StyleIliopoulou, P., & Feloni, E. (2022). Spatial Modelling and Geovisualization of House Prices in the Greater Athens Region, Greece. Geographies, 2(1), 111-131. https://doi.org/10.3390/geographies2010008