1. Introduction
The elbow is the second-most frequently dislocated joint in the body, with posterior/posterolateral dislocations being the most prevalent [
1,
2]. These dislocations involve an anteriorly directed dislocation of the radial head. However, the etiology of isolated radial head dislocations remains poorly understood [
3]. A deeper understanding of the radiocapitellar joint would be beneficial to elucidate the mechanisms behind these injuries.
Osseous stability in the elbow throughout its range of motion is most apparent at the extremes of flexion and extension, where the radial head becomes a key contributor at higher ranges of flexion [
4]. At 90 degrees of elbow flexion, approximately 75% of the elbow joint stability against varus stress is attributed to the joint articulation [
5]. The radial head has been shown to be a critically important secondary stabilizer of the elbow by providing valgus stability [
6]. The radiocapitellar joint not only buttresses against the proximal migration of the radius during elbow flexion, but it has been shown to also transmit approximately 60% of an axial load applied through the elbow [
6,
7]. Additionally, the radial head mediates the role of elbow valgus stabilization from the surrounding ligaments, and moderates the tensioning of the lateral ulnar collateral ligament to stabilize against varus stress [
8]. While soft tissue structures, such as the anterior band of the ulnar collateral ligament, contribute to stability in the mid-ranges of flexion, the osseous constraints of the joint are fundamental to overall elbow stability [
9].
The role of the radiocapitellar joint as an osseous valgus stabilizer is underscored by its involvement in the most common mode of elbow dislocation: posterolateral dislocation. Such dislocations are often associated with persistent valgus instability. A previous study demonstrated a large portion of their patients with persistent valgus instability were found to have cartilage and chondral defects of the capitellum [
10]. Understanding the biomechanics of radiocapitellar osseous stability—specifically the forces required for joint translation and dislocation relative to joint compression forces—is critical to developing strategies to address valgus instability and prevent further chondral damage.
Posterolateral rotatory instability has been identified as the main injury pattern for posterolateral elbow dislocations [
11]. Emerging treatment algorithms for elbow posterolateral rotatory instability, incorporating imaging to characterize the articular congruency [
12]. Recent imaging studies have highlighted the relationship between elbow instability and radiocapitellar incongruity, defined as the distance between the rotational center of the capitellum and the longitudinal axis of the radius through the center of the radial head [
13,
14]. These findings suggest a need to investigate how joint compressive and translational forces interact, particularly in the presence of slight anatomical variations in the congruency of the articulation.
Previous research has examined the bony constraints of the radiocapitellar joint against forced translation [
15], but a biomechanical stability ratio has not been utilized to quantify the stability of the joint. This ratio, defined as the translating force at dislocation divided by the compressive load placed on the joint [
16,
17], provides a more precise characterization of joint stability. The objective of this study was to define and to quantify the stability ratio of the radiocapitellar joint in anterior and posterior directions at various angles of elbow flexion. We hypothesized that the radiocapitellar joint would exhibit a lower stability ratio with anteriorly directed subluxation, indicating inherent instability of the osseus articulation.
2. Material and Methods
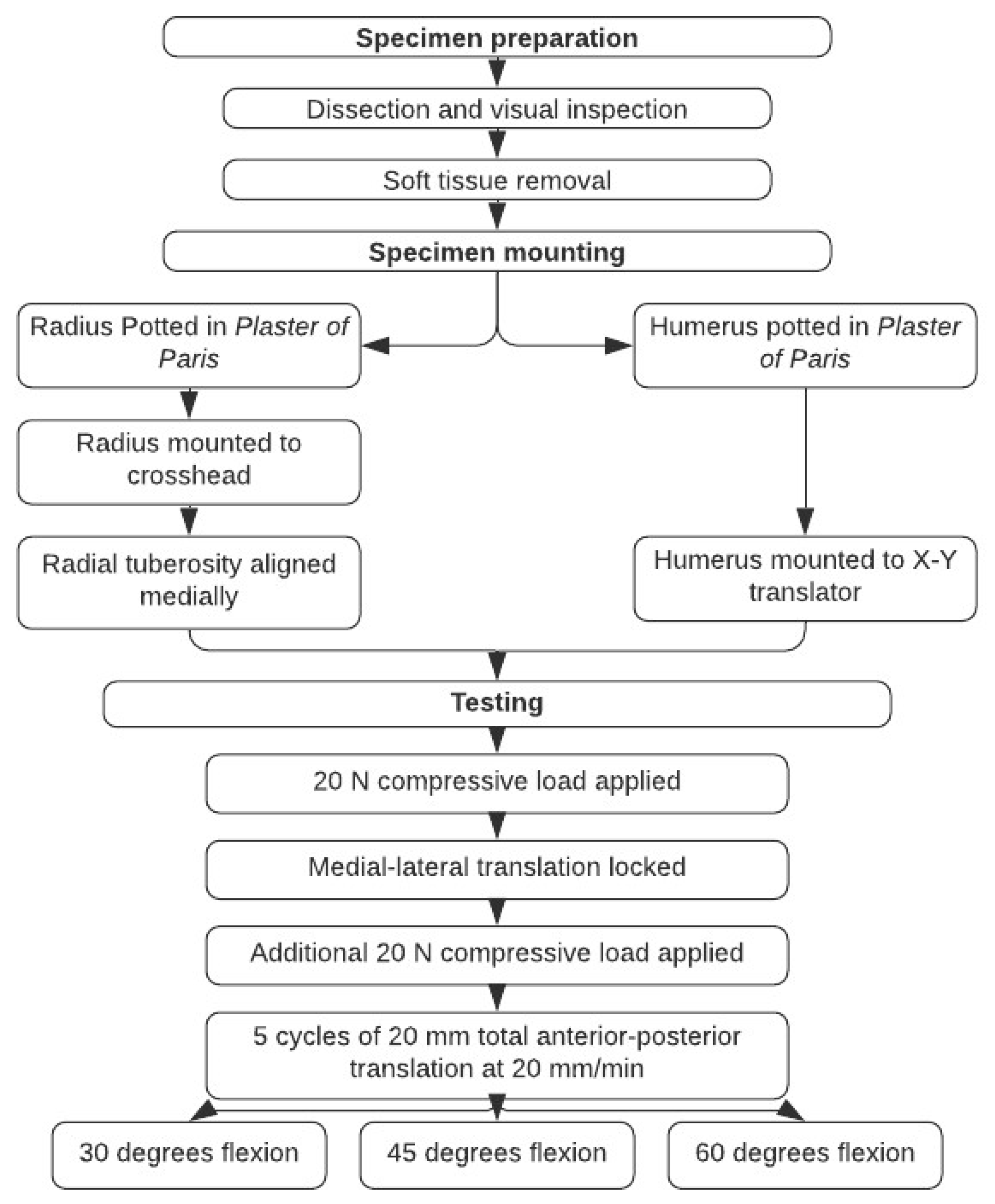
2.1. Specimen Preparation
Eight fresh-frozen cadaveric elbows with a mean age of 68.9 years (range 61–73 years; 3 males and 5 females; 7 left and 1 right) were used. All specimens were macroscopically intact with no evidence of gross abnormalities. The skin, subcutaneous tissue, and all other tissues were removed to isolate the radiocapitellar osseous articulation; removal included the UCL, LCL, and the ulna, which left a completely disarticulated radiocapitellar joint.
The humerus was then cut approximately 6 cm proximal to the lateral epicondylar ridge of the humerus and potted into a 6.5 cm PVC pipe with Plaster of Paris (DAP, Model #10312, Baltimore, MD, USA) ensuring that the epicondylar axis was perpendicular to the long axis of the PVC pipe. Similarly, the radius was cut to approximately 7 cm and potted in a 6 cm PVC pipe with Plaster of Paris so that the radial head was perpendicular to the long axis of the PVC pipe. The radial shaft was then additionally secured using one 5 cm transosseous wood screw. To maintain the cartilaginous properties of the articulating surfaces throughout the preparation and testing process, a 0.9% saline solution was periodically applied to as a precaution for desiccation of the specimen.
The position of the radial tuberosity was identified and marked on the pipe to determine neutral forearm rotation. With respect to the position of the radiocapitellar joint, neutral forearm position has been described in the literature as the alignment of the longest axis of the radial head perpendicular to the forearm plane [
18]. The forearm plane was defined by a line connecting the center of the capitellum and the radial styloid process (processus styloideus), with an average orientation of 158 ± 14° of axial rotation (supination) relative to the radial tuberosity [
18,
19,
20].
2.2. Biomechanical Evaluation
An overview of the experimental protocol is shown in
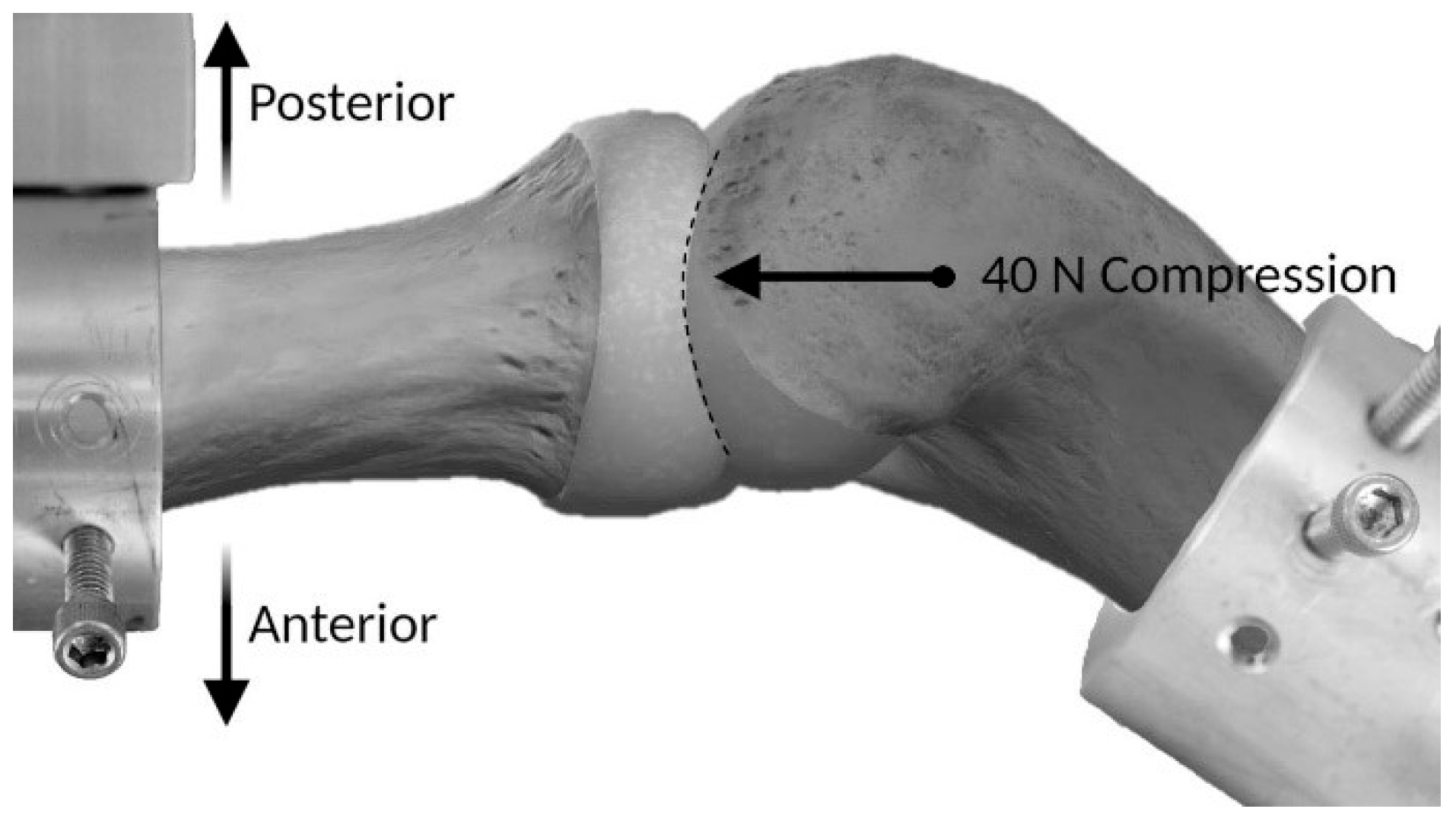
Figure 1. The humerus was mounted on a custom clamp that allowed for flexion–extension adjustment with the epicondylar axis placed parallel with the floor and the crosshead of the testing machine. The clamp was attached to an X-Y translator on the baseplate of a testing machine (Instron Corp, Model #3365, Canton, MA, USA) (
Figure 2 and
Figure 3).
A 20 N compressive force was applied to the radial head from the capitellum by loading through the translator from a hanging weight on a pulley; this initial load application allowed the radial head to find a center position to articulate with the capitellum. The radius was then adjusted to align the radiocapitellar joint congruity and locked in place. The medial–lateral translation was then locked, and the compression–distraction axis was left unconstrained. An additional 20 N of radiocapitellar joint compression was then applied for a total of 40 N. Finally, the crosshead position was adjusted until the load output was zero and then the gauge length was reset to zero.
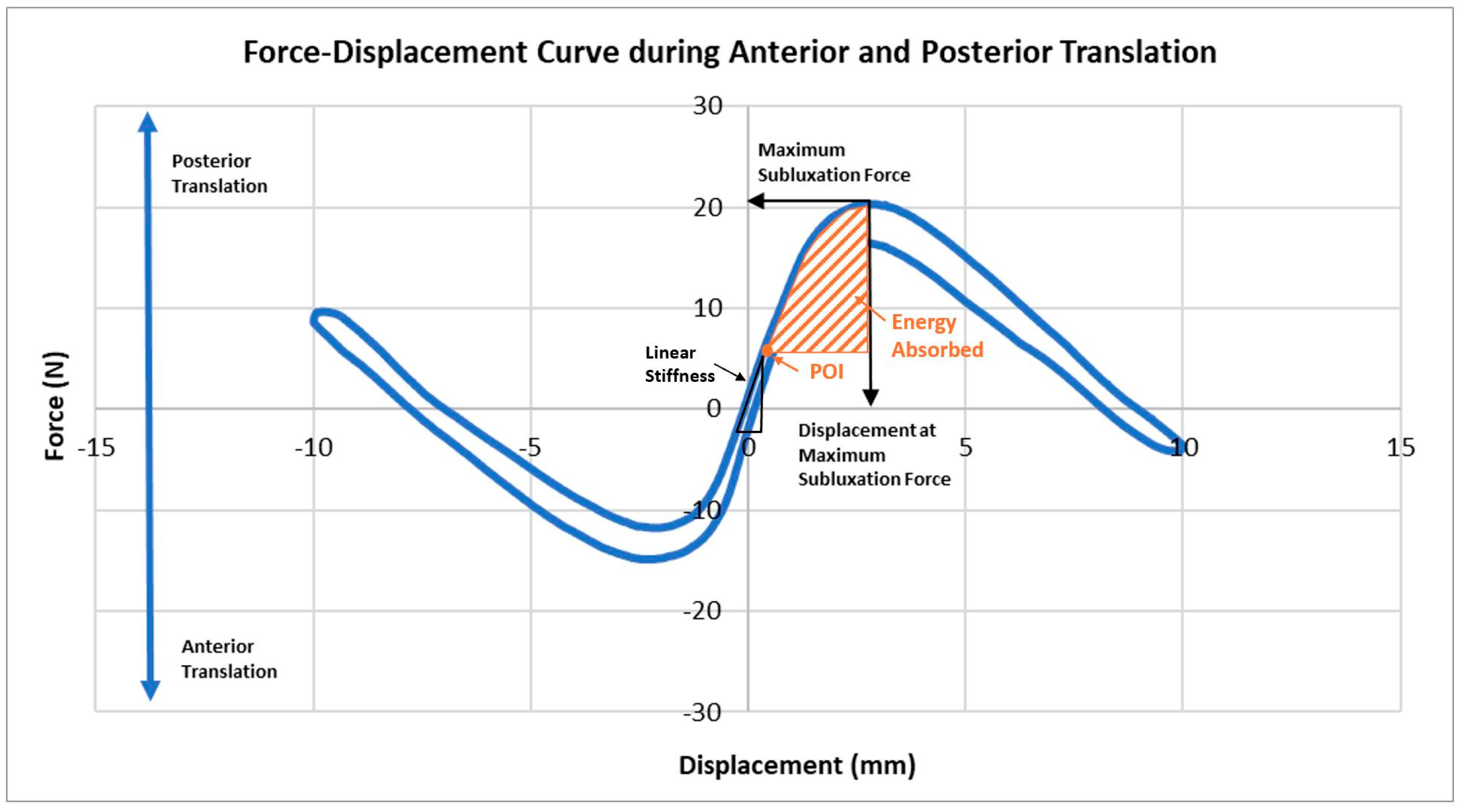
Each specimen underwent 5 cycles of 10 mm anterior and 10 mm posterior translation at a rate of 20 mm/min. The 10 mm translation was not enough to completely dislocate the joint in either direction, but sufficient to achieve a peak subluxation force. Testing was done at 30, 45, and 60 degrees of elbow flexion. After testing was completed, radial head measurements were taken, including medial–lateral and anterior–posterior diameters and radial head depth. Maximum subluxation force and displacement at this force were measured; linear stiffness, stability ratio and energy absorbed were calculated. Linear stiffness was defined as the maximum slope of the load–displacement curve before peak subluxation force was obtained for both anterior and posterior radial head translation. Stability ratio, as defined by Lippitt et al. [
9], was calculated by
. Energy absorbed was calculated as the integral of the load–displacement curve from the point of inflection to the peak subluxation force (
Figure 4).
2.3. Statistics
A sample size calculation was performed based on the average differences and standard deviations in the stability ratio from the first two specimens. Based on the effect size, which varied between 1.5 and 4.0, a sample size of 7 specimens would be needed to show a statistical difference; therefore, we chose to test 8 specimens. Data from cycles 2, 3, and 4 were averaged for each specimen; the averages and standard errors were calculated for the 8 specimens. A test for normality for each outcome was first performed using the Shapiro–Wilk test. For the parameters that data were normally distributed (maximum subluxation force and stability ratio), a repeated measured analysis of variance test was performed to determine statistical significance between flexion angles (IBM SPSS Statistics 25). If a statistical difference was detected, a Bonferroni test for pair-wise comparisons was also performed. To statistically compare between anterior and posterior subluxation directions at each given position, a paired student T-test was conducted. For data that were not normally distributed (displacement at maximum subluxation force, linear stiffness and energy absorbed), a Friedman rank sum test was used to compare across flexion angles and a Wilcoxon rank sum test was used to compare anterior and posterior directions. Effect size was reported using Cohen’s d for normally distributed data and as r, z-statistic divided by the square of the sample size, for the non-normally distributed data. Significance was set at p < 0.05 for all tests. All data are shown as mean ± standard deviation of the mean for normally distributed data and as median (interquartile range) for data that were not normally distributed.
3. Results
3.1. Radial Head Dimensions
Radial head measurements were found to be 22.8 ± 2.3 mm in the medial–lateral plane, 22.5 ± 2.8 mm in the anterior–posterior plane, and 2.3 ± 0.6 mm for the depth. There were no statistical differences comparing medial–lateral and anterior–posterior lengths (p < 0.251).
3.2. Anterior vs. Posterior Translation Parameters at Each Flexion Angle
The maximum subluxation force was significantly higher posteriorly than anterior at all flexion angles (
p < 0.027) (
Table 1).
The posterior translation stability ratio was significantly higher by an average of 39.8 ± 32.6% than the anterior stability ratio at all flexion angles (p < 0.025).
There were no statistically significant differences in displacement at the maximum subluxation force of the anterior compared to the posterior direction at all flexion angles (
p > 0.057) (
Table 1).
There were no significant differences in linear stiffness of the anterior compared to the posterior directions at every elbow flexion angle (
p > 0.441) (
Table 1).
Additionally, energy absorbed had no statistically significant differences when comparing anterior versus posterior directions at each flexion angle (
p > 0.547) (
Table 1).
3.3. Comparison of Parameters Across Flexion Angles
The maximum subluxation force was significantly higher in the anterior direction at 30 degrees compared to 45 degrees of flexion (30 degrees, 13.4 ± 1.7 N; 45 degrees, 12.3 ± 1.9 N; p = 0.005; effect size 0.6). Between 30 degrees and 60 degrees in the anterior direction, there were no statistically significant differences for the maximum subluxation force (p = 0.135). There were no statistically significant differences in maximum subluxation force in the posterior direction across all conditions (p > 0.941).
The stability ratio was significantly higher in the anterior direction at 30 degrees compared to 45 degrees of flexion (30 degrees, 0.34 ± 0.04; 45 degrees, 0.31 ± 0.05; p = 0.007; effect size 0.8). Between 30 degrees and 60 degrees for the anterior direction, there were no statistically significant differences in the stability ratio (p = 0.154). There were no statistically significant differences in stability ratio for the posterior direction across all conditions (p > 0.879).
When comparing the effect of each position of elbow flexion angle on the displacement at the maximum subluxation force, there was an increase with increasing elbow flexion angles, but there were no statistically significant differences in both the anterior (p > 0.658) and posterior directions (p > 0.223) across all conditions.
When comparing the effect of the different elbow positions tested on the linear stiffness, there was a decrease with increasing elbow flexion angles, but there were no statistically significant differences in both the anterior (p > 0.072) and posterior directions (p > 0.250) across all conditions.
There were no statistically significant differences in energy absorbed when comparing between elbow positions in the anterior (p > 0.607) and posterior directions (p > 0.197) across all flexion angles.
4. Discussion
This study is the first to quantify the stability ratio of the radiocapitellar joint, providing insight into the compressive force required to achieve bony stability across various elbow flexion angles in neutral forearm rotation. The results demonstrated that the radiocapitellar articulation is more stable against posterior translation than anterior translation in neutral forearm rotation. This finding suggests reduced bony stability at the posterior portion of the radial rim, potentially explaining the higher frequency of anterior dislocations.
Our results align with those of Jensen et al., who reported the highest resistance to posterior and posteromedial translation of the elbow joint in neutral forearm rotation at elbow flexion angle of 0°, 30°, 60°, and 90° [
15]. They also noted that the tallest portion of the radial rim is located anteriorly to anterolaterally, contributing to increased resistance in these directions [
15]. Similarly, our findings revealed a significantly lower stability ratio for anterior subluxation (0.32) compared to posterior subluxation (0.43), providing a possible biomechanical explanation for the predisposition to anterior dislocations.
The compressive force used in this study (40 N) was chosen to balance the forces used in prior studies by Jensen et al. (23 N) and Shukla et al. (50 N) for their intact control in their studies of radiocapitellar stability in relation to compressive forces [
15,
21]. This force was sufficient to maintain joint integrity without risking cartilage damage. While compressive forces across the elbow joint seen clinically can vary and may exceed the values used in this study, the ratio of dislocation to compressive forces would be similar, such that a higher compressive load would require a higher force for dislocation. Future research utilizing higher compressive loads may further elucidate the stability dynamics of the radiocapitellar joint under greater forces.
In examining maximum subluxation forces, our findings are consistent with Chanlalit et al., who reported a mean peak force of 19 ± 4 N to resist posterior subluxation at 30° of elbow flexion with a 50 N compressive load [
22]. In comparison, the current study found a mean maximum subluxation force of 17.3 ± 3.5 N under 40 N of compressive load. The slight discrepancy is likely due to differences in compressive loads, which previous studies have demonstrated to significantly influence radiocapitellar stability [
22,
23]. While Chanlalit et al. emphasized the role of geometric radial head concavity in stability, this current study’s findings enhance this understanding by incorporating the stability ratio, which quantifies the interplay between compressive and translational force [
22].
The validity of the stability ratio as a measure of osseous joint stability has been well supported in the literature for the glenohumeral joint [
24]. Lippitt et al. [
17] demonstrated glenohumeral joint stability ratios of 0.35 ± 0.11 for anterior dislocation with the labrum intact and 0.28 ± 0.06 with the labrum excised under a 50 N compressive load [
16]. Additionally, posterior dislocations in the shoulder yielded a stability ratio of 0.64 ± 0.08 with the labrum intact and 0.41 ± 0.13 when excised [
16]. Comparing these glenohumeral values to the radiocapitellar stability ratio in this study (0.32 ± 0.04 anteriorly and 0.43 ± 0.07 posteriorly) highlights the similar susceptibility of the radiocapitellar joint to subluxation and dislocation, as well as the corresponding directionality.
Applications of the glenohumeral stability ratio are extensive [
16,
17,
25,
26], and such can be potentially mirrored with the radiocapitellar stability ratio. These include developing joint biomechanical models and improving prosthetic designs [
22,
23,
27,
28]. Clinical implications of the radiocapitellar stability ratio include guiding clinical assessments of posterolateral elbow instability and elucidating the pathomechanics of radiocapitellar injuries. The relatively low stability ratio of the radiocapitellar joint also emphasizes the importance of surrounding soft tissues and ligamentous restraints to stability which should be taken into consideration during surgical treatment. Unlike the glenohumeral joint, where the glenoid labrum deepens the glenoid cavity to help stability, the radiocapitellar joint relies on the concavity and the osteochondral border of the radial head for stability. Findings from this study suggest that the level of contribution by the bony articular surfaces for concavity compression is greater for the radiocapitellar joint compared to the glenohumeral joint, further emphasizing the importance of anatomic restoration of the radial head both in reconstruction and replacement. This study adds to the fundamental understanding of the anatomy and its implication to stability of the radiocapitellar joint; however, further studies are needed to understand the complex interplay that occurs between the bony and soft tissue stabilizers as well as the force couples in the radiocapitellar joint.
Future studies can improve on the several limitations in this study including: (1) the use of cadaveric specimens with a mean specimen age of 68.9 years may not fully represent the properties of younger or healthier joints; (2) only the bony articulation of the radial head was examined—excluding the contributions of the ulnohumeral articulation, musculature, or soft tissue; (3) only neutral forearm rotation position was evaluated as this is where the greatest laxity is found in the intact elbow [
29], limiting generalizability to other forearm positions; (4) a single compressive force (40 N) was used, which may not capture the full range of physiological loading conditions; and 5) medial–lateral stability was not evaluated, which could leave gaps in the understanding of the complete picture of the radiocapitellar articulation.