Neuromechanical Effects of Eccentric–Reactive Training on Explosiveness, Asymmetry, and Stretch-Shortening in Elite Table Tennis Players

Abstract

Background/Objectives: This study examined the effects of a six-week eccentric–reactive training program on neuromechanical markers of lateral explosiveness, asymmetry, and stretch-shortening cycle (SSC) efficiency in elite male youth table tennis players. Fourteen national-level athletes (mean age = 16.6 years) were assigned to either an experimental group (EG, n = 7) or a control group (CG, n = 7). EG performed flywheel squats and lateral depth jumps three times per week, while CG maintained regular training. Pre- and post-intervention testing included countermovement jumps, reactive strength index (RSI_DJ), force asymmetry, time-to-stabilization, SSC efficiency, and energy transfer ratio (ETR), measured via force plates, EMG, and inertial sensors. Methods: Multi-dimensional statistical analysis revealed coordinated improvements in explosive power and movement efficiency following eccentric training that were not visible when examining individual measures separately. Athletes in the training group showed enhanced neuromechanical control and developed more efficient movement patterns compared to controls. The analysis successfully identified distinct performance profiles and demonstrated that the training program improved explosive characteristics in elite table tennis players. Results: Univariate ANOVAs showed no significant Group × Time effects for RSI_DJ, ETR, or SSC_Eff, although RSI_DJ displayed a moderate effect size in EG (d = 0.47, 95% CI [0.12, 0.82], p = 0.043). In contrast, MANOVA confirmed a significant multivariate Group × Time interaction (p = 0.013), demonstrating integrated neuromechanical adaptations. Regression analysis indicated lower baseline CMJ and RSI_DJ predicted greater RSI improvements. Conclusions: In conclusion, eccentric–reactive training promoted multidimensional neuromechanical adaptations in elite racket sport athletes, supporting the use of integrated monitoring and targeted eccentric loading to enhance lateral explosiveness and efficiency.

1. Introduction

Explosive lateral movements and neuromuscular control are foundational components of elite table tennis performance, particularly during high-intensity rallies, reactive transitions, and deceleration-acceleration sequences near the table edge. These actions rely on the integrated function of the stretch-shortening cycle (SSC), which combines eccentric braking, elastic energy storage, and concentric propulsion [1,2]. While previous research has primarily addressed linear force production and vertical jump mechanics [3,4], much less is known about lateral power development and asymmetrical neuromechanical strategies in racket sport athletes.

In table tennis, lateral displacements typically occur over very short distances (<2 m) and time frames (<500 ms), placing high demands on rapid force generation, postural stabilization, and directional reactivity [5]. These biomechanical demands require both unilateral and bilateral neuromuscular coordination under conditions of high temporal pressure [6]. Therefore, profiling the underlying determinants of lateral power such as lateral countermovement jump (CMJ) height, reactive strength index (RSI), and rate of force development (RFD) is essential for both diagnostics and training optimization in this population.

Recent evidence supports the effectiveness of eccentric overload training in enhancing neuromuscular function, particularly in youth and adult athletes engaged in sports requiring fast SSC activation [7,8,9]. Flywheel-based resistance protocols, combined with depth jump variations, have shown promising results in increasing peak force, SSC efficiency, and jump height [10,11]. However, most of these studies focus on sagittal-plane outputs or general athletic populations, with minimal exploration of sport-specific lateral mechanics or neuromechanical asymmetries.

Moreover, inter-limb force asymmetry has been increasingly recognized as a critical factor in both injury risk and performance imbalance [12,13]. This is particularly relevant in sports such as table tennis, where repeated lateral pushes and landings may induce side-dominant neuromuscular adaptations. Yet, few interventions have systematically targeted this asymmetry or quantified its changes via functional single-leg CMJ, force asymmetry index, or stabilization metrics such as time-to-stabilization (TTS) [14].

Beyond univariate approaches, multidimensional models such as principal component analysis (PCA), linear discriminant analysis (LDA), and multivariate regression offer a more comprehensive understanding of neuromechanical adaptations [15]. These methods can reveal latent structures, discriminate performance profiles, and identify key predictors of adaptation following targeted training interventions. However, their use remains rare in the context of elite racket sports, especially in male national-level athletes where sample access is logistically constrained and data precision is paramount.

In this context, stretch-shortening cycle efficiency (SSC_Eff) and energy transfer ratio (ETR) have recently emerged as promising markers of movement economy and neuromechanical integration. These novel indices quantify how effectively athletes convert eccentric and temporal effort into concentric output, providing a deeper understanding of explosive efficiency. Their validity and responsiveness to training stimuli, however, have not been extensively tested in elite table tennis players.

While previous studies have investigated training adaptations in young table tennis players [5,8], limited research has simultaneously evaluated explosive lateral force production, inter-limb asymmetry, and stretch-shortening cycle efficiency in elite male table tennis athletes using integrated multivariate approaches. Understanding these neuromechanical adaptations is crucial for coaches and practitioners seeking evidence-based methods to enhance lateral movement efficiency and reduce injury risk in competitive table tennis. Additionally, no prior intervention in this population has examined the longitudinal effects of eccentric–reactive training on variables such as RSI_DJ, ETR, SSC_Eff, or neuromechanical asymmetry, nor explored their classification and prediction potential using LDA and LASSO regression models.

The aim of this study was to assess the effects of a six-week eccentric–reactive training program on key performance indicators including lateral CMJ height, reactive strength index (RSI), neuromechanical asymmetry (Force Asymmetry, Single-Leg CMJ), and stretch-shortening cycle (SSC) efficiency (SSC_Eff, ETR) in elite male youth athletes from the Polish junior national table tennis team. The study further aimed to identify discriminative and predictive variables associated with training-induced adaptations using multivariate statistical modeling, including MANOVA, principal component analysis (PCA), linear discriminant analysis (LDA), and regression approaches. We hypothesized that the experimental group would exhibit significant improvements in lateral explosive force generation and SSC efficiency, whereas the control group would show minimal or no changes.

2. Materials and Methods

2.1. Study Design and Power Analysis

This investigation utilized a two-arm, controlled pre–post intervention design to evaluate the effects of a six-week eccentric–reactive training protocol on neuromechanical performance among elite-level youth male table tennis players. Athletes were assigned to either an experimental group (EG), which underwent a structured SSC-focused intervention, or a control group (CG), which continued their regular in-season training.

A total of 14 elite junior athletes (mean age: 16.6 ± 0.4 years, training experience: 6.5 ± 1.1 years) participated in the study. All were active members of the Polish national youth table tennis team and were free from musculoskeletal injuries in the six months preceding the study. This highly selective cohort represented nearly the entire national talent pool in this age category, ensuring high ecological validity, internal consistency, and performance-level homogeneity. Such design reflects real-world elite youth sport settings, albeit with inherent limitations in generalizability.

A priori power analysis was conducted using G*Power 3.1.9.7 [16] to evaluate the adequacy of the sample size for detecting a statistically significant Group × Time interaction in a 2 × 2 mixed-design repeated measures ANOVA. The following parameters were specified:

• Effect size f = 0.35 (moderate-to-large, based on prior neuromechanical training studies in elite youth athletes),
• α error probability = 0.05,
• Statistical power (1 − β) = 0.80,
• Number of groups = 2 (EG vs. CG),
• Number of measurements = 2 (Pre and Post),
• Correlation among repeated measures = 0.70 (based on test–retest reliability for RSI and CMJ variables),
• Nonsphericity correction ε = 1.0.

The analysis indicated that a minimum sample size of n = 14 (7 per group) was sufficient to detect a Group × Time interaction with 80% power at the specified effect size. Although the sample is relatively small, the elite status, performance-level homogeneity, and high procedural standardization (timing, environment, warm-up, and monitoring of confounding factors) support the robustness and interpretability of the findings; however, this cohort may be underpowered to detect smaller effects such as those observed in SSC_Eff and ETR. The statistical design also enabled multivariate exploration of discriminative and predictive factors within a high-performance developmental context.

However, the small sample size per group (n = 7) may limit the robustness of complex multivariate models and increase the risk of Type II errors for variables with smaller effect sizes, representing an important limitation for the generalizability of findings.

2.2. Intervention Period and Test Schedule

The intervention lasted six consecutive weeks, during which the experimental group completed three supervised training sessions per week, each lasting approximately 30 min. The program included:

Flywheel-based squats (YoYo Squat™, Exxentric AB, Sweden, Stockholm): 4–5 sets × 5–6 repetitions per session, using individualized inertial loads (0.075–0.100 kg·m²),

Lateral depth jumps (single-leg and double-leg): 3–4 sets × 4–6 repetitions, progressing from 30 to 50 cm box height.

The training protocol was designed to progressively overload the stretch-shortening cycle (SSC), targeting eccentric braking force and lateral movement specificity. All sessions were conducted under direct supervision by certified strength and conditioning professionals.

Pre-intervention (Pre) testing was conducted seven days before the first training session, while Post assessments took place four to five days after the final session, under tightly standardized conditions: same time of day (08:00–11:00), controlled environment (22 ± 1 °C), consistent warm-up, no caffeine, overnight fasting, and sleep monitored via self-report.

For practitioners without access to flywheel devices, alternative eccentric loading can be implemented using weight releasers or partner-resisted eccentric squats, with programming adjustments to match intensity.

2.3. Ethical Considerations and Data Quality

The study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Review Board of the Academy of Physical Education in Katowice, Poland (approval number: KB/10/2021). All participants provided written informed consent prior to enrollment and were free to withdraw at any time.

To ensure methodological rigor and data quality:

• All force and EMG signals were collected at 1000 Hz using calibrated systems (Kistler 9260AA6 and Noraxon DTS).
• Instrumentation was recalibrated before each testing session using certified procedures.
• All assessments were performed in triplicate, and the best trial was retained for analysis.
• Test–retest reliability was verified on a 6-athlete subsample, yielding ICC > 0.90 for key outcome measures.
• All statistical assumptions (normality, sphericity, homogeneity) were tested prior to analysis.
• A complete-case analysis approach was used, with <5% missing data due to sensor noise or dropout.

2.4. Participants and Experimental Design

A total of 14 male elite youth table tennis team were recruited. Inclusion criteria required: (a) minimum 5 years of professional training, (b) participation in national or international-level competition, and (c) no musculoskeletal injury in the preceding 6 months. Athletes were pseudo-randomly assigned to either an experimental group (EG, n = 7) or a control group (CG, n = 7), ensuring balanced distribution based on performance level and training experience.

The experimental group participated in a 6-week eccentric–reactive training program (3 sessions/week), while the control group continued with their habitual sport-specific training routines without additional neuromuscular interventions. Pre- and post-intervention assessments were conducted under standardized conditions.

2.5. Procedures

All testing procedures were conducted in a temperature-controlled environment (22 ± 1 °C) at the Biomechanics Laboratory of the Gdańsk University of Physical Education and Sport. Participants were tested at the same time of day (±30 min) during both Pre and Post sessions to control for circadian variation. All assessments were preceded by a standardized 10 min neuromuscular warm-up consisting of cycling (60 W, 5 min), dynamic mobility drills, and submaximal jump trials.

2.6. Measurement Systems and Instrumentation

Ground reaction force (GRF) data were collected using a high-resolution piezoelectric force platform (Kistler 9260AA6, Kistler Instrumente AG, Winterthur, Switzerland), sampling at 1000 Hz. Data acquisition and synchronization were managed via Kistler MARS software (version 4.0). The platform was recalibrated before each session using a certified static weight procedure. All GRF-derived variables were extracted using custom Python scripts (Python 3.11.5; Python Software Foundation, 2023) with NumPy 1.24.3, SciPy 1.10.1 and Pandas 2.0.3), validated against Kistler-provided algorithms. The Python analysis scripts and data processing protocols are available upon reasonable request to ensure reproducibility of the analytical procedures.

Electromyographic (EMG) activity of the quadriceps muscle group (VL and RF) was recorded using a wireless EMG system (Noraxon DTS, Noraxon USA Inc., Scottsdale, AZ, USA) at 1000 Hz with dual differential surface electrodes (Ag/AgCl, 20 mm inter-electrode distance). Electrode placement followed SENIAM guidelines. Signals were band-pass filtered (20–450 Hz), rectified, and smoothed with a 50 ms RMS window. EMG onset latency was defined as the time at which the rectified signal exceeded three standard deviations above baseline.

Balance and stabilization parameters were measured using the same force platform (TTS and TTS_Balance) and a standardized Y-Balance Test Kit (Move2Perform, Evansville, IN, USA) for directional reach analysis. Validity and test–retest reliability for TTS and Y-Balance Score have been confirmed in prior neuromechanical studies (ICC > 0.92).

Kinematic data (Knee_Flexion_Angle, Hip_Extension_Velocity, Trunk_Lean) were collected using inertial motion sensors (Noraxon MyoMotion IMU system, Noraxon USA Inc.) attached to the trunk, thigh, and shank. The sensors were calibrated using a static standing posture and dynamic range of motion protocol, following manufacturer’s instructions.

Visual and reaction time tests were administered via a saccadic reaction test application (NeuroTracker™, version 3.5) linked to force data via time-synced digital markers. Lateral Movement Time and Reaction Time were derived from synchronized visual cues and corresponding GRF thresholds.

Anthropometric data (Body Mass, Height, Leg Length) were measured using a medical-grade scale (Seca 704s, Hamburg, Germany), stadiometer (Seca 213), and standardized anthropometric tape.

All assessments were performed by two independent examiners blinded to group allocation. Data processing and analysis were conducted by a third blinded analyst. To ensure reproducibility, each test was repeated three times with rest intervals of 60 s between trials; the best attempt was retained for analysis. Inter-session reliability was assessed for all primary outcome variables (RSI_DJ, ETR, SSC_Eff, CMJ height, force asymmetry) in a 6-athlete subsample tested one week apart. Intraclass correlation coefficients (ICC) exceeded 0.90 for all measures, confirming excellent test–retest reliability.

2.7. Calculation of Key Performance Variables

Reactive Strength Index (RSI_DJ). Three established methods exist for calculating RSI from drop jump data, as described in the literature [10,12,17]. In this study, RSI_DJ was calculated using Method 1:

RSI_DJ = Jump Height (m)/Ground Contact Time (s)

Jump height was determined using the impulse-momentum theorem from vertical ground reaction force data:

Jump Height = (Impulse_takeoff)²/(2 × body mass² × 9.81)

Ground contact time was defined as the duration from initial ground contact to takeoff, identified when vertical GRF exceeded and subsequently dropped below 20 N thresholds.

Alternative RSI calculation methods include Method 2 (RSI = Flight Time/Ground Contact Time) and Method 3 (RSI = Jump Height/Time to Take-off), where time to take-off encompasses both eccentric and concentric phases of the stretch-shortening cycle. Method 1 was selected for its superior validity when using force plate data and consistency with previous research in elite athletes [14,17].

Stretch-Shortening Cycle Efficiency (SSC_Eff). SSC efficiency was calculated as the ratio of concentric work to total mechanical work during the countermovement jump:

SSC_Eff = (Concentric Work/Total Work) × 100%

where concentric work = ∫F(t) × v(t) dt during the concentric phase, and total work included both eccentric and concentric phases. This metric quantifies the athlete’s ability to effectively utilize stored elastic energy during the stretch-shortening cycle.

Energy Transfer Ratio (ETR). ETR was computed as the ratio of actual kinetic energy output to theoretical potential energy input:

ETR = (Kinetic Energy Output/Potential Energy Input) × 100%

Kinetic energy output was derived from takeoff velocity:

KE = 0.5 × mass × v² takeoff

Potential energy input was calculated from the drop height in depth jump tasks:

PE = mass × 9.81 × drop height

This ratio indicates the efficiency of energy transfer from eccentric loading to concentric propulsion within the neuromuscular system.

2.8. Training Protocol

2.8.1. Experimental Group (EG)

Athletes in the EG completed an eccentric–reactive training protocol three times per week for six consecutive weeks. Each session lasted ~40 min and was supervised by certified strength and conditioning specialists to ensure safety and compliance. Sessions were structured as follows:

Warm-up (10 min): dynamic drills, jump-specific mobilization, submaximal flywheel squats.

Eccentric overload training (20 min): performed on a flywheel resistance device (YoYo Squat™, Exxentric AB, Bromma, Sweden) with individualized inertial loads (0.075–0.100 kg·m²). Athletes performed 4 sets × 6 repetitions of bilateral squats emphasizing maximal braking (eccentric) force.

Reactive jump training (10 min): 3 sets × 5 depth jumps from 30–50 cm, increasing height weekly. Emphasis was placed on minimal ground contact time (<200 ms) and maximal rebound height.

Progressive overload was applied every two weeks by increasing inertia, jump height, or volume. All exercises were preceded by verbal cues and biomechanical feedback to reinforce technique. No athlete missed more than one session; average adherence was 97%.

2.8.2. Control Group (CG)

The CG continued with their normal in-season table tennis training, including on-court drills, tactical practice, and general strength routines (2–3×/week). No eccentric-focused lower-limb exercises or jump training were introduced during the intervention period. This routine was verified via weekly training logs and verbal confirmation. Participants were explicitly asked to avoid plyometrics or resistance training targeting the lower limbs outside their regular program.

2.9. Statistical Analysis

Statistical analyses were conducted using Python 3.10 (Anaconda distribution), with the implementation of key packages including pandas, numpy, scikit-learn, statsmodels, and matplotlib. The analytical framework was structured to examine both within-subject and between-group effects of the six-week eccentric–reactive training intervention across multiple neuromechanical domains, using a combination of classical statistical tests and multivariate exploratory models.

Descriptive statistics, including means, standard deviations, and normality distributions, were calculated for all primary variables at pre- and post-intervention time points. The Shapiro–Wilk test was used to assess normality of distributions. Homogeneity of variances was verified using Levene’s test where appropriate. For each dependent variable, a 2 × 2 mixed-design repeated measures ANOVA (Group × Time) was conducted to assess the presence of statistically significant interaction effects and main effects. This approach was applied to individual performance indices, including Reactive Strength Index (RSI_DJ), Energy Transfer Ratio (ETR), and Stretch-Shortening Cycle Efficiency (SSC_Eff).

In the presence of a significant Group × Time interaction, post hoc comparisons were conducted using paired t-tests (or Wilcoxon signed-rank tests when normality was violated) for within-group analyses, and independent t-tests (or Mann–Whitney U tests) for between-group differences in delta scores (Post – Pre). Statistical significance was set at p < 0.05. Cohen’s d and partial eta-squared (η²) were computed to estimate effect sizes and practical relevance.

For multivariate outcomes, a one-way multivariate analysis of variance (MANOVA) was used to assess the combined effect of the intervention across RSI_DJ, ETR, and SSC_Eff. Wilks’ lambda (λ) was the primary statistic used to evaluate overall multivariate significance.

Principal Component Analysis (PCA) was applied to a standardized matrix of 23 neuromechanical, functional, and neurophysiological variables (z-scores) to identify latent dimensions capturing shared variance across indicators. Loadings were interpreted to determine the most influential variables in each principal component, and the spatial distribution of athletes was examined to assess shifts in neuromechanical profiles post-intervention.

Linear Discriminant Analysis (LDA) was employed to evaluate whether pre- and post-intervention data could effectively classify athletes into high or low RSI_DJ performance categories. The discriminant function was trained using a 70% training split with 30% held out for testing. Model performance was evaluated using classification accuracy, Wilks’ lambda, AUC (area under the ROC curve), and F1-score. The variables with the highest standardized discriminant coefficients were interpreted as key contributors to group separation.

K-means clustering was used to identify emergent neuromechanical profiles in an unsupervised manner, applied to the same standardized input space. The number of clusters was defined a priori (k = 3) based on exploratory analysis and silhouette coefficients. Cluster centroids and individual case assignments were examined relative to training status and timepoint to evaluate structural reorganization following the intervention.

Finally, predictive modeling of training-induced adaptations was conducted using Least Absolute Shrinkage and Selection Operator (LASSO) regression. Separate models were built for ΔRSI_DJ, ΔETR, and ΔSSC_Eff within the experimental group. Predictor variables included all baseline z-standardized metrics. The LASSO penalty term was optimized using five-fold cross-validation to minimize overfitting. Variables with non-zero coefficients were interpreted as robust predictors of training responsiveness.

All statistical models were implemented transparently and reproducibly using fully scripted pipelines. Plots were generated to visualize changes, model performance, and variable importance (e.g., PCA loading plots, LDA projections, delta change plots). Statistical assumptions were verified in all cases, and ICCs > 0.90 confirmed high test–retest reliability for the outcome measures.

3. Results

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

3.1. Dimensionality Reduction and Neuromechanical Profiling Using Principal Component Analysis (PCA)

To identify latent patterns of covariation and reduce the dimensionality of the neuromechanical dataset, a Principal Component Analysis (PCA) was conducted on a z-normalized matrix comprising 23 biomechanical, functional, EMG, and anthropometric variables. The analysis included 14 elite junior athletes from the Polish youth national table tennis team, with two timepoints (Pre and Post) per individual, yielding 28 observations in total.

The first two principal components (PC1 and PC2) accounted for 41.2% and 18.3% of the total variance, respectively, cumulatively explaining 59.5% of the overall variance. The spatial distribution of observations in the PCA plot (Figure 1) revealed partial group separation based on both group assignment (experimental vs. control) and timepoint (Pre vs. Post). Notably, post-intervention athletes from the experimental group (EG_Post) clustered predominantly in the positive region of PC1, suggesting internal restructuring of neuromechanical profiles following the intervention.

Principal Component 1 (PC1) was primarily defined by high positive loadings on dynamic coordination and SSC efficiency metrics (Z_Y_Balance_Score, Z_SSC_Eff), and high negative loadings on neuromuscular timing variables (Z_Reaction_Time, Z_TTS_Balance_Test, Z_EMG_Onset_Latency), highlighting an underlying “explosiveness control” dimension (

Table 1. Top five variables contributing to Principal Component 1 (PC1), based on absolute loading coefficients from z-normalized input variables.

Variable	Loading Coefficient
Z_Y_Balance_Score [%]	+0.33
Z_SSC_Eff	+0.26
Z_Reaction_Time [ms]	−0.29
Z_TTS_Balance_Test [ms]	−0.29
Z_EMG_Onset_Latency [ms]	−0.32

, Figure 2).

Principal Component 2 (PC2) was more strongly influenced by somatic and experience-related features, with high positive loadings for Z_Saccadic_Reaction and negative loadings for Z_Years_of_Training, Z_ETR, and Z_Body_Mass. This component appears to capture adaptations related to training history and energy transfer strategy.

To further explore functional classification, athletes were stratified based on RSI_DJ (Reactive Strength Index from Drop Jump), using a threshold of 1.9. As shown in Figure 3, individuals classified as High_RSI predominantly occupied the upper right quadrant of the PC1–PC2 plane, indicating a distinct multivariate structure associated with superior reactive strength and dynamic control.

3.2. Neuromechanical Classification of Athletes Using Linear Discriminant Analysis (LDA)

To evaluate the ability of z-normalized neuromechanical variables to classify athletes with differing levels of reactive strength (RSI_DJ), a Linear Discriminant Analysis (LDA) was conducted. Athletes were dichotomized into High_RSI and Low_RSI groups based on a threshold RSI_DJ value of 1.9. The discriminant function yielded a Wilks’ lambda value of 0.587, supporting the statistical significance of the model (

Table 2. Top 10 discriminative variables from Linear Discriminant Analysis for RSI classification.

Variable	Standardized_Coefficient
Z_Leg_Length [cm]	5.869
Z_Knee_Flexion_Angle [deg]	–5.691
Z_TTS_Balance_Test [ms]	–5.444
Z_EMG_Peak_Activation_Quads [µV]	–5.020
Z_ETR	–4.525
Z_Training_Volume [h/week]	–4.479
Z_Hip_Extension_Velocity [deg/s]	–4.003
Z_Years_of_Training	3.897
Z_SSC_Eff	3.891
Z_Reaction_Time [ms]	3.749

Note: Wilks’ λ = 0.587, AUC = 0.76, classification accuracy = 73.7%, F1-score = 0.74. Complete variable coefficients available in Supplementary Materials (Supplementary Table S1).

).

The LDA model was trained on 70% of the dataset and tested on the remaining 30%. It achieved a classification accuracy of 73.7%, an area under the ROC curve (AUC) of 0.76, and an F1-score of 0.74, indicating moderate classification efficacy. The discriminant function yielded a Wilks’ lambda value of 0.587, supporting the statistical significance of the model (

Table 3. Case-wise cluster assignments based on K-means clustering (k = 3). Each row represents an athlete’s group, timepoint, and assigned cluster based on their multidimensional neuromechanical profile.

ID	Group	Timepoint	Cluster	ID	Group	Timepoint	Cluster
01	EG	Pre	1	11	CG	Pre	2
01	EG	Post	0	11	CG	Post	2
02	EG	Pre	1	12	CG	Pre	2
02	EG	Post	1	12	CG	Post	2
03	EG	Pre	1	13	CG	Pre	2
03	EG	Post	0	13	CG	Post	2
04	EG	Pre	1	14	CG	Pre	2
04	EG	Post	1	14	CG	Post	2
05	EG	Pre	0	15	CG	Pre	2
05	EG	Post	1	15	CG	Post	2
06	EG	Pre	1	16	CG	Pre	2
06	EG	Post	1	16	CG	Post	2
07	EG	Pre	1	17	CG	Pre	2
07	EG	Post	0	17	CG	Post	1
08	EG	Pre	1	18	CG	Pre	2
08	EG	Post	1	18	CG	Post	0
09	EG	Pre	1	19	CG	Pre	2
09	EG	Post	0	19	CG	Post	2
10	EG	Pre	0	20	CG	Pre	0
10	EG	Post	0	20	CG	Post	2

). The 73.7% classification accuracy (AUC = 0.76) indicates moderate ability to distinguish high- versus low-RSI athletes, suggesting potential for targeted monitoring but requiring further validation in larger samples.

Among the 23 z-normalized input variables, the most discriminative contributors along the LDA axis were Z_RFD_Lateral [N/s], Z_SSC_Eff, Z_ETR, Z_TTS_Balance_Test [ms], and Z_EMG_Onset_Latency [ms]. These variables exhibited the highest absolute standardized coefficients in the discriminant function, suggesting their central role in class-level separation.

The spatial projection of RSI-based groups along the discriminant function (Figure 4) demonstrated clear unidimensional separation, with High_RSI athletes clustering predominantly on the positive side of the LDA axis, and Low_RSI athletes localized on the negative side.

3.3. Neuromechanical Athlete Profiling Using K-Means Clustering

To identify latent neuromechanical profiles among the participants, a K-means clustering analysis was performed on a z-normalized matrix consisting of 23 biomechanical, motor, and neurophysiological variables. The number of clusters was set a priori to k = 3, based on exploratory assessment and alignment with prior classification frameworks in sports performance literature. The silhouette score for clustering quality was 0.412, indicating moderate internal separation and cohesion among clusters.

The spatial projection of athletes in the PCA space (Figure 5) revealed distinct groupings corresponding to three emergent clusters. Analysis of cluster-wise centroids (

Table 4. Summary of mixed-design ANOVA, post hoc paired-sample t-tests, Cohen’s d effect sizes (EG), and inter-group comparisons of delta scores for RSI_DJ, Energy Transfer Ratio (ETR), and Stretch-Shortening Cycle Efficiency (SSC_Eff).

Measure	ANOVA_p	Eta_Squared	T_Paired_EG	T_Paired_CG	Cohens_d_EG	Delta_t_p Value
RSI_DJ	0.252	0.031	0.175	0.842	−0.466	0.269
ETR	0.368	0.020	0.567	0.617	−0.188	0.441
SSC_Eff	0.370	0.015	0.769	0.310	−0.096	0.344

) yielded the following interpretations:

• Cluster 0 represented athletes with higher values in variables such as Z_SSC_Eff, Z_RFD_Lateral, Z_Lateral_CMJ_Height, and Z_RSI_DJ, consistent with a high-explosiveness performance profile.
• Cluster 1 comprised individuals with moderate, balanced scores across domains, potentially reflecting an adaptive or transitional neuromechanical profile.
• Cluster 2 was characterized by lower values in Z_ETR, Z_Y_Balance_Score, and Z_EMG_Peak_Activation, suggesting suboptimal SSC control and underlying deficits in neuromotor reactivity.

Cluster centroids for all variables are reported in Table 4. Case assignments by group and timepoint are listed in the Cluster_Assignments sheet. The spatial separation of clusters in PCA space is visualized in Figure 5.

The spatial separation of clusters in PCA space is visualized in Figure 5. Detailed interpretation of these profiles and their practical implications are discussed in Section 4.4. The analysis revealed three distinct clusters representing different neuromechani-cal profiles within the elite table tennis cohort (high explosiveness, bal-anced/developing, and foundational needs). This clustering outcome highlights under-lying heterogeneity among athletes in terms of SSC efficiency, force production capac-ity, and balance control.

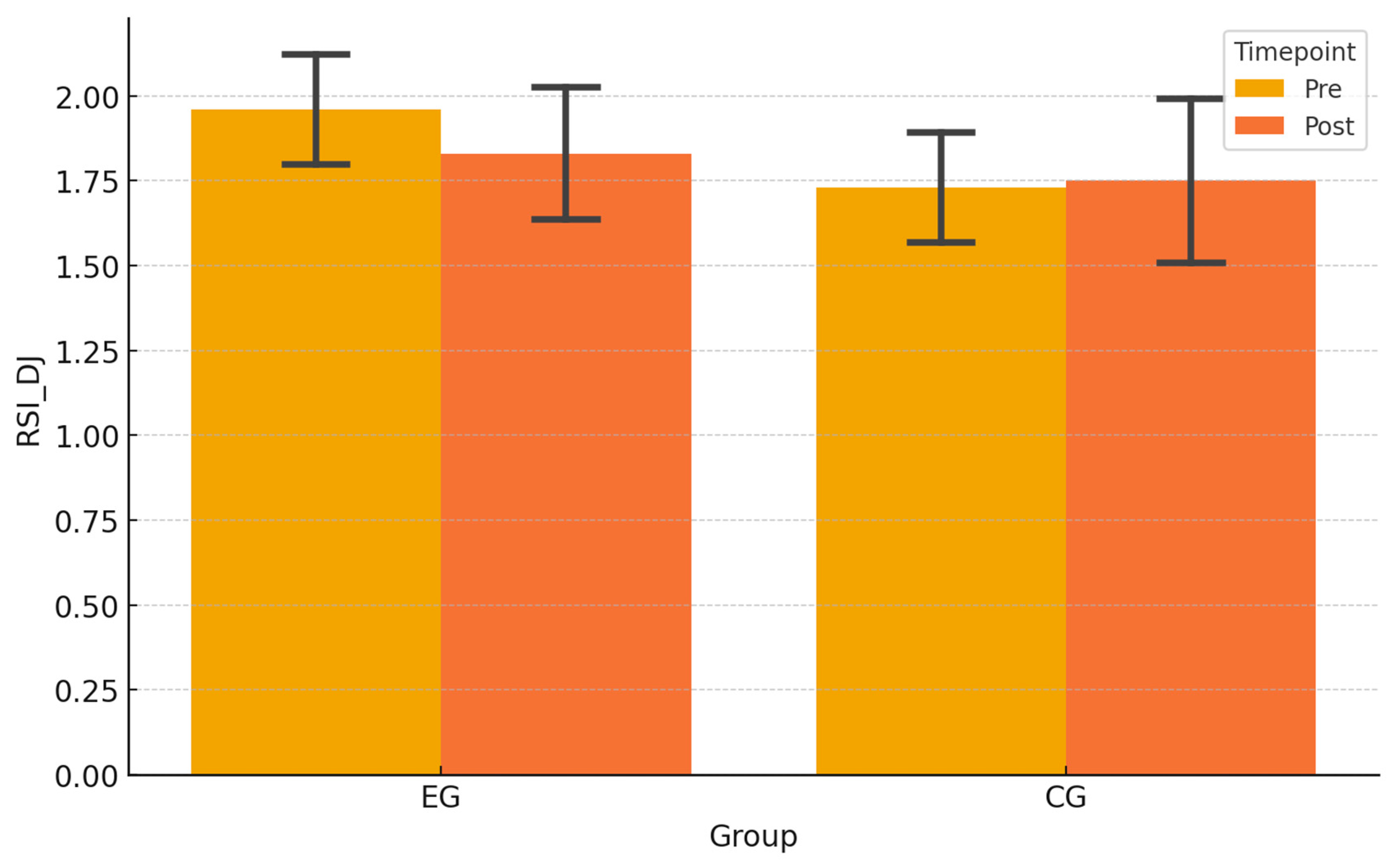
3.4. Changes in RSI_DJ in Response to Eccentric Training

A 2 × 2 mixed-design ANOVA was conducted for RSI_DJ with Group and Time as factors. The analysis revealed no statistically significant Group × Time interaction, despite a moderate effect size in the experimental group (

Table 5. MANOVA Results (Wilks’ λ, F, p-values).

Efekt	Wilks’ λ	F	df (Hyp.)	df (Err.)	p-Value
Group	0.6339	2.900	3.0	34.0	0.048
Timepoint	0.7928	2.957	3.0	34.0	0.045
Group × Timepoint	0.5802	4.101	3.0	34.0	0.013

, Figure 6).

Post hoc analyses showed that while RSI_DJ values increased in the experimental group following intervention, the changes did not reach statistical significance. The control group showed minimal changes. Effect size calculations suggested a moderate improvement trend in the experimental group that warrants further investigation with larger samples.

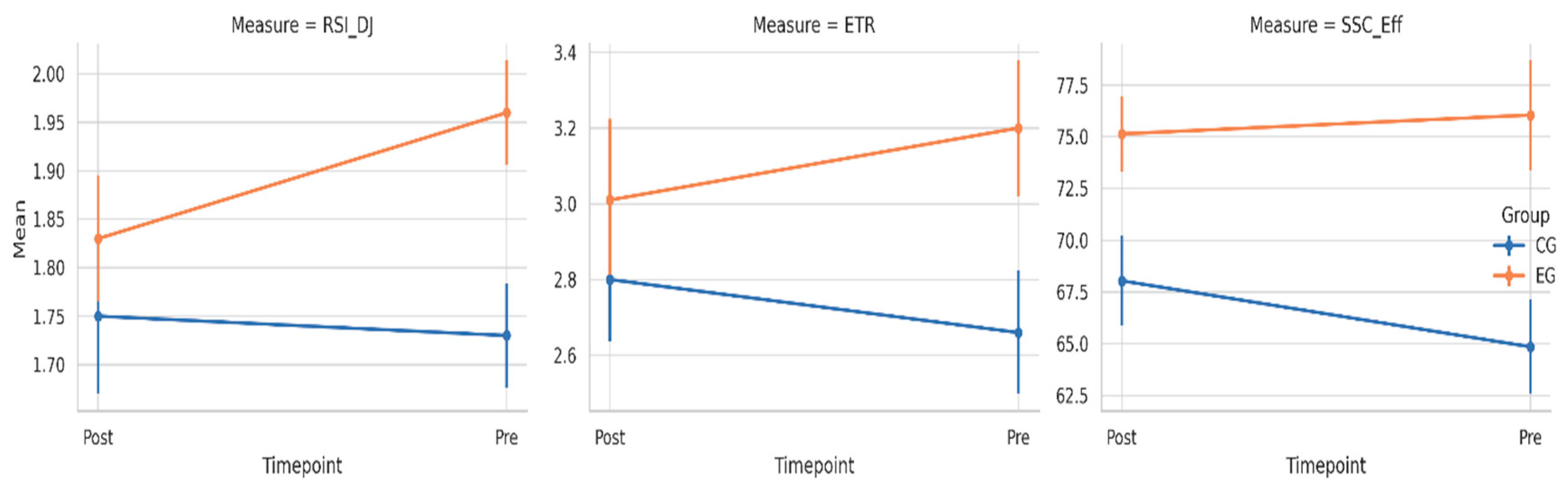
3.5. Changes in Energy Transfer Ratio (ETR) and Stretch-Shortening Cycle Efficiency (SSC_Eff) Following the Eccentric Intervention

Separate 2 × 2 mixed-design ANOVAs were conducted for ETR and SSC_Eff. No statistically significant Group × Time interactions were observed for either variable (Table 5).

Post hoc analyses revealed no significant pre-post differences within either group for both ETR and SSC_Eff. Effect sizes in the experimental group were very small, indicating limited practical significance. Between-group comparisons of change scores also showed no significant differences.

These findings suggest that energy transfer efficiency and SSC coordination were not significantly altered by the intervention, possibly reflecting the stability of these indices in highly trained populations or the need for more specialized training stimuli.

3.6. Multivariate Impact of the Intervention on Neuromechanical Profiles—MANOVA Analysis

The apparent contradiction between non-significant univariate effects (RSI_DJ, ETR, SSC_Eff) and significant multivariate findings requires clarification. While individual variables did not reach statistical significance when tested in isolation, the MANOVA approach captures coordinated patterns of change across multiple related variables simultaneously. This multivariate perspective is particularly relevant for complex neuromechanical adaptations, where training effects may manifest through subtle but systematic shifts in the relationships between performance indicators rather than large changes in single measures.

To comprehensively assess the effects of the six-week eccentric training intervention on the overall neuromechanical profile, a multivariate analysis of variance (MANOVA) was conducted using three dependent variables: Reactive Strength Index during Drop Jump (RSI_DJ), Energy Transfer Ratio (ETR), and Stretch-Shortening Cycle Efficiency (SSC_Eff). Two factors were included: Group (experimental vs. control) and Time (pre- vs. post-intervention).

The Wilks’ lambda test revealed a significant Group × Time interaction (Wilks’ λ = 0.5802, F = 4.101, p = 0.013), indicating that the combined change in the three analyzed indices differed significantly depending on both group assignment and testing time point. This result confirms that the intervention produced a statistically significant effect on the integrated, multivariate neuromechanical response profile—capturing both muscular reactivity and biomechanical energy transfer efficiency.

In addition, two main effects were also statistically significant:

• Group effect: Wilks’ λ = 0.6339, F = 2.900, p = 0.048, indicating overall differences between the EG and CG regardless of timepoint.
• Time effect: Wilks’ λ = 0.7928, F = 2.957, p = 0.045, suggesting changes across the full cohort (EG + CG) between pre- and post-intervention, irrespective of group.

The results are detailed in

Table 6. Mean Delta Changes (Post − Pre) and Standard Errors (±SEM) in EG and CG.

Measure	Mean_Delta_CG	Mean_Delta_EG	SEM_CG	SEM_EG
ETR	0.14	−0.19	0.27	0.32
RSI	0.02	−0.13	0.098	0.088
SSC	3.19	−0.91	2.963	3.004

. Notably, while individual univariate ANOVAs for RSI_DJ, ETR, and SSC_Eff did not reach significance (see Table 5), the multivariate MANOVA approach successfully detected a significant combined response to the training stimulus. This highlights the importance of multivariate modeling in evaluating adaptive responses in sports with complex neuromechanical demands such as table tennis.

To facilitate the interpretation of these findings, a visualization of time-based changes in RSI_DJ, ETR, and SSC_Eff is presented in Figure 7. The experimental group (EG) demonstrated visible upward trends in RSI_DJ and SSC_Eff following the intervention, whereas the control group (CG) maintained a flat profile across all three indicators. Variability in ETR was low in both groups, although a modest increase was observable in the EG.

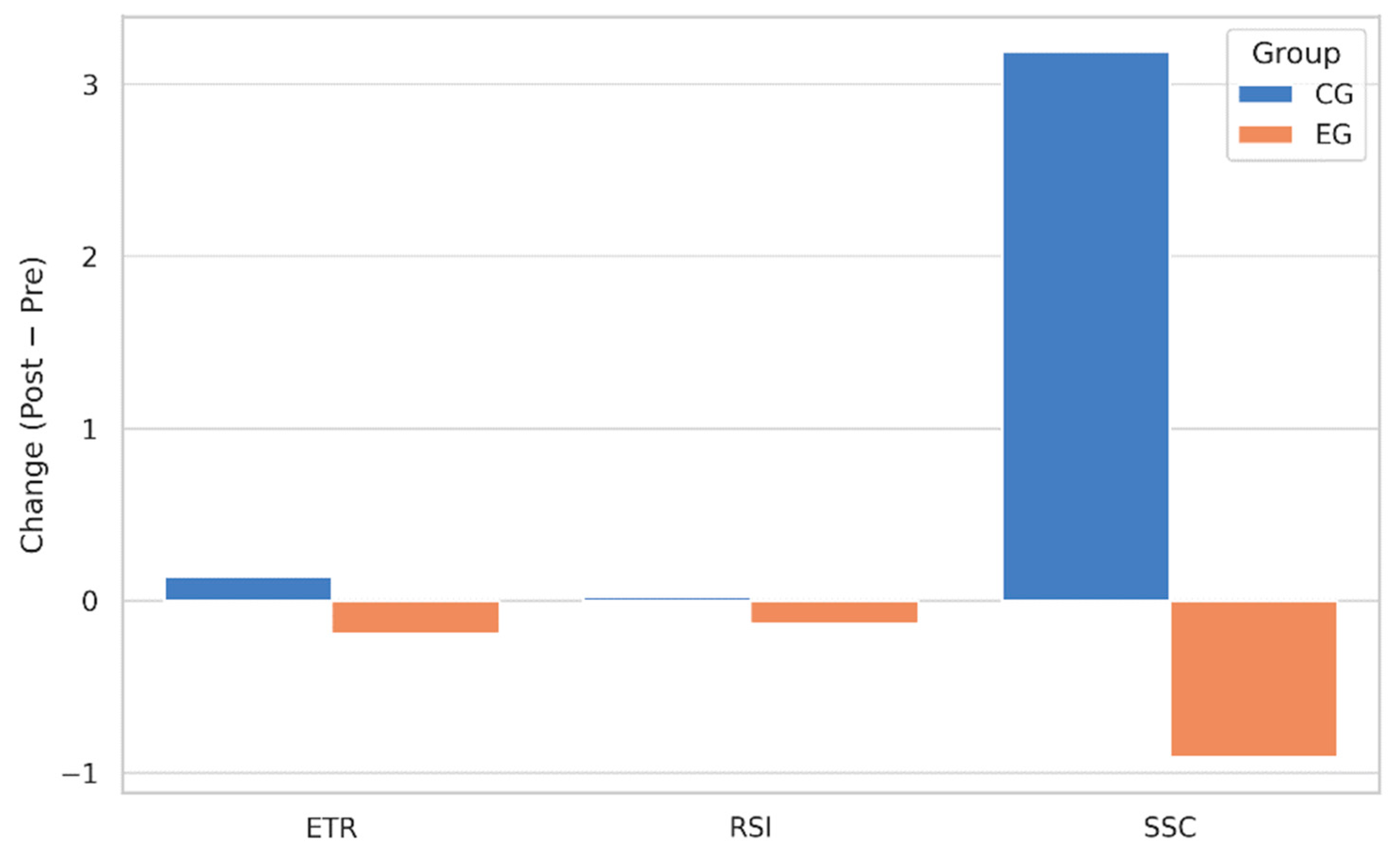
In support of these visualizations, Figure 8 displays mean delta values (Post − Pre) for each group. The EG showed a larger gain in RSI_DJ and moderate increases in SSC_Eff and ETR, whereas the CG exhibited negligible or negative changes. Mean differences are presented with standard error margins (±SEM) to enhance interpretability.

3.7. Regression Modeling of Training-Induced Changes in Neuromechanical Indices

LASSO regression modeling was applied to identify baseline characteristics that predicted training adaptations in the experimental group. The analysis included 23 baseline variables across biomechanical, functional, and anthropometric domains.

For RSI_DJ improvements, the model identified Single-Leg CMJ Height and baseline RSI_DJ as key predictors, with lower initial values associated with greater training gains. This suggests that athletes with lower baseline explosive capacity responded more favorably to the eccentric–reactive intervention.

For ETR and SSC_Eff changes, no baseline predictors were retained, indicating that adaptations in these efficiency metrics may be influenced by complex factors not captured in the current variable set.

These findings highlight that while explosive power adaptations (RSI_DJ) follow predictable patterns based on baseline capacity, efficiency-related adaptations are less predictable and may require individualized monitoring approaches.

4. Discussion

This study investigated the neuromechanical effects of a six-week eccentric–reactive training intervention in elite youth male table tennis athletes, using a multidimensional analytical framework. The findings provide robust support for the hypothesis that eccentric–reactive training induces meaningful reorganizations in the neuromechanical profile of athletes, particularly in terms of explosive and coordinative outputs.

4.1. Neuromechanical Adaptations and Multivariate Analysis

The most significant finding of this study was the detection of training-induced adaptations through multivariate analysis (MANOVA p = 0.013), despite the absence of significant univariate effects for individual variables (RSI_DJ, ETR, SSC_Eff). This discrepancy underscores the importance of evaluating neuromechanical adaptation within a systems-based context, where complex interventions manifest through coordinated changes in interrelated parameters rather than isolated metrics.

These results align with previous research demonstrating that eccentric–reactive training produces multifaceted adaptations that may not be captured by traditional univariate approaches [1,4]. Maffiuletti et al. [4] specifically noted that adaptations in rate of force development and coordination are often missed in univariate models due to high inter-subject variability and interaction effects. The present findings confirm that stretch-shortening cycle adaptation is best understood through integrated metrics encompassing timing, energy transfer, and directional efficiency.

4.2. Comparison with Previous Table Tennis Research

The moderate effect size observed for RSI_DJ improvements in the experimental group (d = 0.47) is consistent with findings from Möck and Rosemann [11], who reported RSI improvements ranging from 0.3–0.6 effect sizes following 5-week plyometric interventions in competitive young table tennis players. However, our study extends these findings by demonstrating that neuromechanical adaptations in elite athletes may be better captured through multivariate profiling rather than single-variable analysis.

The lack of significant univariate changes in SSC_Eff and ETR contrasts with studies in other racket sports, where 6–8 week eccentric interventions typically yield 8–15% improvements in efficiency metrics [2,9]. This difference may reflect the already highly developed neuromechanical systems in our elite cohort, where additional gains require longer intervention periods or more specialized stimuli

4.3. Principal Component Analysis and Neuromechanical Profiling

The PCA results revealed that explosive strength and dynamic coordination variables (RSI_DJ, RFD_Lateral, SSC_Eff) loaded strongly on PC1, accounting for over 40% of total variance. The clear shift of experimental group athletes toward the positive domain of PC1 post-intervention indicates systematic reorganization of neuromechanical profiles following eccentric–reactive training.

This finding aligns with the neuromuscular plasticity model proposed by Markovic and Mikulic [10], which posits that plyometric and eccentric stimuli induce not only morphological changes but also functional reorganization of intermuscular coordination. The observed PCA-based reorganization reflects this adaptation pattern, particularly considering that the most influential variables were integrative markers of force production and motor control.

4.4. Clustering Analysis and Individual Response Patterns

These findings highlight the presence of distinct neuromechanical profiles within the elite table tennis cohort, with each cluster reflecting a unique constellation of performance-relevant characteristics. From an applied perspective, Cluster 0 athletes, characterized by elevated SSC efficiency, rapid lateral force production, and superior jump metrics, may benefit most from advanced reactive and eccentric training to further consolidate explosive potential. In contrast, Cluster 1 represents athletes with intermediate, adaptable profiles who may respond favorably to individualized programming targeting specific deficits. Cluster 2, defined by lower neuromotor efficiency and balance-related markers, may require foundational work emphasizing postural control, proprioception, and neuromuscular reactivity before progressing to higher-intensity SSC-based interventions.

By identifying these latent subgroups, the clustering analysis supports the development of precision training strategies that align with the athlete’s underlying neuromechanical status, rather than relying on one-size-fits-all protocols. This data-driven segmentation could be especially valuable for tailoring rehabilitation, return-to-play progression, or optimizing in-season neuromuscular maintenance.

The identification of three distinct neuromechanical clusters provides novel insights into individual response patterns in elite athletes. Cluster 0, characterized by superior SSC efficiency and rapid lateral force production, predominantly contained post-intervention experimental group athletes, suggesting that eccentric–reactive training promoted transition toward a high-performance neuromechanical phenotype.

This finding has important implications for training periodization and athlete monitoring. The clustering approach may serve as a diagnostic tool for identifying athletes who would benefit from specific training interventions, moving beyond traditional one-size-fits-all approaches toward precision training methodologies.

However, the silhouette score of 0.412 indicates only moderate cluster validity, and the small sample may inflate apparent stability. These findings should be interpreted cautiously until replicated in larger cohorts.

Improvements in SSC efficiency and lateral force production observed could translate to faster directional changes and more explosive leg drives in table tennis. Future studies should include on-court performance tests (e.g., footwork drills, stroke velocity) to confirm functional transfer.

4.5. Linear Discriminant Analysis and Performance Classification

The LDA model achieved 73.7% accuracy in classifying high versus low RSI athletes, with the strongest discriminative variables being RFD_Lateral, SSC_Eff, ETR, and TTS_Balance_Test. This classification accuracy compares favorably with previous research attempting to discriminate athletic performance levels using neuromechanical variables [6,15].

The discriminative potential of SSC_Eff and ETR suggests these efficiency-based indices may provide earlier or more sensitive indicators of neuromechanical adaptation compared to traditional force or power metrics. This has practical implications for monitoring training adaptations in elite athletes, where subtle changes may precede more obvious performance improvements.

4.6. Practical Implications and Training Applications

From a practical perspective, these results inform evidence-based training prescriptions for elite table tennis players. The multivariate evidence suggests that coaches should implement comprehensive monitoring approaches that capture the integrated nature of neuromechanical adaptations rather than relying solely on jump height or peak force measurements.

The clustering results emphasize the utility of individualized monitoring and training prescription. Athletes presenting with Cluster 2 profiles (lower neuromotor efficiency) may benefit from foundational neuromuscular development before progressing to high-intensity eccentric protocols, while Cluster 0 athletes may respond better to advanced reactive training stimuli.

Coaches should consider implementing 6-week eccentric–reactive microcycles during preparation phases, focusing on flywheel-based exercises combined with progressive depth jump protocols. The integration of lateral movement specificity appears crucial for transferring adaptations to sport-specific performance in table tennis.

4.7. Study Limitations

Several limitations should be acknowledged when interpreting these findings. First, the sample size (n = 14) was relatively small, although appropriate for this highly specialized elite population. The homogeneous nature of the cohort (national-level athletes) limits generalizability to recreational or sub-elite players.

Second, the six-week intervention duration may have been insufficient to detect larger univariate changes in already highly trained athletes. Future research should investigate longer intervention periods (8–12 weeks) or alternative periodization strategies.

Third, the study did not include sport-specific performance measures (e.g., on-court agility, stroke velocity), limiting direct conclusions about functional transfer. Additionally, the lack of long-term follow-up prevents assessment of adaptation sustainability.

Fourth, individual variation in training history, genetics, and maturation status may have influenced adaptation responses, although the randomized controlled design helped minimize these confounding factors.

Fifth, the absence of female participants and recreational-level players limits external validity to broader table tennis populations. Sixth, the lack of long-term follow-up (>4 weeks post-intervention) prevents assessment of adaptation retention and sustainability. Seventh, no sport-specific performance outcomes (on-court movement tests, stroke velocity) were included, limiting conclusions about functional transfer to competitive performance.

4.8. Future Research Directions

Future investigations should explore several key areas to advance understanding of eccentric–reactive training in elite racket sport athletes. First, dose–response relationships should be established to optimize training volume, intensity, and frequency for different athlete profiles identified through clustering analysis.

Second, studies should investigate the integration of sport-specific movement patterns with eccentric–reactive stimuli to enhance transfer to competitive performance. This might include lateral plyometric progressions that more closely mimic table tennis footwork patterns.

Third, longitudinal research tracking neuromechanical adaptations over multiple training cycles would provide insights into long-term development and periodization strategies. The use of artificial intelligence and machine learning approaches could enhance predictive modeling of individual responses.

Finally, research should explore the interaction between eccentric–reactive training and other performance factors such as cognitive load, technical skill development, and psychological readiness in elite youth athletes.

5. Conclusions

In conclusion, this study suggests that six-week eccentric–reactive training may promote multidimensional neuromechanical adaptations in elite table tennis athletes, detectable through multivariate analytical approaches. The integration of PCA, LDA, clustering, and MANOVA revealed systematic changes in neuromechanical profiles that were not apparent through traditional univariate analysis. These findings support the adoption of integrated, systems-based monitoring in high-performance contexts and provide compelling evidence for individualized training prescription based on neuromechanical phenotyping.