Feature-Based Modeling of Subject-Specific Lower Limb Skeletons from Medical Images
Abstract
1. Introduction
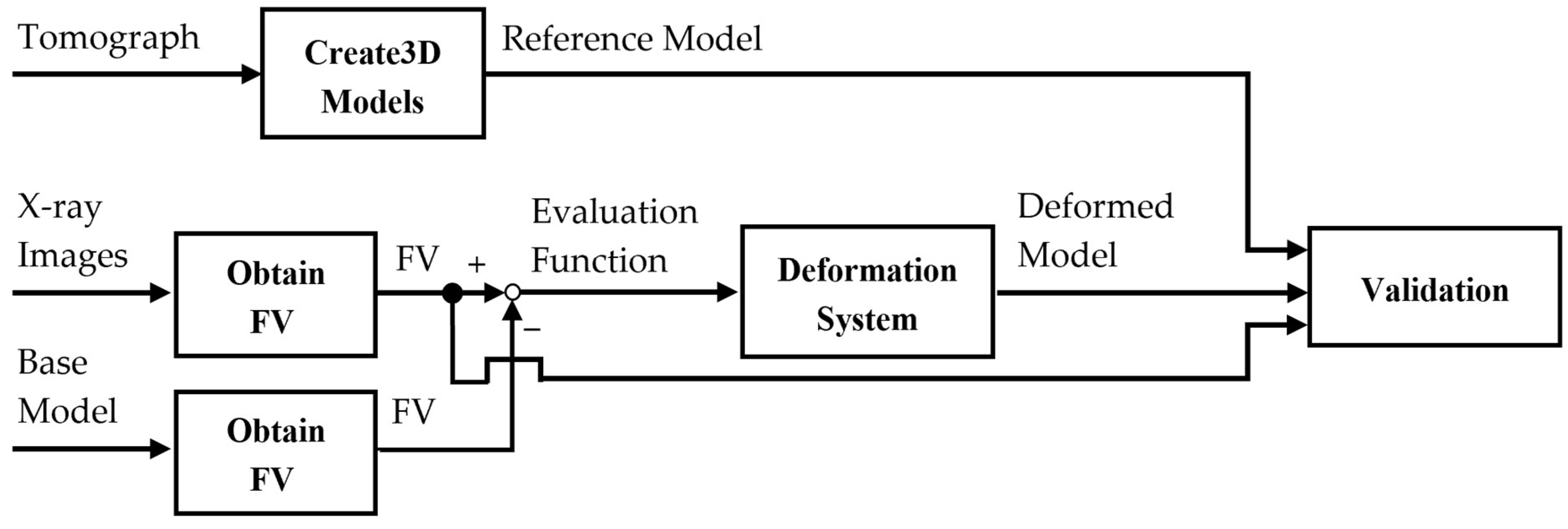
2. Materials and Methods
2.1. Setting the Coordinate System on the Model
2.2. Adjustment of Tilt Between Medical Images and Model
2.3. Acquisition of Feature Points and Feature Values from Medical Images and Shape Model
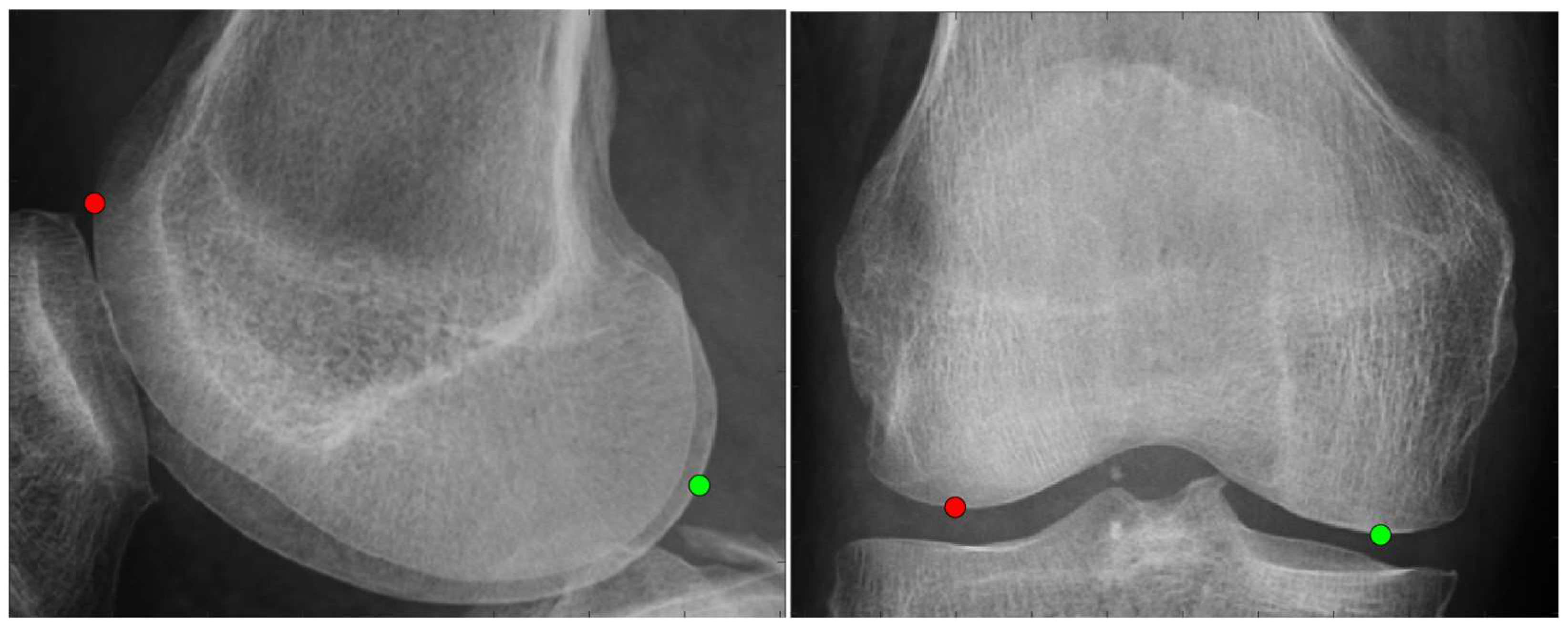
2.3.1. Anatomical Feature Point
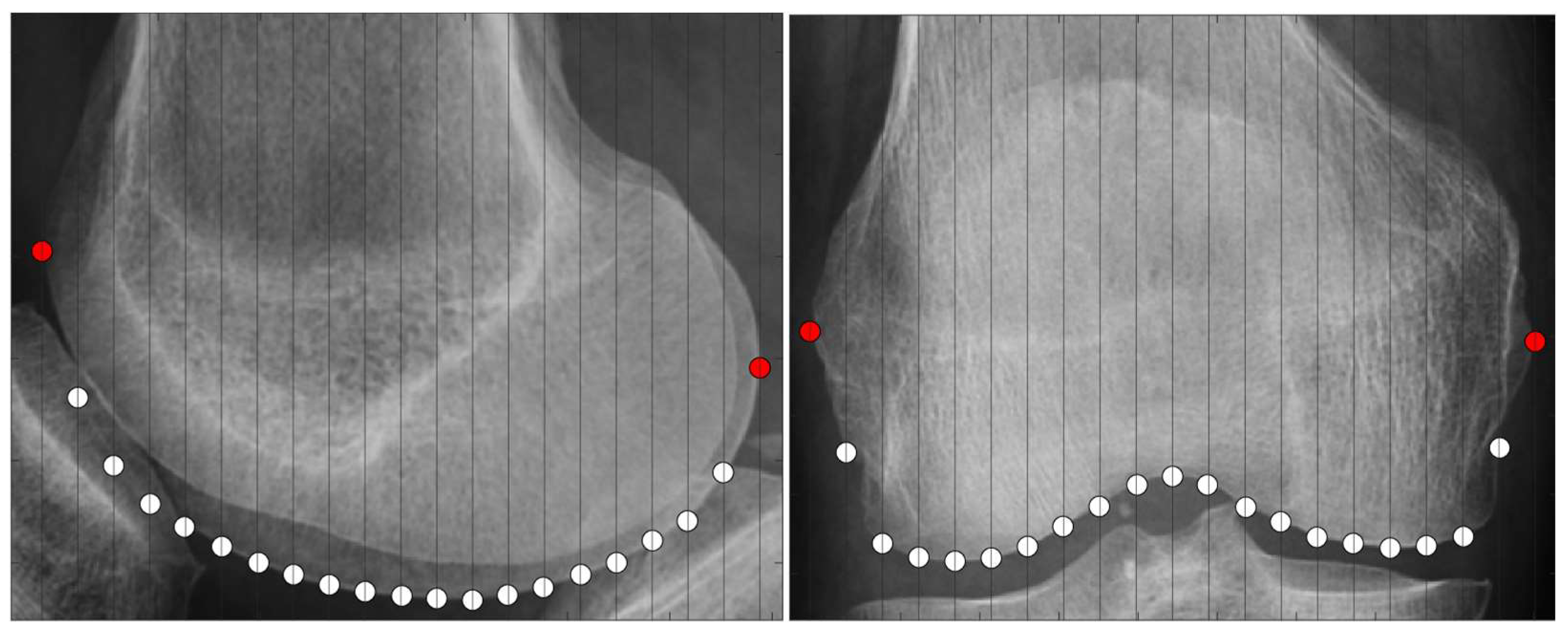
2.3.2. Scanning Feature Values
- Select two points located at both ends.
- Of the two points obtained in step 1, designate the point located posteriorly in the sagittal plane and laterally in the coronal plane as the reference point.
- Draw a perpendicular line on the images that divides the two points into n equal parts.
- Obtain the intersection of the line drawn in step 3 and the bone contour line.
- Calculate the distances between all points and the reference point and use them as the feature values.
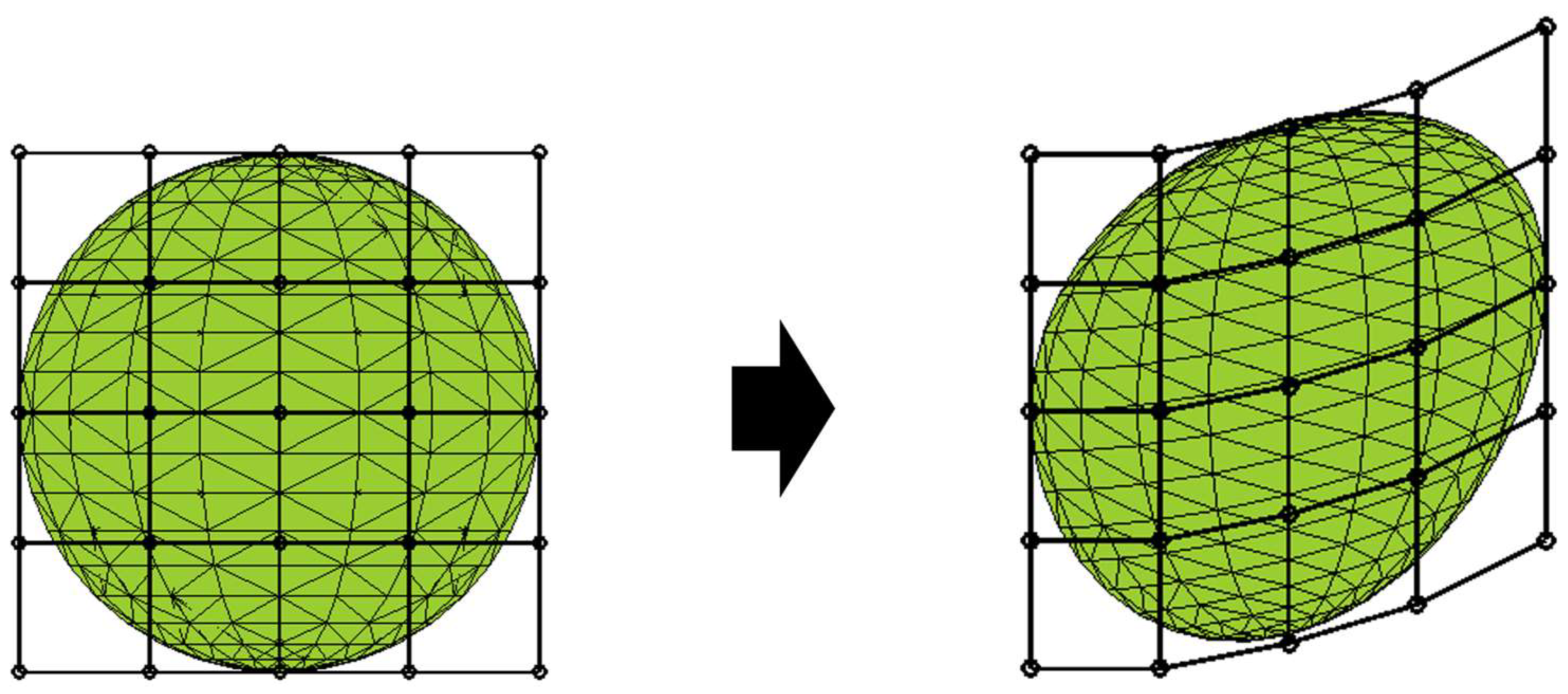
2.4. Deformational Technique
2.5. Optimization Calculation
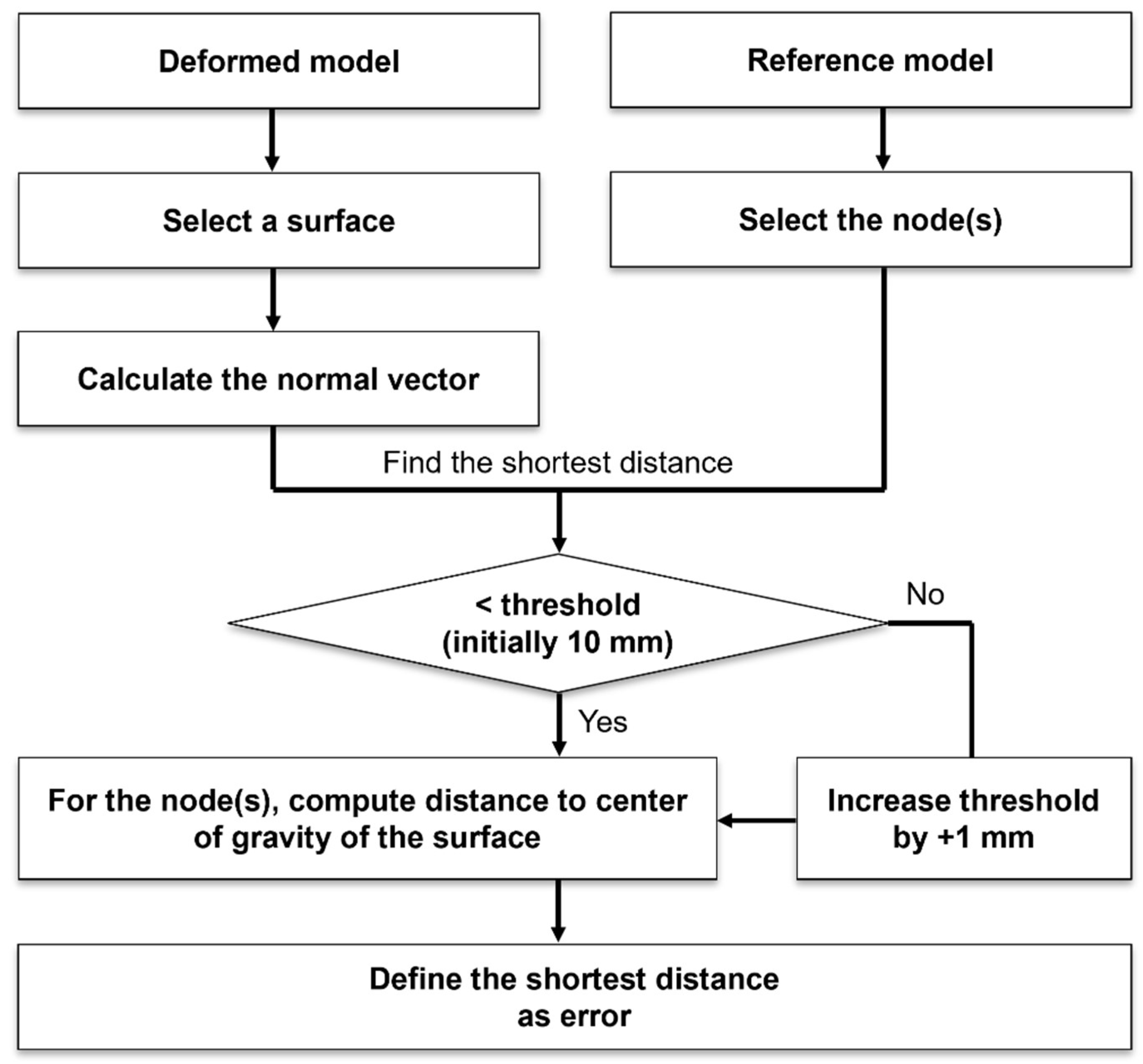
2.6. Evaluation
- Find the normal on any one surface of the deformed model.
- Find the shortest distance between the normal obtained in step 1 and the node point of the reference model.
- Find a node whose shortest distance calculated in step 2 is less than a certain threshold.
- If there is no point below the threshold value in step 3, set the threshold value to +1 mm.
- Find the distance between the point obtained in step 3 and the center of gravity of the surface chosen in step 1.
- Define the point with the shortest distance obtained in step 5 as the closest node point; then, the value of the distance is the error between the model after deformation and the reference model.
- Repeat steps 1 through 6 for all surfaces that make up the deformed model.
3. Results
3.1. Relevance of FFD
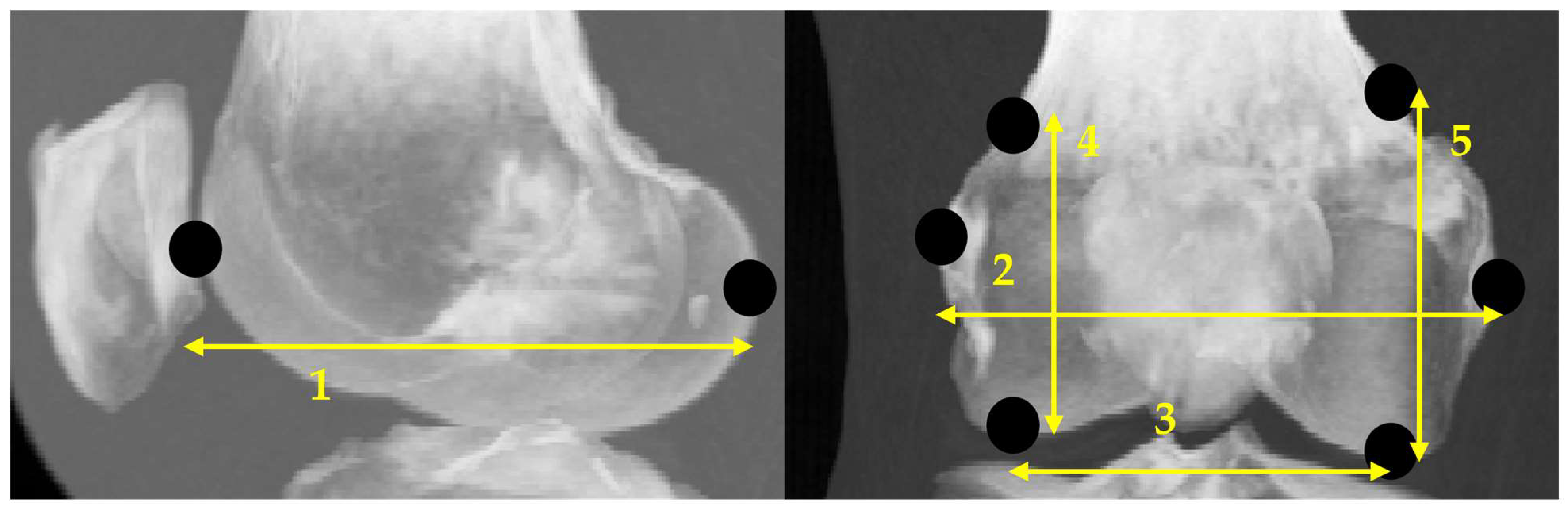
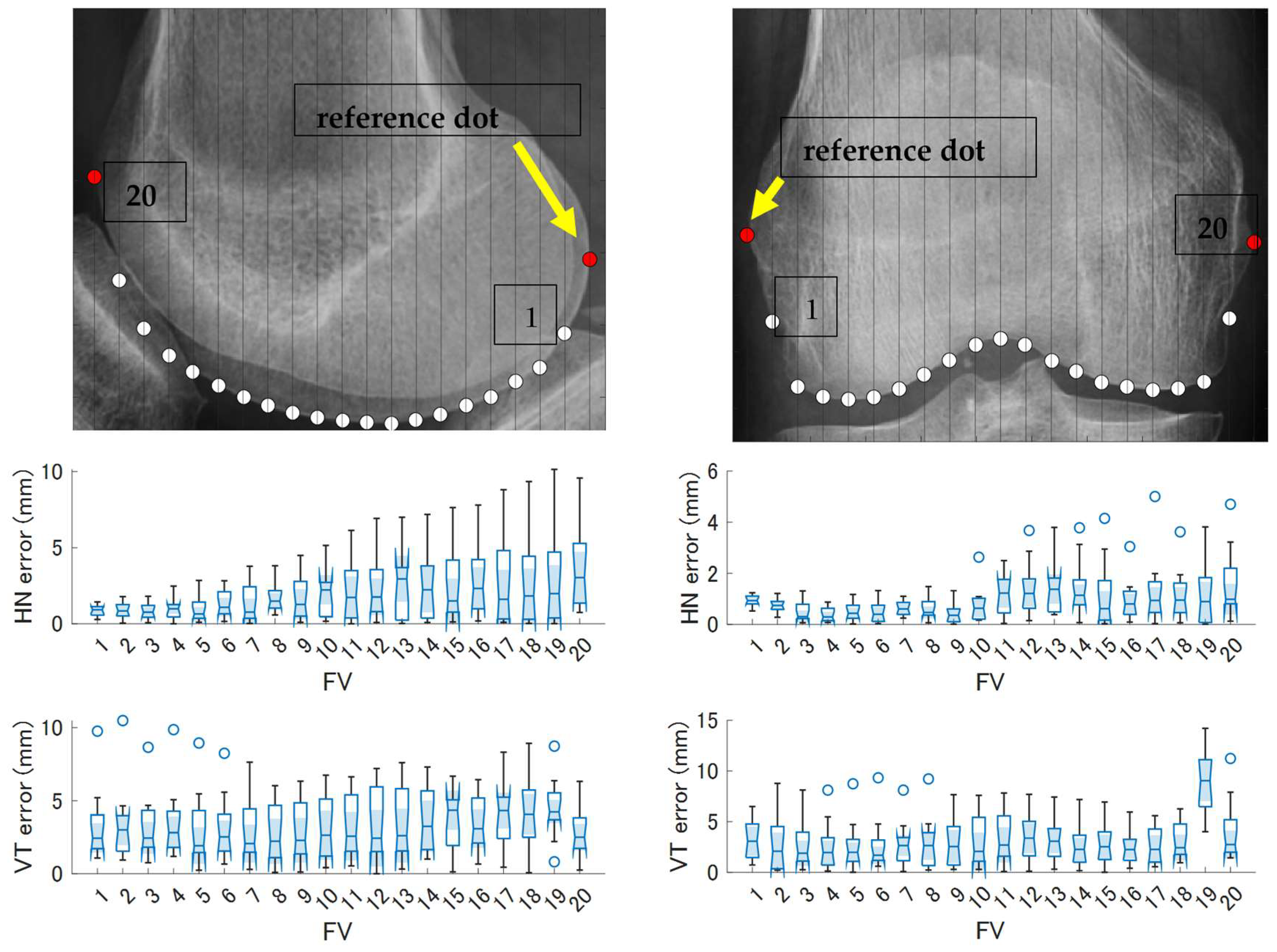
3.2. Comparison and Accuracy of Feature Value Acquisition Methods
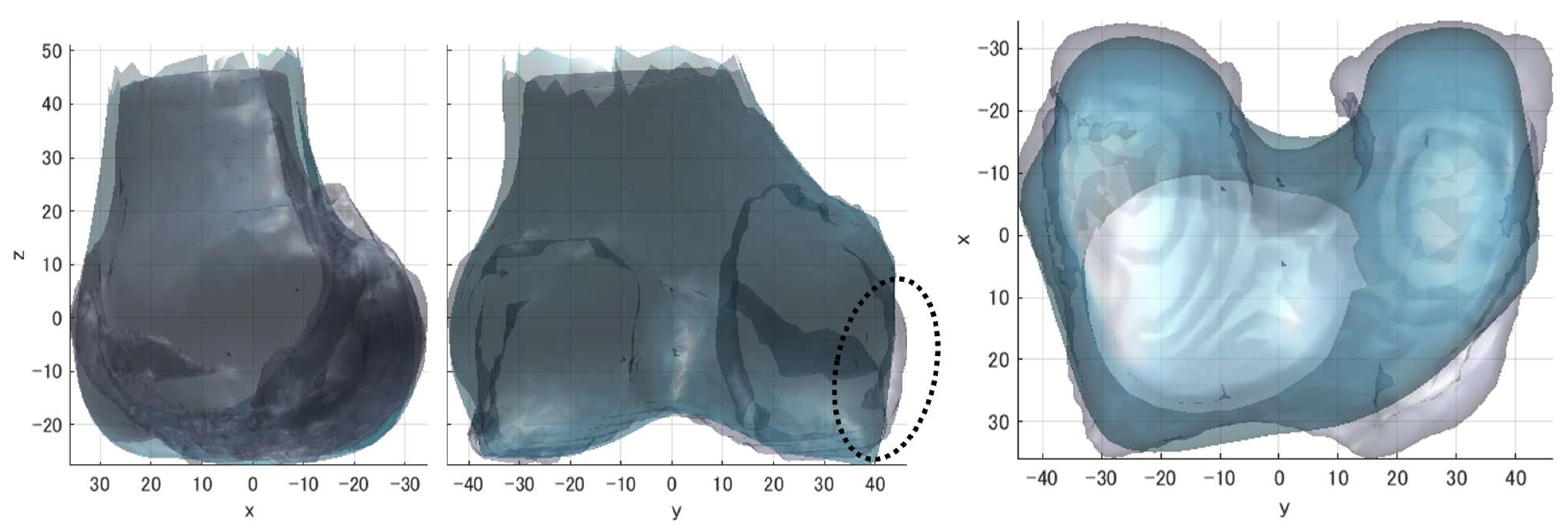
3.3. Evaluation of the Overall Model Shape
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Mercader, A.; Rottinger, T.; Bigdeli, A.; Luth, T.C.; Rottinger, H. A patient-specific 3D model of the knee to compare the femoral rollback before and after total knee arthroplasty (TKA). J. Exp. Orthop. 2021, 8, 2. [Google Scholar] [CrossRef] [PubMed]
- Otomaru, I.; Nakamoto, M.; Takao, M.; Sugano, N.; Kagiyama, Y.; Yoshikawa, H.; Tada, Y.; Sato, Y. Automated preoperative planning of femoral component for total hip arthroplasty (THA) from 3D CT images. JBSE 2008, 3, 478–489. [Google Scholar] [CrossRef]
- Wang, S.; Hase, K.; Ota, S. Development of a lower limb finite element musculoskeletal gait simulation framework driven solely by inertial measurement unit sensors. Biomechanics 2021, 1, 293–306. [Google Scholar] [CrossRef]
- Wang, S.; Hase, K.; Ota, S. A computationally efficient lower limb finite element musculoskeletal framework directly driven solely by inertial measurement unit sensors. J. Biomech. Eng. 2022, 144, 051011. [Google Scholar] [CrossRef] [PubMed]
- Kalra, K.M.; Maher, M.M.; Rizzo, S.; Kanarek, D.; Shephard, O.J. Radiation exposure from chest CT: Issues and strategies. J. Korean Med. Sci. 2004, 19, 159–166. [Google Scholar] [CrossRef]
- Meulepas, J.M.; Ronckers, C.M.; Smets, A.M.J.B.; Nievelstein, R.A.J.; Gradowska, P.; Lee, C.; Jahnen, A.; van Straten, M.; de Wit, M.Y.; Zonnenberg, B.; et al. Radiation exposure from pediatric CT scans and subsequent cancer risk in the Netherlands. JNCI J. Natl. Cancer Inst. 2019, 111, 256–263. [Google Scholar] [CrossRef]
- Shellock, F.G.; Crues, J.V. MR procedures: Biologic effects, safety, and patient care. Radiology 2004, 232, 635–652. [Google Scholar] [CrossRef]
- Inaguma, K.; Kotani, T.; Kishida, S.; Sakuma, T.; Ueno, K.; Iijima, Y.; Kajiwara, D.; Okuyama, K.; Sakashita, K.; Okuwaki, S.; et al. Medical accidents related to ferromagnetic objects brought into the MRI Room: Analysis of the national multicenter database by orthopedic surgeons. SSRR 2023, 7, 96–102. [Google Scholar] [CrossRef]
- Reyes-Santias, F.; Garcia-Garcia, C.; Aibar-Guzman, B.; Garcia-Campos, A.; Cordova-Arevalo, O.; Mendoza-Pintos, M.; Cinza-Sanjurjo, S.; Portela-Romero, M.; Mazon-Ramos, P.; Gonzalez-Juanatey, J.R. Cost analysis of magnetic resonance imaging and computed tomography in Cardiology: A case study of a university hospital complex in the euro region. Healthcare 2023, 11, 2084. [Google Scholar] [CrossRef]
- Bhalodia, R.; Elhabian, S.; Adams, J.; Tao, W.; Kavan, L.; Whitaker, R. Deepssm: A blueprint for Image-to-Shape deep learning models. Med. Image Anal. 2024, 91, 103034. [Google Scholar] [CrossRef]
- Kurazume, R.; Nakamura, K.; Okada, T.; Sato, Y.; Sugano, N.; Koyama, T.; Iwashita, Y.; Hasegawa, T. 3D reconstruction of a femoral shape using a parametric model and two 2D fluoroscopic images. Comput. Vision Image Underst. 2009, 113, 202–211. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Parry, S.R. Free-form deformation of solid geometric models. ACM SIGGRAPH Comput. Graph. 1986, 20, 151–160. [Google Scholar] [CrossRef]
- Jack, D.; Pontes, J.K.; Sridharan, S.; Fookes, C.; Shirazi, S.; Maire, F.; Eriksson, A. Learning Free-Form deformations for 3D object reconstruction. Lect. Notes Comput. Sci. 2018, 11362, 317–333. [Google Scholar]
- Modenese, L.; Renault, J. Automatic generation of personalised skeletal models of the lower limb from Three-Dimensional bone geometries. J. Biomech. 2021, 116, 110186. [Google Scholar] [CrossRef]
- Mohammadi, A.; Myller, K.A.H.; Tanska, P.; Hirvasniemi, J.; Saarakkala, S.; Toyras, J.; Korhonen, R.K.; Mononen, M.E. Rapid CT-based estimation of articular cartilage biomechanics in the knee joint without cartilage segmentation. Ann. Biomed. Eng. 2020, 48, 2965–2975. [Google Scholar] [CrossRef]
- Mochimaru, M.; Kouchi, M.; Fukui, Y.; Tsutsumi, E. Classification of 3D foot shape based on Inter-shape distance using the FFD method. Jpn. J. Ergon. 1997, 33, 229–234. [Google Scholar] [CrossRef][Green Version]
- Laporte, S.; Skalli, W.; de Guise, J.A.; Lavaste, F.; Mitton, D. A biplanar reconstruction method based on 2D and 3D Contours: Application to the distal femur. Comput. Methods Biomech. Biomed. Eng. 2003, 6, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Mitton, D.; Landry, C.; Veron, S.; Skalli, W.; Lavaste, F.; de Guise, J.A. 3D reconstruction method from biplanar radiography using non-stereocorresponding points and elastic deformable meshes. Med. Biol. Eng. Comput. 2000, 38, 133–139. [Google Scholar] [CrossRef] [PubMed]
- Mitulescu, A.; Semaan, I.; de Guise, J.A.; Leborgne, P.; Adamsbaum, C.; Skalli, W. Validation of the non-stereo corresponding points stereoradiographic 3D reconstruction technique. Med. Biol. Eng. Comput. 2001, 39, 152–158. [Google Scholar] [CrossRef]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
- Baka, N.; Kaptein, B.L.; de Bruijne, M.; van Walsum, T.; Gihphart, J.E.; Niessen, W.J.; Lelieveldt, B.P.F. 2D-3D shape reconstruction of the distal femur from stereo X-ray imaging using statistical shape models. Med. Image Anal. 2011, 15, 840–850. [Google Scholar] [CrossRef]
- Marra, M.A.; Vanheule, V.; Fluit, R.; Koopman, B.H.F.J.M.; Rasmussen, J.; Verdonschot, N.; Andersen, M.S. A subject-specific musculoskeletal modeling framework to predict in vivo mechanics of total knee arthroplasty. J. Biomech. Eng. 2015, 137, 020904. [Google Scholar] [CrossRef] [PubMed]
- Lerner, Z.F.; Demers, M.S.; Delp, S.L.; Browning, R.C. How tibiofemoral alignment and contact locations affect predictions of medial and lateral tibiofemoral contact forces. J. Biomech. 2015, 48, 644–650. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, S.; Mizu-uchi, H.; Okazaki, K.; Hamai, S.; Tashiro, Y.; Nakahara, H.; Iwamoto, Y. Two-dimensional planning can result in internal rotation of the femoral component in total knee arthroplasty. Knee Surg. Sports Traumatol. Arthrosc. 2014, 24, 229–235. [Google Scholar] [CrossRef] [PubMed]

| Error | 1 | 2 | 3 | Global |
|---|---|---|---|---|
| Mean | 0.080 | 0.124 | 0.055 | 0.087 |
| RMSE | 0.128 | 0.168 | 0.069 | 0.122 |
| Max. | 0.278 | 0.272 | 0.115 | 0.278 |
| Anatomical | |||||||||||||
| 1 | 2 | 3 | |||||||||||
| Error | Global | ||||||||||||
| Mean | 7.07 | 10.22 | 3.75 | 7.02 | |||||||||
| RMSE | 9.08 | 17.96 | 4.74 | 10.60 | |||||||||
| Max | 18.02 | 39.56 | 8.21 | 39.56 | |||||||||
| Scanning | |||||||||||||
| 1 | 2 | 3 | |||||||||||
| Coronal | Sagittal | Coronal | Sagittal | Coronal | Sagittal | ||||||||
| Error | HN | VY | HN | VT | HN | VT | HN | VT | HN | VT | HN | VT | Global |
| Mean | 0.63 | 3.10 | 1.49 | 2.09 | 0.78 | 3.76 | 2.06 | 4.98 | 0.60 | 3.81 | 4.94 | 3.22 | 2.62 |
| RMSE | 0.80 | 3.72 | 1.86 | 2.95 | 0.98 | 4.21 | 2.60 | 5.25 | 0.77 | 4.13 | 5.97 | 3.45 | 3.06 |
| Max. | 1.62 | 8.70 | 3.22 | 6.73 | 1.90 | 8.09 | 4.10 | 7.01 | 1.55 | 5.88 | 10.14 | 5.21 | 10.14 |
| Error | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | Global |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.53 | 0.18 | 0.36 | 1.43 | 1.84 | 1.17 | 2.31 | 1.92 | 1.88 | 1.66 | 3.13 | 1.56 | 2.05 | 1.54 |
| Max. | 3.60 | 6.78 | 6.20 | 9.55 | 10.97 | 7.58 | 12.88 | 10.45 | 11.99 | 9.90 | 8.36 | 6.21 | 6.26 | 12.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Fujita, I.; Yamauchi, K.; Hase, K. Feature-Based Modeling of Subject-Specific Lower Limb Skeletons from Medical Images. Biomechanics 2025, 5, 63. https://doi.org/10.3390/biomechanics5030063
Wang S, Fujita I, Yamauchi K, Hase K. Feature-Based Modeling of Subject-Specific Lower Limb Skeletons from Medical Images. Biomechanics. 2025; 5(3):63. https://doi.org/10.3390/biomechanics5030063
Chicago/Turabian StyleWang, Sentong, Itsuki Fujita, Koun Yamauchi, and Kazunori Hase. 2025. "Feature-Based Modeling of Subject-Specific Lower Limb Skeletons from Medical Images" Biomechanics 5, no. 3: 63. https://doi.org/10.3390/biomechanics5030063
APA StyleWang, S., Fujita, I., Yamauchi, K., & Hase, K. (2025). Feature-Based Modeling of Subject-Specific Lower Limb Skeletons from Medical Images. Biomechanics, 5(3), 63. https://doi.org/10.3390/biomechanics5030063






