Reliability and Validity of the Articulation Motion Assessment System Using a Rotary Encoder
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Protocol
2.3. Instrumentation
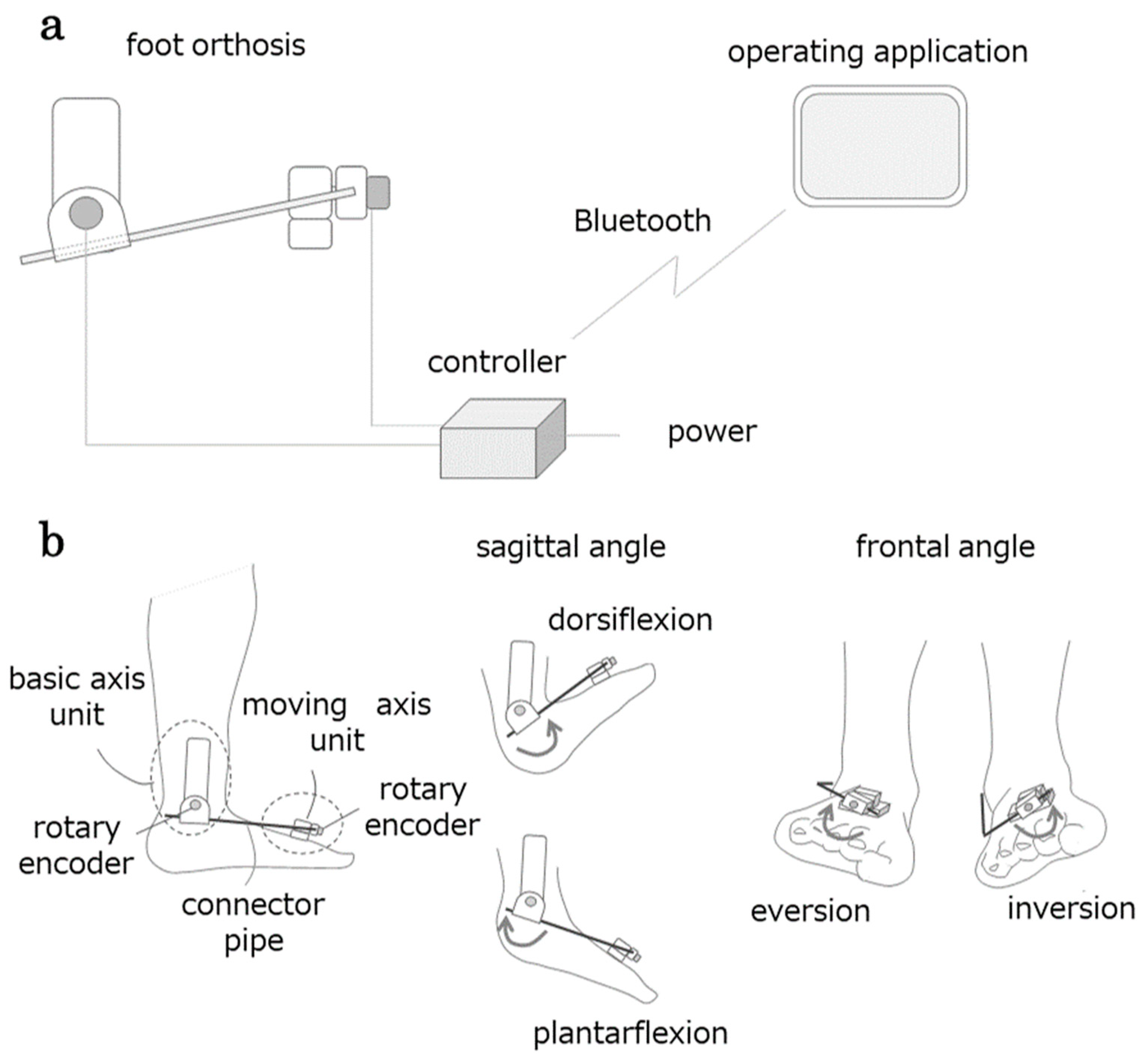
2.3.1. AMAS
2.3.2. A 2D Motion Analysis
2.3.3. Inertial Measurement Unit (IMU)
2.4. Data Analysis
3. Results
3.1. Validity
3.1.1. Comparisons Between Conditions
3.1.2. Criterion Validity
3.1.3. Root Mean Squared Error (RMSE)
3.2. Reliability
3.3. Consistency
4. Discussion
5. Conclusions
6. Practical Applications
7. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schmitt, D. Insights into the evolution of human bipedalism from experimental studies of humans and other primates. J. Exp. Biol. 2003, 206, 1437–1448. [Google Scholar] [CrossRef] [PubMed]
- Mirelman, A.; Shema, S.; Maidan, I.; Hausdorff, J.M. Gait. Handb. Clin. Neurol. 2018, 159, 119–134. [Google Scholar] [CrossRef]
- Baker, J.M. Gait disorders. Am. J. Med. 2018, 131, 602–607. [Google Scholar] [CrossRef]
- Perry, J.; Garrett, M.; Gronley, J.K.; Mulroy, S.J. Classification of walking handicap in the stroke population. Stroke 1995, 26, 982–989. [Google Scholar] [CrossRef] [PubMed]
- Schmid, A.; Duncan, P.W.; Studenski, S.; Lai, S.M.; Richards, L.; Perera, S.; Wu, S.S. Improvements in speed-based gait classifications are meaningful. Stroke 2007, 38, 2096–2100. [Google Scholar] [CrossRef] [PubMed]
- Graf, A.; Judge, J.O.; Õunpuu, S.; Thelen, D.G. The effect of walking speed on lower-extremity joint powers among elderly adults who exhibit low physical performance. Arch. Phys. Med. Rehabil. 2005, 86, 2177–2183. [Google Scholar] [CrossRef] [PubMed]
- Lamontagne, A.; Richards, C.L.; Malouin, F. Coactivation during gait as an adaptive behavior after stroke. J. Electromyogr. Kinesiol. 2000, 10, 407–415. [Google Scholar] [CrossRef] [PubMed]
- Allen, J.L.; Kautz, S.A.; Neptune, R.R. The influence of merged muscle excitation modules on post-stroke hemiparetic walking performance. Clin. Biomech. 2013, 28, 697–704. [Google Scholar] [CrossRef] [PubMed]
- Wade, L.; Birch, J.; Farris, D.J. Walking with increasing acceleration is achieved by tuning ankle torque onset timing and rate of torque development. J. R. Soc. Interface 2022, 19, 20220035. [Google Scholar] [CrossRef]
- Morasso, P. A Vexing question in motor control: The degrees of freedom problem. Front. Bioeng. Biotechnol. 2022, 9, 783501. [Google Scholar] [CrossRef]
- Bernstein, N.A. The Coordination and Regulation of Movements; Pergamon Press: London, UK, 1967; pp. 143–168. [Google Scholar]
- Jenkyn, T.R.; Anas, K.; Nichol, A. Foot segment kinematics during normal walking using a multisegment model of the foot and ankle complex. J. Biomech. Eng. 2009, 131, 034504. [Google Scholar] [CrossRef]
- Farris, D.J.; Kelly, L.A.; Cresswell, A.G.; Lichtwark, G.A. The functional importance of human foot muscles for bipedal locomotion. Proc. Natl. Acad. Sci. USA 2019, 116, 1645–1650. [Google Scholar] [CrossRef] [PubMed]
- Yokoyama, H.; Kaneko, N.; Ogawa, T.; Kawashima, N.; Watanabe, K.; Nakazawa, K. Cortical correlates of locomotor muscle synergy activation in humans: An electroencephalographic decoding study. iScience 2019, 15, 623–639. [Google Scholar] [CrossRef]
- Churchland, M.M.; Cunningham, J.P.; Kaufman, M.T.; Foster, J.D.; Nuyujukian, P.; Ryu, S.I.; Shenoy, K.V. Neural population dynamics during reaching. Nature 2012, 487, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Suresh, A.K.; Goodman, J.M.; Okorokova, E.V.; Kaufman, M.; Hatsopoulos, N.G.; Bensmaia, S.J.; Anatomy; Biology, Q.; Behavior, H.; States, U. Neural population dynamics in motor cortex are different for reach and grasp. eLife 2020, 9, 58848. [Google Scholar] [CrossRef] [PubMed]
- McLoughlin, J. Ten guiding principles for movement training in neurorehabilitation. OpenPhysio J. 2020, 10, 1–17. [Google Scholar] [CrossRef]
- Mehrabi, N.; Schwartz, M.H.; Steele, K.M. Can altered muscle synergies control unimpaired gait? J. Biomech. 2019, 90, 84–91. [Google Scholar] [CrossRef]
- Petersen, T.H.; Willerslev-Olsen, M.; Conway, B.A.; Nielsen, J.B. The motor cortex drives the muscles during walking in human subjects. J. Physiol. 2012, 590, 2443–2452. [Google Scholar] [CrossRef]
- Song, S.; Desai, R.; Geyer, H. Integration of an adaptive swing control into a neuromuscular human walking model. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 4915–4918. [Google Scholar] [CrossRef]
- Akazawa, K.; Fuj, K. Theory of muscle contraction and motor control. Adv. Robot. 1986, 1, 379–390. [Google Scholar] [CrossRef]
- Takei, T.; Lomber, S.G.; Cook, D.J.; Scott, S.H. Transient deactivation of dorsal premotor cortex or parietal area 5 impairs feedback control of the limb in macaques. Curr. Biol. 2021, 31, 1476–1487.e5. [Google Scholar] [CrossRef]
- Minassian, K.; Hofstoetter, U.S.; Dzeladini, F.; Guertin, P.A.; Ijspeert, A. The human central pattern generator for locomotion: Does it exist and contribute to walking? Neuroscientist 2017, 23, 649–663. [Google Scholar] [CrossRef]
- Leiras, R.; Cregg, J.M.; Kiehn, O. Brainstem circuits for locomotion. Annu. Rev. Neurosci. 2022, 45, 63–85. [Google Scholar] [CrossRef]
- Krauth, R.; Schwertner, J.; Vogt, S.; Lindquist, S.; Sailer, M.; Sickert, A.; Lamprecht, J.; Perdikis, S.; Corbet, T.; Millán, J.d.R.; et al. Cortico-muscular coherence is reduced acutely post-stroke and increases bilaterally during motor recovery: A pilot study. Front. Neurol. 2019, 10, 126. [Google Scholar] [CrossRef]
- Liu, J.; Sheng, Y.; Liu, H. Corticomuscular coherence and its applications: A review. Front. Hum. Neurosci. 2019, 13, 100. [Google Scholar] [CrossRef]
- Brockett, C.L.; Chapman, G.J. Biomechanics of the ankle. Orthop. Trauma 2016, 30, 232–238. [Google Scholar] [CrossRef]
- Kim, H.; Cho, J.-E.; Seo, K.-J.; Lee, J. Bilateral ankle deformities affects gait kinematics in chronic stroke patients. Front. Neurol. 2023, 14, 1078064. [Google Scholar] [CrossRef] [PubMed]
- Hong, W.-H.; Wang, C.-M.; Chen, C.-K.; Wu, K.P.-H.; Kang, C.-F.; Tang, S.F. Kinematic features of rear-foot motion using anterior and posterior ankle-foot orthoses in stroke patients with hemiplegic gait. Arch. Phys. Med. Rehabil. 2010, 91, 1862–1868. [Google Scholar] [CrossRef]
- Palumbo, A.; Vizza, P.; Calabrese, B.; Ielpo, N. Biopotential signal monitoring systems in rehabilitation: A review. Sensors 2021, 21, 7172. [Google Scholar] [CrossRef]
- Munro, A.; Herrington, L.; Carolan, M. Reliability of 2-dimensional video assessment of frontal-plane dynamic knee valgus during common athletic screening tasks. J. Sport Rehabil. 2012, 21, 7–11. [Google Scholar] [CrossRef]
- Schurr, S.A.; Marshall, A.N.; Resch, J.E.; A Saliba, S. Two-dimensional video analysis is comparable to 3D motion capture in lower extremity movement assessment. Int. J. Sports Phys. Ther. 2017, 12, 163–172. [Google Scholar]
- Corazza, S.; Mündermann, L.; Gambaretto, E.; Ferrigno, G.; Andriacchi, T.P. Markerless motion capture through visual hull, articulated ICP and subject specific model generation. Int. J. Comput. Vis. 2010, 87, 156–169. [Google Scholar] [CrossRef]
- Simon, S.R. Quantification of human motion: Gait analysis—Benefits and limitations to its application to clinical problems. J. Biomech. 2004, 37, 1869–1880. [Google Scholar] [CrossRef]
- Michelini, A.; Eshraghi, A.; Andrysek, J. Two-dimensional video gait analysis: A systematic review of reliability, validity, and best practice considerations. Prosthet. Orthot. Int. 2020, 44, 245–262. [Google Scholar] [CrossRef] [PubMed]
- Dingenen, B.; Malliaras, P.; Janssen, T.; Ceyssens, L.; Vanelderen, R.; Barton, C.J. Two-dimensional video analysis can discriminate differences in running kinematics between recreational runners with and without running-related knee injury. Phys. Ther. Sport 2019, 38, 184–191. [Google Scholar] [CrossRef] [PubMed]
- Cordova, M.L.; Dorrough, J.L.; Kious, K.; Ingersoll, C.D.; Merrick, M.A. Prophylactic ankle bracing reduces rearfoot motion during sudden inversion. Scand. J. Med. Sci. Sports 2007, 17, 216–222. [Google Scholar] [CrossRef] [PubMed]
- Laidig, D.; Schauer, T.; Seel, T. Exploiting kinematic constraints to compensate magnetic disturbances when calcu-lating joint angles of approximate hinge joints from orientation estimates of inertial sensors. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 971–976. [Google Scholar] [CrossRef]
- McGrath, T.; Stirling, L. Body-Worn IMU-Based Human hip and knee kinematics estimation during treadmill walking. Sensors 2022, 22, 2544. [Google Scholar] [CrossRef]
- Taetz, B.; Bleser, G.; Miezal, M. Towards self-calibrating inertial body motion capture. Int. Conf. Inf. Fusion 2016, 19, 1751–1759. [Google Scholar]
- Chan, P.Y.; Ripin, Z.M.; Halim, S.A.; Tharakan, J.; Muzaimi, M.; Ng, K.S.; Kamarudin, M.I.; Eow, G.B.; Hor, J.Y.; Tan, K.; et al. An in-laboratory validity and reliability tested system for quantifying hand-arm tremor in motions. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 460–467. [Google Scholar] [CrossRef]
- Jaramillo, I.E.; Jeong, J.G.; Lopez, P.R.; Lee, C.-H.; Kang, D.-Y.; Ha, T.-J.; Oh, J.-H.; Jung, H.; Lee, J.H.; Lee, W.H.; et al. Real-time human activity recognition with IMU and encoder sensors in wearable exoskeleton robot via deep learning networks. Sensors 2022, 22, 9690. [Google Scholar] [CrossRef]
- Yang, J.-F.; Scholz, J.P. Learning a throwing task is associated with differential changes in the use of motor abundance. Exp. Brain Res. 2005, 163, 137–158. [Google Scholar] [CrossRef] [PubMed]
- Tseng, Y.-W.; Scholz, J.P.; Schöner, G.; Hotchkiss, L. Effect of accuracy constraint on joint coordination during pointing movements. Exp. Brain Res. 2003, 149, 276–288. [Google Scholar] [CrossRef]
- Gielen, C.; van Bolhuis, B.; Theeuwen, M. On the control of biologically and kinematically redundant manipulators. Hum. Mov. Sci. 1995, 14, 487–509. [Google Scholar] [CrossRef]
- Koster, B.; Deuschl, G.; Lauk, M.; Timmer, J.; Guschlbauer, B.; Lücking, C.H. Essential tremor and cerebellar dysfunction: Abnormal ballistic movements. J. Neurol. Neurosurg. Psychiatry 2002, 73, 400–405. [Google Scholar] [CrossRef] [PubMed]
- Matsugi, A.; Nishishita, S.; Bando, K.; Kikuchi, Y.; Tsujimoto, K.; Tanabe, Y.; Yoshida, N.; Tanaka, H.; Douchi, S.; Honda, T.; et al. Excessive excitability of inhibitory cortical circuit and disturbance of ballistic targeting movement in degenerative cerebellar ataxia. Sci. Rep. 2023, 13, 13917. [Google Scholar] [CrossRef]
- Mihcin, S. Simultaneous validation of wearable motion capture system for lower body applications: Over single plane range of motion (ROM) and gait activities. Biomed. Eng. Biomed. Tech. 2022, 67, 185–199. [Google Scholar] [CrossRef] [PubMed]
- McCurdy, K.; Langford, G. Comparison of unilateral squat strength between the dominant and non-dominant leg in men and women. J. Sports Sci. Med. 2005, 4, 153–159. [Google Scholar] [PubMed]
- Kapreli, E.; Athanasopoulos, S.; Papathanasiou, M.; Van Hecke, P.; Strimpakos, N.; Gouliamos, A.; Peeters, R.; Sunaert, S. Lateralization of brain activity during lower limb joints movement. An fMRI study. NeuroImage 2006, 32, 1709–1721. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.H.; Hijmans, J.M.; Moeini, F.; Rajabi, R.; Ferber, R.; van der Worp, H.; Zwerver, J. Validity and reliability of a smartphone motion analysis app for lower limb kinematics during treadmill running. Phys. Ther. Sport 2020, 43, 27–35. [Google Scholar] [CrossRef]
- Choo, C.Z.Y.; Chow, J.Y.; Komar, J. Validation of the Perception Neuron system for full-body motion capture. PLoS ONE 2022, 17, e0262730. [Google Scholar] [CrossRef] [PubMed]
- Mould, R.F. Introductory Medical Statistics, 3rd ed.; Boca Raton: London, UK, 1998; pp. 177–194. [Google Scholar]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Brookshaw, M.; Sexton, A.; McGibbon, C.A. Reliability and validity of a novel wearable device for measuring elbow strength. Sensors 2020, 20, 3412. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Routledge Academic, Lawrence Erlbaum Associates: New York, NY, USA, 1988; pp. 75–105. [Google Scholar]
- Heuvelmans, P.; Benjaminse, A.; Bolt, R.; Baumeister, J.; Otten, E.; Gokeler, A. Concurrent validation of the Noraxon MyoMotion wearable inertial sensors in change-of-direction and jump-landing tasks. Sports Biomech. 2022, 3, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Rekant, J.; Rothenberger, S.; Chambers, A. Inertial measurement unit-based motion capture to replace camera-based systems for assessing gait in healthy young adults: Proceed with caution. Meas. Sensors 2022, 23, 100396. [Google Scholar] [CrossRef] [PubMed]
- Walmsley, C.P.; Williams, S.A.; Grisbrook, T.; Elliott, C.; Imms, C.; Campbell, A. Measurement of upper limb range of motion using wearable sensors: A systematic review. Sports Med. Open 2018, 4, 53. [Google Scholar] [CrossRef] [PubMed]
- McGrath, T.; Stirling, L. Body-Worn IMU Human skeletal pose estimation using a factor graph-based optimization framework. Sensors 2020, 20, 6887. [Google Scholar] [CrossRef]
- de Vries, W.; Veeger, H.; Baten, C.; van der Helm, F. Magnetic distortion in motion labs, implications for validating inertial magnetic sensors. Gait Posture 2009, 29, 535–541. [Google Scholar] [CrossRef]
- Sprager, S.; Juric, M.B. Inertial sensor-based gait recognition: A review. Sensors 2015, 15, 22089–22127. [Google Scholar] [CrossRef]
- Freeman, C.T.; Rogers, E.; Hughes, A.-M.; Burridge, J.H.; Meadmore, K.L. Iterative learning control in health care: Electrical stimulation and robotic-assisted upper-limb stroke rehabilitation. IEEE Control. Syst. 2012, 32, 18–43. [Google Scholar] [CrossRef]
- Sharma, N.; Stegath, K.; Gregory, C.M.; Dixon, W.E. Nonlinear neuromuscular electrical stimulation tracking control of a human limb. IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 17, 576–584. [Google Scholar] [CrossRef]
- Allen, M.; Zhong, Q.; Kirsch, N.; Dani, A.; Clark, W.W.; Sharma, N. A nonlinear dynamics-based estimator for functional electrical stimulation: Preliminary results from lower-leg extension experiments. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 2365–2374. [Google Scholar] [CrossRef]
- McGinley, J.L.; Baker, R.; Wolfe, R.; Morris, M.E. The reliability of three-dimensional kinematic gait measurements: A systematic review. Gait Posture 2009, 29, 360–369. [Google Scholar] [CrossRef] [PubMed]
- Kwakkel, G.; Van Wegen, E.; Burridge, J.; Winstein, C.; van Dokkum, L.; Murphy, M.A.; Levin, M.; Krakauer, J. Standardised measurement of quality of upper limb movement after stroke: Consensus-based core recommendations from the Second Stroke Recovery and Rehabilitation Roundtable. Int. J. Stroke 2019, 14, 783–791. [Google Scholar] [CrossRef]
- Levin, M.F.; Kleim, J.A.; Wolf, S.L. What do motor “recovery” and “compensation” mean in patients following stroke? Neurorehabilit. Neural Repair 2008, 23, 313–319. [Google Scholar] [CrossRef]
- Bernhardt, J.; Hayward, K.S.; Kwakkel, G.; Ward, N.S.; Wolf, S.L.; Borschmann, K.; Krakauer, J.W.; Boyd, L.A.; Carmichael, S.T.; Corbett, D.; et al. Agreed definitions and a shared vision for new standards in stroke recovery research: The Stroke Recovery and Rehabilitation Roundtable taskforce. Int. J. Stroke 2017, 12, 444–450. [Google Scholar] [CrossRef] [PubMed]
- Maura, R.M.; Parra, S.R.; Stevens, R.E.; Weeks, D.L.; Wolbrecht, E.T.; Perry, J.C. Literature review of stroke assessment for upper-extremity physical function via EEG, EMG, kinematic, and kinetic measurements and their reliability. J. Neuroeng. Rehabil. 2023, 20, 21. [Google Scholar] [CrossRef]


| Subjective Motor Speed | ||||||||
|---|---|---|---|---|---|---|---|---|
| Comfortable | Slow | |||||||
| Activity | Conditions | System | ρ | RMSE | ρ | RMSE | ρ | RMSE |
| Dorsiflexion | maximum | AMAS | 0.69 ** | 9.22 | 0.65 ** | 9.47 | 0.72 ** | 9.04 |
| IMU | 0.44 ** | 17.3 | 0.41 ** | 22.23 | 0.47 ** | 12.73 | ||
| mild | AMAS | 0.54 ** | 7.29 | 0.50 ** | 7.35 | 0.58 ** | 7.25 | |
| IMU | 0.35 ** | 10.19 | 0.28 ** | 10.02 | 0.40 ** | 10.31 | ||
| Plantarflexion | maximum | AMAS | 0.53 ** | 16.23 | 0.66 ** | 14.32 | 0.45 ** | 17.33 |
| IMU | 0.47 ** | 21.26 | 0.38 ** | 22.34 | 0.54 ** | 20.55 | ||
| mild | AMAS | 0.53 ** | 9.95 | 0.59 ** | 9.97 | 0.48 ** | 9.94 | |
| IMU | 0.16 ** | 19.66 | 0.17 ** | 17.12 | 0.16 ** | 21.23 | ||
| Subjective Motor Speed | ||||||||
|---|---|---|---|---|---|---|---|---|
| Comfortable | Slow | |||||||
| Activity | Conditions | System | ρ | RMSE | ρ | RMSE | ρ | RMSE |
| Inversion | maximum | AMAS | 0.69 ** | 14.49 | 0.72 ** | 14.64 | 0.68 ** | 14.38 |
| IMU | 0.02 | 28.82 | −0.08 * | 27.94 | 0.08 ** | 29.42 | ||
| mild | AMAS | 0.55 ** | 13.11 | 0.63 ** | 12.29 | 0.49 ** | 13.63 | |
| IMU | 0.03 | 28.43 | −0.07 * | 29.78 | 0.10 ** | 27.49 | ||
| Eversion | maximum | AMAS | 0.46 ** | 14.74 | 0.39 ** | 15.29 | 0.52 ** | 14.31 |
| IMU | 0.01 | 35.7 | 0.01 | 38.23 | 0 | 33.72 | ||
| mild | AMAS | 0.50 ** | 11.19 | 0.55 ** | 11.15 | 0.46 ** | 11.22 | |
| IMU | −0.06 * | 34.96 | −0.02 | 41.86 | −0.07 * | 28.77 | ||
| Subjective Motor Speed | ||||||||
|---|---|---|---|---|---|---|---|---|
| Comfortable | Slow | |||||||
| Activity | Conditions | System | ρ | RMSE | ρ | RMSE | ρ | RMSE |
| Inversion | maximum | AMAS | 0.48 ** | 17.46 | 0.50 ** | 17.8 | 0.48 ** | 17.22 |
| IMU | 0.18 ** | 24.69 | 0.19 ** | 22.44 | 0.18 ** | 26.16 | ||
| mild | AMAS | 0.49 ** | 12.89 | 0.52 ** | 12.75 | 0.49 ** | 12.98 | |
| IMU | 0.31 ** | 26.32 | 0.23 ** | 27 | 0.35 ** | 25.85 | ||
| Eversion | maximum | AMAS | 0.07 ** | 12.02 | 0.04 | 12.5 | 0.11 ** | 11.65 |
| IMU | 0.02 | 27.49 | 0.13 ** | 28.7 | −0.09 ** | 26.55 | ||
| mild | AMAS | −0.05 * | 11.83 | −0.07 * | 12.49 | −0.04 | 11.32 | |
| IMU | 0.04 | 28.17 | 0.11 ** | 34.04 | −0.03 | 22.84 | ||
| Comfortable | Slow | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ICC | 95% CI | ICC | 95% CI | ||||||
| Lower | Upper | Lower | Upper | ||||||
| Dorsiflexion | maximum | 0.83 | ** | 0.68 | 0.93 | 0.98 | ** | 0.95 | 0.99 |
| mild | 0.95 | ** | 0.89 | 0.98 | 0.93 | ** | 0.87 | 0.98 | |
| Plantarflexion | maximum | 0.93 | ** | 0.85 | 0.97 | 0.87 | ** | 0.75 | 0.95 |
| mild | 0.86 | ** | 0.73 | 0.94 | 0.76 | ** | 0.58 | 0.9 | |
| Inversion | maximum | 0.96 | ** | 0.91 | 0.98 | 0.98 | ** | 0.96 | 0.99 |
| mild | 0.97 | ** | 0.94 | 0.99 | 0.97 | ** | 0.94 | 0.99 | |
| Eversion | maximum | 0.76 | ** | 0.58 | 0.9 | 0.86 | ** | 0.73 | 0.95 |
| mild | 0.9 | ** | 0.8 | 0.96 | 0.94 | ** | 0.88 | 0.98 | |
| Comfortable | Slow | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ICC | 95% CI | ICC | 95% CI | ||||||
| Lower | Upper | Lower | Upper | ||||||
| Dorsiflexion | maximum | 0.96 | ** | 0.91 | 0.99 | 1 | ** | 0.99 | 1 |
| mild | 0.99 | ** | 0.98 | 1 | 0.99 | ** | 0.97 | 0.99 | |
| Plantarflexion | maximum | 0.98 | ** | 0.97 | 0.99 | 0.97 | ** | 0.94 | 0.99 |
| mild | 0.97 | ** | 0.93 | 0.99 | 0.94 | ** | 0.87 | 0.98 | |
| Inversion | maximum | 0.99 | ** | 0.98 | 1 | 1 | ** | 0.99 | 1 |
| mild | 0.99 | ** | 0.99 | 1 | 0.99 | ** | 0.99 | 1 | |
| Eversion | maximum | 0.94 | ** | 0.87 | 0.98 | 0.97 | ** | 0.93 | 0.99 |
| mild | 0.98 | ** | 0.95 | 0.99 | 0.99 | ** | 0.97 | 1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ito, H.; Yamaguchi, H.; Inoue, M.; Nagano, H.; Kitai, K.; Morita, K.; Kodama, T. Reliability and Validity of the Articulation Motion Assessment System Using a Rotary Encoder. Biomechanics 2025, 5, 2. https://doi.org/10.3390/biomechanics5010002
Ito H, Yamaguchi H, Inoue M, Nagano H, Kitai K, Morita K, Kodama T. Reliability and Validity of the Articulation Motion Assessment System Using a Rotary Encoder. Biomechanics. 2025; 5(1):2. https://doi.org/10.3390/biomechanics5010002
Chicago/Turabian StyleIto, Hiroki, Hideaki Yamaguchi, Mari Inoue, Hikaru Nagano, Ken Kitai, Kiichiro Morita, and Takayuki Kodama. 2025. "Reliability and Validity of the Articulation Motion Assessment System Using a Rotary Encoder" Biomechanics 5, no. 1: 2. https://doi.org/10.3390/biomechanics5010002
APA StyleIto, H., Yamaguchi, H., Inoue, M., Nagano, H., Kitai, K., Morita, K., & Kodama, T. (2025). Reliability and Validity of the Articulation Motion Assessment System Using a Rotary Encoder. Biomechanics, 5(1), 2. https://doi.org/10.3390/biomechanics5010002






