Next Article in Journal
The Kinematics and Biomechanics for Non-Contiguous Anterior Cervical Discectomy and Fusion, Cervical Disc Arthroplasty, and Hybrid Cervical Surgery: A Systematic Review
Next Article in Special Issue
Assessing the Shooting Velocity According to the Shooting Technique in Elite Youth Rink Hockey Players
Previous Article in Journal / Special Issue
Performance, Perceptual and Reaction Skills and Neuromuscular Control Indicators of High-Level Karate Athletes in the Execution of the Gyaku Tsuki Punch
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Biomechanics
Volume 3
Issue 3
10.3390/biomechanics3030035
biomechanics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Joint Moment Responses to Different Modes of Augmented Visual Feedback of Joint Kinematics during Two-Legged Squat Training

by
Raviraj Nataraj
1,2,*,
Sean Patrick Sanford
1,2 and
Mingxiao Liu
1,2
1
Department of Biomedical Engineering, Stevens Institute of Technology, Hoboken, NJ 07030, USA
2
Movement Control Rehabilitation Laboratory, Altorfer Complex, Stevens Institute of Technology, Hoboken, NJ 07030, USA
*
Author to whom correspondence should be addressed.
Biomechanics 2023, 3(3), 425-442; https://doi.org/10.3390/biomechanics3030035
Submission received: 2 July 2023 / Revised: 14 August 2023 / Accepted: 22 August 2023 / Published: 7 September 2023
(This article belongs to the Collection Locomotion Biomechanics and Motor Control)
Browse Figures
Versions Notes

Abstract

:
This study examined the effects of different modes of augmented visual feedback of joint kinematics on the emerging joint moment patterns during the two-legged squat maneuver. Training with augmented visual feedback supports improved kinematic performance of maneuvers related to sports or daily activities. Despite being representative of intrinsic motor actions, joint moments are not traditionally evaluated with kinematic feedback training. Furthermore, stabilizing joint moment patterns with physical training is beneficial to rehabilitating joint-level function (e.g., targeted strengthening and conditioning of muscles articulating that joint). Participants were presented with different modes of augmented visual feedback to track a target squat-motion trajectory. The feedback modes varied along features of complexity (i.e., number of segment trajectories shown) and body representation (i.e., trajectories shown as sinusoids versus dynamic stick-figure avatars). Our results indicated that mean values and variability (trial-to-trial standard deviations) of joint moments are significantly (p < 0.05) altered depending on the visual feedback features being applied, the specific joint (ankle, knee, hip), and the squat movement phase (early, middle, or late time window). This study should incentivize more optimal delivery of visual guidance during rehabilitative training with computerized interfaces (e.g., virtual reality).

1. Introduction

Augmented sensory feedback for motion guidance can improve functional performance during and after training [1] associated with rehabilitation [2]. Augmented visual feedback about one’s movements may be provided through various tools, from simple mirrors [3] to highly customizable computerized interfaces (e.g., large-screen displays [4,5] and headsets [6]). Such feedback guidance can improve movement techniques [7] for motor rehabilitation [4,5,8] and minimize the risk of re-injury [9,10]. Augmented feedback can be used to acquire complex motor skills in sports [11] or play instruments [12] for populations that are healthy, diseased, or athletic [13] In addition, augmented cues through virtual reality can cognitively engage and motivate persons to participate in more therapeutic activities [14]. Thus, there is a broad scope of applications and tools in which augmented visual feedback of motion can be leveraged to support better motor performance. However, the impact of augmented visual feedback about joint kinematics upon the intrinsic joint kinetics (e.g., joint moments) that create the observed motions is largely unknown. While internal kinetics and observed motions are naturally coupled through bodily dynamics [15], their relative variabilities can diverge with complex multi-segment movements. Even for stereotypical functions like walking, variability in joint kinetics can increase as a compensatory mechanism to maintain target kinematic profiles pending the functional role and articulating muscles of that joint [16]. Thus, augmented feedback about kinematics may also uniquely impact the underlying joint kinetics during the training of locomotor function [17,18,19].
While joint kinetics can be generally sensitive to external cueing [20], it is unclear if they respond uniquely to particular features in augmented feedback about joint kinematics. Features are the defining characteristics of how the feedback is being provided. These feedback features include what information is provided, how much, and how often it is delivered. Suppose joint kinetics have specific dependencies on feedback features. In that case, we may better consider how we present cues for typically kinematics-focused guidance paradigms [10,21] in rehabilitation to generate more stable patterns in the underlying joint kinetics. The specific features of feedback cues for joint kinematics can then be considered in optimizing task-specific motor training through improved inter-limb coordination [22] and efficiency [16] of joint kinetics. Most importantly, regarding motor rehabilitation, stable and consistent joint kinetic function during physical training may facilitate better outcomes in targeting increases in function and stability (e.g., hip muscle strengthening, recovery after ligament injury) at particular joints [23,24] or reducing the motor variability associated with systemic dysfunction [25,26] (e.g., multiple sclerosis, arthritis).
Understanding how feature-level variations in augmented feedback typically about kinematics [21] can impact joint kinetics may aid in designing rehabilitative training paradigms for broadly improving joint function [27]. The features in augmented feedback of kinematics are temporal and spatial. Spatial features include the provision of target motion trajectories across individual joints and body segments in relative positions to one another. Temporal features include providing guidance feedback continuously or intermittently [5,28,29]. The associated effects of these features should be assessed through changes in motor output across phases of the movement [30]. Furthermore, features in feedback to guide body movements can reflect themselves in variations of complexity and level of body representation. Complexity denotes how much information about the movement is provided. While more information with feedback can theoretically support more accuracy for complex movements [31], it can risk cognitive overloading that worsens performance [1]. Body representation is an essential consideration for movement rehabilitation protocols, especially in the context of visual feedback [32]. Congruency in body representation with feedback is crucial to optimally modulate the reliance on external cues [32,33] and provide clarity of self-recognition in making said movements [34]. Of particular interest is understanding how functional measures with motor rehabilitation are likely to respond to these features. Key functional measures include joint moment means, as an indicator of skeletal muscle function [35] and joint structural health [36], and joint moment variability, as a benchmark for gains in functional capabilities [37,38,39].
Our laboratory has previously investigated the kinematic performance of the two-legged squat under the guidance of various visual feedback modes [4,5]. We define a mode as the specific combination of feedback features applied with training guidance. Such feedback features included complexity and level of body representation of target trajectories of joint kinematics during the squat. Kinematic performance was measured as accuracy (minimal error) and consistency (minimal standard deviation of error) in tracking visual cues expressing target segmental kinematics. The feedback feature of complexity was increased when participants were presented with more body segment trajectories to match concurrently. We also observed improved performance with more complex feedback [4] when coupled with the feature of greater body representation, i.e., joint motion trajectories shown through dynamic stick figure compared to being expressed more abstractly through sinusoids to be traced. We posited that the stick figure facilitated improved performance through a greater sense of embodiment [40].
In this study, we applied inverse dynamics [41] retrospectively to the kinematic (joint angles) and external force (ground reactions) data to compute and evaluate changes in joint moments with various modes of augmented visual feedback to guide squat kinematics. We report results for flexion-extension moments at the hip, knee, and ankle joints produced under four distinct modes of visual feedback. Ultimately, we examined features in augmented visual feedback with clear joint-level implications, i.e., complexity (number of joints displayed concurrently) and body representation (joint kinematics presented as sinusoids or explicitly as stick-figure joints). We posited that these feedback features would significantly and uniquely affect moments at the hip, knee, and ankle joints, given their unique functional roles in load-bearing and balance for the two-legged squat [42,43]. Across feedback modes, we analyzed shifts in mean joint moment values and changes in joint moment variability. With our experimental design, we mainly tested the following hypotheses: (1) Features of visual feedback will significantly affect joint moment mean and variability values; (2) More complex feedback increases joint moment variability; (3) Increased body representation in the feedback reduces joint moment variability. Furthermore, we examined how joint moment effects due to visual feedback features change across specific joints (spatial) and time phases (temporal) of the squat movement. As such, we conduct two-factor analyses at three levels of increasing specificity: (1) across all joints and time phases in the aggregate (overall), (2) across individual joints, and (3) across individual time phases (i.e., early, middle/target, late) of the movement for each joint.

2. Materials and Methods

2.1. Participants

Eighteen able-bodied participants (12 males: 20.4 ± 0.9 years in age, 179 ± 5.0 cm in height, 74.1 ± 7.9 kg in weight. 6 females: 19.7 ± 1.1 years in age, 166 ± 5.1 cm in height, 61.6 ± 7.6 kg in weight) completed this study approved by the local (Stevens Institute of Technology) Institutional Review Board. All participants signed informed consent to participate voluntarily, and none reported any injury to the lower body that would adversely affect their ability to perform the squat maneuver. A power analysis with pilot data indicated twelve participants would generate significant differences across visual feedback modes for alpha equal to 0.05 at 90% power (Cohen’s effect size of 0.5). Participants were expected to be able-bodied with relatively little (minimal to no weekly exercising) experience with the squat maneuver. Varsity athletes were excluded due to their advanced skill with physical training exercises, as they may be more insensitive to external cues while already performing at exceptionally high levels. Other exclusion criteria included (1) Previous surgery to any lower extremity or of the spine/neck; (2) Chronic pain of any lower extremity or the back/neck within the last three months; (3) A musculoskeletal or neurological disease that affects normal gait or standing function; (4) Sub-normal vision that is not correctable; (5) Any cardiovascular issues that make squat exercises difficult; (6) Inability to regularly squat to the maximum squat depth of 70 degrees (angle between the thigh and vertical). The squat depth of 70 degrees is short of a parallel squat (90 degrees) or full squat [44].

2.2. Experimental Task

Visual feedback was provided to guide the performance of a 4-s squat cycle, which begins and returns to an erect standing position. Participants controlled traces or avatars with their movements to match a target movement trajectory displayed over a 4-s time course, thereby naturally adhering participants to the 4-s squat cycle. Any temporal or spatial deviations similarly manifested in errors (i.e., differences between actual and target movement trajectories). The target movement trajectory for each body segment (shank, thigh, and torso) was a symmetric sinusoid representing flexion-extension angular positions during the squat cycle projected to the sagittal plane. The sagittal plane is of primary interest since squat kinematics are most prevalent in this plane [45]. For bilateral body segments (i.e., shank, thigh), the left and right side segments were averaged for projection due to the relatively high degree of symmetry observed for squatting by healthy persons [46]. The maximum squat depth of the target trajectory occurred at the cycle midpoint (i.e., squat cycle time = 2 s). Ideally, the maximum squat depth occurs at the temporal midpoint between when the participant is at the initial erect standing position (at time = 0 s) and return to the erect standing position to complete the squat cycle (at time = 4 s). Angular motions of all three segments were tracked utilizing marker-based motion capture. These motions were displayed against target trajectories as visual feedback to participants in real time.
As described below (abstract versus representative modes), the sinusoidal motion trajectories of body segments are displayed explicitly as sinusoidal traces or stick-figure avatars undergoing the same angular motions. The participant controls the up-down position for sinusoidal trace tracking from their squat depth. In contrast, the left-right position of the participant trace moves at a constant speed across the displayed screen for four seconds, again encouraging participants to perform approximately a four-second squat cycle. The target trajectories are displayed as a fixed sinusoid that participants attempt to track with their moving trace. For stick-figure tracking, both the target and participant trajectories are dynamic and superimposed on top of each other, with participants tasked to follow the target segment trajectories, whose motions again last precisely four seconds.
The primary performance objective for each participant was to move the thigh segment’s angular position to match the target trajectory. The thigh segment was chosen as the primary segment of interest for performance tracking since it undergoes the largest angular changes in dictating knee joint dynamics, the most common rehabilitation target with squat training [47].

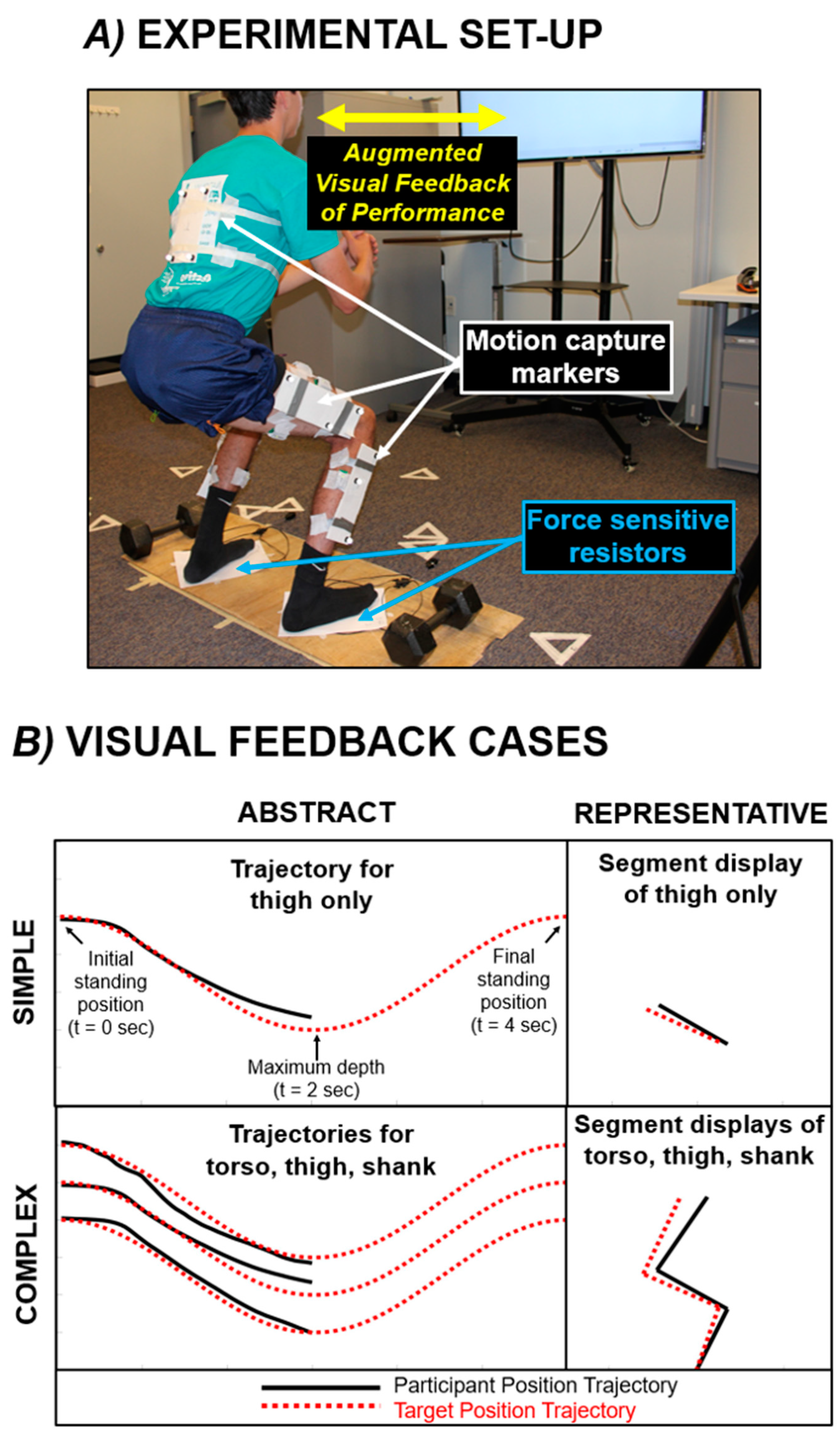
2.3. Experimental Set-Up for Data Collection

As shown in Figure 1A, data collected with each trial included marker-based motion capture (Optitrack®, NaturalPoint Inc., Corvalis, OR, USA) of major body segments and vertical ground reaction forces measured from wireless force-sensitive resistors (FSRs) attached to a standing board. Restricting our ground reaction measures to vertically-directed loads is justified since the mean horizontal ground reaction forces (anterior-posterior, medial-lateral) are <2% body weight for squatting [48]. Nine wide-angle infrared cameras (Prime 17W by Optitrack®) were used for 3-D motion capture of marker clusters affixed to each participant’s shank, thigh, and torso body segments. Each marker cluster comprised three non-collinear retroreflective markers placed on a foam board platform. These marker platforms were then attached with skin-safe adhesive tape. A platform was placed on the lateral side of each shank, positioned equally between the medial malleolus and the middle of the knee joint center of rotation. The platform on each thigh was positioned equally between the lateral epicondyle (knee) and the greater trochanter (hip). A single torso platform, with four markers, was centrally placed between the shoulder blades.
Each platform’s orientation was measured from a global reference frame. The initial setpoint (zero-angle) for orientation was calibrated to coincide with each participant’s erect standing position. Marker position data were streamed in real-time using motion capture software (Version 2.02, Motive by Optitrack®) and processed at 30 frames per second in MATLAB® (Mathworks Inc., Natick, MA, USA) using a desktop computer (Dell Intel® Xeon® CPU E5-1660 v4 @ 3.20 GHz, Round Rock, TX, USA). Visual feedback cues were displayed on a big-screen television (25.8″ H × 44.5″ W, TCL Model:50FS3800). Using sensors from a wireless data acquisition system (Trigno by Delsys), FSR data were collected for estimating the standing center of pressure. Four individual FSR sensors were attached to a solid (wood) board on which subjects would stand. Sensor locations coincided with each subject’s specific foot pressure points (four total for each foot: heel, big toe, 1st metatarsal, 5th metatarsal). FSR data were initially sampled at 1925 Hz (system default) and then re-sampled and synchronized offline to match the 30 Hz real-time display rate of motion data.

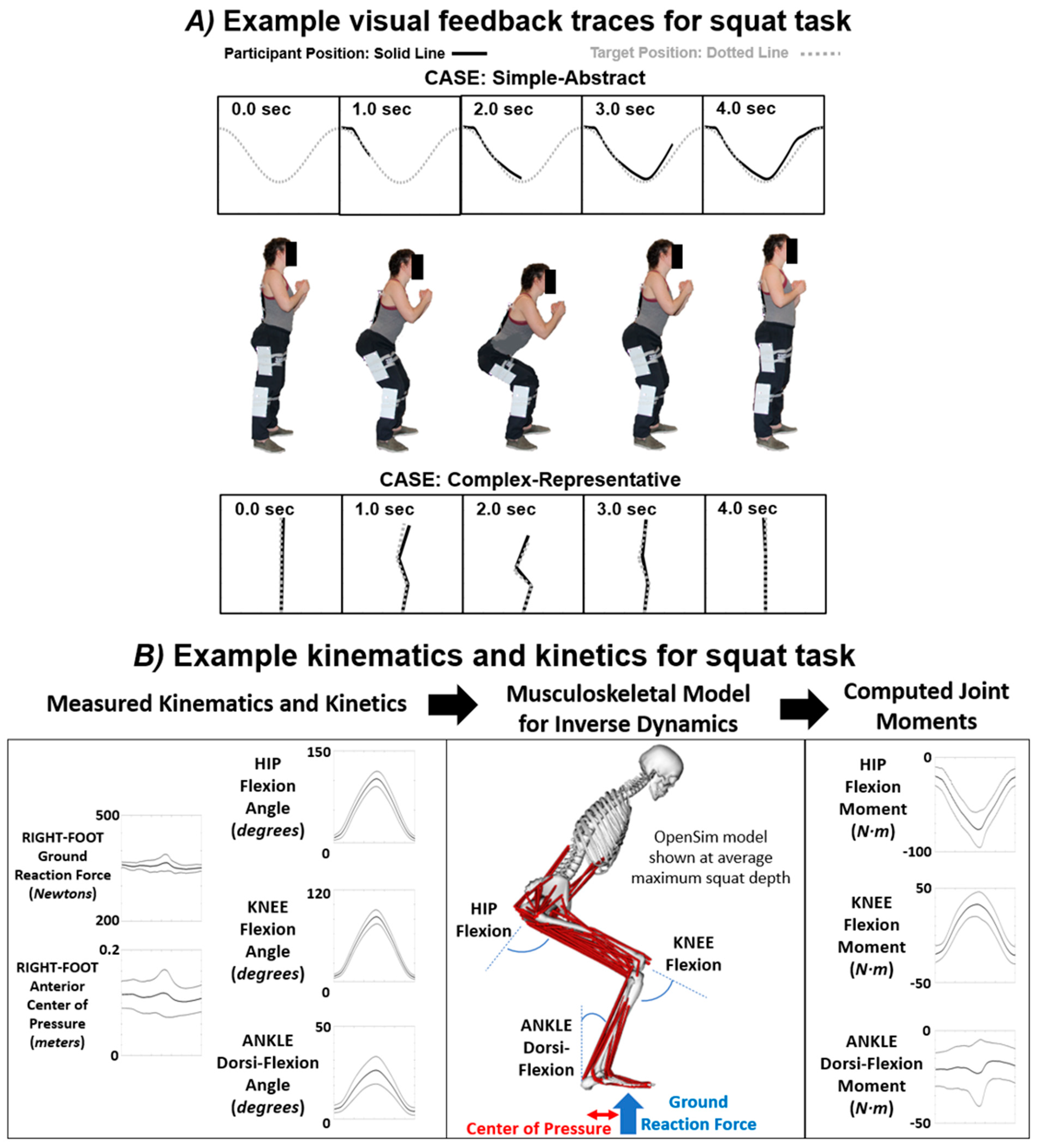
2.4. General Testing Procedure and Visual Feedback Modes

Each participant completed ten consecutive trials for four visual feedback modes. A block of ten training trials, in which concurrent (i.e., while squatting) feedback of actual and target motions was provided. Before each block of official training trials, participants underwent one practice trial and up to three (based on participant preference) to accommodate themselves to the visual mode. Each trial entailed the execution of a single squat repetition. Each mode was defined according to the unique pairing of two primary features (Figure 1B): (1) complexity (simple versus complex) and (2) representation (abstract versus representative). Simple visual feedback only presented spatial information of the participant’s thigh position as a single target to track. Complex visual feedback concurrently displayed the spatial position of the participant’s shank, thigh, and torso segments as three separate targets. Each target trajectory was a single-cycle sinusoid of a segment angular position. The participant was instructed to track all three body segment targets but was aware that the thigh was primarily important for performance.
With abstract feedback, the target trajectory to be traced was displayed on the screen as a sinusoid, while the participant’s actual trajectory moved across the target trajectory with time. Example traces for the time-progressive display of visual feedback are shown in Figure 2A. With representative feedback, the target and the actual motions were displayed as superimposed stick figures (i.e., motion-tracked segments connected and presumed joint locations) moving in the sagittal plane. As such, the defining feature pair for each mode was: simple-abstract (SA), simple-representative (SR), complex-abstract (CA), and complex-representative (CR). The four visual feedback modes were presented in random order to each participant.
For each mode, feedback was presented intermittently, as described in Sanford et al. [5]. The target trajectory disappeared when tracking errors (i.e., the difference between target and actual motions) were less than 5% of a pre-determined mean error. This mean error value was determined from a handful of practice trials (three minimum, up to five pending participant preference) to familiarize participants with the experimental procedures before collecting official data. The target trajectory progressively became more opaque with greater exceeding of this 5% error band to acclimate the participant smoothly to changes in the feedback. As discussed in Sanford et al. [5], this task with associated feedback modes lends itself to the guidance hypothesis whereby intermittent feedback as a function of performance function will promote faster task learning [49].

2.5. Data Analysis

Computation of Joint Angles and Ground Reaction Forces: Angular positions for flexion-extension of the hip, knee, and ankle joints were approximated according to relative changes in the orientation of adjacent body segments. For example, knee joint angles were derived from the angular differences between the thigh and shank segments. Each marker cluster represented a 3D coordinate system assumed to be at a neutral orientation at the erect standing position at the start of each trial. Joint angles for the hips, knees, and ankles were computed based on conventions for anatomical joint rotations computed from adjacent coordinate systems described by Wu et al. [50]. Flexion-extension angles were the primary rotation since participants observed their motions projected onto the sagittal plane where flexion-extension dynamics are dominant [51]. Ground reaction force magnitude and location (i.e., the center of pressure) were estimated for each foot according to the relative voltage readings of the FSR sensors. Each FSR location was registered relative to the global reference frame of the motion capture system using digitization procedures described in Nataraj et al. [52]. When calibrating FSRs (0 to 50 lbs), the estimated resolution for force measures was within 3 N. Furthermore, individual FSR outputs did not saturate for any squat trials.
Inverse Dynamics: Joint angles and ground reaction force data were inputted into OpenSim 3.3, running the model ‘3DGaitModel2392’ to compute respective flexion-extension moments at the hips, knees, and ankles [53]. The software includes a modeling layer that solves equations of motion to compute joint moments from respective kinematic and external force trajectories. This procedural pipeline for computing joint moments for squatting has been validated with a similar use in prior studies [54,55,56]. We compute joint moments for each participant’s left and right sides; however, we assume adequate squat symmetry to report the average joint moments across the left and right sides for subsequent analyses in this paper. This symmetry assumption was justified by observing that the left and right ground reaction forces were within 5% body weight on average across all participants. This procedure to average results across the left and right sides is further reasoned by focusing analysis (and visual feedback) along the flexion-extension plane. The joint moment trajectory was computed over the entire squat maneuver (4 s) for each participant trial. Example traces for joint angles and ground reaction forces (and center of pressure locations) serving as inputs to a computational model to generate corresponding joint moment profiles are shown in Figure 2B.
Statistical Analysis: The mean and variability (standard deviation) of the joint moment traces, across all trials, for each participant and visual feedback mode served as a sample observation. Given only ten training trials per mode, we presume minimal learning for a given mode such that neither trial-to-trial examination nor early-to-late trial comparison is needed. Data were normalized by the overall mean value for each joint when pooling results (overall) across all three joints since each joint expresses considerably different moment magnitudes during the squat maneuver [57]. Otherwise, each joint was treated independently for joint-specific analyses. A two-way (2 × 2) ANOVA was applied to both joint moment mean and variability data during visual feedback training to determine whether significant differences exist across this study’s two primary factors (VF features): (1) simple versus complex feedback and (2) abstract versus representative feedback. If a significant interaction (p < 0.05) was observed, then simple effects (i.e., differences between individual pairs of modes) were also examined. A Bonferroni correction was applied for multiple comparisons. This two-way ANOVA is the primary analysis for this study in testing the main hypotheses. To examine the spatial effects of modes, we repeat the two-way ANOVA for each joint and across all joints (overall) after normalization. To preliminarily investigate any temporal effects of modes, we examined changes in joint moment data based on specific joints and time phases (windows) of the squat movement. Each trial was divided into equal thirds (i.e., 4/3 s) to denote the ‘early’, ‘target’, and ‘late’ time windows of the squat movement cycle. The ‘target’ window represents when participants focus on matching and recovering from the maximum squat depth (at trial time = 2 s). A simple one-way ANOVA was performed across the four visual feedback modes for each pairing of joint and time window to avoid confounding multi-factor analysis of these effects.

3. Results

The effect size for all ANOVA comparisons was moderately large (Cohen’s D > 0.5), and given the n = 18 sample size, the degrees of freedom for one-way and two-way ANOVA were 17 and 18, respectively. There were no outlier trials by any participant (i.e., no trial mean error > 3 standard deviations from the overall mean for the given participant), suggesting the practice trials provided with each visual feedback mode were sufficient for accommodation. The mean joint moment values during training per visual feedback feature (complexity, representation) across all joints (overall) and per joint are shown in Figure 3A. Corresponding results for joint moment variability are shown in Figure 3B. No significant differences were observed with mean joint moment overall nor at the individual joint level except with complexity at the knee joint. Significant increases in joint variability were observed for higher complexity at the hip and ankle joints and across all joints (overall). A significant increase in variability was also observed for abstract feedback for the knee joint. Significant interactions (Table 1) between the factors of complexity and representation were observed only for overall joint variability and specific joints (hip, knee). As such, we report simple effects, i.e., significant differences between individual visual feedback modes, in Table 2 for each joint and overall. Notably, the simple-abstract mode demonstrated the lowest variability and had a significant difference with at least one other mode for every test case (i.e., overall and all three joints).
The mean and variability results for joint moments across time windows (early, target, late) of the squat movement per joint are shown in Figure 4. Within these time windows, one-way ANOVA analyses suggest significant differences exist across visual feedback modes. The p-value and F-stat for each significant difference per joint and time window are shown in Table 3. Notably, the knee joint demonstrates a significant difference in both the mean value and variability of joint moments in each of the three designated windows. The hip joint shows a significant difference in both the mean value and variability of joint moments in the target and late windows. The ankle joint only demonstrates a significant difference in variability and the target and late windows. Although not the focus of the current study, performance results (e.g., kinematic error in tracking target trajectories) reported initially, in part, in [4,5] are provided in Table 4 for comparison.

4. Discussion

To our knowledge, this study is the first to show how visual feedback features (i.e., complexity, level of body representation) used to guide joint kinematics during the two-legged squat uniquely affect internal joint mechanics across spatial (different joints) and temporal (different movement time phases) domains. Such findings indicate how visual guidance for rehabilitative training delivered with technological interfaces, e.g., virtual reality [58,59], can be optimized. The squat task is highly suitable for this pilot examination since it is commonly used for lower-body rehabilitation [2,60], and it is a multi-joint movement that effectively adheres to one degree of freedom (i.e., squat depth), thereby simplifying interpretations. The primary findings from this study are (1) joint moment variability, more than joint moment mean values, was significantly affected by changes in features of visual feedback about kinematics, and (2) the feature of complexity produced more evident changes in joint moments compared to the feature of body representation.
Our previous works [4,5] have shown that the performance of squat kinematics is sensitive to the particular features of visual feedback provided about that performance. In those studies, the primary goal was to examine the effect of training with various visual feedback modes on short-term retention (i.e., performance immediately after feedback is removed). In this study, we more closely examine the effects of these visual feedback modes on internal joint mechanics during training. More specifically, this study now explicitly shows how visual feedback features impact the underlying joint moments, most notably along the dimension of variability. Shifts in motor variability indicate the potential adaptation of control strategies [61] after repeated sessions of guided training. This study suggests that movement tactics with guided training could be actively modulated through intelligent variations in visual feedback features, which may lead to long-term changes in movement strategies. A natural next question is whether it is desirable to prescribe visual feedback features to induce higher or lower joint moment variability during rehabilitative training in maximizing long-term functional outcomes. As mentioned, reducing joint moment variability with rehabilitative practice is naturally beneficial when targeting improved function at particular joints [23,24] or when aiming to mitigate dysfunctional variability related to pathologies [25,26]. Furthermore, lower variability in function typically indicates a higher skill level [62]. However, lowering variability is often achieved progressively with skill development, and it can depend on the nature of the task [63].
However, if the rehabilitation goal is to improve kinematic performance, i.e., recovering motion capabilities after stroke [59], then periods of high motor variability across training sessions may be desirable. Higher variability can reflect a purposeful exploration of the motor space [64] that drives early-stage motor practice. In this study, more visual feedback complexity significantly increased joint moment variability, as hypothesized. Our previous work [4] showed that complex feedback produced improved kinematic (tracking) performance, but only when paired with the body-representative feature. Furthermore, this study suggests a negligible difference in kinetic variability overall between complex-representative and complex-abstract modes despite complex-representative generating superior kinematic performance. Results across both studies indicate that increasing kinetic variability with complex visual feedback could benefit the progressive practice of a rehabilitative motor task such as the squat. The optimal application of different visual feedback features with rehabilitative training may depend on the stage of training (i.e., early versus end), the goals of the rehabilitation paradigm (i.e., kinematic performance versus function of individual joints), and the training task itself (i.e., squat versus gait).
A longitudinal study that evaluates skill transfer [65] on the same group of participants is needed to confirm the effects of higher or lower kinetic variability as kinematic performance evolves with rehabilitation. A major limitation of this study is the lack of repeated measures to examine true motor retention). Our previous work has successfully demonstrated the impact of altered visual feedback on short-term retention [4,5,66,67] (i.e., the relative change in performance immediately after training) and real-time performance [68,69]. While such experimental designs are provocative by inducing immediate behavioral changes, authentic behavioral changes must be demonstrated with follow-up sessions to explore longer-term adaptations and transfer testing of acquired skills [22]. As is, this study successfully showed that applying specific visual feedback features is a potentially viable pathway to modulate joint-level kinetic variability within individual training sessions. Immediately reducing kinetic variability per training dosage can still be beneficial in the functional rehabilitation of particular joints.
Depending on the exercise task, each joint can have unique biomechanical responsibilities (load bearing, finer control, etc.) and be impacted by visual feedback accordingly. This study examined joint-level dependencies of moment variations to visual feedback when training with the squat task. The highest mean peak moments for the squat maneuver are experienced at the hip (~80 N·m extension) and knee (~30 N·m extension) joints in raising the person against gravitational loads. On the other hand, the ankle joint exhibits considerably lower peak moments (~15 N·m plantar-flexion) in primarily stabilizing the center of pressure within the base of support [70,71]. Thus, it is critical for the ankle to constantly make corrective actions, presumably making its joint moment variability more sensitive to changes in visual feedback. Similarly, the hip joint may be more reactive in adjusting the center of mass position, given its relative proximity to the total body center of mass at the erect (quiet) standing position [72]. Thus, variability at the hip and ankle joints may be more sensitive to changes in visual feedback features like complexity due to their fundamental roles in maintaining balance [73].
On the other hand, for the knee, joint moment variability was relatively more impacted by changes in the visual feedback feature of representation. Presumably, joint mechanics modulated by body representation are driven, in part, by feelings of embodiment with the movement feedback [74,75]; however, our study’s limitations in methods are unable to confirm the phenomenon. Still, with this paradigm’s attentive focus on the thigh segment (i.e., primary tracking target), knee joint moment variability may have been particularly sensitive to alterations in how that segment was visually presented (i.e., abstract trajectory versus explicit body segment motions). Although hip angles also depend on thigh orientation, knee dynamics drive the squatting maneuver [2,60] and are more directly determined by thigh angle due to relatively small changes in shank angles. As such, joint moment mean and variability at the knee have more apparent dependencies on visual feedback across temporal phases of the squat. This temporal dependence may also be due to the knee joint exhibiting more complex joint moment patterns, including directional shifts between positive (extension) and negative (flexion) moment values, unlike the hip (~always net extension) and ankle (~always net plantar flexion).
Another limitation of this study is evaluating only joint moments since regulation of joint reaction forces is also of interest with rehabilitative paradigms [76,77,78], which could be addressed with future examinations. Another analysis measure of interest may be “efficiency”, by which we estimate changes in kinematic performance (output) per change in kinetics (input) and as a function of feedback features. While such analyses would further contextualize the impact of visual feedback features for optimizing motor rehabilitation protocols, this study establishes the vital first step in demonstrating that joint moments are responsive to variations in feedback features. Future studies could also address limitations in our protocol by using high-resolution force plates and more complete marker sets designed and calibrated for 3-D anatomical assessment of lower-extremity joint mechanics [79,80]. However, our simplified measures and analyses for joint moments were on par with similar studies for various applications [81,82,83] and, more importantly, were consistent with the visual feedback provided in this study, i.e., three-segment stick figure motions projected onto the sagittal plane. Furthermore, the measurement resolution of our methods did not prevent the identification of significant differences in computed joint moments based on visual feedback features, i.e., the study’s primary goal.

5. Conclusions

In conclusion, visual feedback features (i.e., complexity, level of body representation) can affect the internal mechanics used while training to perform a multi-joint kinematic maneuver. Thus, there is an opportunity to optimize feature elements of augmented feedback training paradigms for motor rehabilitation employing computerized interfaces for guidance. Physical therapy with advanced technologies, such as virtual reality [14,58,84], is increasingly prevalent due to its customizability and capabilities to activate sensory modalities for greater engagement. Delivery of sensory feedback could be strategically optimized with guided training for skill acquisition [85], depending on the movement task, primary joints of interest, and user experience levels with such approaches [86]. Optimizing sensory feedback has clear implications for rehabilitation with visually-driven computerized interfaces such as virtual reality to train improved capabilities in tracking motion [69,87] and force [68] trajectories.

Author Contributions

R.N.—conception and design of the work, analysis/interpretation of data, drafting and revising the manuscript critically, approving the final manuscript, and agreeing to be accountable for all aspects of the work. S.P.S.—conception and design of the work, acquisition of data, approving the final manuscript, and agreeing to be accountable for all aspects of the work. M.L.—acquisition of data, approving the final manuscript, and agreeing to be accountable for all aspects of the work. All authors have read and agreed to the published version of the manuscript.

Funding

This publication was made possible by funding support (startup for Raviraj Nataraj) from the Schaefer School of Engineering and Science at the Stevens Institute of Technology.

Institutional Review Board Statement

All subjects gave their informed consent for inclusion before they participated in the study. The study was conducted in accordance with the Declaration of Helsinki, and the associated protocol 2017-022 was approved by the Institutional Review Board at the Stevens Institute of Technology.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Upon publication, underlying data for this study will be made available upon request from the corresponding author until they are made openly available in a repository (e.g., ResearchGate) that issues DOIs as managed by the corresponding author.

Acknowledgments

The authors would like to acknowledge Troy Bradbury, Elena Davis, Shterna Kuptchik, and Amanda Clemente for assisting in running dynamic simulations performed in OpenSim.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Sigrist, R.; Rauter, G.; Riener, R.; Wolf, P. Augmented visual, auditory, haptic, and multimodal feedback in motor learning: A review. Psychon. Bull. Rev. 2013, 20, 21–53. [Google Scholar] [CrossRef] [PubMed]
  2. Toutoungi, D.; Lu, T.; Leardini, A.; Catani, F.; O’connor, J. Cruciate ligament forces in the human knee during rehabilitation exercises. Clin. Biomech. 2000, 15, 176–187. [Google Scholar] [CrossRef] [PubMed]
  3. Ramachandran, V.S.; Altschuler, E.L. The use of visual feedback, in particular mirror visual feedback, in restoring brain function. Brain 2009, 132, 1693–1710. [Google Scholar] [CrossRef]
  4. Sanford, S.; Liu, M.; Selvaggi, T.; Nataraj, R. Effects of visual feedback complexity on the performance of a movement task for rehabilitation. J. Mot. Behav. 2021, 53, 243–257. [Google Scholar] [CrossRef]
  5. Sanford, S.; Liu, M.; Nataraj, R. Concurrent Continuous Versus Bandwidth Visual Feedback with Varying Body Representation for the 2-Legged Squat Exercise. J. Sport Rehabil. 2021, 30, 794–803. [Google Scholar] [CrossRef]
  6. Karatsidis, A.; Richards, R.E.; Konrath, J.M.; Van Den Noort, J.C.; Schepers, H.M.; Bellusci, G.; Harlaar, J.; Veltink, P.H. Validation of wearable visual feedback for retraining foot progression angle using inertial sensors and an augmented reality headset. J. Neuroeng. Rehabil. 2018, 15, 1–12. [Google Scholar] [CrossRef] [PubMed]
  7. Benjaminse, A.; Welling, W.; Otten, B.; Gokeler, A. Transfer of improved movement technique after receiving verbal external focus and video instruction. Knee Surg. Sports Traumatol. Arthrosc. 2018, 26, 955–962. [Google Scholar] [CrossRef]
  8. Giggins, O.M.; Persson, U.M.; Caulfield, B. Biofeedback in rehabilitation. J. Neuroeng. Rehabil. 2013, 10, 60. [Google Scholar] [CrossRef]
  9. Onate, J.A.; Guskiewicz, K.M.; Sullivan, R.J. Augmented feedback reduces jump landing forces. J. Orthop. Sports Phys. Ther. 2001, 31, 511–517. [Google Scholar] [CrossRef]
  10. Kernozek, T.; Schiller, M.; Rutherford, D.; Smith, A.; Durall, C.; Almonroeder, T.G. Real-time visual feedback reduces patellofemoral joint forces during squatting in individuals with patellofemoral pain. Clin. Biomech. 2020, 77, 105050. [Google Scholar] [CrossRef]
  11. Sigrist, R.; Rauter, G.; Marchal-Crespo, L.; Riener, R.; Wolf, P. Sonification and haptic feedback in addition to visual feedback enhances complex motor task learning. Exp. Brain Res. 2015, 233, 909–925. [Google Scholar] [CrossRef] [PubMed]
  12. Dyer, J.; Stapleton, P.; Rodger, M. Transposing musical skill: Sonification of movement as concurrent augmented feedback enhances learning in a bimanual task. Psychol. Res. 2017, 81, 850–862. [Google Scholar] [CrossRef] [PubMed]
  13. Moinuddin, A.; Goel, A.; Sethi, Y. The role of augmented feedback on motor learning: A systematic review. Cureus 2021, 13, e19695. [Google Scholar] [CrossRef] [PubMed]
  14. Zimmerli, L.; Duschau-Wicke, A.; Mayr, A.; Riener, R.; Lunenburger, L. Virtual reality and gait rehabilitation Augmented feedback for the Lokomat. In Proceedings of the 2009 Virtual Rehabilitation International Conference, Haifa, Israel, June 29–July 2 2009; pp. 150–153. [Google Scholar]
  15. Otten, E. Inverse and forward dynamics: Models of multi–body systems. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2003, 358, 1493–1500. [Google Scholar] [CrossRef]
  16. Winter, D.A. Kinematic and kinetic patterns in human gait: Variability and compensating effects. Hum. Mov. Sci. 1984, 3, 51–76. [Google Scholar] [CrossRef]
  17. Preatoni, E.; Hamill, J.; Harrison, A.J.; Hayes, K.; Van Emmerik, R.E.; Wilson, C.; Rodano, R. Movement variability and skills monitoring in sports. Sports Biomech. 2013, 12, 69–92. [Google Scholar] [CrossRef]
  18. Latash, M.L. On primitives in motor control. Mot. Control 2020, 24, 318–346. [Google Scholar] [CrossRef] [PubMed]
  19. Gerritsen, K.G.; van den Bogert, A.J.; Hulliger, M.; Zernicke, R.F. Intrinsic muscle properties facilitate locomotor control—A computer simulation study. Mot. Control 1998, 2, 206–220. [Google Scholar] [CrossRef]
  20. Wulf, G.; Dufek, J.S. Increased jump height with an external focus due to enhanced lower extremity joint kinetics. J. Mot. Behav. 2009, 41, 401–409. [Google Scholar] [CrossRef]
  21. Weakley, J.; Wilson, K.; Till, K.; Banyard, H.; Dyson, J.; Phibbs, P.; Read, D.; Jones, B. Show me, tell me, encourage me: The effect of different forms of feedback on resistance training performance. J. Strength Cond. Res. 2020, 34, 3157–3163. [Google Scholar] [CrossRef]
  22. Swinnen, S.P.; Lee, T.D.; Verschueren, S.; Serrien, D.J.; Bogaerds, H. Interlimb coordination: Learning and transfer under different feedback conditions. Hum. Mov. Sci. 1997, 16, 749–785. [Google Scholar] [CrossRef]
  23. Schoenfeld, B.J. Squatting kinematics and kinetics and their application to exercise performance. J. Strength Cond. Res. 2010, 24, 3497–3506. [Google Scholar] [CrossRef]
  24. Song, Y.; Li, L.; Albrandt, E.E.; Jensen, M.A.; Dai, B. Medial-lateral hip positions predicted kinetic asymmetries during double-leg squats in collegiate athletes following anterior cruciate ligament reconstruction. J. Biomech. 2021, 128, 110787. [Google Scholar] [CrossRef] [PubMed]
  25. Crenshaw, S.; Royer, T.; Richards, J.; Hudson, D. Gait variability in people with multiple sclerosis. Mult. Scler. J. 2006, 12, 613–619. [Google Scholar] [CrossRef] [PubMed]
  26. Lewek, M.D.; Scholz, J.; Rudolph, K.S.; Snyder-Mackler, L. Stride-to-stride variability of knee motion in patients with knee osteoarthritis. Gait Posture 2006, 23, 505–511. [Google Scholar] [CrossRef] [PubMed]
  27. Welling, W.; Benjaminse, A.; Gokeler, A.; Otten, B. Retention of movement technique: Implications for primary prevention of ACL injuries. Int. J. Sports Phys. Ther. 2017, 12, 908. [Google Scholar] [CrossRef]
  28. Lee, J.H.; Kang, N. Effects of online-bandwidth visual feedback on unilateral force control capabilities. PLoS ONE 2020, 15, e0238367. [Google Scholar] [CrossRef]
  29. Schiffman, J.M.; Luchies, C.W.; Piscitelle, L.; Hasselquist, L.; Gregorczyk, K.N. Discrete bandwidth visual feedback increases structure of output as compared to continuous visual feedback in isometric force control tasks. Clin. Biomech. 2006, 21, 1042–1050. [Google Scholar] [CrossRef]
  30. Yang, C.; Bouffard, J.; Srinivasan, D.; Ghayourmanesh, S.; Cantú, H.; Begon, M.; Côté, J.N. Changes in movement variability and task performance during a fatiguing repetitive pointing task. J. Biomech. 2018, 76, 212–219. [Google Scholar] [CrossRef]
  31. Sigrist, R. Visual and auditory augmented concurrent feedback in a complex motor task. Presence 2011, 20, 15–32. [Google Scholar] [CrossRef]
  32. McCabe, C. Mirror visual feedback therapy. A practical approach. J. Hand Ther. 2011, 24, 170–179. [Google Scholar] [CrossRef] [PubMed]
  33. Roosink, M.; Robitaille, N.; McFadyen, B.J.; Hébert, L.J.; Jackson, P.L.; Bouyer, L.J.; Mercier, C. Real-time modulation of visual feedback on human full-body movements in a virtual mirror: Development and proof-of-concept. J. Neuroeng. Rehabil. 2015, 12, 2. [Google Scholar] [CrossRef] [PubMed]
  34. Hoover, A.E.; Harris, L.R. Detecting delay in visual feedback of an action as a monitor of self recognition. Exp. Brain Res. 2012, 222, 389–397. [Google Scholar] [CrossRef]
  35. Lieber, R.L.; Bodine-Fowler, S.C. Skeletal muscle mechanics: Implications for rehabilitation. Phys. Ther. 1993, 73, 844–856. [Google Scholar] [CrossRef] [PubMed]
  36. Webster, K.E.; Feller, J.A.; Wittwer, J.E. Longitudinal changes in knee joint biomechanics during level walking following anterior cruciate ligament reconstruction surgery. Gait Posture 2012, 36, 167–171. [Google Scholar] [CrossRef] [PubMed]
  37. Hamill, J.; Palmer, C.; Van Emmerik, R.E. Coordinative variability and overuse injury. Sports Med. Arthrosc. Rehabil. Ther. Technol. 2012, 4, 45. [Google Scholar] [CrossRef]
  38. Hubbard, W.A.; McElroy, G. Benchmark data for elderly, vascular trans-tibial amputees after rehabilitation. Prosthet. Orthot. Int. 1994, 18, 142–149. [Google Scholar] [CrossRef]
  39. Rutherford, D.J.; Hubley-Kozey, C. Explaining the hip adduction moment variability during gait: Implications for hip abductor strengthening. Clin. Biomech. 2009, 24, 267–273. [Google Scholar] [CrossRef]
  40. Kilteni, K.; Groten, R.; Slater, M. The sense of embodiment in virtual reality. Presence Teleoperators Virtual Environ. 2012, 21, 373–387. [Google Scholar] [CrossRef]
  41. Pizzolato, C.; Reggiani, M.; Modenese, L.; Lloyd, D. Real-time inverse kinematics and inverse dynamics for lower limb applications using OpenSim. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 436–445. [Google Scholar] [CrossRef]
  42. Donohue, M.R.; Ellis, S.M.; Heinbaugh, E.M.; Stephenson, M.L.; Zhu, Q.; Dai, B. Differences and correlations in knee and hip mechanics during single-leg landing, single-leg squat, double-leg landing, and double-leg squat tasks. Res. Sports Med. 2015, 23, 394–411. [Google Scholar] [CrossRef]
  43. Roos, P.E.; Button, K.; van Deursen, R.W. Motor control strategies during double leg squat following anterior cruciate ligament rupture and reconstruction: An observational study. J. Neuroeng. Rehabil. 2014, 11, 19. [Google Scholar] [CrossRef]
  44. Martínez-Cava, A.; Morán-Navarro, R.; Sánchez-Medina, L.; González-Badillo, J.J.; Pallarés, J.G. Velocity-and power-load relationships in the half, parallel and full back squat. J. Sports Sci. 2019, 37, 1088–1096. [Google Scholar] [CrossRef]
  45. Zawadka, M.; Smolka, J.; Skublewska-Paszkowska, M.; Lukasik, E.; Gawda, P. How Are Squat Timing and Kinematics in The Sagittal Plane Related to Squat Depth? J. Sports Sci. Med. 2020, 19, 500. [Google Scholar]
  46. Webster, K.E.; Austin, D.C.; Feller, J.A.; Clark, R.A.; McClelland, J.A. Symmetry of squatting and the effect of fatigue following anterior cruciate ligament reconstruction. Knee Surg. Sports Traumatol. Arthrosc. 2015, 23, 3208–3213. [Google Scholar] [CrossRef]
  47. Escamilla, R.F. Knee biomechanics of the dynamic squat exercise. Med. Sci. Sports Exerc. 2001, 33, 127–141. [Google Scholar] [CrossRef]
  48. Jung, Y.; Koo, Y.-j.; Koo, S. Simultaneous estimation of ground reaction force and knee contact force during walking and squatting. Int. J. Precis. Eng. Manuf. 2017, 18, 1263–1268. [Google Scholar] [CrossRef]
  49. Park, J.-H.; Shea, C.H.; Wright, D.L. Reduced-frequency concurrent and terminal feedback: A test of the guidance hypothesis. J. Mot. Behav. 2000, 32, 287–296. [Google Scholar] [CrossRef]
  50. Wu, G.; Cavanagh, P.R. ISB recommendations for standardization in the reporting of kinematic data. J. Biomech. 1995, 28, 1257–1262. [Google Scholar] [CrossRef]
  51. Nadeau, S.; McFadyen, B.J.; Malouin, F. Frontal and sagittal plane analyses of the stair climbing task in healthy adults aged over 40 years: What are the challenges compared to level walking? Clin. Biomech. 2003, 18, 950–959. [Google Scholar] [CrossRef]
  52. Nataraj, R.; Li, Z.-M. Integration of marker and force data to compute three-dimensional joint moments of the thumb and index finger digits during pinch. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 592–606. [Google Scholar] [CrossRef] [PubMed]
  53. Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M. OpenSim: Simulating musculoskeletal dynamics and neuromuscular control to study human and animal movement. PLoS Comput. Biol. 2018, 14, e1006223. [Google Scholar] [CrossRef]
  54. Dembia, C.L.; Bianco, N.A.; Falisse, A.; Hicks, J.L.; Delp, S.L. Opensim moco: Musculoskeletal optimal control. PLoS Comput. Biol. 2020, 16, e1008493. [Google Scholar] [CrossRef]
  55. Gallo, C.; Thompson, W.; Lewandowski, B.; Humphreys, B.; Funk, J.; Funk, N.; Weaver, A.; Perusek, G.; Sheehan, C.; Mulugeta, L. computational modeling using opensim to simulate a squat exercise motion. In Proceedings of the NASA Human Research Program Investigators’ Workshop: Integrated Pathways to Mars, Galveston, TX, USA, 13–15 January 2015. [Google Scholar]
  56. Lu, Y.; Mei, Q.; Peng, H.-T.; Li, J.; Wei, C.; Gu, Y. A comparative study on loadings of the lower extremity during deep squat in Asian and Caucasian individuals via OpenSim musculoskeletal modelling. BioMed Res. Int. 2020, 2020, 7531719. [Google Scholar] [CrossRef]
  57. Escamilla, R.F.; Fleisig, G.S.; Lowry, T.M.; Barrentine, S.W.; Andrews, J.R. A three-dimensional biomechanical analysis of the squat during varying stance widths. Med. Sci. Sports Exerc. 2001, 33, 984–998. [Google Scholar] [CrossRef]
  58. Kommalapati, R.; Michmizos, K.P. Virtual reality for pediatric neuro-rehabilitation: Adaptive visual feedback of movement to engage the mirror neuron system. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 5849–5852. [Google Scholar]
  59. Shiri, S.; Feintuch, U.; Lorber-Haddad, A.; Moreh, E.; Twito, D.; Tuchner-Arieli, M.; Meiner, Z. A novel virtual reality system integrating online self-face viewing and mirror visual feedback for stroke rehabilitation: Rationale and feasibility. Top. Stroke Rehabil. 2012, 19, 277–286. [Google Scholar] [CrossRef] [PubMed]
  60. Neitzel, J.A.; Davies, G.J. The benefits and controversy of the parallel squat in strength training and rehabilitation. Strength Cond. J. 2000, 22, 30. [Google Scholar] [CrossRef]
  61. Latash, M.L.; Scholz, J.P.; Schöner, G. Motor control strategies revealed in the structure of motor variability. Exerc. Sport Sci. Rev. 2002, 30, 26–31. [Google Scholar] [CrossRef]
  62. Müller, H.; Sternad, D. Motor learning: Changes in the structure of variability in a redundant task. Prog. Mot. Control 2009, 629, 439–456. [Google Scholar]
  63. Sánchez, C.C.; Moreno, F.J.; Vaíllo, R.R.; Romero, A.R.; Coves, Á.; Murillo, D.B. The role of motor variability in motor control and learning depends on the nature of the task and the individual’s capabilities. Eur. J. Hum. Mov. 2017, 38, 12–26. [Google Scholar]
  64. Dhawale, A.K.; Smith, M.A.; Ölveczky, B.P. The role of variability in motor learning. Annu. Rev. Neurosci. 2017, 40, 479. [Google Scholar] [CrossRef] [PubMed]
  65. Anderson, D.I.; Magill, R.A.; Mayo, A.M.; Steel, K.A. Enhancing motor skill acquisition with augmented feedback. In Skill Acquisition in Sport; Routledge: London, UK, 2019; pp. 3–19. [Google Scholar]
  66. Sanford, S.; Collins, B.; Liu, M.; Dewil, S.; Nataraj, R. Investigating features in augmented visual feedback for virtual reality rehabilitation of upper-extremity function through isometric muscle control. Front. Virtual Real. 2022, 3, 943693. [Google Scholar] [CrossRef]
  67. Liu, M.; Wilder, S.; Sanford, S.; Saleh, S.; Harel, N.Y.; Nataraj, R. Training with agency-inspired feedback from an instrumented glove to improve functional grasp performance. Sensors 2021, 21, 1173. [Google Scholar] [CrossRef] [PubMed]
  68. Nataraj, R.; Sanford, S. Control modification of grasp force covaries agency and performance on rigid and compliant surfaces. Front. Bioeng. Biotechnol. 2021, 8, 574006. [Google Scholar] [CrossRef] [PubMed]
  69. Nataraj, R.; Sanford, S.; Shah, A.; Liu, M. Agency and performance of reach-to-grasp with modified control of a virtual hand: Implications for rehabilitation. Front. Hum. Neurosci. 2020, 14, 126. [Google Scholar] [CrossRef]
  70. Krishnamoorthy, V.; Goodman, S.; Zatsiorsky, V.; Latash, M.L. Muscle synergies during shifts of the center of pressure by standing persons: Identification of muscle modes. Biol. Cybern. 2003, 89, 152–161. [Google Scholar] [CrossRef] [PubMed]
  71. Masani, K.; Vette, A.H.; Kouzaki, M.; Kanehisa, H.; Fukunaga, T.; Popovic, M.R. Larger center of pressure minus center of gravity in the elderly induces larger body acceleration during quiet standing. Neurosci. Lett. 2007, 422, 202–206. [Google Scholar] [CrossRef]
  72. Yu, E.; Abe, M.; Masani, K.; Kawashima, N.; Eto, F.; Haga, N.; Nakazawa, K. Evaluation of postural control in quiet standing using center of mass acceleration: Comparison among the young, the elderly, and people with stroke. Arch. Phys. Med. Rehabil. 2008, 89, 1133–1139. [Google Scholar] [CrossRef]
  73. Horak, F.B.; Nashner, L.M. Central programming of postural movements: Adaptation to altered support-surface configurations. J. Neurophysiol. 1986, 55, 1369–1381. [Google Scholar] [CrossRef]
  74. Garcia-Hernandez, N.; Guzman-Alvarado, M.; Parra-Vega, V. Virtual body representation for rehabilitation influences on motor performance of cerebral palsy children. Virtual Real. 2021, 25, 669–680. [Google Scholar] [CrossRef]
  75. Ventura, S.; Marchetti, P.; Baños, R.; Tessari, A. Body ownership illusion through virtual reality as modulator variable for limbs rehabilitation after stroke: A systematic review. Virtual Real. 2023, 27, 2481–2492. [Google Scholar] [CrossRef]
  76. Li, G.; Kawamura, K.; Barrance, P.; Chao, E.Y.; Kaufman, K. Prediction of muscle recruitment and its effect on joint reaction forces during knee exercises. Ann. Biomed. Eng. 1998, 26, 725–733. [Google Scholar] [CrossRef] [PubMed]
  77. Biscarini, A. Determination and optimization of joint torques and joint reaction forces in therapeutic exercises with elastic resistance. Med. Eng. Phys. 2012, 34, 9–16. [Google Scholar] [CrossRef] [PubMed]
  78. Biscarini, A.; Botti, F.M.; Pettorossi, V.E. Joint torques and joint reaction forces during squatting with a forward or backward inclined Smith machine. J. Appl. Biomech. 2013, 29, 85–97. [Google Scholar] [CrossRef] [PubMed]
  79. Collins, T.D.; Ghoussayni, S.N.; Ewins, D.J.; Kent, J.A. A six degrees-of-freedom marker set for gait analysis: Repeatability and comparison with a modified Helen Hayes set. Gait Posture 2009, 30, 173–180. [Google Scholar] [CrossRef]
  80. Lloyd, C.H.; Stanhope, S.J.; Davis, I.S.; Royer, T.D. Strength asymmetry and osteoarthritis risk factors in unilateral trans-tibial, amputee gait. Gait Posture 2010, 32, 296–300. [Google Scholar] [CrossRef]
  81. Goh, P.; Fuss, F.; Yanai, T.; Ritchie, A. Dynamic intrameniscal stresses measurement in the porcine knee. In Proceedings of the 2006 International Conference on Biomedical and Pharmaceutical Engineering, Singapore, 11–14 December 2006; pp. 194–196. [Google Scholar]
  82. Seibt, E. Force Sensing Glove for Quantification of Joint Torques during Stretching after Spinal Cord Injury in the Rat Model; University of Louisville: Louisville, KY, USA, 2013. [Google Scholar]
  83. Sato, M.; Shimada, Y.; Iwani, T.; Miyawaki, K.; Matsunaga, T.; Chida, S.; Hatakeyama, K. Development of prototype FES-rowing power rehabilitation equipment. In Proceedings of the 10th Annual Conference of the International FES Society, Montreal, QC, Canada, 5–8 July 2005. [Google Scholar]
  84. Robertson, J.V.; Roby-Brami, A. Augmented feedback, virtual reality and robotics for designing new rehabilitation methods. In Rethinking Physical and Rehabilitation Medicine; Springer: Berlin/Heidelberg, Germany, 2010; pp. 223–245. [Google Scholar]
  85. Magill, R.A.; Anderson, D.I. The roles and uses of augmented feedback in motor skill acquisition. In Skill Acquisition in Sport: Research, Theory and Practice; Routledge: London, UK, 2012; pp. 3–21. [Google Scholar]
  86. Gerig, N.; Basalp, E.; Sigrist, R.; Riener, R.; Wolf, P. Visual error amplification showed no benefit for non-naïve subjects in trunk-arm rowing. Curr. Issues Sport Sci. 2019, 4, 13. [Google Scholar] [CrossRef]
  87. Nataraj, R.; Sanford, S.; Liu, M.; Harel, N.Y. Hand dominance in the performance and perceptions of virtual reach control. Acta Psychol. 2022, 223, 103494. [Google Scholar] [CrossRef]
Biomechanics 03 00035 g001
Figure 1. (A) Participant undergoes squat protocol while motion and ground reaction forces are measured. (B) Visual feedback modes defined according to two primary features of complexity (‘simple’ or ‘complex’) and representation (‘abstract’ or ‘representative’). Feedback complexity entails tracking one segment (simple) versus three segments (complex). Representation entails observing feedback explicitly as sinusoids (abstract) versus a stick figure (representative).
Figure 1. (A) Participant undergoes squat protocol while motion and ground reaction forces are measured. (B) Visual feedback modes defined according to two primary features of complexity (‘simple’ or ‘complex’) and representation (‘abstract’ or ‘representative’). Feedback complexity entails tracking one segment (simple) versus three segments (complex). Representation entails observing feedback explicitly as sinusoids (abstract) versus a stick figure (representative).
Biomechanics 03 00035 g001
Biomechanics 03 00035 g002
Figure 2. (A) Example visual traces are shown when feedback is provided across time (0 to 4 sec) for simple-abstract and complex-representative modes. (B) Flow of data processing shown for computing joint moments with inverse dynamics on a musculoskeletal model. Example traces for experimental data used as model inputs (joint angles, ground reaction forces) and corresponding outputs (joint moments) shown as mean (solid center line) ±1 s.d. (denoted by faded outside lines).
Figure 2. (A) Example visual traces are shown when feedback is provided across time (0 to 4 sec) for simple-abstract and complex-representative modes. (B) Flow of data processing shown for computing joint moments with inverse dynamics on a musculoskeletal model. Example traces for experimental data used as model inputs (joint angles, ground reaction forces) and corresponding outputs (joint moments) shown as mean (solid center line) ±1 s.d. (denoted by faded outside lines).
Biomechanics 03 00035 g002
Biomechanics 03 00035 g003
Figure 3. (A) Joint moment mean per visual feedback feature (i.e., complexity, representation) and mode (unique feature pairing) shown overall and for each joint. (B) Joint moment variability per visual feedback feature and mode is shown overall and for each joint. Note: * p < 0.05, ** p < 0.01, *** p < 0.001; Note: complexity is denoted by light gray to dark black, representation is denoted by red (abstract) to body-representative (green), and modes combining features are denoted by the respective combination of red/green color and light/dark.
Figure 3. (A) Joint moment mean per visual feedback feature (i.e., complexity, representation) and mode (unique feature pairing) shown overall and for each joint. (B) Joint moment variability per visual feedback feature and mode is shown overall and for each joint. Note: * p < 0.05, ** p < 0.01, *** p < 0.001; Note: complexity is denoted by light gray to dark black, representation is denoted by red (abstract) to body-representative (green), and modes combining features are denoted by the respective combination of red/green color and light/dark.
Biomechanics 03 00035 g003
Biomechanics 03 00035 g004
Figure 4. (A) Joint moment mean (±1 s.d. dotted lines) per visual feedback mode (unique feature pairing) shown across time windows (early, target, late) for each joint. (B) Joint moment variability (±1 s.d. dotted lines) per visual feedback mode shown across time windows (early, target, late) for each joint. Note: * p < 0.05, ** p < 0.01, *** p < 0.001; Note: complexity is denoted by light gray to dark black, representation is denoted by red (abstract) to body-representative (green) and modes combining features are denoted by the respective combination of red/green color and light/dark.
Figure 4. (A) Joint moment mean (±1 s.d. dotted lines) per visual feedback mode (unique feature pairing) shown across time windows (early, target, late) for each joint. (B) Joint moment variability (±1 s.d. dotted lines) per visual feedback mode shown across time windows (early, target, late) for each joint. Note: * p < 0.05, ** p < 0.01, *** p < 0.001; Note: complexity is denoted by light gray to dark black, representation is denoted by red (abstract) to body-representative (green) and modes combining features are denoted by the respective combination of red/green color and light/dark.
Biomechanics 03 00035 g004
Table 1. Two-Way ANOVA (Factors: Complexity, Representation) Analysis for Joint Moment Mean and Variability during Training per Joint and Overall (Across All Joints).
Table 1. Two-Way ANOVA (Factors: Complexity, Representation) Analysis for Joint Moment Mean and Variability during Training per Joint and Overall (Across All Joints).
Joint Moment Mean
Jointp-Val Complexity
(F-Stat)		Simple
Mean
Value in N·m		Complex Mean
Value
in N·m		p-Val Representation
(F-Stat)		Abstract
Mean
Value
in N·m		Representative
Mean
Value
in N·m		p-Val Interaction
(F-Stat)
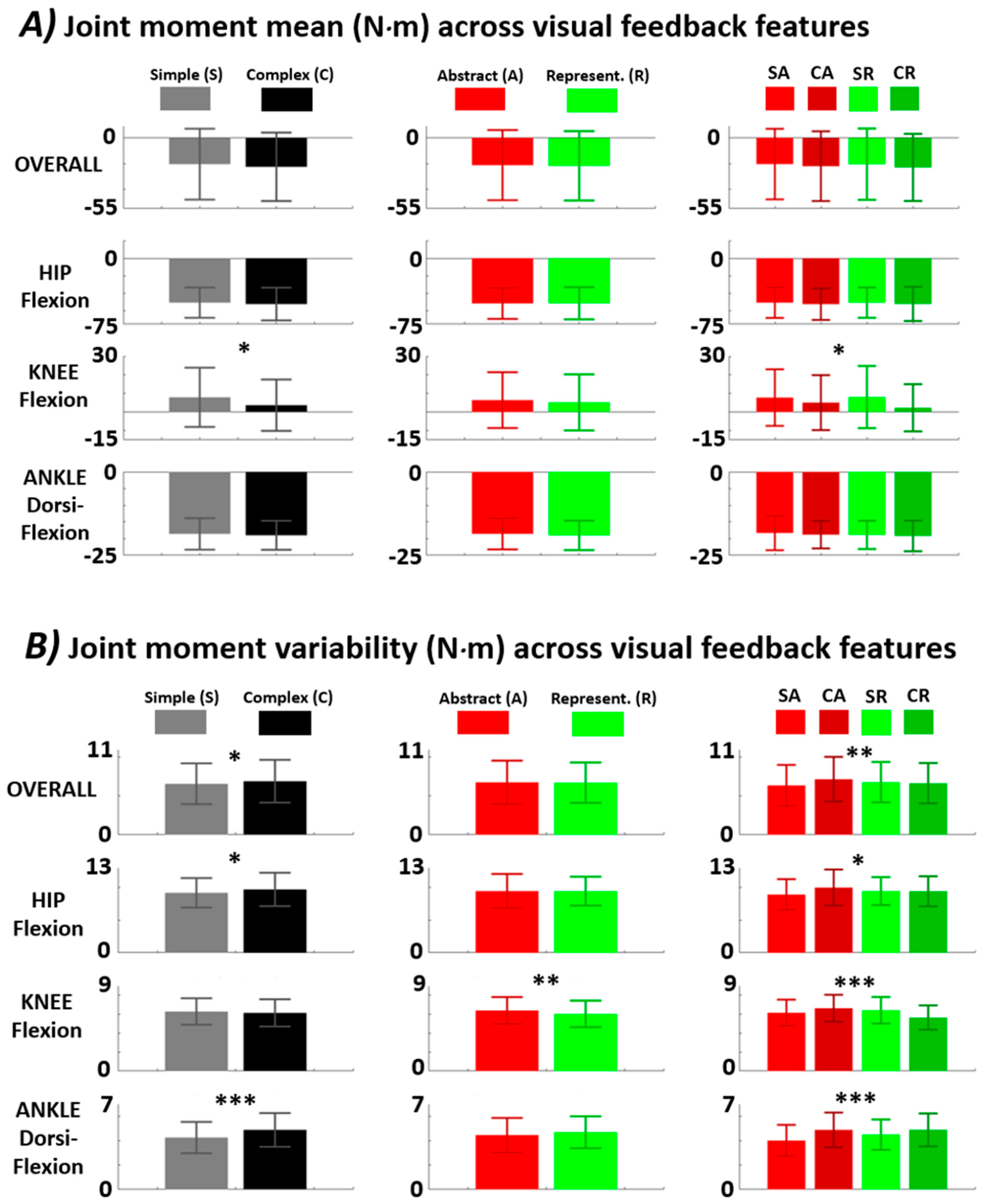
Overall0.19
(1.7)		−20.4 ± 27.6−22.5 ± 26.60.75
(0.11)		−21.2 ± 27.3−21.7 ± 27.00.78
(0.08)
Hip Flexion0.39
(0.74)		−50.5 ± 17.2−52.1 ± 18.70.93
(0.007)		−51.4 ± 17.6−51.2 ± 18.30.95
(0.005)
Knee Flexion5.4 × 10−3
(7.8)		7.8 ± 16.03.6 ± 13.80.42
(0.66)		6.4 ± 15.15.1 ± 15.10.31
(1.0)
Ankle Dorsi-Flexion0.38
(0.77)		−18.6 ± 4.7−19.0 ± 4.30.31
(1.0)		−18.5 ± 4.7−19.0 ± 4.40.83
(0.05)
Joint Moment Variability
tp-Val Complexity
(F-Stat)		Simple
Mean
Value in N·m		Complex Mean
Value
in N·m		p-Val Representation
(F-Stat)		Abstract
Mean
Value
in N·m		Representative
Mean
Value
in N·m		p-Val Interaction
(F-Stat)
Overall0.04
(4.4)		6.6 ± 2.66.9 ± 2.80.77
(0.09)		6.8 ± 2.86.7 ± 2.63.2 × 10−3
(8.8)
Hip Flexion0.04
(4.4)		9.2 ± 2.39.7 ± 2.50.94
(0.03)		9.4 ± 2.69.4 ± 2.20.03
(5.0)
Knee Flexion0.30
(1.1)		6.3 ± 1.46.1 ± 1.40.01
(6.73)		6.4 ± 1.46.0 ± 1.41.1 × 10−5
(19.9)
Ankle Dorsi-Flexion5.0 × 10−6
(21.5)		4.3 ± 1.34.9 ± 1.40.075
(3.2)		4.4 ± 1.44.7 ± 1.30.081
(3.1)
Note: significant p-values (<0.05) are bolded.
Table 2. Simple Effects (Across Visual Feedback Mode Pairs) for Joint Moment Mean and Variability during Training per Joint and Overall.
Table 2. Simple Effects (Across Visual Feedback Mode Pairs) for Joint Moment Mean and Variability during Training per Joint and Overall.
Joint Moment Mean
JointSimple-Abstract
Mean Value
in N·m		Simple-Representative Mean Value
in N·m		Complex-Abstract
Mean Value
in N·m		Complex-Representative Mean Value
in N·m		Significant Difference Pairs
(p-Val)
Overall−20.4 ± 27.5−22.0 ± 27.2−20.4 ± 27.8−23.0 ± 26.2N/A
Hip Flexion−50.5 ± 17.3−52.3 ± 17.9−50.5 ± 17.2−52.0 ± 19.4N/A
Knee Flexion7.7 ± 15.25.0 ± 14.88.0 ± 16.72.2 ± 12.7CA−CR (0.04)
Ankle Dorsi-Flexion−18.3 ± 5.2−18.8 ± 4.1−18.9 ± 4.2−19.2 ± 4.6N/A
Joint Moment Variability
JointSimple-Abstract
Mean Value in N·m		Simple-Representative Mean Value in N·mComplex-Abstract
Mean Value in N·m		Complex-Representative Mean Value in N·mSignificant Difference Pairs
(p-Val)
Overall6.4 ± 2.67.1 ± 2.96.8 ± 2.66.6 ± 2.6SA-SR (2 × 10−3)
Hip Flexion8.9 ± 2.49.9 ± 2.89.4 ± 2.19.4 ± 2.3SA-SR (0.01)
Knee Flexion6.2 ± 1.46.6 ± 1.46.4 ± 1.45.6 ± 1.3SA-CR (0.05), SR-CR (4 × 10−4), CA-CR (6 × 10−4)
Ankle Dorsi-Flexion4.0 ± 1.34.9 ± 1.44.5 ± 1.24.9 ± 1.3SA-SR (4 × 10−5), SA-CA (3 × 10−5)
Note: significant p-values (<0.05) are bolded; p-values are only shown with significant interaction or significant factor effect from two-way ANOVA.
Table 3. One-way ANOVA (i.e., across visual feedback mode pairs) for Joint Moment Mean and Variability Across Movement Phases during Training per Joint and Overall.
Table 3. One-way ANOVA (i.e., across visual feedback mode pairs) for Joint Moment Mean and Variability Across Movement Phases during Training per Joint and Overall.
Ankle Dorsi-FlexionKnee FlexionHip Flexion
EarlyTargetLateEarlyTargetLateEarlyTargetLate
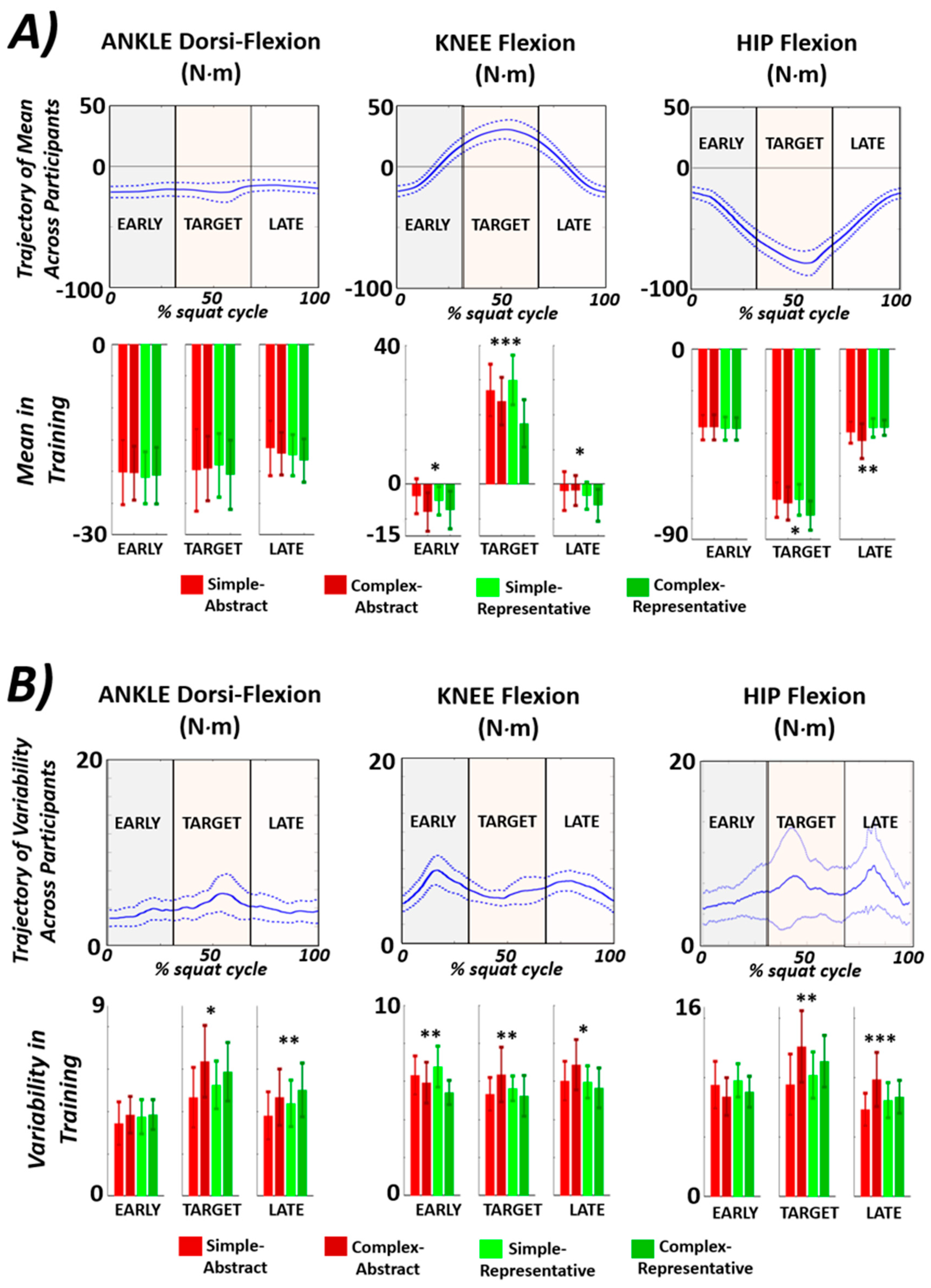
JT Mom Mean
p-val, (F-stat)		0.95
(0.12)		0.90
(0.20)		0.50
(0.79)		0.04
(2.9)		5 × 10−4
(9.15)		0.04
(2.9)		0.98
(0.07)		0.02
(3.5)		7 × 10−3
(4.4)
JT Mom
Variability
p-val (F-stat)		0.48
(0.83)		8 × 10−3
(4.4)		0.04
(2.9)		2 × 10−3
(5.7)		0.02
(3.8)		0.02
(3.8)		0.08
(2.3)		3 × 10−3
(5.1)		7 × 10−4
(6.4)
Note: significant p-values (<0.05) are bolded.
Table 4. Kinematic tracking performance (i.e., error to target trajectory) during training with each visual feedback mode. (note: these results were initially reported in studies [4,5]).
Table 4. Kinematic tracking performance (i.e., error to target trajectory) during training with each visual feedback mode. (note: these results were initially reported in studies [4,5]).
Simple-AbstractSimple-RepresentativeComplex-AbstractComplex-Representative
Accuracy
(mean error, degrees)		5.1 ± 1.33.0 ± 0.64.4 ± 1.45.2 ± 1.3
Consistency/precision
(s.d. of error, degrees)		3.5 ± 1.21.9 ± 0.62.4 ± 0.63.3 ± 0.7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Nataraj, R.; Sanford, S.P.; Liu, M. Joint Moment Responses to Different Modes of Augmented Visual Feedback of Joint Kinematics during Two-Legged Squat Training. Biomechanics 2023, 3, 425-442. https://doi.org/10.3390/biomechanics3030035

AMA Style

Nataraj R, Sanford SP, Liu M. Joint Moment Responses to Different Modes of Augmented Visual Feedback of Joint Kinematics during Two-Legged Squat Training. Biomechanics. 2023; 3(3):425-442. https://doi.org/10.3390/biomechanics3030035

Chicago/Turabian Style

Nataraj, Raviraj, Sean Patrick Sanford, and Mingxiao Liu. 2023. "Joint Moment Responses to Different Modes of Augmented Visual Feedback of Joint Kinematics during Two-Legged Squat Training" Biomechanics 3, no. 3: 425-442. https://doi.org/10.3390/biomechanics3030035

Article Metrics

Back to TopTop