Feasibility of a Full-Field Measurements-Based Protocol for the Biomechanical Study of a Lumbar Belt: A Case Study
Abstract
:1. Introduction
2. Materials and Methods
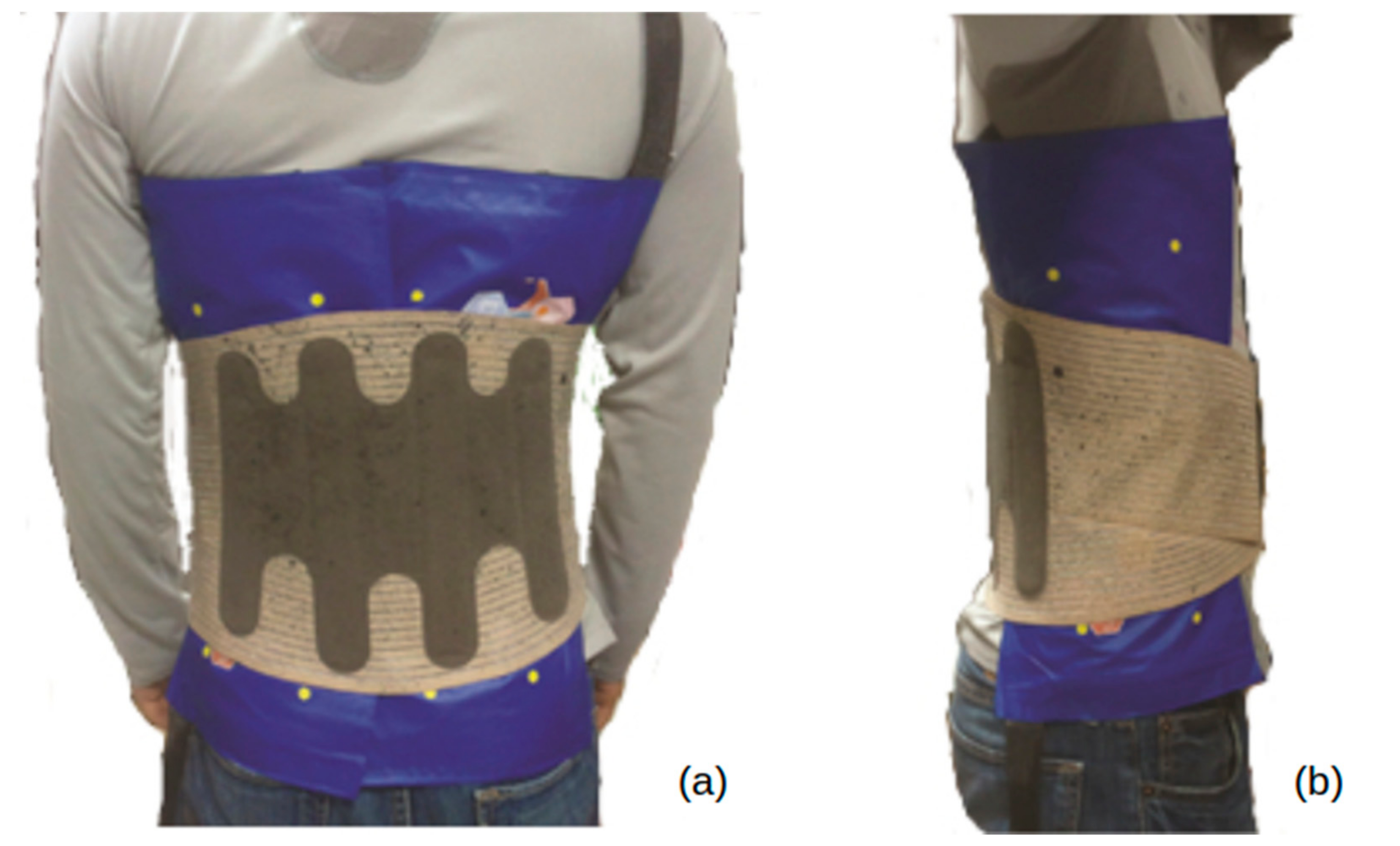
2.1. Study Subject and Lumbar Belts
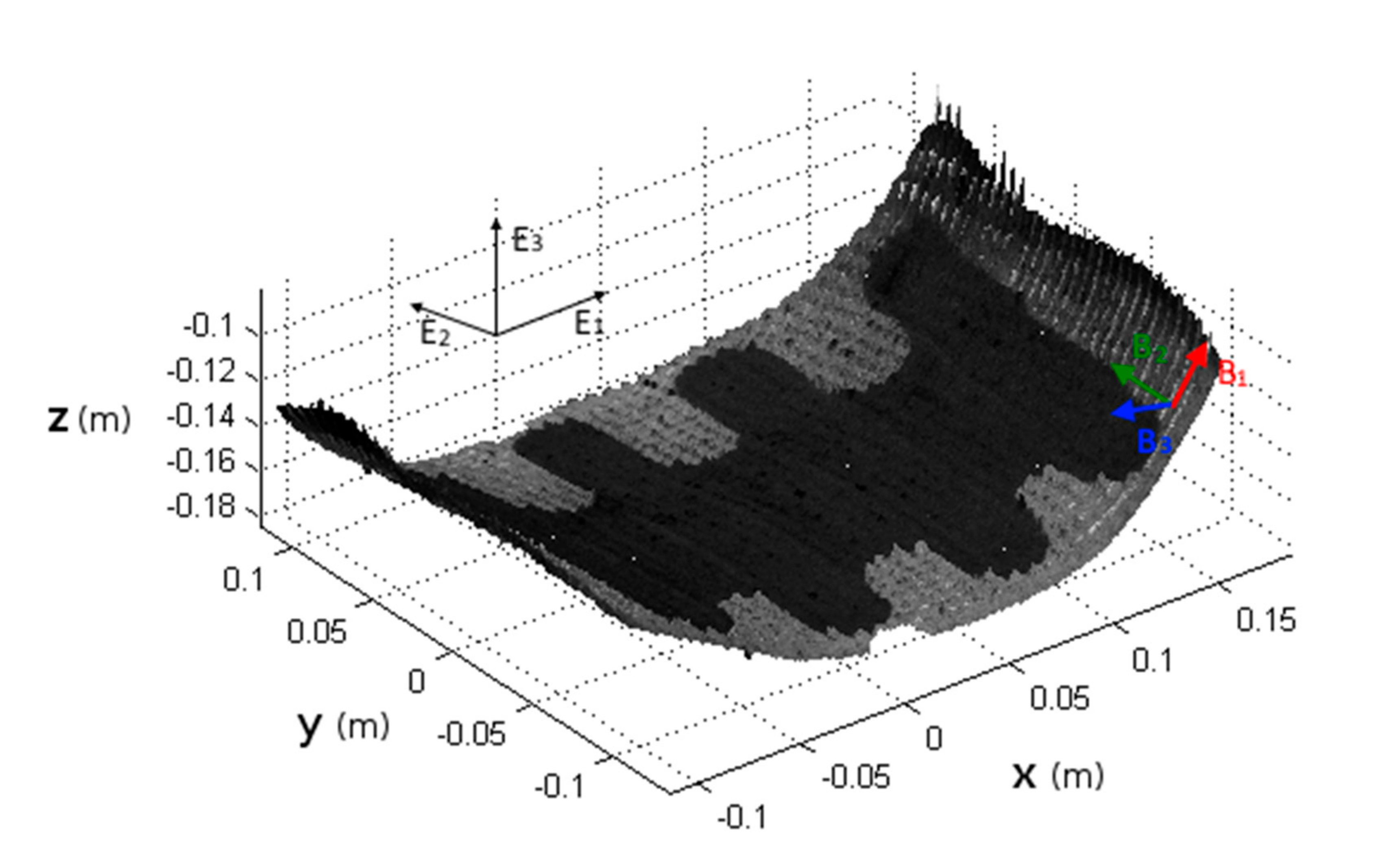
2.2. Measurements of Pressure and Strain
2.3. Measurement Protocol
- the subject puts on the T-shirt,
- the pressure sensor matrices are installed,
- the belt is put in position, flat against the trunk, but is not tightened,
- the shape and the reference images are obtained for the calculation of the displacement,
- the belt is tightened by 20% of its length,
- the deformed images are obtained for the calculation of the displacement and, at the same time, the interface pressure is measured.
2.4. Experimentation 1: Evaluation of the Measurement Protocol
- the T-shirt used to maintain the matrices between the lumbar belts and the trunk, with two different cuts (T-shirt 1 and T-shirt 2);
- the breath holding during the measurement, here breath was held at the end of inspiration or at the end of expiration;
- the position of the arms during the measurement, here, hands on shoulders, arms crossed or hands on shoulders folded to each side (Figure 4);
- In order to ensure that the influence of these parameters, if it exists, was not linked to a specific belt and a height of belt, the influence of the type of belt and its height was also evaluated. Only two belts (Belt A and Belt C) were considered in the study design in order to limit the number of tests. The belts were worn with a 20% overall stretch on the tightening side (right), for all the experiments in this design.
2.5. Experimentation 2: Application on Different Belts
2.6. Statistical Analysis
3. Results
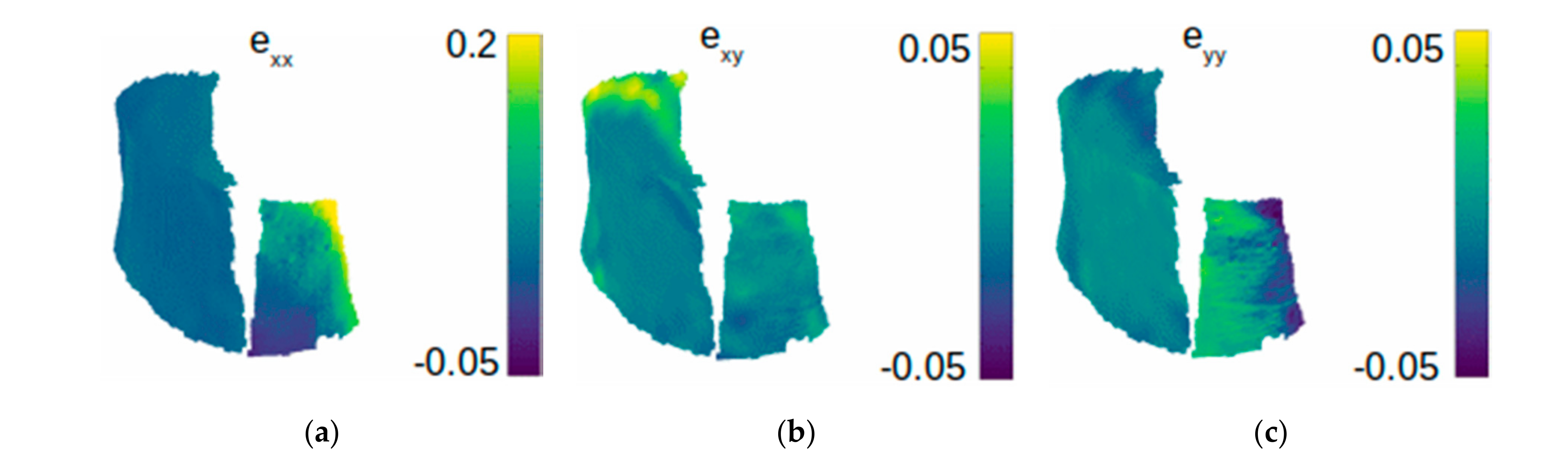
3.1. Experimentation 1: Evaluation of the Measurement Protocol
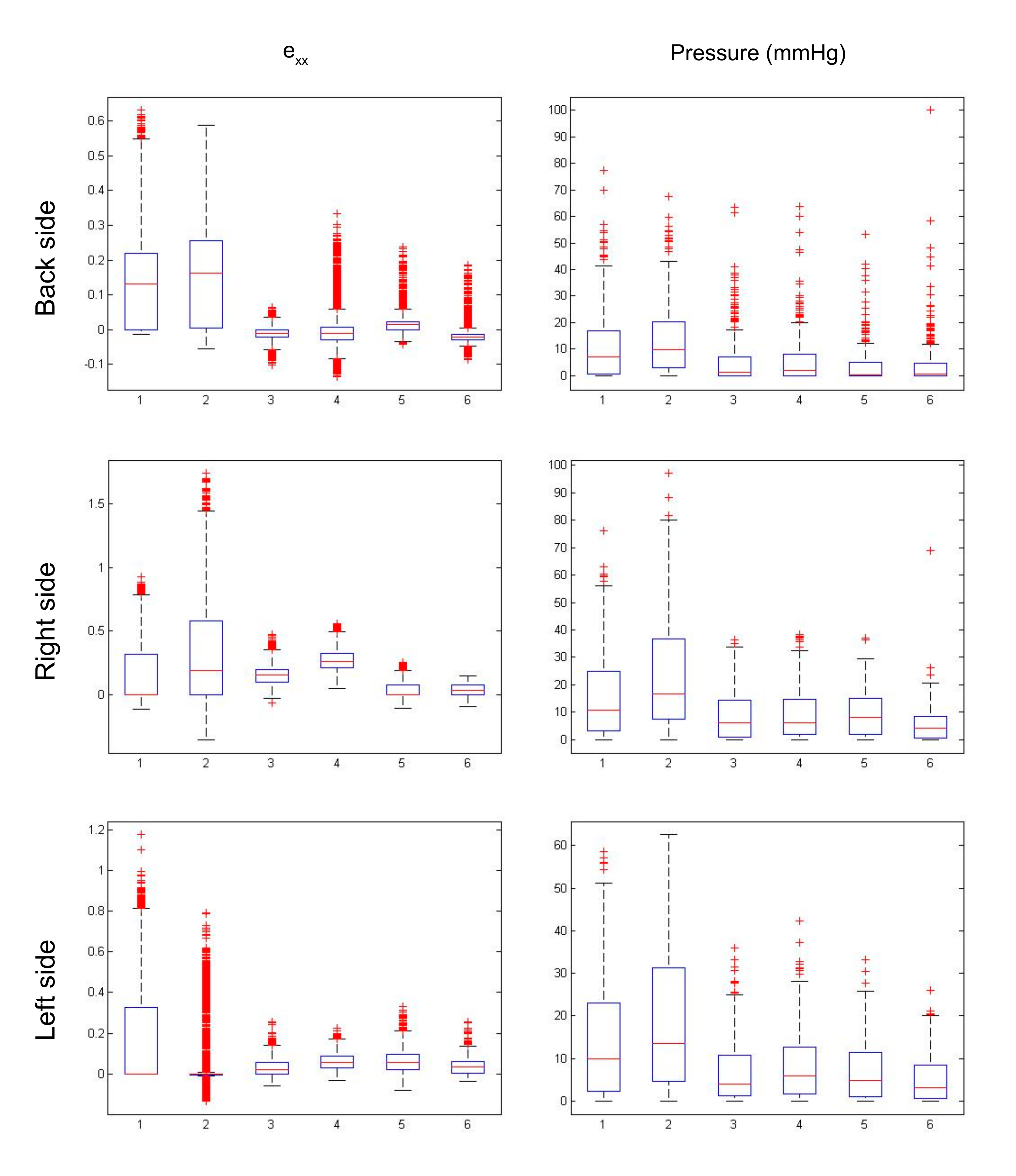
3.2. Experimentation 2: Application on Different Belt Configurations
4. Discussion
4.1. Experimentation 1: Validity of the Measurements
4.2. Experimentation 2: Application on Different Belt Configurations
4.3. Method of Action of Lumbar Belts
4.4. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fassier, J.-B. Prévalence, coûts et enjeux sociétaux de la lombalgie. Rev. Rhum. 2011, 78, S38–S41. [Google Scholar] [CrossRef]
- Krismer, M.; Van Tulder, M. Low back pain (non-specific). Best Practice & Research Clinical. Rheumatology 2007, 21, 77–91. [Google Scholar] [CrossRef]
- Stucki, R.F.; Waldburger, M. Approche multidisciplinaire de la lombalgie commune subaiguë et chronique: Expérience suisse romande. Rev. Rhum. 2001, 68, 178–184. [Google Scholar] [CrossRef]
- Widerström, B.; Olofsson, N.; Arvidsson, I.; Harms-Ringdahl, K.; Larsson, U.E. Inter-examiner reliability of a proposed decision-making treatment based classification system for low back pain patients. Manual. Ther. 2012, 17, 164–171. [Google Scholar] [CrossRef] [Green Version]
- Demoulin, C.; Grosdent, S.; Capron, L.; Tomasella, M.; Somville, P.R.; Crielaard, J.M.; Vanderthommen, M. Intérêt d’une prise en charge multidisciplinaire ambulatoire semi-intensive dans la lombalgie chronique. Rev. Rhum. 2010, 77, 68–73. [Google Scholar] [CrossRef]
- Hill, J.C.; Fritz, J.M. Psychosocial influences on low back pain, disability, and response to treatment. Phys. Ther. 2011, 91, 712–721. [Google Scholar] [CrossRef]
- Martin-Mattera, P.; Thanh-Huê, L.; Garnier, F.; Huez, J.F.; Benoist, V. Chronic low back pain: Symptom or no symptom? Evol. Psychiatr. 2010, 75, 607–620. [Google Scholar] [CrossRef] [Green Version]
- Thoumie, P.; Drape, J.L.; Aymard, C.; Bedoiseau, M. Effects of a lumbar support on spine posture and motion assessed by electrogoniometer and recording. Clin. Biomech. 1998, 13, 18–26. [Google Scholar] [CrossRef]
- Dalichau, S.; Scheele, K. Auswirkungen elastischer lumbal-stützgurte auf den effekt eines muskeltrainingsprogrammes für patienten mit chronischen rückenschmerzen. Z. Orthop. Grenzgeb. 2000, 138, 8–16. [Google Scholar] [CrossRef]
- Cholewicki, J.; Shah, K.R.; McGill, K.C. The effects of a 3-week use of lumbosacral orthoses on proprioception in the lumbar spine. J. Orthop. Sports Phys. 2006, 36, 225–231. [Google Scholar] [CrossRef]
- Han, W.S.; Molimard, J.; Pierrat, B.; Fortas, S.; Pannetier, R.; Convert, R. Biomechanical consequences of lumbar belt design for the therapeutic treatment of low back pain. undefined. Comput. Method Biomech. 2019, 22, S17–S19. [Google Scholar] [CrossRef]
- Bonnaire, R.; Han, W.-S.; Calmels, P.; Convert, R.; Molimard, J. Parametric Study of Lumbar Belts in the Case of Low Back Pain: Effect of Patients' Specific Characteristics. In Computational Biomechanics for Medicine; Nash, M.P., Nielsen, P.M., Wittek, A., Miller, K., Joldes, G.R., Eds.; Springer International Publishing: Heidelberg, Germany, 2020; pp. 43–59. [Google Scholar] [CrossRef]
- Nachemson, A.; Morris, J.M. In vivo measurements of intradiscal pressure: Discometry, a method for the determination of pressure in the lower lumbar discs. J. Bone Jt. Surg. 1964, 46, 1077–1092. [Google Scholar] [CrossRef]
- Andersson, B.J.; Ortengren, R.; Nachemson, A.; Elfstrom, G. Lumbar disc pressure and myoelectric back muscle activity during sitting. Scand. J. Rehabil. Med. 1974, 6, 104–133. [Google Scholar]
- McGill, S.M.; Norman, R.W.; Sharratt, M.T. The effect of an abdominal belt on trunk muscle activity and intra-abdominal pressure during squat lifts. Ergonomics 1990, 33, 147–160. [Google Scholar] [CrossRef]
- Calmels, P.; Fayolle-Minon, I. An update on orthotic devices for the lumbar spine based on a review of the literature. Rev. Rhum. 1996, 63, 285–291. [Google Scholar]
- Fidler, M.W.; Plasmans, C.M. The effect of four types of support on the segmental mobility of the lumbosacral spine. J. Bone Jt. Surg. Am. 1983, 65, 943–947. [Google Scholar] [CrossRef]
- Willner, S. Effect of a rigid brace on back pain. Acta Orthop. 1985, 56, 40–42. [Google Scholar] [CrossRef]
- Valle-Jones, J.C.; Walsh, H.; O’Hara, J.; O’Hara, H.; Davey, N.B.; Hopkin-Richards, H. Controlled trial of a back support (‘lumbotrain’) in patients with non-specific low back pain. Curr. Med. Res. Opin. 1992, 12, 604–613. [Google Scholar] [CrossRef]
- Million, R.; Nilsen, K.H.; Jayson, M.I.; Baker, R.D. Evaluation of low back pain and assessment of lumbar corsets with and without back supports. Ann. Rheum. Dis. 1981, 40, 449–454. [Google Scholar] [CrossRef] [Green Version]
- Kawaguchi, Y.; Gejo, R.; Kanamori, M.; Kimura, T. Quantitative analysis of the effect of lumbar orthosis on trunk muscle strength and muscle activity in normal subjects. J. Orthop. Sci. 2002, 7, 483–489. [Google Scholar] [CrossRef]
- Holmström, E.; Moritz, U. Effects of lumbar belts on trunk muscle strength and endurance: A follow-up study of construction workers. J. Spinal. Disord. Tech. 1992, 5, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Calmels, P.; Queneau, P.; Hamonet, C.; Le Pen, C.; Maurel, F.; Lerouvreur, C.; Thoumie, P. Effectiveness of a lumbar belt in subacute low back pain: An open, multicentric, and randomized clinical study. Spine 2009, 34, 215–220. [Google Scholar] [CrossRef] [PubMed]
- Schott, C.; Zirke, S.; Schmelzle, J.M.; Kaiser, C.; Fernández, L.A.I. Effectiveness of lumbar orthoses in low back pain: Review of the literature and our results. Orthop. Rev. 2018, 10, 7791. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Renya, J.R.; Legget, S.H.; Kenney, K.; Holmes, B.; Mooney, V. The effect of lumbar belts on isolated lumbar muscle. Strength and dynamic capacity. Spine 1995, 20, 68–73. [Google Scholar] [CrossRef]
- Warren, L.P.; Appling, S.; Oladehin, A.; Griffin, J. Effect of soft lumbar support belt on abdominal oblique muscle activity in nonimpaired adults during squat lifting. J. Orthop. Sport Phys. 2001, 31, 316–323. [Google Scholar] [CrossRef] [Green Version]
- Fayolle-Minon, I.; Calmels, P. Effect of wearing a lumbar orthosis on trunk muscles: Study of the muscle strength after 21days of use on healthy subjects. Jt. Bone Spine 2008, 75, 58–63. [Google Scholar] [CrossRef]
- Anders, C.; Hübner, A. Influence of elastic lumbar support belts on trunk muscle function in patients with non-specific acute lumbar back pain. PLoS ONE 2019, 14, e0211042. [Google Scholar] [CrossRef]
- Molimard, J.; Bonnaire, R.; Han, W.S.; Convert, R.; Calmels, P. In-silico pre-clinical trials are made possible by a new simple and comprehensive lumbar belt mechanical model based on the Law of Laplace including support deformation and adhesion effects. PLoS ONE 2019, 14, e0212681. [Google Scholar] [CrossRef]
- Abdul Razak, A.H.; Zayegh, A.; Begg, R.K.; Wahab, Y. Foot Plantar Pressure Measurement System: A Review. Sensors 2012, 12, 9884. [Google Scholar] [CrossRef] [Green Version]
- Romano, E.; Pirozzi, M.; Ferri, M.; Calcante, A.; Oberti, R.; Vitale, E.; Rapisarda, V. The use of pressure mapping to assess the comfort of agricultural machinery seats, Int. J. Ind. Ergonom. 2020, 77, 102835. [Google Scholar] [CrossRef]
- Pierrat, B.; Millot, C.; Molimard, J.; Navarro, L.; Calmels, P.; Edouard, P.; Avril, S. Characterisation of knee brace migration and associated skin deformation during flexion by full-field measurements. Exp. Mech. 2014, 55, 349–360. [Google Scholar] [CrossRef] [Green Version]
- Solav, D.; Moerman, K.M.; Jaeger, A.M.; Genovese, K.; Herr, H.M. MultiDIC: An open-source toolbox for multi-view 3D digital image correlation. IEEE Access 2018, 6, 30520–30535. [Google Scholar] [CrossRef]
- Bonnaire, R.; Verhaeghe, M.; Molimard, J.; Calmels, P.; Convert, R. Characterization of a pressure measuring system for the evaluation of medical devices. Part H J. Eng. Med. 2014, 228, 1264–1274. [Google Scholar] [CrossRef]
- Molimard, J.; Boyer, G.; Zahouani, H. Frequency-based image analysis of random patterns: An alternative way to classical stereocorrelation. J. Korean Soc. Nondestruc. Test. 2010, 30, 181–193. [Google Scholar]
- Chassagne, F.; Martin, F.; Badel, P.; Convert, R.; Giraux, P.; Molimard, J. Experimental investigation of pressure applied on the lower leg by elastic compression bandage. Ann. Biomed. Eng. 2015, 43, 2967–2977. [Google Scholar] [CrossRef] [Green Version]
- Kumar, B.; Das, A.; Alagirusamy, R. Effect of material and structure of compression bandage on interface pressure variation over time. Phlebology 2013, 29, 376–385. [Google Scholar] [CrossRef]
- Partsch, H.; Partsch, B.; Braun, W. Interface pressure and stiffness of ready made compression stockings: Comparison of in vivo and in vitro measurements. J. Vasc. Surg. 2006, 44, 809–814. [Google Scholar] [CrossRef]
- Troynikov, O.; Wardiningsih, W.; Koptug, A.; Watson, C.; Oggiano, L. Influence of material properties and garment composition on pressure generated by sport compression garments. Procedia Eng. 2013, 60, 157–162. [Google Scholar] [CrossRef] [Green Version]
- Aubin, C.-E.; Labelle, H.; Cheriet, F.; Villemure, I.; Mathieu, P.A.; Dansereau, J. Évaluation tridimensionnelle et optimisation du traitement orthopédique de la scoliose idiopathique adolescente. Med. Sci. 2007, 23, 904–909. [Google Scholar] [CrossRef] [Green Version]
- Van den Hout, J.; Van Rhijn, L.; Van den Munckhof, R.; Van Ooy, A. Interface corrective force measurements in Boston brace treatment. Eur. Spine J. 2002, 11, 332–335. [Google Scholar] [CrossRef] [Green Version]
- Gesbert, J.C.; Colobert, B.; Rakotomanana, L.; Violas, P. Idiopathic scoliosis and brace treatment: An innovative device to assess corrective pressure? Comput. Method Biomech. 2021, 24, 131–136. [Google Scholar] [CrossRef] [PubMed]
- Munoz, M.-F.; Salmochi, J.-F.; Rougier, P.; Calmels, P.; Badel, P.; Molimard, J.; Avril, S. New non-invasive and patient-specific method allowing intradiscal pressure change measurement induced by lumbar conservative or surgical treatments. Ann. Phys. Rehab. Med. 2012, 55, e280. [Google Scholar] [CrossRef] [Green Version]



| Experiment | T-Shirts −1: T-Shirt 1 +1: T-Shirt 2 | Position of the Arms −1: Crossed +1: Folded to Each Side | Breathing −1: End of Inspiration +1: End of Expiration | Belt −1: Belt C +1: Belt A | Height −1: 26 cm +1: 21 cm |
|---|---|---|---|---|---|
| #1 | −1 | −1 | −1 | −1 | +1 |
| #2 | +1 | −1 | −1 | −1 | −1 |
| #3 | −1 | +1 | −1 | −1 | −1 |
| #4 | +1 | +1 | −1 | −1 | +1 |
| #5 | −1 | −1 | +1 | −1 | −1 |
| #6 | +1 | −1 | +1 | −1 | +1 |
| #7 | −1 | +1 | +1 | −1 | +1 |
| #8 | +1 | +1 | +1 | −1 | −1 |
| #9 | −1 | −1 | −1 | +1 | −1 |
| #10 | +1 | −1 | −1 | +1 | +1 |
| #11 | −1 | +1 | −1 | +1 | +1 |
| #12 | +1 | +1 | −1 | +1 | −1 |
| #13 | −1 | −1 | +1 | +1 | +1 |
| #14 | +1 | −1 | +1 | +1 | −1 |
| #15 | −1 | +1 | +1 | +1 | −1 |
| #16 | +1 | +1 | +1 | +1 | +1 |
| Sensitivity | p | exx | exy | eyy |
|---|---|---|---|---|
| on the Back | (mmHg) | (10−2 m/m) | (10−2 m/m) | (10−2 m/m) |
| Mean value | 5.395 *** | 8.42 *** | −2.25 *** | 0.03 |
| T-shirt | −0.44 ° | −0.24 | 0.89 ° | −0.35 |
| Arms position | −0.45 ° | −0.78 | 0.77 | −0.56 |
| Breathing | −0.59 * | −0.23 | −0.37 | 0.29 |
| Belt type | −2.68 *** | −6.87 *** | 0.95 ° | 0.23 |
| Belt height | −0.4 | −1.62° | 1.29 * | −0.13 |
| R2 | 0.94 | 0.89 | 0.67 | 0.22 |
| Sensitivity | p | exx | exy | eyy |
| on the right side | (mmHg) | (10−2 m/m) | (10−2 m/m) | (10−2 m/m) |
| Mean value | 9.42 *** | 18.95 *** | −5.44 | 1.04 |
| T-shirt | −1.12 * | −1.21 | −2.75 | −0.76 |
| Arms position | −1.07 * | −2.06 | 2.90 | −2.64 * |
| Breathing | −0.98 ° | 4.09 | 3.87 | −1.96 ° |
| Belt type | −2.35 *** | 7.56 * | −3.37 | −1.86 |
| Belt height | −1.08 * | −8.52 * | −3.37 | 3.34 * |
| R2 | 0.83 | 0.60 | 0.26 | 0.69 |
| Sensitivity | p | exx | exy | eyy |
| on the left side | (mmHg) | (10−2 m/m) | (10−2 m/m) | (10−2 m/m) |
| Mean value | 11.92 *** | 28.18 *** | 2.53 | −7.37 * |
| T-shirt | −1.30 * | −4.88 | −1.84 | 0.96 |
| Arms position | 0.01 | 4.26 | 1.38 | −0.13 |
| Breathing | −0.49 | −5.99 ° | −1.84 | 2.95 |
| Belt type | −4.47 *** | −20.15 *** | −9.87 ° | 8.26 ** |
| Belt height | −2.22 ** | 7.27 ° | −0.28 | 1.45 |
| R2 | 0.92 | 0.82 | 0.43 | 0.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonnaire, R.; Han, W.S.; Convert, R.; Calmels, P.; Molimard, J. Feasibility of a Full-Field Measurements-Based Protocol for the Biomechanical Study of a Lumbar Belt: A Case Study. Biomechanics 2022, 2, 174-188. https://doi.org/10.3390/biomechanics2020015
Bonnaire R, Han WS, Convert R, Calmels P, Molimard J. Feasibility of a Full-Field Measurements-Based Protocol for the Biomechanical Study of a Lumbar Belt: A Case Study. Biomechanics. 2022; 2(2):174-188. https://doi.org/10.3390/biomechanics2020015
Chicago/Turabian StyleBonnaire, Rébecca, Woo Suck Han, Reynald Convert, Paul Calmels, and Jérôme Molimard. 2022. "Feasibility of a Full-Field Measurements-Based Protocol for the Biomechanical Study of a Lumbar Belt: A Case Study" Biomechanics 2, no. 2: 174-188. https://doi.org/10.3390/biomechanics2020015
APA StyleBonnaire, R., Han, W. S., Convert, R., Calmels, P., & Molimard, J. (2022). Feasibility of a Full-Field Measurements-Based Protocol for the Biomechanical Study of a Lumbar Belt: A Case Study. Biomechanics, 2(2), 174-188. https://doi.org/10.3390/biomechanics2020015







