Fluid–Structure Interaction Modeling of Ascending Thoracic Aortic Aneurysms in SimVascular
Abstract
1. Introduction
2. Methods
2.1. Overview of Mathematical Models
2.1.1. Fluid Domain
2.1.2. Solid Domain
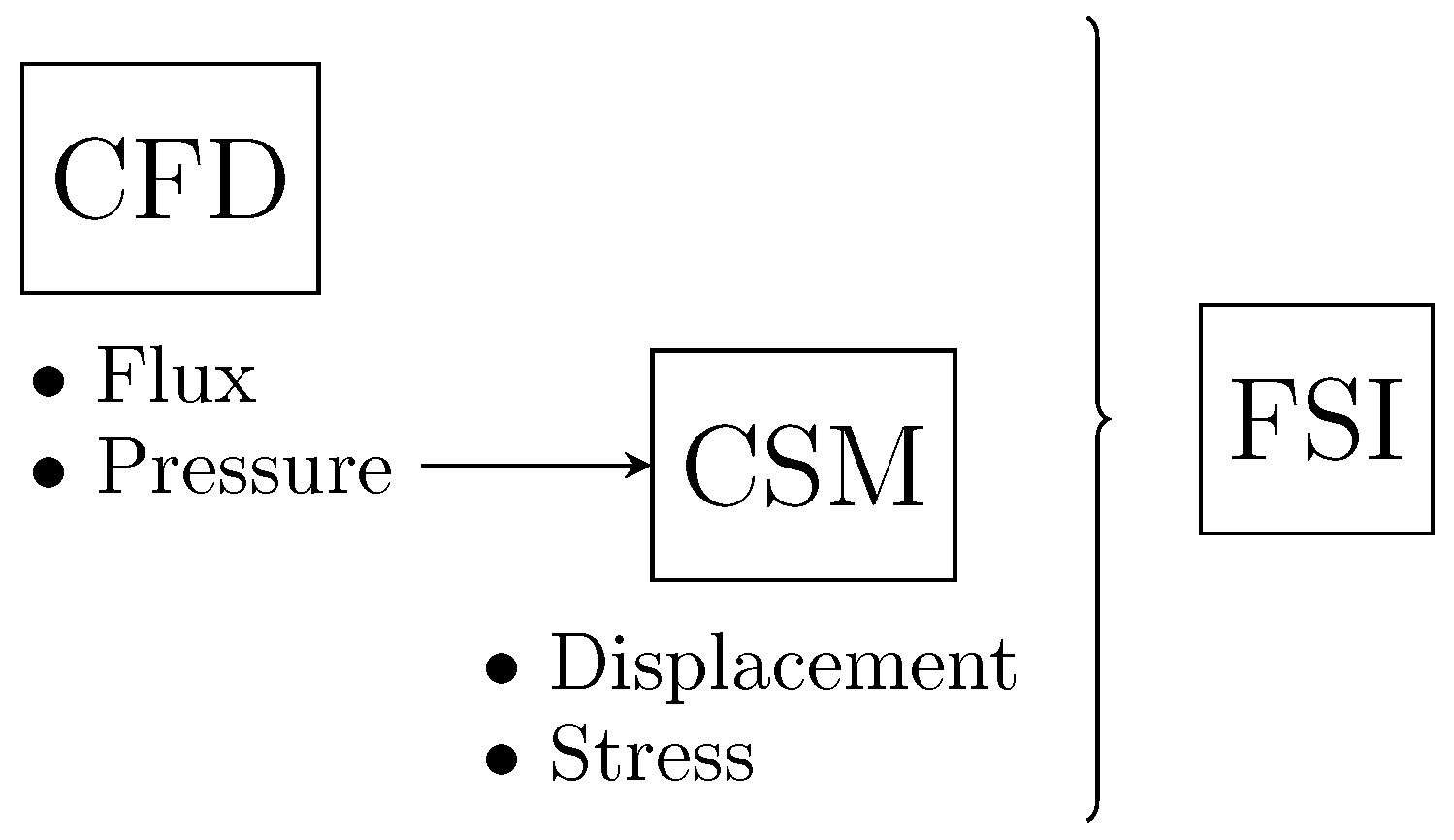
2.1.3. Fluid–Structure Interaction
2.2. Hyperelastic Constitutive Model
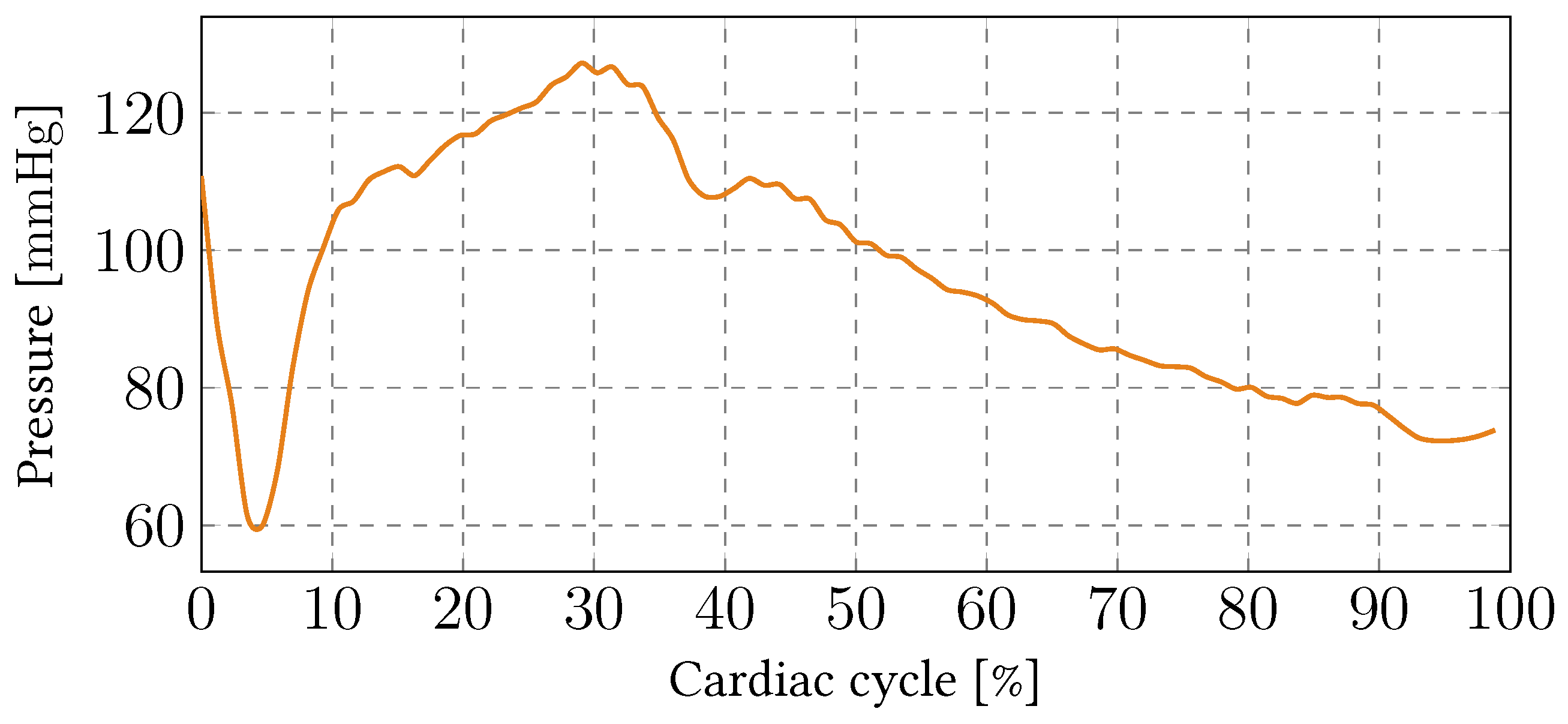
2.3. Boundary Conditions
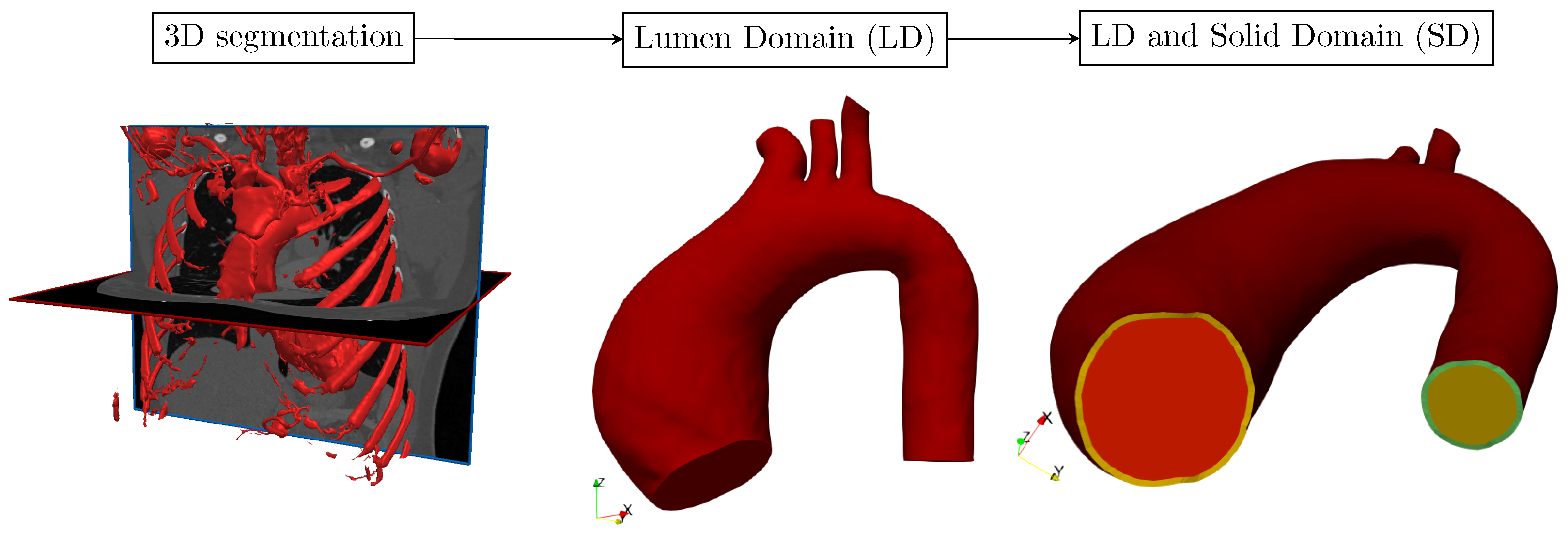
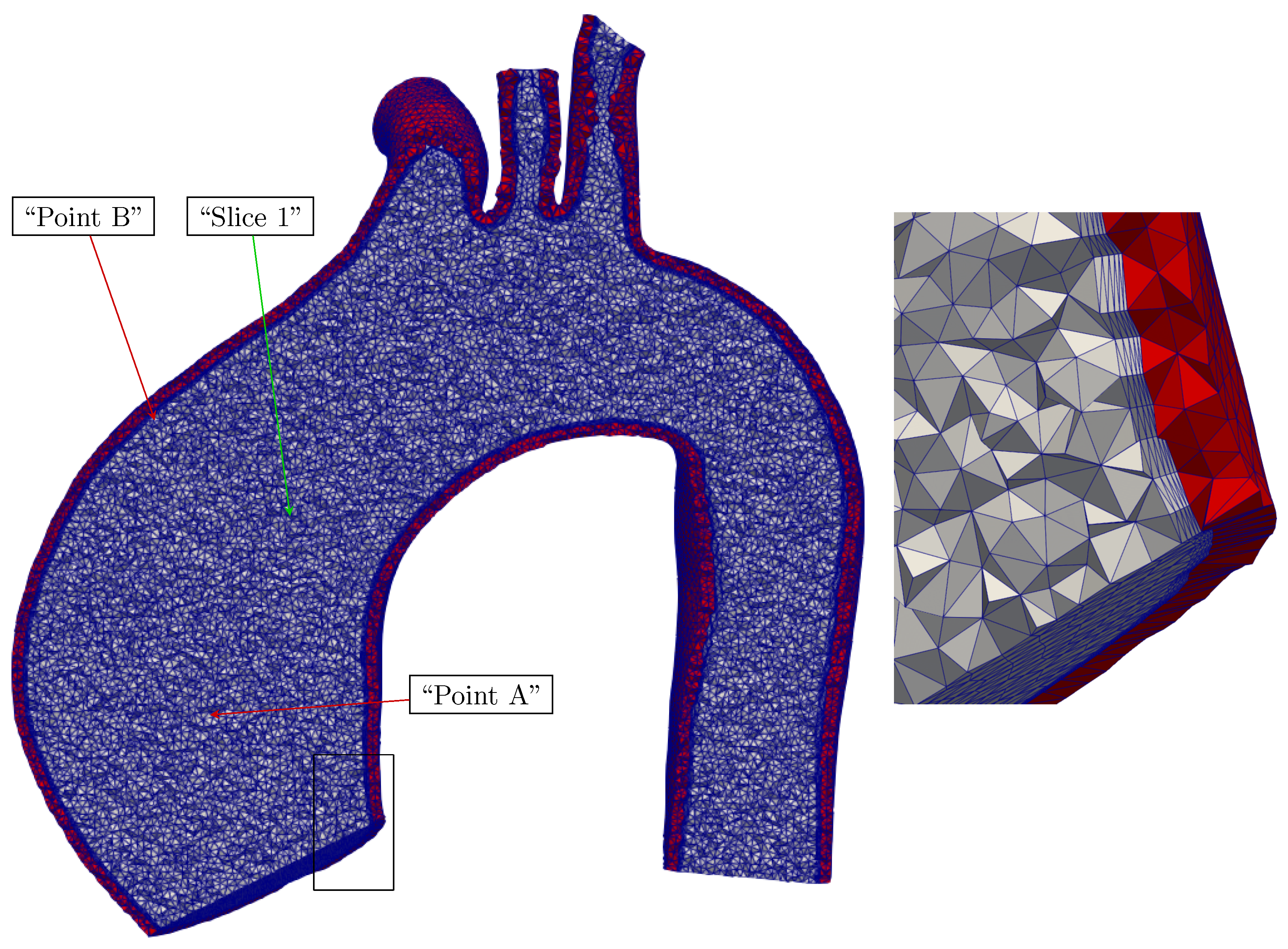
2.4. Mesh Development Workflow in SimVascular
3. Results
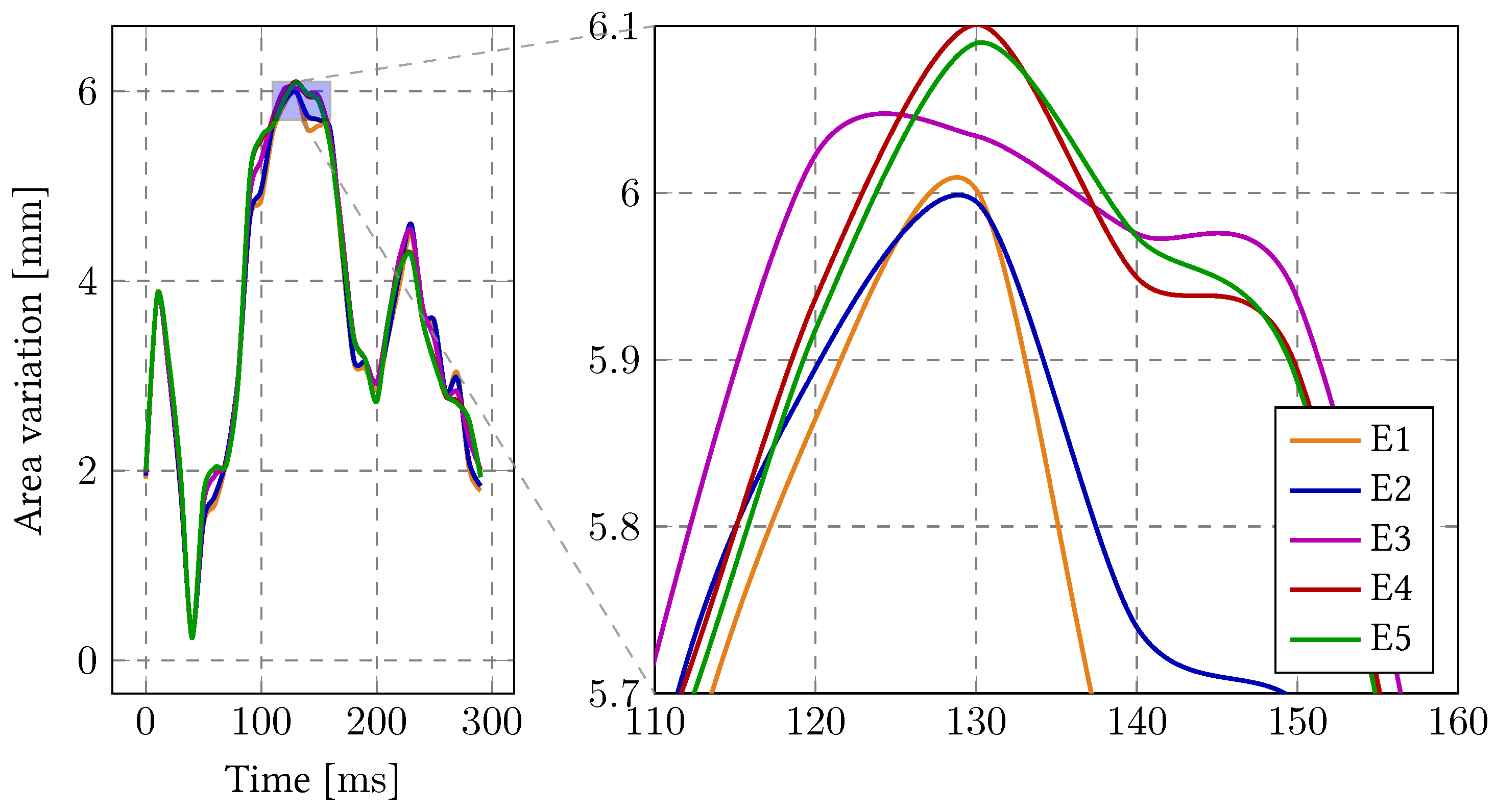
3.1. Sensitivity Analysis
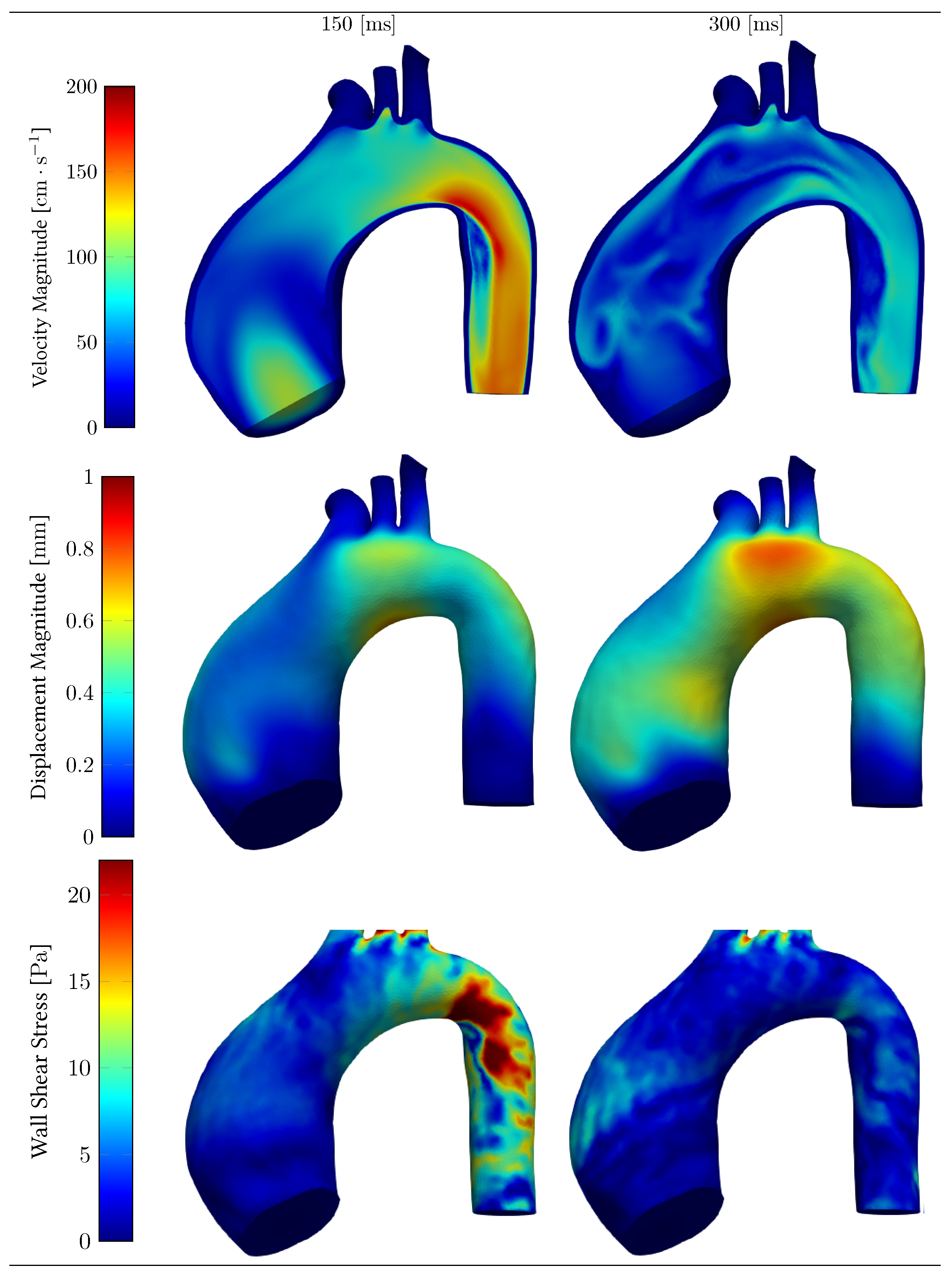
3.2. Hemodynamics and Structural Capabilities
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AD | Aortic Dissection |
| ALE | Arbitrary Lagrangian–Eulerian |
| AI | Artificial Intelligence |
| ATAA | Ascending Thoracic Aortic Aneurysm |
| CSM | Computational Solid Mechanics |
| CFD | Computational Fluid Dynamics |
| CT | Computed Tomography scan |
| ESC | European Society of Cardiology |
| FSI | Fluid–Structure Interaction |
| LD | Luminal Domain |
| MRI | Magnetic Resonance Imaging |
| NAE | Normalized Amplitude Error |
| NPAE | Normalized Phase Amplitude Error |
| ROI | Region of Interest |
| SD | Solid Domain |
| WSS | Wall Shear Stress |
| FEM | Finite Element Method |
| FEA | Finite Element Analysis |
| BAV | Bicuspid Aortic Valve |
References
- Dieter, R.; Dieter, R.; Dieter, R., III. Diseases of the Aorta; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Pasta, S.; Rinaudo, A.; Luca, A.; Pilato, M.; Scardulla, C.; Gleason, T.G.; Vorp, D.A. Difference in hemodynamic and wall stress of ascending thoracic aortic aneurysms with bicuspid and tricuspid aortic valve. J. Biomech. 2013, 46, 1729–1738. [Google Scholar] [CrossRef] [PubMed]
- Erbel, R.; Aboyans, V.; Boileau, C.; Bossone, E.; Bartolomeo, R.D.; Eggebrecht, H.; Evangelista, A.; Falk, V.; Frank, H.; Gaemperli, O.; et al. 2014 ESC guidelines on the diagnosis and treatment of aortic diseases. Eur. Heart J. 2014, 35, 2873–2926. [Google Scholar] [CrossRef]
- Maiti, S.; Thunes, J.R.; Fortunato, R.N.; Gleason, T.G.; Vorp, D.A. Computational modeling of the strength of the ascending thoracic aortic media tissue under physiologic biaxial loading conditions. J. Biomech. 2020, 108, 109884. [Google Scholar] [CrossRef]
- Farzaneh, S.; Trabelsi, O.; Avril, S. Inverse identification of local stiffness across ascending thoracic aortic aneurysms. Biomech. Model. Mechanobiol. 2019, 18, 137–153. [Google Scholar] [CrossRef] [PubMed]
- Trimarchi, S.; Jonker, F.H.; Hutchison, S.; Isselbacher, E.M.; Pape, L.A.; Patel, H.J.; Froehlich, J.B.; Muhs, B.E.; Rampoldi, V.; Grassi, V.; et al. Descending aortic diameter of 5.5 cm or greater is not an accurate predictor of acute type B aortic dissection. J. Thorac. Cardiovasc. Surg. 2011, 142, e101–e107. [Google Scholar] [CrossRef] [PubMed]
- Youssefi, P.; Sharma, R.; Figueroa, C.A.; Jahangiri, M. Functional assessment of thoracic aortic aneurysms—The future of risk prediction? Br. Med. Bull. 2017, 121, 61–71. [Google Scholar] [CrossRef]
- Gzik-Zroska, B.; Joszko, K.; Wolański, W.; Gzik, M. Development of New Testing Method of Mechanical Properties of Porcine Coronary Arteries. In Information Technologies in Medicine; Piętka, E., Badura, P., Kawa, J., Wieclawek, W., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; Volume 472, pp. 289–297. [Google Scholar] [CrossRef]
- Youssefi, P.; Gomez, A.; He, T.; Anderson, L.; Bunce, N.; Sharma, R.; Figueroa, C.A.; Jahangiri, M. Patient-specific computational fluid dynamics—Assessment of aortic hemodynamics in a spectrum of aortic valve pathologies. J. Thorac. Cardiovasc. Surg. 2017, 153, 8–20.e3. [Google Scholar] [CrossRef]
- Mourato, A.; Brito, M.; Xavier, J.; Gil, L.; Tomás, A. On the RANS modelling of the patient-specific thoracic aortic aneurysm. In Advances and Current Trends in Biomechanics; CRC Press: Boca Raton, FL, USA, 2021; pp. 98–102. [Google Scholar]
- Shang, E.K.; Nathan, D.P.; Sprinkle, S.R.; Vigmostad, S.C.; Fairman, R.M.; Bavaria, J.E.; Gorman, R.C.; Gorman, J.H., III; Chandran, K.B.; Jackson, B.M. Peak wall stress predicts expansion rate in descending thoracic aortic aneurysms. Ann. Thorac. Surg. 2013, 95, 593–598. [Google Scholar] [CrossRef]
- Gültekin, O.; Hager, S.P.; Dal, H.; Holzapfel, G.A. Computational modeling of progressive damage and rupture in fibrous biological tissues: Application to aortic dissection. Biomech. Model. Mechanobiol. 2019, 18, 1607–1628. [Google Scholar] [CrossRef]
- Mousavi, S.J.; Jayendiran, R.; Farzaneh, S.; Campisi, S.; Viallon, M.; Croisille, P.; Avril, S. Coupling hemodynamics with mechanobiology in patient-specific computational models of ascending thoracic aortic aneurysms. Comput. Methods Programs Biomed. 2021, 205, 106107. [Google Scholar] [CrossRef]
- Taghizadeh, H.; Tafazzoli-Shadpour, M.; Shadmehr, M.B. Analysis of arterial wall remodeling in hypertension based on lamellar modeling. J. Am. Soc. Hypertens. 2015, 9, 735–744. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Liang, L.; Sun, W. Estimation of in vivo mechanical properties of the aortic wall: A multi-resolution direct search approach. J. Mech. Behav. Biomed. Mater. 2018, 77, 649–659. [Google Scholar] [CrossRef] [PubMed]
- Thunes, J.R.; Phillippi, J.A.; Gleason, T.G.; Vorp, D.A.; Maiti, S. Structural modeling reveals microstructure-strength relationship for human ascending thoracic aorta. J. Biomech. 2018, 71, 84–93. [Google Scholar] [CrossRef] [PubMed]
- Capellini, K.; Vignali, E.; Costa, E.; Gasparotti, E.; Biancolini, M.E.; Landini, L.; Positano, V.; Celi, S. Computational fluid dynamic study for aTAA hemodynamics: An integrated image-based and radial basis functions mesh morphing approach. J. Biomech. Eng. 2018, 140, 111007. [Google Scholar] [CrossRef]
- Thunes, J.R.; Pal, S.; Fortunato, R.N.; Phillippi, J.A.; Gleason, T.G.; Vorp, D.A.; Maiti, S. A structural finite element model for lamellar unit of aortic media indicates heterogeneous stress field after collagen recruitment. J. Biomech. 2016, 49, 1562–1569. [Google Scholar] [CrossRef]
- Ban, E.; Cavinato, C.; Humphrey, J.D. Differential propensity of dissection along the aorta. Biomech. Model. Mechanobiol. 2021, 20, 895–907. [Google Scholar] [CrossRef]
- Wang, R.; Yu, X.; Gkousioudi, A.; Zhang, Y. Effect of Glycation on Interlamellar Bonding of Arterial Elastin. Exp. Mech. 2021, 61, 81–94. [Google Scholar] [CrossRef]
- Mousavi, S.J.; Farzaneh, S.; Avril, S. Patient-specific predictions of aneurysm growth and remodeling in the ascending thoracic aorta using the homogenized constrained mixture model. Biomech. Model. Mechanobiol. 2019, 18, 1895–1913. [Google Scholar] [CrossRef]
- Hackstein, U.; Krickl, S.; Bernhard, S. Estimation of ARMA-model parameters to describe pathological conditions in cardiovascular system models. Inform. Med. Unlocked 2020, 18, 100310. [Google Scholar] [CrossRef]
- Adam, C.; Fabre, D.; Mougin, J.; Zins, M.; Azarine, A.; Ardon, R.; d’Assignies, G.; Haulon, S. Pre-surgical and Post-surgical Aortic Aneurysm Maximum Diameter Measurement: Full Automation by Artificial Intelligence. Eur. J. Vasc. Endovasc. Surg. 2021, 62, 869–877. [Google Scholar] [CrossRef]
- Cao, L.; Shi, R.; Ge, Y.; Xing, L.; Zuo, P.; Jia, Y.; Liu, J.; He, Y.; Wang, X.; Luan, S.; et al. Fully automatic segmentation of type B aortic dissection from CTA images enabled by deep learning. Eur. J. Radiol. 2019, 121, 108713. [Google Scholar] [CrossRef]
- Sazonov, I.; Xie, X.; Nithiarasu, P. An improved method of computing geometrical potential force (GPF) employed in the segmentation of 3D and 4D medical images. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2017, 5, 287–296. [Google Scholar] [CrossRef]
- Rueckel, J.; Reidler, P.; Fink, N.; Sperl, J.; Geyer, T.; Fabritius, M.; Ricke, J.; Ingrisch, M.; Sabel, B. Artificial intelligence assistance improves reporting efficiency of thoracic aortic aneurysm CT follow-up. Eur. J. Radiol. 2021, 134, 109424. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Avril, S.; Lu, J. Prediction of local strength of ascending thoracic aortic aneurysms. J. Mech. Behav. Biomed. Mater. 2021, 115, 104284. [Google Scholar] [CrossRef]
- Lindquist Liljeqvist, M.; Bogdanovic, M.; Siika, A.; Gasser, T.C.; Hultgren, R.; Roy, J. Geometric and biomechanical modeling aided by machine learning improves the prediction of growth and rupture of small abdominal aortic aneurysms. Sci. Rep. 2021, 11, 18040. [Google Scholar] [CrossRef]
- Liu, M.; Liang, L.; Sun, W. Estimation of in vivo constitutive parameters of the aortic wall using a machine learning approach. Comput. Methods Appl. Mech. Eng. 2019, 347, 201–217. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Linka, K.; Sherifova, S.; Cyron, C.J. Predictive constitutive modelling of arteries by deep learning. J. R. Soc. Interface 2021, 18, 20210411. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Yang, W.; Lan, I.S.; Marsden, A.L. Fluid–structure interaction modeling of blood flow in the pulmonary arteries using the unified continuum and variational multiscale formulation. Mech. Res. Commun. 2020, 107, 103556. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Martin, C.; Sun, W. A machine learning approach as a surrogate of finite element analysis–based inverse method to estimate the zero-pressure geometry of human thoracic aorta. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3103. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Liu, M.; Martin, C.; Sun, W. A deep learning approach to estimate stress distribution: A fast and accurate surrogate of finite-element analysis. J. R. Soc. Interface 2018, 15, 20170844. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Q.; Feng, J.; Yu, P.; Zhang, S.; Teng, Z.; Gillard, J.H.; Song, R.; Jing, Z. A pilot study exploring the mechanisms involved in the longitudinal propagation of acute aortic dissection through computational fluid dynamic analysis. Cardiology 2014, 128, 220–225. [Google Scholar] [CrossRef] [PubMed]
- Long Ko, J.K.; Liu, R.W.; Ma, D.; Shi, L.; Ho Yu, S.C.; Wang, D. Pulsatile hemodynamics in patient-specific thoracic aortic dissection models constructed from computed tomography angiography. J. X-ray Sci. Technol. 2017, 25, 233–245. [Google Scholar] [CrossRef]
- Kaspera, W.; Ćmiel Smorzyk, K.; Wolański, W.; Kawlewska, E.; Hebda, A.; Gzik, M.; Ładziński, P. Morphological and Hemodynamic Risk Factors for Middle Cerebral Artery Aneurysm: A Case-Control Study of 190 Patients. Sci. Rep. 2020, 10, 2016. [Google Scholar] [CrossRef]
- Pasta, S.; Agnese, V.; Gallo, A.; Cosentino, F.; Di Giuseppe, M.; Gentile, G.; Raffa, G.M.; Maalouf, J.F.; Michelena, H.I.; Bellavia, D.; et al. Shear Stress and Aortic Strain Associations with Biomarkers of Ascending Thoracic Aortic Aneurysm. Ann. Thorac. Surg. 2020, 110, 1595–1604. [Google Scholar] [CrossRef] [PubMed]
- Condemi, F.; Campisi, S.; Viallon, M.; Troalen, T.; Xuexin, G.; Barker, A.; Markl, M.; Croisille, P.; Trabelsi, O.; Cavinato, C.; et al. Fluid-and biomechanical analysis of ascending thoracic aorta aneurysm with concomitant aortic insufficiency. Ann. Biomed. Eng. 2017, 45, 2921–2932. [Google Scholar] [CrossRef] [PubMed]
- Simão, M.; Ferreira, J.M.; Tomas, A.C.; Fragata, J.; Ramos, H.M. Aorta ascending aneurysm analysis using CFD models towards possible anomalies. Fluids 2017, 2, 31. [Google Scholar] [CrossRef]
- Tomaszewski, M.; Sybilski, K.; Małachowski, J.; Wolański, W.; Buszman, P.P. Numerical and experimental analysis of balloon angioplasty impact on flow hemodynamics improvement. Acta Bioeng. Biomech. 2020, 22, 169–183. [Google Scholar] [CrossRef]
- Yeh, H.H.; Rabkin, S.W.; Grecov, D. Hemodynamic assessments of the ascending thoracic aortic aneurysm using fluid–structure interaction approach. Med. Biol. Eng. Comput. 2018, 56, 435–451. [Google Scholar] [CrossRef]
- Chen, H.; Peelukhana, S.; Berwick, Z.; Kratzberg, J.; Krieger, J.; Roeder, B.; Chambers, S.; Kassab, G. Editor’s Choice–Fluid–Structure Interaction Simulations of Aortic Dissection with Bench Validation. Eur. J. Vasc. Endovasc. Surg. 2016, 52, 589–595. [Google Scholar] [CrossRef]
- Mendez, V.; Di Giuseppe, M.; Pasta, S.; Giuseppe, M.D.; Pasta, S. Comparison of hemodynamic and structural indices of ascending thoracic aortic aneurysm as predicted by 2-way FSI, CFD rigid wall simulation and patient-specific displacement-based FEA. Comput. Biol. Med. 2018, 100, 221–229. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Sherwood, J.M.; Karimpour, M.; Agu, O.; Balabani, S.; Díaz-Zuccarini, V. Aortic dissection simulation models for clinical support: Fluid–structure interaction vs. rigid wall models. Biomed. Eng. Online 2015, 14, 34. [Google Scholar] [CrossRef] [PubMed]
- Zouggari, L.; Bou-said, B.; Massi, F.; Culla, A.; Millon, A. The Role of Biomechanics in the Assessment of Carotid Atherosclerosis Severity: A Numerical Approach. World J. Vasc. Surg. 2018, 1, 1007. [Google Scholar]
- Ateshian, G.A.; Shim, J.J.; Maas, S.A.; Weiss, J.A. Finite Element Framework for Computational Fluid Dynamics in FEBio. J. Biomech. Eng. 2018, 140, 021001. [Google Scholar] [CrossRef] [PubMed]
- Lopes, D.; Agujetas, R.; Puga, H.; Teixeira, J.; Lima, R.; Alejo, J.; Ferrera, C. Analysis of finite element and finite volume methods for fluid–structure interaction simulation of blood flow in a real stenosed artery. Int. J. Mech. Sci. 2021, 207, 106650. [Google Scholar] [CrossRef]
- Wolański, W.; Gzik-Zroska, B.; Joszko, K.; Gzik, M.; Sołtan, D. Numerical Analysis of Blood Flow Through Artery with Elastic Wall of a Vessel. In Innovations in Biomedical Engineering; Gzik, M., Tkacz, E., Paszenda, Z., Piętka, E., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Volume 526, pp. 193–200. [Google Scholar] [CrossRef]
- Donea, J.; Huerta, A.; Ponthot, J. Chapter 14: Arbitrary Lagrangian–Eulerian Methods. Encycl. Comput. 2004, 1, 1–25. [Google Scholar]
- Karimi, S.; Dabagh, M.; Vasava, P.; Dadvar, M.; Dabir, B.; Jalali, P. Effect of rheological models on the hemodynamics within human aorta: CFD study on CT image-based geometry. J. Non–Newton. Fluid Mech. 2014, 207, 42–52. [Google Scholar] [CrossRef]
- Di Martino, E.S.; Guadagni, G.; Fumero, A.; Ballerini, G.; Spirito, R.; Biglioli, P.; Redaelli, A.; Martino, E.S.D.; Guadagni, G.; Fumero, A.; et al. Fluid–structure interaction within realistic three-dimensional models of the aneurysmatic aorta as a guidance to assess the risk of rupture of the aneurysm. Med. Eng. Phys. 2001, 23, 647–655. [Google Scholar] [CrossRef]
- Wan Ab Naim, W.N.; Ganesan, P.B.; Sun, Z.; Chee, K.H.; Hashim, S.A.; Lim, E. A perspective review on numerical simulations of hemodynamics in aortic dissection. Sci. World J. 2014, 2014, 652520. [Google Scholar] [CrossRef]
- Canchi, T.; Kumar, S.D.; Ng, E.Y.K.; Narayanan, S. A Review of Computational Methods to Predict the Risk of Rupture of Abdominal Aortic Aneurysms. BioMed Res. Int. 2015, 2015, 861627. [Google Scholar] [CrossRef]
- Azadani, A.N.; Chitsaz, S.; Matthews, P.B.; Jaussaud, N.; Leung, J.; Tsinman, T.; Ge, L.; Tseng, E.E. Comparison of mechanical properties of human ascending aorta and aortic sinuses. Ann. Thorac. Surg. 2012, 93, 87–94. [Google Scholar] [CrossRef]
- Deplano, V.; Boufi, M.; Gariboldi, V.; Loundou, A.D.; D’Journo, X.B.; Cautela, J.; Djemli, A.; Alimi, Y.S. Mechanical characterisation of human ascending aorta dissection. J. Biomech. 2019, 94, 138–146. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.; Lee, S.B.; Lee, J.; Cho, S.; Park, H.; Yeom, S.; Park, S.H. A comparison among Neo-Hookean model, Mooney-Rivlin model, and Ogden model for chloroprene rubber. Int. J. Precis. Eng. Manuf. 2012, 13, 759–764. [Google Scholar] [CrossRef]
- Bäumler, K.; Vedula, V.; Sailer, A.M.; Seo, J.; Chiu, P.; Mistelbauer, G.; Chan, F.P.; Fischbein, M.P.; Marsden, A.L.; Fleischmann, D. Fluid–structure interaction simulations of patient-specific aortic dissection. Biomech. Model. Mechanobiol. 2020, 19, 1607–1628. [Google Scholar] [CrossRef] [PubMed]
- Vignon-Clementel, I.E.; Alberto Figueroa, C.; Jansen, K.E.; Taylor, C.A. Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Comput. Methods Appl. Mech. Eng. 2006, 195, 3776–3796. [Google Scholar] [CrossRef]
- Hsu, M.C.; Bazilevs, Y. Blood vessel tissue prestress modeling for vascular fluid–structure interaction simulation. Finite Elem. Anal. Des. 2011, 47, 593–599. [Google Scholar] [CrossRef]
- Fonken, J.H.; Maas, E.J.; Nievergeld, A.H.; van Sambeek, M.R.; van de Vosse, F.N.; Lopata, R.G. Ultrasound-Based Fluid–Structure Interaction Modeling of Abdominal Aortic Aneurysms Incorporating Pre-stress. Front. Physiol. 2021, 12, 717593. [Google Scholar] [CrossRef]
- Puyvelde, J.V.; Verbeken, E.; Verbrugghe, P.; Herijgers, P.; Meuris, B. Aortic wall thickness in patients with ascending aortic aneurysm versus acute aortic dissection. Eur. J. Cardio-Thorac. Surg. 2015, 49, 756–762. [Google Scholar] [CrossRef]
- Agnese, V.; Pasta, S.; Michelena, H.I.; Minà, C.; Romano, G.M.; Carerj, S.; Zito, C.; Maalouf, J.F.; Foley, T.A.; Raffa, G.; et al. Patterns of ascending aortic dilatation and predictors of surgical replacement of the aorta: A comparison of bicuspid and tricuspid aortic valve patients over eight years of follow-up. J. Mol. Cell. Cardiol. 2019, 135, 31–39. [Google Scholar] [CrossRef]
- DeCampli, W.M. Ascending aortopathy with bicuspid aortic valve: More, but not enough, evidence for the hemodynamic theory. J. Thorac. Cardiovasc. Surg. 2017, 153, 6–7. [Google Scholar] [CrossRef][Green Version]

| Fluid density | 1.060 | |
| Fluid viscosity | 0.04 | |
| Solid density | 1.120 | |
| Young’s modulus | E | 10 |
| Poisson ratio |
| (dynscm) | C (cmdyn) | (dynscm) | |
|---|---|---|---|
| Thoracic aorta | 39 | 1016 | |
| Brachiocephalic trunk | 139 | 3637 | |
| Left common carotid artery | 520 | 13,498 | |
| Left subclavian artery | 420 | 10,969 |
| Lumen Domain | Solid Domain | |||
|---|---|---|---|---|
| Nomenclature | Elem. Size (mm) | Elem. Number | Elem. Size (mm) | Elem. Number |
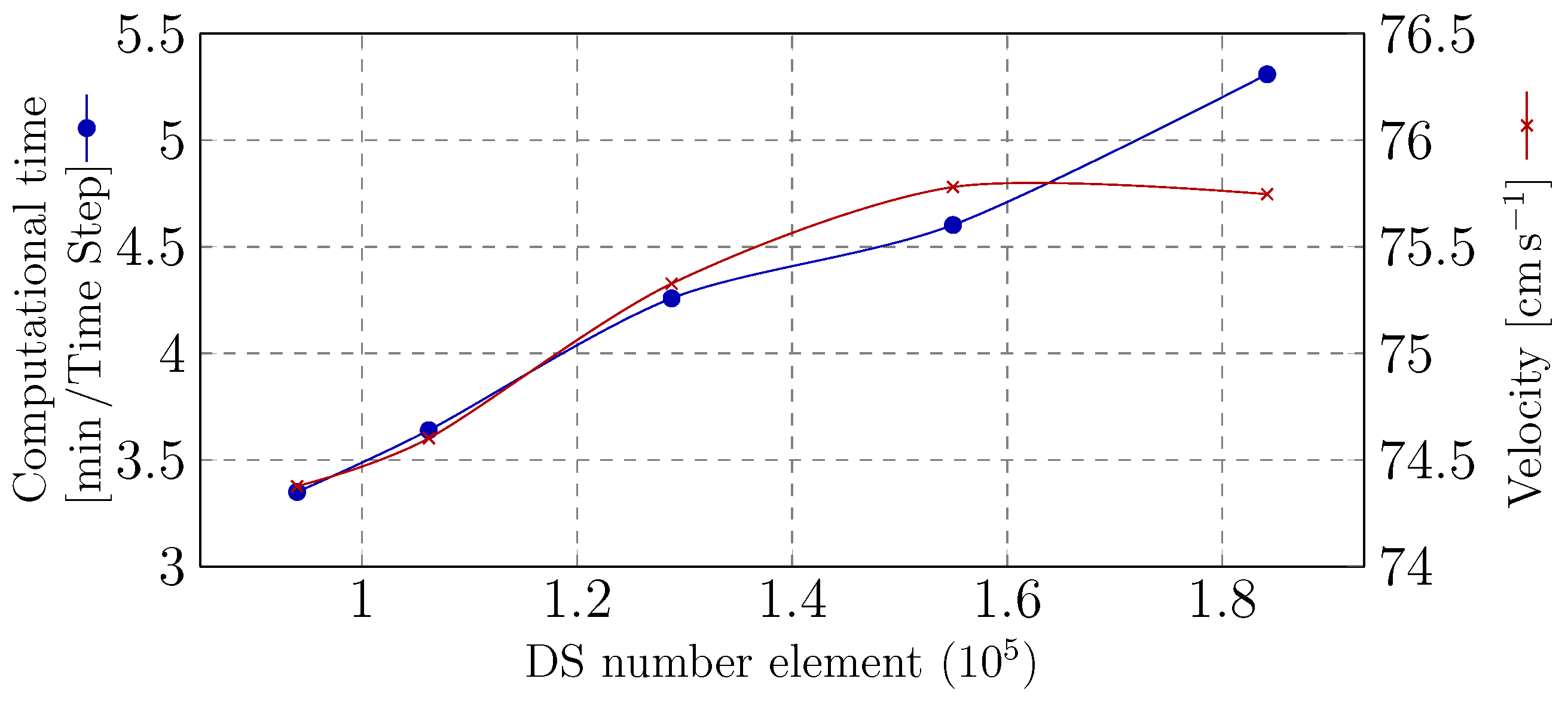
| E1 | 1.5 | 1,132,012 | 1.4 | 93,960 |
| E2 | 1.5 | 1,132,012 | 1.3 | 106,208 |
| E3 | 1.5 | 1,132,012 | 1.2 | 128,791 |
| E4 | 1.5 | 1,132,012 | 1.1 | 154,963 |
| E5 | 1.5 | 1,132,012 | 1.0 | 184,184 |
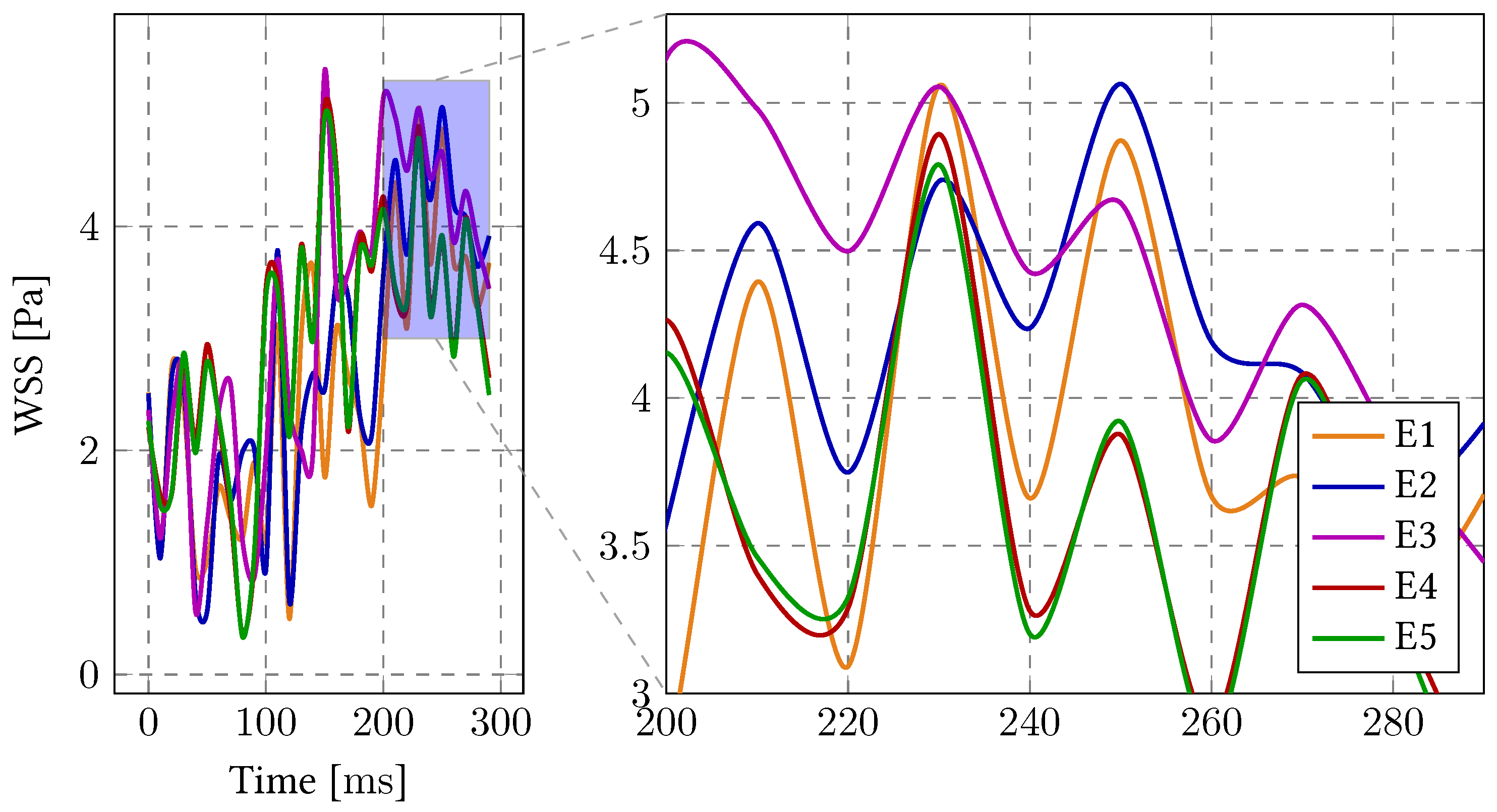
| Error | E1 | E2 | E3 | E4 | E5 | |
|---|---|---|---|---|---|---|
| Velocity | 0.972 | 0.984 | 1.006 | 1.001 | 1 | |
| 0.028 | 0.016 | 0.006 | 0.001 | 0 | ||
| Area Variation | 0.879 | 0.942 | 1.060 | 1.009 | 1 | |
| 0.122 | 0.058 | 0.060 | 0.009 | 0 | ||
| WSS | 0.971 | 1.010 | 1.018 | 0.997 | 1 | |
| 0.029 | 0.010 | 0.018 | 0.003 | 0 |
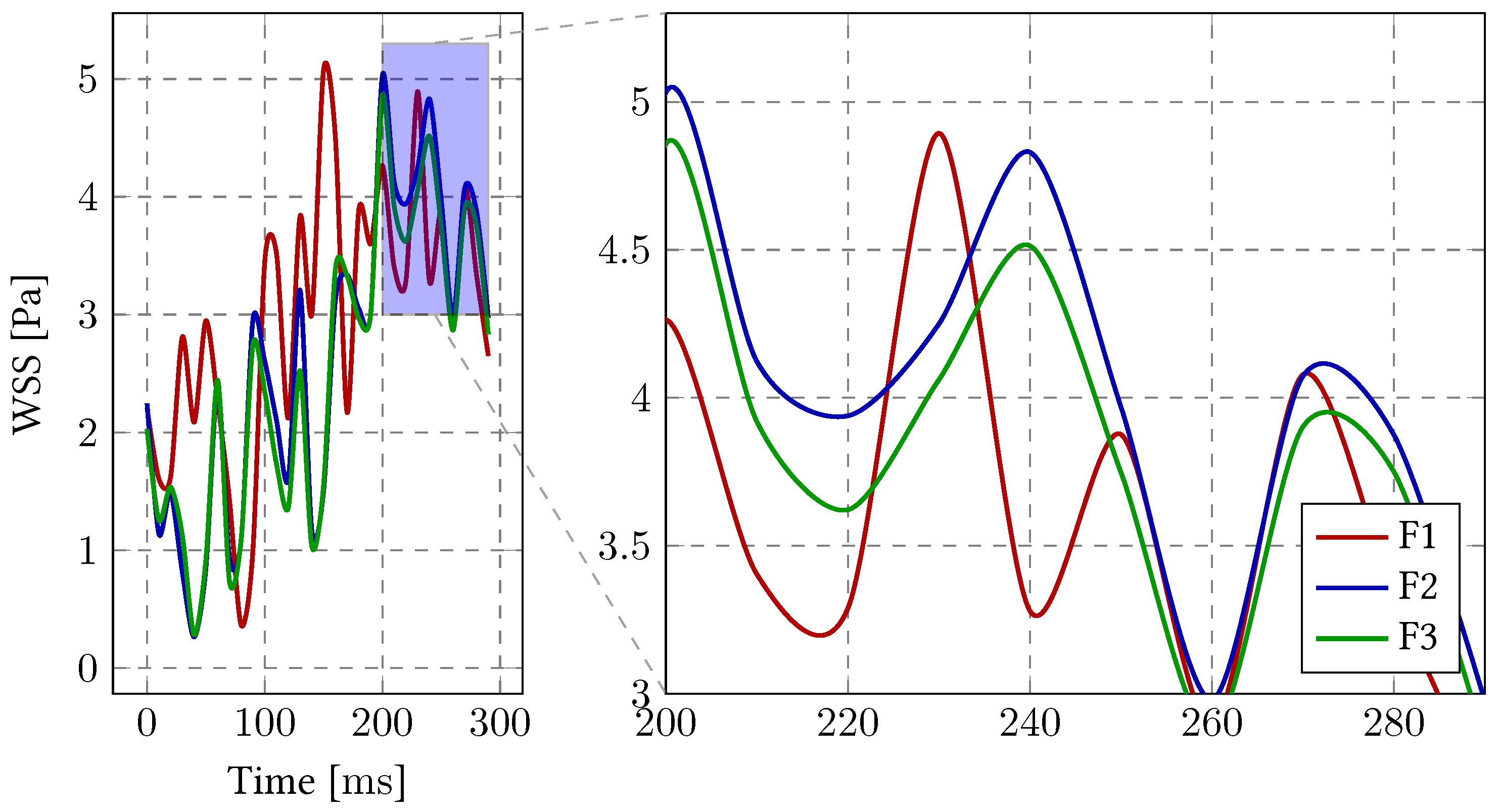
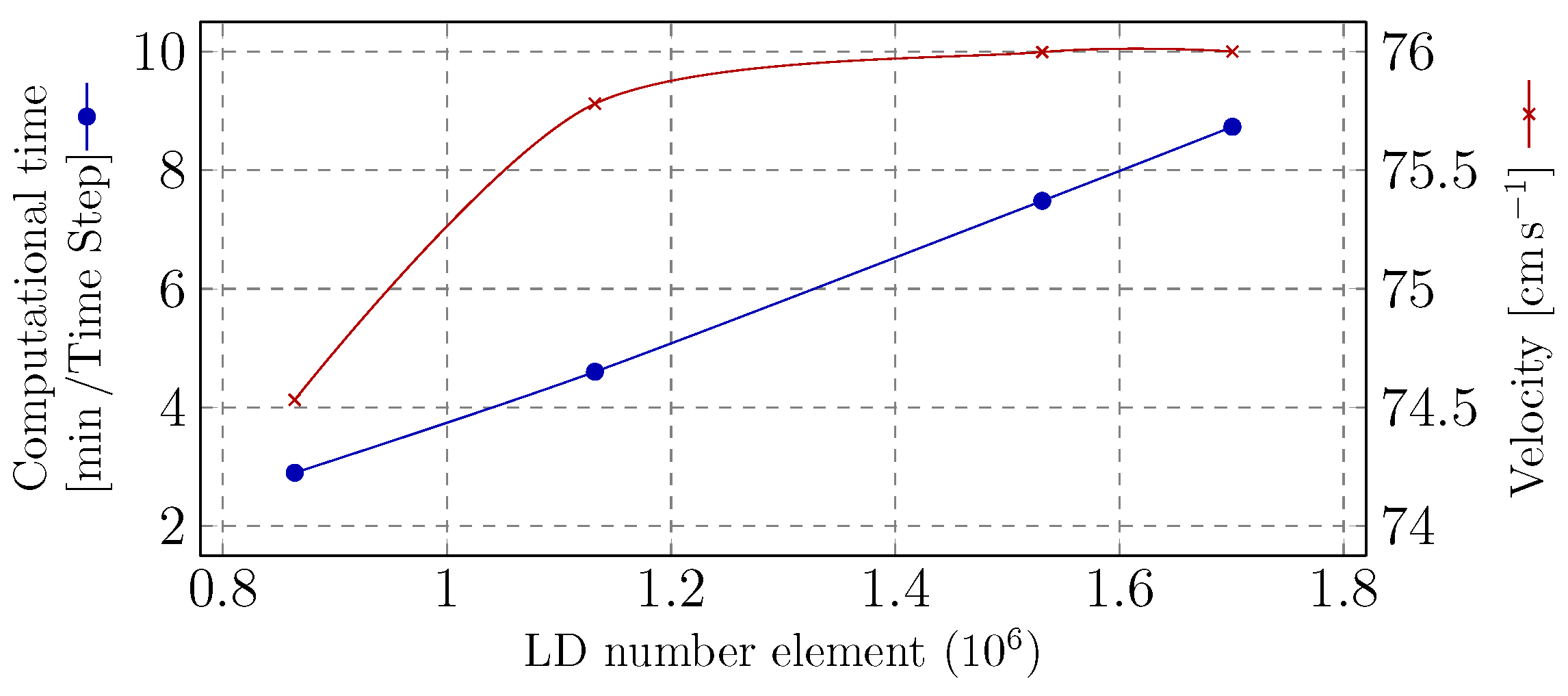
| Lumen Domain | Solid Domain | |||
|---|---|---|---|---|
| Nomenclature | Elem. Size (mm) | Elem. Number | Elem. Size (mm) | Elem. Number |
| F1 | 1.50 | 1,132,012 | 1.1 | 154,963 |
| F2 | 1.35 | 1,531,120 | 1.1 | 264,022 |
| F3 | 1.30 | 1,700,764 | 1.1 | 280,207 |
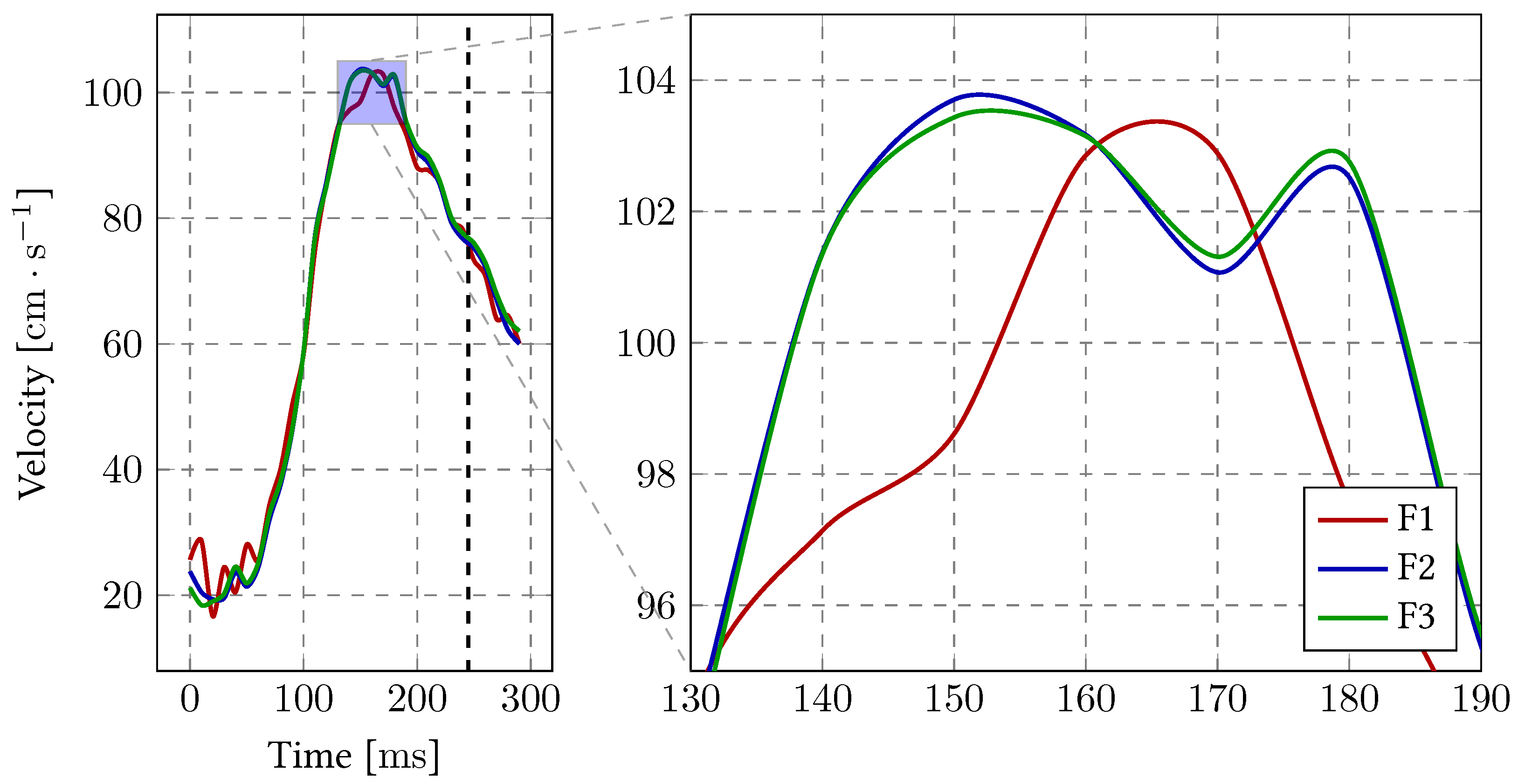
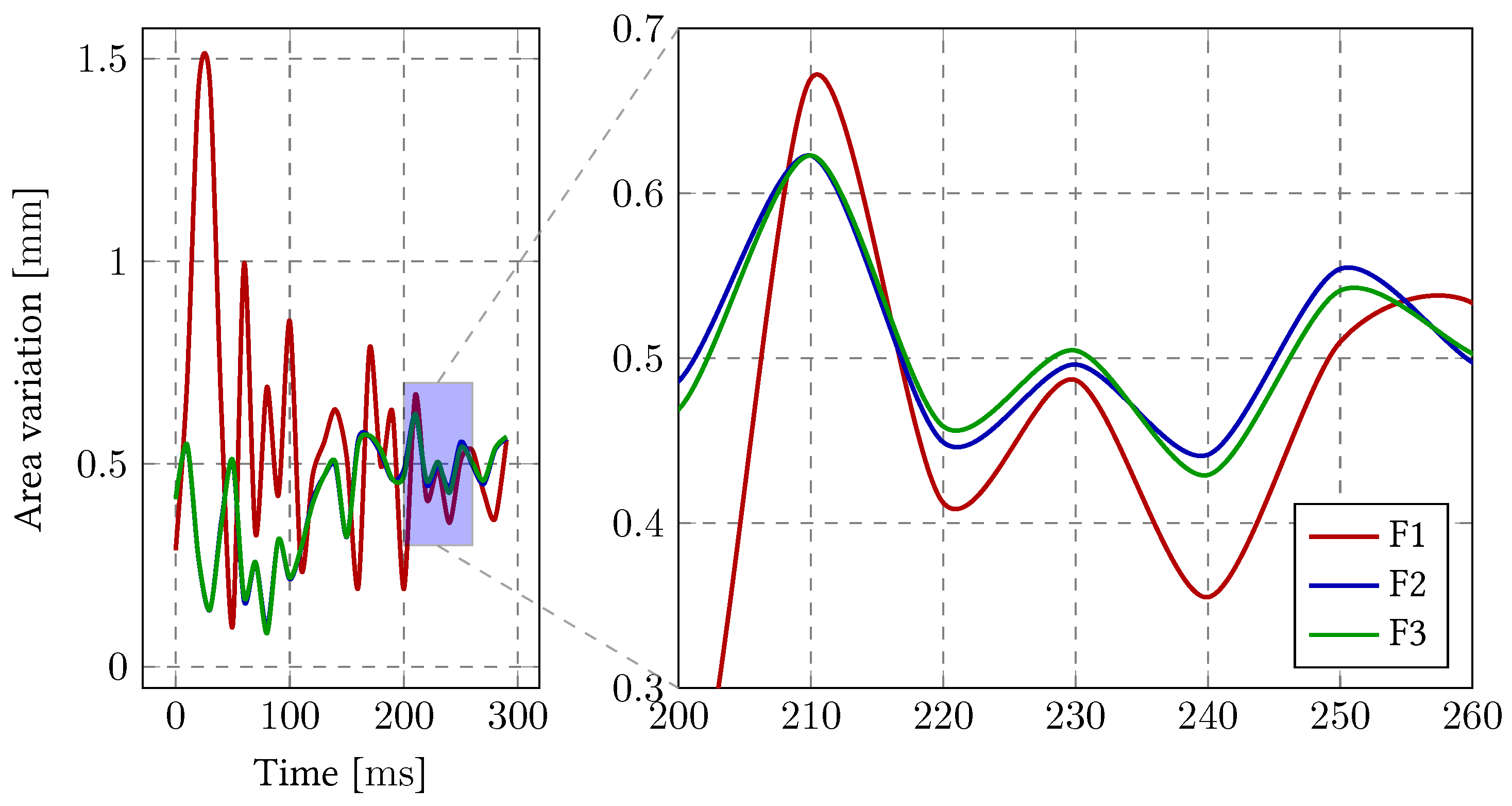
| Error | F1 | F2 | F3 | |
|---|---|---|---|---|
| Velocity | 1.118 | 1.034 | 1 | |
| 0.118 | 0.034 | 0 | ||
| Area Variation | 1.186 | 1.045 | 1 | |
| 0.186 | 0.045 | 0 | ||
| WSS | 1.355 | 0.998 | 1 | |
| 0.355 | 0.001 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valente, R.; Mourato, A.; Brito, M.; Xavier, J.; Tomás, A.; Avril, S. Fluid–Structure Interaction Modeling of Ascending Thoracic Aortic Aneurysms in SimVascular. Biomechanics 2022, 2, 189-204. https://doi.org/10.3390/biomechanics2020016
Valente R, Mourato A, Brito M, Xavier J, Tomás A, Avril S. Fluid–Structure Interaction Modeling of Ascending Thoracic Aortic Aneurysms in SimVascular. Biomechanics. 2022; 2(2):189-204. https://doi.org/10.3390/biomechanics2020016
Chicago/Turabian StyleValente, Rodrigo, André Mourato, Moisés Brito, José Xavier, António Tomás, and Stéphane Avril. 2022. "Fluid–Structure Interaction Modeling of Ascending Thoracic Aortic Aneurysms in SimVascular" Biomechanics 2, no. 2: 189-204. https://doi.org/10.3390/biomechanics2020016
APA StyleValente, R., Mourato, A., Brito, M., Xavier, J., Tomás, A., & Avril, S. (2022). Fluid–Structure Interaction Modeling of Ascending Thoracic Aortic Aneurysms in SimVascular. Biomechanics, 2(2), 189-204. https://doi.org/10.3390/biomechanics2020016










