Influence of Wall Compliance on the Flow Patterns in a Patient-Specific Brachio-Cephalic Arterio-Venous Fistula
Abstract
1. Introduction
2. Materials and Methods
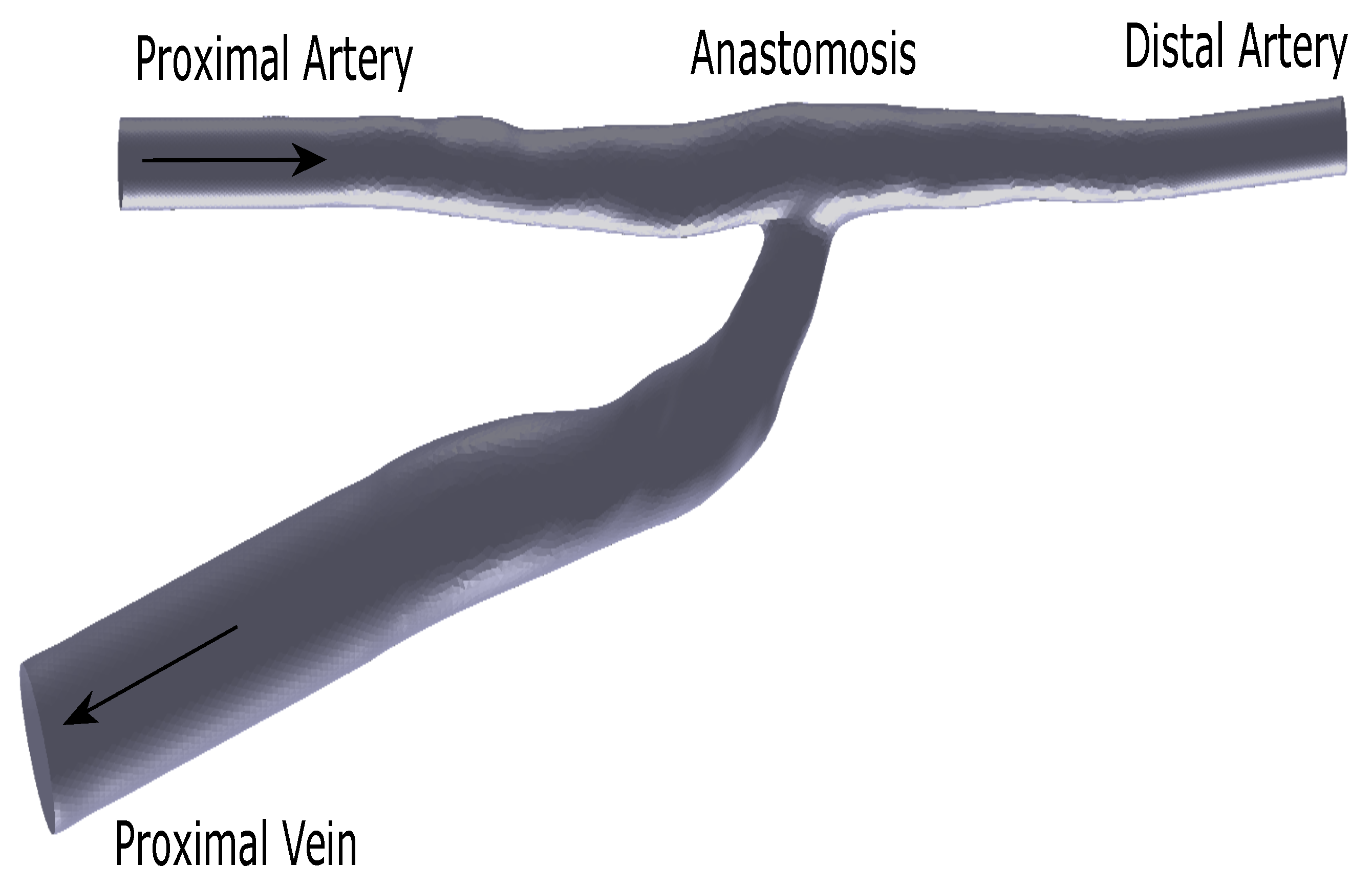
2.1. Flow Phantom
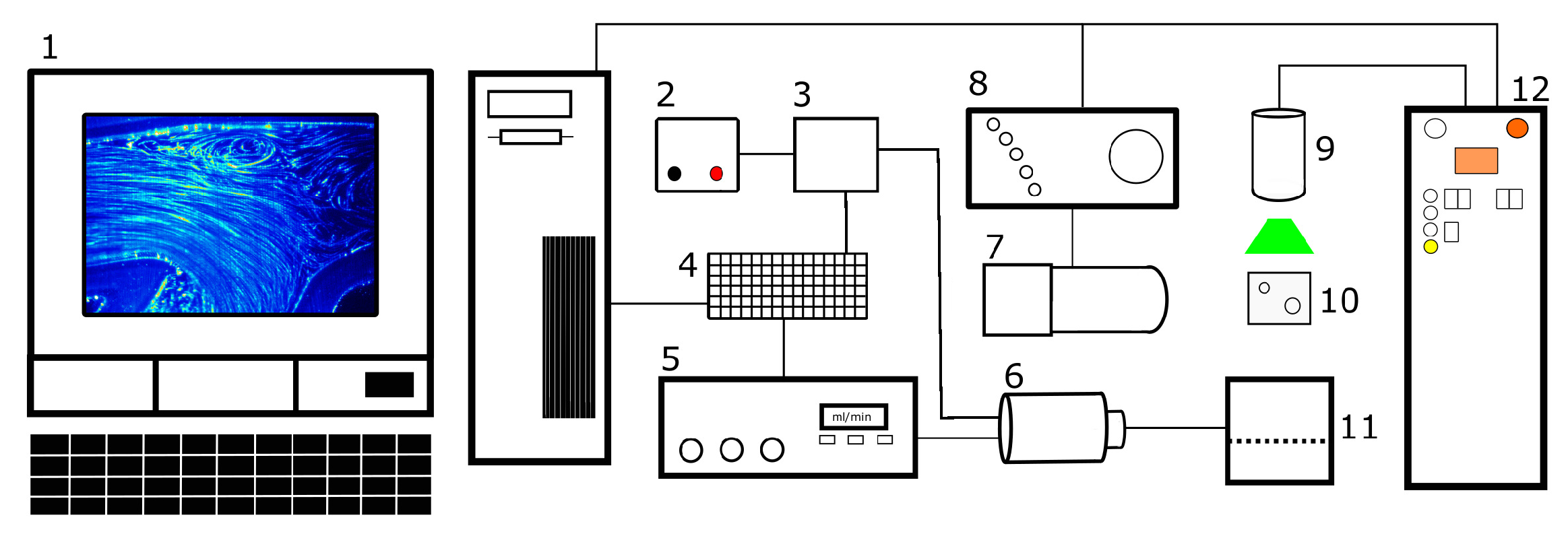
2.2. PIV Setup
2.3. Test Fluid
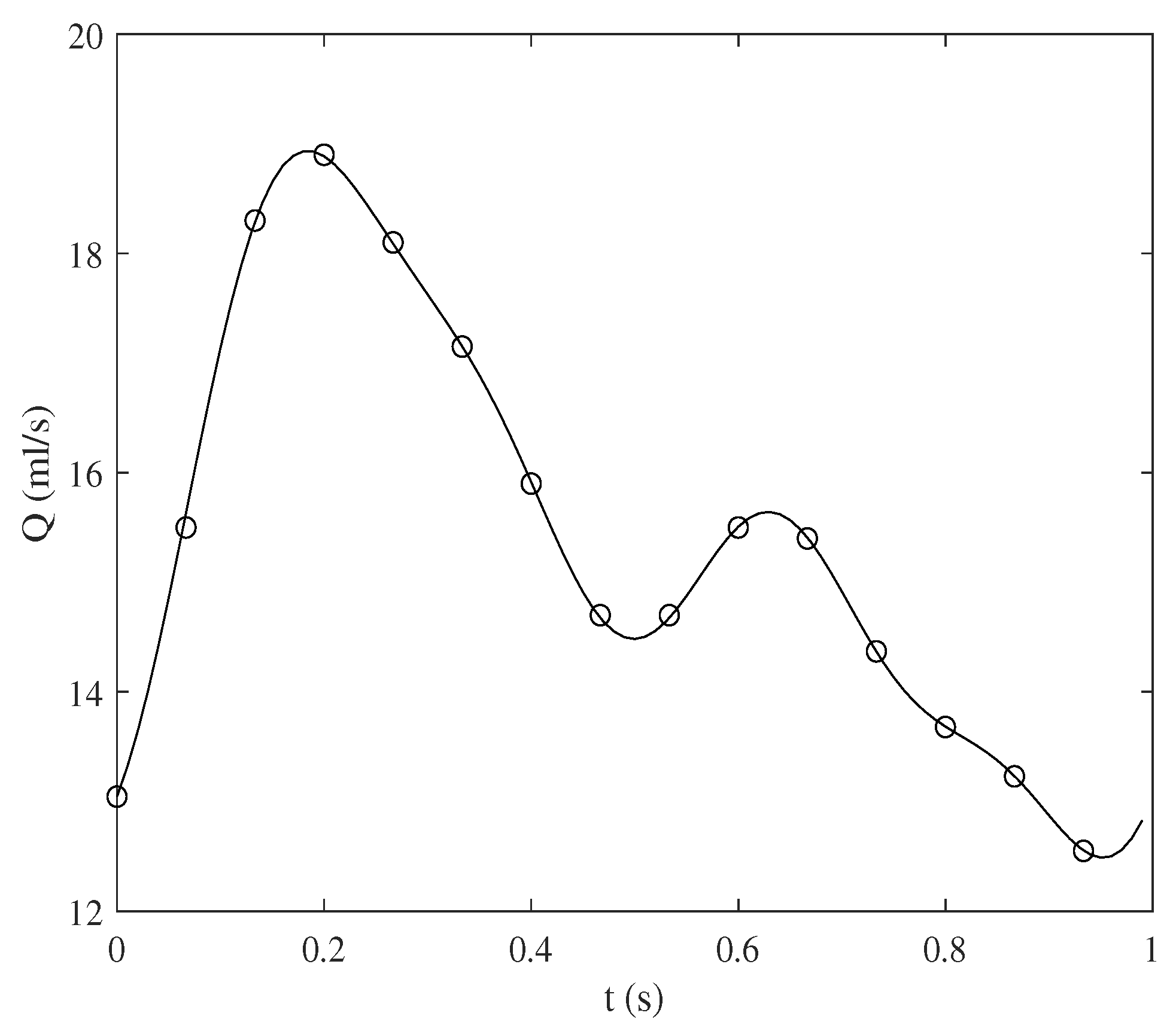
2.4. Experimental Parameters
2.5. Out-of-Plane Velocity Component
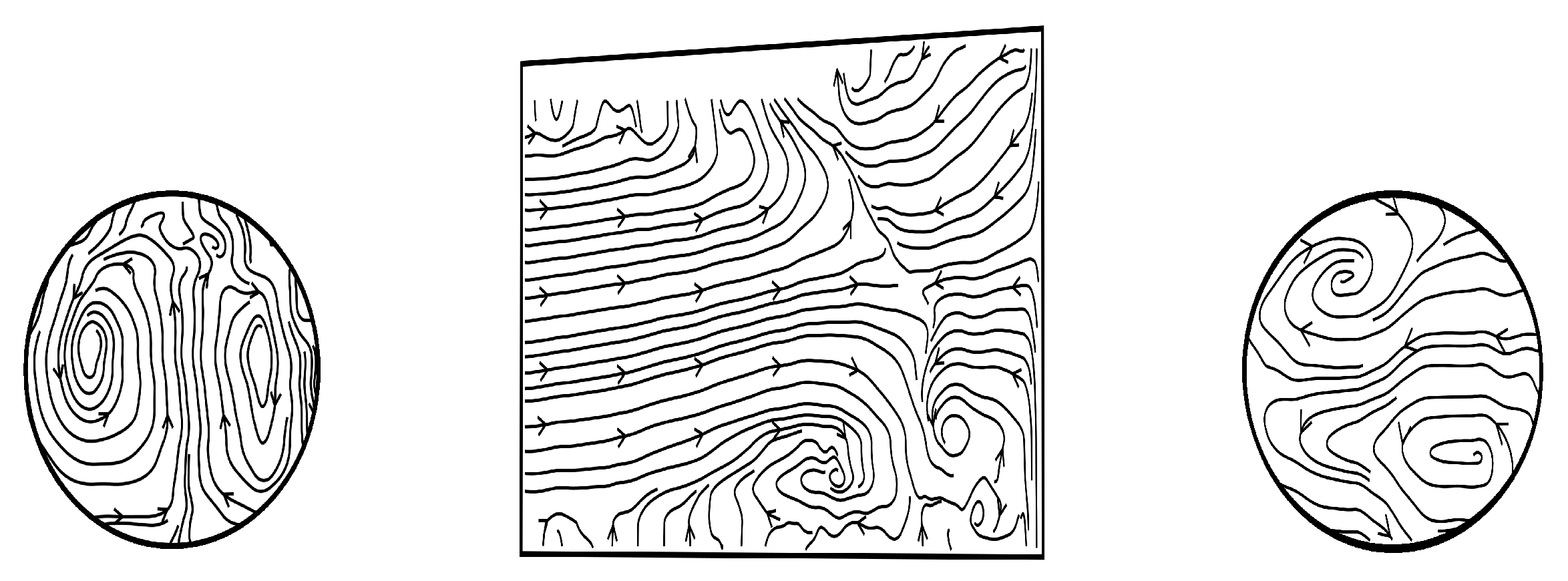
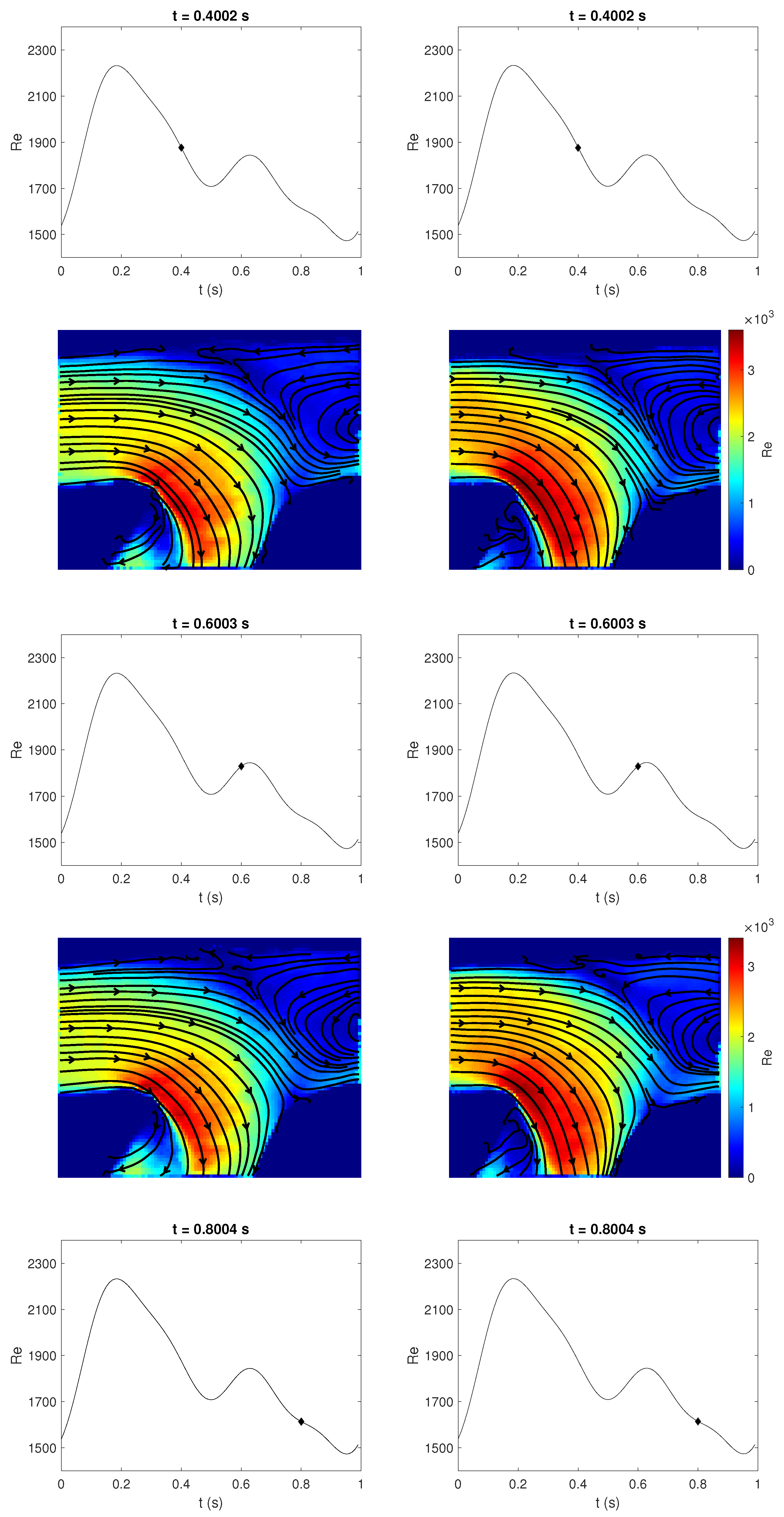
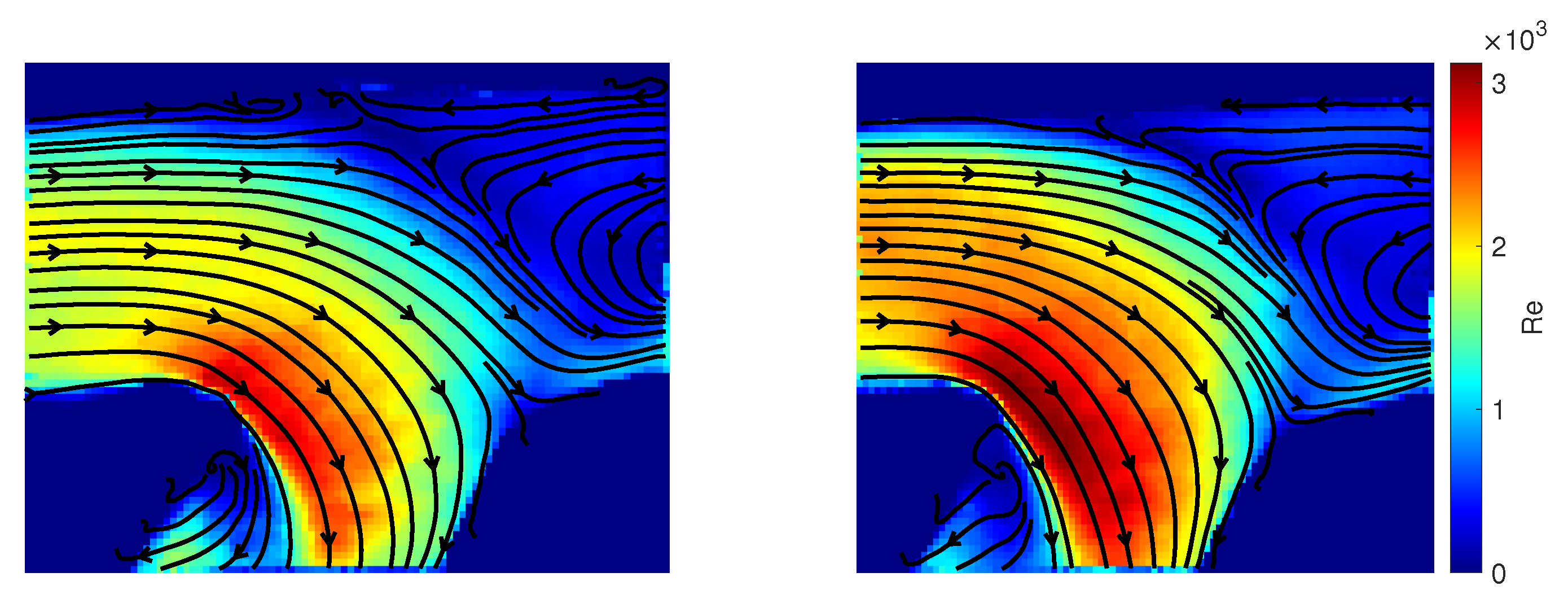
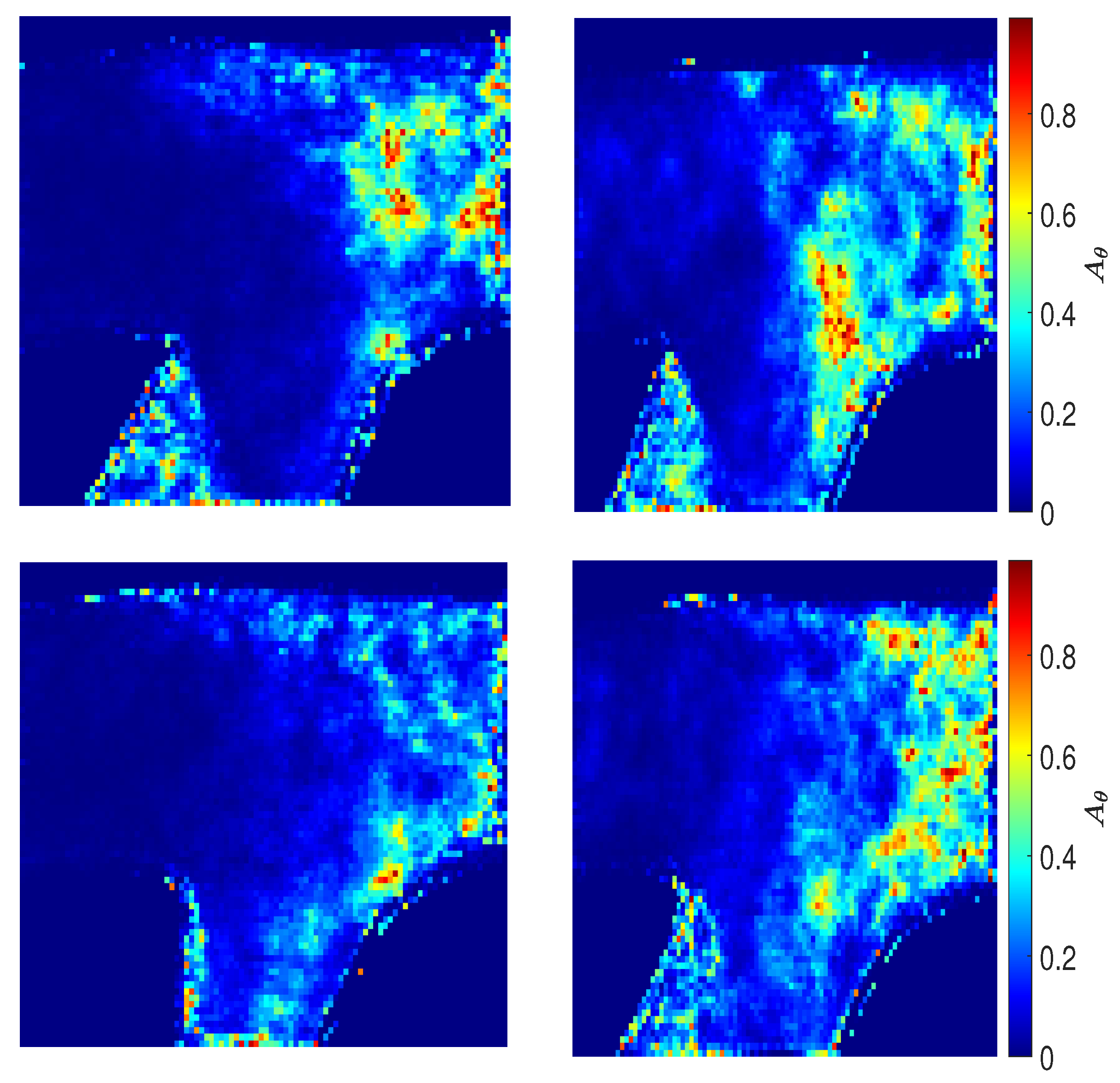
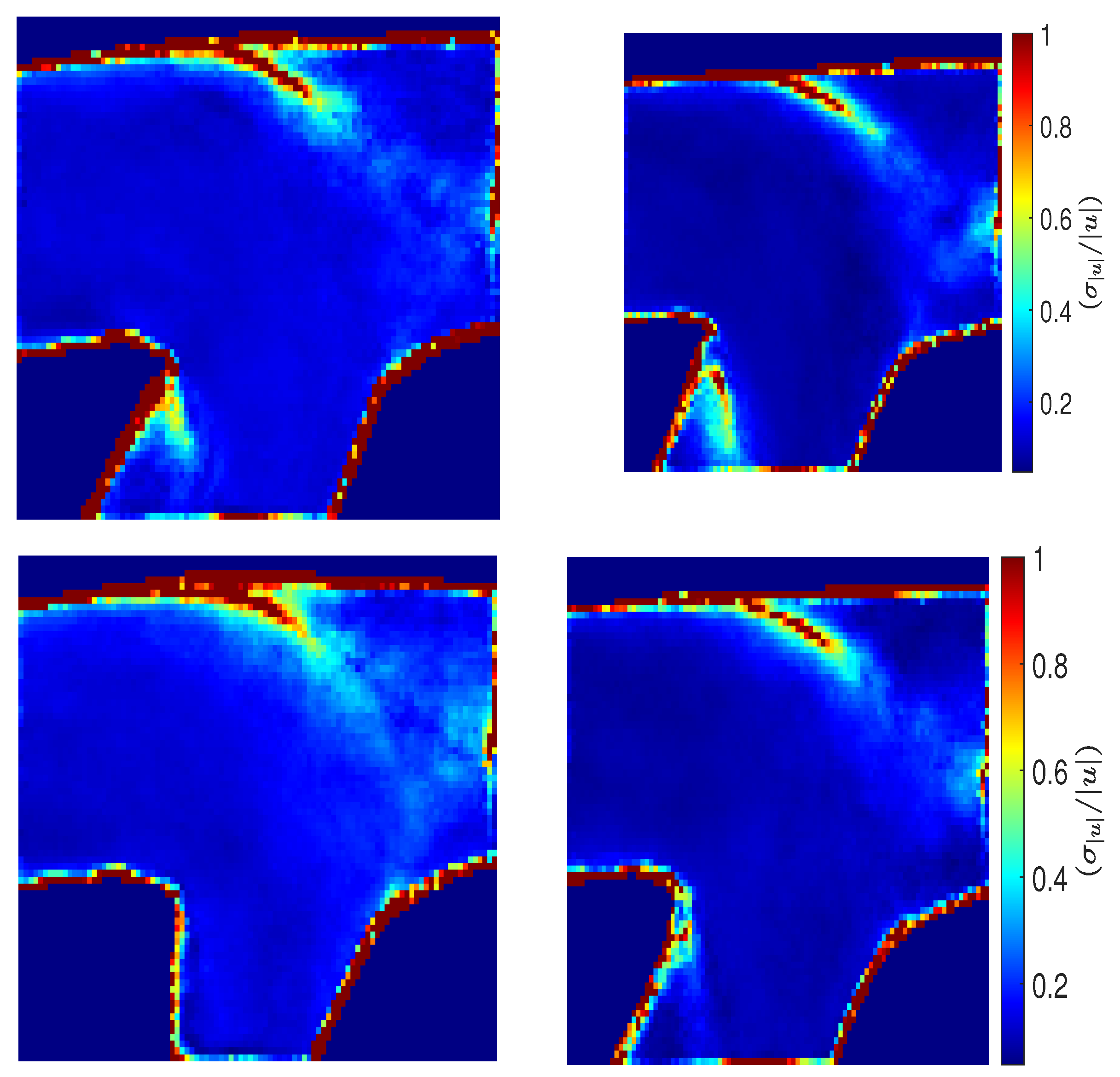
3. Results and Discussion
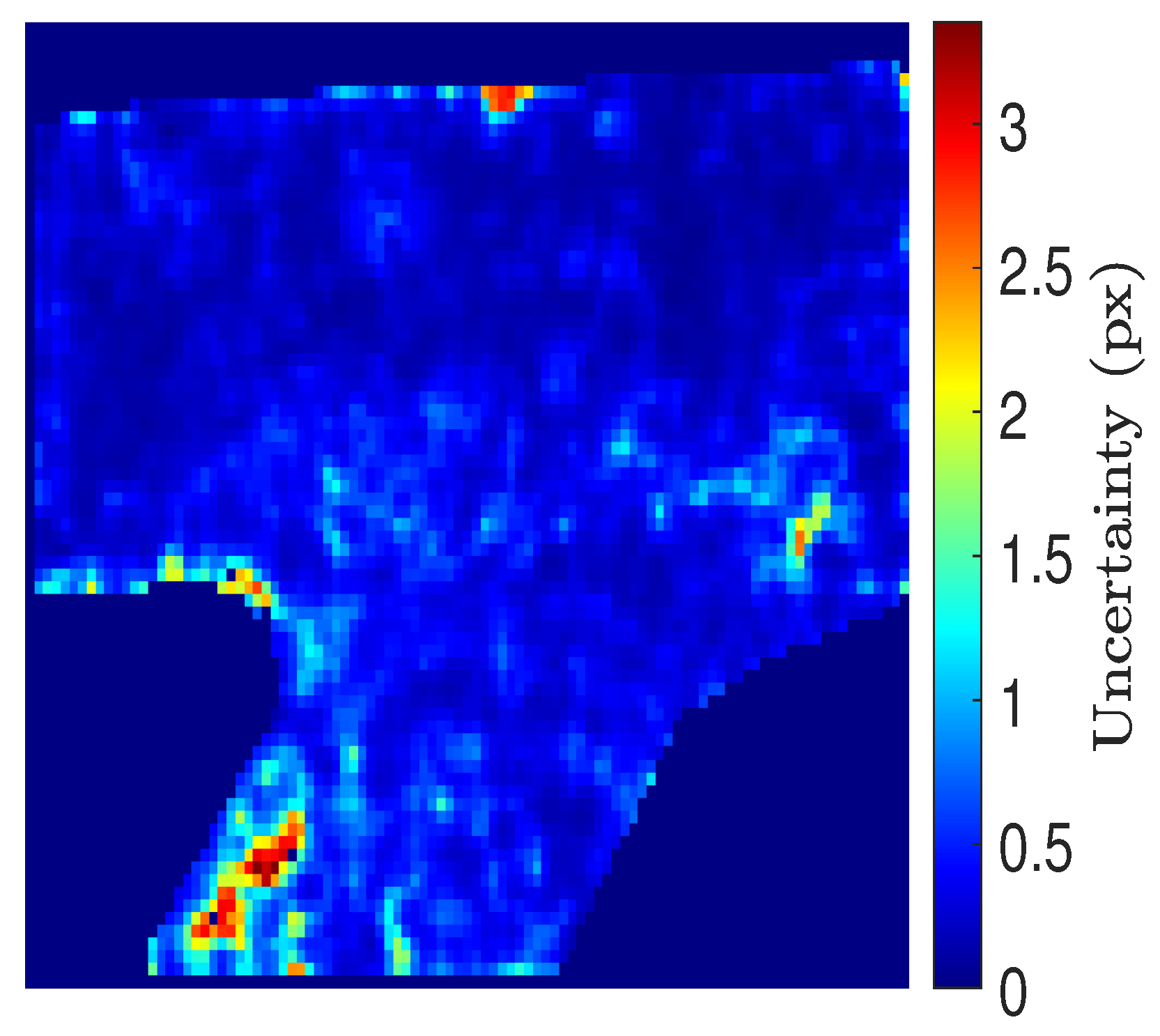
3.1. PIV Uncertainty
3.2. Out-of-Plane Velocity
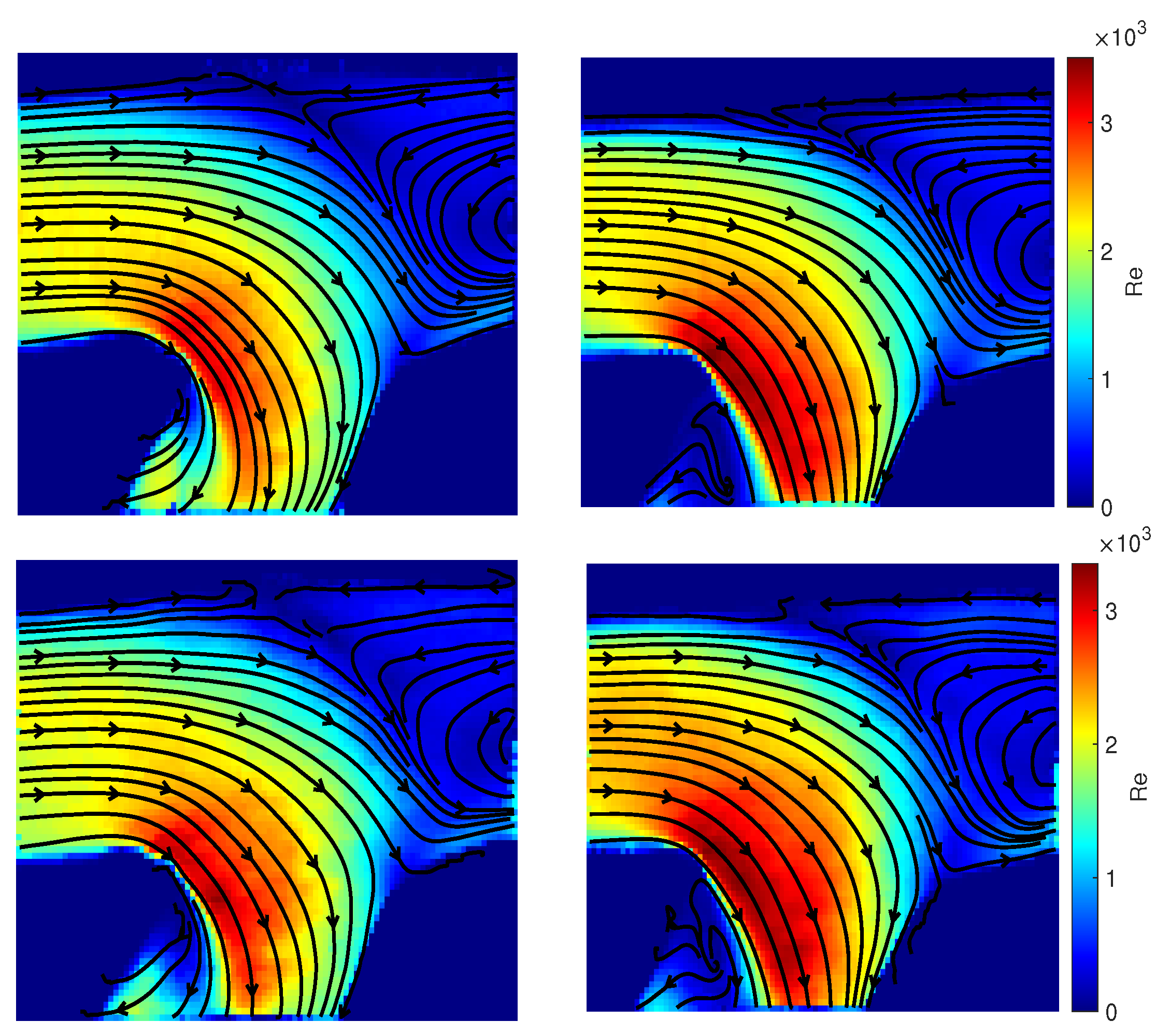
3.3. Qualitative Comparison of Rigid and Compliant Measurements
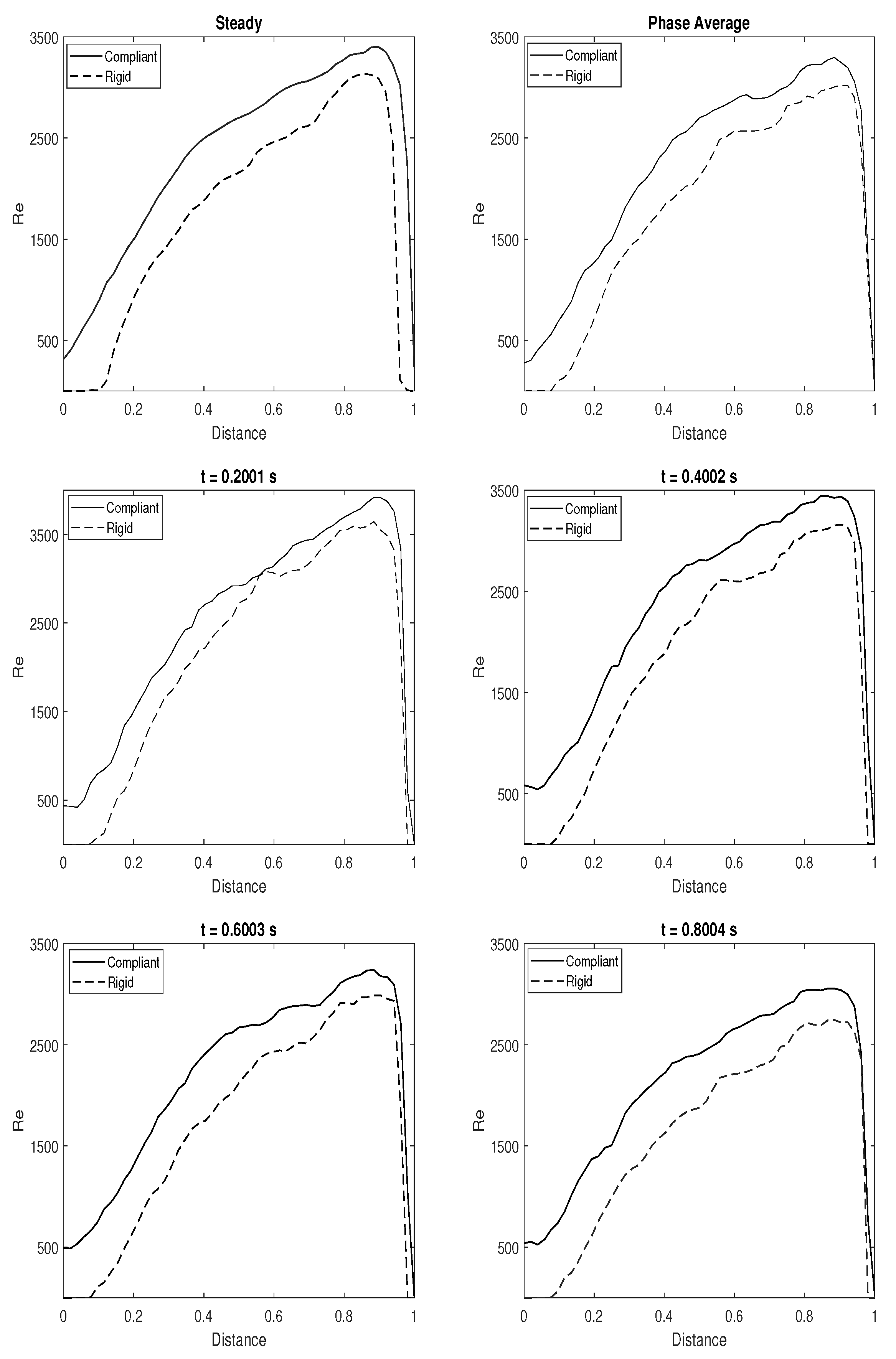
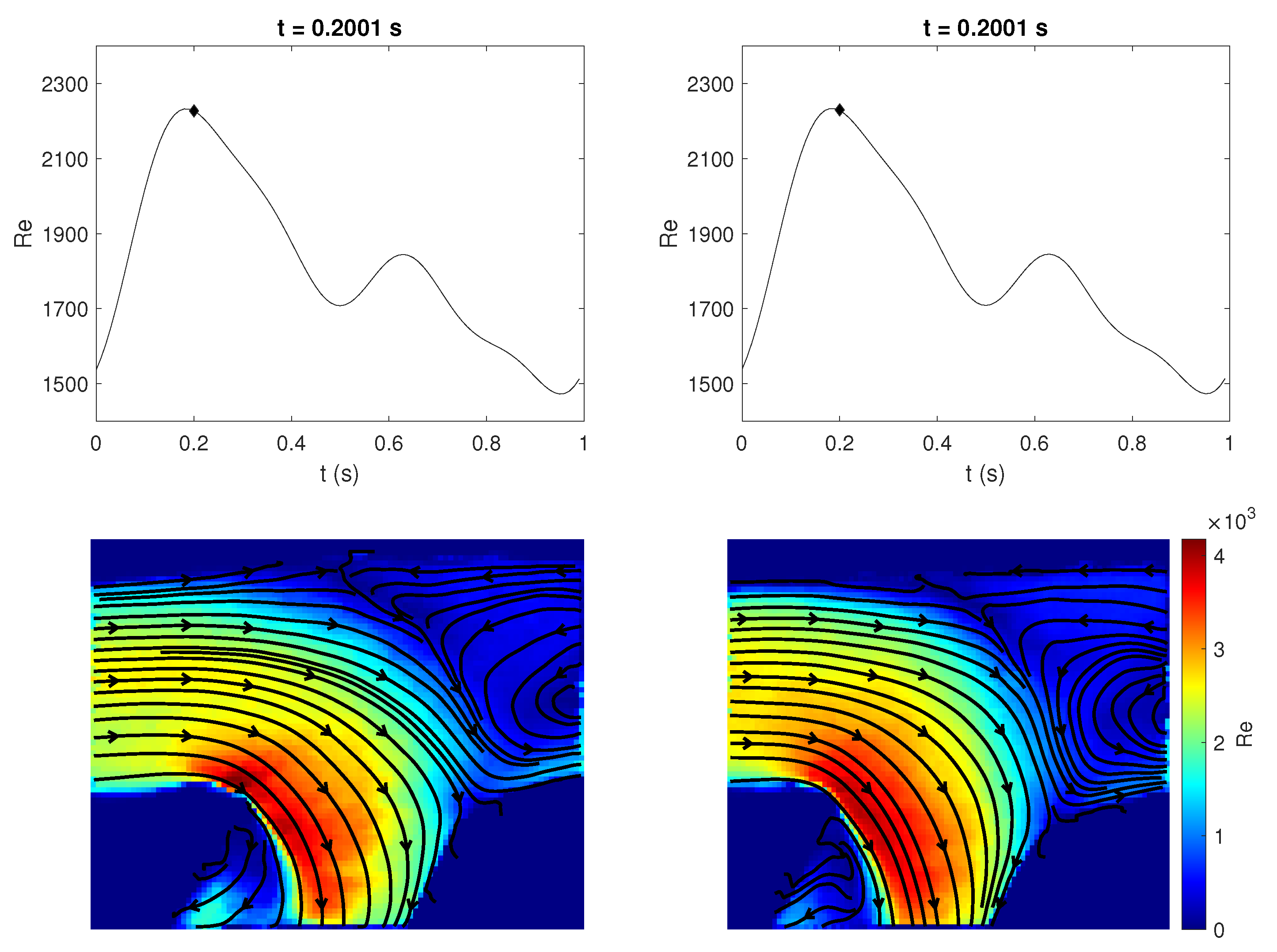
3.4. Quantitative Comparison of Rigid and Compliant Measurements
3.5. Directional Variability and Coefficient of Variation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 3D-3C | Three-Dimensional–Three-Component |
| 4D | Four Dimensional |
| AVF | Arterio-Venous Fistula |
| AVG | Arterio-venous Graft |
| CFD | Computational Fluid Dynamics |
| CKD | Chronic Kidney Disease |
| CVC | Central Venous Catheter |
| ESRD | End Stage Renal Disease |
| FSI | Fluid Structure Interaction |
| MRI | Magnetic Resonance Imaging |
| PI | Pulsatility Index |
| PIV | Particle Image Velocimetry |
| Re | Reynolds Number |
| TAWSS | Time Averaged Wall Shear Stress |
| TransWSS | Transverse Wall Shear Stress |
| TWSSG | Temporal Wall Shear Stress Gradient |
| WSS | Wall Shear Stress |
References
- Chandra, A.; Mix, D.; Varble, N. Hemodynamic study of arteriovenous fistulas for hemodialysis access. Vascular 2013, 21, 54–62. [Google Scholar] [CrossRef] [PubMed]
- Browne, L.D.; Griffin, P.; Bashar, K.; Walsh, S.R.; Kavanagh, E.G.; Walsh, M.T. In Vivo Validation of the In Silico Predicted Pressure Drop Across an Arteriovenous Fistula. Ann. Biomed. Eng. 2015, 43, 1275–1286. [Google Scholar] [CrossRef] [PubMed]
- Park, S.C.; Song, R.; Kim, S.; Kim, H.K.; Kim, S.H.; Lee, J. Fabrication of artificial arteriovenous fistula and analysis of flow field and shear stress by using μ-PIV technology. J. Mech. Sci. Technol. 2016, 30, 5503–5511. [Google Scholar] [CrossRef]
- de Villiers, A.; McBride, A.; Reddy, B.; Franz, T.; Spottiswoode, B. A validated patient-specific FSI model for vascular access in haemodialysis. Biomech. Model. Mechanobiol. 2018, 17, 479–497. [Google Scholar] [CrossRef]
- Jodko, D.M.; Obidowski, D.S.; Reorowicz, P.; Jóźwik, K.; Jodko, D. A two-stage model of an arteriovenous fistula maturation process. Acta Bioeng. Biomech. 2020, 22, 139–153. [Google Scholar] [CrossRef]
- Jodko, D.; Palczynski, T.; Reorowicz, P.; Miazga, K.; Obidowski, D.; Jozwik, K. Determination of a Pressure Drop in the Arteriovenous Fistula With Fluid Structure Interaction Simulations and In Vitro Methods. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, Tampa, FL, USA, 3–9 November 2017; Volume 58363, p. V003T04A016. [Google Scholar]
- Decorato, I.; Kharboutly, Z.; Vassallo, T.; Penrose, J.; Legallais, C.; Salsac, A.V. Numerical simulation of the fluid structure interactions in a compliant patient-specific arteriovenous fistula. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 143–159. [Google Scholar] [CrossRef]
- Decorato, I.; Kharboutly, Z.; Legallais, C.; Salsac, A.V. Comparison of two endovascular treatments of a stenosed arteriovenous fistula: Balloon-angioplasty with and without stenting. Int. J. Artif. Organs 2014, 37, 763–772. [Google Scholar] [CrossRef]
- McGah, P.M.; Leotta, D.F.; Beach, K.W.; Aliseda, A. Effects of wall distensibility in hemodynamic simulations of an arteriovenous fistula. Biomech. Model. Mechanobiol. 2014, 13, 679–695. [Google Scholar] [CrossRef]
- Stewart, S.F.; Paterson, E.G.; Burgreen, G.W.; Hariharan, P.; Giarra, M.; Reddy, V.; Day, S.W.; Manning, K.B.; Deutsch, S.; Berman, M.R.; et al. Assessment of CFD performance in simulations of an idealized medical device: Results of FDA’s first computational interlaboratory study. Cardiovasc. Eng. Technol. 2012, 3, 139–160. [Google Scholar] [CrossRef]
- Hariharan, P.; Giarra, M.; Reddy, V.; Day, S.W.; Manning, K.B.; Deutsch, S.; Stewart, S.F.; Myers, M.R.; Berman, M.R.; Burgreen, G.W.; et al. Multilaboratory particle image velocimetry analysis of the FDA benchmark nozzle model to support validation of computational fluid dynamics simulations. J. Biomech. Eng. 2011, 133, 041002. [Google Scholar] [CrossRef]
- Drost, S.; Alam, N.; Houston, J.; Newport, D. Review of experimental modelling in vascular access for hemodialysis. Cardiovasc. Eng. Technol. 2017, 8, 330–341. [Google Scholar] [CrossRef] [PubMed]
- Sorace, A.G.; Robbin, M.L.; Umphrey, H.; Abts, C.A.; Berry, J.L.; Lockhart, M.E.; Allon, M.; Hoyt, K. Ultrasound measurement of brachial artery elasticity prior to hemodialysis access placement: A pilot study. J. Ultrasound Med. 2012, 31, 1581–1588. [Google Scholar] [CrossRef] [PubMed]
- Colley, E.; Carroll, J.; Thomas, S.; Simmons, A.; Barber, T. Development of a Patient-Specific FSI Model of an Arteriovenous Fistula. Development 2016, 5, 8. [Google Scholar]
- Poelma, C.; Westerweel, J. Generalized displacement estimation for averages of non-stationary flows. Exp. Fluids 2011, 50, 1421–1427. [Google Scholar] [CrossRef][Green Version]
- Drost, S.; de Kruif, B.J.; Newport, D. Arduino control of a pulsatile flow rig. Med. Eng. Phys. 2017, 51, 67–71. [Google Scholar] [CrossRef]
- Wieneke, B. PIV uncertainty quantification from correlation statistics. Meas. Sci. Technol. 2015, 26, 074002. [Google Scholar] [CrossRef]
- Adrian, R.J.; Westerweel, J. Particle Image Velocimetry; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2011; Volume 30. [Google Scholar]
- Botti, L.; van Canneyt, K.; Kaminsky, R.; Claessens, T.; Planken, R.N.; Verdonck, P.; Remuzzi, A.; Antiga, L. Numerical evaluation and experimental validation of pressure drops across a patient-specific model of vascular access for hemodialysis. Cardiovasc. Eng. Technol. 2013, 4, 485–499. [Google Scholar] [CrossRef]
- Browne, L.D.; Walsh, M.T.; Griffin, P. Experimental and numerical analysis of the bulk flow parameters within an arteriovenous Fistula. Cardiovasc. Eng. Technol. 2015, 6, 450–462. [Google Scholar] [CrossRef]
- Kharboutly, Z.; Deplano, V.; Bertrand, E.; Legallais, C. Numerical and experimental study of blood flow through a patient-specific arteriovenous fistula used for hemodialysis. Med. Eng. Phys. 2010, 32, 111–118. [Google Scholar] [CrossRef]
- Javadzadegan, A.; Myo Lwin, N.; Asyraf, M.; Simmons, A.; Barber, T. Analysis of blood flow characteristics in a model of a mature side-to-side arteriovenous fistula. Artif. Organs 2017, 41, E251–E262. [Google Scholar] [CrossRef]
- Sivanesan, S.; How, T.; Black, R.; Bakran, A. Flow patterns in the radiocephalic arteriovenous fistula: An in vitro study. J. Biomech. 1999, 32, 915–925. [Google Scholar] [CrossRef]
- Decorato, I.; Kharboutly, Z.; Legallais, C.; Salsac, A.V. Numerical study of the influence of wall compliance on the haemodynamics in a patient-specific arteriovenous fistula. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 121–123. [Google Scholar] [CrossRef]
- Bozzetto, M.; Ene-Iordache, B.; Remuzzi, A. Transitional flow in the venous side of patient-specific arteriovenous fistulae for hemodialysis. Ann. Biomed. Eng. 2016, 44, 2388–2401. [Google Scholar] [CrossRef] [PubMed]
- Fulker, D.; Ene-Iordache, B.; Barber, T. High-resolution computational fluid dynamic simulation of haemodialysis cannulation in a patient-specific arteriovenous fistula. J. Biomech. Eng. 2018, 140, 031011. [Google Scholar] [CrossRef]
- Mohamied, Y.; Rowland, E.M.; Bailey, E.L.; Sherwin, S.J.; Schwartz, M.A.; Weinberg, P.D. Change of direction in the biomechanics of atherosclerosis. Ann. Biomed. Eng. 2015, 43, 16–25. [Google Scholar] [CrossRef]
- Kharboutly, Z.; Fenech, M.; Treutenaere, J.; Claude, I.; Legallais, C. Investigations into the relationship between hemodynamics and vascular alterations in an established arteriovenous fistula. Med. Eng. Phys. 2007, 29, 999–1007. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, N.; Newport, D. Influence of Wall Compliance on the Flow Patterns in a Patient-Specific Brachio-Cephalic Arterio-Venous Fistula. Biomechanics 2022, 2, 158-173. https://doi.org/10.3390/biomechanics2020014
Alam N, Newport D. Influence of Wall Compliance on the Flow Patterns in a Patient-Specific Brachio-Cephalic Arterio-Venous Fistula. Biomechanics. 2022; 2(2):158-173. https://doi.org/10.3390/biomechanics2020014
Chicago/Turabian StyleAlam, Neda, and David Newport. 2022. "Influence of Wall Compliance on the Flow Patterns in a Patient-Specific Brachio-Cephalic Arterio-Venous Fistula" Biomechanics 2, no. 2: 158-173. https://doi.org/10.3390/biomechanics2020014
APA StyleAlam, N., & Newport, D. (2022). Influence of Wall Compliance on the Flow Patterns in a Patient-Specific Brachio-Cephalic Arterio-Venous Fistula. Biomechanics, 2(2), 158-173. https://doi.org/10.3390/biomechanics2020014





