Abstract
The liver and kidneys are the most commonly injured organs due to traumatic impact forces applied to the abdomen and pose a challenge to physicians due to a hard-to-diagnose risk of internal bleeding. A better understanding of the mechanism of injury will improve diagnosis, treatment, forensics, and other fields. Finite element modelling is a tool that can aid in this understanding, but accurate material properties are required including the strain rate dependency and the feasibility of using animal tissue properties instead of human. The elastic modulus in a probing protocol and the elastic modulus, failure stress, and failure strain in a compression protocol were found for both liver and kidney tissue from human and porcine specimens at varying strain rates. Increases in the elastic modulus were seen for both the human kidney and liver, but only for the porcine kidney, when comparing the unconfined compression and probing protocols. A strain rate dependency was found for both the liver and kidney properties and was observed to have a larger saturation effect at higher rates for the failure stress than for the elastic modulus. Overall, the material properties of intact liver and kidney were characterized, and the strain rate dependency was numerically modelled. The study findings suggest that some kidney and liver material properties vary from human to porcine tissue. Therefore, it is not always appropriate to use material properties of porcine tissue in computational or physical models of the human liver and kidney.
1. Introduction
Abdominal injuries sustained during impact events such as motor vehicle crashes are noteworthy in their severity. A study by Klinich et al. [1] that examined data from a National Automotive Sampling Study of motor vehicle crashes in the United States from 1998–2004 reported that although abdominal organ injuries make up only a small percentage of overall traumas, they account for 13% of critical injuries. Amongst abdominal injuries, two of the most commonly injured organs from impact forces are the kidneys and liver; whether it be from a car accident, explosion, or impact from a projectile [2,3,4]. Due to the quantity of injuries, and the life-threatening impact of these injuries, studies investigating the injury mechanism have become increasingly common to improve understanding in a variety of fields such as safety, forensics, diagnostic medicine, etc.
Although crash test dummies are often used to model human response during motor vehicle accidents and other impacts, including physical abdominal organ models capable of measuring and predicting injuries is difficult and requires a large amount of resources [5]. Instead, a tool that is commonly used to gain insight into the mechanism of abdominal injury is finite element simulation. Many models have been created to aid in investigating abdominal tissue trauma [6,7,8,9,10,11,12,13,14]. The model results are dependent on the tissue material properties, and models in the literature use properties derived from a variety of methods not always reflective of the model application. Since the tissue mechanical properties are dependent on the testing methodology, using properties from incompatible testing could lead to inaccurate results. For example, many organs exhibit differing properties when tested in tension versus compression [15], and most human tissue shows dependence on the loading rate for the elastic modulus (E) and failure properties [5,6,7,8,9,10,11,12,13,14,15,16,17,18].
It has been reported that, during blunt traumatic injury, the liver and kidneys are placed in compression at dynamic rates [19]. However, much of the current literature utilizes methods other than whole organ compression, which is the loading condition experienced in-vivo, such as tension testing, which involves dissecting the whole organ into several pieces in order to standardize the specimens and to control the location where nonlinear behavior and/or failure occurs [5,20,21,22,23,24,25,26,27,28,29,30]. Other methods include probing, which utilizes a compression testing protocol with a loading apparatus that is significantly smaller than the surface area of the organ [5,29,31]. Probing methodologies do not reflect the loading scenario caused by blunt traumatic injury, and thus, material properties derived using such methods might not be appropriate. However, probing at low levels of force and deformation can be used on live specimens [32]. The underlining assumption of tension testing or probing studies are that the properties measured for a portion of the organ are representative of those for a whole intact organ. Comparison of the results from previous studies that used different testing methods reveals variation in failure stress and strain up to 300% [5,25,30,33]. The wide range of published results supports the statement that utilizing a testing methodology that is reflective of the loading scenario being modeled is important to obtaining accurate results.
Only a select few studies have investigated the material properties of the liver and kidney under compression and/or at dynamic rates [31,33], but they did not investigate the properties of intact organs. Instead, they used partial specimens, which has been shown to affect the measured properties [16]. Snedeker [34] measured the elastic modulus of the parenchyma of human and porcine kidneys under quasi-static compressive loading. Umale [5] also performed dynamic compression testing on the porcine kidney parenchyma at rates of 1.5 to 2 m/s but did not report any of the material parameters, but rather provided fit data for an Ogden model. Indentation (probing) testing was performed by Umale [5] and Lu [29] on human and porcine kidneys at quasi-static loading rates. Previous studies of the liver followed the same testing procedures and loading rates, with most testing performed on partial specimens under tension. Of the few compression tests, the majority were at quasi-static rates [5,21,26,35]. Only a single study [36] tested the liver under dynamic compression using a Kolsky Bar technique, and did not report the material properties directly but only through a custom mathematical model.
Furthermore, several studies utilize organs from non-human hosts, such as porcine, bovine, or monkeys, as it is often difficult to obtain human specimens [5,20,24,30,31,33,37]. Very few studies directly compare the results from human and non-human hosts [17,18], and only one study for kidney and another for liver tissue has investigated the feasibility of using porcine tissue properties as a substitute for human tissue parameters [34,38]. The study involving the kidney only investigated the tissue from the two hosts using quasi-static tension testing of the kidney capsule. It was found that the elastic modulus differed significantly, but the failure properties did not, and thus porcine kidney tissue is a justifiable surrogate for human tissue [34]. It is still unknown whether these findings hold true at dynamic rates or when tested on an intact organ. The study that compared human and porcine liver failure stress also investigated bovine liver properties and the effect of loading rate through comparing results with two similar studies [38]. It was found that all three hosts demonstrated strain-rate dependent characteristics but that the specific results varied greatly between hosts. Moreover, the findings were compared to other published results that did not use the same methods and all the studies used partial specimens rather than intact livers.
There remain several gaps in knowledge regarding the response of the kidneys and liver to compressive loading. First, the stress-strain behavior, including failure properties, has not been extensively studied and reported for full organ testing. Second, the strain rates at which testing has been performed are limited, and little or no data is available at higher strain rates. Finally, the suitability of using porcine organ results as a substitute for human organ properties has not been fully explored, particularly under compression and at the strain rates of interest for many blunt trauma incidents. This study is the first to investigate these topics in depth and to compare the results using multiple testing methodologies.
The goals of this research are to characterize the material properties of the intact liver and kidney in compression using two protocols, full unconfined compression and probing, at varying strain rates for human and porcine tissues. Specifically, the aims are to determine the feasibility of using porcine tissue as a model for human tissue, compare the results using the two testing protocols, evaluate the impact of using intact organs, and quantify the relationship between strain rate and the elastic modulus (E), failure stress (σf), and failure strain (ef) of the liver and kidney individually. These parameters were chosen since they are required for developing numerical models and for interpreting the results regarding injury. It is hypothesized that there will be no differences between the material properties of human and porcine tissues, and also that increasing strain-rate will increase the E, σf and εf. Further characterizing the material properties of these organs will lead to improved computational and physical models for a range of dynamic loading conditions.
2. Materials and Methods
2.1. Specimens
Specimens were obtained from both human and porcine hosts. Three cadavers (ages 76–98 years), cleared from transmittable diseases, were procured from the Medical College of Wisconsin which resulted in six kidney (height: 21.9–29.35 mm; area: 1677–4700 mm2) and three liver specimens (height: 43.99–54.21 mm; area: 13,500–19,600 mm2). The 32 fresh kidneys (height: 26.21–34.9 mm; area: 5200–12,600 mm2) and 23 fresh livers (height: 31.42–55.5 mm; area; 18,800–92,300 mm2) from porcinis were obtained from a local slaughterhouse. All porcinis (ages 100–150 days) were used for other purposes, and thus no animals were euthanized specifically for this study. All tissue testing occurred as soon as possible after death of the host. Tissue was kept refrigerated at 4 degrees Celsius when storage was required, and prior to testing organs were brought to room temperature.
2.2. Material Testing Devices
Three types of material testing were performed: destructive compression testing, nondestructive compression testing, and probing. A Material Testing System (MTS) was used for both destructive and nondestructive compression testing (Figure 1). The compressive force and displacement were sampled at a rate of 4096 Hz. The load placed on the human and porcine tissue was measured using 15 kN and 2.5 kN load cells.

Figure 1.
Experimental set up of the kidney in the unconfined compression testing protocol that is identical for the liver tissue.
The third type of material testing was a probing protocol that used a Mark-10 force gauge with an EMSL-301 test stand that collected both force and displacement at 50 Hz. The end of the probe in contact with the organs was a flat circular (4.9 mm diameter) loading surface.
2.3. Experimental Protocol
Nondestructive and destructive testing was performed using the unconfined compression protocol. The methodology involved placing either a liver or kidney between two compression plates that fully cover the specimen. In nondestructive testing, the top plate compresses the organ up to 30% strain (below the failure point as seen in Figure 2), while destructive testing compresses the organ until failure. Nondestructive testing tests were repeated at varying strain rates on the same organ, with sufficient time between tests to allow the organ to return to its initial height. In order to further minimize the effects of prior testing, the strain rate testing order was randomized for each specimen. Destructive tests allowed only one strain rate to be used per specimen but rates were varied between specimens (Table 1 and Table 2). Both testing types were displacement controlled. Force and displacement were used to calculate engineering stress and engineering strain (Equations (1) and (2)). Engineering stress and strain were chosen for reporting due to their general use in the literature [21] and the inability to obtain the exact current loaded area during testing for these specimens and protocols.
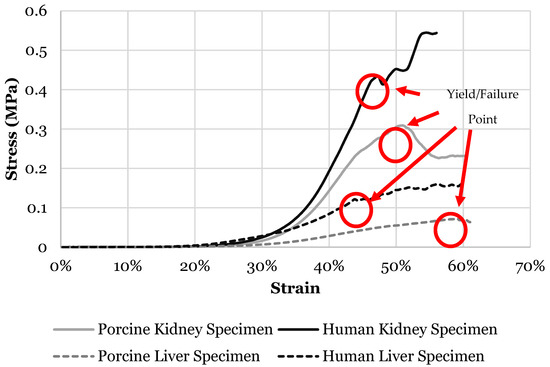
Figure 2.
Stress versus strain curve of liver and kidney specimens from both human and porcine showing failure/yield point.

Table 1.
Strain rates used in each of the protocols in the kidney experimental testing.

Table 2.
Strain rates used in each of the protocols in the liver experimental testing.
All organs were placed on graph paper with known area to estimate the surface area (Figure 3). The E was calculated by taking the secant slope at the most linear portion of the curve. σf and εf were recorded during destructive testing. Failure was defined as a 10% drop in force or an increase of 3% strain with no increase in force.

Figure 3.
Porcine kidney (a) and liver (b) placed on graph paper used to estimate surface area.
The probing methodology indented human and porcine specimens at the tallest point of the organ using rates of 1%/s and 25%/s up to 30% strain. The stress for the probing method was calculated using Equation (3).
2.4. Data Analysis
A mathematical model (Equation (4)) was used to describe the stress-strain relationship that was observed in the experimental testing [39]. The parameters consist of the E in the toe region (Etoe), the E in the terminal region (Eterm), the center strain of the inflection region (εc), and a parameter describing the curvature of the inflection region (ψ).
where E and ε are the current values.
The parameters that best fit the experimental curves were found for each of the strain rates. Changes in the material model parameters between different strain-rates were analyzed. In order to determine model fit, the R2 of the line produced by plotting experimental results on the y-axis with the modeled results on the x-axis was found. Equation (5) was developed to determine the relationship between the material properties and strain rate through an optimization process within Excel (Microsoft, Redmond, WA, USA) that maximized the R2.
The factor of strain rate on the porcine material properties was tested using a one-way ANOVA for all protocols. Two sample t-test was used to determine the statistical differences between human and porcine results at each rate. Alpha value of 0.05 was used for all statistical tests.
3. Results
3.1. Kidney
A material model (Equation (4)) was used to describe the stress–strain relationship of both human and porcine kidneys (Table 3). A dependency in strain rate was observed in the model for both human and porcine kidney. The Etoe for the human model increased by 0.009 MPa from 1%/s to 5%/s and by 0.003 from 5%/s to 25%/s while no changes were observed in the porcine results. The curvature of the inflection region was inconsistent between rates with large deviations. Porcine curvature of the inflection region was more consistent with a maximum standard deviation of 3.00. Finally, both human and porcine Eterm increased with each increase in rate. The largest increase was 0.0041 MPa for the human model and 0.008 MPa for the porcine model between the rates of 5%/s to 25%/s. Overall, the rest of the parameters were unaffected by the strain rate.

Table 3.
Average and standard deviation of the model parameters and R2 of model fit to experimental results for the kidney at tested strain rates for each host in the nondestructive testing protocol.
Porcine kidney E was measured to be stiffer than human at all rates in the unconfined compression protocol (p < 0.05) (Table 4). Human kidney E ranged from 0.005 MPa at 1%/s to 0.01 MPa at 25%/s on average, while porcine specimens ranged from 0.03 MPa at 1%/s to 0.045 MPa at 25%/s. Although not statistically significant, the human E increased with every increase in strain rate.

Table 4.
Elastic modulus of human and porcine kidneys from rates of 1%/s to 25%/s for the unconfined compression protocol.
The E of the porcine kidney was measured at rates ranging from 1%/s to 1000%/s (Figure 4). On average, the specimens became stiffer as the strain rate increased (p < 0.001). From 1%/s to 100%/s no statistical difference in E was found, but rates above 100%/s were statistically higher than at 1%/s and 5%/s, and 1000%/s was statistically stiffer than rates below 500%/s. The model relating E to strain rate (Equation (5)) has an R2 of 0.98 (Figure 4), and the parameters for porcine kidneys are shown in Table 5. The behavior of the kidney E is sensitive to the strain rate at low strain rates up to 100%/s and then this dependency starts to saturate.
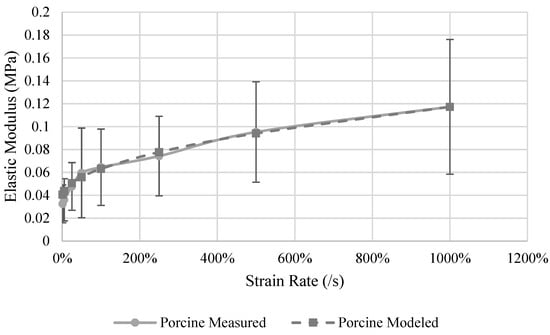
Figure 4.
Measured and model predicted elastic modulus of the porcine kidney.

Table 5.
Parameters for the material model that describes the relationship between strain rate and elastic modulus for porcine kidneys.
No differences were observed in the E of the two hosts when tested at 1%/s and 25%/s using the probing protocol (Table 6). A 95% increase in E was measured in the human kidney when testing at 25%/s versus 1%/s (p = 0.006), and a 20% increase was observed between the same rates for the porcine specimens (p > 0.05).

Table 6.
Elastic modulus for both human and porcine kidney tissue in the probing protocol at varying strain rates.
Other than at a relative low strain rate (5%/s), the human specimens had a σf 16% to 25% higher than the porcine specimens (Figure 5). The largest difference was at the rate of 100%/s where the human kidney failed at 0.36 MPa while the porcine kidney failed at 0.26 MPa. An increase of 0.13 MPa was observed between the rates of 100%/s and 500%/s for the porcine specimens, which was the largest increased observed between all rates. Failure stress was observed to be generally dependent on strain rate for both human and porcine specimens (Figure 5). The strain-rate dependence model (Equation (5)) for porcine specimens (Table 7) has an R2 of 0.97. The behavior of the kidney sf is sensitive to the strain rate at rates up to 100%/s and then this dependency starts to saturate.
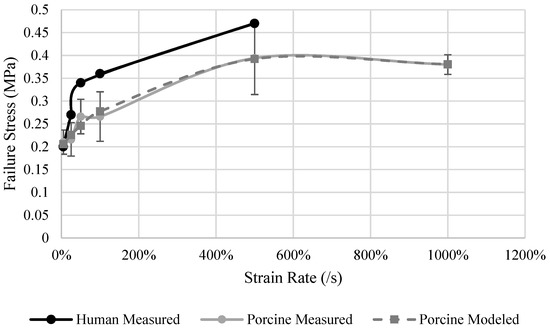
Figure 5.
Measured human and porcine and porcine model predicted failure stress of the kidney.

Table 7.
Parameters for the material model that describes the relationship between strain rate and failure stress for porcine kidneys.
Failure strain was nearly identical between the two hosts. Both human and porcine εf was observed to be independent of strain rate. On average the εf was 49% and ranged from 41% to 57%.
3.2. Liver
Equation (4) was also used to describe the stress-strain behavior of the human and porcine liver specimens between the rates of 1%/s to 25%/s (Table 8). An effect of strain rate was observed for all four parameters for both human and porcine specimens only after the strain rate was increased to 25%/s. Little to no changes were observed in the Etoe parameter for both human and porcine livers between all rates. An increase of 50% was observed for the Eterm parameter between the rates of 5%/s and 25%/s for the modeled human stress-strain curve, and 40% for the modeled porcine results. The parameter describing the curvature of the inflection region dropped by 6% with each increase in strain rate for the porcine results, while human modeled results had a drop of 30% from 1%/s to 5%/s and 23% from 5%/s to 25%/s. Little to no changes were observed between the rest of the parameters between the rates of 5%/s to 25%/s for both human and porcine modeled results.

Table 8.
Average and standard deviation of the model parameters and R2 of model fit to experimental results for the liver at tested strain rates for each host in the nondestructive testing protocol.
Small differences were observed in the E between human and porcine hosts tested in unconfined compression. Porcine hosts were stiffer by only 0.004 MPa, 0.013 MPa, and 0.02 MPa for the rates of 1%/s, 5%/s, and 25%/s respectively (Table 9). The average E for the human specimens ranged from 0.04 MPa at 1%/s to 0.06 MPa at 25%/s. Porcine specimens became stiffer as strain rate increased ranging from 0.032 MPa at 1%/s to 0.06 MPa at 500%/s on average (p = 0.016). Only the rates above 100%/s were statistically significantly greater than the E measured at 1%/s (Figure 6). The strain rate dependency model (Equation (5)) results (Table 10) has an R2 of 0.98 (Figure 6). Porcine liver E was found to be sensitive to the strain rate between 5%/s and 50%/s. As the rates increase above 50%/s, the dependency becomes linear.

Table 9.
Elastic modulus of human and porcine liver specimens at varying strain rates in unconfined compression.
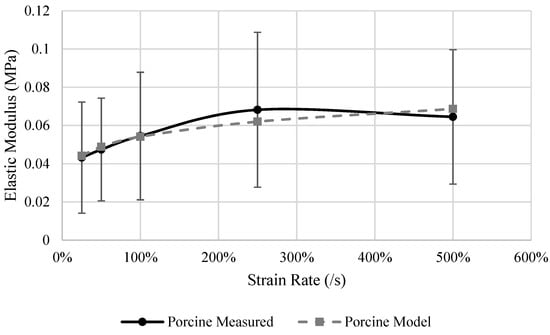
Figure 6.
Measured and model predicted elastic modulus of the porcine liver.

Table 10.
Parameters for the material model that describes the relationship between strain rate and porcine liver elastic modulus.
Human livers were approximately 0.13 MPa softer at 1%/s and 0.16 MPa stiffer at 25%/s strain rate (p = 0.027 and 0.033) for the probing protocol. E increased by 33% from the rate of 1%/s to 25%/s for the porcine hosts and 55% for the human liver but both increases were not statistically significant (p > 0.05) (Table 11).

Table 11.
Human and porcine liver elastic modulus at varying strain rates in the probing methodology.
Human livers had a higher σf than the porcine specimens at every tested strain rate. The largest difference, a 135% increase, was observed at the rate of 25%/s, and the smallest difference, a 62% increase, was observed at 500%/s. Strain rate dependency was observed for the σf in both human and porcine livers (Figure 7). Human livers tested at a rate of 25%/s had a σf of 0.11 MPa, which increased by 54% to 0.17 MPa when tested at 500%/s. Similarly, the porcine specimen σf increased from 0.04 MPa to 0.11 MPa from the rate of 25%/s to 500%/s. σf dependence on strain rate was statistically significant (p = 0.011) for the porcine results. The strain rate dependence model (Equation (5)) of the porcine σf results (Table 12) has an R2 of 0.98 (Figure 7). The liver σf is sensitive to the strain rate between the rates of 5%/s to 500%/s. A slight pause is observed between the rates of 25%/s to 100%/s but then a slight increase in σf was observed from 100%/s to 500%/s.
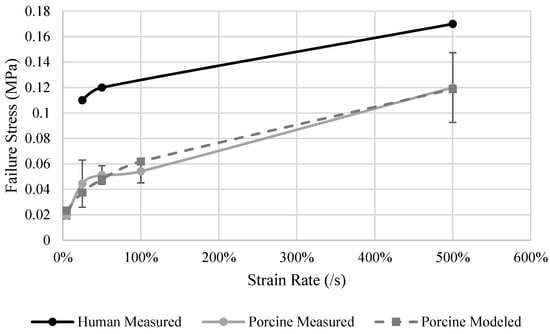
Figure 7.
Human and porcine measured and porcine model predicted failure stress of the liver.

Table 12.
Parameters for the material model that describes the relationship between strain rate and porcine liver failure stress.
A strain rate dependency was observed for εf in human and porcine livers (Figure 8). No differences were observed between the rates of 25%/s and 50%/s, but the εf increased 20% when tested at 500%/s for human specimens. For porcine specimens, it was found that εf increased with each incremental increase in strain rate, ranging from 50% strain at 5%/s to 75% strain at 500%/s (p = 0.01). ef at rates of 100%/s and 500%/s were statistically higher than at a rate of 5%/s, and only 500%/s was statistically higher than at the rate of 25%. The strain rate dependence model (Equation (5)) results (Table 13) an R2 of 0.96 (Figure 8). The behavior of the liver εf is sensitive to the strain rate between the rates of 5%/s to 50%/s. As the rates increase above 50%/s, the material property dependency on strain rate saturates.
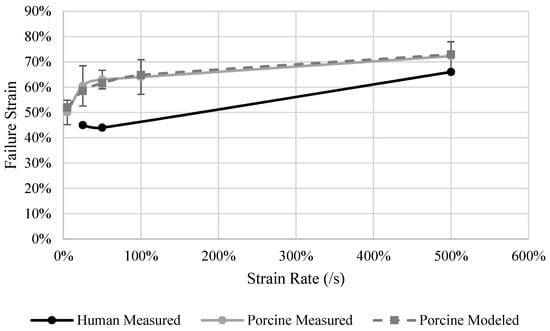
Figure 8.
Human and porcine measured and porcine model predicted failure strain of the liver.

Table 13.
Parameters for the material model that describes the relationship between strain rate and porcine liver failure strain.
4. Discussion
4.1. Kidney
An unconfined compression and probing protocol were used to characterize the mechanical properties of the intact human and porcine kidney. The results from the unconfined compression protocol determined that porcine tissue stiffness (E) was 4 times larger than for the human kidneys. This finding indicates that substituting E from porcine tissue testing for human properties is not justified. However, little to no differences were observed in σf and εf and therefore porcine values are suitable for use in human models for those parameters. A study by Giraud [40] has identified many anatomical similarities between human and porcine kidneys, but the large disparity in E between the two hosts could be due to the difference in specimen age. It has been previously determined that aging has a significant impact on the elastin content within tissue which effects stiffness [35]. The porcinis were estimated to be within 2% of their expected lifespan when the organs were procured, while human specimens were procured from cadavers that had reached their natural lifespan.
One of the unique aspect that this research offers is the testing of whole intact kidneys, in contrast to previous studies that tested only single components or pieces from the organ. The current study found E of the whole porcine kidney to be 0.033 MPa at 1%/s strain rate while compression testing of the parenchyma by Umale [5] at quasi-static rates found E to be 0.015 MPa. This comparison demonstrates the substantial difference in properties between testing whole organs and dissected pieces, which indicates that testing a whole intact organ, as was done in the current study, should provide the most realistic material properties for use in modeling, as the kidney is a combination of all of its components.
Comparing the results from applying two different testing methodologies to the same specimens has not previously been performed on the kidneys. A similar relationship of E with strain rate was observed between the unconfined compressions and probing protocols. However, the E in the probing protocol was higher for both hosts. The human and porcine kidneys geometries are similar, thus the comparable trend in E and its variation with strain rate was expected. The increase in E seen in the probing protocol could be due to compressing a smaller area of the tissue and the involvement of surrounding tissue is not directly addressed in the calculation of modulus, highlighting the need to test using an appropriate protocol for the expected application of the results.
Unconfined compression tests were performed at higher rates for the porcine specimens due to the availability of specimens, and the effect of strain rate on E was determined. An increase in E with an increase in strain rate was observed for both human and porcine kidneys. E increased linearly with strain rate at a rate of 0.05 MPa per 1%/s increase in strain rate, but after 50%/s this dependence saturates and the rate of change in E decreases to 0.006 MPa per 1%/s increase in strain rate from the rates of 100%/s to 1000%/. Thus the kidney tissue E is more sensitive to strain rate changes at lower rates. A similar relationship between strain rate and σf was observed for porcine kidneys. A linear relationship with an increase of 0.16MPa with every 1%/s increase in strain rate was found up to 50%/s. The strain rate dependency saturates at this point and no difference was found between 500%/s and 1000%/s. A previous study on kidney capsule tissue only [34] found similar relationships of E with strain rate under tension testing, but the saturation occurred 150%/s. No strain rate effect was observed for εf in this study between human and porcine kidneys, in contrast to σf and E.
4.2. Liver
The material properties of an intact liver were characterized for both human and porcine specimens. No statistically significant differences were found between E and εf of the human and porcine liver in unconfined compression. Although geometrically different, on a tissue level the porcine and human liver are similar [41,42] and thus, similar results were expected. The current study found the porcine modulus at 1%/s strain rate to be 0.032 MPa while a previous study that tested only the porcine liver parenchyma under quasi-static loading [5] reported a modulus of 0.002 MPa for small strains. These findings underscore the importance of using whole intact organs for determining material properties for subsequent modeling. A large difference in E, between the human and porcine livers, was found for the probing protocol, in contrast to the unconfined compression protocol results. The difference in geometry between hosts could drive this difference. In the unconfined compression protocol, the entire organ was compressed at once and thus the geometrical differences have a lesser influence. However, in the probing protocol, a small portion of the liver is being compressed. For both hosts the highest point of the liver was probed. Human livers have two lobes of which the right lobe is often larger, thus the probe compressed the right lobe. For porcine livers, there are four lobes that are all connected at the center, which is the highest point. Compressing the porcine liver via probe allows for the four lobes to move somewhat relative to each other as the pressure increases, thus lowering the measured E. These differences in probing results again indicate the need to test using a loading methodology and protocol similar to what is experienced in-vivo if the results are to produce accurate models.
Another difference found between the two hosts was higher σf in human specimens versus the porcine specimens. Amongst other factors such as disease, aging, and previous injury, alcohol can have a significant effect on the collagen content of the liver [43,44], which may impact the failure properties in human livers.
A strain rate dependency was observed for the E, σf, and εf in unconfined compression. The dependency on strain rate saturates after 50%/s for E and εf for both hosts. The strain rate effect is greatest going from quasi-static to slow dynamic rates which is described using a mathematical model. This study tested at several different rates which allowed for the model development that describes the point where the ἑ dependency saturates. No previous studies of the liver had described the relationship between E, σf, and εf and strain rate. Thus, the strain rate dependence models developed in this study provide more accurate information regarding the material properties at higher load rates which can allow for a wider range of modeling applications.
One of the limitations in this study is that the testing device used for the probing protocol limited the maximum strain rate. However, an impact of strain rate, similar to that in unconfined compression, was still able to be identified at the lower rates. This study also obtained a limited number of human specimens that were also of advanced age. This may pose some limitation on the range of data but should not affect the overall results with respect to strain rate dependency, protocol differences, etc., nevertheless statistical significance was not achieved for the human specimens.
5. Conclusions
Overall this study provides detailed new information regarding human and porcine kidney and liver properties at multiple strain rates for whole intact organs that was not available from previous studies. The goals of this study were four fold: (i) quantify the E, σf, and εf at multiple strain rates of kidney and liver; (ii) examine the impact of whole intact organ versus partial specimens testing; (iii) compare results from unconfined compression and probing testing protocols; (iv) investigate the feasibility of using porcine liver and kidney mechanical properties as substitutes for human tissue parameters.
The findings for kidney material properties include:
- Kidney modulus and failure stress are dependent on the strain rate while failure strain was largely independent of strain rate. The strain rate dependence saturated at rates greater than 100%/s.
- Kidney modulus measured using whole organ testing was approximately twice as stiff as previously reported for kidney parenchyma specimens. Caution must be exercised when using material parameters derived from partial kidney specimens.
- Kidney modulus measured using the probing protocol was larger than under unconfined compression for both hosts. Therefore the results from two testing methods are not interchangeable.
- Porcine kidney was found to be four times stiffer than human kidney tissue and therefore the elastic modulus of porcine kidney cannot be used for human tissue modeling. Nevertheless, the failure stress and failure strain of the kidney from both hosts was found to be similar.
The results of the mechanical property testing on liver are as follows:
- Liver modulus, failure stress, and failure strain are dependent on the strain rate. Failure strain dependence on rate saturated at rates greater than 50%/s.
- Liver modulus measured using whole organ testing was much larger than previously reported for liver parenchyma specimens. Caution must be exercised when using material parameters derived from partial liver specimens.
- Liver modulus measured using the probing protocol was four times larger than under unconfined compression for the human specimens and twice as large for porcine livers. Therefore the results from two testing methods are not interchangeable.
- Porcine liver mechanical properties were found to be an adequate substitute for human kidney properties for elastic modulus and failure strain, but not for failure stress.
The results from this study will aid in the development of more accurate and comprehensive computational and physical models and better understanding of the behavior of the liver and kidney to dynamic impacts or loading.
Author Contributions
Conceptualization, N.C.-K.; Methodology, N.C.-K. and B.J.; Software, B.J.; Validation, B.J. and N.C.-K.; Formal Analysis, B.J., S.C. and N.C.-K.; Investigation, B.J. and N.C.-K.; Resources, N.C.-K.; Data Curation, B.J.; Writing—Original Draft Preparation, B.J., S.C. and N.C.-K.; Writing—Review & Editing, B.J., S.C. and N.C.-K.; Visualization, B.J. and S.C.; Supervision, N.C.-K.; Project Administration, N.C.-K.; Funding Acquisition, N.C.-K. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the United States Department of Defense grant #4892-ARMY-DHP-ELVIS Phase II.
Institutional Review Board Statement
The study was exempt from the IRB of the University of Wisconsin-Milwaukee and approved by US Army Medical Research and Materiel Command (USAMRMC) Office of Research Protections (ORP) Protocol #A-17744.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to acknowledge the tissue donors and the financial support of the United States Department of Defense.
Conflicts of Interest
The authors declare no conflict of interest.
Notations and Abbreviations
| E | Elastic modulus |
| Eterm | Elastic modulus of terminal region |
| Etoe | Elastic modulus of toe region |
| ε | Engineering strain |
| εc | Center strain of inflection point |
| εf | Failure strain |
| Strain rate | |
| σ | Stress |
| σf | Failure stress |
| σND | Stress for non-destructive methodology |
| σP | Stress for probing methodology |
| ψ | Parameter describing the curvature of inflection region |
References
- Klinich, K.; Flannagan, C.; Nicholson, K.; Schneider, L.; Rupp, J. Abdominal Injury in Motor Vehicle Crashes; UMTRI-2008-40; University of Michigan: Ann Arbor, MI, USA, 2008. [Google Scholar]
- Asensio, J.; Trunkey, D. Current Therapy of Trauma and Surgical Critical Care E-Book; Elsevier Health Sciences: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Chauhan, N.; Badgurjar, M.K.; Saxena, P. A Prospective Study of Assessment of Solid Organs in Cases of Blunt Abdominal Trauma. Int. J. Sci. Res. 2019, 8, 48–50. [Google Scholar]
- Loftis, K.; Edward, L.; Mazuchowski, L.; Clouser, M.; Gillich, P. Prominent Injury Types in Vehicle Underbody Blast. Mil. Med. 2019, 184, 261–264. [Google Scholar] [CrossRef]
- Umale, S.; Deck, C.; Bourdet, N.; Dhumane, P.; Soler, L.; Marescaux, J.; Willinger, R. Experimental Mechanical Characterization of Abdominal Organs: Liver, Kidney & Spleen. J. Mech. Behav. Biomed. Mater. 2013, 17, 22–33. [Google Scholar]
- Lizee, E.; Robin, S.; Song, E.; Bertholon, N.; Le Coz, J.-Y.; Besnault, B.; Lavaste, F. Development of a 3D Finite Element Model of the Human Body. SAE Trans. 1998, 107, 2760–2782. [Google Scholar]
- Bass, C.; Davis, M.; Rafaels, K.; Rountree, M.; Harris, R.; Sanderson, E.; Andrefsky, W.; DiMarco, G.; Zielinski, M. A Methodology for Assessing Blast Protection in Explosive Ordnance Disposal Bomb Suits. Int. J. Occup. Saf. Ergon. 2005, 11, 347–361. [Google Scholar] [CrossRef]
- Roberts, J.; Merkle, A.; Biermann, P.; Ward, E.; Carkhuff, B.; Cain, R.; O’Connor, J. Computational and Experimental Models of the Human Torso for Non-Penetrating Ballistic Impact. J. Biomech. 2007, 40, 125–136. [Google Scholar] [CrossRef] [PubMed]
- Ward, E.; Merkle, A.; Harrigan, T.; Roberts, J. Comparing Blast Effects on Human Torso Finite Element Model Against Existing Lethality Curves. In Proceedings of the Department of Defense Explosive Safety Board Seminar, Portland, OR, USA, 13–15 July 2010; Volume 34. [Google Scholar]
- Chen, Z.; Joli, P.; Feng, Z.-Q. Finite Element Modeling of Interactions Between Pelvic Organs Due to Pressure. In Proceedings of the 10e Colloque National En Calcul Des Structures, Giens, France, 9–13 May 2011. [Google Scholar]
- Gayzik, F.; Moreno, D.; Vavalle, N.; Rhyne, A.; Stitzel, J. Development of the Global Human Body Models Consortium Mid-Sized Male Full Body Model. In International Workshop on Human Subjects for Biomechanical Research; National Highway Traffic Safety Administration: Washington, DC, USA, 2011; Volume 39. [Google Scholar]
- Beillas, P.; Berthet, F. Performance of a 50th Percentile Abdominal Model for Impact: Effects of Size and Mass. J. Biomech. 2012, 45, S83. [Google Scholar] [CrossRef]
- Golman, A.; Danelson, K.; Miller, L.; Stitzel, J. Injury Prediction in a Side Impact Crash Using Human Body Model Simulation. Accid. Anal. Prev. 2014, 64, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, D.; Guleyupoglu, B.; Koya, B.; Stitzel, J.; Gayzik, F. Development of a Computationally Efficient Full Human Body Finite Element Model. Traffic Inj. Prev. 2015, 16, S49–S56. [Google Scholar] [CrossRef]
- Tamura, A.; Omori, K.; Miki, K.; Lee, J.; Yang, K.; King, A. Mechanical Characterization of Porcine Abdominal Organs; SAE Technical Paper, No. 2002-22-0003; SAE: Warrendale, PA, USA, 2002. [Google Scholar]
- Kemper, A.; Santago, A.; Stitzel, J.; Sparks, J.; Duma, M. Biomechanical Response of Human Spleen in Tensile Loading. J. Biomech. 2012, 45, 348–355. [Google Scholar] [CrossRef] [PubMed]
- Johnson, B.; Campbell, S.; Campbell-Kyureghyan, N. The Differences in Measured Prostate Material Properties Between Probing and Unconfined Compression Testing Methods. Med Eng. Phys. 2020, 80, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Johnson, B.; Campbell, S.; Campbell-Kyureghyan, N. Biomechanical Properties of Abdominal Organs Under Tension with Special Reference to Increasing Strain Rate. J. Biomech. 2020, 109, 109914. [Google Scholar] [CrossRef]
- Roberts, J.; O’Connor, J.; Ward, E. Modeling the Effect of Nonpenetrating Ballistic Impact as a Means of Detecting Behind-Armor Blunt Trauma. J. Trauma Acute Care Surg. 2005, 58, 1241–1251. [Google Scholar] [CrossRef]
- Hollenstein, M.; Nava, A.; Valtorta, D.; Snedeker, J.; Mazza, E. Mechanical Characterization of the Liver Capsule and Parenchyma. In International Symposium on Biomedical Simulation; Springer: Berlin/Heidelberg, Germany, 2006; pp. 150–158. [Google Scholar]
- Chui, C.; Kobayashi, E.; Chen, X.; Hisada, T.; Sakuma, I. Transversely Isotropic Properties of Porcine Liver Tissue: Experiments and Constitutive Modelling. Med Biol. Eng. Comput. 2007, 45, 99–106. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Shojaei, A. Measurement of the Mechanical Properties of the Human Kidney. IRBM 2017, 38, 292–297. [Google Scholar] [CrossRef]
- Rosen, J.; Brown, J.; De, S.; Sinanan, M.; Hannaford, B. Biomechanical Properties of Abdominal Organs in Vivo and Postmortem Under Compression Loads. J. Biomech. Eng. 2008, 130, 021020. [Google Scholar] [CrossRef] [PubMed]
- Santago, A.; Kemper, A.; McNally, C.; Sparks, J.; Duma, S. The Effect of Temperature on the Mechanical Properties of Bovine Liver. Biomed. Sci. Instrum. 2009, 45, 376–381. [Google Scholar]
- Brunon, A.; Bruyere-Garnier, K.; Coret, M. Mechanical Characterization of Liver Capsule Through Uniaxial Quasi-Static Tensile Tests Until Failure. J. Biomech. 2010, 43, 2221–2227. [Google Scholar] [CrossRef]
- Gao, Z.; Lister, K.; Desai, J. Constitutive Modeling of Liver Tissue: Experiment and Theory. Ann. Biomed. Eng. 2010, 38, 505–516. [Google Scholar] [CrossRef]
- Kemper, A.; Santago, A.; Stitzel, J.; Sparks, J.; Duma, S. Biomechanical Response of Human Liver in Tensile Loading. In Annals of Advances in Automotive Medicine/Annual Scientific Conference; Association for the Advancement of Automotive Medicine: Chicago, IL, USA, 2010; Volume 54, p. 15. [Google Scholar]
- Chatelin, S.; Oudry, J.; Perichon, N.; Sandrin, L.; Allemann, P.; Soler, L.; Willinger, R. In Vivo Liver Tissue Mechanical Properties by Transient Elastography: Comparison with Dynamic Mechanical Analysis. Biorheology 2011, 48, 75–88. [Google Scholar] [CrossRef]
- Lu, Y.-C.; Untaroiu, C. Effect of Storage Methods on Indentation-Based Material Properties of Abdominal Organs. Proc. Inst. Mech. Eng. Part H 2013, 227, 293–301. [Google Scholar] [CrossRef]
- Lu, Y.-C.; Kemper, A.; Untaroiu, C. Effect of Storage on Tensile Material Properties of Bovine Liver. J. Mech. Behav. Biomed. Mater. 2014, 29, 339–349. [Google Scholar] [CrossRef]
- Miller, K. Constitutive Modelling of Abdominal Organs. J. Biomech. 2000, 33, 367–373. [Google Scholar] [CrossRef]
- Carter, F.J.; Frank, T.G.; Davies, P.J.; McLean, D.; Cuschieri, A. Measurements and Modelling of the Compliance of Human and Porcine Organs. Medical Image Anal. 2001, 5, 231–236. [Google Scholar] [CrossRef]
- Dương, M.; Huynh Nguyễn, N.; Ngọc Trần, T.; Tolba, R.H.; Staat, M. Influence of Refrigerated Storage on Tensile Mechanical Properties of Porcine Liver and Spleen. Int. Biomech. 2015, 2, 79–88. [Google Scholar] [CrossRef][Green Version]
- Snedeker, J.; Niederer, P.; Schmidlin, F.R.; Farshad, M.; Demetropoulos, C.K.; Lee, J.B.; Yang, K.H. Strain-Rate Dependent Material Properties of the Porcine and Human Kidney Capsule. J. Biomech. 2005, 38, 1011–1021. [Google Scholar] [CrossRef] [PubMed]
- Roan, E.; Vemaganti, K. The Nonlinear Material Properties of Liver Tissue Determined From No-Slip Uniaxial Compression Experiments. J. Biomech. Eng. 2007, 129, 450–456. [Google Scholar] [CrossRef] [PubMed]
- Saraf, H.; Ramesh, K.; Lennon, A.; Merkle, A.; Roberts, J. Mechanical Properties of Soft Human Tissues Under Dynamic Loading. J. Biomech. 2007, 40, 1960–1967. [Google Scholar] [CrossRef] [PubMed]
- Tay, B.K.; Kim, J.; Srinivasan, M. In Vivo Mechanical Behavior of Intra-Abdominal Organs. IEEE Trans. Biomed. Eng. 2006, 53, 2129–2138. [Google Scholar] [CrossRef]
- Kemper, A.; Santago, A.; Stitzel, J.; Sparks, J.; Duma, S. Effect of Strain Rate on the Material Properties of Human Liver Parenchyma In Unconfined Compression. J. Biomech. Eng. 2013, 135, 104503. [Google Scholar] [CrossRef]
- Campbell-Kyureghyan, N.; Marras, W. Combined Experimental and Analytical Model of the Lumbar Spine Subjected to Large Displacement Cyclic Loads Part II–Model Validation. Int. J. Comput. Vis. Biomech. 2009, 2, 95–104. [Google Scholar]
- Giraud, S.; Favreau, F.; Chatauret, N.; Thuillier, R.; Maiga, S.; Hauet, T. Contribution of Large Pig For Renal Ischemia-Reperfusion and Transplantation Studies: The Preclinical Model. BioMed Res. Int. 2011, 2011, 532127. [Google Scholar] [CrossRef] [PubMed]
- Sherratt, M.J. Tissue Elasticity and The Ageing Elastic Fibre. Age 2009, 31, 305–325. [Google Scholar] [CrossRef] [PubMed]
- Nykonenko, A.; Petr, V.; Zonča, P. Anatomic Peculiarities of Pig and Human Liver. Exp. Clin. Transplant. 2017, 15, 21–26. [Google Scholar]
- Neuman, R.E.; Logan, M. The Determination of Collagen and Elastin in Tissues. J. Biol. Chem. 1950, 186, 549–556. [Google Scholar] [CrossRef]
- Rojkind, M.; Marie-Adele, G.; Biempica, L. Collagen Types in Normal and Cirrhotic Liver. Gastroenterology 1979, 76, 710–719. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).