A Proposed Method for Evaluating Drop Jump Performance with One Force Platform
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
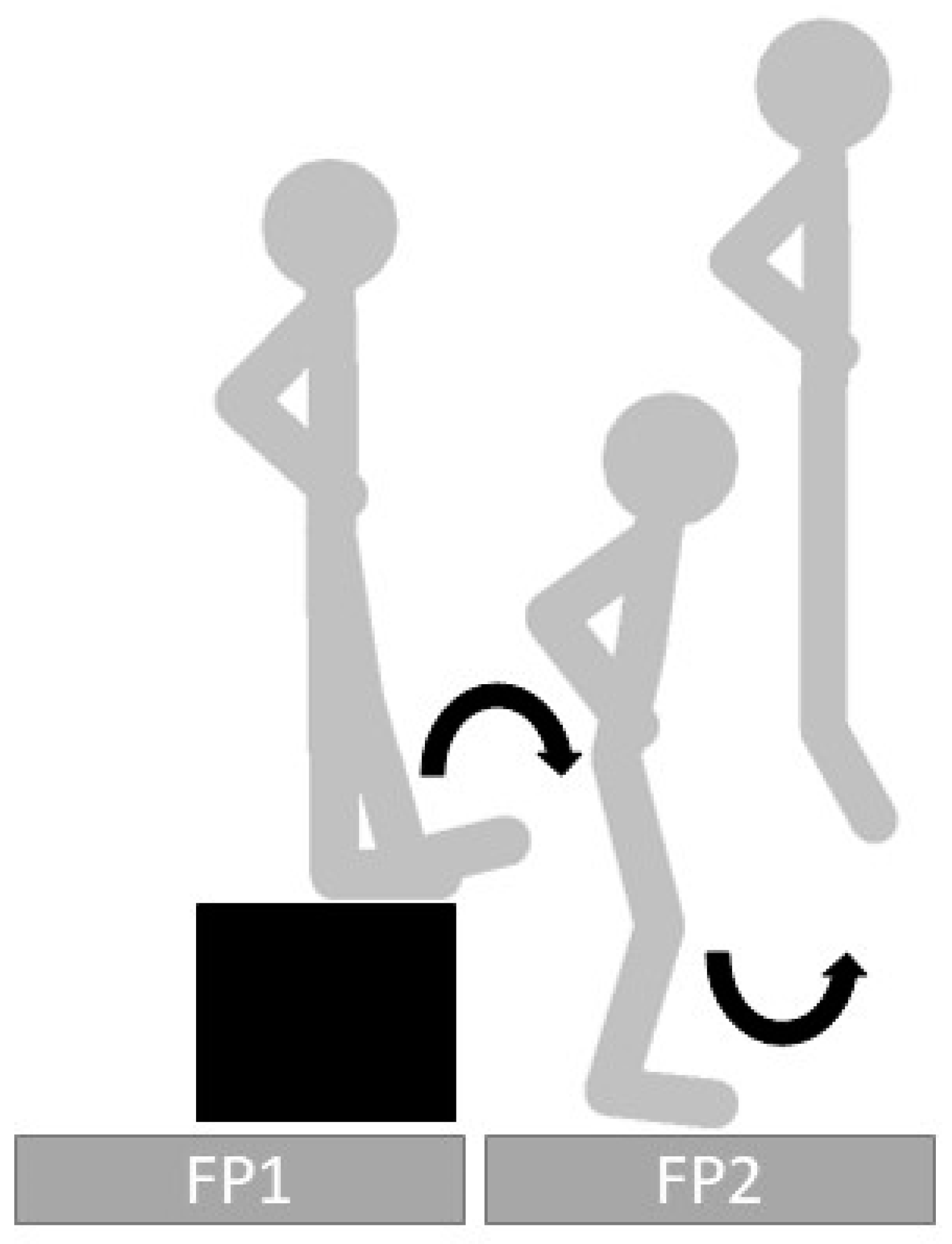
2.2. Experimental Design
2.3. Statistical Analysis
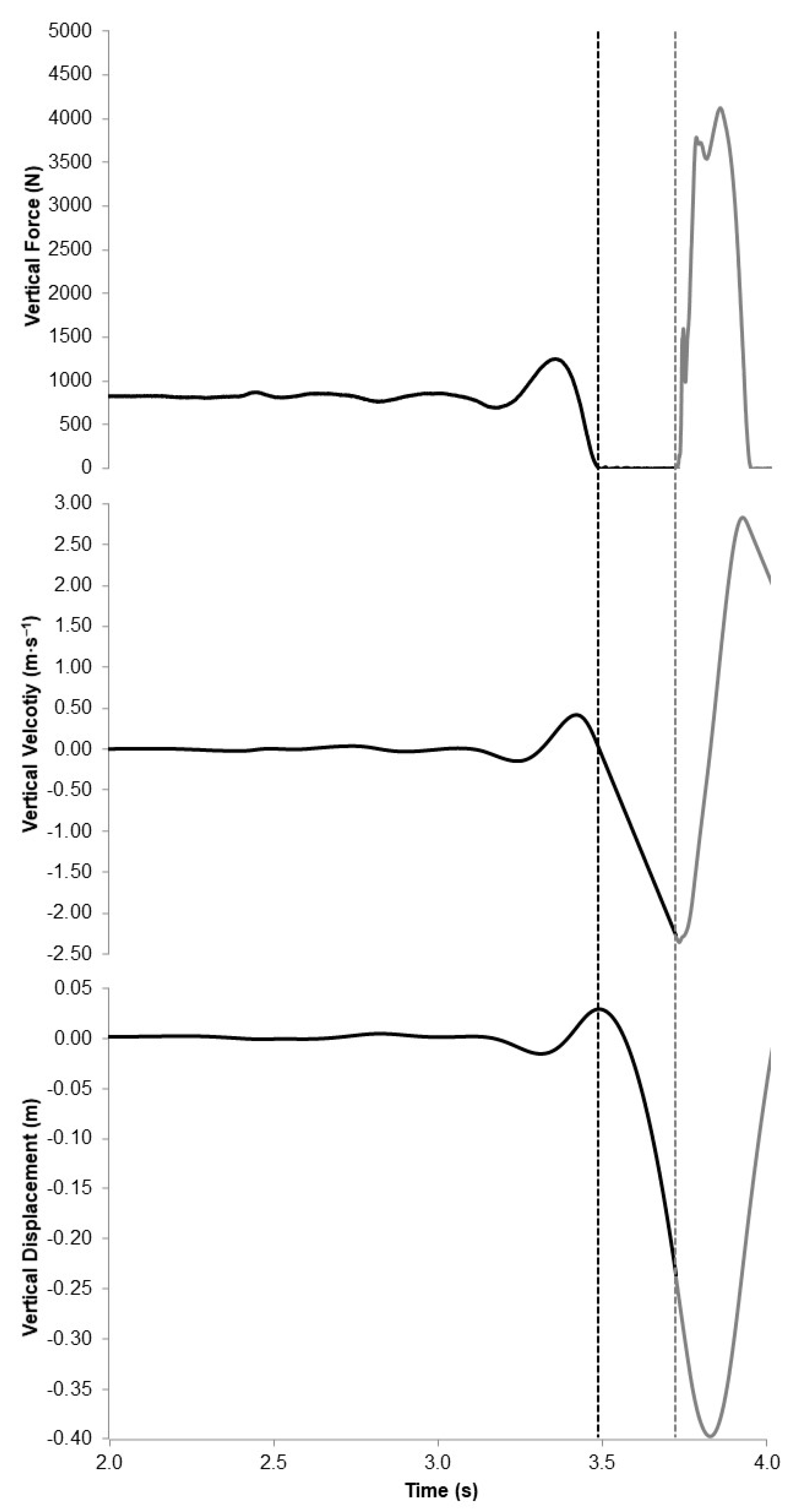
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pedley, J.S.; Lloyd, R.S.; Read, P.; Moore, I.S.; Oliver, J.L. Drop jump: A technical model for scientific application. Strength Cond. J. 2017, 39, 36–44. [Google Scholar]
- Byrne, P.J.; Moran, K.; Rankin, P.; Kinsella, S. A comparison of methods used to identify â€~optimal’drop height for early phase adaptations in depth jump training. J. Strength Cond. Res. 2010, 24, 2050–2055. [Google Scholar]
- Schmidtbleicher, D. Training for power events. In The Encyclopedia of Sports Medicine; Komi, P.V., Ed.; Blackwell Science: Oxford, UK, 1992; pp. 381–395. [Google Scholar]
- Geraldo, G.F.; Bredt, S.T.; Menzel, H.J.; Peixoto, G.H.; Carvalho, L.A.; Lima, F.V.; Soares, J.S.; Andrade, A.G. Drop height is influenced by box height but not by individual stature during drop jumps. J. Phys. Educ. 2019, 30, e-3078. [Google Scholar]
- Costley, L.; Wallace, E.; Johnston, M.; Kennedy, R. Reliability of bounce drop jump parameters within elite male rugby players. J. Sports Med. Phys. Fit. 2018, 58, 1390–1397. [Google Scholar]
- Suchomel, T.J.; McMahon, J.J.; Lake, J.P. Combined assessment methods. In Performance Assessment in Strength and Conditioning; Comfort, P., Jones, P.A., McMahon, J.J., Eds.; Routledge: London, UK, 2019. [Google Scholar]
- Baca, A. A comparison of methods for analyzing drop jump performance. Med. Sci. Sports Exerc. 1999, 31, 437–442. [Google Scholar]
- Kibele, A. Technical Note: Possible errors in the comparative evaluation of drop jumps from different heights. Ergonomics 1999, 42, 1011–1014. [Google Scholar]
- Palazzi, D.; Williams, B. Accuracy and precision of the kinetic analysis of drop jump performance. In Proceedings of the 30 International Conference on Biomechanics in Sports (2012), Melbourne, Australia, 2–6 July 2012. [Google Scholar]
- Bobbert, M.F.; Huijing, P.A.; van Ingen Schenau, G.J. Drop jumping. II. The influence of dropping height on the biomechanics of drop jumping. Med. Sci. Sports Exerc. 1987, 19, 339–346. [Google Scholar]
- Lake, J.P.; Augustus, S.; Austin, K.; Mundy, P.; McMahon, J.J.; Comfort, P.; Haff, G.G. The Validity of the Push Band 2. 0 during Vertical Jump Performance. Sports 2018, 6, 140. [Google Scholar]
- Lake, J.; Mundy, P.; Comfort, P.; McMahon, J.J.; Suchomel, T.J.; Carden, P. Concurrent Validity of a Portable Force Plate Using Vertical Jump Force-Time Characteristics. J. Appl. Biomech. 2018, 34, 410–413. [Google Scholar]
- Stratford, C.; Dos’ Santos, T.; McMahon, J.J. The 10/5 Repeated Jumps Test: Are 10 repetitions and three trials necessary? Biomechanics 2021, 1, 1–14. [Google Scholar]
- Stratford, C.; Dos’Santos, T.; McMahon, J.J. Comparing drop jumps with 10/5 repeated jumps to measure reactive strength index. Prof. Strength Cond. 2020, 57, 23–28. [Google Scholar]
- McMahon, J.J.; Suchomel, T.J.; Lake, J.P.; Comfort, P. Relationship between reactive strength index variants in rugby league players. J. Strength Cond. Res. 2021, 35, 280–285. [Google Scholar]
- Laffaye, G.; Bardy, B.; Taiar, R. Upper-limb motion and drop jump: Effect of expertise. J. Sports Med. Phys. Fit. 2006, 46, 238. [Google Scholar]
- Owen, N.J.; Watkins, J.; Kilduff, L.P.; Bevan, H.R.; Bennett, M.A. Development of a Criterion Method to Determine Peak Mechanical Power Output in a Countermovement Jump. J. Strength Cond. Res. 2014, 28, 1552–1558. [Google Scholar]
- Moir, G.L. Three Different Methods of Calculating Vertical Jump Height from Force Platform Data in Men and Women. Meas. Phys. Educ. Exerc. Sci. 2008, 12, 207–218. [Google Scholar]
- Dowling, J.J.; Vamos, L. Identification of Kinetic and Temporal Factors Related to Vertical Jump Performance. J. Appl. Biomech. 1993, 9, 95–110. [Google Scholar]
- Linthorne, N.P. Analysis of standing vertical jumps using a force platform. Am. J. Phys. 2001, 69, 1198–1204. [Google Scholar]
- Mullineaux, D.R.; Barnes, C.A.; Batterham, A.M. Assessment of bias in comparing measurements: A reliability example. Meas. Phys. Educ. Exerc. Sci. 1999, 3, 195–205. [Google Scholar]
- Ludbrook, J. A primer for biomedical scientists on how to execute model II linear regression analysis. Clin. Exp. Pharmacol. Physiol. 2012, 39, 329–335. [Google Scholar]
- McMahon, J.J.; Lake, J.P.; Suchomel, T.J. Vertical jump testing. In Performance Assessment in Strength and Conditioning; Comfort, P., Jones, P.A., McMahon, J.J., Eds.; Routledge: London, UK, 2018; pp. 96–116. [Google Scholar]
- Yamashita, D.; Murata, M.Y.I. Effect of Landing Posture on Jump Height Calculated from Flight Time. Appl. Sci. 2020, 10, 776. [Google Scholar]



| Criterion (Mean ± SD) | Alternative (Mean ± SD) | Mean Difference | Slope 95% CI | Intercept 95% CI | |
|---|---|---|---|---|---|
| Actual Drop Height (m) | 0.27 ± 0.03 | 0.27 ± 0.03 | 0.002 | −0.028 −0.069 to 0.013 | 1.112 0.960 to 1.264 |
| Touchdown Velocity (m·s−1) | 2.30 ± 0.13 | 2.29 ± 0.12 | 0.010 | −0.263 −0.638 to 0.112 | 1.119 0.956 to 1.282 |
| Jump Height (m) | 0.28 ± 0.06 | 0.28 ± 0.06 | −0.001 | −0.004 −0.025 to 0.018 | 1.009 0.931 to 1.087 |
| Braking Phase Time (s) | 0.098 ± 0.014 | 0.098 ± 0.014 | 0.000 | −0.001 −0.006 to 0.004 | 1.015 0.958 to 1.072 |
| Propulsion Phase Time (s) | 0.134 ± 0.020 | 0.134 ± 0.020 | 0.000 | 0.001 −0.005 to 0.005 | 0.989 0.958 to 1.033 |
| Braking Displacement (m) | −0.13 ± 0.02 | −0.13 ± 0.02 | −0.001 | 0.01 −0.008 to 0.027 | 1.082 0.945 to 1.219 |
| Propulsion Displacement (m) | 0.23 ± 0.04 | 0.23 ± 0.04 | −0.001 | −0.001 −0.020 to 0.019 | 0.997 0.907 to 1.088 |
| Mean Braking Force (N) | 2763.39 ± 391.78 | 2761.56 ± 393.59 | 1.831 | 14.576 −6.610 to 35.762 | 0.995 0.988 to 1.003 |
| Mean Propulsion Force (N) | 2223.28 ± 299.84 | 2225.55 ± 297.18 | −2.271 | 23.991 −7.450 to 55.219 | 0.991 0.977 to 1.006 |
| Criterion (Mean ± SD) | Alternative (Mean ± SD) | Mean Difference | Slope 95% CI | Intercept 95% CI | |
|---|---|---|---|---|---|
| Actual Drop Height (m) | 0.35 ± 0.03 | 0.34 ± 0.03 | 0.004 | −0.035 −0.084 to 0.014 | 1.114 0.975 to 1.252 |
| Touchdown Velocity (m·s−1) | 2.60 ± 0.13 | 2.59 ± 0.12 | 0.013 | −0.273 −0.667 to 0.120 | 1.110 0.961 to 1.260 |
| Jump Height (m) | 0.28 ± 0.07 | 0.28 ± 0.07 | −0.003 | 0.002 −0.009 to 0.012 | 0.982 0.943 to 1.022 |
| Braking Phase Time (s) | 0.101 ± 0.018 | 0.101 ± 0.017 | 0.000 | 0.000 −0.003 to 0.003 | 1.005 0.976 to 1.034 |
| Propulsion Phase Time (s) | 0.134 ± 0.022 | 0.135 ± 0.022 | 0.000 | −0.001 −0.004 to 0.002 | 1.000 0.978 to 1.024 |
| Braking Displacement (m) | −0.15 ± 0.02 | −0.15 ± 0.02 | −0.001 | −0.001 −0.004 to 0.002 | 1.056 0.819 to 1.294 |
| Propulsion Displacement (m) | 0.23 ± 0.04 | 0.23 ± 0.04 | −0.002 | 0.002 −0.009 to 0.013 | 0.982 0.935 to 1.030 |
| Mean Braking Force (N) | 2962.35 ± 389.96 | 2959.99 ± 391.12 | 2.358 | 11.165 −9.216 to 31.546 | 0.997 0.990 to 1.004 |
| Mean Propulsion Force (N) | 2208.32 ± 292.64 | 2212.73 ± 292.43 | −4.402 | −6.063 −32.025 to 19.899 | 1.001 0.988 to 1.013 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McMahon, J.J.; Lake, J.P.; Stratford, C.; Comfort, P. A Proposed Method for Evaluating Drop Jump Performance with One Force Platform. Biomechanics 2021, 1, 178-189. https://doi.org/10.3390/biomechanics1020015
McMahon JJ, Lake JP, Stratford C, Comfort P. A Proposed Method for Evaluating Drop Jump Performance with One Force Platform. Biomechanics. 2021; 1(2):178-189. https://doi.org/10.3390/biomechanics1020015
Chicago/Turabian StyleMcMahon, John J., Jason P. Lake, Callum Stratford, and Paul Comfort. 2021. "A Proposed Method for Evaluating Drop Jump Performance with One Force Platform" Biomechanics 1, no. 2: 178-189. https://doi.org/10.3390/biomechanics1020015
APA StyleMcMahon, J. J., Lake, J. P., Stratford, C., & Comfort, P. (2021). A Proposed Method for Evaluating Drop Jump Performance with One Force Platform. Biomechanics, 1(2), 178-189. https://doi.org/10.3390/biomechanics1020015







