Comparative Biomechanical Study of Screw Fixation Techniques in Periacetabular Osteotomy
Abstract
:1. Introduction
2. Materials and Methods
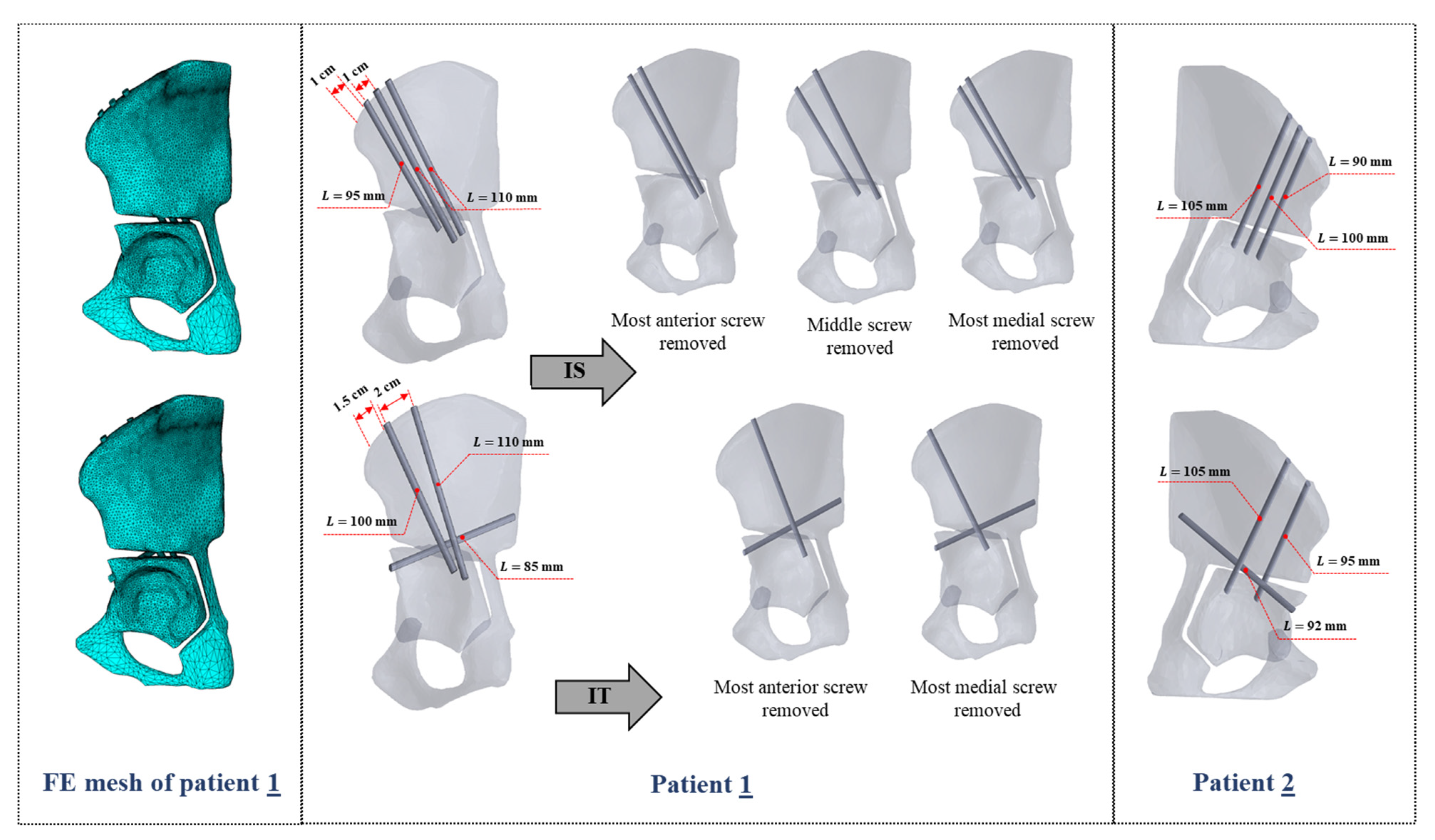
2.1. Geometrical Modeling
2.2. Finite Element Simulation
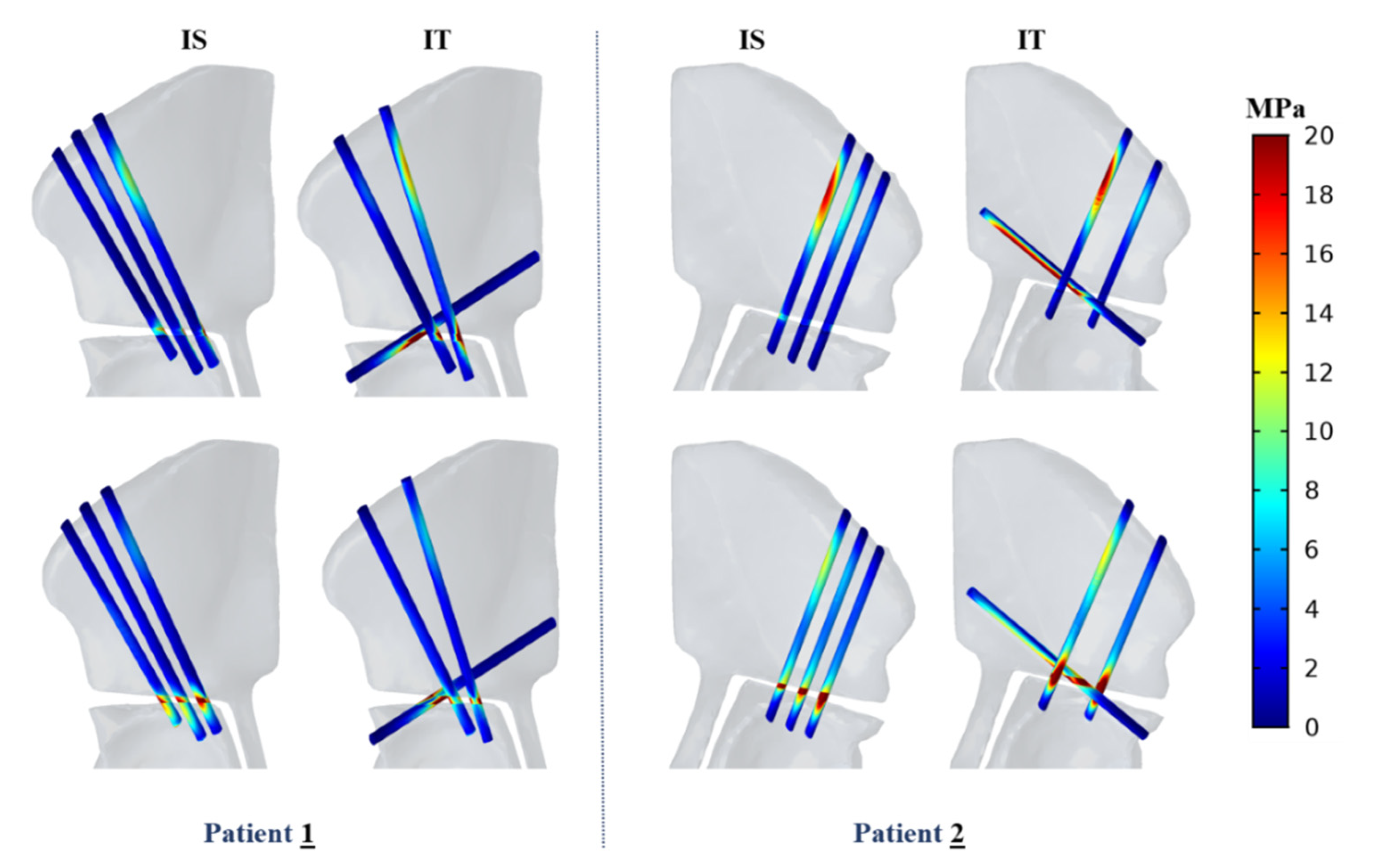
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cooperman, D.R.; Wallensten, R.; Stulberg, S.D. Acetabular dysplasia in the adult. Clin. Orthopaed. Related Res. 1983, 175, 79–85. [Google Scholar] [CrossRef]
- Ganz, R.; Klaue, K.; Vinh, T.S.; Mast, J.W. A new periacetabular osteotomy for the treatment of hip dysplasias technique and preliminary results. Clin. Orthopaed. Related Res. 1988, 232, 26–36. [Google Scholar] [CrossRef]
- Armand, M.; Lepistö, J.; Tallroth, K.; Elias, J.; Chao, E. Outcome of periacetabular osteotomy: Joint contact pressure calculation using standing AP radiographs, 12 patients followed for average 2 years. Acta Orthopaed. 2005, 76, 303–313. [Google Scholar] [CrossRef] [Green Version]
- Lepistö, J.; Armand, M.; Armiger, R.S. Periacetabular osteotomy in adult hip dysplasia–developing a computer aided real-time biomechanical guiding system (BGS). Suomen Ortoped. Traumatol. Ortoped. Traumatol. Finland Finn. J. Orthopaed. Traumatol. 2008, 31, 186. [Google Scholar]
- Armiger, R.S.; Armand, M.; Tallroth, K.; Lepistö, J.; Mears, S.C. Three-dimensional mechanical evaluation of joint contact pressure in 12 periacetabular osteotomy patients with 10-year follow-up. Acta Orthopaed. 2009, 80, 155–161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, C.; Ltcl, L.H.; Wwdm, H.P. Stress Distribution of a Modified Periacetabular Osteotomy for Treatment of Dysplastic Acetabulum. J. Med. Biol. Eng. 2010, 31, 53–58. [Google Scholar]
- Zou, Z.; Chávez-Arreola, A.; Mandal, P.; Board, T.N.; Alonso-Rasgado, T. Optimization of the position of the acetabulum in a ganz periacetabular osteotomy by finite element analysis. J. Orthopaed. Res. 2013, 31, 472–479. [Google Scholar] [CrossRef]
- Niknafs, N.; Murphy, R.J.; Armiger, R.S.; Lepisto, J.; Armand, M. Biomechanical factors in planning of periacetabular osteotomy. Front. Bioeng. Biotechnol. 2013, 1, 20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gaffney, B.M.; Clohisy, J.C.; Van Dillen, L.R.; Harris, M.D. The association between periacetabular osteotomy reorientation and hip joint reaction forces in two subgroups of acetabular dysplasia. J. Biomech. 2020, 98, 109464. [Google Scholar] [CrossRef] [PubMed]
- Park, S.-J.; Lee, S.-J.; Chen, W.-M.; Park, J.-H.; Cho, Y.-S.; Shin, T.; Kwon, S.-Y. Computer-Assisted Optimization of the Acetabular Rotation in Periacetabular Osteotomy Using Patient’s Anatomy-Specific Finite Element Analysis. Appl. Bion. Biomech. 2018, 2018, 9730525. [Google Scholar] [CrossRef] [Green Version]
- De Raedt, S.; Mechlenburg, I.; Stilling, M.; Rømer, L.; Murphy, R.J.; Armand, M.; Lepistö, J.; de Bruijne, M.; Søballe, K. Reliability of computer-assisted periacetabular osteotomy using a minimally invasive approach. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 2021–2028. [Google Scholar] [CrossRef] [PubMed]
- An, K.; Himeno, S.; Tsumura, H.; Kawai, T.; Chao, E. Pressure distribution on articular surfaces: Application to joint stability evaluation. J. Biomech. 1990, 23, 1013–1020. [Google Scholar] [CrossRef]
- Li, G.; Sakamoto, M.; Chao, E.Y. A comparison of different methods in predicting static pressure distribution in articulating joints. J. Biomech. 1997, 30, 635–638. [Google Scholar] [CrossRef]
- Matheney, T.; Kim, Y.-J.; Zurakowski, D.; Matero, C.; Millis, M. Intermediate to long-term results following the Bernese periacetabular osteotomy and predictors of clinical outcome. J. Bone Jt. Surg. 2009, 91, 2113–2123. [Google Scholar] [CrossRef]
- Hussell, J.G.; Rodriguez, J.A.; Ganz, R. Technical complications of the Bernese periacetabular osteotomy. Clin. Orthopaed. Related Res. 1999, 363, 81–92. [Google Scholar] [CrossRef]
- Babis, G.C.; Trousdale, R.T.; Jenkyn, T.R.; Kaufman, K. Comparison of two methods of screw fixation in periacetabular osteotomy. Clin. Orthopaed. Related Res. 2002, 403, 221–227. [Google Scholar] [CrossRef]
- Widmer, B.J.; Peters, C.L.; Bachus, K.N.; Stevens, P.M. Initial stability of the acetabular fragment after periacetabular osteotomy: A biomechanical study. J. Pediat. Orthopaed. 2010, 30, 443–448. [Google Scholar] [CrossRef] [PubMed]
- Crockarell, J.; Trousdale, R.T.; Cabanela, M.E.; Berry, D.J. Early experience and results with the periacetabular osteotomy. The Mayo Clinic experience. Clin. Orthopaed. Related Res. 1999, 363, 45–53. [Google Scholar] [CrossRef]
- Matta, J.M.; Stover, M.D.; Siebenrock, K. Periacetabular osteotomy through the Smith-Petersen approach. Clin. Orthopaed. Related Res. 1999, 363, 21–32. [Google Scholar]
- Yassir, W.; Mahar, A.; Aminian, A.; Newton, P.; Wenger, D. A comparison of the fixation stability of multiple screw constructs for two types of pelvic osteotomies. J. Pediatric Orthopaed. 2005, 25, 14–17. [Google Scholar]
- Murphy, R.J.; Armiger, R.S.; Lepistö, J.; Mears, S.C.; Taylor, R.H.; Armand, M. Development of a biomechanical guidance system for periacetabular osteotomy. Int. J. Comput. Assist. Radiol. Surg. 2015, 10, 497–508. [Google Scholar] [CrossRef] [Green Version]
- Murphy, R.J.; Armiger, R.S.; Lepistö, J.; Armand, M. Clinical evaluation of a biomechanical guidance system for periacetabular osteotomy. J. Orthopaed. Surg. Res. 2016, 11, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Pieper, S.; Halle, M.; Kikinis, R. 3D Slicer. In Proceedings of the 2004 2nd IEEE International Symposium on Biomedical Imaging: Nano to Macro, Arlington, VA, USA, 18–18 April 2004; pp. 632–635. [Google Scholar]
- Becker, R.; Rannacher, R. An optimal control approach to a posteriori error estimation in finite element methods. Acta Numer. 2001, 10, 1–102. [Google Scholar] [CrossRef]
- Eriksson, K.; Estep, D.; Hansbo, P.; Johnson, C. Introduction to adaptive methods for differential equations. Acta Numer. 1995, 4, 105–158. [Google Scholar] [CrossRef]
- Dalstra, M.; Huiskes, H.; van Erning, L. Development and validation of a three-dimensional finite element model of the pelvic bone. J. Biomech. Eng. Trans. ASME 1995, 117, 272–278. [Google Scholar] [CrossRef] [Green Version]
- Anderson, A.E.; Peters, C.L.; Tuttle, B.D.; Weiss, J.A. Subject-specific finite element model of the pelvis: Development, validation and sensitivity studies. J. Biomech. Eng. 2005, 127, 364–373. [Google Scholar] [CrossRef] [Green Version]
- Dalstra, M.; Huiskes, R.; Odgaard, A.v.; Van Erning, L. Mechanical and textural properties of pelvic trabecular bone. J. Biomech. 1993, 26, 523–535. [Google Scholar] [CrossRef] [Green Version]
- Tanino, H.; Ito, H.; Higa, M.; Omizu, N.; Nishimura, I.; Matsuda, K.; Mitamura, Y.; Matsuno, T. Three-dimensional computer-aided design based design sensitivity analysis and shape optimization of the stem using adaptive p-method. J. Biomech. 2006, 39, 1948–1953. [Google Scholar] [CrossRef]
- Volokh, K.; Chao, E.; Armand, M. On foundations of discrete element analysis of contact in diarthrodial joints. Mol. Cell. Biomech. MCB 2007, 4, 67. [Google Scholar]
- Bergmann, G.; Deuretzbacher, G.; Heller, M.; Graichen, F.; Rohlmann, A.; Strauss, J.; Duda, G. Hip contact forces and gait patterns from routine activities. J. Biomech. 2001, 34, 859–871. [Google Scholar] [CrossRef]
- Yosibash, Z.; Tal, D.; Trabelsi, N. Predicting the yield of the proximal femur using high-order finite-element analysis with inhomogeneous orthotropic material properties. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 2707–2723. [Google Scholar] [CrossRef]
- Basafa, E.; Armiger, R.S.; Kutzer, M.D.; Belkoff, S.M.; Mears, S.C.; Armand, M. Patient-specific finite element modeling for femoral bone augmentation. Med. Eng. Phys. 2013, 35, 860–865. [Google Scholar] [CrossRef] [Green Version]
- Pistoia, W.; Van Rietbergen, B.; Lochmüller, E.-M.; Lill, C.; Eckstein, F.; Rüegsegger, P. Estimation of distal radius failure load with micro-finite element analysis models based on three-dimensional peripheral quantitative computed tomography images. Bone 2002, 30, 842–848. [Google Scholar] [CrossRef]
- Rhyu, K.; Kim, Y.; Park, W.; Kim, K.; Cho, T.-J.; Choi, I. Application of finite element analysis in pre-operative planning for deformity correction of abnormal hip joints–a case series. Proc. Instit. Mech. Eng. Part H J. Eng. Med. 2011, 225, 929–936. [Google Scholar] [CrossRef]
- Phillips, A.; Pankaj, P.; Howie, C.; Usmani, A.; Simpson, A. Finite element modelling of the pelvis: Inclusion of muscular and ligamentous boundary conditions. Med. Eng. Phys. 2007, 29, 739–748. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.-T.; Tsai, M.-T.; Chang, C.-H.; Fuh, L.-J.; Lai, K.-A.; Liu, Z.-L.; Tu, M.-G.; Huang, H.-L. Finite element analysis of the effects of sizes of acetabular components on the initial stability of the acetabular cup. J. Med. Biol. Eng. 2008, 28, 59–63. [Google Scholar]
- Sucato, D.J.; Tulchin, K.; Shrader, M.W.; DeLaRocha, A.; Gist, T.; Sheu, G. Gait, Hip Strength and Functional Outcomes After a Ganz Periacetabular Osteotomy for Adolescent Hip Dysplasia. J. Pediatric Orthopaed. 2010, 30, 344–350. [Google Scholar] [CrossRef] [PubMed]
- Mechlenburg, I.; Nyengaard, J.; Rømer, L.; Søballe, K. Changes in load-bearing area after Ganz periacetabular osteotomy evaluated by multislice CT scanning and stereology. Acta Orthopaed. Scand. 2004, 75, 147–153. [Google Scholar] [CrossRef] [PubMed]
- Gahramanov, A.; İnanıcı, F.; Çağlar, Ö.; Aksoy, C.; Tokgözoğlu, A.M.; Güner, S.; Baki, A.; Atilla, B. Functional Results in Periacetabular Osteotomy: Is it Possible to Obtain a Normal Gait after the Surgery? HIP Int. 2017, 27, 449–454. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, M.; Takahira, N.; Fukushima, K.; Yamamoto, T.; Moriya, M.; Uchiyama, K. Early gait analysis after curved periacetabular osteotomy for acetabular dysplasia. Orthoped. Res. Rev. 2015, 7, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, C.; Zavala, L.; Opstedal, L.; Becker, J. Recovery of Lower Extremity Function in the Initial Year Following Periacetabular Osteotomy: A Single Subject Analysis. Physiother. Theory Pract. 2020, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Swarup, I.; Zaltz, I.; Robustelli, S.; Sink, E. Outcomes of periacetabular osteotomy for borderline hip dysplasia in adolescent patients. J. Hip Preservat. Surg. 2020, 7, 249–255. [Google Scholar] [CrossRef] [PubMed]





| Mesh Iteration | Initial Mesh | One Step Refinement | Two Step Refinement | Four Step Refinement |
|---|---|---|---|---|
| Number of elements | 217,390 | 100,462 | 100,419 | 100,380 |
| Maximum von Mises Stress (MPa) | 104.59 | 140.48 | 140.33 | 140.26 |
| Model | Number of Elements |
|---|---|
| Patient 1 | |
| IS | 100,380 |
| IT | 102,424 |
| IS first screw removed | 76,999 |
| IS middle screw removed | 74,900 |
| IS third screw removed | 73,455 |
| IT first screw removed | 76,401 |
| IT second screw removed | 73,448 |
| Patient 2 | |
| IS | 203,057 |
| IT | 226,367 |
| Patient 1 | Patient 2 | |||
|---|---|---|---|---|
| IS | IT | IS | IT | |
| Peak von Mises stress in osteotomized pelvic fragment (MPa) | 58.0 | 70.1 | 28.5 | 76.4 |
| Peak von Mises stress in acetabular fragment (MPa) | 24.1 | 29.9 | 26.5 | 48.3 |
| Peak compressive strain in both fragments (%) | 3.7 | 2.5 | 5.2 | 4.8 |
| Peak normal stress in fixation screws (MPa) | 56.0 | 74.8 | 67.3 | 103 |
| Peak shear stress in fixation screws (MPa) | 37.8 | 49.8 | 45.7 | 73.6 |
| Peak normal stress in interface (MPa) | 31.3 | 52.5 | 35.2 | 59.8 |
| Peak shear stress in interface (MPa) | 30.1 | 36.3 | 27.7 | 40.2 |
| Bone stiffness (N/mm) | 1677 | 1703 | 755 | 760 |
| Bone yield load (N) | 9232 | 10,107 | 14,534 | 15,111 |
| IS | IT | ||||
|---|---|---|---|---|---|
| A: Most Anterior Screw Removed | B: Middle Screw Removed | C: Most Medial Screw Removed | D: Most Anterior Screw Removed | E: Most Medial Screw Removed | |
| Peak von Mises stress in osteotomized pelvic fragment (MPa) | 114 | 58.3 | 71.5 | 100 | 104 |
| Peak von Mises stress in acetabular fragment (MPa) | 40.3 | 25.5 | 27.2 | 11.6 | 13.8 |
| Peak compressive strain in both fragments (%) | 6.2 | 3.4 | 4.0 | 2.3 | 2.6 |
| Peak normal stress in fixation screws (MPa) | 226 | 80.0 | 140 | 121 | 144 |
| Peak shear stress in fixation screws (MPa) | 119 | 59.2 | 66.1 | 74.4 | 77.9 |
| Peak normal stress in interface (MPa) | 189 | 55.3 | 83.9 | 87.8 | 92.8 |
| Peak shear stress in interface (MPa) | 68.5 | 36.3 | 38.0 | 53.0 | 53.2 |
| Bone stiffness (N/mm) | 1509 | 1665 | 1541 | 1657 | 1609 |
| Bone yield load (N) | 5380 | 8485 | 6419 | 7924 | 6828 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakhtiarinejad, M.; Farvardin, A.; Murphy, R.J.; Grupp, R.B.; Tis, J.E.; Sponseller, P.D.; Armand, M. Comparative Biomechanical Study of Screw Fixation Techniques in Periacetabular Osteotomy. Biomechanics 2021, 1, 131-144. https://doi.org/10.3390/biomechanics1010010
Bakhtiarinejad M, Farvardin A, Murphy RJ, Grupp RB, Tis JE, Sponseller PD, Armand M. Comparative Biomechanical Study of Screw Fixation Techniques in Periacetabular Osteotomy. Biomechanics. 2021; 1(1):131-144. https://doi.org/10.3390/biomechanics1010010
Chicago/Turabian StyleBakhtiarinejad, Mahsan, Amirhossein Farvardin, Ryan J. Murphy, Robert B. Grupp, John E. Tis, Paul D. Sponseller, and Mehran Armand. 2021. "Comparative Biomechanical Study of Screw Fixation Techniques in Periacetabular Osteotomy" Biomechanics 1, no. 1: 131-144. https://doi.org/10.3390/biomechanics1010010
APA StyleBakhtiarinejad, M., Farvardin, A., Murphy, R. J., Grupp, R. B., Tis, J. E., Sponseller, P. D., & Armand, M. (2021). Comparative Biomechanical Study of Screw Fixation Techniques in Periacetabular Osteotomy. Biomechanics, 1(1), 131-144. https://doi.org/10.3390/biomechanics1010010





