Atomic Many-Body Selectivity in Cubic CsPbI3 Solar Cell Memristor
Abstract
1. Introduction
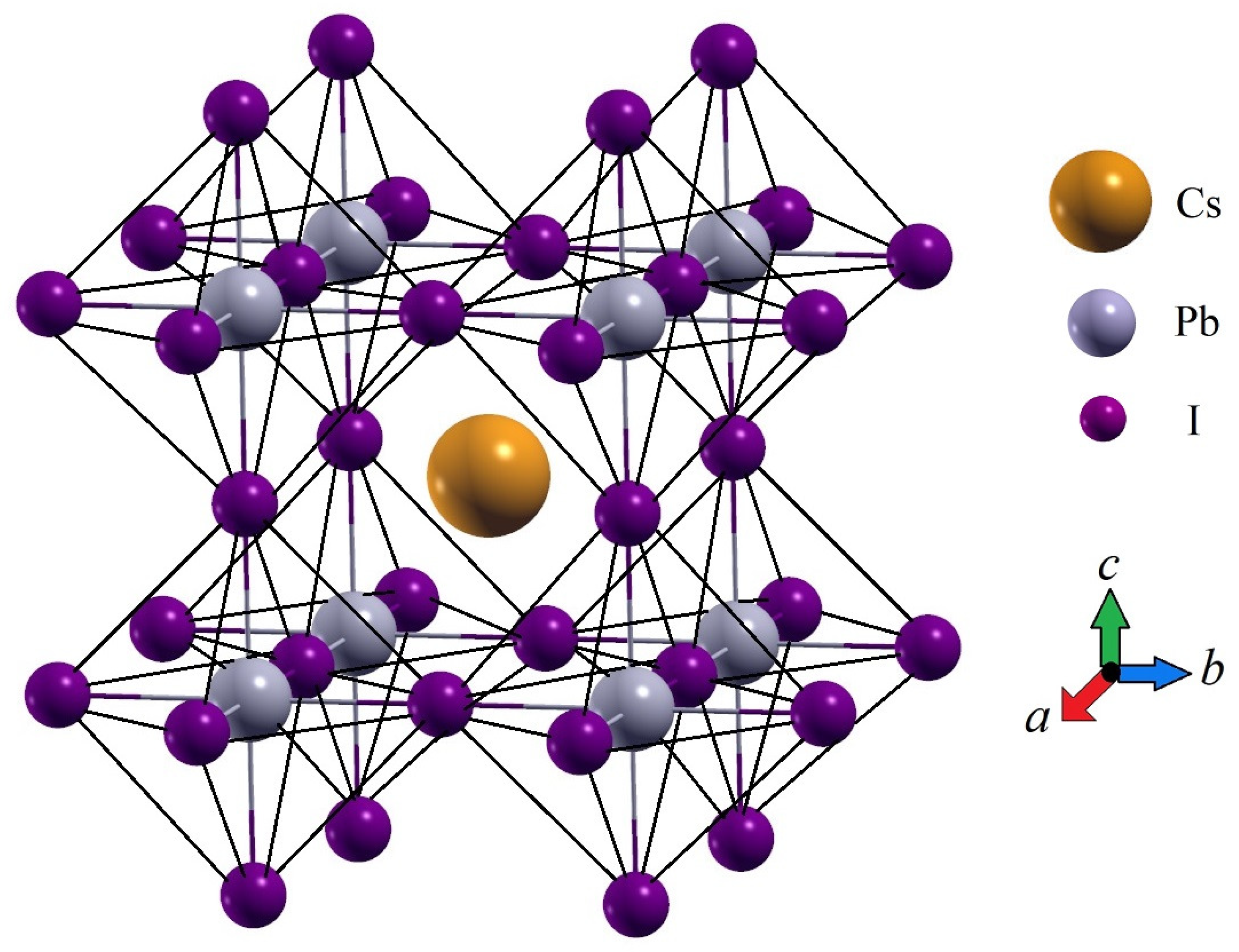
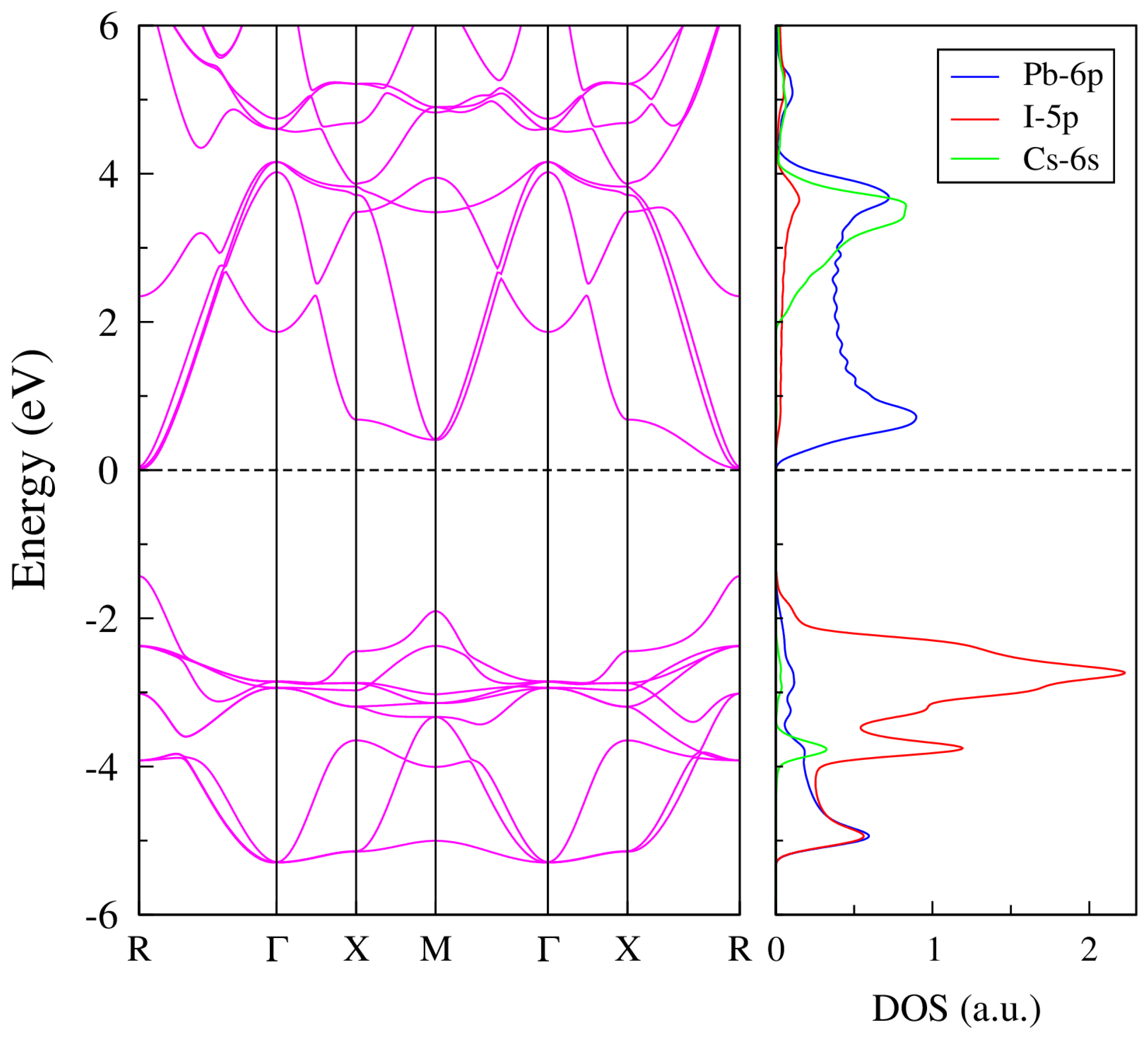
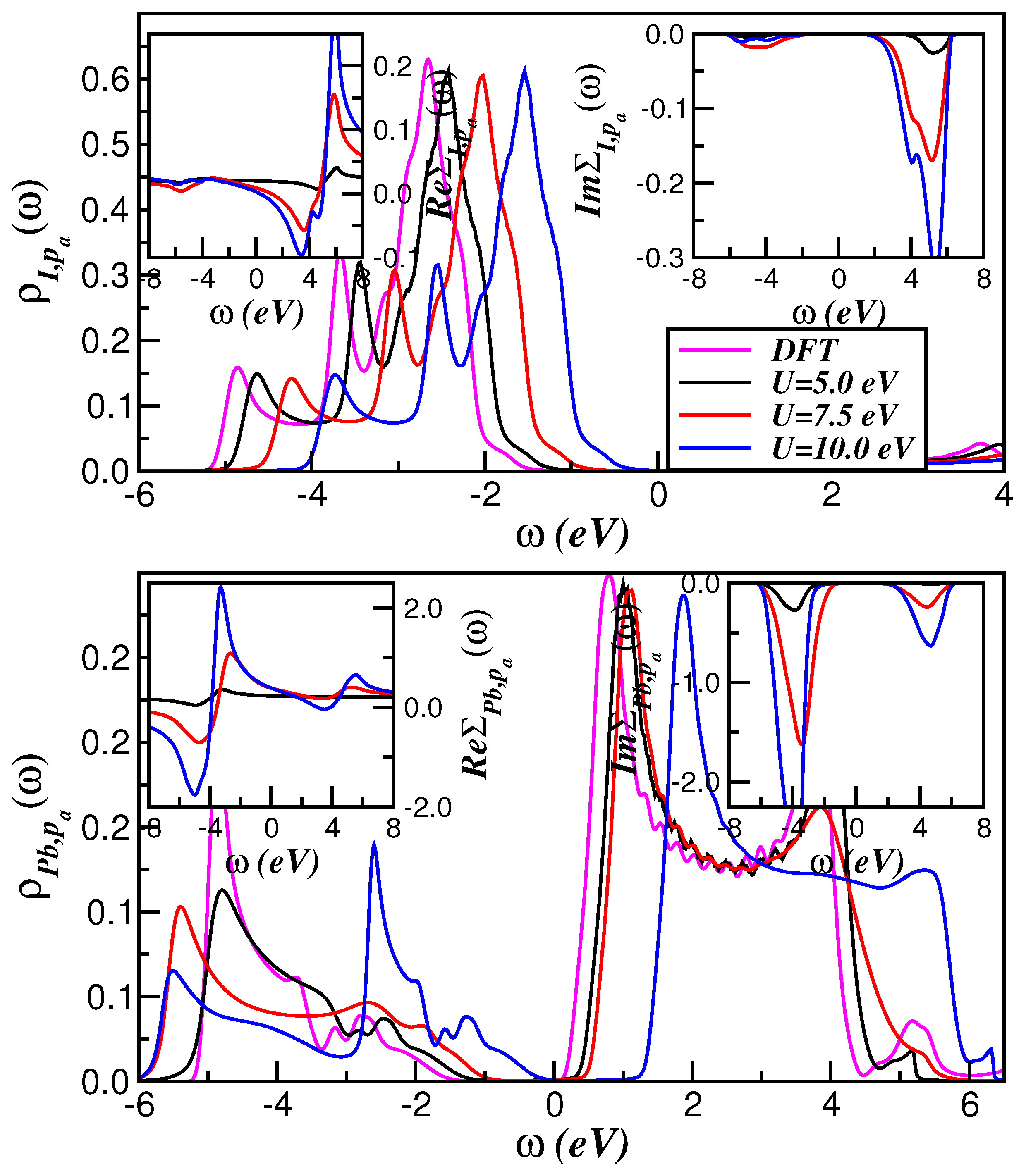
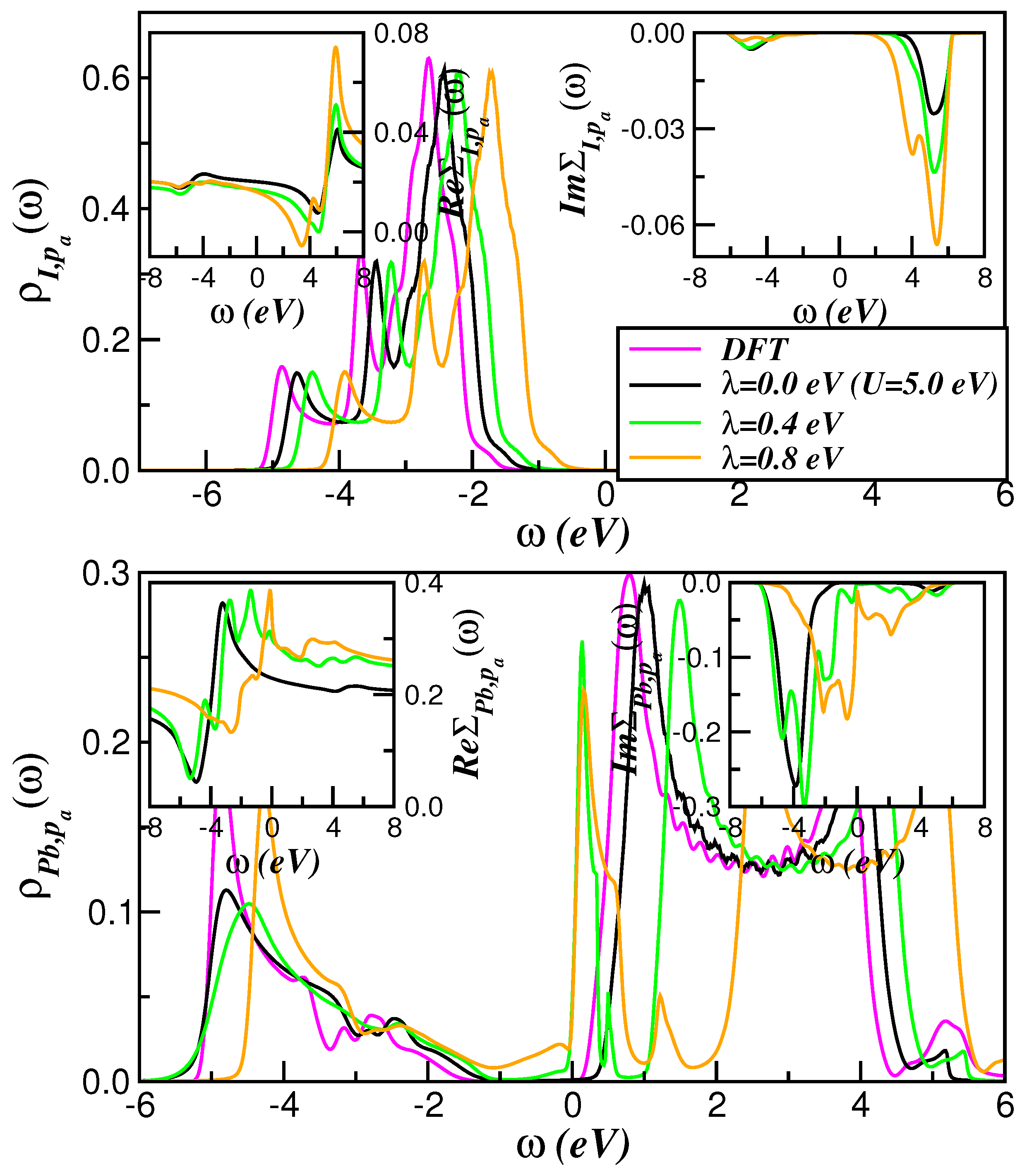
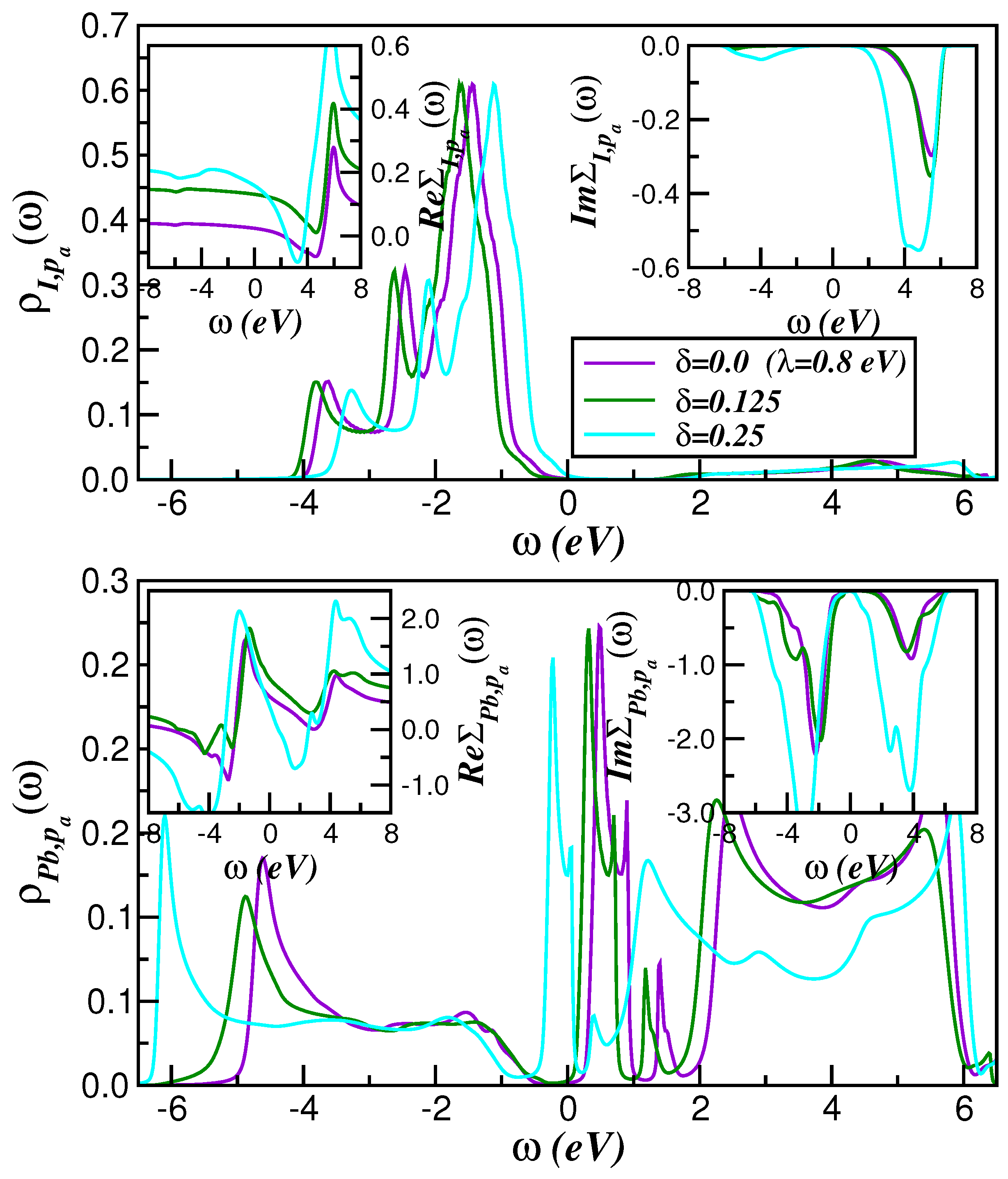
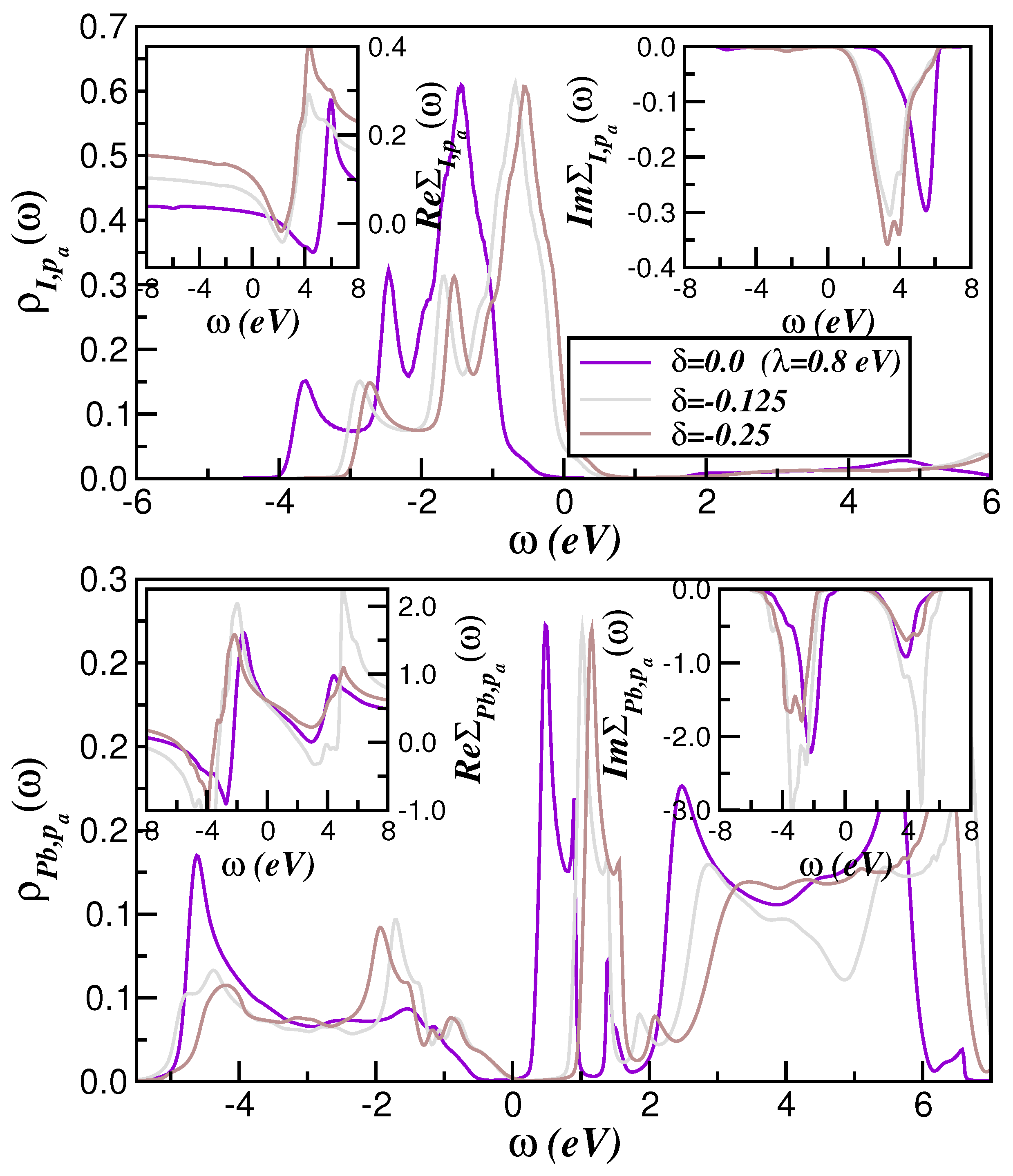
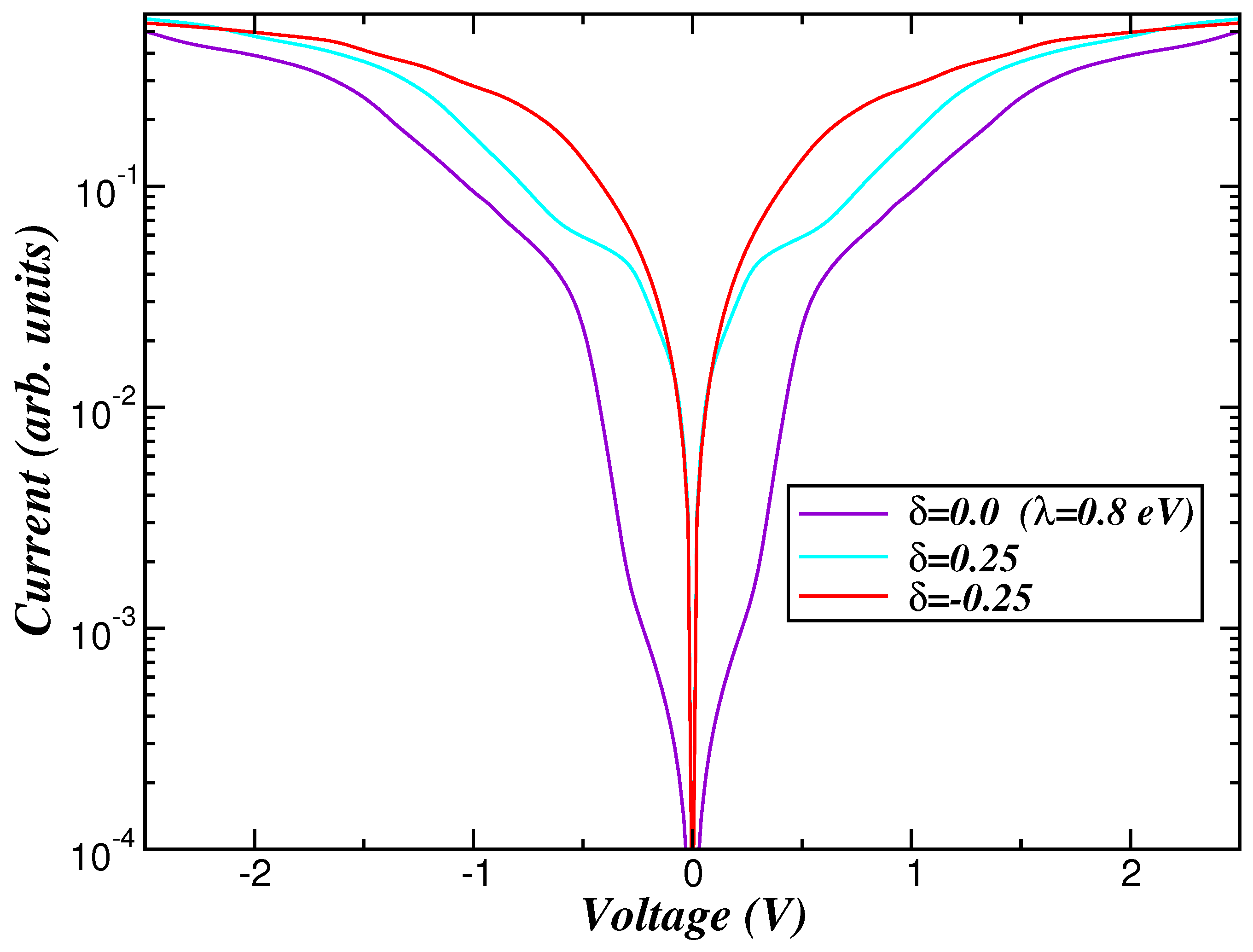
2. Theory and Results
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, W.; Wang, Z.; Deschler, F.; Gao, S.; Friend, R.H.; Cheetham, A.K. Chemically diverse and multifunctional hybrid organic–inorganic perovskites. Nat. Rev. Mater. 2017, 2, 16099. [Google Scholar] [CrossRef]
- García-Fernández, A.; Juarez-Perez, E.J.; Bermúdez-García, J.M.; Llamas-Saiz, A.L.; Artiaga, R.; López-Beceiro, J.J.; Señarís-Rodríguez, M.A.; Sánchez-Andújar, M.; Castro-García, S. Hybrid lead halide [(CH3)2NH2]PbX3 (X = Cl− and Br−) hexagonal perovskites with multiple functional properties. J. Mater. Chem. C 2019, 7, 10008. [Google Scholar] [CrossRef]
- Rao, C.N.R.; Cheetham, A.K.; Thirumurugan, A. Hybrid inorganic–organic materials: A new family in condensed matter physics. J. Phys. Condens. Matter 2008, 20, 083202. [Google Scholar] [CrossRef]
- Zhang, W.; Xiong, R.-G. Ferroelectric metal–organic frameworks. Chem. Rev. 2012, 112, 1163. [Google Scholar] [CrossRef]
- Jain, P.; Ramachandran, V.; Clark, R.J.; Hai, D.Z.; Toby, B.H.; Dalal, N.S.; Krotom, H.W.; Cheetham, A.K. Multiferroic behavior associated with an order-disorder hydrogen bonding transition in metal-organic frameworks (MOFs) with the perovskite ABX3 architecture. J. Am. Chem. Soc. 2009, 131, 13625. [Google Scholar] [CrossRef]
- Gómez-Aguirre, L.C.; Pato-Doldaán, B.; Mira, J.; Castro-García, S.; Senãrís-Rodríguez, M.A.; Sánchez-Andúar, M.; Singleton, J.; Zapf, V.S. Magnetic ordering-induced multiferroic behavior in [CH3NH3][Co(HCOO)3] metal–organic framework. J. Am. Chem. Soc. 2016, 138, 1122. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050. [Google Scholar] [CrossRef]
- Xiao, Z.; Yuan, Y.; Shao, Y.; Wang, Q.; Dong, Q.; Bi, C.; Sharma, P.; Gruverman, A.; Huang, J. Giant switchable photovoltaic effect in organometal trihalide perovskite devices. Nat. Mater. 2015, 14, 193. [Google Scholar] [CrossRef]
- Brivio, F.; Butler, K.T.; Walsh, A.; van Schilfgaarde, M. Relativistic quasiparticle self-consistent electronic structure of hybrid halide perovskite photovoltaic absorbers. Phys. Rev. B 2014, 89, 155204. [Google Scholar] [CrossRef]
- Ahmadi, S.S.; Amiri, P.; Salehi, H. Structural, electronic, optical, and thermoelectric properties of CsPbI3−yBry (y=0.5, 1.5, 2.5) compounds: First-principle study. J. Taiwan Inst. Chem. Eng. 2024, 155, 105304. [Google Scholar] [CrossRef]
- Han, J.S.; Le, Q.V.; Choi, J.; Hong, H.; Moon, C.W.; Kim, T.L.; Kim, H.; Kim, S.Y.; Jang, H.W. Air-stable cesium lead iodide perovskite for ultra-low operating voltage resistive switching. Adv. Funct. Mater. 2018, 28, 1705783. [Google Scholar] [CrossRef]
- Ge, S.; Huang, Y.; Chen, X.; Zhang, X.; Xiang, Z.; Zhang, R.; Li, W.; Cui, Y. Silver iodide induced resistive switching in CsPbI3 perovskite-based memory device. Adv. Mater. Interfaces 2019, 6, 1802071. [Google Scholar] [CrossRef]
- You, Y.-M.; Liao, W.-Q.; Zhao, D.; Ye, H.-Y.; Zhang, Y.; Zhou, Q.; Niu, J.; Wang, X.; Li, P.-F.; Fu, D.-W.; et al. An organic-inorganic perovskite ferroelectric with large piezoelectric response. Science 2017, 357, 306. [Google Scholar] [CrossRef]
- Bermúdez-García, J.M.; Sánchez-Andújar, M.; CastroGarcía, S.; López-Beceiro, J.; Artiaga, R.; Señarís-Rodríguez, M.A. Giant barocaloric effect in the ferroic organic-inorganic hybrid [TPrA][Mn(dca)3] perovskite under easily accessible pressures. Nat. Commun. 2017, 8, 15715. [Google Scholar] [CrossRef]
- Coudert, F.-X. Responsive metal–organic frameworks and framework materials: Under pressure, taking the heat, in the spotlight, with friends. Chem. Mater. 2015, 27, 1905. [Google Scholar] [CrossRef]
- García-Fernández, A.; Marcos-Cives, I.; Platas-Iglesias, C.; Castro-García, S.; Vázquez-García, D.; Fernández, A.; Sánchez-Andújar, M. Diimidazolium halobismuthates [Dim]2[Bi2X10] (X = Cl−, Br−, or I−): A new class of thermochromic and photoluminescent materials. Inorg. Chem. 2018, 57, 7655. [Google Scholar] [CrossRef]
- Saparov, B.; Mitzi, D.B. Organic-inorganic perovskites: Structural versatility for functional materials design. Chem. Rev. 2016, 116, 4558. [Google Scholar] [CrossRef]
- Gu, C.; Lee, J.-S. Flexible hybrid organic-norganic perovskite memory. ACS Nano 2016, 10, 5413. [Google Scholar] [CrossRef]
- Waser, R.; Dittmann, R.; Staikov, G.; Szot, K. Redox-based resistive switching memories-nanoionic mechanisms, prospects, and challenges. Adv. Mater. 2009, 21, 2632. [Google Scholar] [CrossRef]
- Waser, R.; Aono, M. Nanoionics-based resistive switching memories. Nat. Mater. 2007, 6, 833. [Google Scholar] [CrossRef]
- Lee, M.M.; Teuscher, J.; Miyasaka, T.; Murakami, T.N.; Snaith, H.J. Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites. Science 2012, 338, 643. [Google Scholar] [CrossRef] [PubMed]
- Kwon, K.C.; Hong, K.; Le, Q.V.; Lee, S.Y.; Choi, J.; Kim, K.B.; Kim, S.Y.; Jang, H.W. Inhibition of ion migration for reliable operation of organolead halide perovskite-based metal/semiconductor/metal broadband photodetectors. Adv. Funct. Mater. 2016, 26, 4213. [Google Scholar] [CrossRef]
- Tan, Z.-K.; Moghaddam, R.S.; Lai, M.L.; Docampo, P.; Higler, R.; Deschler, F.; Price, M.; Sadhanala, A.; Pazos, L.M.; Credgington, D.; et al. Bright light-emitting diodes based on organometal halide perovskite. Nat. Nanotechnol. 2014, 9, 687. [Google Scholar] [CrossRef]
- Nie, W.; Blancon, J.-C.; Neukirch, A.J.; Appavoo, K.; Tsai, H.; Chhowalla, M.; Alam, M.A.; Sfeir, M.Y.; Katan, C.; Even, J.; et al. Light-activated photocurrent degradation and self-healing in perovskite solar cells. Nat. Commun. 2016, 7, 11574. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.; Song, J.; Xiao, L.; Zeng, H.; Sun, H. All-inorganic colloidal perovskite quantum dots: A new class of lasing materials with favorable characteristics. Adv. Mater. 2015, 27, 7101. [Google Scholar] [CrossRef]
- Jong, U.-G.; Yu, C.-J.; Kim, Y.-S.; Kye, Y.-H.; Kim, C.-H. First-principles study on the material properties of the inorganic perovskite Rb1−xCsxPbI3 for solar cell applications. Phys. Rev. B 2018, 98, 125116. [Google Scholar] [CrossRef]
- Song, J.; Li, J.; Li, X.; Xu, L.; Dong, Y.; Zeng, H. Quantum dot light-emitting diodes based on inorganic perovskite cesium lead halides (CsPbX3). Adv. Mater. 2015, 27, 7162. [Google Scholar] [CrossRef]
- Saliba, M.; Matsui, T.; Seo, J.-Y.; Domanski, K.; Correa-Baena, J.-P.; Nazeeruddin, M.K.; Zakeeruddin, S.M.; Tress, W.; Abate, A.; Hagfeldt, A.; et al. Cesium-containing triple cation perovskite solar cells: Improved stability, reproducibility and high efficiency. Energy Environ. Sci. 2016, 9, 1989. [Google Scholar] [CrossRef]
- Long, Z.; Qiu, X.; Chan, C.L.J.; Sun, Z.; Yuan, Z.; Poddar, S.; Zhang, Y.; Ding, Y.; Gu, L.; Zhou, Y.; et al. A neuromorphic bionic eye with filter-free color vision using hemispherical perovskite nanowire array retina. Nat. Commun. 2023, 14, 1972. [Google Scholar] [CrossRef]
- Marronnier, A.; Roma, G.; Boyer-Richard, S.; Pedesseau, L.; Jancu, J.-M.; Bonnassieux, Y.; Katan, C.; Stoumpos, C.C.; Kanatzidis, M.G.; Even, J. Anharmonicity and disorder in the black phases of cesium lead iodide used for stable inorganic perovskite solar cells. ACS Nano 2018, 12, 3477. [Google Scholar] [CrossRef]
- Trots, D.M.; Myagkota, S.V. High-temperature structural evolution of caesium and rubidium triiodoplumbates. J. Phys. Chem. Solids 2008, 69, 2520. [Google Scholar] [CrossRef]
- Sutton, R.J.; Filip, M.R.; Haghighirad, A.A.; Sakai, N.; Wenger, B.; Giustino, F.; Snaith, H.J. Cubic or orthorhombic? Revealing the Crystal structure of metastable black-phase CsPbI3 by theory and experiment. ACS Energy Lett. 2018, 3, 1787. [Google Scholar] [CrossRef]
- Wang, Z.; Malyi, O.I.; Zhao, X.; Zunger, A. Mass enhancement in 3d and s-p perovskites from symmetry breaking. Phys. Rev. B 2021, 103, 165110. [Google Scholar] [CrossRef]
- Moller, C.K. Crystal structure and photoconductivity of caesium plumbohalides. Nature 1958, 182, 1435. [Google Scholar] [CrossRef]
- Yuan, Y.; Huang, J. Ion migration in organometal trihalide perovskite and its impact on photovoltaic efficiency and stabilty. Accounts Chem. Res. 2016, 49, 286. [Google Scholar] [CrossRef]
- Xia, G.; Huang, B.; Zhang, Y.; Zhao, X.; Wang, C.; Jia, C.; Zhao, J.; Chen, W.; Li, J. Nanoscale insights into photovoltaic hysteresis in triple-cation mixed-halide perovskite: Resolving the role of polarization and ionic migration. Adv. Mater. 2019, 31, 1902870. [Google Scholar] [CrossRef]
- Loizos, M.; Rogdakis, K.; Luo, W.; Zimmermann, P.; Hinderhofer, A.; Lukić, J.; Tountas, M.; Schreiber, F.; Milić, J.V.; Kymakis, E. Resistive switching memories with enhanced durability enabled by mixed-dimensional perfluoroarene perovskite heterostructure. Nanoscale Horizons 2024, 9, 1146. [Google Scholar] [CrossRef]
- Futscher, M.H.; Milić, J.V. Mixed conductivity of hybrid halide perovskites: Emerging opportunities and challenges. Front. Energy Res. 2021, 9, 629074. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Fu, L.; Yu, T.; Zhou, S.; Zhang, L.; Yin, L. Surface passivation engineering strategy to fully-inorganic cubic CsPbI3 perovskites for high-performance solar cells. Nat. Commun. 2018, 9, 1076. [Google Scholar] [CrossRef]
- Eperon, G.E.; Paternó, G.M.; Sutton, R.J.; Zampetti, A.; Haghighirad, A.A.; Cacialli, F.; Snaith, H.J. Inorganic caesium lead iodide perovskite solar cells. J. Mater. Chem. A 2015, 3, 19688. [Google Scholar] [CrossRef]
- Niu, G.; Li, W.; Li, J.; Liang, X.; Wang, L. Enhancement of thermal stability for perovskite solar cells through cesium doping. RSC Adv. 2017, 7, 17473. [Google Scholar] [CrossRef]
- Yu, C.-J.; Ko, U.-H.; Hwang, S.-G.; Kim, Y.-S.; Jong, U.-G.; Kye, Y.-H.; Ri, C.-H. First-principles study on material properties and stability of inorganic halide perovskite solid solutions CsPb(I1−xBrx). Phys. Rev. Mater. 2020, 4, 045402. [Google Scholar] [CrossRef]
- Bekenstein, Y.; Koscher, B.A.; Eaton, S.W.; Yang, P.; Alivisatos, A.P. Highly luminescent colloidal nanoplates of perovskite cesium lead halide and their oriented assemblie. J. Am. Chem. Soc. 2015, 137, 16008. [Google Scholar] [CrossRef] [PubMed]
- Mondal, N.; Samanta, A. Complete ultrafast charge carrier dynamics in photo-excited all-inorganic perovskite nanocrystals (CsPbX3). Nanoscale 2017, 9, 1878. [Google Scholar] [CrossRef]
- Hutter, E.M.; Sutton, R.J.; Chandrashekar, S.; Abdi-Jalebi, M.; Stranks, S.D.; Snaith, H.J.; Savenije, T.J. Vapour-deposited cesium lead iodide perovskites: Microsecond charge carrier lifetimes and enhanced photovoltaic performance. ACS Energy Lett. 2017, 2, 1901. [Google Scholar] [CrossRef]
- Craco, L.; Leoni, S. Magnetoresistance in the spin-orbit Kondo state of elemental bismuth. Sci. Rep. 2015, 5, 13772. [Google Scholar] [CrossRef]
- Craco, L.; Leoni, S. Bulk quantum correlations and doping-induced nonmetallicity in the Bi2Se3 topological insulator. Phys. Rev. B 2012, 85, 075114. [Google Scholar] [CrossRef]
- Craco, L.; Leoni, S. Tunable Kondo-Mott physics in bulk Bi2Te2Se topological insulator. Phys. Rev. B 2012, 85, 195124. [Google Scholar] [CrossRef]
- Amadon, B. First-principles DFT+DMFT calculations of structural properties of actinides: Role of Hund’s exchange, spin-orbit coupling, and crystal structure. Phys. Rev. B 2016, 94, 115148. [Google Scholar] [CrossRef]
- Facio, J.I.; Mravlje, J.; Pourovskii, L.; Cornaglia, P.S.; Vildosola, V. Spin-orbit and anisotropic strain effects on the electronic correlations in Sr2RuO4. Phys. Rev. B 2018, 98, 085121. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Brgoch, J.; Lehner, A.J.; Chabinyc, M.; Seshadri, R. Ab initio calculations of band gaps and absolute band positions of polymorphs of RbPbI3 and CsPbI3: Implications for main-group halide perovskite photovoltaics. J. Phys. Chem. C 2014, 118, 27721. [Google Scholar] [CrossRef]
- Giorgi, G.; Fujisawa, J.-I.; Segawa, H.; Yamashita, K. Cation role in structural and electronic properties of 3D organic-inorganic halide perovskites: A DFT analysis. J. Phys. Chem. C 2014, 118, 12176. [Google Scholar] [CrossRef]
- Huang, L.-Y.; Lambrecht, W.R.L. Electronic band structure, phonons, and exciton binding energies of halide perovskites CsSnCl3, CsSnBr3, and CsSnI3. Phys. Rev. B 2013, 88, 165203. [Google Scholar] [CrossRef]
- Umari, P.; Mosconi, E.; De Angelis, F. Relativistic GW calculations on CH3NH3PbI3 and CH3NH3SnI3 perovskites for solar cell applications. Sci. Rep. 2014, 4, 4467. [Google Scholar] [CrossRef]
- Amat, A.; Mosconi, E.; Ronca, E.; Quarti, C.; Umari, P.; Nazeeruddin, M.K.; Grätzel, M.; De Angelis, F. Cation-induced band-gap tuning in organohalide perovskites: Interplay of spin-orbit coupling and octahedra tilting. Nano Lett. 2014, 14, 3608. [Google Scholar] [CrossRef]
- Hirasawa, M.; Ishihara, T.; Goto, T. Exciton features in 0-, 2-,and 3-dimensional networks of [PbI6]4-octahedra. Phys. Soc. Jpn. 1994, 63, 3870. [Google Scholar] [CrossRef]
- Tanaka, K.; Takahashi, T.; Ban, T.; Kondo, T.; Uchida, K.; Miura, N. Comparative study on the excitons in lead-halide-based perovskite-type crystals CH3NH3PbBr3CH3NH3PbI3. Sol. State Commun. 2003, 127, 619. [Google Scholar] [CrossRef]
- Even, E.; Pedesseau, L.; Jancu, J.-M.; Katan, C. Importance of spin-orbit coupling in hybrid organic/inorganic perovskites for photovoltaic applications. J. Phys. Chem. Lett. 2013, 4, 2999. [Google Scholar] [CrossRef]
- Kotliar, G.; Savrasov, S.Y.; Haule, K.; Oudovenko, V.S.; Parcollet, O.; Marianetti, C. A Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865. [Google Scholar] [CrossRef]
- Mott, N.F. The basis of the electron theory of metals, with special reference to the transition metals. Proc. Phys. Soc. A 1949, 62, 416. [Google Scholar] [CrossRef]
- Imada, I.; Fujimori, A.; Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 1998, 70, 1039. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Louie, S.G. Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies. Phys. Rev. B 1986, 34, 5390. [Google Scholar] [CrossRef]
- Chemla, D.S.; Shah, J. Many-body and correlation effects in semiconductors. Nature 2001, 411, 549. [Google Scholar] [CrossRef]
- Tuan, D.V.; Dery, H. Excitons and trions in monolayer semiconductors with correlated electrons. Phys. Rev. B 2023, 108, 085303. [Google Scholar] [CrossRef]
- Craco, L.; Carara, S.S.; da Silva Barbosa, E.; Milošević, M.V.; Pereira, T.A.S. Electronic and valleytronic properties of crystalline boron-arsenide tuned by strain and disorder. RSC Adv. 2023, 13, 17907. [Google Scholar] [CrossRef]
- Rozenberg, M.J.; Inoue, I.H.; Sánchez, M.J. Strong electron correlation effects in non-volatile electronic memory devices. Appl. Phys. Lett. 2006, 88, 033510. [Google Scholar] [CrossRef]
- Blom, P.W.M.; Wolf, R.M.; Cillessen, J.F.M.; Krijn, M.P.C.M. Ferroelectric Schottky diode. Phys. Rev. Lett. 1994, 73, 2107. [Google Scholar] [CrossRef]
- Beck, A.; Bednorz, J.G.; Gerber, C.; Rossel, C.; Widmer, D. Reproducible switching effect in thin oxide films for memory applications. App. Phys. Lett. 2000, 77, 139. [Google Scholar] [CrossRef]
- Chen, W.; Song, L.; Wang, S.; Zhang, Z.; Wang, G.; Hu, G.; Gao, S. Essential characteristics of memristors for neuromorphic computing. Adv. Electron. Mater. 2023, 9, 2200833. [Google Scholar] [CrossRef]
- Gao, S.; Zeng, F.; Wang, M.; Wang, G.; Song, C.; Pan, F. Implementation of complete boolean logic functions in single complementary resistive switch. Sci. Rep. 2015, 5, 15467. [Google Scholar] [CrossRef] [PubMed]
- Taylor, D.M.; Millis, C.A. Memory effect in the current-voltage characteristic of a low-band gap conjugated polymer. J. Appl. Phys. 2001, 90, 306. [Google Scholar] [CrossRef]
- Ma, L.P.; Pyo, S.; Ouyang, J.; Xu, Q.F.; Yang, Y. Nonvolatile electrical bistability of organic/metal-nanocluster/organic system. Appl. Phys. Lett. 2003, 82, 1419. [Google Scholar] [CrossRef]
- Wang, R.; Yang, J.-Q.; Mao, J.-Y.; Wang, Z.-P.; Wu, S.; Zhou, M.; Chen, T.; Zhou, Y.; Han, S.-T. Recent advances of volatile memristors: Devices, mechanisms, and applications. Adv. Intell. Syst. 2020, 2, 202000055. [Google Scholar] [CrossRef]
- Zhou, Y.; Ramanathan, S. Mott memory and neuromorphic devices. Proc. IEEE. 2015, 103, 1289. [Google Scholar] [CrossRef]
- Zhang, H.-T.; Panda, P.; Lin, J.; Kalcheim, Y.; Wang, K.; Freeland, J.W.; Fong, D.D.; Priya, S.; Schuller, I.K.; Sankaranarayanan, S.K.R.S.; et al. Organismic materials for beyond von Neumann machines. Appl. Phys. Rev. 2020, 7, 011309. [Google Scholar] [CrossRef]
- Pickett, M.D.; Medeiros-Ribeiro, G.; Williams, R.S. A scalable neuristor built with Mott memristors. Nat. Mater. 2013, 12, 114. [Google Scholar] [CrossRef]
- Ignatov, M.; Ziegler, M.; Hansen, M.; Petraru, A.; Kohlstedt, H. A memristive spiking neuron with firing rate coding. Front. Neurosci. 2015, 9, 376. [Google Scholar] [CrossRef]
- Loizos, M.; Rogdakis, K.; Kymakis, E. Sustainable mixed-halide perovskite resistive switching memories using self-assembled monolayers as the bottom contact. J. Phys. Chem. Lett. 2024, 15, 7635. [Google Scholar] [CrossRef]
- Kumar, S.; Pickett, M.D.; Strachan, J.P.; Gibson, G.; Nishi, Y.; Williams, R.S. Local temperature redistribution and structural transition during joule-heating-driven conductance switching in VO2. Adv. Mater. 2013, 25, 6128. [Google Scholar] [CrossRef] [PubMed]
- Madan, H.; Jerry, M.; Pogrebnyakov, A.; Mayer, T.; Datta, S. Quantitative mapping of phase coexistence in Mott-Peierls insulator during electronic and thermally driven phase transition. ACS Nano 2015, 9, 2009. [Google Scholar] [CrossRef] [PubMed]
- Pickett, M.D.; Williams, R.S. Sub-100 fJ and sub-nanosecond thermally driven threshold switching in niobium oxide crosspoint nanodevices. Nanotechnology 2012, 23, 215202. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Wang, Z.; Davila, N.; Kumari, N.; Norris, K.J.; Huang, X.; Strachan, J.P.; Vine, D.; Kilcoyne, A.L.D.; Nishi, Y.; et al. Physical origins of current and temperature controlled negative differential resistances in NbO2. Nat. Commun. 2017, 8, 658. [Google Scholar] [CrossRef]
- Brockman, J.S.; Gao, L.; Hughes, B.; Rettner, C.T.; Samant, M.G.; Roche, K.P.; Parkin, S.S.P. Subnanosecond incubation times for electric-field-induced metallization of a correlated electron oxide. Nat. Nanotechnol. 2014, 9, 453. [Google Scholar] [CrossRef]
- Funck, C.; Menzel, S.; Aslam, N.; Zhang, H.; Hardtdegen, A.; Waser, R.; Hoffmann-Eifert, S. Multidimensional simulation of threshold switching in NbO2 based on an electric field triggered thermal runaway model. Adv. Electron. Mater. 2016, 2, 1600169. [Google Scholar] [CrossRef]
- Salev, P.; Fratino, L.; Sasaki, D.; Berkoun, R.; del Valle, J.; Kalcheim, Y.; Takamura, Y.; Rozenberg, M.; Schuller, I.K. Transverse barrier formation by electrical triggering of a metal-to-insulator transition. Nat. Commun. 2021, 12, 5499. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. II. Operators for fast iterative diagonalization. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef]
- Kleinman, L.; Bylander, D. Efficacious form for model pseudopotentials. Phys. Rev. Lett. 1982, 48, 1425. [Google Scholar] [CrossRef]
- Junquera, J.; Paz, Ó.; Sánchez-Portal, D.; Artacho, E. Numerical atomic orbitals for linear-scaling calculations. Phys. Rev. B 2001, 64, 235111. [Google Scholar] [CrossRef]
- Moreno, J.; Soler, J.M. Optimal meshes for integrals in real- and reciprocal-space unit cells. Phys. Rev. B 1992, 45, 13891. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13. [Google Scholar] [CrossRef]
- Fujimoto, S. Topological order and non-Abelian statistics in noncentrosymmetric s-wave superconductors. Phys. Rev. B 2008, 77, 220501(R). [Google Scholar] [CrossRef]
- Yu, S.-L.; Xie, X.C.; Li, J.-X. Mott physics and topological phase transition in correlated Dirac fermions. Phys. Rev. Lett. 2011, 107, 010401. [Google Scholar] [CrossRef]
- Craco, L. Insulator-to-metal crossover induced by local spin fluctuations in strongly correlated systems. J. Phys. Condens. Matter 2001, 13, 263. [Google Scholar] [CrossRef]
- Merkel, M.E.; Tehrani, A.M.; Ederer, C. Probing the Mott insulating behavior of Ba2MgReO6 with DFT+DMFT. Phys. Rev. Res. 2024, 6, 023233. [Google Scholar] [CrossRef]
- Sorgenfrei, F.; Alouani, M.; Schött, J.; Jönsson, H.J.M.; Eriksson, O.; Thunström, P. Theory of X-ray absorption spectroscopy for ferrites. Phys. Rev. B 2024, 109, 115126. [Google Scholar] [CrossRef]
- Pesin, D.A.; Balents, L. Mott physics and band topology in materials with strong spin–orbit interaction. Nat. Phys. 2010, 6, 376. [Google Scholar] [CrossRef]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 398. [Google Scholar] [CrossRef]
- Craco, L. Quantum orbital entanglement: A view from the extended periodic Anderson model. Phys. Rev. B 2008, 77, 125122. [Google Scholar] [CrossRef]
- Freelon, B.; Liu, Y.H.; Chen, J.-L.; Craco, L.; Laad, M.S.; Leoni, S.; Chen, J.; Tao, L.; Wang, H.; Flauca, R.; et al. Mott-Kondo insulator behavior in the iron oxychalcogenides. Phys. Rev. B 2015, 92, 155139. [Google Scholar] [CrossRef]
- Coleman, P.; Schofield, A.J. Quantum criticality. Nature 2005, 433, 226. [Google Scholar] [CrossRef]
- Lu, C.-P.; Li, G.; Mao, J.; Wang, L.-M.; Andrei, E.Y. Bandgap, mid-gap states, and gating effects in MoS2. Nano Lett. 2014, 14, 4628. [Google Scholar] [CrossRef]
- Koga, A.; Kawakami, N.; Peters, P.; Pruschke, T. Quantum phase transitions in the extended periodic Anderson model. Phys. Rev. B 2008, 77, 045120. [Google Scholar] [CrossRef]
- Meir, Y.; Wingreen, N.S. Landauer formula for the current through an interacting electron region. Phys. Rev. Lett. 1992, 68, 2512. [Google Scholar] [CrossRef]
- Craco, L.; Kang, K. Perturbation treatment for transport through a quantum dot. Phys. Rev. B 1999, 59, 12244. [Google Scholar] [CrossRef]
- Cuniberti, G.; Craco, L.; Porath, D.; Dekker, C. Backbone-induced semiconducting behavior in short DNA wires. Phys. Rev. B 2002, 65, 241314(R). [Google Scholar] [CrossRef]
- Bao, X.-X.; Wang, X.-F. Effects of long-range dispersive interaction on the electron transport in short single strands of guanine bases. Int. J. Quantum Chem. 2023, 1, e27251. [Google Scholar] [CrossRef]
- Craco, L.; Chagas, E.F.; Carara, S.S.; Freelon, B. Atomristor Mott theory of Sn adatom adlayer on a Si surface. Condens. Matter 2024, 9, 32. [Google Scholar] [CrossRef]
- Ming, F.; Mulugeta, D.; Tu, W.; Smith, T.S.; Vilmercati, P.; Lee, G.; Huang, Y.-T.; Diehl, R.D.; Snijders, P.C.; Weitering, H.H. Hidden phase in a two-dimensional Sn layer stabilized by modulation hole doping. Nat. Commun. 2017, 8, 14721. [Google Scholar] [CrossRef]
- Fisk, Z.; Sarrao, J.L.; Cooper, S.L.; Nyhus, P.; Boebinger, G.S.; Passner, A.; Canfield, P.C. Kondo insulators. Phys. B Condens. Matter 1996, 409, 223–224. [Google Scholar]
- Shiga, M.; Teramoto, T.; Harada, T.; Takahashi, T.; Iga, F.; Kawae, T. Kondo breakdown in the topological Kondo insulator Smb6 studied by point-contact Andreev reflection spectroscopy. Phys. Rev. B 2023, 108, 195130. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Craco, L.; Carara, S.S. Atomic Many-Body Selectivity in Cubic CsPbI3 Solar Cell Memristor. Compounds 2025, 5, 7. https://doi.org/10.3390/compounds5010007
Craco L, Carara SS. Atomic Many-Body Selectivity in Cubic CsPbI3 Solar Cell Memristor. Compounds. 2025; 5(1):7. https://doi.org/10.3390/compounds5010007
Chicago/Turabian StyleCraco, Luis, and Sabrina S. Carara. 2025. "Atomic Many-Body Selectivity in Cubic CsPbI3 Solar Cell Memristor" Compounds 5, no. 1: 7. https://doi.org/10.3390/compounds5010007
APA StyleCraco, L., & Carara, S. S. (2025). Atomic Many-Body Selectivity in Cubic CsPbI3 Solar Cell Memristor. Compounds, 5(1), 7. https://doi.org/10.3390/compounds5010007






